Received 22 June 2015; accepted 11 October 2015; published 15 October 2015

ABSTRACT

Shock induced symmetric compression has been studied in a spherical target. The shock induced interfacial radius will shrink and would reach a minimum point during implosion situation. However, after implosion the plasma tries to expand in blow off/explosion situation and as a result the interfacial radius will increase. Effects of plasma parameters like density and temperature have been studied numerically. It is seen that the density increases many times due to the mass conservation in imploding situation of a compressible shell like ICF. However, temperature will change rapidly due to change of inner density and so would be the pressure of compressible fluid following adiabatic law. Our analytical results agree qualitatively with those of simulation results in spherical geometry and also experimental observations conducted in cylindrical container.

Keywords:

Two Fluid Interface Instability, Shock Impingement, Adiabatic Symmetric Compression, Implosion

1. Introduction

Dynamics of interfacial radius of an imploded spherical shell like ICF is an interesting task to the fusion community. The motion of the interface of two fluids and the effects of the plasma parameters like density and temperature on the motion have been studied both analytically and numerically. This study can explain the underwater explosion [1] or find out the time taken in filling up the cavity suddenly formed inside an incompressible fluid [2] . Stability conditions of symmetric compression for incompressible and immiscible viscous fluids were discussed earlier by Plesset [1] considering a source and sink at the origin of the spherical shells. Linear perturbation method shows that the thermal electron conduction may be symmetric in laser driven fusion [3] [4] . In both cases, analytical results predict that spherical shell will shrink depending on the pressure difference at the fluid interface [5] . However, implosion dynamics has been studied in spherical targets con- sidering the solid compressibility and the mass loss by ablation [6] . Later, he described the two layer spherical shell target implosion considering a single pressure [7] . Mikaelian [8] considered only radial incompressible flow to explain RT and RM growth in a cylindrical target. Later, he pointed out that smooth density gradient at the interface could stabilize the fluid instabilities after considering the constant steep density gradient at the multiple-shell interface [9] in ICF related problems. Again, the problem of implosion and explosion has been studied in spherical geometry [10] [11] . In ICF, deuterium-tritium fuel is kept in a micro balloon surrounded by a foam like target. The laser shock immediately produces the target into plasma which tries to expand whereas shock velocity impinges inside the lighter DT fluid. In this stage hydrodynamic instabilities arise, which oppose to efficient compression. There are several answers to consider the potential flow model to describe the motion of the interface. Hwang et al. considered potential flow model for incompressible fluid of a hydromagnetic situation to study the linear behavior of the dynamic effects of plasma in the cylindrical geometry [12] . The problem of implosion in cylindrical geometry under a variety of physical conditions has recently been in- vestigated both experimentally and numerically [13] -[15] . The results of these studies show that during a laser induced implosion (deceleration phase), the interface of cylinder/spherical target is compressed and the radius of the cylinder/sphere decreases and consequently, the density of the internal plasma increases [16] [17] and reaches a maximum value for a critical value of the two fluid interface radius. This is followed by a blow off stage when the interfacial radius expands with associated lowering of density. These features characterize the compression in ICF process. The interfacial radius will shrink due to shock impingement at the interface and reaches a minimum during implosion situation. However, after implosion the plasma expands due to blow off/ explosion situation and consequently the interfacial radius will increase.

In this paper, we have shown that the interfacial radius will shrink due to the shock impingement producing the interfacial velocity and the density will increase many times due to the mass concentrated in imploding situation of a compressible shell like ICF. However, temperature also changes the inner shell obeying adiabatic compression for very fast process. Our analytical results are found to agree qualitatively with recent simulation and experimental results obtained in cylindrical geometry. Also in the spherical geometry, during compression the density of the DT fuel increases many times more than the density of the DT gas [18] [19] in the compressed shell within the core of the spherical target.

We have described the paper as follows: In section 2, we describe the geometry and physical situation of the problem with analytical results. Numerical results and its discussion has been given in section 3.

2. Formulation of the Problem: Spherical Target

In this paper, we assume a model which focuses on the post shock phenomena of interface motion during implosion-explosion situation and thereby changes density, temperature. Consider two concentric spherical shells containing two different fluids of different densities: fluid having density 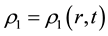in the inner shell having radius 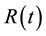and another fluid of constant density of 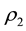in the outer shell with radius 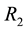where we have taken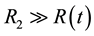. The inner shell with radius is set in motion by impingement of a shock. We are interested in the dynamics of the interface leading to consequent compression of the contained fluid and the effects of plasma parameters like density and temperature on the dynamics (Figure 1).

Assuming mass conservation relation for inner fluid, we can write for fluid density: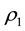

(1)

Now,we have the equation of continuity

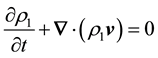(2)

where v is interface velocity after passage of shock.

Assuming that the impingement of shock gives rise to uniform compression from all directions so that the above equation may be considered to be independent of angular variable. In spherical coordinates, Equation (2) can be written as

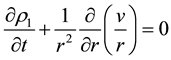(3)

Solving it one can get the expression of velocity in the following form

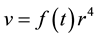(4)

Using the boundary conditions that at the two fluid interface

(5)

where 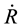is the shock generated interfacial velocity. Then velocity of the interface in Equation (4) leads to

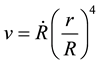(6)

Now assuming the potential flow motion, we can write

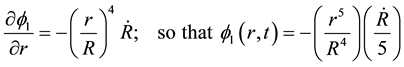(7)

Since, there is no source/sink of velocity at the origin, the integration constant can be neglected. Now, we employ Bernoulli’s equation for compressible fluid in inner shell

(8)

where is the minimum value of can reach. is internal pressure of lighter fluid.

To calculate the r.h.s term of the above equation, we assume adiabatic compression i.e., for very fast process as in ICF situation, which leads to

(9)

After some straightforward algebraic calculation and keeping terms up to third order of the ratio, we

arrive at the following equation

(10)

where are the pressure at and, respectively.

However, outer shell fluid satisfy the Laplace’s equation,

(11)

Using the boundary condition at the interface

(12)

the solution of Laplace’s Equation (11) becomes

(13)

Bernoulli’s equation for the fluid with constant, gives

(14)

Using as given by Equation (13) we get,

(15)

where are the pressure at very large distance from the interface and, respectively. Also, we have

neglected 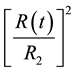for. Using boundary condition and combining

Equations (10) and (15) we arrive at the following equation for,

(16)

which will describe the evolution of the interface and other parameters.

Equation (16) can be integrated once to obtain a relation between and (Figure 2).

(17)

where.

3. Numerical Results and Discussions

To solve Equation (16), we first make the equation dimensionless and write a set of first order equations,

(18)

(19)

where normalized variables are.

Now, we solve the set of Equations (18) and (19) using Runge-Kutta-Fehlberg technique and plot interface and its velocity in Figure 3(a) and Figure 3(b). It is seen that the induced shock compresses the interface which

reaches a minimum point near the origin of the target during deceleration phase. This is the implosion situation. Mass conservation suggests that since the volume is reduced, the density increases and reaches a maximum corresponding to the minimum of interfacial radius. Then plasma tries to expand in acceleration phase. Thus interfacial radius increases with time. This is the explosion situation. The interfacial radius reaches minimum at stagnation time

(20)

At this instant the density attains its maximum value

(21)

It is shown in Figure 4(a). Again, the velocity changes like a shock during changing of implosion state to explosion state. It has been shown in Figure 3(b). It is to be noted that in our uniform compression model predicts a good qualitative agreement with the corresponding experimental and simulation results for both cylindrical [13] -[15] and spherical geo- metries [18] [19] . However, there may be more complicated physics behind the compression during stagnation time.

Finally, if we assume that the compression of the inner spherical shell fluid occurs adiabatically and that there occurs little or no conduction of heat across the interfacial radius, the shell fluid temperature

varies as, where is the adiabatic constant. Thus the time evolution of the temperature

follows the same pattern as the density. In Figure 4(b) we have plotted against

(g ® adiabatic index). It is to be noted that the time dependence of temperature thus exhibited also agrees qualitatively with experimental and simulation results in cylindrical geometry [15] .

Acknowledgements

This work is supported by the Department of Science & Technology, Government of India under grant no. SR/S2/ HEP-007/2008. Author L. K. Mandal is thankful to Prof. S. Ghosh and Dr. N. Chakraborty for helpful discussion.

Cite this paper

LabakantaMandal,SouravRoy,ManoranjanKhan,R.Roychoudhury, (2015) Shock Induced Symmetric Compression in a Spherical Target. Journal of Modern Physics,06,1769-1775. doi: 10.4236/jmp.2015.613178

References