Journal of Modern Physics
Vol.06 No.12(2015), Article ID:60105,15 pages
10.4236/jmp.2015.612174
Local Particle-Ghost Symmetry
Yoshiharu Kawamura
Department of Physics, Shinshu University, Matsumoto, Japan
Email: haru@azusa.shinshu-u.ac.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
We study the quantization of systems with local particle-ghost symmetries. The systems contain ordinary particles including gauge bosons and their counterparts obeying different statistics. The particle-ghost symmetries are new type of fermionic symmetries between ordinary particles and their ghost partners, different from the space-time supersymmetry and the BRST symmetry. There is a possibility that they are useful to explain phenomena of elementary particles at a more fundamental level, by extension of our systems. We show that our systems are formulated consistently or subsidiary conditions on states guarantee the unitarity of systems, as the first step towards the construction of a realistic fundamental theory.
Keywords:
Fermionic Symmetry, BRST Quantization, Quartet Mechanism

1. Introduction
Graded Lie algebras or Lie superalgebras have been frequently used to formulate theories and construct models in particle physics. Typical examples are supersymmetry (SUSY) [1] -[4] and BRST symmetry [5] - [7] .
The space-time SUSY [8] [9] is a symmetry between ordinary particles with integer spin and those with half- integer spin, and the generators called supercharges are space-time spinors that obey the anti-commutation relations [10] [11] .
The BRST symmetry is a symmetry concerning unphysical modes in gauge fields and abnormal fields called Faddeev-Popov ghost fields [12] . Though both gauge fields and abnormal fields contain negative norm states, theories become unitary on the physical subspace, thanks to the BRST invariance [13] [14] . The BRST and anti-BRST charges are anti-commuting space-time scalars.
Recently, models that contain both ordinary particles with a positive norm and their counterparts obeying different statistics have been constructed and those features have been studied [15] - [18] . Models have fermionic symmetries different from the space-time SUSY and the BRST symmetry. We refer to this type of novel symmetries as “particle-ghost symmetries”.
The particle-ghost symmetries have been introduced as global symmetries, but we do not need to restrict them to the global ones. Rather, it would be meaningful to examine systems with local particle-ghost symmetries from following reasons. It is known that any global continuous symmetries can be broken down by the effect of quantum gravity such as a wormhole [19] . Then, it is expected that a fundamental theory possesses local symmetries, and global continuous symmetries can appear as accidental ones in lower-energy scale. In the system with global particle-ghost symmetries, the unitarity holds by imposing subsidiary conditions on states by hand. In contrast, there is a possibility that the conditions are realized as remnants of local symmetries in a specific situation. Hence, it is interesting to investigate features of particle-ghost symmetries more closely and widely, and to apply them on a microscopic theory beyond the standard model.
In this paper, we study the quantization of systems with local particle-ghost symmetries. The systems contain ordinary particles including gauge bosons and their counterparts obeying different statistics. We show that our systems are formulated consistently or subsidiary conditions on states guarantee the unitarity of systems, as the first step towards the construction of a realistic fundamental theory. The conditions can be originated from constraints in case that gauge fields have no dynamical degrees of freedom.
The contents of this paper are as follows. We construct models with local fermionic symmetries in Section 2, and carry out the quantization of the system containing scalar and gauge fields in Section 3. Section 4 is devoted to conclusions and discussions on applications of particle-ghost symmetries. In the Appendix Section, we study the system that gauge fields are auxiliary ones.
2. Systems with Local Fermionic Symmetries
2.1. Scalar Fields with Local Fermionic Symmetries
Recently, the system described by the following Lagrangian density has been studied [15] -[18] ,
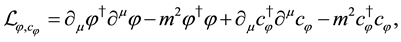 (1)
(1)
where 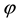 is an ordinary complex scalar field and
is an ordinary complex scalar field and 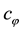 is the fermionic counterpart obeying the anti-commu- tation relations. The system has a global
is the fermionic counterpart obeying the anti-commu- tation relations. The system has a global  symmetry that consists of U(1) and fermionic symmetries. The unitarity holds by imposing suitable subsidiary conditions relating the conserved charges on states.
symmetry that consists of U(1) and fermionic symmetries. The unitarity holds by imposing suitable subsidiary conditions relating the conserved charges on states.
Starting from (1), the model with the local 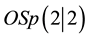 symmetry is constructed by introducing gauge fields. The resultant Lagrangian density is given by
symmetry is constructed by introducing gauge fields. The resultant Lagrangian density is given by
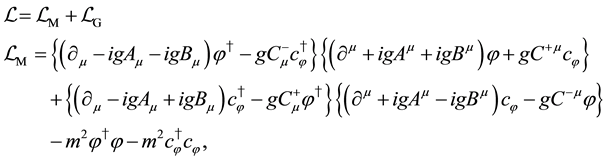 (2)
(2)
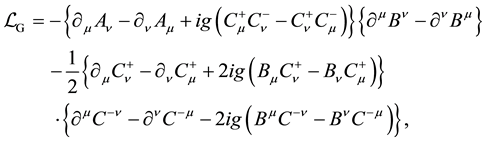 (3)
(3)
where 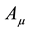 and
and 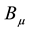 are the gauge fields relating the (diagonal) U(1) symmetries,
are the gauge fields relating the (diagonal) U(1) symmetries, 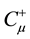 and
and  are gauge fields relating the fermionic symmetries, and g is the gauge coupling constant. The quantized fields of
are gauge fields relating the fermionic symmetries, and g is the gauge coupling constant. The quantized fields of 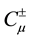 obey the anti-commutation relations.
obey the anti-commutation relations.
The 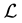 is invariant under the local U(1) transformations,
is invariant under the local U(1) transformations,
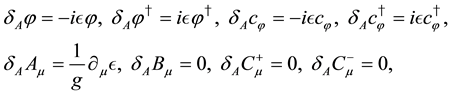 (4)
(4)
 (5)
(5)
and the local fermionic transformations,
 (6)
(6)
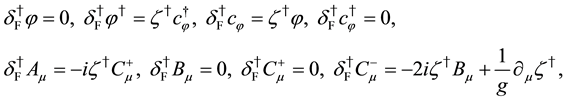
where 
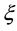
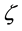
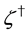
The 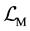

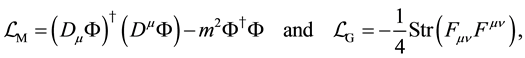
respectively. In
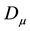
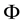
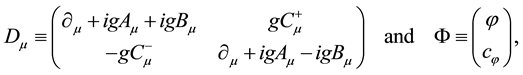
respectively. In
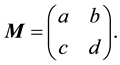
The 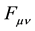
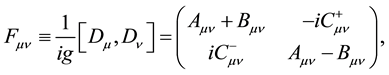
where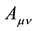



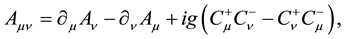
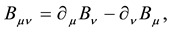


Under the transformations (4)-(7), the field strengths are transformed as

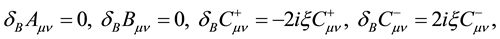
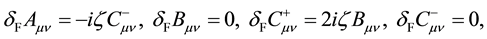
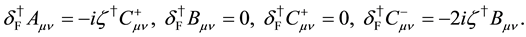
Using the global fermionic transformations,
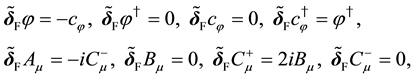
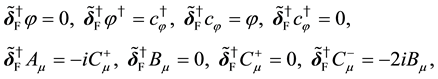
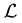

where 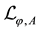
2.2. Spinor Fields with Local Fermionic Symmetries
For spinor fields, we consider the Lagrangian density,
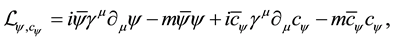
where 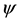
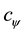
Starting from (24), the Lagrangian density with local symmetries is constructed as
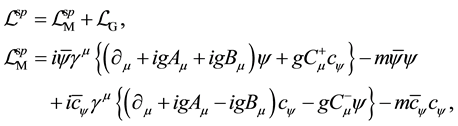
where 
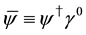
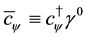
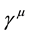
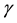
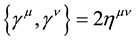
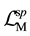

where 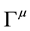
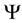
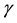
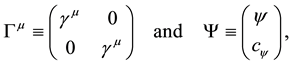
respectively.
The 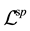
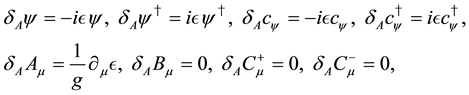

and the local fermionic transformations,
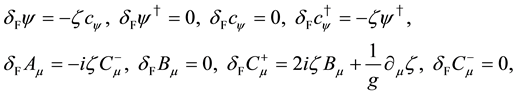
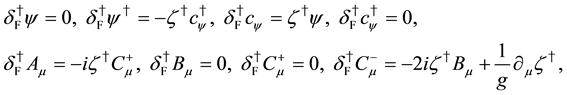
where 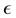
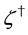
Using the global fermionic transformations,
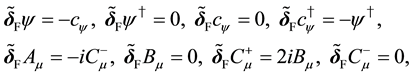
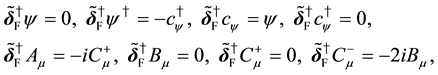

where 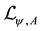
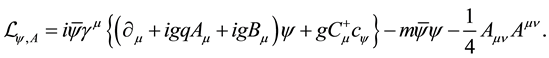
3. Quantization
We carry out the quantization of the system with scalar and gauge fields described by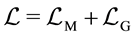
3.1. Canonical Quantization
Based on the formulation with the property that the hermitian conjugate of canonical momentum for a variable is just the canonical momentum for the hermitian conjugate of the variable [16] , the conjugate momenta are given by
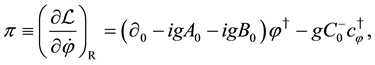
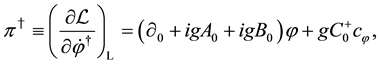
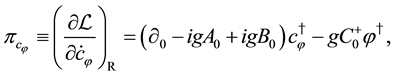
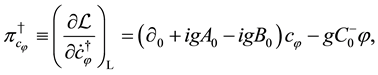
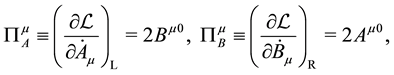
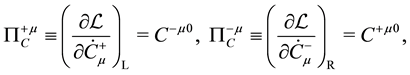
where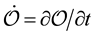
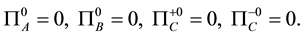
Using the Legendre transformation, the Hamiltonian density is obtained as
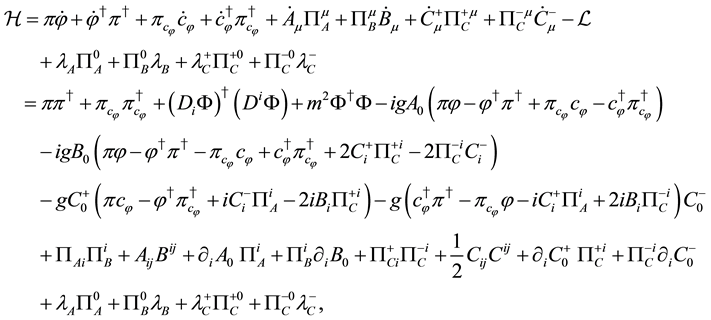
where Roman indices i and j denote the spatial components and run from 1 to 3, 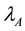
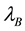

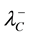
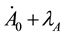
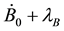
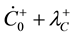
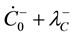
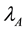
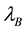

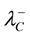
Secondary constraints are obtained as follows,
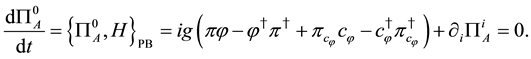
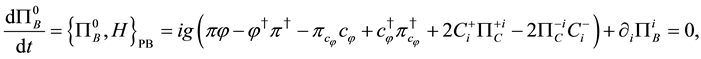
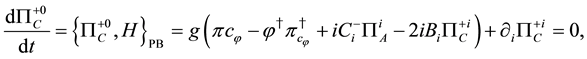
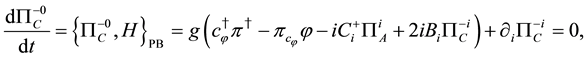
where H is the Hamiltonian 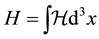
system with canonical variables 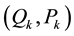
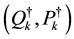
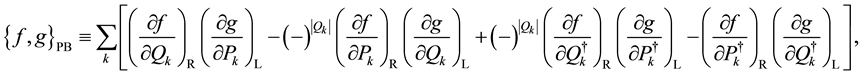
where 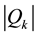
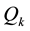


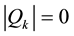
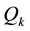
We take the gauge fixing conditions,
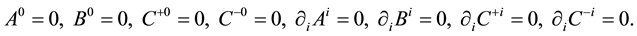
The system is quantized by regarding variables as operators and imposing the following relations on the canonical pairs,
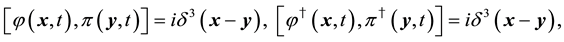
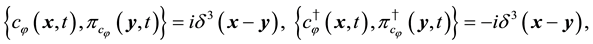
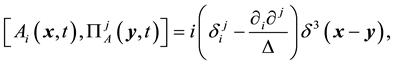
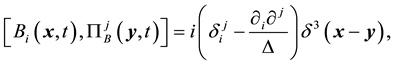
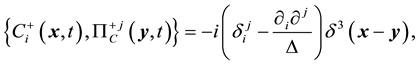
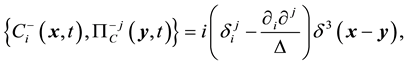
where

On the reduced phase space, the conserved U(1) charges 
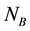
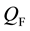
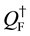
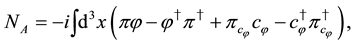

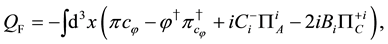

The following algebraic relations hold:
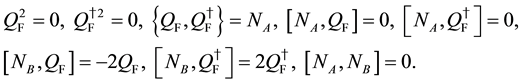
The above charges are generators of global U(1) and fermionic transformations such that
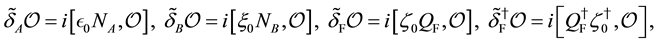
where 
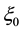
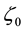
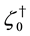
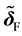
in (20) and (21) are related to 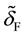
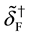
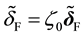

The system contains negative norm states originated from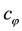
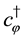
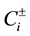
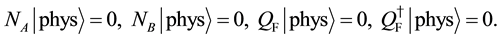
In the Appendix, we point out that subsidiary conditions corresponding to (62) can be realized as remnants of local symmetries in a specific case.
3.2. Unitarity
Let us study the unitarity of physical S matrix in our system, using the Lagrangian density of free fields,
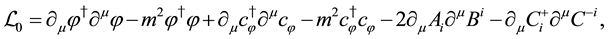
where the gauge fixing conditions (49) are imposed on. The 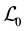
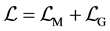
From (63), free field equations for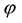
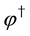
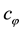

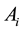
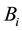
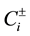
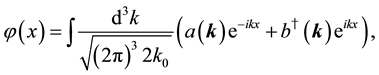
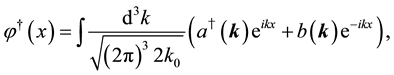
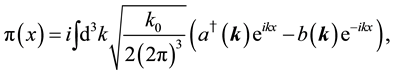


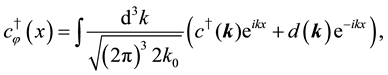

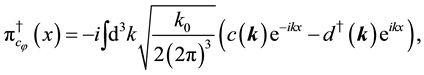
where 
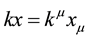
In the same way, by solving the free Maxwell equations, we obtain the solutions,

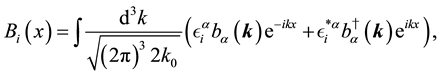
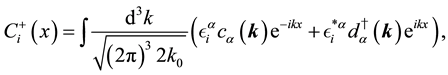
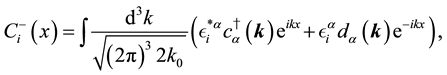
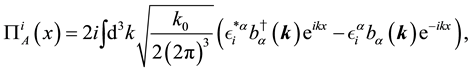
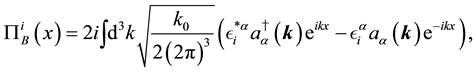
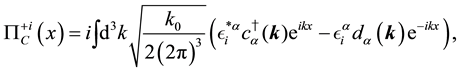
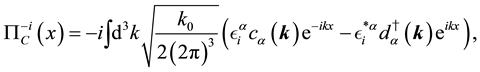
where 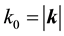

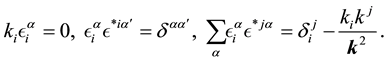
The index 
By imposing the same type of relations as (50) - (55), we have the relations,

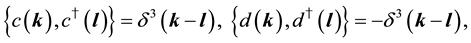
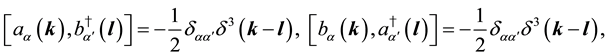
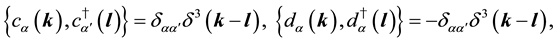
and others are zero.
The states in the Fock space are constructed by acting the creation operators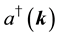
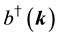
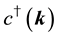


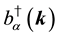
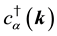
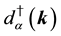
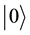
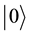
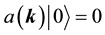


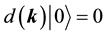
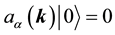
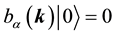
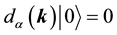
We impose the following subsidiary conditions on states to select physical states,
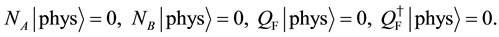
Note that 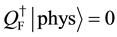
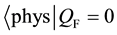
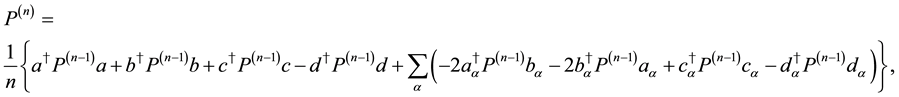
where 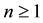

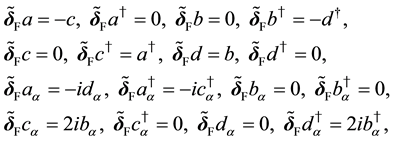

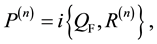
where 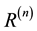
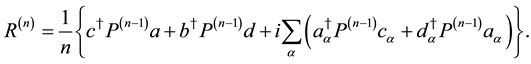
From (88), we find that any state with 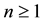
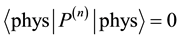

The system is also formulated using hermitian fermionic charges defined by 
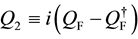
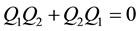
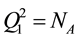
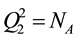

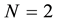
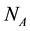
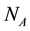
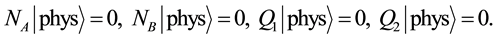
It is also understood that our fermionic symmetries are different from the space-time SUSY, from the fact that Q1 and Q2 are scalar charges. They are also different from the BRST symmetry, as seen from the algebraic relations among charges.
The system with spinor and gauge fields described by 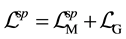
3.3. BRST Symmetry
Our system has local symmetries, and it is quantized by the Faddeev-Popov (FP) method. In order to add the gauge fixing conditions to the Lagrangian, several fields corresponding to FP ghost and anti-ghost fields and auxiliary fields called Nakanishi-Lautrup (NL) fields are introduced. Then, the system is described on the extended phase space and has a global symmetry called the BRST symmetry. We present the gauge-fixed Lagrangian density and study the BRST transformation properties.
According to the usual procedure, the Lagrangian density containing the gauge fixing terms and FP ghost terms is constructed as

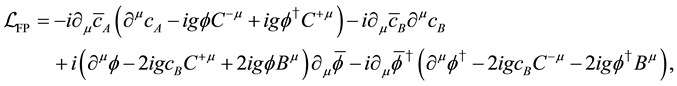
where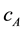
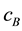
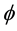

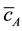
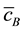
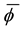
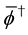
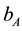
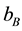
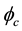
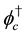
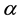
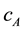

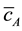
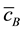
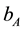

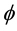
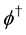
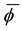
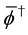
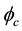
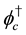
The 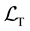

where the transformations for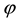
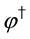
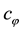
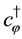
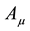
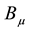
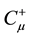
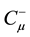
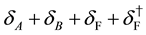
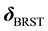
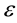

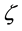
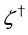
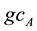
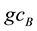
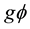
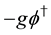
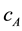
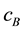

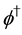
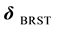
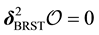
The sum of the gauge fixing terms and FP ghost terms is simply written as
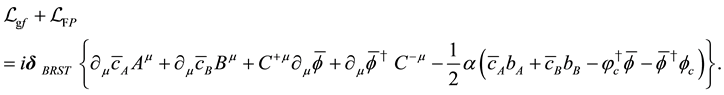
According to the Noether procedure, the BRST current 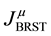
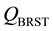
and

respectively. Here we use the field equations. The BRST charge is a conserved charge (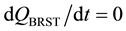

By imposing the following subsidiary condition on states,
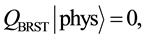
it is shown that any negative norm states originated from time and longitudinal components of gauge fields as well as FP ghost and anti-ghost fields and NL fields do not appear on the physical subspace, through the quartet mechanism. There still exist negative norm states come from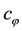
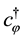
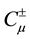
4. Conclusions and Discussions
We have studied the quantization of systems with local particle-ghost symmetries. The systems contain ordinary particles including gauge bosons and their counterparts obeying different statistics. There exist negative norm states come from fermionic scalar fields (or bosonic spinor fields) and transverse components of fermionic gauge fields, even after reducing the phase space due to the first class constraints and the gauge fixing conditions or imposing the subsidiary condition concerning the BRST charge on states. By imposing additional subsidiary conditions on states, such negative norm states are projected out on the physical subspace and the unitarity of systems hold. The additional conditions can be originated from constraints in case that gauge fields have no dynamical degrees of freedom.
The systems considered are unrealistic if this goes on, because they are empty leaving the vacuum state alone as the physical state. Then, one might think that it is better not to get deeply involved them. Although they are still up in the air at present, there is a possibility that a formalism or concept itself is basically correct and is useful to explain phenomena of elementary particles at a more fundamental level. It is necessary to fully understand features of our particle-ghost symmetries, in order to appropriately apply them on a more microscopic system.
We make conjectures on some applications. We suppose that particle-ghost symmetries exist and the system contains only a few states including the vacuum as physical states at an ultimate level. Most physical particles might be released from unphysical doublets that consist of particles and their ghost partners. A release mechanism has been proposed based on the dimensional reduction by orbifolding [17] .
After the appearance of physical fields, 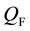


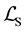
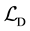

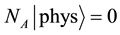
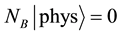
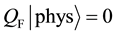

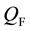
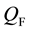
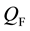
The system seems to be same as that described by 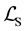
In most cases, our ghost fields require non-local interactions [15] and the change of degrees of freedom can occur in systems with infinite numbers of fields [17] . Then, they might suggest that fundamental objects are not point particles but extended objects such as strings and membranes. Hence, it would be interesting to explore systems with particle-ghost symmetries and their applications in the framework of string theories1.
Acknowledgements
The author thanks the Editor and the referee for their comments. This work was supported in part by scientific grants from the Ministry of Education, Culture, Sports, Science and Technology under Grant No. 22540272.
Cite this paper
YoshiharuKawamura, (2015) Local Particle-Ghost Symmetry. Journal of Modern Physics,06,1721-1736. doi: 10.4236/jmp.2015.612174
References
- 1. Neveu, A. and Schwarz, J.H. (1971) Nuclear Physics B, 31, 86-112.
http://dx.doi.org/10.1016/0550-3213(71)90448-2 - 2. Ramond, P. (1971) Physical Review D, 3, 2415-2418.
http://dx.doi.org/10.1103/PhysRevD.3.2415 - 3. Aharonov, Y., Casher, A. and Susskind, L. (1971) Physics Letters B, 35, 512-514.
http://dx.doi.org/10.1016/0370-2693(71)90386-8 - 4. Gervais, J.L. and Sakita, B. (1971) Nuclear Physics B, 34, 632-639.
http://dx.doi.org/10.1016/0550-3213(71)90351-8 - 5. Becchi, C., Rouet, A. and Stora, R. (1975) Communications in Mathematical Physics, 42, 127-162.
http://dx.doi.org/10.1007/BF01614158 - 6. Becchi, C., Rouet, A. and Stora, R. (1976) Annals of Physics, 98, 287-321.
http://dx.doi.org/10.1016/0003-4916(76)90156-1 - 7. Tyutin, V. (1975) Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. Lebedev Physical Institute Report No.39, arXiv:0812.0580 [hep-th].
- 8. Wess, J. and Zumino, B. (1974) Nuclear Physics B, 70, 39-50.
http://dx.doi.org/10.1016/0550-3213(74)90355-1 - 9. Wess, J. and Bagger, J. (1991) Supersymmetry and Supergravity. 2nd Edition. Princeton University Press, Princeton.
- 10. Salam, A. and Strathdee, J. (1975) Physical Review D, 11, 1521-1535.
http://dx.doi.org/10.1103/PhysRevD.11.1521 - 11. Haag, R., Lopuszański, J.T. and Sohnius, M. (1975) Nuclear Physics B, 88, 257-274.
http://dx.doi.org/10.1016/0550-3213(75)90279-5 - 12. Faddeev, L.D. and Popov, N. (1967) Physics Letters B, 25, 29-30.
http://dx.doi.org/10.1016/0370-2693(67)90067-6 - 13. Kugo, T. and Ojima, I. (1978) Physics Letters B, 73, 459-462.
http://dx.doi.org/10.1016/0370-2693(78)90765-7 - 14. Kugo, T. and Ojima, I. (1979) Progress of Theoretical Physics Supplement, 66, 1-130.
http://dx.doi.org/10.1143/PTPS.66.1 - 15. Kawamura, Y. (2015) International Journal of Modern Physics A, 30, Article ID: 1550153.
http://dx.doi.org/10.1142/S0217751X15501535 - 16. Kawamura, Y. (2014) Fermionic Scalar Field.
http://arxiv.org/abs/1406.6155 - 17. Kawamura, Y. (2015) International Journal of Modern Physics A, 30, Article ID: 1550056.
http://dx.doi.org/10.1142/S0217751X15500566 - 18. Kawamura, Y. (2015) Quantization of Systems with OSp(2|2) Symmetry.
http://arxiv.org/abs/1502.00751 - 19. Giddings, S. and Strominger, A. (1988) Nuclear Physics B, 306, 890-907.
http://dx.doi.org/10.1016/0550-3213(88)90446-4 - 20. Parisi, G. and Sourlas, N. (1979) Physical Review Letters, 43, 744-745.
http://dx.doi.org/10.1103/PhysRevLett.43.744 - 21. Witten, E. (1982) Journal of Differential Geometry, 17, 661-692.
- 22. Kawamura, Y. (2015) International Journal of Modern Physics A, 30, Article ID: 1550109.
http://dx.doi.org/10.1142/S0217751X15501092 - 23. Okuda, T. and Takayanagi, T. (2006) Journal of High Energy Physics, 2006, 62.
- 24. Terashima, S. (2006) Journal of High Energy Physics, 2006, 67.
Appendix
A1. System with Auxiliary Gauge Fields
Let us study the system without 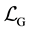
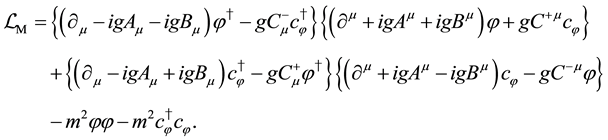
In this case, gauge fields do not have any dynamical degrees of freedom, and are regarded as auxiliary fields. The conjugate momenta of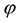
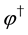
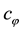
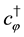
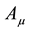
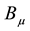
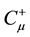
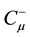
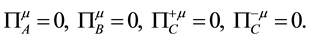
Using the Legendre transformation, the Hamiltonian density is obtained as
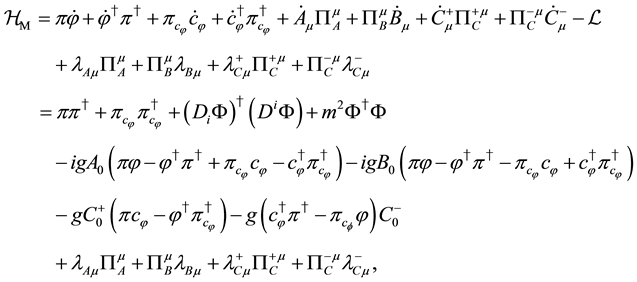
where

Secondary constraints are obtained as
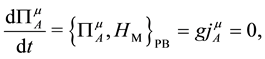
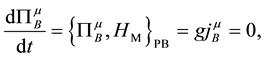
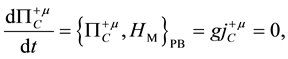
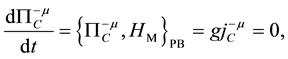
where 
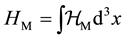
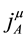
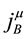
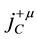
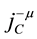
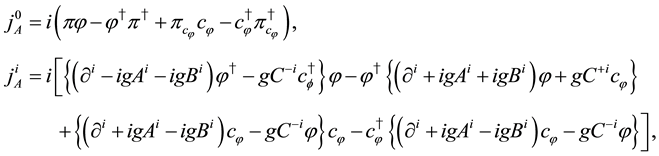
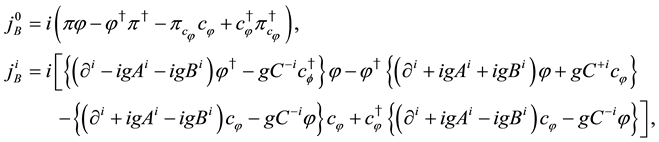
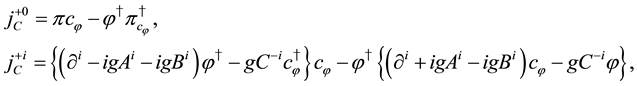
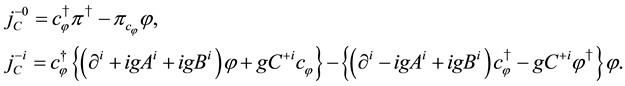
In the same way, tertiary constraints are obtained as
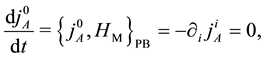
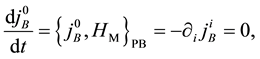

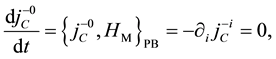
from the invariance under the time evolution of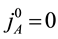
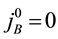
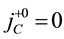
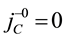
the conditions
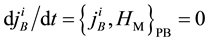
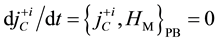
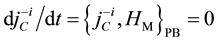
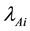
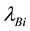
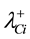
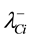
thermore, new constraints do not appear from the conditions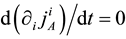
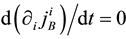
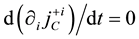
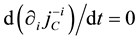
The constraints are classified into the first class ones
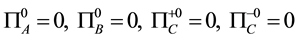
and the second class ones
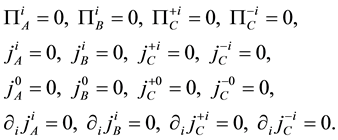
The determinant of Poisson bracket between second class ones does not vanish on constraints.
Using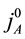
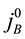
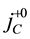
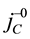
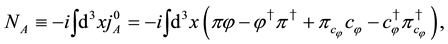
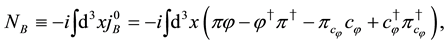
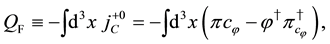
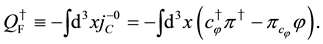
The same algebraic relations hold as those in (60).
The above charges are conserved and generators of global U(1) and fermionic transformations for scalar fields. They satisfy the relations,
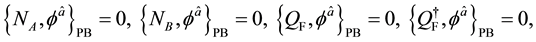
where 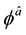
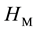
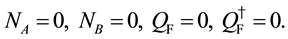
After taking the following gauge fixing conditions for the first class ones (113),
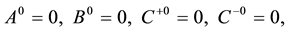
the system is quantized by regarding variables as operators and imposing the same type of relations (50) and (51) on the canonical pairs. From (120), it is reasonable to impose the following subsidiary conditions on states,
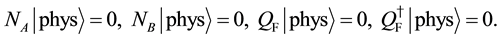
Then, they guarantee the unitarity of our system, though it contains negative norm states originated from 
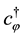
NOTES
1Objects called ghost D-branes have been introduced as an extension of D-brane and their properties have been studied [23] [24] .