Journal of Modern Physics
Vol.06 No.09(2015), Article ID:58533,3 pages
10.4236/jmp.2015.69122
One Dimensional Relativistic Particle in a Quadratic Dissipative Medium Subjected to a Force That Depends on the Position
Federico Petrovich
Departamento de Fisica, Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires Ciudad Universitaria, Buenos Aires, Argentina
Email: fedepetrov@df.uba.ar
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 31 July 2015; published 3 August 2015
ABSTRACT
We will find a constant of motion with energy units for a relativistic particle moving in a quadratic dissipative medium subjected to a force which depends on the position. Then, we will find the Lagrangian and the Hamiltonian of the equation of motion in a time interval such that the velocity does not change its sign. Finally, we will see that the Lagrangian and Hamiltonian have some problems.
Keywords:
Lagrangian, Hamiltonian, Constant of Motion, Dissipation, Relativistic

1. Introduction
It is well known that the Lagrangian and Hamiltonian approaches for dissipative systems have some problems [1] -[5] . One of these problems consists of the possibility of having two different Hamiltonians to the same classical system [6] , implying that one will have two different quantizations for that system. Another problem consists that for some dissipative systems, the trajectories on the space (x, v) have a good expected behavior but on the space (x, p) have an odd behavior. However, the interest in having Hamiltonian for dissipative system continues [7] [8] .
In this paper, we will find a constant of motion, the Lagrangian and the Hamiltonian of the equation of motion of a one-dimensional relativistic particle in a quadratic dissipative medium subjected to a force that depends of the position, in a time interval such that the velocity does not change its sign.
This problem is already solved if we consider the classical second Newtons law [9] , i.e., when the equation of motion of the particle is the following:
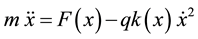 (1)
(1)
where m is the mass of the particle, x is the position, F is the force, q is the sign of the velocity and k is the dissipative parameter that can depend on x.
In this case, it is known that the following quantity is a constant of motion:
 (2)
(2)
where v is the velocity, q is the sign of v, 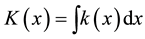 and
and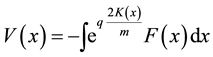 .
.
From this constant, the Lagrangian, the momentum and the Hamiltonian of the system are obtained [9] :
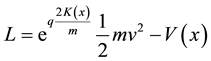 (3)
(3)
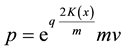 (4)
(4)
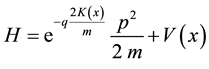 (5)
(5)
Note that since q can be 1 or −1, then there are two possible Lagrangians and Hamiltonians. Note also that in the free particle case, i.e., if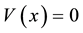 , considering
, considering 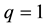 (
(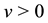 ) and
) and , we can see in Equation (2) that the trajectories in the space (x, v) have a good expected behavior (
, we can see in Equation (2) that the trajectories in the space (x, v) have a good expected behavior (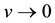 when
when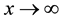 ), but we can see in Equation (5) that the trajectories in the space (x, p) have an odd behavior (
), but we can see in Equation (5) that the trajectories in the space (x, p) have an odd behavior (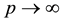 when
when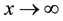 ).
).
If we consider the relativistic second Newtons law, this problem is solved only in the free particle case and considering 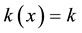 [10] , i.e., when the equation of motion is the following:
[10] , i.e., when the equation of motion is the following:

where 

In this case, the constant of motion is the following:

From this constant, the Lagrangian, the momentum and the Hamiltonian of the system are also obtained and they have the same problems (see reference [10] ).
2. Constant of Motion
If we consider the relativistic second Newtons law, the equation of motion of the particle is the following:

On the one hand, this equation can be written as the following system:

On the other hand, a constant of motion of this equation is a function 

Using Equations (9) and (10) we arrive to:

We will propose the following quantity as a solution of this equation:

We have that:


Hence we arrive to:
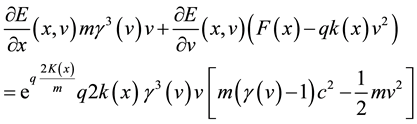
If we consider 


in Equation (12) is a constant of motion.
Note that if we take 


3. Lagrangian, Momentum and Hamiltonian
The Lagrangian of the system can be consistently deduced from the known expression [4] [11] [12] :

Hence we have that:
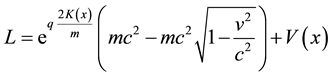
From this Lagrangian, we can find the momentum by doing

The inverse relation of this equation is given by:

Replacing this expression in Equation (12) we obtain the Hamiltonian:

Note that if we consider 




4. Conclusion
We obtained a constant of motion, the Lagrangian and the Hamiltonian for a one-dimensional relativistic particle in a quadratic dissipative medium subjected to a force that depends of the position, in a time interval such that the velocity does not change its sign. We could generalize Equations (3)-(5) to the relativistic case and we saw that the problems we had in the classic case continue. This suggests that the Hamiltonian approach applied to dissipation problem may bring about incorrect solutions if it is directly applied to quantum mechanics or statistical physics.
Cite this paper
FedericoPetrovich, (2015) One Dimensional Relativistic Particle in a Quadratic Dissipative Medium Subjected to a Force That Depends on the Position. Journal of Modern Physics,06,1185-1188. doi: 10.4236/jmp.2015.69122
References
- 1. Dodonov, V.P., Manko, V.I. and Skarzhinsky, V.D. (1981) Hadronic Journal, 4, 1734.
- 2. Okubo, S. (1980) Physical Review D, 22, 919. http://dx.doi.org/10.1103/PhysRevD.22.919
- 3. Glauber, R. and Manko, V.I. (1984) Soviet Physics JETP, 60, 450.
- 4. Lpez, G. (1996) Annals of Physics, 251, 372-383. http://dx.doi.org/10.1006/aphy.1996.0118
- 5. Lpez, G. (1998) International Journal of Theoretical Physics, 37, 1617-1623.
http://dx.doi.org/10.1023/A:1026628221912 - 6. Lpez, G., Lpez, X.E. and Gonzlez, G. (2007) International Journal of Theoretical Physics, 46, 149-156.
http://dx.doi.org/10.1007/s10773-006-9224-y - 7. Musielak, Z.E. (2008) Journal of Physics A: Mathematical and Theoretical, 41, Article ID: 055205.
http://dx.doi.org/10.1088/1751-8113/41/5/055205 - 8. Carinena, J.F. and Ranada, M.F. (2005) Journal of Mathematical Physics, 46, Article ID: 062703.
- 9. Sa Borges, J., Epele, L.N., Fanchiotti, H., Garca Canal, C.A. and Simao, F.R.A. (1987) The Quantization of Quadratic Friction Revisited.
http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/19/006/19006200.pdf - 10. Lpez, G.V., Montes, G.C. and Zanudo, J.G.T. (2015) Journal of Modern Physics, 6, 121-125.
http://dx.doi.org/10.4236/jmp.2015.62016 - 11. Leubner, C. (1987) Physical Review A, 86, 9.
- 12. Yan, C.C. (1981) American Journal of Physics, 49, 269. http://dx.doi.org/10.1119/1.12632

