Journal of Modern Physics
Vol.06 No.10(2015), Article ID:59222,8 pages
10.4236/jmp.2015.610143
Gravireception in Phycomyces: Threshold Determination on the Sounding Rocket TEXUS 50
Werner Schmidt1,2
1Fachbereich Biologie, Philipps-Universität Marburg, Marburg, Germany
2Fachbereich Biologie, Universität Konstanz, Konstanz, Germany
Email: w.2.schmidt@gmx.de
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
Under parabolic flight conditions microgravity is not lower than 3 to 5 times 10−2 g. In contrast to parabolic flights, sounding rocket flights are virtually vibrational-free allowing microgravity as low as 10−5 g. Thus, a rotating platform serving as centrifuge allows the precise generation of gravitational forces ranging from 5 to 100 mg (not possible during parabolic flights). On this basis we determined the threshold1 for optical reflection/absorption changes in Phycomyces to be lower than 25 × 10−3 g. This compares well with the threshold determination of gravitropism in Phycomyces on a clinostat centrifuge. Kinetics of gravity-induced absorption changes and gravity as generated by the on-board centrifuge do not coincide but show a distinctive hysteresis with a latency of 4 s (75 mg-ramp, pull-up).
Keywords:
MDWS (Micro-Dual Wavelength Spectrophotometer), Δ GIAC (Differential Gravity-Induced Absorption Change), Phycomyces blakesleeanus, Sporangiophore, Micro- and Hypergravity, Texus 50, Sounding Rocket, Gravireception

1. Introduction
In 1999 we detected that dark grown sporangiophores of the fungus Phycomyces blakesleeanus exhibited a small but significant and reversible rapid change in optical absorption/reflection if placed horizontally [1] . In various spectroscopic experiments performed on the AIRBUS ZERO G in the years 2002 to 2012 we analyzed these changes as a result of gravitational changes in Arabidopsis, Phycomyces sporangiophores, Avena or maize cole- optiles as measured with a homemade micro-dual wavelength spectrophotometer detecting optical absorption changes lower than 10−5 A. However, microgravity attained during parabolic flights is not lower than 3 to 5 times 10−2 g. In addition, the vibrational input is significant leading to high frequency gravitational impact larger than 1 g, even under “microgravity”.
Gravitropism, the directional bending that plants and fungi display in response to acceleration forces, is generally assumed to be mediated by statoliths, dense cell organelles that function as gravisusceptors (reviews: [2] - [5] ). It is a widely accepted concept that the displacement of statoliths and the concomitant pressure acting on a gravireceptor elicit differential cell wall growth and thus bending [6] - [8] . Alternatively, other cell components could be associated with graviperception, e.g. the cytoskeleton or flexure of cell wall controlling membrane channels. The onset of the bending responses occurs relatively slowly in the order of minutes. Sporangiophores of Phycomyces blakesleeanus, for example, possess gravitropic latencies ranging from 5 to 20 min [9] [10] .
The absolute sensitivity of SPPHs of Phycomyces to centrifugal acceleration with 25 × 10−3 g [11] is moderate in comparison to that of Avena coleoptiles. These display on the same clinostat centrifuge an approximate threshold of about 10−3 g. The gravitropic sensitivity of Phycomyces is about 10 to 200 times smaller than that of Avena coleoptiles and 3 to 4 orders of magnitude smaller than that of Avena roots [12] . These huge differences can be explained by the fact that the weight of all crystals in the growing zone corresponds to that of only a single amyloplast in plants.
Even though the bending responses are slow, the gravitational forces act instantaneously. The time that elapses between the primary reaction of the yet unidentified gravireceptor and the onset of the bending is caused by the subsequent steps of the transduction chain that finally lead to differential growth. Though great insight has been gained during the past decades about the details of essential components of the transduction chain, e.g. ion mobilization, auxin transport [13] , PIN-proteins [14] , the primary responses that are associated with gravireception have remained elusive. As long as the gravirecepor proper remains unidentified, investigations of the primary responses of graviperception will be severely hampered. It appears, however, logically stringent and necessary that i) primary graviresponses need to be “fast”, and as a consequence, that ii) the latency of an acceleration-mediated response can serve as a criterion for assessing the question how “close” the response is associated with the gravireceptor.
The fastest graviresponses so far determined were found for sporangiophores (fruiting bodies) of the single- celled fungus Phycomyces blakesleeanus. Sporangiophores that are exposed to sudden acceleration changes display nearly instantaneous absorption changes, so-called GIACs [15] . In highly scattering samples such as SPPHs absorbance and reflection of light are intimately correlated [16] justifying the term “GIAC”, even if reflection is measured. The biological relevance of these empirical signals can be seen from the observation that the threshold for the GIACs―as described in the present work―is identical with that of gravitropism. The following arguments strongly support the idea that GIACs take place close to the initial end of the dose response curve:
・ The fact that the GIACs are absent in the gravi-defective mutant A909 madJ indicates that they are specific for graviperception and that they are not spurious by products of gravistimulation or instrumental artefacts. Also the observation that the GIACs are expressed well only in horizontal sporangiophores, not however, in vertical ones supports the notion that the GIACs are specific for the transduction chain of gravitropism.
・ Very pertinent for understanding the nature of the gravitropic signal is the observation that GIACs elicited by tilting differ with respect to their sign from those that are elicited by centrifugation or acceleration changes during flight parabolas.
・ The observed GIACs are specific for the apical growing zone, because they were not detectable in the lower part of the sporangiophore. This observation is crucial, because only the growing zone of the sporangiophore manifests differential growth (tropism) and light sensitivity.
・ Dummies, i.e. dead SPPHs (killed by ethanol!) or thin copper wires (comparable to SPPHs in thickness), don’t show hysteresis.
・ There is a pronounced spectral dependency of GIACs in wild type sporangiophores, not observed in gravi- defective mutants.
The responses cited above are faster than the electrical signals that are triggered in plants after gravistimulation. The shortest latencies of such gravi-elicited electrical signals are 8 s [17] ; typically they are, however, longer amounting to some 30 s [18] or even several minutes [19] - [22] . Using a sounding rocket allows to eliminate vibrational impact present in parabolic flights [23] and thus allows to determining the threshold of gravitropism.
2. Material and Methods
2.1. Sounding Rocket TEXUS 50
We participated in the 50th jubilee sounding rocket campaign taking place from the 1st to 14th of April (http://www.sscspace.com/esrange-space-center-3). The Texus 50 was started on the 12th of April 2013, burn out of the first rocket motor after 12.2 s at a height of about 8 km, burn out of the second rocket motor after 43.9 s at a height of about 100 km reaching a velocity of app. 10100 km∙h−1. After “YoYo-despin” the rocket is completely rotational-free as tested by a three-dimensional on-board magnetometer, “falling” for 381.3 s (6.36 min) through the parabola shown in Figure 1. The greatest height of 261.2 km is reached after 261.9 s. During the whole phase of microgravity (<10−4 g) the payload remains completely stable in space as sketched allowing the fine-tuned application of gravitational forces by the rotary platform. Gravitational ramps of 5, 25, 50, 75 and 100 mg were applied, giving rise to the accompanying GIACs looked for.
2.2. Strains and Culture Conditions
The wild-type strain of Phycomyces blakesleeanus (Figure 2, Burgeff) is NRRL1555 (-) originally obtained
Figure 1. Left: Sketch of the complete parabola flown by Texus 50 including the crude dimensions and time points. Microgravity lower than 10−4 g is attained at a height of 100 km and after 63.8 s. It lasts for 381 s (6.35 min). During the whole period of microgravity up to reentry into the atmosphere (449.5 s) the rocket points upwards and does not rotate at all. This allows the precise action of the build-in centrifuge and the five gravitational ramps of 5, 25, 50, 75 and 100 mg. After reentry the status of the rocket is no longer controlled leading to a muddle-headed movement. After the main parachute release the rocket-again-hangs upwards till landing to be picket up by a helicopter. The maximum gravitational impact in the start phase is 6.1 g, still accepted by the vertical SPPH. However, maximum reentry deceleration of 37.8 g destroys the SPPH as shown by the recovered samples. Right: sketch of the complete payload of the rocket including three experiments and essential parts without the two motors. The experiment in the lowest part and described here is termed TEM 06-33. The total length of the rocket is about 13 m, the length of the payload 5.189 m.
Figure 2. Microscopic picture of a single sporangium of a sporangiophore. Highest geo- (and photo-) sensitivity is just below the spherical sporangium as shown.
from the Northern Regional Research Laboratory, USDA, Peoria, IL, USA. Sporangiophores of Phycomyces were raised as described previously [15] . For short, they were grown in glass shell vials (1 cm diameter × 4 cm height; Flachbodengläser, AR Klarglas, Münnerstädter Glaswarenfabrik, Münnerstadt, Germany) on a synthetic solid medium with glucose. Until the appearance of stage-4b sporangiophores (i.e. with sporangium) of 2.5 cm length the material was kept in transparent plastic boxes at ambient temperature (19˚C - 21˚C) under white incandescent light fluence rate (0.5 Wm−2).
2.3. Micro-Dual Wavelength Spectrophotometer
Gravity-Induced Absorption Changes (GIACs) were detected in vivo with a home-made micro-dual wavelength spectrophotometer (MDWS) as described previously [23] [24] (Figure 3). Because of the structure of SPPHs and for technical reasons we measure reflectance rather than absorption as suggested by its name. Since A ~ - log R at very small reflection changes as in the present case, DR is proportional to DA = log Rl2/Rl1, where R is the reflected light at the wavelengths l1 and l2. The MDWS is capable of measuring extremely small optical reflection changes (<10−5 A) and is app. 100 to 1000 times more sensitive than common double beam spectrophotometers [25] . The extreme sensitivity of the dual wavelength method originates i) in its high chopping frequency (0.5 kHz) significantly diminishing the so-called 1/f-noise4 [26] and ii) in its “self-compensating” properties: any change (temperature, air pressure, humidity) not caused by the specific optical change (GIAC) looked for is fairly suppressed.
Based on the action spectrum of GIACs [26] in the visible wavelength range we selected LEDs in the blue and in the red (l1 = 460 nm and l2 = 660 nm, Roithner Lasertechnik, Wien, Austria). The phase of the lock-in amplifier was chosen to deliver an increasing GIAC-signal upon increasing absorbance in the blue (i.e. decreasing reflectance), and vice versa. The chopped measuring light beams of wavelengths l1 and l2 impinge on the sample and are reflected back to the photomultiplier module (UV-VIS: H5773-01, Hamamatsu Photonics Deutschland GmbH, Herrsching, Germany). A lock-in amplifier (LIA-MV-200-H; FEMTO Messtechnik GmbH, Berlin, Germany) obtains the reference signal from the LED-control unit and converts the chopped and reflected light stream into the analogues GIAC-signal. This is finally fed to the AD-converter (16 bit dynamical resolution), additional electronics and the transmission line between rocket and the base station. GIAC-signals typically suffer from baseline shifts, which have to be controlled both during the flight and often have to be corrected for when evaluating the data. The individual vial (sample) typically includes 10 to 20 SPPHs. In a sense this represents an exaggerated high degree of averaging for the individual sample/measurement with good repeatability.
Figure 3. Sketch of the Micro-Dual Wavelength Spectrophotometer (MDWS). Main components are the two LEDs set to wavelengths, between which the reflection/absorption change is expected (right site). These focus their conic beams (app. 30˚) chopped with a phase shift of 180˚ and 0.5 kHz as indicated onto the “hedge” of app. 10 to 20 SPPHs. The isotropically reflected light pulses (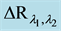 ) are detected by a mini photomultiplier module. The chopped signal is fed to a lock-in amplifier and further processed as absorbance change (GIAC =
) are detected by a mini photomultiplier module. The chopped signal is fed to a lock-in amplifier and further processed as absorbance change (GIAC =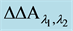 ) and transmitted from the capsule electronics down into the control room (ZARM).
) and transmitted from the capsule electronics down into the control room (ZARM).
Due to the relative small amount of reflected light per pulse reaching the cathode of the photomultiplier only a poor SNR3 is attained, anyway. However, by FFT-smoothing using a suitable kernel for the integral valuable information can be extracted even from noisy signals [27] .
The computer program originally designed for the MDWS on board the Airbus 300 Zero G was originally written by K. Dörnemann (Univ. Marburg), further developed by Multimedia and Software GmbH, Erlangen, Germany and adopted/adapted by Astrium for usage on board the TEXUS 50.
Prior to start of TEXUS 50 a simple test of the activity of the sample to fly offers itself: We monitor the DGIAC signal in the inactive vertical position of the SPPHs. Than we tilt the SPPHs including the whole light fiber arrangement into the horizontal position. This results in the expected DGIAC signal (Figure 4).
2.4. Telemetry
The on board experiment is completely controlled and monitored from the base station via radio signals (TCE64-Telecommand-Encoder for 64 digital signals). Common module data such as GPS, battery voltage, currents, temperatures, adjustment of both LEDs of the MDWS, amplification, time delay of the lock-in, high voltage of the photomultiplier are monitored at 5 Hz. GIAC data are monitored with 16 bit resolution at 0.5 kHz and completely stored on the on board micro-PC. For reasons of velocity only 1/16 of all GIAC-data are transferred to the ground station via a Kayser-Threde-Module for numerical and graphical display on the screen on ground. In addition to GIAC-recording, this allows the on-line baseline correction by the experimenter.
3. Results and Discussion
Some 10 years ago the threshold in Phycomyces was determined using an earth bound clinostat [11] . These authors presented a threshold of 2 × 10−2 g. This is in perfect agreement with the lower limit of 25 mg (2.5 × 10−2 g) as optically determined on the TEXUS 50 sounding rocket and described here. Both methods are based on theoretically quite different approaches: measurement of bending is on the response site; measurement of GIACs is close to the graviperception site leading to comparable values. This supports the assumption of a linear data flow between reception of the stimulus and the resulting response.
Figure 5 represents the main result of this campaign as monitored during the whole phase of microgravity (381 s). Increasing gravitational ramps g were generated by a centrifuge. Gravity-induced absorbance changes clearly show GIAC signals pointing upwards correlating with the ramps between 25 and 100 mg limiting the threshold to be lower than 25 mg. These changes indicate either a decrease of blue light reflection or an increase
Figure 4. Prior to inserting the sample vials into the late access chambers Phycomyces is tested for its activity with the MDWS-spectrophotometer which is used for parabolic flight experiments and which is installed for this purpose in our ESRANGE laboratory. After inserting the sample the MDWS is carefully calibrated for a good balance of both 180˚ shifted light pulses, beginning with lowest sensitivity (±4.25 units) and stepwise increasing amplification of 105. Tilting the sample chamber by 90˚ with the present sample leads to the signal increase by 1.5 units. First the samples stand upward and the trace shows a moderate shift. Clearly, the tilting process causes irregular kinetic shifts particularly of the upper signal. This corresponds to a decrease of blue light respectively increase of red light reflection.
Figure 5. This figure represents the main result of this campaign as monitored during the whole phase of microgravity. g: gravitational ramps (mg) as generated by the centrifuge. GIAC: gravity-induced absorbance changes. Baseline, dotted curve: the main structure of the GIAC-kinetics was fitted by a polynomial of 3rd order, largely eliminating the unavoidable shift of the GIAC-signal, but saving the “fine structure”. GIACcorr represents the corrected GIAC-kinetics, multiplied with 4. GIACsmoothed is the corrected and noise-free GIAC- kinetics as smoothed by FFT using a suitable inner Kernel. Clearly, there is a significant correlation to the applied gravitational ramps (top). 25 mg still show up in the GIAC-kinetics, limiting the threshold to lower than this value. Remarkable: during the constant maximum value of the individual ramps the GIAC-kinetics are still shifting upwards. The zero-g-phases between the ramps clearly show small upward-bumps as indicated by the arrows.
of red light reflection.
To correct the unavoidable shift of the GIAC-signal, the crude structure was fitted by a polynom of 3rd order, saving the “fine structure” such as bumps and short-term shifts during gravity (dotted curve). GIACcorr represents the difference of the original GIAC-kinetics minus the calculated fit, multiplied with 4. Finally, this still noisy kinetics is smoothed by FFT-analysis [27] using a suitable inner Kernel (GIACsmoothed). Note, during the constant maximum value of the individual ramps, the GIAC-kinetics are still shifting upwards, stronger and opposite to the baseline shift. In addition, during the zero-G-phases among the ramps, small but significant upward-bumps show up as indicated by the arrows. Is this a transient response of the SPPHs to the transition of gravity to complete weightlessness? So far its explanation remains obscure.
Referring to our previous work on GIAC-hystereses [28] , exemplarily the hysteresis of the GIAC-peak at 75 mg (after further correction of the remaining shift) and the appendant gravity-ramp are shown in Figure 6. Top:
Figure 6. As experienced by our former parabolic flight experiments [28] , exemplarily and after proper FFT-smoothing we worked out the hysteresis for the 75 mg ramp. Top: Both kinetics (GIAC, blue, and g, black) do not coincide. Bottom: This is further shown by the hysteresis loop (GIAC vs. gravity g) as calculated from the individual kinetics, exhibiting a significant area: a measure of internal molecular action (cf. [28] ). This strongly supports the biological relevance of GIACs.
Both kinetics (GIAC and g) do not coincide. Upon onset of the 75 mg gravitational ramp the GIAC is about 4 s delayed. Bottom: This is further expressed by the hysteresis loop (GIAC vs. gravity) as calculated from the individual kinetics, exhibiting a significant area―a measure of internal molecular action. This observation strongly supports the biological relevance of GIACs.
So far the identities of molecular components involved in GIACs still remain unknown. We still cannot exclude that GIACs are a trivial byproduct of the primary sensory transduction process of gravitropism.
We further hypothesize―parallel to the better understood blue light responses―the involvement of various electrons transfer components such as flavins, flavosemiquinones, cytochromes or pterins which spectrally cover the whole visible action spectrum [29] [30] . They undergo complex reactions during hyper- and particularly microgravity, in agreement with previous findings in drop tower experiment lasting only 4.7 s (cf. Figure 1 in [31] ).
Acknowledgements
The work was supported by grant 50WB1025 from the DLR/BMWI (Deutsches Zentrum für Luft- und Raum- fahrt, and Bundesministerium für Wirtschaft). First of all I thank my college Prof. Galland for helpful discussion of this paper and various suggestions. We greatly acknowledge the excellent implementation and miniaturization of our various spectrophotometers (MDWS and RSS) as formerly used for parabolic flights and now for sounding rocket campaigns by the whole team of Astrium (Bremen, Dep. TO4-BEOS, Astrium, 28199 Bremen, GmbH) particularly Thomas Hülsing and Burkhard Schmitz. The engineers of the former Kayser-Threde GmbH (München) are thanked for their excellent work controlling the flight of the rocket (since 1st Sept. 2014 they are fused with OHB Systems under the name OHB System AG, Oberpfaffenhofen, Germany).
Cite this paper
WernerSchmidt,11, (2015) Gravireception in Phycomyces: Threshold Determination on the Sounding Rocket TEXUS 50. Journal of Modern Physics,06,1381-1389. doi: 10.4236/jmp.2015.610143
References
- 1. Schmidt, W. and Galland, P. (2000) Planta, 210, 848-852.
http://dx.doi.org/10.1007/s004250050689 - 2. Morita, M.T. (2010) Annual Review of Plant Biology, 61, 705-720.
http://dx.doi.org/10.1146/annurev.arplant.043008.092042 - 3. Corrochano, L.M. and Galland, P. (2006) Photomorphogenesis and Gravitropism in Fungi. In: Kues, U. and Fischer, R., Eds., The Mycota I, Growth, Differentiation and Sexuality, Springer-Verlag, Berlin, Heidelberg, 231-257.
http://dx.doi.org/10.1007/3-540-28135-5_13 - 4. Sack, F. (1991) International Review of Cytology, 127, 193-252.
http://dx.doi.org/10.1016/S0074-7696(08)60695-6 - 5. Kiss, J.Z., Hertel, R. and Sack, F.R. (1989) Planta, 177, 198-206.
http://dx.doi.org/10.1007/BF00392808 - 6. Volkmann, D. and Sievers, A. (1979) Graviperception in Multicellular Organs. In: Haupt, W. and Feinleib, M.E., Eds., Encyclopedia of Plant Physiology, Physiology of Movements, Vol. 7, Springer, Berlin, Heidelberg, New York, 573-600.
- 7. Sack, F. (1997) Planta, 203, 63-68.
http://dx.doi.org/10.1007/PL00008116 - 8. Boonsirichai, K., Guan, C., Chen, R. and Masson, P.H. (2002) Annual Review of Plant Biology, 53, 421-447.
http://dx.doi.org/10.1146/annurev.arplant.53.100301.135158 - 9. Dennison, D.S. (1961) The Journal of General Physiology, 45, 23-38.
http://dx.doi.org/10.1085/jgp.45.1.23 - 10. Dennison, D.S. and Shropshire Jr., W. (1984) The Journal of General Physiology, 84, 845-859.
http://dx.doi.org/10.1085/jgp.84.6.845 - 11. Galland, P., Finger, H. and Wallacher, Y. (2004) Journal of Plant Physiology, 161, 733-739.
http://dx.doi.org/10.1078/0176-1617-01082 - 12. Shen-Miller, J., Hinchmann, R.R. and Gordon, S.A. (1968) Plant Physiology, 43, 338-344.
http://dx.doi.org/10.1104/pp.43.3.338 - 13. Wabnik, K., Govaerts, W., Friml, J. and Kleine-Vehn, J. (2011) Molecular BioSystems, 7, 2352-2359.
- 14. Blilou, I., Xu, J., Wildwater, M., Willemsen, V., Papanov, I., Friml, J., Heidstra, R., Aöda, M., Palme, K. and Scheres, B. (2005) Nature, 433, 39-44.
http://dx.doi.org/10.1038/nature03184 - 15. Schmidt, W. and Galland, P. (2004) Plant Physiology, 135, 183-192.
http://dx.doi.org/10.1104/pp.103.033282 - 16. Kubelka, P. and Munk, F. (1931) Zeitschrift für Technische Physik, 12, 593-601.
- 17. Behrens, H.M., Gradmann, D. and Sievers, A. (1985) Planta, 163, 463-472.
http://dx.doi.org/10.1007/BF00392703 - 18. Behrens, H.M., Weisenseel, M.H. and Sievers, A. (1079) Plant Physiology, 70, 1079-1083.
http://dx.doi.org/10.1104/pp.70.4.1079 - 19. Björkmann, T. (1988) Botanical Research, 15, 1-41.
http://dx.doi.org/10.1016/S0065-2296(08)60043-9 - 20. Sievers, A., Sondag, C., Trebacz, K. and Hejnowicz, Z. (1995) Planta, 197, 392-398.
http://dx.doi.org/10.1007/BF00202662 - 21. Shigematsu, H., Toko, K., Matsunoand, T. and Yamafuji, K. (1994) Plant Physiology, 105, 875-880.
- 22. Weisenseel, M.H. and Meyer, A.J. (1997) Planta, 203, 98-106.
http://dx.doi.org/10.1007/PL00008122 - 23. Schmidt, W. (2004) Microgravity—Science and Technology, 15, 42-48.
http://dx.doi.org/10.1007/BF02870951 - 24. Schmidt, W. (2004) Journal of Biochemical and Biophysical Methods, 58, 15-24.
http://dx.doi.org/10.1016/S0165-022X(03)00153-2 - 25. Schmidt, W. (2007) Microgravity—Science and Technology, 19, 11-15.
http://dx.doi.org/10.1007/BF02870983 - 26. Schmidt, W. (2006) Protoplasma, 229, 125-131.
http://dx.doi.org/10.1007/s00709-006-0217-8 - 27. Schmidt, W. (2005) Optical Spectroscopy in Life Sciences and Chemistry: An Introduction. Wiley-VCH, Weinheim, 369.
- 28. Schmidt, W. (2011) Microgravity Science and Technology, 23, 356-364.
http://dx.doi.org/10.1007/s12217-010-9255-0 - 29. Schmidt, W., Galland, P., Senger, H. and Furuya, M. (1990) Planta, 182, 375-381.
http://dx.doi.org/10.1007/BF02411388 - 30. Schmidt, W. and Galland, P. (1999) Planta, 208, 274-282.
http://dx.doi.org/10.1007/s004250050559 - 31. Schmidt, W. (2010) Microgravity Science and Technology, 22, 79-85.
http://dx.doi.org/10.1007/s12217-009-9113-0 - 32. Johnson, J.B. (1928) Physical Review, 32, 97-109.
http://dx.doi.org/10.1103/PhysRev.32.97
Abbreviations
DLR: Deutsches Zentrum für Luft- und Raumfahrt
ESRANGE: European Space and Sounding Rocket Range (near Kiruna, Sweden)
FFT2: Fast Fourier Transform
GIAC: Gravity-Induced Absorption Change
LIAC: Light-Induced Absorption Change
MDWS: Micro-Dual Wavelength Spectrophotometer
RSS: Rapid Scan Spectrophotometer
SNR3: Signal to Noise Ratio
1/f-noise4: Also called flicker noise or Pink noise
SPPH: Phycomyces sporangiophore
TEXUS 50: 50th sounding rocket campaign, April 2013
ZARM: Center for Applied Space Technology and Microgravity
NOTES

1The terminus “threshold” is adopted (i) from the biophysical theory of nerve signal propagation and (ii) from the physical theory of field-effect transistors (FETs). Both thresholds are typical all or none reactions; i.e. ion respectively electrical conductivity changes abruptly only if a well defined voltage, the “threshold voltage” is applied. In the theory of nerve conductivity the membrane potential must be depolarized to a precise extend in order to initiate an action potential. The threshold voltage of a field-effect transistor is the minimum gate-to-source voltage differential that is needed to create a conducting path between the source and drain terminals (e.g. representing a switch). Threshold potentials are necessary in order to regulate and propagate signals in both the central nervous system and the peripheral nervous system. However, so far it is common custom in plant physiology also to speak of “threshold of gravitropism” even if the questioned reaction is decreasing monotonously to zero upon decreasing gravi-stimuli and does not represent an all or none reaction. The “threshold” is the smallest stimulus where a response is observed. It depends on the sensitivity of the measuring set-up.
2There are many different FFT algorithms involving a wide range of mathematics, from simple complex-number arithmetic to group theory and number theory. Here it is used for smoothing.
3Signal-to-noise ratio (abbreviated SNR) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise.
41/f noise or Pink noise (sometimes also called flicker noise) is a signal or process with a frequency spectrum such that the power spectral density (energy or power per Hz) is inversely proportional to the frequency of the signal since its discovery by Johnson [32] . 1/f fluctuations are widely found in nature, physics, technology, biology, astrophysics or geophysics. The theory is highly complex and so far not well understood, but nevertheless for optospectroscopic measurements very useful and simple: the SNR3 is inversely proportional to the chopping frequency of the MDWS.









