Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57048,7 pages
10.4236/jmp.2015.67089
The Study of Optoacoustic First and Second Sound Waves in Superfluid Helium under the Effect of Gaussian Laser Light Considering Electrostriction Mechanism
Leyla Safaei Kouchaksaraei
Physics Science and Research Institute, Tajik National University, Dushanbe, Tajikistan
Email: ley_safaee@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 May 2015; accepted 8 June 2015; published 11 June 2015
ABSTRACT
The present paper is aimed to study the effect of Gaussian laser light on first and second sound waves in superfluid helium theoretically using optoacoustic method. The mechanism applied in this study is electrostriction mechanism. This study considers crystal parts of superfluid helium with a zero absorption coefficient applying electrostriction mechanism. Affecting Gaussian laser light on these crystal parts, a spectrum of cylindrical first and second sound waves and cylindrical slow and rapid waves is obtained. Meanwhile, frequency of waves amplitudes proportionate to time period of laser light is calculated.
Keywords:
Electrostriction Mechanism, First and Second Sound Waves, Gaussian Laser Light, Superfluid Helium

1. Introduction
A superfluid is a state of matter that behaves like a fluid with zero viscosity and zero entropy. The substance which looks like a normal fluid will flow without friction past any surface, which allows it to continue to circulate over obstructions and through pores in containers which hold it, subject only to its own inertia.
Known as a major facet in the study of quantum hydrodynamics and macroscopic quantum phenomena superfluidity effect was discovered by Pyotr Kapitsa [1] , John. F. Allen and Don Meisner [2] in 1937. It has since been described through phenomenological and microscopic theories by different physicists. The formation of the superfluid is known to be related to the formation of a Bose-Einstein condensate. This is made obvious by the fact that superfluidity occurs in liquid helium-4 at far higher temperatures than it does in helium-3. Each atom of helium-4 is a boson particle, by virtue of its zero spin. Helium-3, however, is a fermion particle, which can form bosons only by pairing with itself at much lower temperatures, in a process similar to the electron pairing in superconductivity.
Superfluidity in liquid helium4 occurs at 2.186 kelvin degrees. Helium-4 in temperature of 2.186 kelvin degrees has a lambda shape phase transition and this temperature point is called lambda point. This phase transition divides helium into two parts. Those parts of helium that are below 2.186 kelvin degrees have superfluidity properties and it is called superfluid helium or helium II. This part is responsive for unit and unique properties of liquid helium. These properties include a zero viscosity coefficient, zero entropy, efficient heat transition and obvious vortex and a thermodynamic effect. Those parts of helium-4 that are above 2.186 k degrees are called normal helium or helium I. Helium below 2.186 k degrees can moves out easily and rapidly through capillarity tubes and this is the superfluidity property discovered by Kapitsa. Since the viscosity coefficient is not zero at temperatures above 2.186 k degrees there is no superfluidity property and this part is called normal helium. Helium I has transition properties like classic gas because of its low density. Helium II is similar to quantum liquid because of its unlimited thermal conductivity [3] .
In the 1950s, Hall and Vinen performed experiments establishing the existence of quantized vortex lines in superfluid helium [4] . In the 1960s, Rayfield and Reif established the existence of quantized vortex rings [5] . Packard has observed the intersection of vortex lines with the free surface of the fluid [6] , and Avenel and Varoquaux have studied the Josephson effect in superfluid helium-4 [7] . In 2006, a group at the University of Maryland visualized quantized vortices by using small tracer particles of solid hydrogen [8] .
Figure 1 is the phase diagram of 4He [9] . It is a p-T diagram indicating the solid and liquid regions separated by the melting curve (between the liquid and solid state) and the liquid and gas region, separated by the vapor- pressure line. This latter ends in the critical point where the difference between gas and liquid disappears. The diagram shows the remarkable property that 4He is liquid even at absolute zero. Helium four is only solid at pressures above 25 bar.
Figure 1 also shows the λ-line. This is the line that separates two fluid regions in the phase diagram indicated by He-I and He-II. In the He-I region the helium behaves like a normal fluid; in the He-II region the helium is superfluid.
The name lambda-line comes from the specific heat ? temperature plot which has the shape of the Greek letter λ [10] [11] . See Figure 2, which shows a peak at 2.172 K, the so-called λ-point of 4He.
Below the lambda line, the liquid can be described by the so-called two-fluid model. It behaves as if it consists of two components: a normal component, which behaves like a normal fluid, and a superfluid component with zero viscosity and zero entropy. The ratios of the respective densities ρn/ρ and ρs/ρ, with ρn(ρs) the density of the normal
Figure 1. Phase diagram of 4He. The λ-line is also given in this diagram.
(superfluid) component, and ρ (the total density), depends on temperature and is represented in Figure 3 [12] . By lowering the temperature, the fraction of the superfluid density increases from zero at Tλ to one at zero kelvin. Below 1 K the helium is almost completely superfluid.
It is possible to create density waves of the normal component (and hence of the superfluid component since ρn + ρs = constant) which are similar to ordinary sound waves. This effect is called second sound. Due to the temperature dependence of ρn (Figure 3) these waves in ρn are also temperature waves.
Equations related to first sound waves propagation (propagation of pressure vibration) and second sound waves propagation (propagation of temperature vibration) are calculated by applying optoacoustic relations and linear hydrodynamic equations.
In fact, the first sound wave is a pressure wave that is continuously decreasing while the temperature is increasing, and it has a discontinuity in the lambda point. Also second sound wave is a thermal wave that is observed in Figure 4 [3] . There are other sound waves in superfluid helium than first and second sound waves that are not the subject of study in this paper.
Observing waves equations of pressure and temperature, we see that there are two mechanisms in Helium superfluid: thermal and electrostriction mechanisms [13] . Romanov V. P. and Salikhov T. Kh. studied optoacoustic
Figure 2. Heat capacity of liquid 4He at saturated vapor pressure as function of the temperature. The peak at T = 2.17 K marks a (second-order) phase transition.
Figure 3. Temperature dependence of the relative superfluid and normal components ρn/ρ and ρs/ρ as functions of T.
Figure 4. Diagram of sound velocities as per temperature (Kelvin) in superfluid helium.
methods for producing second sound waves in superfluid helium theoretically in 1991 [14] . Salikhov T. Kh. studied laser production of first and second sound waves in superfluid helium in 2000 [15] . Theoretical study about a spectrum of transition functions of optoacoustic first and second sound signals in superfluid helium considering thermal mechanism was implemented by T. Kh. Salikhov and O. Sh. Odilov [16] . These two scientists also studied the photoacoustic effect in superfluid helium [17] . The present paper considers crystal parts of superfluid helium. Since coefficient of absorption in these parts is nearly zero, the only effective mechanism in these parts is electrostriction one.
Electrostriction Mechanism is an elastic deformation which is created by electric field. On this basis the mechanical intensity which is independent from reverse field direction is in contrast to the piezoelectric effect.
When we affect the laser light on superfluid helium, the electric field causes an expansion and contraction in the sample that is the elastic deformation. Laser light does not create any heat in this state. Electrostriction in solid dielectrics is tiny and have a second rate effect. On the other hand the piezoelectric materials have a linear effect [18] [19] .
2. Effect of Gaussian Laser Light on Superfluid Helium
Obviously these waves are produced theoretically through effecting Gaussian laser light on cylindrical cells filled with superfluid helium. Here laser light is as per time period of laser 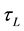 and power
and power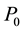 .
.
Systems related to waves equations for acoustic vibrations of pressure and temperature ignoring dispersion coefficient are as follows:
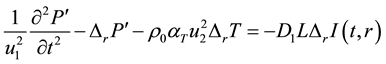 (1)
(1)
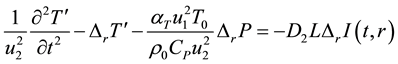 (2)
(2)
Here parameters in Equations (1) and (2) are as follows:
 , , ,
, , ,
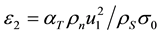 , ,
, ,
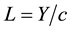 ,
,
that are optoacoustic coupling parameters. Here, c is light velocity,  is coefficient of thermal expansion, and
is coefficient of thermal expansion, and 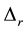 is radial part of Laplace indicator.
is radial part of Laplace indicator.
When Gaussian laser light effect on superfluid helium, it has the following intensity:
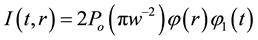
Here, w is laser light radius,  and
and  are functions of radial and time divisions of laser light. If we effect Fourier transformation to t and Hankel transformation to r in Equations (1) and (2) as
are functions of radial and time divisions of laser light. If we effect Fourier transformation to t and Hankel transformation to r in Equations (1) and (2) as

we obtain Equations (3) and (4) as follows:


Here, 




Meanwhile, the roots of dispersion equation can be calculated as follows:
Solving this equation, we obtain the these expressions: 
Here, we have

Through effecting Hankel reverse transformation on the Equations (5) and (6), we obtain the following equations:


Here, 


Solving the Equations (7) and (8), we obtain Equations (9) and (10) as follows:


Here, 

Therefore, the Equations (9) and (10) can be written as follows:






The Equations (11) to (16) show that cylindrical first and second sound waves including two parts are exited in helium superfluid. The Equation (13) is related to cylindrical normal first sound wave and a similar sound is observed in the Equation (14) moving with velocity of 






The Equations (17) to (20) show that the intensity of produced acoustic waves in low frequencies increase according to relation of
3. Conclusions
The researcher presented theoretically production of first and second sound waves in superfluid helium through emitting Gaussian laser light with electrostrictive mechanism consideration. An exited spectrum of cylindrical first and second sound waves including slow and rapid parts was obtained simultaneously in the applied system. When we observe the equations resulted through theoretical computations we conclude that the presence of factor 


In low frequencies, the intensity of produced acoustic first and second sound waves was calculated according to the relation of
Acknowledgements
The quality of this study was greatly enhanced by the gracious assistance of the author’s advisor, Professor T. Kh. Salikhov. The author is grateful to him, for his great help and fruitful comments. She also would like to thank all her colleagues who contributed to this study.
References
- Kapitsa, P. (1938) Nature, 141, 74.
- Allen, J.F. and Misener, A.D. (1938) Nature, 142, 643. http://dx.doi.org/10.1038/142643a0
- Frank, P. (1992) Matter and Methods at Low Temperatures. 2nd Edition, Springer, Berlin, 20-30.
- Hall, H.E. and Vinen, W.F. (1956) Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sci- ences, 238, 215. http://dx.doi.org/10.1098/rspa.1956.0215
- Rayfield, G. and Reif, F. (1964) Physical Review, 136, A1194. http://dx.doi.org/10.1103/PhysRev.136.A1194
- Packard, R.E. (1982) Physica B+C, 109-110, 1474.
- Avenel, O. and Varoquaux, E. (1985) Physical Review Letters, 55, 2704-2707. http://dx.doi.org/10.1103/PhysRevLett.55.2704
- Bewley, G.P., Lathrop, D.P. and Sreenivasan, K.R. (2006) Nature, 441, 588. http://dx.doi.org/10.1038/441588a
- Swenson, C. (1950) Physical Review, 79, 626. http://dx.doi.org/10.1103/PhysRev.79.626
- Keesom, W.H. and Keesom, A.P. (1935) Physica, 2, 557. http://dx.doi.org/10.1016/S0031-8914(35)90128-8
- Buckingham, M.J. and Fairbank, W.M. (1961) The Nature of the λ-Transition. In: Gorter, C.J., Ed., Progress in low Temperature Physics, North-Holland, Amsterdam, 80.
- Andronikashvili, E.L. (1948) Journal of Experimental and Theoretical Physics (JETP) (Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki), 18, 424.
- Salikhov, T.K. and Leyla, S.K. (2012) Generation of the Optoacoustic Impulses of the First and Second Sounds in Superfluid Helium through Electrostriction Mechanism. Payam Scientific Journal of Tajik National University (Вестник Таджикского национального университета), 1/1,99. http://www.tnu.tj
- Romanov, V.P. and Salikhov, T.K. (1991) Physics Letters A, 161, 161-163.
- Salikhov, T.K. (2000) The Theory of Lasers Generation First and Second Sounds in Superfluid Helium. Proceedings of the 11th International Conference on Photoacoustic and Photothermal Phenomena, Kyoto, 25-29 June 2000, 4-10.
- Salikhov, T.K. and Odilov, O.S. (2007) The Spectrum of Transfer Functions of Optoacoustic Signals of the First and Second Sounds in Superfluid Helium. Proceedings of the 14th International Conference on Photoacoustic and Photothermal Phenomena, Cairo, 6-9 January 2007, 145.
- Salikhov, T.K. and Odilov, O.S. (2009) The Photoacoustic Effect in the Superfluid Helium. Proceedings of the 15th International Conference on Photoacoustic and Photothermal Phenomena, Leuven, 19-23 July 2009, 208.
- Gusev, V., Picart, P., Mounier, D. and Breteau, J.-M. (2002) Optics Communications, 204, 229-236. http://dx.doi.org/10.1016/S0030-4018(02)01211-7
- Gusev, V., Picart, P., Mounier, D. and Breteau, J.M. (2003) Review of Scientific Instrument, 74, 901.














