Received 19 January 2015; accepted 7 September 2015; published 10 September 2015

ABSTRACT

Quantum electrodynamics (QED) is built on the original Dirac equation, an equation that exhibits perfect symmetry in that it is symmetric under charge conjugation (C), space (P) and time (T) reversal and any combination of these discrete symmetries. We demonstrate herein that while the proposed Lorentz invariant Curved Spacetime Dirac Equations (CSTD-equations) obey C, PT and CPT-symmetries, these equations readily violate P, T, CP and CT-symmetries. Realising this violation, namely the T and CT-violation, we take this opportunity to suggest that the Curved Spacetime Dirac Equations may help in solving the long standing riddle and mystery of the preponderance of matter over antimatter. We come to the tentative conclusion that if these CSTD-equations are to explain the preponderance of matter over antimatter; then, photons are to be thought of as described by the spherically curved version of this set of equations, while ordinary matter is to be explained by the parabolically and hyperbolically curved spacetime versions of this same set of equations.

Keywords:

Antimatter Asymmetric, CP-Violation, Curved Spacetime Dirac Equation

“Science is a way of thinking much more than it is a body of knowledge.”

―Carl Edward Sagan (1934-1996)

1. Introduction

The Dirac equation is a relativistic quantum mechanical wave equation serendipitously discovered by the eminent British physicist, Professor Paul Adrien Maurice Dirac [1] [2] . This equation possesses perfect symmetry in that it is invariant under charge (C), space (P), time (T) reversal operations and any combination of these discrete symmetries i.e. CP, CT, PT and CPT-symmetries. The fact that it is symmetric under C-symmetry implies that the Universe must constitute matter and antimatter in equal proportions, the resultant meaning of which is that the Universe must be a radiation bath since matter and antimatter annihilate to form photons. The fact that this prediction of the successful Dirac equation is completely at variance with physical and natural reality has worried scientists ever-since this dearth came to notice. This reading works-out the symmetries of the proposed curved spacetime Dirac equations [3] and uses them to make a suggestion on this riddle of why the Dirac equation’s predictions on matter-antimatter proportions are at odds with physical and natural reality.

The Dirac equation was discovered as part of an effort (by Dirac) to overcome the criticism levelled against the Klein-Gordon equation [4] . The Klein-Gordon equation [4] gave negative probabilities and this was considered to be physically meaningless. Despite this fact, this equation [the Klein-Gordon equation] accounts very well for spin-zero Bosons. Though this criticism levelled against the Klein-Gordon equation could be overcome without the need for the Dirac equation [5] , this criticism motivated Dirac to successfully seek an equation devoid of negative probabilities, whereupon he discovered the Dirac equation. By giving the correct gyromagnetic ratio of the Electron which at the time was a mystery, the Dirac equation gave an accurate description of the Electron and was thus largely believed to be an equation for the Electron.

The Dirac equation applies to a flat Minkowski spacetime. Thus, it was born without the corresponding curved spacetime version. Realising this gap to be filled, several researchers proposed their own versions of the curved spacetime versions of the Dirac equation [6] -[14] . In our modest view, save for the introduction of a seemingly mysterious four vector potential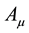, what makes the curved spacetime version of the Dirac equations presented in the reading [3] stands-out over other attempts in that the method used in arriving at these curved spacetime Dirac equations [3] is exactly the same as that used by Professor [1] [2] . As will be demonstrated shortly, this method used in [3] appears to us as the most straight forward and logical manner in which to arrive a curved spacetime version of the Dirac equation. All that has been done in [3] is to decompose the general metric in a manner that allows us to apply Professor [1] [2] ’s prescription at arriving at our proposed curved spacetime Dirac equation.

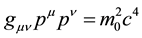
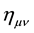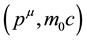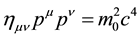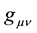As is well known, Dirac [1] [2] ’s original equation is arrived at from the famous Einstein momentum-energy equation, namely where is the usual Minkowski metric, are the four momentum and rest mass of the particle in question respectively and c is the usual speed of light in a vacuum. In curved spacetime, we know very well that the equation is given by where is the general metric of a curved spacetime manifold. If a curved spacetime version of the Dirac equation is to be derived, shouldn’t it be derived from the fundamental equation in the same way the flat spacetime Dirac equation is derived from the fundamental equation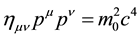? Dirac derived his equation by taking the “square-root” of the equation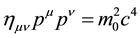: like Dirac, shouldn’t we derive the curved spacetime Dirac equation by taking the “square-root” of the equation? I think so―if it is possible, we must!

Along the same line as that Dirac used in his derivation, it is a fundamental mathematical fact that a two-rank tensor (such as the metric tensor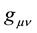) can be written as a sum of the product of a vector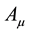, i.e.:

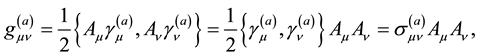(1)

where the matrices are 4 × 4 matrices such that and -matrices¹ are defined such that:

(2)

where is the 2 × 2 identity matrix, matrices are the usual 2 × 2 Pauli matrices and the 0’s are 2 × 2 null matrices and such that for:

(3)

The index “a” is not an active index as are the Greek indices―its an index which labels a particular representation of the metric―it labels a particular curvature of spacetime i.e. whether spacetime is spherically², parabolically or hyperbolically curved. Written in full, the three metric tensors, and are given by:

(4)

Especially for a scientist and/or mathematician, there is little if anything they can do but accept facts as they

stand and present them-self thus the writing of as is to be accepted as a legiti-

mate mathematical fact for as long as is a tensor. Since is a vector and the -matrices are all constant scaler matrices, is a tensor. Therefore, it follows that the equation can now be

written as. As clearly demonstrated in [3] , if we are to have the equation written in the decomposed form, and one where to follow Dirac [1] [2] ’s original derivation method, they will arrive at the three curved spacetime Dirac equations, namely:

(5)

It is not a difficult exercise to show that multiplication of (5) from the left hand-side by the conjugate operator leads us to the Klein-Gordon equation, , provided we have the

gauge condition, where is a non-zero constant (see, [15] -[17] , for an exposition of the this modified Lorenz gauge). The condition, should be taken as a gauge condition restricting this four vector. For the case, if, we have the original Dirac equation.

As it stands, Equation (5) would be a horrible equation insofar as its solutions are concerned because the vector is expected to be a function of space and time i.e.. Other than a numerical solution, there is no foreseeable way to obtain an exact solution is if that is the case. However, we found a way round the problem; fortunately, in the readings [18] [19] , we realised that this vector could actually be used to arrive at a general spin Dirac equation thereby drastically simplifying the equation so that it now was given by:

(6)

where now the matrices were such that:

(7)

where was the spin quantum number [18] [19] . In Equation (6), the vector has completely disappeared from our midst thus drastically simplifying the resultant equation in the process. For the purposes of the present reading, we will consider (6) and not (5). The vector appearing in (5) will be taken as presenting this electromagnetic of the particle. This idea finds support from our on-going work on an all- encompassing Unified Field Theory of all the Forces of Nature (see [17] ).

2. Symmetries

Now, on the main business of the day: we shall work-out the symmetries of the curved spacetime Dirac equations for the case. We shall assume as is the case with the Dirac equation that the electromagnetic four potential is a real function and that the components of this vector are zero-rank objects. Before that, we need to consider first how the electric (E) and magnetic fields (B), currents (J) and charges (ρ) behave under C, p and T-transformations. Under a P-transformation, the positions of electrical charges will be interchanged and so the electric field will change sign as a consequence. Currents will flow in opposite direction so they also will change sign as a result. Since the magnetic field is proportional to J × r, its sign will be preserved. All this can be summarised as:

(8)

Under a T-transformation, the charges and positions will remain unchanged, whereas the currents will flow in opposite direction, in which case we will get:

(9)

Using similar arguments as above, we will get for the C-transformation, the following:

(10)

Finally under the combined CPT-transformation the charges and currents change sign and the electric and magnetic fields will retain their signs. These properties can be summarised in terms of the four vector potential of the ambient electromagnetic field as:

(11)

Of particular importance here is the transformations (11) of the four vector potential, this the reader will have to know as we will not remind them in the derivations that follow.

2.1. C-Symmetry Observance

To demonstrate the symmetries of the CSTD-equations under charge conjugation, we proceed as usual, that is, we bring the curved spacetime Dirac particle under the influence of an ambient electromagnetic magnetic field (which is a real function). Having done this, the normal procedure of incorporating this ambient electromagnetic magnetic field into the Dirac equation is by making the transformation, hence Equation (6) will now be given by:

(12)

Equation (12) represents the curved spacetime Dirac particle which is immersed in an ambient electromagnetic magnetic field. If we are to reverse the particle’s electromagnetic field and that of the ambient electromagnetic magnetic field i.e., then, (12) becomes:

(13)

If the CSTD-equations is symmetric under charge conjugation, then, there must exist some mathematical transformation, which if applied to (13) would lead us back to an equation that is equivalent to (12).

Starting from (13), in-order to revert back to (12), the first mathematical operation to be applied to (13) the complex conjugate operation on the entire equation. So doing, we will have:

(14)

If (12) is invariant under charge conjugation, then, there must exist a matrix, such that:

(15)

If such a matrix where to exist, then, multiplying (14) from the left by, will lead us to the equation:

(16)

where. We shall prove in the section “Proof” below, that the matrix exists, hence, the CSTD-equations for which are symmetric under charge conjugation.

Proof

We shall prove that the matrix does exist. First we must realise that the matrices can be written as:

(17)

Taking the complex conjugate on both-sides of (17) and knowing that, we will have:

(18)

By some legitimate mathematical operation, we need to remove the complex conjugate on in (18). We know that and as-well that, therefore:

(19)

Multiplying both-sides of (19) by and knowing that, it follows that:

(20)

so that:

(21)

and from this, it follows that we must have. For this acting on, we will have:

(22)

therefore:

(23)

as desired in (15).

2.2. P-Symmetry Violation

A parity transformation requires that we reverse the space coordinates i.e. and this implies that. So doing, we will have (6) now being given by:

(24)

If (6) is invariant under a parity transformation, then, there must exist a matrix, such that:

(25)

There does not exist such a matrix that fullfils the conditions (25) because this would require that, and, which is impossible for non-null matrix. Therefore, the CSTD-equations for the case are not symmetric under space reversal.

2.3. T-Symmetry Violation

A time reversal transformation requires that we reverse the time coordinate i.e. and this implies. So doing, we will have (6) now being given by:

(26)

If (6) is invariant under a time reversal transformation, then, there must exist a matrix, such that:

(27)

There does not exist such a matrix that fullfils the conditions (27) because this would require that, and, which is impossible for non-null matrix. Therefore, the CSTD-equations for the case are not symmetric under time reversal.

2.4. CP-Symmetry Violation

A simultaneous charge conjugation and parity transformation requires that we reverse the particle’s electromagnetic field and that of the ambient electromagnetic magnetic field i.e. and as-well the space coordinates i.e. and this will lead to. Effecting all these transformations in (12), we will have:

(28)

If (12) is invariant under a simultaneous charge conjugation and parity transformation, then, there must exist a matrix, such that:

(29)

This matrix is the same matrix as, thus by the same arguments as those presented for, there does not exist this matrix that fullfils the conditions (29). Therefore, the CSTD-equations is not symmetric under a simultaneous reversal of charge and space.

2.5. CT-Symmetry Violation

A simultaneous charge conjugation and time reversal requires that we reverse the ambient electromagnetic magnetic field i.e. and as-well the time coordinate i.e. and this effectively will lead to. Effecting all these transformations into (12), we will have:

(30)

If (12) is invariant under a simultaneous charge conjugation and time transformation, then, there must exist a matrix, such that:

(31)

This matrix is the same matrix as, thus by the same arguments as those presented for, there does not exist this matrix that fullfils the conditions (31). Therefore, the CSTD-equations is not symmetric under a simultaneous reversal of charge and time.

2.6. PT-Symmetry Observance

If we are to reverse the spacetime coordinates, that is, and thereafter multiply the resulting equation by from the left and then make use of the fact that, it is seen that the resulting equation is equivalent to the original. Thus, the CSTD-equations for the case are symmetric under PT-transformations.

2.7. CPT-Symmetry Observance

If we are to reverse the ambient electromagnetic magnetic field together with the spacetime coordinates i.e., then, for the ambient electromagnetic magnetic field we will have i.e., it will remain invariant, thus inserting these transformations into (12), it is seen that for the resulting equation, if we take apply the complex conjugate operation on both-sides and the follows up with a multiplication on both- sides by, the resultant equation is exactly the same as the original. Thus, the CSTD-equations for the case are not only symmetric under CPT-transformations, but completely, wholly and totally invariant as no extra mathematical operations are required in-order to revert to the original equation.

2.8. Summary

In Table 1, we give a summary of the symmetries of all the three CSTD-equations. The flat CSTD-equations (in which the Dirac equation emerges on the condition) is in complete observance of all the symmetries while the parabolic and hyperbolic curved spacetime components of this set of equations only observe C, PT, CPT-symmetries and violate P, T, CP and CT-symmetries. Other than the C, P and the T symmetries and their different combinations, there is another symmetry that is allowed by the CSTD-equations and this is the symmetry under the reversal of the spin quantum number i.e.. Let S be the operator corresponding to this symmetry.

Now, without simultaneously acting on the CSTD-equations with the parity operator (P), the effect of acting exclusively on the CSTD-equations with the spin operator (S) is the same as exclusively acting on this same equation with the P-operator. What this effectively means is that the spherically curved CSTD-equations i.e., the case is symmetric under a reversal of the spin of the particle because this same equation is symmetric under a reversal of the space coordinates and on the same footing, the parabolic and hyperbolically curved spacetime versions of this set of equations, these equations will violate the S-symmetry since this same equations are asymmetric under a reversal of the space coordinates. In the subsequent section, we shall

demonstrate how the violation of the P, T, CP and S-symmetries can be used harmoniously to explain Universe that we live in. These three CSTD-equations together with these symmetry violations neatly explain the existence of radiation and the preponderance of matter over antimatter.

3. General Discussion

The symmetries of the Lorentz invariant CSTD-equations have here been worked out and we have shown that the parabolic and hyperbolic curved spacetime components of this set of equations, while they are in complete and total observance of C, PT and CPT-symmetries, these same equations readily violate P, T, CP and CT-symmetries. Of particular interest to us here is the CPT-violation. In the present discussion, we would like to point out that these three equations combined, may help in unlocking and solving the long standing riddle and mystery of the preponderance of matter over antimatter.

3.1. Problems with the Perfect Dirac Symmetries

In our view―insofar as the preponderance of matter over antimatter is concerned, one of the problems with the original Dirac equation is that it was born solo, as an equation explaining a Minkowski flat spacetime particle with no curved spacetime version of it. Realising the clear evident gap, over the years, researches proposed curved spacetime versions of the Dirac equation (cf. Refs.: [6] -[14] ). The problem with most of these proposed curved spacetime Dirac equations [6] -[14] , is that they preserve the symmetries of the original Dirac equation. This means that insofar as the preponderance of matter over antimatter is concerned, these equations [6] -[14] do no better job than the original Dirac equation.

If the predictions of the original Dirac equations together with its descendants [6] -[14] are to hold, then, it would mean that the Laws of Nature explaining the existence and production of matter, all but point to the fact that there must exist at the instant of creation of matter, equal positions of matter and antimatter. This obviously throws us into a conundrum because as far as experimental and observational evidence is concerned, we live in a matter dominated Universe. Our manned and unmanned exploration of the Solar system and the most distant portions of the heavens (using radio astronomy and cosmic ray detection), tell us that the Universe is made up of the same stuff as the Earth. The currently accepted and most favoured explanation as to how our Universe comes to be dominated by matter is that handed down to us by Professor Andrei Dimitriev Sakharov (1921-1989) in 1967.

3.2. Sakharov Conditions

In 1967, Professor Andrei Dimitriev Sakharov described three minimum properties of Nature which are required for any baryogenesis to occur, regardless of the exact mechanism leading to the excess of baryonic matter. In his seminal paper, Sakharov [20] did not list the conditions explicitly. Instead, he described the evolution of a Universe which goes from a Baryon-excess (B-excess) while contracting in a Big Crunch to an anti-B-excess after the resultant Big Bang. In summary, his three key assumptions are now known as they Sakharov Conditions, and these are:

1) At least one B-number violating process.

2) C and CP-violating processes.

3) Interactions outside of thermal equilibrium.

These conditions must be met by any explanation in which during the Big Bang but is very high in the present day. They are necessary but not sufficient―thus scientists seeking an explanation of the currently obtaining matter asymmetry on this basis (Sakhorov conditions) must describe the specific mechanism through which baryogenesis happens. Much theoretical work in cosmology and high-energy physics revolves around finding physical processes and mechanism which fit the three Sakhorov pre-conditions and correctly predicting the observed baryon density.

3.3. Current Research Efforts

Therefore, the current thrust in research especially at CERN³ is to search for physical processes in Nature that violate CP-symmetry. In 2011 during high-energy Proton collisions in the LHCb experiment [21] , scientists working at CERN created mesons―i.e. hadronic subatomic particles comprised of one quark and one antiquark―inside the LHCb experiment [21] and this experiment seems to have yeilded some very interesting results insofar as the Sakhorov conditions are concerned. By observing the rapid decay of the, physicists of the LHCb-Collaboration [21] were able to identify the neutral particle’s decay products―i.e. the particles that it decayed into. After a significantly large number of Proton collisions and decay events, the LHCb-Colla- boration [21] concluded that more matter particles where generated than antimatter during neutral decays.

The first violations of CP-symmetry was first documented in Brookhaven Laboratory in the US in the 1960s in the decay of neutral Kaon particles. Since then, Japanese and US labs forty years later found similar behaviour in B⁰-mesons systems where they detected similar CP-symmetry violations. LHCb-Collaboration [21] results indicating that antimatter decays at a faster rate than antimatter only come in as further supporting evidence and from a [20] standpoint, these observations certainly provide key insights into the problem of the preponderance of matter over antimatter.

3.4. Solution Inaccordance with the Present Work

This is not the case with the CSTD-equations which clearly predict T, CT and CP-violation as a permissible Laws of Nature. That is to say, in as much as the Dirac equation is taken as a Law of Nature, here we have (if we accept these equations) these CSTD-equations standing as candidate Laws of Nature in which case they predict T, CT and CP-violation. If we accept them as legitimate equations of physics as is the case with the Dirac equation, then, we can use them to explain the apparent preponderance of matter without the need for the Sakhorov conditions.

The Sakhorov conditions assume that the Laws of Nature are symmetric with respect to matter and antimatter. According to these pre-conditions, the preponderance of matter will arise in a Universe whose laws are perfectly symmetric with respect to matter and antimatter if there exists physical mechanisms and processes satisfying these conditions. If however the Laws of Nature are asymmetric with respect to matter and antimatter, there is no need for the Sakhorov conditions to explain the preponderance of matter over antimatter.

If all the three CSTD-equations are to operate simultaneously in the same Universe (there is nothing stopping this occurrence), then, the spherically curved spacetime version of the CSTD-equations, i.e., the case should lead to the production of equal portions of matter and antimatter. This matter-antimatter concoction should annihilate to form radiation i.e., to form a photon bath. The parabolic and hyperbolically curved spacetime version of the CSTD-equations, i.e., the case will lead to the exclusive production of matter with no production of antimatter as the Laws of Nature leading to the production of this matter are asymmetric with respect to matter and antimatter. What is needed for this is T and CT-symmetry violation only. To see this, we provide the reasoning below.

First we must realise that each of the four discrete symmetries C, P, T and S have two states. If all of them where obeyed, then, a shown in Table 2, there would be sixteen types of Electrons. For example, , is one of the states representing a left handed Electron that travels forward in time and has a positive spin. The up-arrow in the bracket indicates that this Electron travels forward in time and likewise a downward arrow would indicate that this Electron travels backwards in time; the arrow of time is a property of the T-opera- tion. The clockwise circular arrow in the bracket indicates a positive spin and likewise, an anticlockwise circular arrow would indicate a negative spin; spin is a property of the S-operation. The subscript-L in indicates a left handed Electron and likewise, a subscript-R indicates a left handed Electron; handedness a property of the P-operation. The superscript in indicates the sign of the electrical charge whether it is positive or negative; charge is a property of the C-operation and all antimatter particle are represented in Table 2 with an over-bar. We are now going to argue that of these sixteen Electrons, the symmetry violations of the CSTD-equations allow only one and only one of the sixteen Electrons to exist.

1) Clearly, T-violation implies that only Electrons moving forward in time will be allowed to exist. This means the eight Electrons [,;,;,;,] under the column with are all ruled out as candidate Electrons in our Universe. Only eight of the sixteen now remain as candidates and these are,;,;,;,. We should note that all the antiparticles appearing in Table 2 have their hand of time in the forward direction; this means that they must have negative energy.

2) S-violation implies that exclusively positive or negative spin Electrons will be allowed in the Universe. This means of the eight candidate Electrons [,;,;,;,], we have to drop four. We shall drop the negative spin Electrons, thus we will remain with only four candidate Electrons and these are,;,.

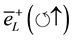
3) P-violation implies that exclusively left or right handed Electrons will be allowed in the Universe. This means of the remaining four candidate Electrons [,;,], we have to drop two. We shall drop the right handed Electrons, thus we will remain with only two candidate Electrons and these are,.

4) Finally, we must realise that of the two remaining Electrons, , one has positive energy while the other has negative energy. Now, for a final answer, we appeal to Professor Richard Phillips Feynman (1918-1988)’s interpretation of antiparticles where instead of antiparticles having negative energy-mass as is the case here, they have positive energy and their hand of time is reversed [22] . With this intepretation, the Electron becomes a positive energy particle if we reverse its hand of time so that it is now given by. This Electron is a CT-symmetric partner to. According to CT-violation of the CSTD-equations, this particle can not exist simultaneously with in the same Universe. This leaves us with just one Electron out a of possible sixteen. Thus, one can safely say that the CSTD-equations lead to the exclusive production of matter while the case will lead to the productive of both matter and antimatter which will annihilate to produce radiation. In short, this can be summarised as follows:

(32)

Clearly, there here is no need for the Sakhorov conditions in-order for there to be a preponderance of matter over antimatter. We do not say nor make the claim that this is “The Solution” to the long-standing problem of the preponderance of matter over antimatter, but that, it is (perhaps) a viable solution worthy of consideration.

4. Conclusions

The present work is to be taken as work in progress toward a Unified Field Theory [17] that would encompass all the Forces of Nature; thus the conclusions we here make are only tentative. Be that it may, our strong feeling is that when the entire work is finally brought to its logical and final conclusion, the present conclusion regarding the CSTD-equations will still hold; thus, assuming the correctness or acceptability of the ideas presented herein, we hereby make the following conclusion (tentative):

1) The parabolic and hyperbolically curved spacetime components of Lorentz invariant CSTD-equations [3] uphold C, PT and CPT-Symmetries, and these same equations readily violate P, T, CP and CT-Symmetries.

2) If the Lorentz invariant CSTD-equations are to explain the prepondarance of matter over antimatter, then, photons are to be thought of as obeying the flat CSTD-equations i.e., the CSTD-equations for which, while ordinary matter is to be explained by the parabolic and hyperbolically curved spacetime versions of this set of equations.

Acknowledgements

We are grateful to the National University of Science & Technology (NUST)’s Research & Innovation Department and Research Board for their unremitting support rendered toward our research endeavours; of particular mention, Prof. Dr. Mundy, Dr. P. Makoni and Prof. Dr. Y. S. Naiks unwavering support. This paper is dedicated to my mother Setmore Nyambuya and to the memory of departed father Nicholas Nyambuya (1947-1999).

Cite this paper

Golden GadzirayiNyambuya, (2015) On the Preponderance of Matter over Antimatter. Journal of Modern Physics,06,1441-1451. doi: 10.4236/jmp.2015.611148

References

NOTES

¹In Equation (1) above, the term must be treated as a single object with one index. This is what this object is. One can set. The problem with this setting (i.e.) is that we need to have the objects, and, clearly visible in our Curved Spacetime Dirac Equation (5). This issue of why we need the term appearing with the double-m index is well explained in [3] .

²By spherically curved, it here is not meant that the metric has no off diagonal terms. On the same footing, by parabolically curved spacetime, it meant that metric has positive off diagonal terms and likewise, a hyperbolically curved spacetime, it meant that metric has negative off diagonal terms.

³European Organization for Nuclear Research (CERN) is located at the France-Swiss border near Geneva Swirtherland.