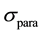Journal of Modern Physics
Vol.05 No.17(2014), Article ID:51419,7 pages
10.4236/jmp.2014.517179
Numerical Investigation of a UCN Source Based on Solid Deuterium by Combining a Simulation Code with an Analytical Approach
Habib Mohammadi1, Mohammad Mehdi Firoozabadi1, Rouhollah Gheisari2
1Department of Physics, University of Birjand, Birjand, Iran
2Physics Department, Persian Gulf University, Bushehr, Iran
Email: mohammadi@birjand.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 September 2014; revised 8 October 2014; accepted 5 November 2014
ABSTRACT
At thermal ultra-cold neutron (UCN) sources (neutrons in thermal equilibrium with the moderator) only a very small fraction of neutrons have velocities ~6 m/s. Therefore, the UCN production rate cannot be substantially increased by simply lowering the temperature of the moderator. The new approach is to use the super-thermal principle, i.e., neutrons not in thermal equilibrium with the converter. We want to investigate scattering kernels for a super-thermal UCN source based on a two-layer arrangement of D2O and solid D2. The solid D2 (sD2) at temperature 8 K is kept in close contact with D2O moderator at room temperature. Using the MCNP code, the fast neutron flux on the spallation target, the thermal flux in the D2O near the sD2, and the cold flux in the sD2 are simulated. For a given cold flux, neutron transport equations are calculated. In order to obtain precise neutron scattering kernels, and consequently UCN flux and density, 330 neutron energy groups have been taken. The coupled energy dependent transport equations have been solved by combining MCNPX code with an analytical approach and using implicit method in MATLAB. We have obtained an optimal dimension for the UCN source. A suitable space step has been taken for the numerical stability.
Keywords:
Two-Layer UCN Source Based on D2O/sD2, Scattering Kernel, Monte Carlo Method, Implicit Method, Super-Thermal Principle

1. Introduction
Ultra-cold neutron (UCN) can be used in fundamental physics experiments, such as neutron electric dipole moment and life-time measurements, which require low velocities and long interaction and observation times [1] [2] . The accuracy of such measurements is limited mainly by statistics [3] , and significantly higher UCN densities will allow more tests of the standard model. Several projects have the goal to build new UCN sources in order to provide the required increase in UCN density and flux. Two main source types having the potential to produce substantially higher UCN densities, are based on using either super-fluid helium [4] - [7] or solid deuterium (sD2) to down scatter cold neutrons [8] [9] . Basic research to produce experimental UCN converters was done by using D2, O2, and CD4 [10] [11] . These converters reduce the speed of the cold neutron (CN) to that of UCN. The research works have shown that deuterium can be used in different states of gas, liquid, and solid. The sD2 has more applicants [12] [13] . In UCN sources, CN neutrons have a mean energy of ~meV. Considerable fractions of these neutrons slow down to ~neV. We have the goal to study UCN density and flux of a UCN source based on a two-layer arrangement of D2O and sD2 by combining MCNPX2.4.0 code with an analytical approach. In Section 2, mathematical tools are presented. The CN flux in the sD2 is simulated with MCNPX code. This result for the CN flux is then used as boundary condition to calculate the UCN flux and density. The results and discussion are presented in Section 3. Finally, the summary and conclusions are given in Section 4.
2. Material and Methods
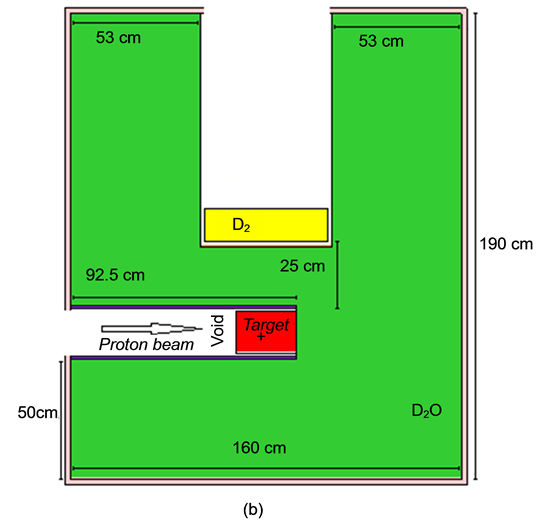
A scheme of the UCN source under consideration is shown in Figure 1. Fast neutrons are produced by a proton beam hitting spallation target. In the heavy water (D2O) moderator at room temperature, the mean kinetic energy of fast neutrons (spallation neutrons) is reduced, and consequently thermal neutrons are produced. Some of the thermal neutrons are cooled and eventually converted to UCN (inside the sD2). In Table 1, the proton beam and spallation target parameters have been given as well as UCN source geometry factors, and materials. The sD2 must be almost pure, to reduce up-scattering on para-D2. Here the sD2 layer, with a number density of 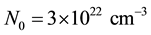 and a high ortho-concentration
and a high ortho-concentration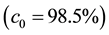 , is considered at temperature of T = 8 K to prevent the dispersion of each UCN. Using the MCNPX code, the fast neutron flux on the target, the thermal
, is considered at temperature of T = 8 K to prevent the dispersion of each UCN. Using the MCNPX code, the fast neutron flux on the target, the thermal
Figure 1. (a) Schematic drawing of a UCN two-layer arrangement of D2O/sD2. The incoming fast neutrons (spallation neutrons) are thermalized in the D2O moderator. The thermal neutrons are being transported throughout the sD2 layer, until large fractions of these neutrons are cooled at d = 4 cm. The cold neutrons (CN) are converted to UCN everywhere in the sD2. x denotes one-dimensional position; (b) Geometric description of the UCN setup used in the MC calculations.
Table 1. Main description of proton beam, spallation target, UCN source geometry, and material.
aThe optimized length and the corresponding volume (see Table 3); bThe inner and outer side walls have been made from Zr and Steel, respectively. Here Steel material contains 72% 56Fe, 18% 52Cr, 8% 58Ni, and 2% 55Mn; cThe thicknesses of the inner side outer side walls equal 0.05 and 0.3 mm, respectively.
flux in the heavy water near the sD2, and the CN flux in the sD2 are simulated. Cold and thermal neutrons are being transported throughout sD2 and UCN are being produced everywhere in the sD2. The CN flux increases (versus position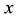 ) and reaches a maximum value at
) and reaches a maximum value at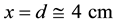 . We assume that these processes can be treated as one-dimension. The CN flux values at
. We assume that these processes can be treated as one-dimension. The CN flux values at 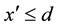 are used as boundary conditions. We may write the neutron transport equation as follow.
are used as boundary conditions. We may write the neutron transport equation as follow.
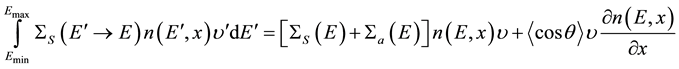 (1)
(1)
The scattering kernel
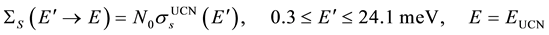 (2)
(2)
Is considered for CN neutrons which are directly converted to UCN. We use
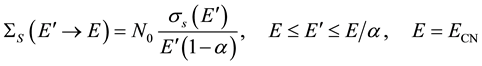 (3)
(3)
For description of CN neutrons which slow down and don't fall below about 0.1 meV. The definitions of the symbols used in Equations (1)-(3) are:
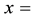 position of CN or UCN in sD2
position of CN or UCN in sD2
 scattering kernel
scattering kernel
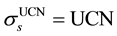 production cross-section
production cross-section
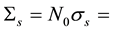 macroscopic scattering cross-section
macroscopic scattering cross-section
 macroscopic absorption cross-section
macroscopic absorption cross-section
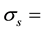
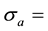
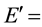
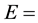
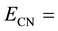


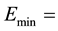
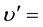
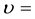
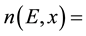
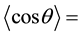
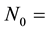
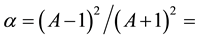
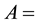
When a neutron has low energy, scattering occurs by means of 
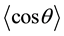
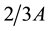
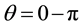
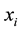
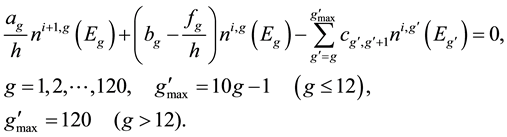
Substituting Equation (2) into Equation (1) and after discretization we obtain the following algebraic equations.

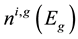
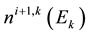
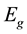
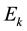
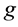
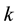
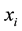
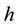
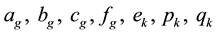
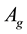
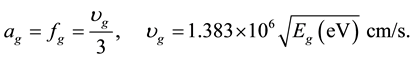

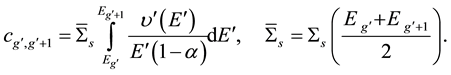
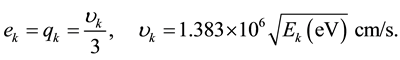
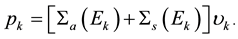
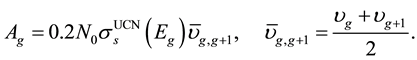
For solving Equations (4) and (5) we take the energy difference between each two neighboring energy groups as
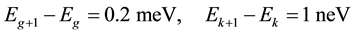
The boundary condition is as follow:

The 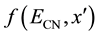
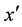

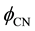
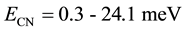
3. Results and Discussion
We have considered a UCN two-layer source of D2O/sD2 and calculated its UCN yield. In the D2O moderator the incoming fast neutrons (spallation neutrons) slow down to thermal region at room temperature. They decelerate in the sD2 fairly and have a velocity distribution in the energy range of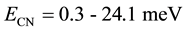
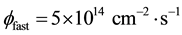
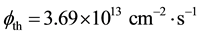
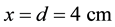
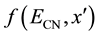

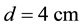
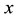
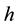
Table 2. The simulation results of the neutron flux (cm−2・s−1).
aThe fast flux on the spallation target is 5 × 1014 cm−2・s−1. The fast flux, the thermal flux, and the cold flux in the D2O near the sD2 approximately equal to 2.12 × 1011, 3.69 × 1013 and 1.73 × 1013 cm−2・s−1, respectively.
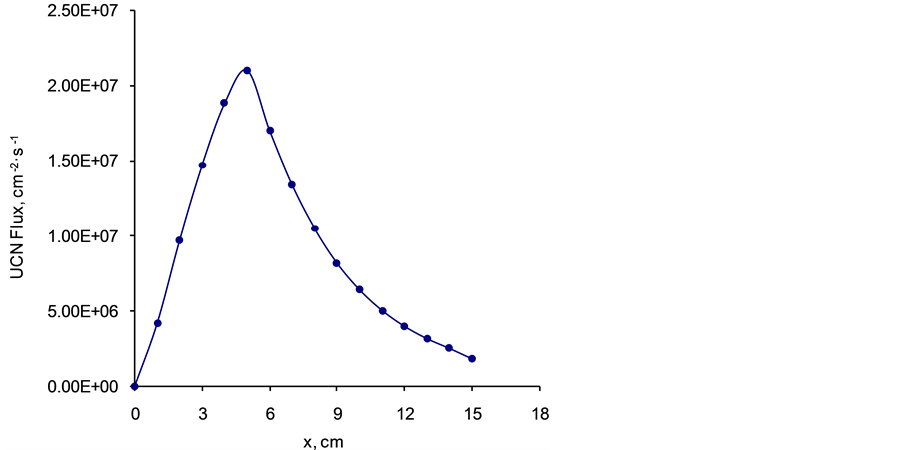
Figure 2. UCN flux versus thickness x of the sD2 (see Figure 1(a)). The curve reaches to a maximum at x = 4.3 cm. Data points represent UCNs in the energy range of 40 - 250 neV.
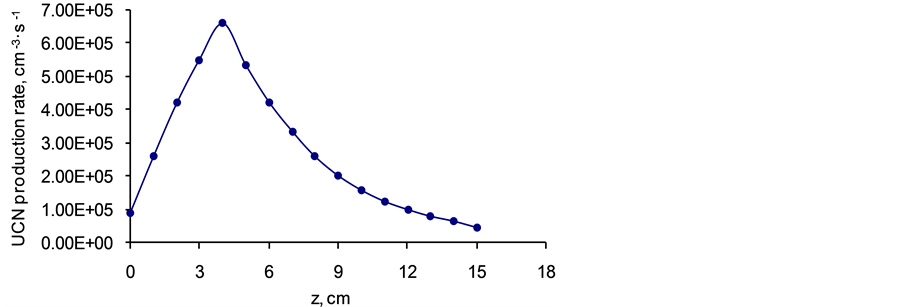
Figure 3. UCN production rate versus thickness x of the sD2 (see Figure 1(a)). The curve reaches to a maximum at x ≈ 4 cm. Data points repre- sent UCNs in the energy range of 40 - 250 neV.
4. Summary and Conclusions
In the present work, a UCN source based on D2O/sD2 has been studied. The sD2 at 8 K is kept in close contact with the D2O moderator at room temperature. The sD2 layer, with a number density of 
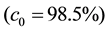
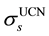
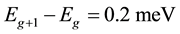
Table 3. The numerical results of average UCN flux, density and production in the sD2a.
aThe calculations have been performed without taking temperature increase; bAt PSI, the UCN production rate is expected to be 2.9 × 105 cm−3・s−1. The volume of sD2 is disk shaped (with 27 liters in volume and 50 cm in diameter) [20] [21] .
tioning that this value is smaller than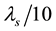

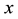
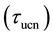
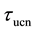
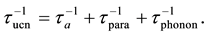
Here, 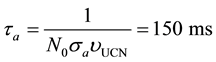
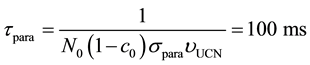
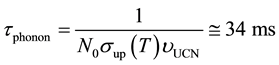
and 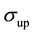
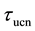

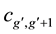
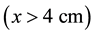
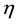
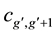
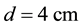
Acknowledgements
The authors wish to thank Birjand University, Birjand, Iran, for their support.
References
- Ignatovich, V.K. (1990) Ultracold Neutrons. Clarendon Press, Oxford.
- Golub, R., Richardson, D.J. and Lamoreaux, S.K. (1991) Ultra-Cold Neutrons. Hilger, Bristol.
- Steyerl, A., et al. (1986) Physics Letters A, 116, 347. http://dx.doi.org/10.1016/0375-9601(86)90587-6
- Golub, R. and Pendlebury, J.M. (1977) Physics Letters A, 62, 337. http://dx.doi.org/10.1016/0375-9601(77)90434-0
- Brome, C.R., Butterworth, J.S., Dzhosyuk, S.N., Mattoni, C.E.H., McKinsey, D.N., et al. (2001) Physical Review C, 63, Article ID: 055502. http://dx.doi.org/10.1103/PhysRevC.63.055502
- Masuda, Y., Kitagaki, T., Hatanaka, K., Higuchi, M., Ishimoto, S., et al. (2002) Physical Review Letters, 89, Article ID: 284801. http://dx.doi.org/10.1103/PhysRevLett.89.284801
- Zimmer, O., Baumann, K., Fertl, M., Franke, B., Mironov, S., et al. (2007) Physical Review Letters, 99, Article ID: 104801. http://dx.doi.org/10.1103/PhysRevLett.99.104801
- Serebrov, A.P. (2000) Nuclear Instruments and Methods in Physics Research Section A, 440, 653. http://dx.doi.org/10.1016/S0168-9002(99)01057-8
- Saunders, A., Anaya, J.M., Bowles, T.J., Filippone, B.W., Geltenbort, P., et al. (2004) Physics Letters B, 593, 55. http://dx.doi.org/10.1016/j.physletb.2004.04.048
- Atchison, F., Blau, B., Bodek, K., Van den Brandt, B., Brys, T., et al. (2009) Nuclear Instruments and Methods in Physics Research Section A, 611, 252. http://dx.doi.org/10.1016/j.nima.2009.07.072
- Frei, A., Gutsmiedl, E., Morkel, C., Muller, A.R., Paul, S. and Urban, M. (2009) Physical Review B, 80, Article ID: 064301. http://dx.doi.org/10.1103/PhysRevB.80.064301
- Atchsion, F., Blau, B., Bodek, K., Van den Brandt, B., Brys, T. and Fierlinger, P. (2007) Physical Review Letters, 99, Article ID: 262502. http://dx.doi.org/10.1103/PhysRevLett.99.262502
- Altarev, I., Daum, M., Frei, A., Gutsmiedl, E., Hampel, G., Hartmann, F.J., et al. (2008) The European Physical Journal A, 37, 9-14. http://dx.doi.org/10.1140/epja/i2008-10604-8
- Sekimoto, H. (2007) Nuclear Reactor Theory. Tokyo Institute of Technology Press, Tokyo.
- Atchsion, F., Blau, B., Bodek, K., Van den Brandt, B., Brys, T., Fierlinger, P., et al. (2005) Physical Review Letters, 95, Article ID: 182502. http://dx.doi.org/10.1103/PhysRevLett.95.182502
- MacFarlane, R.E. and Muir, D.W. (1994) The NJOY Nuclear Data Processing Systems Version 91, LA-12740-M. Los Alamos National Laboratory, Los Alamos.
- Kasprzak, M. (2004) Thermal Up-Scattering of Very Cold and Ultra-Cold Neutrons in Solid Deuterium. Master’s Thesis, Jagiellonian University Press, Krakow.
- Frei, A., Gutsmiedl, E., Morkel, C., Muller, A.R., Paul, S., Rols, S., et al. (2010) Europhysics Letters, 92, Article ID: 62001. http://dx.doi.org/10.1209/0295-5075/92/62001
- Kasprzak, M. (2008) Ultra-Cold Neutron Converters. Ph.D. Thesis, University of Vienna, Vienna.
- Atchsion, F., Van den Brandt, B., Brys, T., Fierlinger, P., Hautle, P., Henneck, R., et al. (2005) Physical Review C, 71, Article ID: 054601. http://dx.doi.org/10.1103/PhysRevC.71.054601
- The PSI UCN Website: http://ucn.web.psi.ch/
- Atchison, F. (2002) Internal Report, TM-14-02-02, Part I and II.