Journal of Modern Physics
Vol.06 No.03(2015), Article ID:54197,12 pages
10.4236/jmp.2015.63024
Gas-Dust Protoplanetary Disc: Modeling Collisional Interaction of Primordial Bodies
M. Ya. Marov, A. V. Rusol
Vernadsky Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, Moscow, Russia
Email: marovmail@yandex.ru, fermata@inbox.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2015; accepted 16 February 2015; published 25 February 2015
ABSTRACT
One of the key problems in the concept of planetary systems origin and early evolution is solid bodies formation in the protoplanetary gas-dust disc around young stars. Dust particles interactions inside the original fluffy dust clusters of fractal nature resulted from gravitational instability and fragmentation in the disc’s central plane areassumed as the most plausible mechanism of primary bodies set up owing to particles integration within the clusters. Follow upcollisions are regarded to be responsible for eventual growth of primary bodies to the size of planetesimals. We discuss this scenario including chemical nature of particles depending on the disc’s radial temperature distribution and phase transitions. The mathematical model is developed based on the method of penetrating particles with the account for internal structure/properties of bodies involved, complicated patterns of their interaction, and phenomenological approach to describe energy distribution in the contact zone. The model is mainly addressed to the stage of formed solid bodies collisions. The results of numerical evaluation of the model are described involving some constraints for complete or partial destruction of colliding bodies followed by either scattering of collisional fragments orpartial back accumulation.
Keywords:
Planetary System, Origin, Evolution, Protoplanetary Disc, Fluffy Cluster, Permeable Particles, Numerical Modeling, Collision, Icy-Stone Body

1. Introduction
Study of planetary systems origin and early evolution is a key fundamental problem of the modern astrophysics. It is rooted in accretion discs formation around single, close binary and even multiple stars. The great progress in the field was accomplished for the last decades due to ground based and space observations that allowed us to trace disc structure, composition and properties at the different stages of evolution [1] . However, we still have very limited knowledge about the physical processes responsible for growth of bodies of progressively larger size from an original gas-dust matter of the accretion discs resulting in planetesimals set up with the focus placed especially on young solar type stars. Mathematical models developed to describe the process are mostly speculative because are not supported and verified by the data of observations. Basically, the models proceed from an idea of successive growth of solid particles due to simply their collisional interactions in the disc matter since the very beginning although such a scenario is poorly justified. Moreover, it contradicts to the laboratory experiments of particle collisions under rather high velocities which are assumed to occur in the real conditions. From the physical viewpoint, mechanism of collisional interaction of original dust clusters resulted from gravitational instability and fragmentation of subdisk in the disc central plane seems more justified [2] [3] . Particles growth inside fluffy dust clusters of fractal nature is addressed as more feasible process giving rise eventually to original asteroid-size bodies [4] [5] . Anyway, physical mechanism of particle interactions is a key to ensure the follow up processes of primordial bodies and ultimately planets formation.
2. Gas-Dust Protoplanetary Disc Evolution
The entire set of observations for young solar-type stars has confirmed two facts that were previously only reasonable theoretical assumptions: the Sun and its surrounding protoplanetary gas-dust disk were formed jointly from a single mass in a single process and the process of planetary formation begins in this gas-dust disk. In this section we will follow the basic concepts developed in [3] .
The solar system is currently believed to have formed through the gravitational collapse of a dense fragment (core) of an interstellar molecular cloud with a density
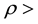 10 - 20 g・cm−3, a temperature T~10 K, a mass larger than the solar one by 10% - 30%, and a dust mass fraction of ~1% [6] . The collapse gave rise to a single protostar surrounded by a gas-dust disk of the axisymmetric and flattened shape whose evolution ended with the ultimate formation of a planetary system. All of the events from the onset of star formation in the molecular cloud to the formation of giant planets in the protoplanetary gas-dust disk fit in a time interval of ~10 Myr. The latter is confirmed by observations of young stars, including those with massive planets. Given the age of the oldest meteoritic material (CAIs) known from radioisotopic studies, the age of the solar system is 4.57 Gyr [7] [8] . Note that the age of the Moon’s oldest anorthosite rocks and the Earth’s zircons is only slightly younger and is estimated to be ~4.4 Gyr [9] .
10 - 20 g・cm−3, a temperature T~10 K, a mass larger than the solar one by 10% - 30%, and a dust mass fraction of ~1% [6] . The collapse gave rise to a single protostar surrounded by a gas-dust disk of the axisymmetric and flattened shape whose evolution ended with the ultimate formation of a planetary system. All of the events from the onset of star formation in the molecular cloud to the formation of giant planets in the protoplanetary gas-dust disk fit in a time interval of ~10 Myr. The latter is confirmed by observations of young stars, including those with massive planets. Given the age of the oldest meteoritic material (CAIs) known from radioisotopic studies, the age of the solar system is 4.57 Gyr [7] [8] . Note that the age of the Moon’s oldest anorthosite rocks and the Earth’s zircons is only slightly younger and is estimated to be ~4.4 Gyr [9] .
The circumsolar gas-dust disk was 98% molecular hydrogen and helium by mass in the ratio 70.5%:27.5%, which corresponds to a ratio of ~10:1 by the number of particles, while 2% were accounted for by the remaining elements and compounds, including the hydrogen compounds. Some of them were also in the gaseous state (from 0.5% to 1.5%, depending on the temperature), while others were in the form of ices (from 1.5% to 0.5%, respectively). The constraints on the initial angular momentum of the circumsolar protoplanetary disk J with allowance made for the physical processes at the early evolutionary stage of the solar system and for the chemical and isotopic compositions of chondrites lead to
 g・cm2・s?1 [10] -[13] .
g・cm2・s?1 [10] -[13] .
The disk around the protostar and the accretion of gas from the disk onto the protostarsatisfying the spectroscopicobservational data give a disk mass estimate of
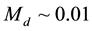 - 0.5 MS (MS is the present-day solar mass); the range
- 0.5 MS (MS is the present-day solar mass); the range
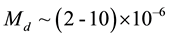 MS/yr was obtained for the mass flux from the envelope onto the disk (the total accretion mass flux). This corresponds to the accretion time scale for a solar-mass protostellar object
MS/yr was obtained for the mass flux from the envelope onto the disk (the total accretion mass flux). This corresponds to the accretion time scale for a solar-mass protostellar object
 yr [14] [15] .
yr [14] [15] .
Analysis of the spectral energy distribution for the disks and high-resolution observations of the thermal radiation in the millimeter wavelength range around T Tauri stars (variable stars with a mass
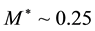 - 11 МS surrounded by accretion gas-dust disks and exhibiting irregular brightness variations) show that the bulk of the matter is concentrated in an inner region with a radius of ~40 AU [16] . The Sun passed through such a stage at its early evolution. Gas-dust disks have been discovered around most of the observed T Tauri stars with ages £106 yr and around ~20% - 30% of the stars with ages £107 yr [16] [17] with a mean lifetime of 3 - 6 Myr [18] . These disks were probable precursors of planetary systems. In addition, scattered-light observations and spectroscopic data in a wide wavelength range show that the dust particle sizes in the disks reach 0.1 - 1 cm, which are much larger the interstellar ones [19] [20] . This may be indicative of the initial particles’ integration in the disks.
- 11 МS surrounded by accretion gas-dust disks and exhibiting irregular brightness variations) show that the bulk of the matter is concentrated in an inner region with a radius of ~40 AU [16] . The Sun passed through such a stage at its early evolution. Gas-dust disks have been discovered around most of the observed T Tauri stars with ages £106 yr and around ~20% - 30% of the stars with ages £107 yr [16] [17] with a mean lifetime of 3 - 6 Myr [18] . These disks were probable precursors of planetary systems. In addition, scattered-light observations and spectroscopic data in a wide wavelength range show that the dust particle sizes in the disks reach 0.1 - 1 cm, which are much larger the interstellar ones [19] [20] . This may be indicative of the initial particles’ integration in the disks.
The most adequate theoretical model for the dissipation of the disks surrounding young stars is the combination of viscous evolution and photoevaporation of the disk [16] [21] . At the stage of viscous evolution lasting several million years, the bulk of the turbulent gas together with dust falls onto the central star, while the gas on the disk periphery together with fine dust moves outward in view of the angular momentum conservation. However, this process, which reduces considerably the disk mass, cannot dissipate it completely but facilitates the photoevaporation of disk material under intense ultraviolet radiation from the young star. The photoevaporation mechanism can provide the removal of gas from the disk as the dissipation of the disk as a whole in a time interval <1 Myr.
The estimates of the temperature and pressure and their radial distributions are the most important information in constructing and verifying cosmochemical numerical models for the structure of the circumsolar protoplanetary gas-dust disk at various stages of its evolution. In contrast to the “cold” accumulation of solar system bodies we proceed from the “hot” protoplanetary disk model that is based on the accumulated experimental data on the discrepancy between the abundances of many elements on the Sun, in undifferentiated meteorites [3] . In particular, it was established that all chondrites (except CI) and our planet are depleted in moderately volatile (Na, K, Rb, Sn, etc.) and highly volatile (Cs, Pb, etc.) elements relative to the solar abundances coincident with their abundances in carbonaceous CI chondrites [22] . The depletion is most pronounced for such elements as Bi, Cd, Cs, Hg, In, Pb, Se, Te, Tl, Zn, S, etc. [23] . Subsequently, the depletion in these elements was found to be typical not only for various types of chondrites but also for the bulk composition of the terrestrial planets and some large planetesimals (for example, the parent bodies of eucrites). Hence it was concluded that the differentiation of moderately and highly volatile elements was an important large-scale process at the early evolutionary stages of the solar nebula and the protoplanetary disk.
Evidently, the higher the volatility of an element, the greater the depletion. Thermodynamic calculations [24] [25] showed that temperatures of no lower than 1200 - 900 K are required in both partial evaporation and incomplete condensation of the primordial matter of planets and the parent bodies of chondrites. However, the fractional evaporation mechanism has found neither theoretical nor experimental confirmation [3] . The condensation mechanism for the differentiation of moderately and highly volatile elements accompanied by their incomplete accumulation in the protomatter of planets and the parent bodies of chondrites seems more justified. Indeed, for most elements, there is a clear correlation between the degree of depletion and the temperature of its condensation (50%) from a solar-composition gas [26] . It is most likely attributable to the influence of the kinetic constraints on the heterogeneous reactions in a gas-solid system associated with the reduction of the reaction surface of small dust particles during their accumulation and some other factors [27] . The above arguments lead us to conclude that, first, much of the chondritic material formed through the condensation of the gas phase of the protoplanetary disk and, second, the maximum temperatures in the circumsolar disk in the formation zone of the chondritic material (r~2 - 3.5 AU) reached Т~1200 - 900 K.
Apart from mineral phases containing moderately volatile elements, there are crystalline Mg- and Fe-bearing silicates in the material of chondrites, although a significant fraction of them were modified by secondary processes in the parent bodies. The crystalline Fe-Mg silicates most likely form in high-temperature processes in the envelopes of giant stars of some classes [28] . However, subsequently, they are subjected to decrystallization under the influence of various external factors [29] and, therefore, the silicates in the interstellar medium [30] and diffuse and dense molecular clouds are also in an amorphous form [31] [32] . They enter into the composition of dust (d £ 0.1 μm) made up mainly of amorphous olivine (85%) and pyroxene (15%) in a ratio Fe/Mg » 1. Observations of protoplanetary disks around T Tauri stars showed that the silicate dust grains in them are larger in size than those in molecular clouds, d~2 µm [33] and incorporate a mixture of amorphous and crystalline silicates [34] [35] .
Thus, the available data on the presence of crystalline silicates in various cosmochemical objects lead to the conclusion that the temperature in the protoplanetary disk at r £ 1 - 1.5 AU reached ~1500 - 1300 K. However, the material of chondrites also contains evidence that there were higher temperatures in the circumsolar disk as well. This is suggested by the refractory CAIs, whose sizes vary between several microns and several centimeters. They account for 0.1 - 13 vol.% of the chondritic material [36] . The inclusions are enriched in the most refractory elements (such as Са and Al as well as the rare Hf, Sc, Lu, etc.). It is these elements that enter into the composition of the first condensed phases forming when a solar-composition gas cools down. Experimental studies [37] and thermodynamic simulations [38] suggest that CAIs are the earliest condensate formed near the Sun (r < 0.5 AU) at Т~2000 - 1700 K and partially carried outward through the radial drift up to the formation zone of the parent bodies of chondrites.
The above estimates have been supported by the numerical modeling based on the developed theoretical approach rooted in heterogeneous mechanics and the improved technique of simulation of a multiphase multicomponent turbulent mediumin differentially rotating disc matter with allowance made for the inertial properties of the polydisperse admixture of solid particles, coagulation, and radiation [39] - [41] . This allowed us to calculate the radial temperature and pressure distributions in the circumsolar protoplanetary disk at the successive stages of its evolution, including the period of the dust layer (subdisk) formation and evolution in the disk midplane. The overall pattern of change of the temperature conditions in the protoplanetary disk in the course of its evolution was evaluated: initially, the gas and dust gradually cooled down; subsequently, as the dust particles settled and the dust layer became denser, the subdisk could be heated during the formation of dust clumps, provided that the particles were sufficiently small. At the end of the first evolutionary stage of the protoplanetary disk, the maximum temperature, pressure, and density were reached in it. These largely determined the composition of the planetary bodies formed at the second stage. In the Earth’s formation region (at r ≈ 1 AU), the temperature in the disk midplane (after the subdisk formation) gradually decreased from the condensation temperature of magnesia silicates and iron (³1400 K) to 700 - 500 K. In the succeeding period, the temperature in the disk (above the subdisk) continued to decrease due to the settling of dust, but it could also slightly rise inside the subdisk as it contracted until the formation of dust clumps.
Therefore, as follows from the calculated models, the probable temperatures of the Earth’s protomatter at this stage were between 300 and 500 K. Consequently, no carbonaceous CI chondrites dominated of hydrosilicates could be formed in this region. Indeed, since the temperature in this zone of the protoplanetary disk was above the H2O ice condensation temperature, the solid particles and bodies could not accumulate water. As a result, the vast bulk of the Earth’s (and Venus’s and Mars’) protomatter had a reduced composition. No hydrosilicates could be formed in gas-solid reactions due to the low partial water vapor pressure in the protoplanetary disk with a protosolar (nearly solar) composition. Therefore, the solid phase could not contain water or water-containing compounds similar to those observed in carbonaceous chondrites. In other words, the volatile and moderately volatile components were deficient in the iner regions of the solar system. According to the models developed [42] [43] the bulk of Earth’s ad terrestrial planets water was obtained later on through migration of volatile-rich objects (comets ad asteroids) from the outer regions of the solar system, mainly from its outskirt in the Kuiper belt, which was responsible for heterogeneous accretion of these planets mostly during period of the Late Heavy Bombardment (LHB).
Subsequent evolution of dust clumps formed in dense dust layer of the compacted subdisc as a result of its gravitational instability are assumed to involve the follow up clumps contraction accompanied by coagulation and coalescence (stiking together) of populated particles during mutual collisions. Collisions used to be regarded responsible for the eventual growth of larger bodies (up to planet embryos) from primary (pertinent to nebula) and secondary (condensed) dust particles. However, the experimental data do not confirm the possibility of such growth in the collisional processes for bodies in the range of sizes from 1 - 10 cm to 100 m, because neither the surface forces nor the gravitational ones are efficient in this range. It is worth to note that dust clustering can be enforced in turbulent eddies attributable to the emergence of order in a turbulent medium [41] . Anyway, direct collisional integration of relatively large particles under moderate velocities seems less probable than mechanism of collective interaction of original fluffy clusters, basically of fractal structure [2] [4] . In general, individual interaction of dust particles within colliding clusters, as well as interaction of particles with the surrounding gas in the subdisc are required.
As our study showed [3] [41] , at the earliest evolutionary stage of the protoplanetary disk, submicron and micron-size particles (of an interstellar origin) could stick together under the action of surface forces at collision velocities Vc < 1 m/s to form very porous fluffy dust aggregates with a fractal dimension Df ≈ 1.4 - 1.9. During the collisions of such aggregates with sizes d ~ 10 - 100 µm, they can stick together at Vc £ 0.2 m/s and are destroyed at Vc ³ 1 m/s. When the sizes of the aggregates reach d ~ 1 cm, they are compacted (Df approaches 3), turning into compact particles. For bodies with d ~ 1 - 10 cm, sticking turned out to be possible only during collisions with velocities Vc < 1 cm/s, under additional assumptions, for example, in the case of frost-coated surfaces [44] . At higher velocities, the collisions of aggregates between themselves or with individual small particles can lead to their sticking due to the dissipation of energy through compaction [45] . Once compaction has given rise to fairly dense (though porous) particles with a fractal dimension Df ≈ 3, the resource of further energy dissipation during collisions turns out to be exhausted and initially the loss of the individual particles constituting an aggregate and subsequently its complete destruction and fragmentation begins [46] [47] .
On the whole, the experimental and theoretical results on the sticking of particles in the protoplanetary disk suggest that the sticking probability decreases
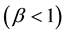 when the particle sizes become larger than d~0.1 - 1 cm, while this probability approaches zero
when the particle sizes become larger than d~0.1 - 1 cm, while this probability approaches zero
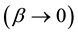 as the sizes increase to
as the sizes increase to
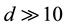 cm. Thus, bodies with sizes d ³ 1 - 10 cm similar in size to pebbles or cobblestones are formed. A further growth of such bodies beyond the range d~0.1 - 1 m during collisions through the surface forces is unlikely to be possible. Therefore, one should not expect that the coalescence of particles during their collisions could give rise to large boulders with sizes d~ 1 - 10 m [48] [49] . At such size and velocity scales, the surface molecular forces no longer work, while the self-gravity is not yet efficient due to the smallness of these bodies. It is well known that only bodies with sizes larger than 0.1 - 1 km can keep smaller bodies and particles on their surface through their self-gravity [50] - [54] .
cm. Thus, bodies with sizes d ³ 1 - 10 cm similar in size to pebbles or cobblestones are formed. A further growth of such bodies beyond the range d~0.1 - 1 m during collisions through the surface forces is unlikely to be possible. Therefore, one should not expect that the coalescence of particles during their collisions could give rise to large boulders with sizes d~ 1 - 10 m [48] [49] . At such size and velocity scales, the surface molecular forces no longer work, while the self-gravity is not yet efficient due to the smallness of these bodies. It is well known that only bodies with sizes larger than 0.1 - 1 km can keep smaller bodies and particles on their surface through their self-gravity [50] - [54] .
Yet another important argument against the formation of planetesimals through a direct growth during pair collisions of particles is the rapid drift of bodies toward the Sun as a result of the angular momentum loss during their deceleration by the gas. The deceleration occurs due to the slightly higher revolution velocity of the bodies around the Sun than that of the gas (because the force of attraction of the gas to the Sun is weakened by the radial gas pressure gradient). Bodies with d~1 m have the highest drift velocity toward the Sun; as a result, they approach the Sun from the radial distance r = 1 AU in a time interval, ~100 yr, that is very short compared to the hypothetical time of their coalescence into planetesimals.
We may conclude that collisional interaction of fractal fluffy clusters should be addressed as the most probable and realistic mechanism of the particle original integration and follow up growth to larger size bodies. Nonetheless, it is paramount to consider physical processes of interaction of bodies in rather wide range of the parameters involved, which is addressed as unavoidable mechanism of solid bodies collisions at the follow up stages of a protoplanetary disk evolution. In the following sections we will deal with this mechanism based on the developed model and analysis of the results of its numerical evaluation.
3. Prerequisite of the Collisions Modeling
Before you begin to format your paper, first write and save the content as a separate text file. Keep your text and graphic files separate until after the text has been formatted and styled. Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads―the template will do that for you.
Basically, for more or less adequate description of primary objects behavior in the protoplanetary nebula methods of either continuous mechanics or molecular dynamics can be utilized. The former one when applied to assemble of bodies of complicated structure requires their properties to be averaged over some volumes that prevent to investigate local processes for which composed particles are responsible. The method of molecular dynamics dealing with particle interactions seems more appropriate though some modifications are necessary in specific applications.
A few methods of modeling particle dynamics in a gas-dust medium depending on the mode of their interaction at the collisions are known. Two models are usually applied: either method of molecular dynamics when elastic particles interact in one point, or method of “hydrodynamics of smoothed particles” with averaging their properties in the contact zone. Based on the pattern of interacting forces, three computational models, sometimes referred to as classical ones, are possible:
・ Particle-Particle (PP);
・ Particle-Mesh (PM);
・ Particle-Particle-Particle-Mesh (P3M).
PP model is the simplest approach of particles interaction in terms of modeling when pair interactions for all particles are calculated based on the known particles distribution. This approach results, however, to significant loss of computing time when dealing with large massive of particles, with some exception only for short-acting particles interaction forces.
PM model uses both the field equation for the total potential of particles system and a single particle behavior in the field. This approach allows us to decrease significantly time calculation of forces acting on a particle though less accurately than in the PP model. Another disadvantage of the РМ model is that when introducing the total potential one need to utilize more detailed grid in order to investigate local behavior of particles.
P3M model allows us to integrate advantages of both РР and РM models and to simulate large particle systems with far-acting forces because based on this approach splitting of acting forces into two parts is possible: non-zero short-acting ones on characteristic distances between particles, and far-acting ones correctly repre- sented by the grid itself.
Unfortunately, for the case under consideration the above models of particles interaction are not quite appropriate. Indeed, an accurate evaluation of the processes in contact zone of particles interaction requires the solution of complicated contact problem taking into account both geometrical and physical non-linearity. When dealing with interactions of many ten thousands particles such an approach seems unfeasible and even hardly justified. This is why more relevant approach has been suggested―the so called method of permeable particles representing modification of the known method of particles in molecular dynamics [55] . Its advantage is in the capacity to provide interaction of colliding bodies depending on their internal structure involving properties of forming particles and collision’s velocity which gives rise to complete or partial destruction of one or both objects followed by either fragments scattering, or by their full or partial inverse accumulation into single body. Structure properties of the bodies, such as their densities, rate of differentiation and density distribution in depth depending on the composed particles characteristics, as well as relative velocities bodies in space are introduced as entry parameters of the model.
In the method of permeable particles processes of energy re-distribution in the contact zone should be taken into account. Because of complexity of the process some approximation are to be used in order to minimize the computing procedure when dealing with many particles. Let us note that this method is regarded as the most adequate in the study of the above mentioned fluffy dust clusters when mutual penetration of particles in some depth occurs resulting in the new particle bounds and dust aggregates of different fractal dimensions.
In our study, modeling bodies were represented as one or several sets of N particles of the different physical properties underlined by the above discussed chemical nature and they are either localized in a multilayer object or chaotically distributed over the given volume. Besides, internal structure and energy redistribution in the contact zone is taken into account, as well as the fact that in contrast to point contact of rigid particles, the topology of close package of balls possesses a porosity and dispersion of their diameters that complicates numerical realization of the model. Hence, the above mentioned model of particles has been significantly modified in terms of mathematical treatment of the model.
We also used phenomenological description of energy distribution in the contact zone aimed to ensure relevance of the numerical model to physical behavior of collide particles and to avoid at the same time complexity of calculations. Dependence of expended energy on particles density and size, as well as relative collisional velocity was implemented. This mechanism is capable to account for proportional energy distribution over processes in the contact zone, in particular, heat release, phase transitions, deformation and destruction.
4. Mathematical Model
The method of permeable particles allowed us to take into consideration internal structure of particles and complicated patterns of their interactions. Basically, we are aware that in the original configurations formation and permanent time step intersections of interacting particles may set up. Proceeding from physical properties of particles and their relative velocities the reconstruction coefficient modeling collisional process
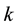 was introduced. Approximate relations for this coefficient were designed in order to account sufficiently well how various physical-mechanical properties effect the contact zone.
was introduced. Approximate relations for this coefficient were designed in order to account sufficiently well how various physical-mechanical properties effect the contact zone.
The Newton model of collisions was taken as the basic one [56] was advanced in terms of the introduced the k coefficient, depending on the distance between particle centers, collisional velocity, and physical nature of particles involved. The following dependence of k on distance, velocity, and density of colliding particles was utilized:
 (1)
(1)
Here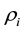 ,
,
 ,
,
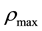 aredensitiesofthecollidedparticlesandmaximumdensityadmittedbythemodel, respectively;
aredensitiesofthecollidedparticlesandmaximumdensityadmittedbythemodel, respectively;
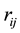 are distances between centers of particles;
are distances between centers of particles;
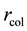 is the distance qual to the sum of particles radii;
is the distance qual to the sum of particles radii;


Parameter



where


As critical velocity

The following set of


where












5. The Model Evaluation
A few special constraints are placed when evaluating

In turn, these requirements place constraints on numerical methods utilization. In particular, Runge-Kutt technique of any order turns out inappropriate since it requires large amount of calculations at every time step. Verlet algorithm [57] [58] is more relevant and effective though less accurate. In this approach, particle position at the next time step is calculated using its current position


where

Forces

Let us note that in the Verlet algorithm expressions particle velocities are not shown explicitly while they can be evaluated using routine expressions for central velocities:

Different modifications of the Verlet algorithm were suggested in order to minimize errors of calculations. One of the most efficient is the leapfrog scheme, such that the first half of particle position change is caused by its velocity at the previous step and the second half―by its velocity at the current step:

Such an approach allows us to calculate quite efficiently both positions and velocities of particles and to keep admittable accuracy when modeling collisional processes of dust component in the protoplanetary disc. It is also possible to extend it over the study of larger solid bodies (planetesimals) evolution.
6. The Model Verification and Discussion of the Results
6.1. Model Verification
The developed method of permeable particles has been numerically evaluated using the above described technique and applied to the study of several problems:
・ collisional evolution of bodies in the protoplanetary disc;
・ asteroid Vesta impact and aftermath;
・ icy-stone body destruction within the Roche lobe of Saturn.
The model and its relevance to the problem under consideration including the introduced coefficients accuracy can be verified if to utilize the modeling approach to some objects with the well known basic parameters and characteristics of collisional evolution and to compare the results.
Asteroids of the Main Belt with evolution patterns deduced from the astronomical observations and the known matter properties from meteorites analysis, best fit to the purpose. For the test model some basic parameters, such as bodies’ size distribution and Kepler velocities disturbances, are needed. Gravity perturbations exerted by giant planets embryos, first of all Jupiter, may be assumed as the most probable source of velocities dispersion in the early solar system [59] . Densities of projectile and target were taken 3.0 g/сm3 corresponding to iron-silicate bodies. Non-disturbed relative velocity of collisions for the Main Belt bodies varies from 10 to 500 m/s while with the account for perturbations from massive Jupiter-like bodies it may amount to 10 km/s. As far as energy required to destroy bodies of different size is concerned, the relations incorporating data of observations and numerical modeling can be used [60] [61] , which is reasonably well qualitative approximation. It is plotted in Figure 1.

Figure 1. Destruction energy

6.2. Collisions of Bodies: Analog of the Protoplanetary Disc Collisional Evolution
The results of numerical experiments for a set of selected targets and projectiles are summarized in Table 1. Examples of modeling are also shown in Figures 2-8.
Obviously, aftermath of solid bodies’ collisions in the protoplanetary disc are crucially dependent on size of both target and projectile and projectile’s velocity. The key parameters are the kinetic energy of projectile and energy of the particles’ coupling in a solid body ensuring target’s integrity. In particular, as Figure 9 testifies, while energy of the projectile was sufficient to destroy the target, the fragments left coalesced rather than to be scattered.
Table 1. The results of modeling two bodies interaction in the Main Asteroid Belt (Densities of projectile and target are 3.0 g/сm3).
Figure 2. Collision of projectile of 2 m in diameter with a target of 20 m in diameter under velocity 50 m/s.
Figure 3. Collision of projectile of 2 m in diameter with a target of 20 m in diameter under velocity 1 km/s.
Figure 3. Collision of projectile of 2 m in diameter with a target of 20 m in diameter under velocity 1 km/s.
Figure 4. Collision of projectile of 20 m in diameter with a target of 200 m in diameter under velocity 50 m/s.
Figure 5. Collision of projectile of 20 m in diameter with a target of 200 m in diameter under velocity 1 km/s.
Figure 6. Collision of projectile of 1 km in diameter with a target of 10 km in diameter under velocity 50 m/s.
Figure 7. Collision of projectile of 1 km in diameter with a target of 10 km in diameter under velocity 1 km/s.
Figure 8. Collision of projectile of 1 km in diameter with a target of 10 km in diameter under velocity 5 km/s.
Figure 9. Model of the crater formation and fragments scattering on asteroid Vesta.
There was assumed that an analog of large primary bodies interaction in the protoplanetary disc could be found modeling collisions in the Main Asteroid Belt. As an example asteroid Vesta―the differentiated body of 529 ± 10 km in size having 25 - 40 km thick basaltic crust has been selected. Heavy cratered terrain of the Vesta surface bring evidence of numerous impacts throughout its evolution including giant crater of 460 km across formation from catastrophic impact of a large body. Reconstruction of such an event allowed us to derive the following estimation: size of the impacted projectile was ~35 km and the velocity of collision ~5 km/s, in accord with the results obtainein [62] . Sequence of the crater formation and fragments of impacted body and projectile scattering are shown in Figure 9.

Figure 10. Model sequence of tidal destruction of a body entering within the Saturn’s Roche lobe.
Finally, we simulate an icy-stone body destruction within the Roche Lobe of a large body. This is of special interest in terms of planetesimals behavior around a formed planet, as well as satellite system evolution around giants in the solar system. In Figure 10 the results of modeling of tidal destruction of a differentiated icy-stone body of radius ~600 km and mass 1023 - 1024g migrated within the Roche limit of Saturn (~1.5 Rs) is shown. Such an event can be relevant to both early evolution of planetesimals when forming of giant planets with the systems of satellites and later trap of bodies migrated from outskirt of the solar system.
7. Conclusions
The model of collisional interaction of bodies in the evolved protoplanetary gas-dust disc at the stage of planetesimals formation was developed. Mathematical evaluation of the model is based on the method of permeable particles allowing us to take into account internal structure of bodies involved and complicated patterns of their interaction. Phenomenological approach to describe energy distribution in the contact zone ensured the numerical model high capacity, in particular its relevance to physical behavior of particles with no significant raising the complexity. In the numerical evaluation, there found some constraints for complete or partial destruction of colliding bodies, following by either scattering of collisional fragments or their partial back accumulation.
Verification of the model for different basic entry data allowed us to conclude that the suggested phenomenological approach of different dynamical processes in the contact zone of colliding bodies is rather adequately describe the real energy re-distribution. The model therefore is regarded as a good approximation to the study of collisional dynamics in the gas-dust disc at the stage of early evolution following primary solid bodies formation from original dusty fluffy clumps of fractal nature.
References
- Marov, M.Ya. (2014) Fundamentals of the Modern Astophysics: From the Home Planet to Space Frontiers. Springer.
- Marov, M.Ya. (2005) Adv.in Phys. Sci. (Uspechi Phys. Nauk), 175, 668-678.
- Marov, M.Ya., Kolesnichenko, A.V., Makalkin, A.B., Dorofeeva, V.A., Ziglina, I.N. and Chernov, A.V. (2011) From the Protosolar Cloud to the Planetary System: A Model for the Evolution of the Gas-Dust Disk. In: Galimov, E.M., Ed., Problems of Biosphere Origin and Evolution, Nova Publishers, 319-404.
- Kolesnichenko, A.V. and Marov, M.Ya. (2012) Solar System Research, 46.
- Kolesnichenko, A.V. and Marov, M.Ya. (2014) Solar System Research, 48, 354-365. http://dx.doi.org/10.1134/S0038094614050037
- Reipurth, B., Jewitt, D. and Keil, K., Eds. (2007) Protostars and Planets V. University of Arizona Press, Tucson.
- Shukolyukov, A. and Lugmair, G.W. (2003) Chronology of Asteroid Accretion and Differentiation. In: Bottke, W., Cellino, A., Paolicchi, P. and Binzel, R.P., Eds., Asteroids III, University of Arizona Press, Tucson, 687-695.
- Connelly, J.N., Bizzarro, M., Krot, A.N., Nordlund, Å., Wielandt, D. and Ivanova, M.A. (2012) Science, 38, 651. http://dx.doi.org/10.1126/science.1226919
- de Pater, I. and Lissauer, J.J. (2004) Planetary Sciences. Cambridge University Press, Cambridge.
- Cassen, P. (1994) Icarus, 112, 405-429. http://dx.doi.org/10.1006/icar.1994.1195
- Cassen, P. (2001) Meteoritics & Planetary Science, 36, 671-700. http://dx.doi.org/10.1111/j.1945-5100.2001.tb01908.x
- Makalkin, A.B. (2004) Solar System Research, 38, 491-507. http://dx.doi.org/10.1007/s11208-005-0021-6
- Ruzmaikina, T.V. and Makalkin, A.B. (1991) Formation and Evolution of the Protoplanetary Disk. In: Donahue, T.M., Ed., Planetary Sciences: American and Soviet Research, National Academies Press, Washington DC, 44-60.
- Eisner, J.A., Hillenbrand, L.A., Carpenter, J.M. and Wolf, S. (2005) The Astrophysical Journal, 635, 396-421. http://dx.doi.org/10.1086/497161
- White, R.J., Greene, T.P., Doppmann, G.W., et al. (2007) Stellar Properties of Embedded Protostars. In: Reipurth, B., Jewitt, D. and Keil, K., Eds., Protostars and Planets V, University of Arizona Press, Tucson, 117-132.
- Beckwith, S.V.W. and Sargent, A.I. (1996) Nature, 383, 139-144. http://dx.doi.org/10.1038/383139a0
- Cieza, L.A., Kessler-Silacci, J.E., Jaffe, D.T., Harvey, P.M. and Evans II, N.J. (2005) The Astrophysical Journal, 635, 422-441. http://dx.doi.org/10.1086/497325
- Haisch, K.E., Lada, E.A. and Lada, C.J. (2001) The Astrophysical Journal, 553, L153-L156. http://dx.doi.org/10.1086/320685
- Beckwith, S.V.W., Henning, T. and Nakagawa, Y. (2000) Dust Properties and Assembly of Large Particles in Protoplanetary Disks. In: Mannings, V., Boss, A.P. and Rassell, S.S., Eds., Protostars and Planets IV, University of Arizona Press, Tucson, 533-558.
- Natta, A., Testi, L., Calvet, N., et al. (2007) Dust in Proto-Planetary Disks: Properties and Evolution. In: Reipurth, B., Jewitt, D. and Keil, K., Eds., Protostars and Planets V, University of Arizona Press, Tucson, 767-781.
- Alexander, R.D., Clarke, C.J. and Pringle, J.E. (2006) Monthly Notices of the Royal Astronomical Society, 369, 229- 239. http://dx.doi.org/10.1111/j.1365-2966.2006.10294.x
- Lodders, K. (2003) The Astrophysical Journal, 591, 1220-1247. http://dx.doi.org/10.1086/375492
- Palme, H. and Boyton, W.V. (1993) Meteoritic Constraints on Conditions in the Solar Nebula. In: Levy, E.H. and Lunine, J.I., Eds., Protostars and Planets III, University of Arizona Press, Tucson, 979-1004.
- Saxena, S.K. and Eriksson, G. (1986) Chemistry of the Formation of Terrestrial Planets. In: Saxena, S.K., Ed., Chemistry and Physics of Terrestrial Planets (Advances in Physical Geochemistry), Volume 6, Springer, New York, 30-105.
- Petaev, M.I. and Wood, J.A. (1998) Meteoritics & Planetary Science, 33, 1123-1137. http://dx.doi.org/10.1111/j.1945-5100.1998.tb01717.x
- Palme, H., Larimer, J.W. and Lipschutz, M.E. (1988) Moderately Volatile Elements. In: Kerridge, J.F. and Mathews, M.S., Eds., Meteorites and the Early Solar System, University of Arizona Press, Tucson, 436-461.
- Fegley Jr., B. (2000) Space Science Reviews, 92, 177-200. http://dx.doi.org/10.1023/A:1005286910756
- Jones, A.P. (2001) Philosophical Transactions of the Royal Society A, 359, 1961-1972. http://dx.doi.org/10.1098/rsta.2001.0890
- Alexander, C.M.O’.D., Boss, A.P., Keller, L.P., et al. (2007) Astronomical and Meteoritic Evidence for the Nature of Interstellar Dust and Its Processing in Protoplanetary Disks. In: Reipurth, B., Jewitt, D. and Keil, K., Eds., Protostars and Planets V, University of Arizona Press, Tucson, 801-813.
- Zubko, V., Dwek, E. and Arendt, R.G. (2004) The Astrophysical Journal Supplement Series, 152, 211-249. http://dx.doi.org/10.1086/382351
- Tielens, A.G.G.M. (1998) The Astrophysical Journal, 499, 267-272. http://dx.doi.org/10.1086/305640
- Watson, D.M., Kemper, F., Calvet, N., Keller, L.D., Furlan, E., Hartmann, L., et al. (2004) The Astrophysical Journal Supplement Series, 154, 391-395. http://dx.doi.org/10.1086/422918
- Kessler-Silacci, J.E., Hillenbrand, L.A., Blake, G.A. and Meyer, M.R. (2005) The Astrophysical Journal, 622, 404-429. http://dx.doi.org/10.1086/427793
- Ciardi, D.R., Telesco, C.M., Packham, C., Martin, C.G., Radomski, J.T., De Buizer, J.M., et al. (2005) The Astrophysical Journal, 629, 897-902. http://dx.doi.org/10.1086/431548
- Honda, M., Kataza, H., Okamoto, Y.K., Miyata, T., Yamashita, T., Sako, S., et al. (2003) The Astrophysical Journal, 585, L59-L63. http://dx.doi.org/10.1086/374034
- MacPherson, G.J. (2005) Calcium-Aluminum-Rich Inclusions in Chondritic Meteorites. In: Davis, A.M., Ed., Meteorites, Comets and Planets, Elsevier-Pergamon, Oxford, 201-246.
- Meibom, A., Krot, A.N., Robert, F., Mostefaoui, S., Russell, S.S., Petaev, M.I. and Gounelle, M. (2007) The Astrophysical Journal, 656, L33-L36. http://dx.doi.org/10.1086/512052
- Grossman, L., Ebel, D.S. and Simon, S.B. (2002) Geochimica et Cosmochimica Acta, 66, 145-161. http://dx.doi.org/10.1016/S0016-7037(01)00731-1
- Kolesnichenko, A.V. and Marov, M.Ya. (2006) Solar System Research, 40, 1-56. http://dx.doi.org/10.1134/S0038094606010011
- Kolesnichenko, A.V. and Marov, M.Ya. (2008) Solar System Research, 42, 226-255. http://dx.doi.org/10.1134/S0038094608030040
- Marov, M.Ya. and Kolesnichenko, A.V. (2013) Turbulence and Self-Organization: Modeling Astrophysical Objects. Springer, Berlin.
- Marov, M.Ya. and Ipatov, S.I. (2001) Volatiles Inventory and Formation of Planetary Atmospheres. In: Marov, M.Ya. and Rickman, H., Eds., Collisions in the Solar System, Kluwer Academic Publishers, 223-247. http://dx.doi.org/10.1007/978-94-010-0712-2_14
- Marov, M.Ya. and Ipatov, S.I. (2005) Solar System Research, 39, 374-380. http://dx.doi.org/10.1007/s11208-005-0050-1
- Supulver, K.D., Bridges, F.G., Tiscareno, S. and Lievore, J. (1997) Icarus, 129, 539-554. http://dx.doi.org/10.1006/icar.1997.5801
- Wurm, G., Paraskov, G. and Krauss, O. (2005) Icarus, 178, 253-263. http://dx.doi.org/10.1016/j.icarus.2005.04.002
- Blum, J. and Wurm, G. (2000) Icarus, 143, 138-146. http://dx.doi.org/10.1006/icar.1999.6234
- Dominik, C. and Tielens, A.G.G.M. (1997) The Astrophysical Journal, 480, 647-673. http://dx.doi.org/10.1086/303996
- Sekiya, M. and Takeda, H. (2005) Icarus, 176, 220-223. http://dx.doi.org/10.1016/j.icarus.2005.01.008
- Chiang, E.I. (2004) Dust in Protoplanetary Disks. In: Witt, A.N., Clayton, G.C. and Draine, B.T., Eds., Astrophysics of Dust (ASP Conference Series: Volume 309), Astronomical Society of the Pacific, San Francisco, 213.
- Safronov, V.S. (1994) Astronomicheskii Vestnik, 28, 3-9.
- Vityazev, A.V., Pechernikova, G.V. and Safronov, V.S. (1990) Planetyzemnoigruppy: Proiskhozhdenieirannyayaevolyutsiya (The Terrestrial Planets: Origin and Early Evolution). Nauka, Moscow.
- Weidenschilling, S.J. (1984) Icarus, 60, 553-567. http://dx.doi.org/10.1016/0019-1035(84)90164-7
- Weidenschilling, S.J. (2000) Space Science Reviews, 92, 295-310. http://dx.doi.org/10.1023/A:1005259615299
- Weidenschilling, S.J. (2006) Icarus, 181, 572-586. http://dx.doi.org/10.1016/j.icarus.2005.11.017
- Hockney, R. and Eastwood, J. (1984) Computer Simulation Using Particles. McGraw-Hill, New York.
- Panovko, Ya.G. (1976) Fundamentals of Applied Theory for Vibration and Impact. Mashinostroenie, Leningrad. (In Russian)
- Koonin, S.E. (1990) Computational Physics: FORTRAN Version. Addison Wesley, Redwood City.
- Rit, M. (2003) Nano Design in Science and Technology. WSP, New York.
- Morbidelli, A., Bottke, W., Nesvorny, D. and Levison, H.F. (2009) Icarus, 204, 558-573.
- Holsapple, K., et al. (2003) Asteroid Impacts: Laboratory Experiments and Scaling Laws. In: Bottke, W., Cellino, A., Paolicchi, P. and Binzel, R.P., Eds., Asteroids III, University of Arizona Press, Tucson, 443-461.
- Davis, D.R., Chapman, C.R., Weidenschilling, S.J. and Greenberg, R. (1985) Icarus, 62, 30-53. http://dx.doi.org/10.1016/0019-1035(85)90170-8
- Asphaug, E., Ryan, E. and Zuber, M. (2003) Asteroid Interiors. In: Bottke, W., Cellino, A., Paolicchi, P. and Binzel, R.P., Eds., Asteroids III, University of Arizona Press, Tucson.


