Received 19 August 2014; revised 15 September 2014; accepted 6 October 2014

ABSTRACT

Static, spherically symmetric bodies are studied by the use of flat space-time theory of gravitation. In empty space a singularity at a Euclidean distance from the centre can exist. But the radius of this singular sphere is smaller than the radius of the body. Hence, there is no event horizon, i.e. black holes do not exist. Escape of energy and information is possible. Flat space-time theory of gravitation and quantum mechanics do not contradict to one another.

Keywords:

Gravitation, Flat Space-Time, Spherical Symmetry, Black Holes

1. Introduction

In this paper the theory of gravitation in flat space-time [1] [2] is applied to static, spherically symmetric bodies. The study of this paper follows along the lines of article [3] . There can exist a spherically symmetric, singular sphere in empty space. But the radius of the singular sphere is smaller than the radius of the body. Hence, this singular sphere doesn’t exist. This means that there is no event horizon, i.e., black holes in the sense of general relativity do not exist. Information and energy are not lost. Hence, theory of gravitation in flat space-time and quantum mechanics do not contradict to one another. The results of this article can also be found in my book [4] . It is worth mentioning that the system of differential of a non-stationary, spherically symmetric, collapsing body is given in Chapter III of [4] . A solution of these differential equations is not known. We also mention that flat space-time theory of gravitation implies no big bang for homogeneous, isotropic, cosmological models. The universe contracts to a positive minimum (corresponding to the big bang of general relativity) and then it expands for all times. This result can be found in the book [4] and in the article [5] . Lastly let us mention the comparison of the theory of gravitation in flat space-time with the theory of general relativity [6] .

In a recent article of Hawking [7] and in the cited references therein, essays to the resolution of the paradox of black holes of general relativity are studied.

2. Gravitation in Flat Space-Time

We shortly summarize the theory of gravitation in flat space-time. Let 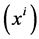be a four-vector of space-time and 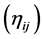a symmetric metric tensor of flat space-time with the line-element

. (2.1)

A special case is the pseudo-Euclidean metric where 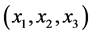are Cartesian coordinates, 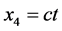and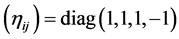. The gravitational field is described by a symmetric tensor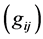. The proper-time is defined by

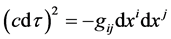. (2.2)

Put

Define 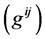by

.

The Lagrangian for the gravitational potentials is given by

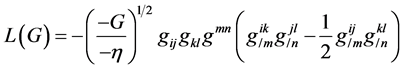(2.3)

where the bar / denotes the covariant derivative relative to the metric (2.1). Let k be the gravitational constant. Put

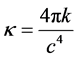
and define the differential operator of order two

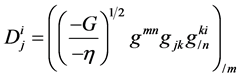. (2.4)

Then, the field equations for the potentials from the Lagrangian (2.3) are

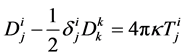(2.5)

where is the total energy-momentum tensor of matter and of the gravitational field, i.e.

.

It is worth to mention that the energy-momentum of the gravitational field is a tensor contrary to the one of general relativity.

The equations of motion for matter are

. (2.6)

The derivative of these results can be found in the articles [1] [2] and in the book [5] .

3. Static Spherically Symmetric Gravitational Field

Here, we follow along the lines of paper [3] . Let us consider a spherically symmetric body at rest with non-va- nishing pressure.

We set with.

The potential are

. (3.1)

A body at rest has the four-velocity

. (3.2)

The matter tensor can be written in the form

(3.3)

where and are pressure and density of matter.

We use the abbreviation

and define

, (3.4a)

. (3.4b)

Then the energy-momentum tensor of the gravitational field is

. (3.5)

The differential equations for the gravitational field have the form

, (3.6a)

, (3.6b)

. (3.6c)

In addition, there are boundary conditions for and for which are omitted. Let r₀ denote the boundary of the spherically symmetric body which gives.

Put

(3.7a)

then we get the gravitational mass

. (3.7b)

Elementary calculations give by a suitable linear combination of the Equations (3.6) and the boundary conditions

. (3.8)

It is worth to mention that static, spherically, symmetric bodies with pressure equal to zero do not exist. It holds (see [3] )

. (3.9)

The derivation of all these results can be found in the article [3] and in the book [4] .

4. The Gravitational Field in the Exterior of the Body

The gravitational field in the exterior of the body, i.e., is described by the differential equations (see (3.6))

, (4.1a)

, (4.1b)

(4.1c)

with

. (4.2)

It follows from (4.1) by the substitution

(4.3)

, (4.4a)

, (4.4b)

. (4.4c)

Elementary calculations give the asymptotic solutions, i.e. for by the use of the boundary condition

(4.5a)

(4.5b)

(4.5c)

where the parameter A must be fixed by the use of the interior solution. It is worth to mention that no additional parameter arises by the use of general relativity.

Numerical methods are used to get the solutions in the exterior of the body for different parameters A. For small values the solutions (4.5) are used and for increasing the system of differential equations (4.4) is numerically solved.

There are different types of solutions:

1) regular solutions, i.e. for all the functions f, g and h exist and are positive. This is in particular the case for A ≥ 0.2.

2) singular solutions, i.e. there exist a critical value depending on A such that f, g and h do not exist or vanish for. This is the case for all negative values and for small positive values of A. It is worth to

mention that this singularity arises at the Euclidean distance r_c from the centre of the body. It is real and not a property of the coordinate system as by the use of the general theory of relativity which implies an event horizon.

All these results can be found in the article [3] and in the book [4] .

5. Study of Singular Solutions

We will now study the solutions in case (2) in the neighbourhood of, i.e.. We start from (4.4) and we get for the essential part of the solutions near:

(5.1)

With suitable constants. This gives near the singularity

(5.2)

with positive constant A₀, B₀, C₀. We get by the substitution of (5.1) and (5.2) into the Equation (4.4c)

implying

. (5.3a)

The differential Equation (4.4b) gives by (5.1) and (5.2)

(5.3b)

without fixing. The same method yields by the use of (4.4a)

. (5.3c)

The relations (5.3a) and (5.3c) imply

.

Hence we have

. (5.4)

It follows from (5.4) that the inequality (5.3b) is fulfilled for

. (5.5)

This inequality is in agreement with (5.4) and

Summarizing, we have

(5.6)

Hence, β and γ are always positive whereas is positive for and negative for. The absolute radial velocity of light is near the critical value

for.

We get by the use of (5.2) and (5.5) that the solution cannot be continued to. Hence, static, spherically

symmetric bodies with radius do not exist. This is quite different to the results of general relativity

but in analogy to Rosen’s biometric theory of gravitation [8] .

We will now study a spherically symmetric body with radius.

We get from the relations (5.1) and (5.2) by the use of (4.3) for

, (5.7a)

, (5.7b)

. (5.7c)

Therefore, it follows from (5.7) for with (4.2)

.

Hence, relation (3.8) yields for by the use of (3.5), (3.7a) and the assumption that the energy of the gravitational field is non-negative

. (5.8)

It follows from (5.8)

.

We get from this inequality

. (5.9)

The condition P = 0 implies that the mass M = 0 by virtue of Furthermore, relation (5.9) gives

implying

. (5.10)

The equation of state

gives

in contradiction to (5.10).

Hence, there exists no static, spherically symmetric body with Euclidean radius, i.e. every static, spherically symmetric body has a radius.

Summarizing, we can state that static, spherically symmetric bodies have no singular solutions. There exists no event horizon, i.e. black holes do not exist.

This result is in agreement with quantum mechanics in contrast to black holes of the general theory of relativity.

The differential equations for a collapsing, spherically symmetric body are given in Chapter III of the book [4] . The final state of the solution of these equations cannot be a black hole but a solution of these equations is not known.

References