Journal of Modern Physics
Vol.5 No.10(2014), Article
ID:47425,11
pages
DOI:10.4236/jmp.2014.510095
Sedeonic Equations of Gravitoelectromagnetism
Victor L. Mironov1,2, Sergey V. Mironov1
1Institute for Physics of Microstructures RAS, Nizhniy Novgorod, Russia
2Lobachevsky State University of Nizhniy Novgorod, Nizhniy Novgorod, Russia
Email: mironov@ipmras.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2014; revised 21 April 2014; accepted 15 May 2014
Abstract
In present paper we develop the description of massless fields on the basis of space-time algebra of sixteen-component sedeons. The generalized sedeonic second-order equation for unified gravito-electromagnetic (GE) field describing simultaneously weak gravity and electromagnetism is proposed. The relations for the GE field energy, momentum and Lorentz invariants are derived. The special case of GE field described by first-order sedeonic wave equation is also discussed.
Keywords:Gravitoelectromagnetism, Clifford Algebra, Space-Time Sedeons

1. Introduction
The analogy between electromagnetic and gravitational fields was discussed by many researchers starting from J. C. Maxwell and O. Heaviside [1] [2] . This analogy motivated many attempts to reformulate the equations of Newtonian gravitation in the form similar to the Maxwell equations in electrodynamics. Such approach is based on two general assumptions. First is the existence of gravitomagnetic field connected with moving masses. Second is the hypothesis that the speed of gravitational field propagation is equal to the speed of light. These assumptions enable the formulation of phenomenological Maxwell-like equations for gravitational field [3] [4] . On the other hand, recently it was shown that linearized weak field equations of general relativity [5] -[9] can be represented as the set of Maxwell-like equations for the vectorial gravitational field and now this linear approximation (so-called “post-Newtonian approximation”) is widely used in astrophysics for the analysis of interactions between moving and spinning masses [8] -[13] . However, the Heaviside-Gibbs vector algebra, which is usually used for the formulation of electromagnetism and linear gravity, does not adequately specify the spacetime properties of gravitational and electromagnetic fields. Since the Maxwell equations are the system of four equations for scalar, pseudoscalar, vector and pseudovector values, the application of multi-component algebras is more appropriate. There are different approaches based on algebra of hypercomplex numbers and Clifford algebras to formulate electromagnetism [14] -[20] and linear gravity [21] -[23] taking into account above mentioned space symmetry. However, the consideration of total relativistic space-time field’s symmetry requires the introduction of sixteen-component space-time values. There are some attempts to develop a field theory on the basis of sixteen-component structures such as hypercomplex sedenions [24] -[27] and hypercomplex multivectors generating associative space-time Clifford algebras [28] [29] . Recently S. Demir and M. Tanisli [27] reported the compactification of the linear field equations for gravitational and electromagnetic fields on the basis of conic sedenions. They have shown that formally electromagnetism and gravity can be described by single unified equation for the conic sedenionic potentials. However, the sedenions is nonassociative algebra that leads to the problems in calculating the second-order relations for unified field. Besides, the inclusion of negative energy and negative Pointing vector of gravitational field in a mathematical structure of the unified field equation was not considered.
Recently we proposed the sixteen-component associative space-time algebra of scalar-vector objects named by sedeons [30] . The sedeons have the clearly defined geometric meaning, take into account the symmetry of physical values to the space-time inversion and realize the scalar-vector representation of Poincare group. In present paper we develop the description of massless fields on the basis of sedeonic potentials. We show that sedeonic approach enables the introduction of unified sedeonic gravito-electromagnetic (GE) field describing simultaneously weak gravity and electromagnetism.
2. Linear Equations of Gravitation in Flat Space-Time
In this section we reproduce the arguments leading to the linear equations of the weak gravitational field. As is well known [6] , Einstein’s equation for gravitational field is written as
 , (1)
, (1)
where 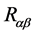 is Ricci curvature tensor,
is Ricci curvature tensor, 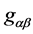 is metric tensor,
is metric tensor,  is the speed of light,
is the speed of light, ![]() is the gravitational constant,
is the gravitational constant, 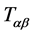 is the tensor of energy-momentum of matter (Greek indexes are 0, 1, 2, 3, Latin indexes are 1, 2, 3). In linear approximation [6] -[9] this equation has the following form
is the tensor of energy-momentum of matter (Greek indexes are 0, 1, 2, 3, Latin indexes are 1, 2, 3). In linear approximation [6] -[9] this equation has the following form
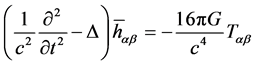 , (2)
, (2)
where 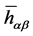 is the deviation from Minkovski metric tensor
is the deviation from Minkovski metric tensor 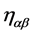 defined as
defined as
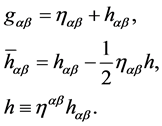 (3)
(3)
The deviation 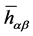
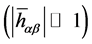 satisfies the gauge condition
satisfies the gauge condition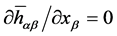 . Introducing mater density
. Introducing mater density  and density of mater current
and density of mater current  according
according
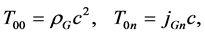 (4)
(4)
as well as the scalar 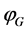 and vector
and vector  potentials according
potentials according
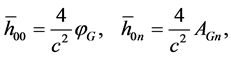 (5)
(5)
the Equation (2) can be represented as the set of wave equations for potentials
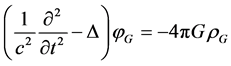 , (6)
, (6)
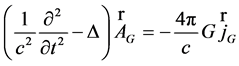 , (7)
, (7)
with gauge condition
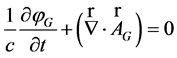 . (8)
. (8)
The analogy with electrodynamics is evident. It allows one to introduce the gravitoelectric 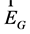 and gravitomagnetic
and gravitomagnetic 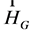 fields
fields
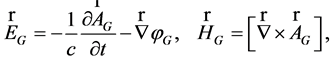 (9)
(9)
which satisfy the following Maxwell-like equations written in Heaviside-Gibbs algebra:
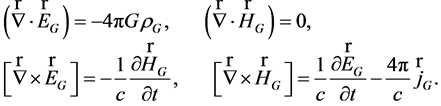 (10)
(10)
3. Symmetry of Electrical and Gravitational Charges
It is known that Coulomb’s law for the force of electrical interaction between two charged point bodies is written as follows:
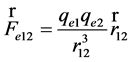 , (11)
, (11)
where 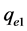 and
and  are electrical charges,
are electrical charges, ![]() is a vector directed from body 1 to body 2,
is a vector directed from body 1 to body 2, ![]() is the separation between point bodies, which is equal to modulus of
is the separation between point bodies, which is equal to modulus of![]() . For a symmetric description of electromagnetic and gravitational phenomena, we introduce the gravitational charge
. For a symmetric description of electromagnetic and gravitational phenomena, we introduce the gravitational charge 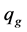 (considered previously in [3] and [31] ) as
(considered previously in [3] and [31] ) as
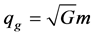 , (12)
, (12)
where 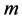 is a mass of gravitating body. Then Newton’s law for gravitational force between two point bodies can be written in the form of Coulomb’s law:
is a mass of gravitating body. Then Newton’s law for gravitational force between two point bodies can be written in the form of Coulomb’s law:
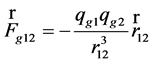 . (13)
. (13)
Simultaneous consideration of gravitational and electric fields leads us to another symmetry connected with charge conjugation. The idea consists in an introduction of two additional units associated with electrical and gravitational charges. First one is electrical unit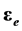 , which is changed (in sign) under electrical charge conjugation. Second one is gravitational unit
, which is changed (in sign) under electrical charge conjugation. Second one is gravitational unit![]() , which is changed (in sign) under gravitational charge conjugation. Since in the classical gravitoelectrodynamics there is no direct interaction between gravitational and electrical charges, the rules of multiplication for units
, which is changed (in sign) under gravitational charge conjugation. Since in the classical gravitoelectrodynamics there is no direct interaction between gravitational and electrical charges, the rules of multiplication for units 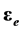 and
and ![]() should be chosen in accordance with Table1 Besides, we suppose the anticommutativity of these units and assume that the priority of commutation is higher than multiplication, so that
should be chosen in accordance with Table1 Besides, we suppose the anticommutativity of these units and assume that the priority of commutation is higher than multiplication, so that
 . (14)
. (14)
Following this approach, the generalized gravito-electromagnetic charge 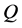 can be presented as
can be presented as
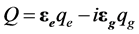 (15)
(15)
and generalized Newton-Coulomb law can be written in the following symmetric form:
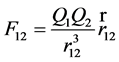 . (16)
. (16)
Indeed, using (15) and (16) we obtain correct expression for the force between two massive electrically charged point bodies
 . (17)
. (17)
Using algebra of gravitoelectrical units we can introduce the following operations of charge conjugations:
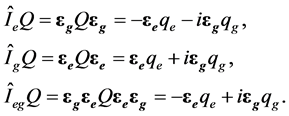 (18)
(18)
4. Sedeonic Equations for GE Field
The space-time scalar-vector sixteen-component sedeon ![]() is defined as [30] :
is defined as [30] :
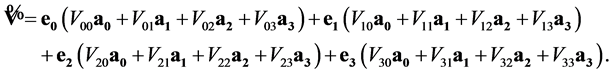 (19)
(19)
The values![]() ,
, ![]() ,
, ![]() ,
, ![]() are scalar-vector basis, where the value
are scalar-vector basis, where the value 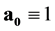 is absolute scalar unit and the values
is absolute scalar unit and the values![]() ,
, ![]() ,
, ![]() are absolute unit vectors generating the right Cartesian basis. The values
are absolute unit vectors generating the right Cartesian basis. The values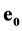 ,
,  ,
, 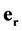 ,
, 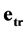 are space-time scalar units, where value
are space-time scalar units, where value 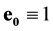 is an absolute scalar unit;
is an absolute scalar unit; 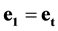 is a time scalar unit;
is a time scalar unit; 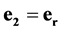 is a space scalar unit;
is a space scalar unit;  is a space-time scalar unit. The multiplication and commutation rules for sedeonic absolute unit vectors
is a space-time scalar unit. The multiplication and commutation rules for sedeonic absolute unit vectors![]() ,
, ![]() ,
, ![]() and space-time units
and space-time units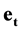 ,
, 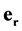 ,
,  are presented in Table 2 and Table 3 respectively. In the tables and further the value
are presented in Table 2 and Table 3 respectively. In the tables and further the value ![]() is the imaginary unit
is the imaginary unit . Note that sedeonic units
. Note that sedeonic units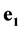 ,
,  ,
, 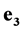 and unit vectors
and unit vectors![]() ,
, ![]() ,
, ![]() generate the anticommutative algebras, but
generate the anticommutative algebras, but ,
, 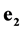 ,
, 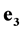 commute with
commute with![]() ,
, ![]() ,
,![]() :
:
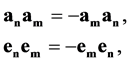 for
for  and
and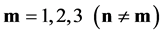 , (20)
, (20)
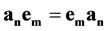 , for any
, for any 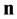 and
and![]() . (21)
. (21)
The sedeonic formalism enables the representation of gravitational and electromagnetic fields as one unified gravito-electromagnetic field. Indeed, the sedeonic second-order equation for massless field can be presented in the following form [30] :
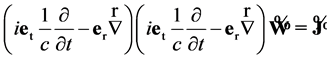 . (22)
. (22)
Let us consider the potential of GE field as:
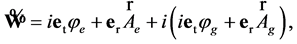 (23)
(23)
where![]() ,
, 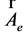 ,
, 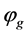 , and
, and 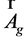 are scalar and vector potentials of electromagnetic (index e) and gravitational (index g) fields. Hereafter we mean that electrical values contain
are scalar and vector potentials of electromagnetic (index e) and gravitational (index g) fields. Hereafter we mean that electrical values contain  and gravitational values contain
and gravitational values contain ![]() units, but we omit them to simplify farther expressions. Let us also consider the sedeonic source of GE field
units, but we omit them to simplify farther expressions. Let us also consider the sedeonic source of GE field
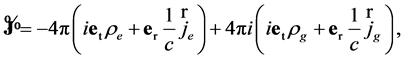 (24)
(24)
where 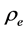 is a volume density of electrical charge;
is a volume density of electrical charge; 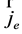 is a density of electrical current;
is a density of electrical current; 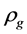 is a volume density of gravitational charge;
is a volume density of gravitational charge; ![]() is a density of gravitational current [3] . Then the sedeonic Equation (22) describes simultaneously electromagnetic and gravitational fields. Performing sedeonic multiplication of operators in the left part of (22) we get the system of wave equations for the components of GE potential
is a density of gravitational current [3] . Then the sedeonic Equation (22) describes simultaneously electromagnetic and gravitational fields. Performing sedeonic multiplication of operators in the left part of (22) we get the system of wave equations for the components of GE potential
 , (25)
, (25)
which is equivalent to the four equations for![]() ,
, 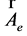 ,
, 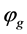 , and
, and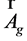 . On the other hand, the sedeonic Equation (22) can be represented as the system of first-order Maxwell equation for electromagnetic and gravitational fields. Indeed, introducing scalar and vector strengths of GE field as
. On the other hand, the sedeonic Equation (22) can be represented as the system of first-order Maxwell equation for electromagnetic and gravitational fields. Indeed, introducing scalar and vector strengths of GE field as

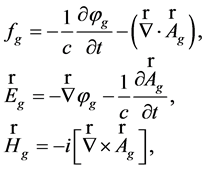 (26)
(26)
we get
 (27)
(27)
and the second-order wave Equation (22) can be represented in the following form:
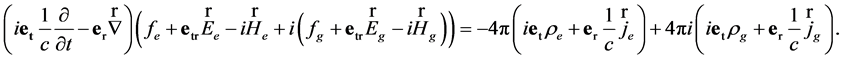 (28)
(28)
Applying operator 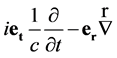 to both parts of expression (28) one can obtain the second-order wave equations for the field strengths in the following form:
to both parts of expression (28) one can obtain the second-order wave equations for the field strengths in the following form:
 , (29)
, (29)
 , (30)
, (30)
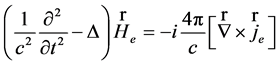 , (31)
, (31)
 , (32)
, (32)
 , (33)
, (33)
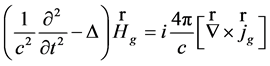 . (34)
. (34)
In the absence of processes of matter nucleation and annihilation, we can assume the conservation laws
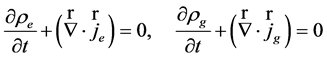 (35)
(35)
and on the basis of Equations (29) and (32) we can take the scalar fields ![]() and
and  equal to zero. This is equivalent to the Lorentz gauge conditions (see expressions (26)):
equal to zero. This is equivalent to the Lorentz gauge conditions (see expressions (26)):
 (36)
(36)
Taking into account these gauge conditions the Equation (28) is rewritten as
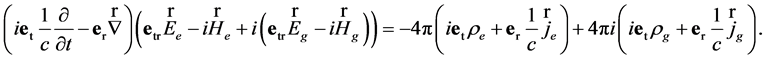 (37)
(37)
Performing sedeonic multiplication in the left part of Equation (37) and separating terms with different space-time and charge (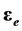 and
and![]() ) properties, we obtain two systems of Maxwell equations for electromagnetic and gravitational fields:
) properties, we obtain two systems of Maxwell equations for electromagnetic and gravitational fields:
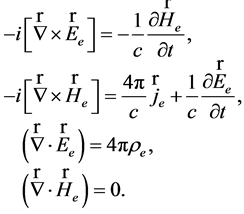
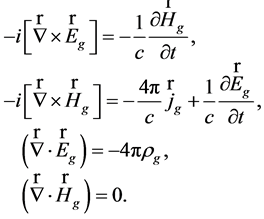 (38)
(38)
Thus, we have shown that the generalized sedeonic Equation (22) correctly describes the unified GE field. Further, we will assume the performing of gauge conditions (36).
4.1. Relations for Energy and Momentum of GE Field
The sedeonic wave equation allows one to derive the generalized Pointing theorem for unified GE field [18] .
Multiplying the expression (37) on the sedeon 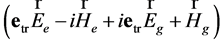 from the left and separating components with different space-time and charge properties, we obtain following equations:
from the left and separating components with different space-time and charge properties, we obtain following equations:
 (39)
(39)
 (40)
(40)
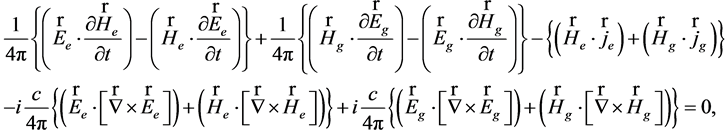 (41)
(41)
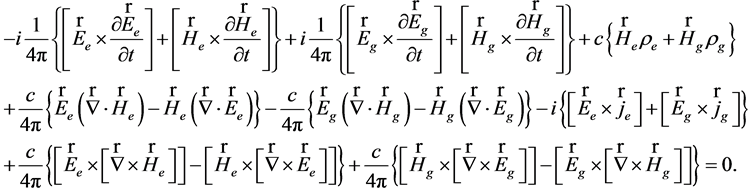 (42)
(42)
The system of (39)-(42) is the generalized Pointing theorem for the GE field. The value 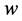
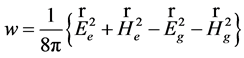 (43)
(43)
plays the role of volume density of GE field energy, while vector 
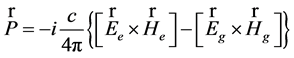 (44)
(44)
plays the role of Pointing vector of GE field.
4.2. Lorentz Invariants of GE Field
The sedeonic algebra allows one to obtain relations for the Lorentz invariants [18] of GE field. Let us multiply expression (37) on the sedeon 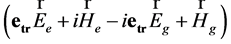 from the left. Then performing sedeonic multiplication, and equating the components with different space-time and charge properties, we get following equations:
from the left. Then performing sedeonic multiplication, and equating the components with different space-time and charge properties, we get following equations:
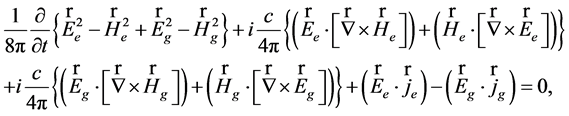 (45)
(45)
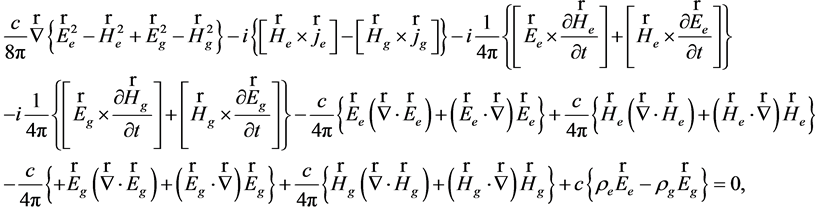 (46)
(46)
 (47)
(47)
 (48)
(48)
The expressions (45)-(48) are the equations for the Lorentz invariants 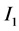 and
and  of GE field:
of GE field:
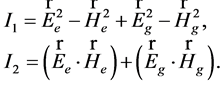 , (49)
, (49)
5. First-Order Equation of GE Field
Let us consider the special case of massless GE field, which is described by sedeonic first-order equation
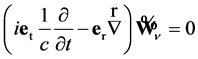 . (50)
. (50)
Here the potential of GE field is
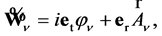 (51)
(51)
where 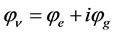 and
and . The sedeonic Equation (50) is equivalent to the following system:
. The sedeonic Equation (50) is equivalent to the following system:

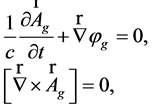 (52)
(52)
with gauge conditions:
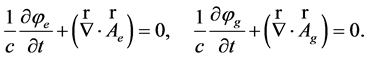 ( 53)
( 53)
In fact Equation (52) describe the GE field with zero field strengths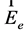 ,
, 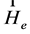 ,
,  ,
,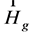 .
.
5.1. Analogue of Poynting Theorem and Lorentz Invariants for the First-Order Equation
Multiplying the Equation (50) on sedeon 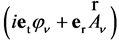 from the left and separating parts with different spacetime properties (and taking into account
from the left and separating parts with different spacetime properties (and taking into account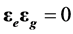 ) we get the following second-order equations for the field potentials:
) we get the following second-order equations for the field potentials:
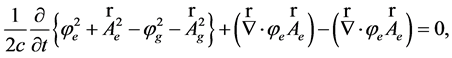 (54)
(54)
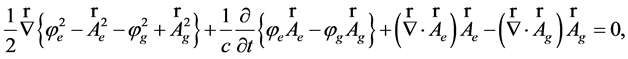 (55)
(55)
 (56)
(56)
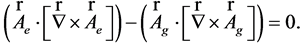 (57)
(57)
On the other hand, multiplying (50) on sedeon 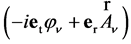 from the left and separating values with different space-time and charge properties we obtain the following four equations:
from the left and separating values with different space-time and charge properties we obtain the following four equations:
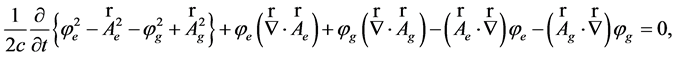 (58)
(58)
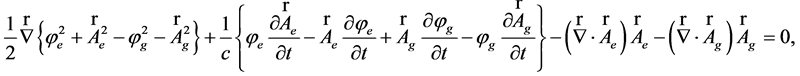 (59)
(59)
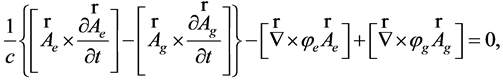 (60)
(60)
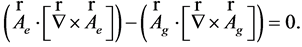 (61)
(61)
The expressions (54)-(57) and (58)-(61) are the analogs of Poynting theorem and Lorentz invariants relations for the field, which is described by first-order equation.
5.2. Plane Wave Solution of Sedeonic First-Order Equation
Let us consider the plane wave solution of Equation (50). In this case the potential can be written as:
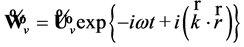 , (62)
, (62)
where  is a frequency,
is a frequency,  is an absolute wave vector and the wave amplitude
is an absolute wave vector and the wave amplitude 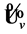 does not depend on coordinates and time. The dependence of the frequency on the wave vector has two branches:
does not depend on coordinates and time. The dependence of the frequency on the wave vector has two branches:
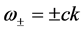 , (63)
, (63)
where  is the module of wave vector
is the module of wave vector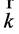 . In general, the plane wave solution for the Equation (50) can be written in the following sedeonic form [30] :
. In general, the plane wave solution for the Equation (50) can be written in the following sedeonic form [30] :
 , (64)
, (64)
where  is an arbitrary sedeon with constant components. Note that the internal structure of this wave is changed under space and time conjugation. Let us analyze the structure of the plane wave (64) in detail. We suppose that wave vector
is an arbitrary sedeon with constant components. Note that the internal structure of this wave is changed under space and time conjugation. Let us analyze the structure of the plane wave (64) in detail. We suppose that wave vector 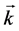 is directed along z axis. Then the first-order Equation (50) can be rewritten in the following equivalent form:
is directed along z axis. Then the first-order Equation (50) can be rewritten in the following equivalent form:
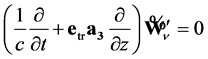 , (65)
, (65)
where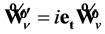 . Using (63) and (64) we can write solution of (65) in the following form:
. Using (63) and (64) we can write solution of (65) in the following form:
 , (66)
, (66)
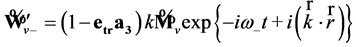 . (67)
. (67)
Note that the wave function 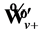 describes the positive branch of dispersion law (63) that corresponds, for example, to the “antiparticle”, while
describes the positive branch of dispersion law (63) that corresponds, for example, to the “antiparticle”, while 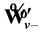 describes the negative branch that corresponds to the “particle” state. The wave functions (66) and (67) are the eigenfunctions of spin operator [32] :
describes the negative branch that corresponds to the “particle” state. The wave functions (66) and (67) are the eigenfunctions of spin operator [32] :
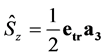 . (68)
. (68)
Indeed, it is simple to check that
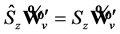 , (69)
, (69)
where eigenvalue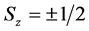 . It is seen that plane wave
. It is seen that plane wave 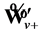 describes “antiparticle” state with spirality
describes “antiparticle” state with spirality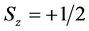 , while
, while 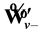 describes “particle” state with spirality
describes “particle” state with spirality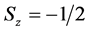 .
.
6. Discussion
From a mathematical point of view, the analogy between electromagnetism and weak gravity leads us to integrating these fields into unified equation, which describes the interaction between electrically charged and gravitating bodies.
On the other hand, from a physical point of view, the phenomena of electricity and gravity are absolutely inseparable from each other. Naturally, all electrically charged particles have the masses and consequently they are involved in both electromagnetic and gravitational interactions. Therefore, all processes involving charged particles should be considered from a unified concept of gravitoelectromagnetism. For example, the electron transitions between excited and ground states in an atom should be accompanied by simultaneous irradiation (absorption) of electromagnetic and gravitational waves (gravito-electromagnetic waves), since in these processes both electric and gravitational interactions of the electron with the atomic nucleus are changed. Also, the processes of particle-antiparticle pair’s nucleation (or annihilation) should be accompanied by absorption (or emission) of gravito-electromagnetic waves. At last, any antennas radiate gravito-electromagnetic waves since an alternating current in the radiating and receiving antennas has both electrical and gravitational components. Thus, the gravitational waves exist everywhere around us. For the sake of justice, it should be noted that the energy of gravitational wave’s components is very small and in general all effects of the interaction between radiation and matter are determined by electromagnetic component.
Furthermore, the concept of gravitational charge allows separating the effects of inertia associated with inertial mass and the effects of gravity associated with gravitational charge of the particles. For example, the quantum sedeonic wave equation [30] for a quantum particle in a gravitational field can be written as
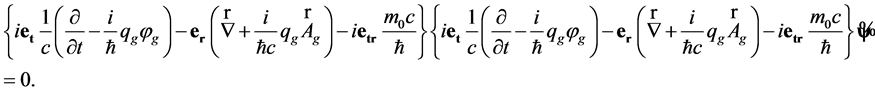 (70)
(70)
Here the parameter 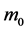 is the inertial rest mass of particle, while
is the inertial rest mass of particle, while  is the gravitational charge. This opens the way for the quantum description of gravitational interactions of particles.
is the gravitational charge. This opens the way for the quantum description of gravitational interactions of particles.
Moreover the operation of charge conjugation allows one to describe the particles with opposite gravitational charges (antimatter [33] ) and suppose the repulsive matter-antimatter gravitational interaction.
Finally, we showed that the sedeonic first-order Equation (50) describes massless particles with spin 1/2. We believe that this equation can be considered for modeling a neutrino field including electromagnetic and gravitational components.
Acknowledgements
The authors are very thankful to Mironova, G.V. for help and moral support. We also thank Korolev, S. for assistance.
References
- Maxwell, J.C. (1865) Philosophical Transactions of the Royal Society of London, 155, 459-512.http://dx.doi.org/10.1098/rstl.1865.0008
- Heaviside, O. (1893) The Electrician, 31, 281-282. https://archive.org/stream/electromagnetict01heavrich#page/454/mode/2up
- Majernik, V. (1971) Astrophysics and Space Science, 14, 265-285. http://dx.doi.org/10.1007/BF00653317
- Singh, A. (1981) Lettere Al Nuovo Cimento, 32, 231-234. http://dx.doi.org/10.1007/BF02799188
- Weinberg, S. (1972) Gravitation and Cosmology. John Wiley, New York.
- Landau, L.D. and Lifschitz, E.M. (1987) The Classical Theory of Fields. Pergamon Press, Oxford.
- Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. Freeman W.H. and Company, San Francisco.
- Ruggiero, M.L. and Tartaglia, A. (2002) Il Nuovo Cimento B, 117, 743-768.
- Mashhoon, B. (2007) Gravitoelectromagnetism: A Brief Review. In: Iorio, L., Ed., The Measurement of Gravitomagnetism: A Challenging Enterprise, NOVA Science, Hauppauge, New York, 29-39.
- Kaplan, J.D., Nichols, D.A. and Thorne, K.S. (2009) Physical Review D, 80, 124014. http://dx.doi.org/10.1103/PhysRevD.80.124014
- Kopeikin, S.M. (2006) International Journal of Modern Physics D, 15, 305-320. http://dx.doi.org/10.1142/S0218271806007663
- Iorio, L. (2007) Recent Developments in Testing Gravitomagnetism with Satellite Laser Ranging. In: Iorio, L., Ed., The Measurement of Gravitomagnetism: A Challenging Enterprise, NOVA Science, Hauppauge, New York, 103-136.
- Schafer, G. (2009) Space Science Review, 148, 37-52. http://dx.doi.org/10.1007/s11214-009-9537-2
- Majernik, V. (1999) Advances in Applied Clifford Algebras, 9, 119-130. http://dx.doi.org/10.1007/BF03041944
- Imaeda, K. (1976) Il Nuovo Cimento B, 32, 138-162. http://dx.doi.org/10.1007/BF02726749
- Gamba, A. (1998) Il Nuovo Cimento A, 111, 293-302.
- Tolan, T., Ozdas, K. and Tanisli, M. (2006) Il Nuovo Cimento B, 121, 43-55.
- Mironov, V.L. and Mironov, S.V. (2009) Journal of Mathematical Physics, 50, 012901. http://dx.doi.org/10.1063/1.3041499
- Chanyal, B.C., Bisht, P.S. and Negi, O.P.S. (2010) International Journal of Theoretical Physics, 49, 1333-1343. http://dx.doi.org/10.1007/s10773-010-0314-5
- Shaarawi, A.M. (2000) Foundations of Physics, 30, 1911-1941. http://dx.doi.org/10.1023/A:1003762405951
- Majernik, V. (1982) Astrophysics and Space Science, 84, 191-204. http://dx.doi.org/10.1007/BF00713636
- Ulrych, S. (2006) Physics Letters B, 633, 631-635. http://dx.doi.org/10.1016/j.physletb.2005.12.050
- Demir, S., Tanisli, M. and Tolan, T. (2013) International Journal of Modern Physics A, 28, 1350112. http://dx.doi.org/10.1142/S0217751X13501121
- Imaeda, K. and Imaeda, M. (2000) Applied Mathematics and Computation, 115, 77-88. http://dx.doi.org/10.1016/S0096-3003(99)00140-X
- Carmody, K. (1988) Applied Mathematics and Computation, 28, 47-72. http://dx.doi.org/10.1016/0096-3003(88)90133-6
- Carmody, K. (1997) Applied Mathematics and Computation, 84, 27-47. http://dx.doi.org/10.1016/S0096-3003(96)00051-3
- Demir, S. and Tanisli, M. (2012) International Journal of Theoretical Physics, 51, 1239-1253. http://dx.doi.org/10.1007/s10773-011-0999-0
- Joyce, W.P. (2001) Journal of Physics A: Mathematical and General, 34, 1991-2005. http://dx.doi.org/10.1088/0305-4470/34/10/304
- Cafaro, C. and Ali, S.A. (2007) Advances in Applied Clifford Algebras, 17, 23-36. http://dx.doi.org/10.1007/s00006-006-0014-7
- Mironov, V.L. and Mironov, S.V. (2013) Applied Mathematics, 4, 53-60. http://dx.doi.org/10.4236/am.2013.410A3007
- Schwebel, S. (1970) International Journal of Theoretical Physics, 3, 315-330. http://dx.doi.org/10.1007/BF00669760
- Mironov, V.L. and Mironov, S.V. (2009) International Journal of Modern Physics A, 24, 6237. http://dx.doi.org/10.1142/S0217751X09047739
- Hajdukovic, D.S. (2013) Astrophysics and Space Science, 339, 1-5. http://dx.doi.org/10.1007/s10509-012-0992-y


