Journal of Modern Physics
Vol.5 No.6(2014), Article ID:44621,10 pages DOI:10.4236/jmp.2014.56041
Some Success Applications for Local-Realism Quantum Mechanics: Nature of Covalent-Bond Revealed and Quantitative Analysis of Mechanical Equilibrium for Several Molecules
Runsheng Tu
Agency of Product Quality Inspection of Huangshi, Huangshi City, China
Email: 2run3@sina.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 5 February 2014; revised 28 February 2014; accepted 14 March 2014
ABSTRACT
With local realism quantum mechanics established, we can simply describe an extranuclear electron as a large-scale elastic ring with an elastic phase trajectory. Several small molecules can thus be strictly calculated through the logical method of establishing an accurate mechanical equilibrium equation describing the molecular structure, then solving the strict solutions of this mechanical equation and the corresponding wave equation. The results (bond length and dissociation energy) are in good agreement with observed results—i.e. if it is only coincidence, there should not be such a high probability of agreement between calculated and observed results. The method of local realism quantum mechanics is no longer the semi-empirical method. The method to calculate the electron pairing energy uses a linear regression of the ionization energy obtained through experiment. Nonetheless, it is exciting that there are diatomic molecules such as Na2, K2 and asymmetric HF molecules that possess a non-zero non-bonding electron number in the calculation examples. Moreover, the molecular structures are very intuitive, and the calculation method is much simpler than existing methods.
Keywords:Local Realism Quantum Mechanics, Large-Scale Elastic Ring, Phase Trajectory, Bond Length, Dissociation Energy, Nature of Covalent Bond

1. Introduction
Reference [1] establishes the theoretical system describing local realism quantum mechanics (LRQM), which is a quantum mechanics (QM) model whose logic system is exactly the same as existing QM theory except that the probability interpretation has been eliminated. In LRQM, volatility and the nature of a particle are compatible; the transition between classical mechanics and wave mechanics is no longer a sudden process, but a process of gradual change. From the structure diagram of the hydrogen molecular ion (Figure 1), we can see that the bonding electron moves between the two hydrogen nuclei, no superluminal interaction—the extranuclear electron is local. If the bonding electron between the two nuclei is the phase trajectory ring, the relationship between each particle is the exact causation, and this extranuclear electron must be in reality. Thus, the bonding electrons are always in two nuclei (or atomic cores) for the covalent molecular bonds calculated in this work, which means the molecules can achieve a mechanical equilibrium state and the mechanical equilibrium equations have a specific solution. Reference [2] has proven that the uncertainty relation possesses a double meaning of determinism and indeterminism, which raises the stakes for LRQM; even if the proof for LRQM is insufficient, this paper also shows that the results are very interesting when we use extranuclear electron as a large scale elastic ring.
LRQM think: the structure of a ground hydrogen-atom state is that there is a proton in the central of a phasetrajectory electronic ring [1] . Therefore, an electron which rotates around a nucleus is equivalent to an entity ring rotates outside the nucleus. The planetary motion of the point electron in Bohr model of the hydrogen atom has been replaced by the rotation of phase-trajectory electronic ring. Since the mass and charge of the electron is distributed in the ring, calculation method of hydrogen atoms can be the same as Bohr’s planetary model. Owing to the phase-trajectory ring that is enclosed by a quantum of circularly polarized light and that is electromagnetic wave, Schrödinger method for solving the wave equation can also be applied to calculating the hydrogen atom. The calculations in this article are based on the calculation of hydrogen-like ions. The molecular structures shown by Figure 1, Figure 2 are the classic framework. Although there are one or two electrons outside the nucleus
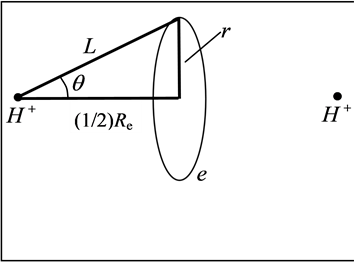
Figure 1. Hydrogen molecule-ion .
.
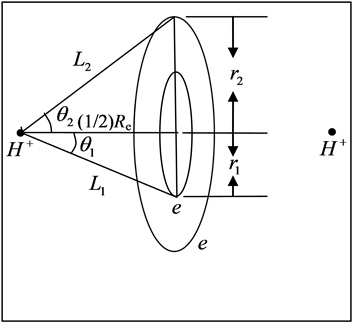
Figure 2. Hydrogen molecule H2 of excited state.
calculating them is entirely independent of quantum entanglement and quantum teleportation. Visible, extranuclear electron in the movement process neither is superluminal, nor cannot be divided with environment (That is, there are precise causal association between extranuclear and surroundings rather than the presence and movement in the peculiar way of indeterminism). In the molecule shown by Figure 1, Figure 2, there is the process of quantum teleportation, and even there is the quantum entanglement phenomenon which also did not affect the intramolecular interaction. This determines that the method used by this paper is the method of local realism.
LRQM does not use the probability interpretation of a wave function in a stable quantum system. If we assume admittance of an electron described by a minimal circularly polarized quantum, then the phase trajectory of the extranuclear electron, in the absence of random disturbances, is an elastic large-scale ring, which we refer to as an electronic ring. Thus, electron pairing occurs when two single electron rings completely coincide. For example, the hydrogen atom is an atom whose extranuclear electron is a lone electron ring whose movement is equal to the ring-like electric charge rotation. This movement produces a non-zero magnetic moment, where the magnetic moment caused by the electron spin remains is partly offset by the nuclear spin magnetic moment. Note that this magnetic moment can be observed macroscopically. This hypothesis relates to some current research works [3] -[5] as well as to a number of previous studies [6] -[15] .
2. The Paired Energy of Electrons
The difference in ionizing energy for the two electrons in the electronic pair come from the interaction between the two electrons; in the electronic pair the ionization of the first electron requires interaction with another electron and the nucleus at the same time, but the ionization of the second electron only requires the nucleus. This means that the difference in ionizing energy is the interaction energy between the two paired electrons. In the past, this energy has been referred to as the infinitesimal disturbance energy, and has been an energy term of some annoyance. However, in LRQM, it can be solved by known ionization energy (We take the helium atom as an example: 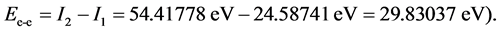 Its approximate value is Ee-e = 15Z*/n2. The precise formula may be obtained by using the following method:
Its approximate value is Ee-e = 15Z*/n2. The precise formula may be obtained by using the following method:
(a) Lists the relation form of the difference of ionizing energy between two electrons of the n = 1 energy level of various elements [ΔI(1s2)] to the effective nuclear charge number (see Figure 3, Table 1).
(b) Extracts the regression equation

Figure 3. The relations between the ionizing energy of two 1s2 electrons and the effective nuclear charge number.
Table 1. The relations between the ionizing energy of two 1s2 electrons and the effective nuclear charge number.
 (1)
(1)
(c) Use Ee-e to express the interaction energy between the two paired-electrons outside the nuclear (their size equal mark opposite with the dissociation energy of paired electrons), promotes from n = 1 to n = n (n is the natural number also is principal quantum number).
 . (2)
. (2)
For a molecule, Z* may be ΣZ*. When Z* = 0, Ee-e = −3.1613/n2 is the pairing energy of electrons, and Ee-e = −3.1613 eV is the pairing energy of free electrons. In order to confirm the accuracy of Equation (2), substituting Z = 11 into Equation (2), results in Ee-e[Na(1s2)] = 183.399 eV. This is difference between I11 and the I10 of sodium element. The actual value is .
.
3. Several Atoms and Molecules to Be Calculated by the Method of LRQM
The logic system underpinning LRQM and existing QM theory is the same, where LRQM contains all of the positive aspects from original quantum theory and current QM. In looking at structure, the original researchers of quantum theory believed that the position and movement properties of electrons were different for atoms and molecules. Thus, because of the same underlying logic system, Schrödinger’s methods and Bohr’s method are still available in LRQM to calculate the energy of the hydrogen atom. This is the source of the value for the hydrogen atom energy E = −13.606Z2/n2. The following calculations are carried out according to the hydrogen-like ions.
3.1. Hydrogen Atom, Helium Atom and Negative Hydrogen-Ion
The potential energy function of electron in a hydrogen atom is V = Ze2/r = e2/r, the ground state energy is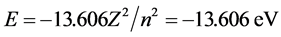 . For a helium atom in the ground state, the spin of the two electrons are opposite, i.e. are an electron pair, and so become a double electric ring. The potential energy function of the double electron in a helium atom is V = −2e2/r, and the potential energy function of the single electron is V = −e2/r. In the ground state helium atom, the sum of the energy of the two electrons (the interaction energy between the nucleus and the electrons) is
. For a helium atom in the ground state, the spin of the two electrons are opposite, i.e. are an electron pair, and so become a double electric ring. The potential energy function of the double electron in a helium atom is V = −2e2/r, and the potential energy function of the single electron is V = −e2/r. In the ground state helium atom, the sum of the energy of the two electrons (the interaction energy between the nucleus and the electrons) is 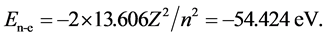 Thus, the energy of each electron is 27.212 eV without distinction. The radius of the phase-orbit-line circle for each of the two 1 s electrons is equally large, and one electron does not have to shield the other.
Thus, the energy of each electron is 27.212 eV without distinction. The radius of the phase-orbit-line circle for each of the two 1 s electrons is equally large, and one electron does not have to shield the other.
For helium molecule, the paired energy of 1s2 electrons is Ee-e(He) = 29.930 eV (it is obtained by substituting n = 1 and Z = 2 into Equation (2)). After solving the calculation of electron pairing energy, it is easy to calculate the helium atom: 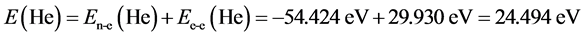 (where, En-e(He) = Z2/n2). The computational method about helium atom will be used frequently in behind. The structure of H− (1s2) ion is similar with the one of helium atom, therefore, ground state
(where, En-e(He) = Z2/n2). The computational method about helium atom will be used frequently in behind. The structure of H− (1s2) ion is similar with the one of helium atom, therefore, ground state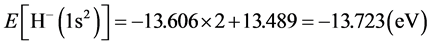 .
.
Another kind of hydrogen negative ion is H−(1s12s1), the radius of the electron ring of H−(1s1) is r(1s) = a0, the radius of the electron ring of H−(2s1) is r(2s) = 22a0, when the two electronic rings are in the identical plane, interaction between the two electrons is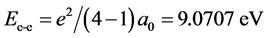 . The energy of H−(1s12s1) is
. The energy of H−(1s12s1) is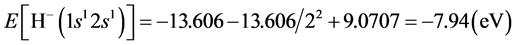 . Because of the spinning of 1s1 electron is opposite with the electron’s of 2s1, therefore, the orbital magnetic moment of hydrogen negative ion H−(1s12s1) is also zero.
. Because of the spinning of 1s1 electron is opposite with the electron’s of 2s1, therefore, the orbital magnetic moment of hydrogen negative ion H−(1s12s1) is also zero.
3.2. Hydrogen Molecular Ion
According to the above atomic structure model, we also know the structure of some small molecule. For example, the structure of hydrogen molecule-ion is that the both sides of a phase-orbit-line ring have a proton respectively (seen in Figure 1). It is also a mechanical balance system, the mechanical balance equation of state in the two nuclei connection direction is
 . (3)
. (3)
This equation is obtained by quantum to be local, quantum to be in reality, Electromagnetics and Geometry. It cannot be obtained by existing quantum mechanics. The general solution of this equation is
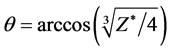 . (4)
. (4)
where Z* is the effective nuclear charge number of one side in the symmetrical covalent molecule. Both Equations (3) and (4) is the situation of the covalent molecule for the single bonding electrons. For the covalent molecule that the bonding electrons are paired, they become 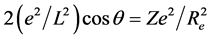 and
and 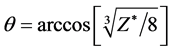
separately. In this example Z = 1, θ = 50˚57'10" (i.e. 50.953˚). The total potential energy function of 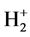 is
is
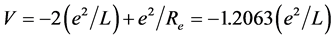 .
.
Computation treated as hydrogenic ion, the energy is
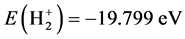 .
.
The electronic potential energy function in 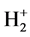 is
is
 .
.
Similarly computation treated as hydrogenic ion, corresponding energy is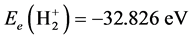 . The difference between
. The difference between  and
and 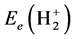 is the interaction energy between nuclei:
is the interaction energy between nuclei: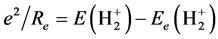 , the nuclear separation of diatomic molecules can be calculated by using following formula:
, the nuclear separation of diatomic molecules can be calculated by using following formula:
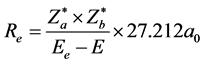 . (5)
. (5)
Therefore,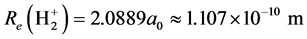 . The dissociation energy of
. The dissociation energy of 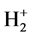 is
is
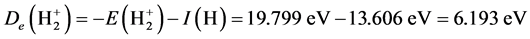 .
.
The corresponding experimental values are 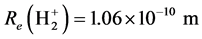 and
and . The bonding electrons do not to pair. In the hydrogen molecular ion, the spinning magnetic moment is not zero, there is the magnetic moment interaction between the two nuclei, and make hydrogen molecular ion become an asymmetrical molecule. Computing to treat it as the symmetrical molecular, the error is inevitably big. This causes the accurate degree of the calculating result for the hydrogen molecular ion to be inferior to the one of hydrogen molecule.
. The bonding electrons do not to pair. In the hydrogen molecular ion, the spinning magnetic moment is not zero, there is the magnetic moment interaction between the two nuclei, and make hydrogen molecular ion become an asymmetrical molecule. Computing to treat it as the symmetrical molecular, the error is inevitably big. This causes the accurate degree of the calculating result for the hydrogen molecular ion to be inferior to the one of hydrogen molecule.
The excited state energy and the bond length of hydrogen molecular ion are also can be calculated. May see from Equation (4), the angle θ is only related with the bonding electronic number and the nuclear charge number, but has nothing to do with the energy level. Therefore, the angle θ in excited state  is the same with the one in the ground state
is the same with the one in the ground state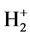 . Corresponding energy is the 1/n2 time of the one of the ground state. E = −4.950 eV, Ee = −8.207 eV. Substituting these two into Equation (5), may result in
. Corresponding energy is the 1/n2 time of the one of the ground state. E = −4.950 eV, Ee = −8.207 eV. Substituting these two into Equation (5), may result in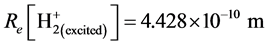 ,
,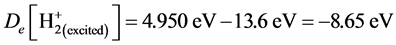 .
.
3.3. Hydrogen Molecule
The mechanical structure of hydrogen molecule (H2) is very similar with the one of hydrogen molecular ion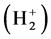 , but the phase-orbit-line between the two nuclei is a dielectronic ring. The solution of the equation of mechanical equilibrium state in the system is θ = π/3. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy function of the system is
, but the phase-orbit-line between the two nuclei is a dielectronic ring. The solution of the equation of mechanical equilibrium state in the system is θ = π/3. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy function of the system is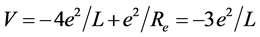 . Calculating to regard it as a helium-like ion (i.e. two hydrogenic ions of V = −(3/2)e2/L), the corresponding total energy is
. Calculating to regard it as a helium-like ion (i.e. two hydrogenic ions of V = −(3/2)e2/L), the corresponding total energy is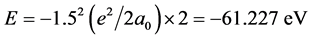 ). In H2, the potential energy of the pure electrons is
). In H2, the potential energy of the pure electrons is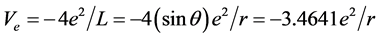 . Calculating to regard it as helium-like ionthe corresponding electronic energy is
. Calculating to regard it as helium-like ionthe corresponding electronic energy is . Similarly we have:
. Similarly we have: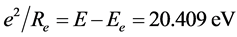 ,
,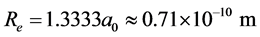 . Since the two-electron in the ground H2’s state and the two-electron in He have the same environment (n = 1, Z = 2), then the interaction energy of the two electrons in H2 also is Ee-e(H2) = 29.830 eV. So the dissociation energy of H2 is
. Since the two-electron in the ground H2’s state and the two-electron in He have the same environment (n = 1, Z = 2), then the interaction energy of the two electrons in H2 also is Ee-e(H2) = 29.830 eV. So the dissociation energy of H2 is
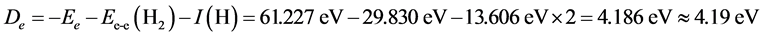 .
.
The corresponding experimental values are: De = 4.75 eV, Re = 0.74 × 10−10 meters.
The first excited state of H2 is the state which the one of its ground state bonding electron was stimulated to the 2s energy level. Its symbolic representation is H2(1s12s1). The bonding electrons have constituted two concentric circles to be in among two protons. Its mechanical balance equation is
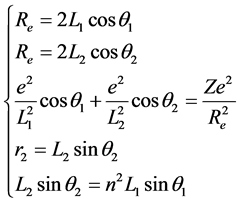 . (6)
. (6)
Last equality is obtained by according to the relations between the radius of phase-orbit-line ring and the main quantum number (rn = n2rground state). This equation set has the solution. Substitute the first equality and the fifth equality separately the second equality and the third equality may eliminate Re,
 . (7)
. (7)
Let conθ1 = x, conθ2 = y, considered Z = 1, n = 2, we have: ;
;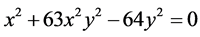 . x graphed as y, result in the intersection point of the two curves. Hence, conθ1 = 0.62652, conθ2 = 0.15982; θ1 = 51.206˚, θ2 = 80.8035˚. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy function of the system is
. x graphed as y, result in the intersection point of the two curves. Hence, conθ1 = 0.62652, conθ2 = 0.15982; θ1 = 51.206˚, θ2 = 80.8035˚. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy function of the system is
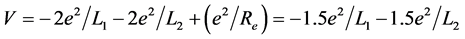 .
.
Calculating to regard it as a helium-like ion (i.e. Two hydrogenic atoms of V = −(3/2)e2/L), 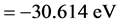
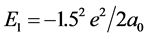 ,
, 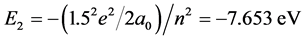 , The total energy of this system is E(1s1 + 2s1) = −38.267 eV. The potential energy of pure electrons in H2(1s12s1) is
, The total energy of this system is E(1s1 + 2s1) = −38.267 eV. The potential energy of pure electrons in H2(1s12s1) is
 .
.
Calculating to regard as a helium-like ion, the corresponding electronic energy is
 .
.
Likewise we have: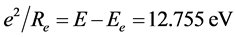 , substituting it into Equation (5),
, substituting it into Equation (5),
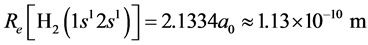
can be obtained. The interaction energy of the two electrons in H2(1s12s1) is
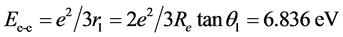 .
.
The dissociation energy is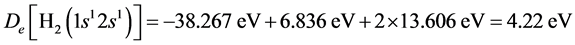 .
.
The chemical bond in the excited state hydrogen molecule H2(1s12s1) is a duplet bond formed by two single electrons.
If the molecular structure shown in Figure 1, Figure 2 is stable, so, the molecule of “part of electron cloud or wave function overlap between the two atoms” described by existing valence bond theory is unstable (the mechanical equilibrium state cannot be achieved).
3.4. Helium Molecule-Ion  et# and Helium Molecule He2
et# and Helium Molecule He2
The structure of 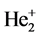 is similar with the one of
is similar with the one of  extremely. When the ground state helium atom ionizes, the nuclear charge number felt by the fled electron (effective nuclear charge number) may be calculated (supposing that the inner electron doesn’t rearrange). According to central-field model, the calculation formula of the first ionization energy is I1(He) = (Z*)2(e2/2a0). Substituting I1(He) = 24.587 eV into it, result in Z* = 1.3443. Regarding He+ as a point charge whose effective nuclear charge number is 1.3443. The solution of the equation of state of mechanical equilibrium in the system is θ = 45.9527˚. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy is
extremely. When the ground state helium atom ionizes, the nuclear charge number felt by the fled electron (effective nuclear charge number) may be calculated (supposing that the inner electron doesn’t rearrange). According to central-field model, the calculation formula of the first ionization energy is I1(He) = (Z*)2(e2/2a0). Substituting I1(He) = 24.587 eV into it, result in Z* = 1.3443. Regarding He+ as a point charge whose effective nuclear charge number is 1.3443. The solution of the equation of state of mechanical equilibrium in the system is θ = 45.9527˚. The interaction between electrons to be not temporarily considered is convenient to calculate the nuclear distance. The total potential energy is
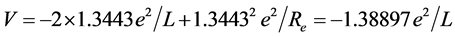 .
.
Calculating to regard it as a hydrogenic atom, the corresponding electronic energy is
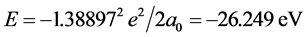 .
.
The potential energy of bonded electrons in 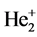 is
is
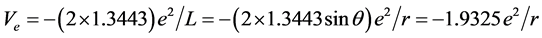 Calculating to regard it as a hydrogenic atom, the corresponding bonding electronic energy is
Calculating to regard it as a hydrogenic atom, the corresponding bonding electronic energy is
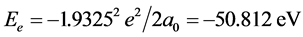 .
.
the interaction energy between the two He+ ions is
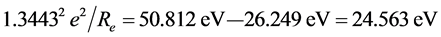 ,
,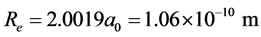 .
.
The dissociation energy of 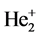 is
is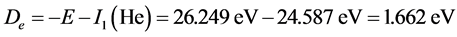 . The corresponding experimental values are: Re = 1.08 × 10−10 m, De = 3 eV. If considering electron-pairing energy, we may some revise.
. The corresponding experimental values are: Re = 1.08 × 10−10 m, De = 3 eV. If considering electron-pairing energy, we may some revise.
The two electrons for the opposite spin to pair give out energy, this kind of energy actually is the electron-pairing energy Δ. According to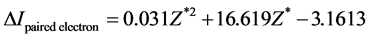 , we know that ΔIpaired electron = ‒3.1613 eV when Z* = 0. This is the electron-pairing energy Δ = 3.1613 eV (the positive value express to give out energy). The superconductivity theory to be becoming popular has used this kind of interaction. When Z* = 0, the extranuclear electron is just free electron, Δ = 3.1613 eV is also electrons-pairing energy. The ionization energy needed by the first electron in an electron-pair dissociating is the sum of the doing work to remove the first electron and the electron pairing energy Δ. Thus we have
, we know that ΔIpaired electron = ‒3.1613 eV when Z* = 0. This is the electron-pairing energy Δ = 3.1613 eV (the positive value express to give out energy). The superconductivity theory to be becoming popular has used this kind of interaction. When Z* = 0, the extranuclear electron is just free electron, Δ = 3.1613 eV is also electrons-pairing energy. The ionization energy needed by the first electron in an electron-pair dissociating is the sum of the doing work to remove the first electron and the electron pairing energy Δ. Thus we have , so that, Z* = 1.25488. Substituting Z* = 1.25488 into Equation (4), result in cosθ = 0.679486, θ = 47.1965˚, sinθ = 0.733688. We also have following corresponding results (The succinct form see the second line in Table 2):
, so that, Z* = 1.25488. Substituting Z* = 1.25488 into Equation (4), result in cosθ = 0.679486, θ = 47.1965˚, sinθ = 0.733688. We also have following corresponding results (The succinct form see the second line in Table 2):
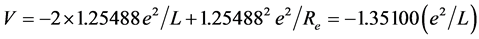 .
.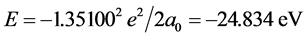 ;
;
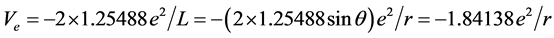 ;
; ;
;
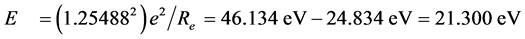 ,
,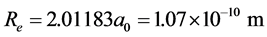 ;
;
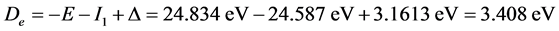 .
.
Table 2. The calculation results for ground state HF molecule and so on.
We examine the stability of helium molecule He2. Substituting Z* = 1.2674 into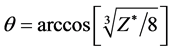 , result in θ = 57.2416˚. Other computed results see the third line in Table 2. The dissociation energy being negative value expressed to give out energy when it dissociate, He2 cannot freely exist under the normal condition. The mechanical balance equation has the solution indicated that He2 may exist in the extra energy’s environment (e.g. has glare to shine or high temperature).
, result in θ = 57.2416˚. Other computed results see the third line in Table 2. The dissociation energy being negative value expressed to give out energy when it dissociate, He2 cannot freely exist under the normal condition. The mechanical balance equation has the solution indicated that He2 may exist in the extra energy’s environment (e.g. has glare to shine or high temperature).
3.5. Lithium Molecule Li2
The structure of Li2 is similar with the one of H2, yet the two bonded electrons are in the energy level of n = 2. The first ionization energy of Li is I1(Li) = 5.39172 eV. According to central field model we know: that the calculation formula of the first ionization energy is 5.39172 eV = (Z*2/22)e2/2a0, Z*[Li(1s)] = 1.2590. The computed results are Re = 2.56 ´ 10−10 m, De = 1.19 eV (see Table 2). The corresponding experimental values are: Re = 2.67 ´ 10−10 m, De = 1.06 eV.
3.6. Lithium Molecule Na2
The structure of Na2 is similar with the one of Li2 and H2, yet the two bonding electrons are in the energy level of n = 3. The first ionization energy of Na is I1(Na) = 5.13908 eV. According to central field model we know: 5.13908 eV = (Z*/n)2e2/2a0, Z*[Na(1s)] = 1.84374. De = 16.013 − 6.516 − 5.13908 × 2 = −0.78 eV. Other computed results Re = 5.08 × 10−10 m (see the 10th line in Table 2). The corresponding experimental values are: Re = 3.8 × 10−10 m, De = 3116 cm−1 = 0.37 eV. The sodium atomic radius should be the electronic ring radius of most outer layer. According to the first ionizing energy, we may estimate the radius of sodium atom. The potential energy of 3s1 electron in sodium atom is 2 times its total energy: Z*e2/r[Na(4s1)] = 2 ´ 5.13908 eV. There is r[Na(4s1)] = 1.8437(13.606/5.13908)a0 = 2.57 × 10−10 m.
3.7. Potassium Molecule K2
The structure of K2 is similar with the one of Na2, Li2 and H2, yet the two bonded electrons are in the energy level of n = 4. The first ionization energy of K is I1(K) = 4.34066 eV. According to central field model we know: 4.34066 eV = (Z*/n)2e2/2a0, Z*(K+) = 2.2593. Other computed results are Re = 8.52 × 10−10 m and De = 0.314 eV (see the 11th line in Table 2). The corresponding experimental values are: Re = 4.8 × 10−10 m, De = 4457 cm−1 =
0.55 eV. From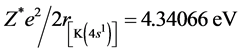 , we know the radius of potassium atom
, we know the radius of potassium atom
 .
.
The error source is coming from that the effective nuclear charge number felt by the bonding electron in the molecule is inaccurate.
3.8. Ground State Hydrogen Fluoride Molecule HF
Hydrogen fluoride HF is a symmetric molecule, but it may also achieve the mechanical balance state, the bonding electron is an electron provided by the hydrogen atom. Its structure is similar with the one of hydrogen molecular ion. The mechanical balance state equation and the relation between sides and angles of HF are

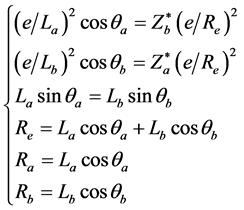 (8)
(8)
The two independent equations may be obtained by substitution
 (9)
(9)
Let cosθa = x, conθb = y, above equations can become:
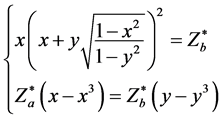 (10)
(10)
The first ionization energy of F is I1(F) = 17.42282eV. According to central-field model we know: 17.42282 eV = (Z*/n)2(e2/2a0), 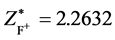 ,
,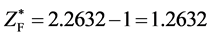 . Considering
. Considering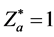 ,
, 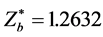 , based on Equation (10), x graphed as y, we may obtain the intersection point of two curves and result in: θa = θH = 61.900˚, θb = θF = 37.200˚. Owing to the bonding electron in HF is provided by atom H, so n = 1. Other computed results see Table 2. The corresponding experimental values are: Re = 0.92 × 10−10 m, De = 5.7 eV.
, based on Equation (10), x graphed as y, we may obtain the intersection point of two curves and result in: θa = θH = 61.900˚, θb = θF = 37.200˚. Owing to the bonding electron in HF is provided by atom H, so n = 1. Other computed results see Table 2. The corresponding experimental values are: Re = 0.92 × 10−10 m, De = 5.7 eV.
3.9. Ground State Sodium Hydride NaH
In the different energy level, electron pairing is quite difficult, the bond of Na‒H is a one-electron bond, the bonding electron is in the energy level of n = 1. It is provided by hydrogen atom. The one side of the molecule structure is similar with .
.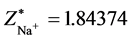 ,
,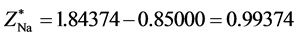 . The state equation of mechanics balance is Equation (8). For this molecule NaH, the concrete form of Equation (10) is
. The state equation of mechanics balance is Equation (8). For this molecule NaH, the concrete form of Equation (10) is
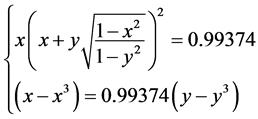 (11)
(11)
x graphed as y, we may obtain the crossover coordinate and θa = θH = 50.5340˚, θb = θM = 51.4697˚. The calculation results for energy and the distance between two nuclei are as in Table 2. The value in literature is De = 10131.58 cm−1 = 1.25 eV. The calculation results about NaH are only indicated: Under this article model, the system of NaH may achieve balanced, uses the same asymptotic method there is hope of approach to obtain the reasonable result.
4. Conclusions
The old theory of covalent bonds assumes that two electron clouds overlap in between the two nuclei. However, this structure is not sufficient to overcome the powerful force of internuclear repulsion, and so the theory predicts that the molecule should be unstable most of the time. The accurate calculation results in this paper show that it is only the bonding electron that is always in between the two atoms (as shown in Figure 1, Figure 2), which allows for the observed stability of the molecule.
Compared with the old valence bond theory, the theory described by this work offers several advantages. First, the molecular structure is simple and clear and we can accurately quantify the mechanical equilibrium state. Second, the calculation method is very simple, the logic is strong and does not require a tentative function, and the theory removes any requirement for a semi-empirical approach. Finally, the theory implies a sufficient stability of covalent molecules that they can withstand analysis by mechanical and kinetic means.
Many people believe that the standard model theory has many loopholes, and as such cannot be used as an absolute standard to invalidate other theories. This article does not support the standard model theory. Is the method introduced in this paper a new development direction for quantum chemistry? Can you put forward any other reasonable suggestions for solving the electronic shape of p, d and f?
Finally, this author asks readers to help accomplish two things. The first is to judge whether the calculated case in this paper is a successful application of local realism QM. The second thing is to, if possible, implement the verification experiments and the predictions in Reference [1] .
Competing Financial Interests Statement
All the work was completed by me. I take full responsibility for the article. For this work that I done, I not employed by any organization, all the work is done at their own expense. I (this paper author) declare no competing financial interests.
References
- Tu, R.S. (2013) Trying to Establish Local Realism Quantum Mechanics. International Journal of Modern Theoretical Physics, 3, 118-152.
- Tu, R.S. (2013) The Formula Whose Shape Is Similar to a Heisenberg Relation Possesses the Double Meanings of Determinism and Indeterminism. Infinite Energy, 107, 44-46.
- Tu, R.S. (1999) The Uncertainty Relation Has the Determinism and the Indeterminism Double Meaning. Journal of Shandong Normal University (Natural Science Edition), 3, 64-65.
- Tu, R.S. (2000) One Kind of Plan to Beautify Quantum Mechanics. Journal of Shandong Normal University, 1, 31-33.
- Tu, R.S. (1998) A Concise Description Way of Quantum Mechanics. Journal of Ningsia Institute of Technology (Nature science), 1, 117-123.
- Guangjing, N. and Suqing, C. (2005) Advanced Quantum Mechanics (3rd Edition) [491]. Fudan University Press, Shanghai.
- Dürr, S., Nonn, T. and Rempe, G. (1998) Origin of Quantum-Mechanical Complementarity Probed by a “Which-Way” Experiment in an Atom Interferometer. Nature, 395, 33. http://dx.doi.org/10.1038/25653
- Xiaofeng, P. (2009) Nonlinearity Quantum Mechanics. [317]. Electronics Industry Press, Beijing.
- Changpu, S. (2006) Quantum Mechanics Survey Question and Quantum Information. http://www.vtimes.net/bbs/dispost.asp?boardid=10&postid=184
- Guowen, W. (2009) The Error and Disaster of Wave Function Collapsing Supposition. http://blog.sciencenet.cn/home.php?mod=space&uid=212815&do=blog&id=271791
- Tianrong, T. (1995) Quantum Mechanics Realism Really Didn’t Lose. Journal of Wugang Workers’ College, 4, 61-69.
- Hailin, Z. (1998) Binding Force in Wave-Particle Interaction. Nuclear Fusion and Plasma Physics, 1, 11-16.
- Wilson, C.M., et al. (2011) Observation of the Dynamical Casimir Effect in a Superconducting Circuit. http://arxiv.org/abs/1105.4714.
- Youchang, X. and Meicheng, S. (1979) Structure Chemistry . People’s Education Press, Beijing.
- Lendau, L.D. (1990) Quatum Mechanics: Theoretical Physics Concise Course (Vol. 2) [Fulin, L.] [1-324]. Advanced Education Press, 231-233.


