Journal of Modern Physics
Vol.05 No.09(2014), Article ID:47002,17 pages
10.4236/jmp.2014.59083
Cumulant Structure Factors of Jellium
P. Ziesche1, J. Cioslowski1,2
1Max-Planck-Institut für Physik Komplexer Systeme, Dresden, Germany
2Institute of Physics, University of Szczecin, Szczecin, Poland
Email: pz@pks.mpg.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2014; revised 25 February 2014; accepted 21 March 2014
ABSTRACT
For the ground state of the homogeneous electron gas (jellium), it is shown how the cumulant de- composition of the 2-matrix leads to the cumulant decomposition of the structure factors Sa,p(q) for the antiparallel (a) and parallel (p) spin pairs and how it simultaneously allows one to derive the momentum distribution n(k), which is a one-body quantity [Phys. Rev. A 86, 012508 (2012), A 89, 059902 (E)(2014)]. The small-q and large-q behavior of Sa,p(q), and their normalizations are de- rived and compared with the results of P. Gori-Giorgi et al. [Physica A 280, 199 (2000) and Phys. Rev. B 61, 7353 (2000)].
Keywords:
Jellium, Reduced Density Matrices, Pair Densities, Coulomb Hole, Fermi Hole, Structure Factors, Cumulant Decomposition

1. Introduction
This paper deals with the ground state of an extended spin-unpolarized (paramagnetic) homogeneous electron gas (HEG), which is one of the most widely studied systems with correlated electrons [1] . The gas is assumed to be uniform in space with the electron density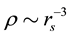 . Other characteristic quantities that depend parametrical- ly on rs are the total energy per electron e, from which follows the interaction energy
. Other characteristic quantities that depend parametrical- ly on rs are the total energy per electron e, from which follows the interaction energy 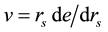 [2] , the momentum distribution
[2] , the momentum distribution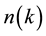 , and the static structure factors (SFs)
, and the static structure factors (SFs)  with “a” standing for electron pairs with antiparallel spins and “p” for pairs with parallel spins. For recent papers on the HEG, also known as jellium, see for example [3] - [15] . Recent GWA and QMC calculations for
with “a” standing for electron pairs with antiparallel spins and “p” for pairs with parallel spins. For recent papers on the HEG, also known as jellium, see for example [3] - [15] . Recent GWA and QMC calculations for 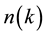 are [3] [4] . (For comparison with experiment see [5] . The value of
are [3] [4] . (For comparison with experiment see [5] . The value of 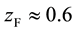 for rs = 3.9 agrees with the results, obtained in Refs. [6] [7] .)
for rs = 3.9 agrees with the results, obtained in Refs. [6] [7] .)
Overhauser considered the pair densities PDs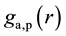 , which follow from the SFs by Fourier transform, and parameterized them in terms of certain 2-body wave functions (known as geminals) [16] . More general geminals should allow one to calculate not only the 2-body quantities
, which follow from the SFs by Fourier transform, and parameterized them in terms of certain 2-body wave functions (known as geminals) [16] . More general geminals should allow one to calculate not only the 2-body quantities , but also the 1-body quantity
, but also the 1-body quantity . Searching in this direction, one immediately encounters the hierarchy of the reduced density matrices (RDMs) and their cumulant decomposition. (The concept of RDM is of great importance in quantum chemistry, see [17] - [22] .) Here it is assumed that the 2-body RDM (2-matrix) is available from perturbation theory or otherwise (hierarchy truncation etc.) and, with the spin structure as a decisive point, it is elucidated how the contraction has to be performed for an extended system in such a way that the 1-body density
. Searching in this direction, one immediately encounters the hierarchy of the reduced density matrices (RDMs) and their cumulant decomposition. (The concept of RDM is of great importance in quantum chemistry, see [17] - [22] .) Here it is assumed that the 2-body RDM (2-matrix) is available from perturbation theory or otherwise (hierarchy truncation etc.) and, with the spin structure as a decisive point, it is elucidated how the contraction has to be performed for an extended system in such a way that the 1-body density 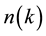 is obtained. In view of the thermodynamic limit, this procedure calls for the cumulant decomposition of the 2-matrix into its Hartree- Fock part
is obtained. In view of the thermodynamic limit, this procedure calls for the cumulant decomposition of the 2-matrix into its Hartree- Fock part 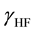 and its nonreducible remainder, the cumulant 2-matrix
and its nonreducible remainder, the cumulant 2-matrix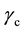 , which proves to be the source of both
, which proves to be the source of both  and
and  [10] . Diagonalization of
[10] . Diagonalization of  yields cumulant geminals and the corresponding weights (i.e. the spectral resolution).
yields cumulant geminals and the corresponding weights (i.e. the spectral resolution).
A side product of this geminal analysis is the following. Usually the partitioning 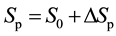 involves an unperturbed (ideal Fermi gas) term S0 and the interaction-induced term
involves an unperturbed (ideal Fermi gas) term S0 and the interaction-induced term ![]() arising from the pairwise Cou- lomb repulsion [15] . In contrast to that approach, an alternative partitioning is presented here as a consequence of the cumulant decomposition of the 2-matrix, namely
arising from the pairwise Cou- lomb repulsion [15] . In contrast to that approach, an alternative partitioning is presented here as a consequence of the cumulant decomposition of the 2-matrix, namely![]() , with the Hartree-Fock term
, with the Hartree-Fock term ![]() [con- structed from the correlated
[con- structed from the correlated![]() ] and a nonreducible remainder, i.e. the cumulant parallel-spin SF
] and a nonreducible remainder, i.e. the cumulant parallel-spin SF![]() . The advantage of such a partitioning stems from the fact that the cumulant SFs
. The advantage of such a partitioning stems from the fact that the cumulant SFs ![]() are given within perturbation theory by linked (and therefore size-extensive) diagrams with two open particle-hole lines and arbitrary numbers of closed loops. As usual, the divergent terms are eliminated by a partial summation known as “the random phase approximation” (RPA) with the physical meaning of long-range correlations (screening), which becomes exact at the high-density limit of
are given within perturbation theory by linked (and therefore size-extensive) diagrams with two open particle-hole lines and arbitrary numbers of closed loops. As usual, the divergent terms are eliminated by a partial summation known as “the random phase approximation” (RPA) with the physical meaning of long-range correlations (screening), which becomes exact at the high-density limit of ![]() [23] [24] . RPA is a general method to treat the quantum-mechanical many-body problem, successfully applied not only to the HEG. It is now implemented in electronic structure codes for both solids and molecules [25] . A recent discussion concerns its failure when applied to the dissocia- tion of
[23] [24] . RPA is a general method to treat the quantum-mechanical many-body problem, successfully applied not only to the HEG. It is now implemented in electronic structure codes for both solids and molecules [25] . A recent discussion concerns its failure when applied to the dissocia- tion of![]() : it is exact at the dissociation limit, but very inaccurate at intermediate internuclear distances, see Figure 1 in [26] . This RPA has been applied to the HEG quantities e,
: it is exact at the dissociation limit, but very inaccurate at intermediate internuclear distances, see Figure 1 in [26] . This RPA has been applied to the HEG quantities e, ![]() , n(k), and
, n(k), and![]() . There have been recent efforts to obtain n(k) and S(q) beyond RPA [7] [15] . In those publications, analytical constraints and fit- ting procedures to quantum-Monte-Carlo data (as “amends” for experimental data) have been combined for the best possible results. Other attempts to go beyond RPA and quantum-Monte-Carlo calculations are the operator- product expansion (OPE) [27] and the machine learning methods [28] . In the following text, the RPA is com- bined with the cumulant analysis described above. Altogether, the available data on the static SFs
. There have been recent efforts to obtain n(k) and S(q) beyond RPA [7] [15] . In those publications, analytical constraints and fit- ting procedures to quantum-Monte-Carlo data (as “amends” for experimental data) have been combined for the best possible results. Other attempts to go beyond RPA and quantum-Monte-Carlo calculations are the operator- product expansion (OPE) [27] and the machine learning methods [28] . In the following text, the RPA is com- bined with the cumulant analysis described above. Altogether, the available data on the static SFs ![]() of the HEG are compiled and analyzed from a new viewpoint, namely the cumulant decomposition, continuing earlier attempts in that direction [7] [10] [29] - [32] . From a formal point of view, the present study is closely re- lated to the work of P. Gori-Giorgi et al. [15] .
of the HEG are compiled and analyzed from a new viewpoint, namely the cumulant decomposition, continuing earlier attempts in that direction [7] [10] [29] - [32] . From a formal point of view, the present study is closely re- lated to the work of P. Gori-Giorgi et al. [15] .
The paper is organized as follows. In Section 2, the 2-matrix ![]() and its cumulant decomposition is intro- duced. It is shown how the SFs
and its cumulant decomposition is intro- duced. It is shown how the SFs ![]() and
and ![]() follow from
follow from![]() . Their relation to the PDs
. Their relation to the PDs ![]() via the Fourier transform is elucidated in Appendix A, where the cusp and curvature theorems are summarized as well. In Section 3, the antiparallel-spin SFs are derived within RPA [the necessary technical details (particle- hole propagator, etc.) being given in Appendix B]. The normalization of
via the Fourier transform is elucidated in Appendix A, where the cusp and curvature theorems are summarized as well. In Section 3, the antiparallel-spin SFs are derived within RPA [the necessary technical details (particle- hole propagator, etc.) being given in Appendix B]. The normalization of ![]() yields the short-range correla- tion parameter
yields the short-range correla- tion parameter![]() . In Section 4, the cumulant decomposition of the parallel-spin SFs with a complicated exchange integral is presented. The fourth moment of
. In Section 4, the cumulant decomposition of the parallel-spin SFs with a complicated exchange integral is presented. The fourth moment of ![]() yields another short-range correlation parameter, namely
yields another short-range correlation parameter, namely![]() . Table 1 and Table 2 summarize the small- and large-q behavior and the normalization of the SFs. Section 5 concludes the paper with a summary and an outlook.
. Table 1 and Table 2 summarize the small- and large-q behavior and the normalization of the SFs. Section 5 concludes the paper with a summary and an outlook.
2. Basic Equations
The functions mentioned above, i.e. ![]() and
and![]() , determine the total energy
, determine the total energy ![]() via the kinetic energy
via the kinetic energy ![]() and the interaction energy
and the interaction energy![]() ,
,
![]() (2.1)
(2.1)
respectively. In Equation (2.1), ![]() is the classical plasma frequency with
is the classical plasma frequency with![]() . The momenta
. The momenta ![]() are measured in units of
are measured in units of![]() , energies (including
, energies (including![]() ) in units of
) in units of ![]() [in a.u. it is
[in a.u. it is![]() ]. The GGSB analysis [15] is based upon the decomposition
]. The GGSB analysis [15] is based upon the decomposition ![]() with the term
with the term
![]() (2.2)
(2.2)
of the ideal Fermi gas with ![]() and the term
and the term ![]() vanishing at the high-density limit
vanishing at the high-density limit![]() , which corresponds to “no Coulomb repulsion”. The linear-cubic combination
, which corresponds to “no Coulomb repulsion”. The linear-cubic combination ![]() that appears sever- al times in the following derivations may be regarded as the ideal-Fermi-gas term.
that appears sever- al times in the following derivations may be regarded as the ideal-Fermi-gas term. ![]() has a simple geome- trical meaning: it is the average volume accessible to the occupied momentum when excited by a transfer mo- mentum of amplitude
has a simple geome- trical meaning: it is the average volume accessible to the occupied momentum when excited by a transfer mo- mentum of amplitude ![]() [33] . The interaction energy in the lowest order [i.e. with
[33] . The interaction energy in the lowest order [i.e. with![]() ] equals
] equals![]() .
.
It is interesting to note that the plasmon sum rule [34] requires ![]() to possess the small-q asymptotics of
to possess the small-q asymptotics of
![]() , where
, where ![]() is the classical plasma frequency (in units of
is the classical plasma frequency (in units of![]() ). [From the f-sum rule or Thomas-Reich-Kuhn sum rule of the dynamic SF
). [From the f-sum rule or Thomas-Reich-Kuhn sum rule of the dynamic SF ![]() follows the plasmon sum rule
follows the plasmon sum rule ![]() of the static SF
of the static SF![]() .] At first glance, this asymptotic behavior appears incom- patible with the linear dependence of
.] At first glance, this asymptotic behavior appears incom- patible with the linear dependence of ![]() on
on ![]() around
around![]() . However, these two observations are rea- dily reconciled by writing
. However, these two observations are rea- dily reconciled by writing
![]() (2.3)
(2.3)
where ![]() is a function with the asymptotics
is a function with the asymptotics ![]() and
and![]() .
.
In this paper, an alternative is presented, namely
![]() (2.4)
(2.4)
Note that what is called ![]() in [10] is named here
in [10] is named here![]() . Equation (2.4) is the so-called cumulant de-
. Equation (2.4) is the so-called cumulant de-
composition into the “Hartree-Fock” component![]() , reducible to the 1-body quantity
, reducible to the 1-body quantity![]() , which fol- lows from the exact 1-matrix, and the non-reducible “cumulant” component
, which fol- lows from the exact 1-matrix, and the non-reducible “cumulant” component![]() , such that for
, such that for ![]() it is
it is ![]() and consequently
and consequently![]() . In this cumulant decomposition, the Coulomb repulsion
. In this cumulant decomposition, the Coulomb repulsion ![]() enters the SF
enters the SF ![]() at two places: 1) the “Fock term”
at two places: 1) the “Fock term” ![]() via the correlated momentum distribution
via the correlated momentum distribution ![]() and 2) the cumulant SF
and 2) the cumulant SF ![]() via linked diagrams, whereas in the GGSB decomposition the Coulomb repulsion is hidden only in
via linked diagrams, whereas in the GGSB decomposition the Coulomb repulsion is hidden only in ![]() that (in the cumulant “language”) equals
that (in the cumulant “language”) equals ![]() with
with ![]() [which results from
[which results from![]() ]. For plots of
]. For plots of ![]() see Figure 1 in paper I of [35] . The Fock term
see Figure 1 in paper I of [35] . The Fock term ![]() brings in the momentum distribution
brings in the momentum distribution ![]() with its nonanalytical pecu- liarities, caused by the RPA long-range correlation. The complexity of the HEG manifests itself in nonanalytici- ties or singularities of the type
with its nonanalytical pecu- liarities, caused by the RPA long-range correlation. The complexity of the HEG manifests itself in nonanalytici- ties or singularities of the type ![]() or
or![]() , see e.g.
, see e.g. ![]() or
or![]() . This gives rise to the k- or q-dependences in relation to the dependence on rs. For example, according to the perturbation theory,
. This gives rise to the k- or q-dependences in relation to the dependence on rs. For example, according to the perturbation theory, ![]() should behave like
should behave like ![]() for small rs. This is true for k values away from the Fermi edge (i.e.
for small rs. This is true for k values away from the Fermi edge (i.e. ![]() and
and![]() ). However, at the Fermi edge
). However, at the Fermi edge ![]() involves terms like
involves terms like ![]() or it jumps as
or it jumps as![]() . This im- plies a contribution
. This im- plies a contribution ![]() that equals
that equals![]() , see [29] .
, see [29] .
The cumulant decomposition seems to be more complicated than its conventional counterpart but, on the oth- er hand, it may be considered a more natural partitioning. This is so because, within the many-body perturbation theory, the cumulant SF ![]() is given by linked diagrams, whereas
is given by linked diagrams, whereas ![]() contains also unlinked diagrams.
contains also unlinked diagrams.
As already mentioned above, the spin-summed SF is given by![]() . In terms of the cumu- lant SFs
. In terms of the cumu- lant SFs![]() , these quantities read
, these quantities read
![]() (2.5)
(2.5)
where![]() , in agreement with Equation (2.4). The negative sign in front of
, in agreement with Equation (2.4). The negative sign in front of ![]() en- sures the positive normalization of the cumulant SFs. Note that
en- sures the positive normalization of the cumulant SFs. Note that ![]() (the perfect screening sum rule) implies
(the perfect screening sum rule) implies ![]() and
and![]() , the latter relating the 1-body quantity
, the latter relating the 1-body quantity ![]() to the 2-body quantities
to the 2-body quantities![]() . The analogs of Equations (2.4) and (2.5) in the direct space, including Fourier transforms and normalizations, are given in Appendix A together with the cusp and curvature theorems for
. The analogs of Equations (2.4) and (2.5) in the direct space, including Fourier transforms and normalizations, are given in Appendix A together with the cusp and curvature theorems for ![]() and
and![]() , respectively, which are short-range correlation parameters of
, respectively, which are short-range correlation parameters of![]() .
.
The original definitions of the 1- and 2-body RDMs in terms of the anticommuting creation and annihiliation operators ![]() and
and![]() , respectively, are given by
, respectively, are given by
![]() (2.6)
(2.6)
The short hands ![]() and
and ![]() are used throughout the text,
are used throughout the text, ![]()
![]() [instead of
[instead of![]() ].
].
The hermiticity of ![]() is obvious and the permutational antisymmetry means that
is obvious and the permutational antisymmetry means that ![]() when 1 and 2 or 1' and 2' are interchanged.
when 1 and 2 or 1' and 2' are interchanged. ![]() is the total particle-number operator. The ground state
is the total particle-number operator. The ground state ![]() is an
is an ![]() - body state, hence
- body state, hence ![]() and
and ![]() are
are ![]() -body states, and thus
-body states, and thus
![]() (2.7)
(2.7)
holds for the normalization. The corresponding contraction sum rule
![]() (2.8)
(2.8)
describes how the 1-matrix ![]() for finite
for finite ![]() results from the 2-matrix
results from the 2-matrix![]() . Equation (2.8) does not permit the above mentioned thermodynamic limit.
. Equation (2.8) does not permit the above mentioned thermodynamic limit.
A way towards a size-extensive contraction is the cumulant decomposition. This means to define the cumulant 2-matrix ![]() with
with
![]() (2.9)
(2.9)
This matrix obviously has the spin structure
![]() (2.10)
(2.10)
with the symmetric and antisymmetric 2-body spin functions
![]() (2.11)
(2.11)
Equations (2.10) and (2.11) define ![]() (which does not change sign under the exchange
(which does not change sign under the exchange ![]() or
or![]() ) and
) and ![]() (which changes sign under these exchanges). With
(which changes sign under these exchanges). With ![]() , the dimensionless cumulant 2-matrices
, the dimensionless cumulant 2-matrices ![]() are introduced. The next step involves deriving
are introduced. The next step involves deriving ![]() (for electron pairs with antiparallel spins) and
(for electron pairs with antiparallel spins) and ![]() (for electron pairs with parallel spins) from
(for electron pairs with parallel spins) from![]() . With
. With ![]() and
and ![]() together with
together with ![]() for “a” or
for “a” or ![]() for “p”, Equation (2.10) leads to
for “p”, Equation (2.10) leads to
![]() (2.12)
(2.12)
respectively. Here and in the following, the arguments ![]() of these matrices are suppressed for the sake of convenience. Their diagonals (for which
of these matrices are suppressed for the sake of convenience. Their diagonals (for which ![]() and
and![]() ) are denoted by
) are denoted by ![]() and
and![]() . They determine the normalizations
. They determine the normalizations
![]() (2.13)
(2.13)
where![]() . Their Fourier transforms (with the integral operator
. Their Fourier transforms (with the integral operator![]() ) yield the desired cumulant SFs,
) yield the desired cumulant SFs,
![]() (2.14)
(2.14)
see also Appendix A. A consequence of Equation (2.14) and Equations (A.6)-(A.8) is that the short-range cor- relation determines the asymptotic large-q behavior of the SFs and their normalizations.
Where do the cumulant 2-matrices ![]() come from? As mentioned above, they are given by linked diagrams. Each direct diagram
come from? As mentioned above, they are given by linked diagrams. Each direct diagram ![]() with two open particle-hole lines (one running from
with two open particle-hole lines (one running from ![]() to
to ![]() and another one from
and another one from ![]() to
to![]() ) is associated with an exchange diagram
) is associated with an exchange diagram![]() , see for example Figure 2(a) and Figure 3(a). Thus, a series of diagram pairs
, see for example Figure 2(a) and Figure 3(a). Thus, a series of diagram pairs ![]() exists from which the building elements
exists from which the building elements ![]() and
and ![]() follow. The next step defines the singlet/triplet components
follow. The next step defines the singlet/triplet components ![]() in terms of these diagrams, the relations
in terms of these diagrams, the relations
![]() (2.15)
(2.15)
following from Equation (2.12). So, the spin-averaged sum ![]() can be written differently: The a- and p-compo- nents
can be written differently: The a- and p-compo- nents ![]() are equally weighted, whereas the singlet- and triplet-components
are equally weighted, whereas the singlet- and triplet-components ![]() have the weights equaling 1/4 and 3/4, and the components
have the weights equaling 1/4 and 3/4, and the components ![]() have the weights equaling 1 and
have the weights equaling 1 and![]() , respectively. The same holds for the PDs
, respectively. The same holds for the PDs![]() . On the other hand, for the cumulant SFs
. On the other hand, for the cumulant SFs ![]() one has:
one has:
![]() (2.16)
(2.16)
Note the slightly different definitions of the spin-summed quantities![]() ,
, ![]() , and
, and ![]() on one hand, and
on one hand, and ![]() and
and ![]() on the other.
on the other.
With ![]() and
and ![]() given from the Feynman diagrams and with
given from the Feynman diagrams and with ![]() and
and ![]() following from them, the spin-resolved components of the interaction energy
following from them, the spin-resolved components of the interaction energy ![]() are
are
![]() (2.17)
(2.17)
and
![]() (2.18)
(2.18)
which can be written as![]() . Thus,
. Thus, ![]() ,
,![]() . In the following, RPA is used (index “r”) and the terms
. In the following, RPA is used (index “r”) and the terms ![]() and
and ![]() mean all the (hopefully small) contributions beyond RPA:
mean all the (hopefully small) contributions beyond RPA: ![]() and
and![]() .
.
3. Antiparallel Spins: The Coulomb Hole
We move through the chain![]() , where “a” means antiparallel spins and “d” means “direct” diagrams (of the type depicted in Figure 2(a)). In its Cartesian space representation,
, where “a” means antiparallel spins and “d” means “direct” diagrams (of the type depicted in Figure 2(a)). In its Cartesian space representation, ![]() is given by (using the definitions of Appendix B)
is given by (using the definitions of Appendix B)
![]() (3.1)
(3.1)
with the abbreviations ![]() and
and![]() . [Remember to read
. [Remember to read ![]() instead of
instead of![]() .] The integral operator
.] The integral operator ![]() generalizes the particle-hole propagator
generalizes the particle-hole propagator![]() , see Equation (B.4). The diagonal elements
, see Equation (B.4). The diagonal elements ![]() define the cumulant PD [see Equation (B.5)]
define the cumulant PD [see Equation (B.5)]
![]() (3.2)
(3.2)
When going from Equation (3.1) to Equation (3.2), the contour integration![]() , which replaces the fre- quency integration by the velocity integration, leads to the real function
, which replaces the fre- quency integration by the velocity integration, leads to the real function ![]() for the particle- hole propagator, see e.g. Equation (B.1) in [11] . This leads to Equation (B.5) taking the form
for the particle- hole propagator, see e.g. Equation (B.1) in [11] . This leads to Equation (B.5) taking the form ![]()
![]() , where
, where ![]() is referred to as the Macke function [23] [36] [37] . The effective interaction
is referred to as the Macke function [23] [36] [37] . The effective interaction
![]() is the RPA screened Coulomb interaction with a Yukawa-like cut-off
is the RPA screened Coulomb interaction with a Yukawa-like cut-off![]() ,
,![]() . The reverse replacement
. The reverse replacement ![]() can- cels out with
can- cels out with![]() , thus restoring the original perturbation expression in the lowest order. The
, thus restoring the original perturbation expression in the lowest order. The
qualitative behavior of ![]() is depicted in Figure 11 of [7] ; it begins at
is depicted in Figure 11 of [7] ; it begins at ![]() as a positive number and then decreases, becoming negative, and finally approaches zero from below, ensuring that its normalization vanishes, see Equation (A.6).
as a positive number and then decreases, becoming negative, and finally approaches zero from below, ensuring that its normalization vanishes, see Equation (A.6).
The Fourier transform of ![]() is the cumulant SF
is the cumulant SF ![]() within RPA:
within RPA:
![]() (3.3)
(3.3)
[38] . Note that ![]() parametrically depends on
parametrically depends on![]() , approaching the Macke function
, approaching the Macke function ![]() for
for ![]() [with the properties (B.8), see also Figure 4];
[with the properties (B.8), see also Figure 4]; ![]() may be referred to as the “generalized Macke function”.
may be referred to as the “generalized Macke function”. ![]() determines
determines ![]() via
via![]() , which yields the interaction energy of the antiparallel spin pairs
, which yields the interaction energy of the antiparallel spin pairs
![]() (3.4)
(3.4)
with ![]() at the high-density limit. The short-range correlation parameter
at the high-density limit. The short-range correlation parameter
![]() (3.5)
(3.5)
also follows from ![]() in RPA with
in RPA with
![]() (3.6)
(3.6)
at the high-density limit [38] - [40] . Actually, it is exactly this high-density behavior of ![]() and
and ![]() for
for ![]() that results from the ladder theory, which constitutes the best method to treat the short-range correlation [41] - [46] (for the recent developments see [27] ). The correctness of Equations (3.3)-(3.6) confirms the starting point (3.1).
that results from the ladder theory, which constitutes the best method to treat the short-range correlation [41] - [46] (for the recent developments see [27] ). The correctness of Equations (3.3)-(3.6) confirms the starting point (3.1).
How does ![]() behave for small
behave for small![]() ?
?
![]() (3.7)
(3.7)
in agreement with an ansatz of Iwamoto [47] . The coefficients ![]() are due to multipair and quasiparticle-qua- sihole excitations, respectively. They follow from
are due to multipair and quasiparticle-qua- sihole excitations, respectively. They follow from ![]() as
as ![]() and
and ![]() [48] . Note that the region
[48] . Note that the region ![]() shrinks with decreasing
shrinks with decreasing ![]() and finally vanishes for
and finally vanishes for![]() . As
. As ![]() contains (in the paramagnetic gas) half of the plasmon term, the other half has to come from
contains (in the paramagnetic gas) half of the plasmon term, the other half has to come from![]() , which also has to compensate the (
, which also has to compensate the (![]() -independent) ideal-Fermi-gas term.
-independent) ideal-Fermi-gas term.
In the transitional region between the small and large values of ![]() there is a peculiar point. Namely, upon approaching from below the transition momenta of
there is a peculiar point. Namely, upon approaching from below the transition momenta of![]() , the topology changes from two overlapping to two non-overlapping Fermi spheres. This topology change causes a jump discontinuity in
, the topology changes from two overlapping to two non-overlapping Fermi spheres. This topology change causes a jump discontinuity in ![]() and
and ![]() at
at ![]() [36] , namely
[36] , namely
![]() (3.8)
(3.8)
the ellipsis representing the terms beyond RPA. In the Cartesian space these jump discontinuities cause the Friedel oscillations in![]() . They make interpolations between
. They make interpolations between ![]() and
and ![]() with Padé approximants [49] or the robust interpolation scheme [50] questionable.
with Padé approximants [49] or the robust interpolation scheme [50] questionable.
How does ![]() of Equation (3.3) behave for
of Equation (3.3) behave for![]() ? As the large-q asymptotics does not require the RPA, the perturbation theory holds in the lowest order, hence in Equation (3.3) the “descreening” replacement
? As the large-q asymptotics does not require the RPA, the perturbation theory holds in the lowest order, hence in Equation (3.3) the “descreening” replacement ![]() is possible. The integration over
is possible. The integration over ![]() yields the Macke function
yields the Macke function ![]() with the large-q asymp- totics (B.8) starting with
with the large-q asymp- totics (B.8) starting with![]() . Thus, for
. Thus, for ![]() one has
one has
![]() (3.9)
(3.9)
Are there perhaps corrections due to terms beyond RPA? Indeed, the electron-electron coalescence cusp theo- rem ![]() together with the Kimball trick [51] makes the first term
together with the Kimball trick [51] makes the first term ![]() decorated with an additional factor
decorated with an additional factor![]() . One may expect the next term to be modified in a similar way, thus
. One may expect the next term to be modified in a similar way, thus
![]() (3.10)
(3.10)
with unknown correlation parameters ![]() and
and ![]() vanishing for
vanishing for ![]() and with the beyond-RPA term
and with the beyond-RPA term ![]() different from
different from![]() . The meaning of Equation (3.10) is as follows: the short-range correlation parameter
. The meaning of Equation (3.10) is as follows: the short-range correlation parameter ![]() determines the large-wavenumber asymptotics of
determines the large-wavenumber asymptotics of ![]() [41] [51] [52] . Because
[41] [51] [52] . Because ![]() depends on the parameter
depends on the parameter![]() , one may read Equation (3.5) as an integral equation to be solved iteratively. One may also ask how to modify the RPA-result
, one may read Equation (3.5) as an integral equation to be solved iteratively. One may also ask how to modify the RPA-result ![]() of Equation (3.3) in such a way that it absorbs the correct large-q behavior (3.10).
of Equation (3.3) in such a way that it absorbs the correct large-q behavior (3.10).
4. Parallel Spins: The Fermi Hole
For the parallel-spin, SF it is appropriate to write it as ![]() with
with![]() ,
, ![]() , and
, and![]() . Thus besides
. Thus besides ![]() one also needs the quantities
one also needs the quantities ![]() and
and![]() , which arise from the same source, namely
, which arise from the same source, namely![]() .
. ![]() and
and ![]() do not contribute to the normalization of
do not contribute to the normalization of![]() , but they do contri- bute to the interaction energy
, but they do contri- bute to the interaction energy ![]() [Equation (2.13)] and to the on-top Fermi hole curvature [Equation (4.12)]. Whereas
[Equation (2.13)] and to the on-top Fermi hole curvature [Equation (4.12)]. Whereas ![]() describes the smooth transition from 0 for small
describes the smooth transition from 0 for small ![]() to 1 for
to 1 for ![]() as it is known from the ideal- Fermi gas, the term
as it is known from the ideal- Fermi gas, the term ![]() describes the interaction induced corrections.
describes the interaction induced corrections.
![]() is known to some extent (at least sufficient for a qualitative discussion). As it can be seen from Figure 1 of [35] , it is
is known to some extent (at least sufficient for a qualitative discussion). As it can be seen from Figure 1 of [35] , it is ![]() for
for ![]() and
and ![]() for
for ![]() with
with ![]() defining
defining![]() . The Fock function
. The Fock function ![]() defined in Equation (2.4) contributes to
defined in Equation (2.4) contributes to![]() . It has the properties (4.1)-(4.4):
. It has the properties (4.1)-(4.4):
![]() (4.1)
(4.1)
The quantity ![]() is referred to as the Löwdin parameter or the index of non-idempotency. [P.-O. Löwdin was first to address the meaning of the trace of the squared 1-matrix.] It is a correlation parameter that measures the correlation-induced non-idempotency of the momentum distribution
is referred to as the Löwdin parameter or the index of non-idempotency. [P.-O. Löwdin was first to address the meaning of the trace of the squared 1-matrix.] It is a correlation parameter that measures the correlation-induced non-idempotency of the momentum distribution ![]() and vanishes for
and vanishes for![]() . For the dependence of
. For the dependence of ![]() on
on ![]() see [7] . For the kinetic part of the correlation energy
see [7] . For the kinetic part of the correlation energy ![]() it holds
it holds
![]() (4.2)
(4.2)
The small- and large-q asymptotics of ![]() are
are
![]() (4.3)
(4.3)
respectively. The small ![]() behavior has been demonstrated with the decomposition
behavior has been demonstrated with the decomposition![]() , where
, where ![]() is continuous (jump-free), see Equation (3.8) in [7] or Equation (5.1) in [35] . The quantity
is continuous (jump-free), see Equation (3.8) in [7] or Equation (5.1) in [35] . The quantity ![]() is the quasiparticle weight with
is the quasiparticle weight with ![]() within RPA. Note the non- analytical behavior of
within RPA. Note the non- analytical behavior of ![]() with terms
with terms ![]() and note that here the prefactor of the ideal-Fermi-gas term depends on
and note that here the prefactor of the ideal-Fermi-gas term depends on![]() . The Löwdin parameter
. The Löwdin parameter ![]() and the term quadratic in
and the term quadratic in ![]() have to be canceled out by
have to be canceled out by ![]() and replaced by the other half of the plasmon term. The large-q behavior arises from
and replaced by the other half of the plasmon term. The large-q behavior arises from ![]() [52] [53] , which is influenced by the short-range correlation parameter
[52] [53] , which is influenced by the short-range correlation parameter![]() , in analogy to
, in analogy to ![]() in Equations (3.10) and (4.12), respectively. At
in Equations (3.10) and (4.12), respectively. At![]() , there is a singular (topologically caused) jump
, there is a singular (topologically caused) jump
![]() (4.4)
(4.4)
Together with ![]() that arises from
that arises from![]() , it contributes to
, it contributes to![]() , the source of the Friedel oscillations in
, the source of the Friedel oscillations in![]() , whereas Equation (3.8) leads to the Friedel oscillations of
, whereas Equation (3.8) leads to the Friedel oscillations of![]() .
.
Next, ![]() is to be considered. It follows from the Feynman diagrams that
is to be considered. It follows from the Feynman diagrams that![]() , where “p” means parallel spins and “x” stands for exchange. According to Figure 3(a), the exchange counterpart to
, where “p” means parallel spins and “x” stands for exchange. According to Figure 3(a), the exchange counterpart to ![]() is given by
is given by
![]() (4.5)
(4.5)
Its diagonal elements define the cumulant PD (within RPA)
![]() (4.6)
(4.6)
and (after a tedious derivation) its Fourier transform turns out to be equal
![]() (4.7)
(4.7)
Unfortunately this complicated integral is not known so far as an explicit function of ![]() and
and![]() . If it is approximately substituted by
. If it is approximately substituted by![]() , then the integration over
, then the integration over ![]() yields the well-known energy denominator for the exchange term:
yields the well-known energy denominator for the exchange term:
![]() (4.8)
(4.8)
resulting in
![]() (4.9)
(4.9)
with![]() , in analogy to Equation (3.3).
, in analogy to Equation (3.3). ![]() is referred to as the Gutlé function [33] ; for its definition and properties see Equations (B.9), (B.10), and Figure 4. The quantity
is referred to as the Gutlé function [33] ; for its definition and properties see Equations (B.9), (B.10), and Figure 4. The quantity ![]() introduced above in Equation (4.7) can be regarded as its generalization. It is worth mentioning that, whereas in
introduced above in Equation (4.7) can be regarded as its generalization. It is worth mentioning that, whereas in ![]() the screened interaction
the screened interaction ![]() is necessary to remove the long-range divergences of the bare interaction
is necessary to remove the long-range divergences of the bare interaction![]() , this is not the case for
, this is not the case for ![]() as it follows from
as it follows from
![]() (4.10)
(4.10)
This is the famous result of Onsager, Mittag, and Stephen [54] [55] . The total interaction energy equals ![]() with
with![]() ,
, ![]() , and
, and![]() .
.
Within the approximation![]() , the exchange analog of Equation (3.5) reads
, the exchange analog of Equation (3.5) reads
![]() (4.11)
(4.11)
which agrees with Equation (3.5) in the corresponding approximation ![]() thanks to
thanks to![]() , see Equations (B.8) and (B.9).
, see Equations (B.8) and (B.9).
Furthermore, the on-top curvature ![]() of the Fermi hole follows from
of the Fermi hole follows from ![]() and, vice versa, it de- termines the large-q asymptotics of
and, vice versa, it de- termines the large-q asymptotics of![]() ,
,
![]() (4.12)
(4.12)
![]() does not contribute to the
does not contribute to the ![]() -term because its expansion begins with
-term because its expansion begins with![]() . The proof of Equation (4.12) employs the curvature theorem (A.11) and the Kimball trick. With
. The proof of Equation (4.12) employs the curvature theorem (A.11) and the Kimball trick. With ![]() and Equation (4.2) it is
and Equation (4.2) it is
![]() (4.13)
(4.13)
Note, that ![]() begins at the second order with
begins at the second order with ![]() and
and![]() , see Equation (B.8). The terms proportional to
, see Equation (B.8). The terms proportional to![]() , which would cause the integral
, which would cause the integral ![]() to diverge, cancel each other. At the high-density limit one has [56] [57]
to diverge, cancel each other. At the high-density limit one has [56] [57]
![]() (4.14)
(4.14)
with![]() .
.
Next the small-q behavior of ![]() is studied. Since the integral that enters Equation (4.7) is not known in a closed form, understanding the small-q behavior of
is studied. Since the integral that enters Equation (4.7) is not known in a closed form, understanding the small-q behavior of ![]() is not as straightforward as that of
is not as straightforward as that of![]() . For
. For ![]() with Equation (3.3) for
with Equation (3.3) for ![]() and Equation (4.7) for
and Equation (4.7) for ![]() it holds
it holds
![]() (4.15)
(4.15)
where the first ellipsis stands for higher-order terms [of the order ![]() or
or![]() ] of Equation (3.3) and the second ellipsis means the beyond-RPA terms
] of Equation (3.3) and the second ellipsis means the beyond-RPA terms ![]() beginning with
beginning with![]() . With
. With ![]() introduced above, for
introduced above, for ![]() it follows (within RPA) that
it follows (within RPA) that
![]() (4.16)
(4.16)
What contributes to the second term as a function of ![]() and
and ![]() remains to be studied. If we assume that its power expansion begins with
remains to be studied. If we assume that its power expansion begins with ![]() then, in analogy with Equation (3.7), one obtains
then, in analogy with Equation (3.7), one obtains
![]() (4.17)
(4.17)
and thus (again for![]() )
)
![]() (4.18)
(4.18)
in agreement with the plasmon sum rule and [15] . Note that ![]() and
and ![]() [from which
[from which ![]() follows] are indirectly related due to the fact that they have their common origin in the same Feynman diagrams. Namely, the starting point is the 4-point function
follows] are indirectly related due to the fact that they have their common origin in the same Feynman diagrams. Namely, the starting point is the 4-point function ![]() (see Figure 3(a) and also Figure 3(a) in [10] ). Upon carrying out the contraction procedure
(see Figure 3(a) and also Figure 3(a) in [10] ). Upon carrying out the contraction procedure![]() , followed by integration over
, followed by integration over ![]() and the Fourier transform for
and the Fourier transform for![]() , the source quantity for the momentum distribution
, the source quantity for the momentum distribution ![]() emerges, see [10] . On the other hand, upon taking the diagonal elements
emerges, see [10] . On the other hand, upon taking the diagonal elements ![]() and
and ![]() and carrying out the Fourier transform for
and carrying out the Fourier transform for ![]() one obtains
one obtains![]() . Certainly a further study of
. Certainly a further study of ![]() and
and ![]() within RPA and the beyond-RPA terms is warranted.
within RPA and the beyond-RPA terms is warranted.
Next, the large-q behavior of ![]() is studied. For
is studied. For![]() , the RPA quantity
, the RPA quantity ![]() approaches
approaches![]() . Thus, with the large-q asymptotics of
. Thus, with the large-q asymptotics of ![]() [see Equation (B.9)] and the beyond RPA-corrections analogue Equation (3.9), one obtains
[see Equation (B.9)] and the beyond RPA-corrections analogue Equation (3.9), one obtains
![]() (4.19)
(4.19)
perhaps with an additional correlation parameter![]() . In comparison with Equation (3.10), the
. In comparison with Equation (3.10), the ![]() tail is strongly enhanced (i.e. four times larger). Note that the difference of the prefactors is just
tail is strongly enhanced (i.e. four times larger). Note that the difference of the prefactors is just![]() . The large-q asymptotics of
. The large-q asymptotics of ![]() begins with the same expression as
begins with the same expression as![]() , thus
, thus ![]() begins with a term proportional to
begins with a term proportional to![]() :
:
![]() (4.20)
(4.20)
which makes ![]() and even
and even ![]() integrable, see Equation (A.14). Comparison with Equation (A.13), that follows from the curvature theorem [Equation (A.11)], shows that
integrable, see Equation (A.14). Comparison with Equation (A.13), that follows from the curvature theorem [Equation (A.11)], shows that ![]() as a sum rule, hence the asymptotics (4.12) is recovered.
as a sum rule, hence the asymptotics (4.12) is recovered.
The asymptotics of the SFs are summarized in Table 1 and Table 2; for the high-density limit with ![]() and
and![]() , the decoration drops off and the RPA limiting values reemerge. They show once more how the short-range correlation parameters determine the large-q asymptotics of the SFs, what is effected by the cusp and curvature theorems. As a side result, the on-top curvature of the Fermi hole is rederived in terms of
, the decoration drops off and the RPA limiting values reemerge. They show once more how the short-range correlation parameters determine the large-q asymptotics of the SFs, what is effected by the cusp and curvature theorems. As a side result, the on-top curvature of the Fermi hole is rederived in terms of![]() , see Equation (4.12). As it follows from Table 2 the function
, see Equation (4.12). As it follows from Table 2 the function![]() , defined at the beginning, see Equation (2.3), has the asymptotics
, defined at the beginning, see Equation (2.3), has the asymptotics ![]() and
and![]() . Besides, for
. Besides, for ![]() the inflexion point of
the inflexion point of ![]() is
is![]() ,
,![]() . For
. For ![]() this means
this means![]() . The inflexion-point trajectory for
. The inflexion-point trajectory for![]() , namely
, namely![]() , is in agreement with the slope of the ideal-Fermi-gas term at
, is in agreement with the slope of the ideal-Fermi-gas term at![]() .
.
5. Summary and Outlook
The focus of this paper is on the mathematics of the HEG, which on one hand is only a marginal point in the broad realm of correlated systems lacking rigorous solutions, but on the other constitutes an archetype of an extended many-body Fermi system. The small-q and large-q behaviors of the cumulant structure factors ![]() and the structure factors
and the structure factors ![]() as well as their normalizations are summarized in Table 1 and Table 2, respectively. In these tables, “a” stands for the electron pairs with antiparallel spins and “p” stands for the pairs with parallel spins. This analysis is based upon rigorous constraints such as the perfect screening sum rule (or the charge neutrality condition), the plasmon sum rule with its inflexion-point trajectory, the on-top (the zero electron-electron distance) theorems for the pair densities (cusp for “a” and curvature for “p”) and the “old” RPA (with the Feynman diagrams like those depicted in Figure 2(a) and Figure 3(a) giving exact results for
as well as their normalizations are summarized in Table 1 and Table 2, respectively. In these tables, “a” stands for the electron pairs with antiparallel spins and “p” stands for the pairs with parallel spins. This analysis is based upon rigorous constraints such as the perfect screening sum rule (or the charge neutrality condition), the plasmon sum rule with its inflexion-point trajectory, the on-top (the zero electron-electron distance) theorems for the pair densities (cusp for “a” and curvature for “p”) and the “old” RPA (with the Feynman diagrams like those depicted in Figure 2(a) and Figure 3(a) giving exact results for![]() ). They are all summarized in a way similar to the GGSB paper [15] (where
). They are all summarized in a way similar to the GGSB paper [15] (where ![]() has been pa- rameterized by combining analytical constraints with fitting of numerical data), but modified here under the novel cumulant point of view. This is done under the premise that the cumulant decompositions (2.4), (2.5), and (A.2) are more fundamental than the seemingly simpler decomposition
has been pa- rameterized by combining analytical constraints with fitting of numerical data), but modified here under the novel cumulant point of view. This is done under the premise that the cumulant decompositions (2.4), (2.5), and (A.2) are more fundamental than the seemingly simpler decomposition ![]() into the ideal-Fermi- gas component
into the ideal-Fermi- gas component ![]() and the interaction-induced remainder
and the interaction-induced remainder![]() . A formal analysis is presented with the spin structure (2.10) as a decisive point, leaving the task to parameterize
. A formal analysis is presented with the spin structure (2.10) as a decisive point, leaving the task to parameterize ![]() analytically as functions of
analytically as functions of ![]() and
and ![]() in a manner similar to that carried out in the GGSB paper [15] . The agreement of Equation (3.5) with the results of Macke [23] and Gell-Mann/Brueckner [24] and of Equation (4.10) with the calculations of Onsager et al. [54] also confirms the expressions (3.1) for “dr” and (4.5) for “xr”, where “r” means RPA and “d” and “x” mean direct and exchange Feynman diagrams, respectively, see Figure 2(a) and Figure 3(a). A complete and self-consistent RPA description needs both
in a manner similar to that carried out in the GGSB paper [15] . The agreement of Equation (3.5) with the results of Macke [23] and Gell-Mann/Brueckner [24] and of Equation (4.10) with the calculations of Onsager et al. [54] also confirms the expressions (3.1) for “dr” and (4.5) for “xr”, where “r” means RPA and “d” and “x” mean direct and exchange Feynman diagrams, respectively, see Figure 2(a) and Figure 3(a). A complete and self-consistent RPA description needs both![]() , which is available from Equation (3.3), and
, which is available from Equation (3.3), and![]() , which is actually given by a complicated exchange integral in Equation (4.7). This is needed for
, which is actually given by a complicated exchange integral in Equation (4.7). This is needed for ![]() in the combination
in the combination![]() , where the Fock term
, where the Fock term ![]() appears, which brings in the correlated momentum distribution
appears, which brings in the correlated momentum distribution ![]() with such terms as
with such terms as ![]() (i.e. the Löwdin or idempotency parameter) and
(i.e. the Löwdin or idempotency parameter) and ![]() (i.e. the jump of
(i.e. the jump of ![]() at
at![]() ), the quantity c to be compensated by
), the quantity c to be compensated by![]() . With
. With ![]() and
and![]() , the final expression for
, the final expression for ![]() is
is![]() . The combination
. The combination ![]() makes the term
makes the term ![]() to have the correct prefactor
to have the correct prefactor![]() , such that it disappears in
, such that it disappears in![]() , leaving twice the half plasmon term. One may ask how the Fock term
, leaving twice the half plasmon term. One may ask how the Fock term![]() , respectively the combination
, respectively the combination ![]() influences the PD
influences the PD![]() ?
?
It may be that in the present paper a deeply lying confrontation emerges, namely between 1) perturbation theory, which is linear in the Feynman diagrams, and 2) the cumulant decomposition, for which higher-order reduced density matrices in terms of products of lower-order ones are characteristic.
Going back to the starting point, which rests upon the belief that the geminals and the corresponding weights that diagonalize the cumulant 2-matrix, are the most “natural” 2-body quantities to describe an extended many- body Fermi system, establishes the direction of the future studies. If these quantities are known, then they de- termine the structure factors, the interaction energy ![]() and?according to [10] ?also the momentum dis- tribution
and?according to [10] ?also the momentum dis- tribution ![]() in terms of closed-form expressions. The next task would be to derive an effective approximate 2-body scheme (a modified 2-body Schrödinger equation or the Bethe-Salpeter equation?) from the hierarchy of contracted Schrödinger equations such that it yields the cumulant geminals and their weights.
in terms of closed-form expressions. The next task would be to derive an effective approximate 2-body scheme (a modified 2-body Schrödinger equation or the Bethe-Salpeter equation?) from the hierarchy of contracted Schrödinger equations such that it yields the cumulant geminals and their weights.
Note added in proof: Equations (4.7) and (4.16), Figure 3, and Ref. [25] at the middle of Section 1 are related to attempts around RPA+SOSEX, see [58] - [61] .
Acknowledgements
The authors thank P. Gori-Giorgi in particular for drawing their attention to the Kimball trick, and are grateful to C. Gutlé, and M. Holzmann for valuable discussions and to U. Saalmann for critically reading the manuscript. They acknowledge P. Fulde and the Max Planck Institute for the Physics of Complex Systems Dresden for supporting this work. One of the authors (J. C.) also acknowledges funding from NCN (Poland) under grant DEC-2012/07/B/ST4/00553.
References
- Fulde, P. (2012) Correlated Electrons in Quantum Matter. World Scientific, Singapore City.
- March, N.H. (1958) Physical Review, 110, 604.
- Olevano, V., Titov, A., Ladisa, M., Hämäläinen, K., Huotari, S. and Holzmann, M. (2012) Physical Review B, 86, Article ID: 195123.
- Holzmann, M., Bernu, B., Pierleoni, C., McMinis, J., Ceperley, D.M., Olevano, V. and Site, L.D. (2011) Physical Review Letters, 107, Article ID: 110402.
- Huotari, S., Soininen, J.A., Pylkkänen, T., Hämäläinen, K., Issolah, A., Titov, A., McMinis, J., Kim, J., Esler, K., Ceperley, D.M., Holzmann, M. and Olevano, V. (2010) Physical Review Letters, 105, Article ID: 086403.
- Nechaev, I.A. and Chulkov, E.V. (2006) Physical Review B, 73, Article ID: 165112.
- Gori-Giorgi, P. and Ziesche, P. (2002) Physical Review B, 66, Article ID: 235116.
- Ziesche, P. and Tasnádi, F. (2004) Annalen der Physik (Leipzig), 13, 124. (2004) 13, 623(E).
- Loos, P.-F. and Gill, P.W. (2011) Physical Review B, 84, Article ID: 033103.
- Ziesche, P. (2012) Physical Review A, 86, Article ID: 012508. (2014) Physical Review A, 89, 059902(E).
- Ziesche, P. (2010) Annals of Physics (Berlin), 522, 739.
- Sun, J., Perdew, J.P. and Seidl, M. (2010) Physical Review B, 81, Article ID: 085123.
- Gori-Giorgi, P. and Savin, A. (2006) Physical Review A, 73, Article ID: 032506.
- Diez Muiño, R., Nagy, I. and Echenique, P.M. (2005) Physical Review B, 72, Article ID: 075117.
- Gori-Giorgi, P., Sacchetti, F.and Bachelet, G.B. (2000) Physical Review B, 61, 7353. (2002) Physical Review B, 66, Article ID: 159901(E).
- Overhauser, A.W. (1995) Canadian Journal of Physics, 73, 683-686. http://dx.doi.org/10.1139/p95-101
- Coleman, A.J. and Yukalov, V.I. (2000) Reduced Density Matrices. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-58304-9
- Cioslowski, J. (2000) Many-Electron Densities and Reduced Density Matrices. Kluwer/Plenum, New York. http://dx.doi.org/10.1007/978-1-4615-4211-7
- Kong, L. and Valeev, E.F. (2011) Journal of Chemical Physics, 134, Article ID: 214109. http://dx.doi.org/10.1063/1.3596948
- Mazziotti, D.A. (2007) Reduced Density Matrices: With Applications to Many-Electron Atoms and Molecules. Wiley- Blackwell, Hoboken.
- Juhasz, T. and Mazziotti, D.A. (2006) Journal of Chemical Physics, 125, Article ID: 174105.
- Kutzelnigg, W. and Mukherjee, D. (1999) Journal of Chemical Physics, 110, 2800. http://dx.doi.org/10.1063/1.478189
- Macke, W. and Naturf, Z. (1950) Zeitschrift für Naturforschung, 5a, 192.1
- Gell-Mann, M. and Brueckner, K. (1957) Physical Review, 106, 364. http://dx.doi.org/10.1103/PhysRev.106.364
- Ren, X., Rinke, P., Joas, C. and Scheffler, M. (2012) Journal of Materials Science, 47, 7447-7471. http://dx.doi.org/10.1007/s10853-012-6570-4
- Heß elmann, A. and Andreas, A. (2011) Physical Review Letters, 106, Article ID: 093001.
- Hofmann, J., Barth, M. and Zwerger, W. (2013) Physical Review B, 87, Article ID: 235125.
- Bartók, A.B., Gillan, M.J., Manby, F.R. and Csányi, G. (2013) Physical Review B, 88, Article ID: 054104. http://dx.doi.org/10.1103/PhysRevB.88.054104
- Ziesche, P. and Cioslowski, J. (2005) Physica A, 356, 598-608.2 2>http://dx.doi.org/10.1016/j.physa.2005.04.0062
- Ziesche, P. (1992) Solid State Communications, 82, 597-602. http://dx.doi.org/10.1016/0038-1098(92)90108-L
- Ziesche, P. (2002) International Journal of Quantum Chemistry, 90, 342-354.3 http://dx.doi.org/10.1002/qua.969
- Ziesche, P. in , p. 33.
- Gutlé, C. (2006) Computer Physics Communications, 174, 836-845. http://dx.doi.org/10.1016/j.cpc.2005.12.010
- Pines, D. and Nozières, P. (1966) The Theory of Electron Liquids, Vol. I. Benjamin, New York.
- Ziesche, P. (2004) Physica Status Solidi (b), 241, 3544(I). (2005) (b) 242, 2051 (II).4
- Ziesche, P. (2007) Physica Status Solidi (b), 244, 2022.5
- Hoffman, G.G. (1992) Physical Review B, 45, 8730. http://dx.doi.org/10.1103/PhysRevB.45.8730
- Kimball, J.C. (1976) Physical Review B, 14, 2371. http://dx.doi.org/10.1103/PhysRevB.14.2371
- Geldart, D.J. (1967) Canadian Journal of Physics, 45, 3139-3161. http://dx.doi.org/10.1139/p67-260
- Geldart, D.J.W., Houghton, A. and Vosko, S.H. (1964) Canadian Journal of Physics, 42, 1938-1968. http://dx.doi.org/10.1139/p64-183
- Yasuhara, H. (1972) Solid State Communications, 11, 1481-1483. http://dx.doi.org/10.1016/0038-1098(72)90504-2
- Herbert, J.M. (2002) Physical Review A, 66, Article ID: 052502. http://dx.doi.org/10.1103/PhysRevA.66.052502
- Asgari, R., Polini, M., Davoudi, B. and Tosi, M.P. (2003) Solid State Communications, 125, 139-142. http://dx.doi.org/10.1016/S0038-1098(02)00782-2
- Qian, Z. (2006) Physical Review B, 73, Article ID: 035106. http://dx.doi.org/10.1103/PhysRevB.73.035106
- Cioslowski, J. and Ziesche, P. (2005) Physical Review B, 71, Article ID: 125105. (2005) Physical Review B, 72, Article ID: 239901 (E). http://dx.doi.org/10.1103/PhysRevB.71.125105
- Yasuhara, H. (1974) Physica, 78, 420-434. http://dx.doi.org/10.1016/0031-8914(74)90372-3
- Iwamoto, N. (1986) Physical Review A, 33, 1940.
- Wolfram Research Inc. (2012) Mathematica, Version 8.0. Wolfram Research Inc., Champaign.
- Wang, Y. and Perdew, J.P. (1991) Physical Review B, 44, 13298. http://dx.doi.org/10.1103/PhysRevB.44.13298
- Cioslowski, J. (2012) Journal of Chemical Physics, 136, Article ID: 044109. http://dx.doi.org/10.1063/1.3679657
- Kimball, J.C. (1973) Physical Review A, 7, 1648. http://dx.doi.org/10.1103/PhysRevA.7.1648
- Kimball, J.C. (1975) Journal of Physics A, 8, 1513. http://dx.doi.org/10.1088/0305-4470/8/9/021
- Yasuhara, H. and Kawazoe, Y. (1976) Physica A, 85, 416-424. http://dx.doi.org/10.1016/0378-4371(76)90060-1
- Onsager, L., Mittag, L. and Stephen, M.J. (1966) Annalen der Physik (Leipzig), 18, 71.6
- Glasser, M.L. (1984) Journal of Computational and Applied Mathematics, 10, 293-299. http://dx.doi.org/10.1016/0377-0427(84)90041-4
- Rassolov, V.A., Pople, J.A. and Ratner, M.A. (2000) Physical Review B, 62, 2232. http://dx.doi.org/10.1103/PhysRevB.62.2232
- Rajagopal, A.K., Kimball, J.C. and Banerjee, M. (1978) Physical Review B, 18, 2339. http://dx.doi.org/10.1103/PhysRevB.18.2339
- Freeman, D.L. (1977) Physical Review B, 15, 5512. http://dx.doi.org/10.1103/PhysRevB.15.5512
- Booth, G.H., Grüneis, A., Kresse, G. and Alavi, A. (2013) Nature, 493, 365-370. http://dx.doi.org/10.1038/nature11770
- Shepherd, J.J. and Grüneis, A. (2013) Physical Review Letters, 110, 22640. http://dx.doi.org/10.1103/PhysRevLett.110.226401
- Hummel, F. and Kresse, G. (2014) Verhandlungen der Deutschen Physikalischen Gesellschaft, Tieftemperaturphysik, 84.1.
Appendix A: The Cumulant Pair Densities and Their Cusp and Curvature Theorems
The analogue of Equation (2.4) in the direct space is
![]() (A.1)
(A.1)
with ![]() being the (dimensionless) 1-matrix [and
being the (dimensionless) 1-matrix [and ![]() of Equation (2.4) being the Fourier transform of
of Equation (2.4) being the Fourier transform of![]() ]. Equation (2.5) corresponds to the Coulomb and Fermi holes,
]. Equation (2.5) corresponds to the Coulomb and Fermi holes,
![]() (A.2)
(A.2)
with the spin-summed PDs ![]() and
and![]() . For the qualitative behavior of
. For the qualitative behavior of ![]() see Figure 11 in [7] or Figure 2 and Figure 3 in [31] . The PDs are the Fourier transformed SFs,
see Figure 11 in [7] or Figure 2 and Figure 3 in [31] . The PDs are the Fourier transformed SFs,
![]() (A.3)
(A.3)
![]() (A.4)
(A.4)
and
![]() (A.5)
(A.5)
The definition of the spin-summed SFs, namely ![]() and
and![]() , brings about the factors 1/2 in Equations (A.5)-(A.7). Note also the asymmetry with respect to “a” (Coulomb hole) and “p” (Fermi hole). The conditions
, brings about the factors 1/2 in Equations (A.5)-(A.7). Note also the asymmetry with respect to “a” (Coulomb hole) and “p” (Fermi hole). The conditions ![]() fix the normalizations of
fix the normalizations of![]() , known as the perfect screening sum rule, whereas the coalescing (or the on-top) values
, known as the perfect screening sum rule, whereas the coalescing (or the on-top) values ![]() and
and ![]() (as a conse- quence of the Pauli principle) fix the normalizations of
(as a conse- quence of the Pauli principle) fix the normalizations of ![]() and
and![]() , respectively, and
, respectively, and ![]() fixes the fourth moment of
fixes the fourth moment of![]() . In the following, the identities [obtained from Equations (A.3)-(A.5), res- pectively]
. In the following, the identities [obtained from Equations (A.3)-(A.5), res- pectively]
![]() (A.6)
(A.6)
![]() (A.7)
(A.7)
and
![]() (A.8)
(A.8)
are also used. For plots of ![]() with various values of the parameter
with various values of the parameter ![]() see [7] , Figure 11. For the on-top (the zero electron-electron distance) curvature of the Fermi hole, it holds according to Equation (A.2) that
see [7] , Figure 11. For the on-top (the zero electron-electron distance) curvature of the Fermi hole, it holds according to Equation (A.2) that
![]() (A.9)
(A.9)
as the consequence of![]() . Note that
. Note that ![]() and
and![]() .
.
Cusp and curvature theorems: The large-q behavior of ![]() is related to the electron-electron coal- escence theorems (a.k.a. the cusp theorems, “a” denoting antiparallel spin pairs) [31] [51] [52] [57]
is related to the electron-electron coal- escence theorems (a.k.a. the cusp theorems, “a” denoting antiparallel spin pairs) [31] [51] [52] [57]
![]() (A.10)
(A.10)
and the curvature theorems (with “p” standing for parallel spin pairs) [57]
![]() (A.11)
(A.11)
respectively. Therefore, the short-range parameters ![]() and
and ![]() determine their derivatives
determine their derivatives ![]() and
and![]() , respectively. These theorems allow one to correct the large-q behavior of the SFs and of
, respectively. These theorems allow one to correct the large-q behavior of the SFs and of ![]() and
and ![]() beyond RPA.
beyond RPA.
Proof of Equation (4.12): The Kimball trick is used [51] thanks to P. Gori-Giorgi. Namely, a function ![]() with the asymptotics of
with the asymptotics of ![]() for
for ![]() is defined first through
is defined first through![]() . Then, from the Fourier transform (A.4) and with the help of the Mathematica software [48] , one obtains
. Then, from the Fourier transform (A.4) and with the help of the Mathematica software [48] , one obtains
![]() (A.12)
(A.12)
from which the derivatives of ![]() [including
[including![]() ] follow. With the above curvature theorem (A.11), it finally results in Equation (A.9), which is equivalent with
] follow. With the above curvature theorem (A.11), it finally results in Equation (A.9), which is equivalent with
![]() (A.13)
(A.13)
Comparing this result with Equation (3.10), allows one to conclude that the sum rule ![]() holds. A side product of this analysis is
holds. A side product of this analysis is
![]() (A.14)
(A.14)
Proof: As an intermediate step towards the above expression for![]() , one derives (with the help of the Mathematica software [48] ) the equations
, one derives (with the help of the Mathematica software [48] ) the equations
![]() (A.15)
(A.15)
which lead to the first equation of Equation (A.14). From this result, the second equation follows by means of
![]() and Equation (A.9). Remark on the sign of
and Equation (A.9). Remark on the sign of![]() : According to Equation (A.7), the integral
: According to Equation (A.7), the integral ![]() has to vanish. This is because the negative asymptotics (4.16) of
has to vanish. This is because the negative asymptotics (4.16) of ![]() is compensated by the positive branch (4.17) for small
is compensated by the positive branch (4.17) for small![]() . An additional factor
. An additional factor ![]() suppressing the latter and enhancing the former. This makes the integral
suppressing the latter and enhancing the former. This makes the integral ![]() negative, implying
negative, implying![]() . For the function
. For the function![]() , see for example [7] .
, see for example [7] .
Appendix B: The Particle-Hole Propagator and the Special Functions I(q) and Ix(q)
The building elements of the RPA Feynman diagrams (cf. Figure 1, Figure 2(a), Figure 3(a)) are the Coulomb repulsion ![]() with the coupling constant
with the coupling constant ![]() and the one-body Green’s function of free electrons with
and the one-body Green’s function of free electrons with![]() ,
,
![]() (B.1)
(B.1)
From![]() , it follows that the particle-hole propagator
, it follows that the particle-hole propagator ![]() within RPA, given by
within RPA, given by
![]() (B.2)
(B.2)
results in
![]() (B.3)
(B.3)
The denominators contain the excitation energy ![]() to create a hole with the momentum
to create a hole with the momentum ![]() inside the Fermi sphere and a particle with the momentum
inside the Fermi sphere and a particle with the momentum ![]() outside the Fermi sphere. A complicated step function, defined by
outside the Fermi sphere. A complicated step function, defined by ![]() for
for ![]() and
and![]() , and 0 otherwise, arises from the Pauli principle. A ge- neralization of Equation (B.3) reads
, and 0 otherwise, arises from the Pauli principle. A ge- neralization of Equation (B.3) reads
![]() (B.4)
(B.4)
defining the integral operator![]() ,
,![]() .
.
In calculations of the cumulant SF ![]() (see Figure 2(b) with the bare Coulomb repulsion), the Macke function
(see Figure 2(b) with the bare Coulomb repulsion), the Macke function ![]() appears via
appears via
![]() (B.5)
(B.5)
When dealing with the corresponding exchange term ![]() (see Figure 3(b) with the bare Coulomb repulsion), one obtains by means of contour integration
(see Figure 3(b) with the bare Coulomb repulsion), one obtains by means of contour integration
![]() (B.6)
(B.6)
where
![]() (B.7)
(B.7)
defines the exchange counterpart ![]() of the Macke function
of the Macke function![]() . The functions
. The functions ![]() and
and ![]() have the following properties
have the following properties
![]()
![]()
![]()
![]() (B.8)
(B.8)
and
![]()
![]()
![]()
![]()
![]() (B.9)
(B.9)
see Figure 4. ![]() is known from the work of Macke [23] ; it is explicitly presented e.g. in [36] , where also
is known from the work of Macke [23] ; it is explicitly presented e.g. in [36] , where also ![]() is given, see Equation (C.2).
is given, see Equation (C.2). ![]() is known from Gutlé [33] . The original expression for
is known from Gutlé [33] . The original expression for ![]() can be markedly simplified for
can be markedly simplified for![]() , in which case
, in which case
![]() (B.10)
(B.10)
The small-q behavior ![]() causes the “Heisenberg divergence”. The asymptotics
causes the “Heisenberg divergence”. The asymptotics ![]() ensures finiteness of the integral
ensures finiteness of the integral![]() , which has been congenially calculated by Onsager et al. [54] , see Equation (4.10). The flattening in the small-q region, observed upon going from
, which has been congenially calculated by Onsager et al. [54] , see Equation (4.10). The flattening in the small-q region, observed upon going from ![]() to
to![]() , together with the “area conservation”
, together with the “area conservation”![]() , is partly compensated by the heavy enhancement of the
, is partly compensated by the heavy enhancement of the ![]() tail (from 2/5 to 8/5), see Figure 4. Both
tail (from 2/5 to 8/5), see Figure 4. Both ![]() and
and ![]() consist of two branches,which encounter each other at the Fermi edge with transition momenta
consist of two branches,which encounter each other at the Fermi edge with transition momenta![]() . They have a simple analytical behavior for
. They have a simple analytical behavior for ![]() and
and![]() , but “in between”, namely at
, but “in between”, namely at ![]() it is
it is
![]() (B.11)
(B.11)
with![]() ,
, ![]() for
for ![]() and
and![]() ,
, ![]() for
for![]() . For
. For ![]() it similarly holds
it similarly holds
![]() (B.12)
(B.12)
with (for![]() )
)
![]() (B.13)
(B.13)
The analog case ![]() is not known so far. The peculiar behavior at
is not known so far. The peculiar behavior at ![]() reminds of the behavior of
reminds of the behavior of ![]() near
near![]() , see [7] , Equations (6) and (7).
, see [7] , Equations (6) and (7).
Remark on the types: Note that indices like pl, a, p, d, x, dr, xr are to be represented by upright types, not by italics as this is falsely partly the case e.g. in Table 1 and Table 2.
NOTES
![]()
1Another approach with the same result and coining of the term “RPA” is due to D. Bohm and D. Pines (1953).
2In Equation (27) the correct prefactor is 2αrs/(5π).
3The last sentence of the Abstract should be deleted.
![]()
4It is shown, that the pair-density geminals, see [16] , do not satisfy the plasmon sum rule.
5In Appendix C the Macke function I(q) is explicitly given. The extension to the spinpolarized electron gas is in [37] .
6Here the exchange integral of the 3-dimensional HEG has been evaluated analytically. This rather herculean work was extended to the d-dimensional electron gas by M. L. Glasser [55] .




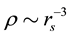 . Other characteristic quantities that depend parametrical- ly on rs are the total energy per electron e, from which follows the interaction energy
. Other characteristic quantities that depend parametrical- ly on rs are the total energy per electron e, from which follows the interaction energy 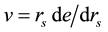 [2] , the momentum distribution
[2] , the momentum distribution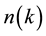 , and the static structure factors (SFs)
, and the static structure factors (SFs)  with “a” standing for electron pairs with antiparallel spins and “p” for pairs with parallel spins. For recent papers on the HEG, also known as jellium, see for example [3] - [15] . Recent GWA and QMC calculations for
with “a” standing for electron pairs with antiparallel spins and “p” for pairs with parallel spins. For recent papers on the HEG, also known as jellium, see for example [3] - [15] . Recent GWA and QMC calculations for 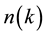 are [3] [4] . (For comparison with experiment see [5] . The value of
are [3] [4] . (For comparison with experiment see [5] . The value of 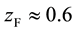 for rs = 3.9 agrees with the results, obtained in Refs. [6] [7] .)
for rs = 3.9 agrees with the results, obtained in Refs. [6] [7] .)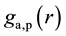 , which follow from the SFs by Fourier transform, and parameterized them in terms of certain 2-body wave functions (known as geminals) [16] . More general geminals should allow one to calculate not only the 2-body quantities
, which follow from the SFs by Fourier transform, and parameterized them in terms of certain 2-body wave functions (known as geminals) [16] . More general geminals should allow one to calculate not only the 2-body quantities , but also the 1-body quantity
, but also the 1-body quantity . Searching in this direction, one immediately encounters the hierarchy of the reduced density matrices (RDMs) and their cumulant decomposition. (The concept of RDM is of great importance in quantum chemistry, see [17] - [22] .) Here it is assumed that the 2-body RDM (2-matrix) is available from perturbation theory or otherwise (hierarchy truncation etc.) and, with the spin structure as a decisive point, it is elucidated how the contraction has to be performed for an extended system in such a way that the 1-body density
. Searching in this direction, one immediately encounters the hierarchy of the reduced density matrices (RDMs) and their cumulant decomposition. (The concept of RDM is of great importance in quantum chemistry, see [17] - [22] .) Here it is assumed that the 2-body RDM (2-matrix) is available from perturbation theory or otherwise (hierarchy truncation etc.) and, with the spin structure as a decisive point, it is elucidated how the contraction has to be performed for an extended system in such a way that the 1-body density 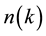 is obtained. In view of the thermodynamic limit, this procedure calls for the cumulant decomposition of the 2-matrix into its Hartree- Fock part
is obtained. In view of the thermodynamic limit, this procedure calls for the cumulant decomposition of the 2-matrix into its Hartree- Fock part 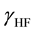 and its nonreducible remainder, the cumulant 2-matrix
and its nonreducible remainder, the cumulant 2-matrix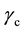 , which proves to be the source of both
, which proves to be the source of both  and
and  [10] . Diagonalization of
[10] . Diagonalization of  yields cumulant geminals and the corresponding weights (i.e. the spectral resolution).
yields cumulant geminals and the corresponding weights (i.e. the spectral resolution).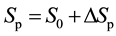 involves an unperturbed (ideal Fermi gas) term S0 and the interaction-induced term
involves an unperturbed (ideal Fermi gas) term S0 and the interaction-induced term 












































































































































































































































































































































































































































































































































































































































































