Journal of Modern Physics
Vol.5 No.12(2014), Article
ID:47739,4
pages
DOI:10.4236/jmp.2014.512106
Perturbation of Hydrogen Degenerate Levels and SO(4)
Enrico Onofri1,2
1Dipartimento di Fisica e Scienze della Terra, Università di Parma, Parma, Italy
2INFN, Gruppo Collegato di Parma, Parma, Italy
Email: enrico.onofri@unipr.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 22 February 2014; revised 21 March 2014; accepted 14 April 2014
ABSTRACT
We present a short note about the perturbative correction to Rydberg energies under a perturbation cosθ/rμ and discuss the role of SO(4) symmetry.
Keywords:Rydberg States, SO(4) Symmetry, Runge-Lenz-Pauli Vector

1. Introduction
The subject of this short note stems from a classroom exercise. I proposed my students to evaluate the effect on the degenerate levels of the hydrogen atom of a perturbation with potential energy . At the first order in perturbation theory this problem requires the diagonalization of the matrix representing the perturbation restricted to the
. At the first order in perturbation theory this problem requires the diagonalization of the matrix representing the perturbation restricted to the 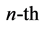 degenerate subspace (see Appendix A).
degenerate subspace (see Appendix A).
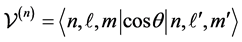 (1)
(1)
The problem in itself appears to involve a rather standard (and boring) calculation based on the properties of Laguerre and Legendre functions. To save time one can attack the problem using a computer algebra system, like Mathematica1 and the matrix  can be readily constructed; if we are lucky enough, its spectrum could be exhibited in closed form or at least in numerical terms. Now, the surprise is that the eigenvalues turn out to be all simple rationals of the form
can be readily constructed; if we are lucky enough, its spectrum could be exhibited in closed form or at least in numerical terms. Now, the surprise is that the eigenvalues turn out to be all simple rationals of the form  where m runs from
where m runs from  to
to  and they are
and they are  degenerate. The result is so simple that one cannot be satisfied by the brute-force calculation, and he or she is forced to look for some explanation. Obviously the first idea that comes to mind is that this result should rely on some Lie-algebraic property. In the following I’m going to explain how hydrogen’s
degenerate. The result is so simple that one cannot be satisfied by the brute-force calculation, and he or she is forced to look for some explanation. Obviously the first idea that comes to mind is that this result should rely on some Lie-algebraic property. In the following I’m going to explain how hydrogen’s 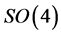 symmetry accounts for the result.
symmetry accounts for the result.
2. Dipole Operators and the SO(4) Generators
The origin of the Lie-theoretic explanation lies in one of the first papers about quantum mechanics [1] . In the book by Gottfried and Yan [2] 2 one can find all details in a masterly presentation. In this note, however, we present a somewhat simpler derivation, suitable for an introductory Quantum Mechanics course. In particular we give a simple derivation of Pauli’s link between  Casimir operator and the Hamiltonian, which cannot be found in most textbooks (see Appendix B). Other relevant information is contained in the recent paper [3] with generalization to higher multipoles.
Casimir operator and the Hamiltonian, which cannot be found in most textbooks (see Appendix B). Other relevant information is contained in the recent paper [3] with generalization to higher multipoles.
The fact is: hydrogen atom, in its simplest terms, described by the Hamiltonian , exhibits a larger degeneracy than required by rotational invariance, the
, exhibits a larger degeneracy than required by rotational invariance, the 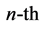 level being
level being  degenerate. This fact was related, since Pauli’s paper, to the presence of an extra conserved vector quantity, which in classical mechanics is known as the Laplace-Runge-Lenz vector and was used by Pauli in the calculation of the spectrum. This should be considered as the first example of dynamical symmetry in Quantum Mechanics. The quantum conserved vector is
degenerate. This fact was related, since Pauli’s paper, to the presence of an extra conserved vector quantity, which in classical mechanics is known as the Laplace-Runge-Lenz vector and was used by Pauli in the calculation of the spectrum. This should be considered as the first example of dynamical symmetry in Quantum Mechanics. The quantum conserved vector is
 (2)
(2)
where 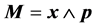 and
and . Since
. Since ![]() commutes with the Hamiltonian it can be normalized by adding a factor
commutes with the Hamiltonian it can be normalized by adding a factor 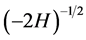 in such a way that
in such a way that  and
and 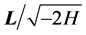 close the Lie algebra of
close the Lie algebra of 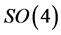 under commutation. In his 1926 paper Pauli showed that this fact was sufficient to derive Balmer’s formula and the “dipole matrix elements”
under commutation. In his 1926 paper Pauli showed that this fact was sufficient to derive Balmer’s formula and the “dipole matrix elements” 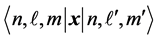 in terms of the matrix of
in terms of the matrix of 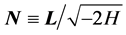 in the same
in the same 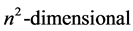 degenerate subspace. Denoting by
degenerate subspace. Denoting by  the orthogonal projector on the
the orthogonal projector on the 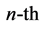 degenerate subspace, it is immediately realized that
degenerate subspace, it is immediately realized that ; no contributions arise from the term
; no contributions arise from the term 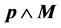 which has vanishing matrix elements between degenerate states since it coincides with the commutator
which has vanishing matrix elements between degenerate states since it coincides with the commutator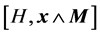 . Now, since N belongs to the Lie algebra of the symmetry group
. Now, since N belongs to the Lie algebra of the symmetry group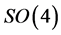 , its spectrum is fixed by group theory alone. Simply enough,
, its spectrum is fixed by group theory alone. Simply enough, 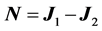 where
where 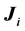 are the generators of the two
are the generators of the two 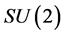 factors of
factors of . Since
. Since  and
and 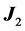 commute, and the total angular momentum is
commute, and the total angular momentum is 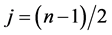 for each of them, the spectrum is simply given by
for each of them, the spectrum is simply given by 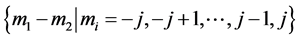 that is
that is  with degeneracy
with degeneracy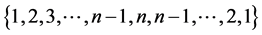 . As a result the spectrum of the matrix
. As a result the spectrum of the matrix 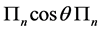 is precisely given, as anticipated, by
is precisely given, as anticipated, by
 (3)
(3)
For the sake of completeness we recall the detailed expression for the eigenfunctions and the matrix elements in appendix.
3. Conclusion
It is clear that the use of a symbolic algebra system can easily give the spectrum of the dipole x or, more generally, . For instance one can check immediately that the matrix identically vanishes for
. For instance one can check immediately that the matrix identically vanishes for , the case of the electric dipole perturbation. However the connection with group theory gives a deeper insight into the result, which by itself could remain a simple mathematical curiosity. Let us notice that in the classical book [4] by Condon and Shortley the calculations of the Stark effect perturbative corrections to the Balmer energies are beautifully obtained using parabolic coordinates, but the result of Equation (3) takes on a new light when interpreted group-theoretically.
, the case of the electric dipole perturbation. However the connection with group theory gives a deeper insight into the result, which by itself could remain a simple mathematical curiosity. Let us notice that in the classical book [4] by Condon and Shortley the calculations of the Stark effect perturbative corrections to the Balmer energies are beautifully obtained using parabolic coordinates, but the result of Equation (3) takes on a new light when interpreted group-theoretically.
Acknowledgements
This paper has a mere didactic interest and it is related to my thesis of 1968. It is my pleasure to thank Prof. Massimo Pauri, then my advisor and today Professor Emeritus at our Department, who taught me quite a lot about symmetry and group theory in Quantum Mechanics.
References
- Pauli, W. (1926) Zeitschrift fur Physik, 36, 336-363. http://dx.doi.org/10.1007/BF01450175
- Gottfried, K. and Yan, T.-M. (2004) Quantum Mechanics, Fundamentals. 2nd Edition, Springer, New York.
- Ostrovsky, V.N., Vrinceanu, D. and Flannery, M.R. (2006) Physical Review A, 74, Article ID: 022720.
- Condon, E.U. and Shortley, G.H. (1964) The Theory of Atomic Spectra. Cambridge University Press, Cambridge.
Appendix A
We adopt the convention for the hydrogen eigenfunctions as follows:

The non-vanishing matrix elements for 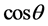 are explicitly given by
are explicitly given by
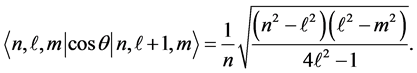
Appendix B
We prove the relation
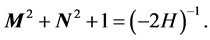 (4)
(4)
In classical mechanics it holds  which clearly cannot hold in quantum mechanics, since the left hand side annihilates the ground state. Quantum commutators provide the
which clearly cannot hold in quantum mechanics, since the left hand side annihilates the ground state. Quantum commutators provide the 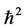 shift which fixes the ground state. This was emphasized by Pauli in [1] . Now to the proof: since the action of
shift which fixes the ground state. This was emphasized by Pauli in [1] . Now to the proof: since the action of  spans the whole energy level and the identity links together
spans the whole energy level and the identity links together  invariants, we can limit ourselves to check the validity of Equation (4) to
invariants, we can limit ourselves to check the validity of Equation (4) to  states. So we may reduce the proof to the more tractable identity
states. So we may reduce the proof to the more tractable identity
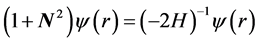
or, by defining , we are left to prove
, we are left to prove
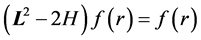 (5)
(5)
Now, on s-states the definition of ![]() gives
gives
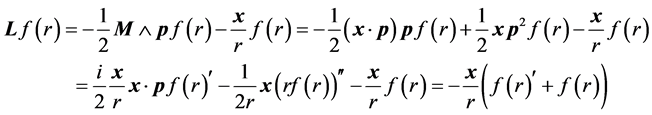
For instance ![]() annihilates
annihilates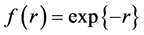 ,
,  has the value
has the value 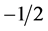 and the relation is satisfied. Now in general, instead of evaluating
and the relation is satisfied. Now in general, instead of evaluating  it’s easier to check Equation (5) on the quadratic form
it’s easier to check Equation (5) on the quadratic form

Indeed,
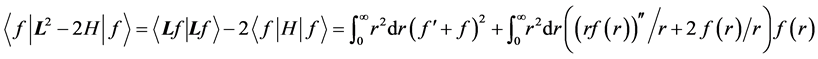
NOTES

1©Wolfram Research.

2I am indebted to Prof. G. Cicuta for attracting my attention to this reference.

