Received 17 November 2013; revised 16 December 2013; accepted 12 January 2014

ABSTRACT

We start recalling with critical eyes the mathematical methods used in gauge theory and prove that they are not coherent with continuum mechanics, in particular the analytical mechanics of rigid bodies (despite using the same group theoretical methods) and the well known couplings existing between elasticity and electromagnetism (piezzo electricity, photo elasticity, streaming birefringence). The purpose of this paper is to avoid such contradictions by using new mathematical methods coming from the formal theory of systems of partial differential equations and Lie pseudo groups. These results finally allow unifying the previous independent tentatives done by the brothers E. and F. Cosserat in 1909 for elasticity or H. Weyl in 1918 for electromagnetism by using respectively the group of rigid motions of space or the conformal group of space-time. Meanwhile we explain why the Poincaré duality scheme existing between geometry and physics has to do with homological algebra and algebraic analysis. We insist on the fact that these results could not have been obtained before 1975 as the corresponding tools were not known before.

Keywords:

Gauge Theory; Curvature; Torsion; Maurer-Cartan Forms; Maurer-Cartan Equations; Lie Groups; Lie Pseudo Groups; Differential Sequence; Janet Sequence; Spencer Sequence; Differential Module; Homological Algebra; Extension Modules

1. Introduction

It is usually accepted today in the literature that the physical foundations of what we shall simply call (classical) “gauge theory” (GT) can be found in the paper published by C.N. Yang and R.L. Mills in 1954 [1] . Having in mind the space-time formulation of electromagnetism (EM), the rough idea is to start with a manifold and a group in order to exhibit a procedure leading to a physical theory, namely a way to obtain fields and field equations from geometrical arguments on one side, both with a dual variational counterpart providing inductions and induction equations on the other side. Accordingly, the mathematical foundations of GT can be found in the references existing at this time on differential geometry and group theory, the best and most quoted one being the survey book [2] published by S. Kobayashi and K. Nomizu in 1963 (see also [3] -[6] ). The aim of this Introduction is to revisit these foundations and their applications with critical eyes, recalling them in a quite specific and self-contained way for later purposes.

The word “group” has been introduced for the first time in 1830 by Evariste Galois (1811-1832). Then this concept slowly passed from algebra (groups of permutations) to geometry (groups of transformations). It is only in 1880 that Sophus Lie (1842-1899) studied the groups of transformations depending on a finite number of parameters and now called Lie groups of transformations.

Let 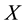be a manifold with local coordinates and 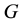be a Lie group, that is another manifold with local coordinates 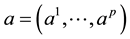called parameters with a composition 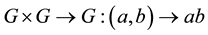, an inverse 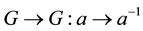and an identity 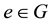satisfying:

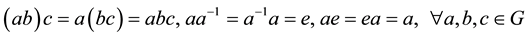
Then 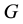is said to act on 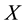if there is a map 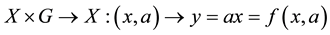such that 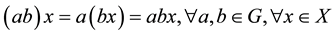and, for simplifying the notations, we shall use global notations even if only local actions are existing. The action is said to be effective if. A subset 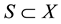is said to be invariant under the action of if 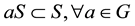and the orbit of is the invariant subset. If acts on two manifolds and, a map is said to be equivariant if. For reasons that will become clear later on, it is often convenient to introduce the graph of the action. In the product, the first factor is called the source while the second factor is called the target.

We denote as usual by the tangent bundle of, by the cotangent bundle, by the bundle of r-forms and by the bundle of q-symmetric tensors. Moreover, if are two vector fields on, we may define their bracket by the local formula

leading to the Jacobi identity

allowing to define a Lie algebra. We have also the useful formula

where is the tangent mapping of a map. Finally, when is a multi-index, we may set and introduce the exterior derivative with in the Poincaré sequence:

In order to fix the notations, we quote without any proof the “three fundamental theorems of Lie” that will be of constant use in the sequel (See [7] for more details):

FIRST FUNDAMENTAL THEOREM 1.1: The orbits satisfy the system of PD equations with. The vector fields are called infinitesimal generators of the action and are linearly independent over the constants when the action is effective.

In a rough way, we have and is thus a family of right invariant 1-forms on called Maurer-Cartan forms or simply MC forms.

SECOND FUNDAMENTAL THEOREM 1.2: If are the infinitesimal generators of the effective

action of a lie group on, then where the are the structure cons-

tants of a Lie algebra of vector fields which can be identified with the tangent space to at the identity by using the action as we already did. Equivalently, introducing the non-degenerate inverse matrix of right invariant vector fields on, we obtain from crossed-derivatives the compatibility conditions (CC) for the previous system of partial differential (PD) equations called Maurer-Cartan equations or simply MC equations, namely:

(care to the sign used) or equivalently (See [7] for more details).

Using again crossed-derivatives, we obtain the corresponding integrability conditions (IC) on the structure constants and the Cauchy-Kowaleski theorem finally provides:

THIRD FUNDAMENTAL THEOREM 1.3: For any Lie algebra defined by structure constants satisfying:

one can construct an analytic group such that by recovering the MC forms from the MC equa- tions.

EXAMPLE 1.4: Considering the affine group of transformations of the real line, the orbits are defined by, a definition leading to and thus

. We obtain therefore and

with .

GAUGING PROCEDURE 1.5: If with a time depending orthogonal matrix (rotation) and a time depending vector ( translation) describes the movement of a rigid body in, then the projection of the absolute speed in an orthogonal frame fixed in the body is the so-called relative speed and the kinetic energy/Lagrangian is a quadratic function of the 1-forms. Meanwhile, taking into account the preceding example, the Eulerian speed only depends on the 1-forms. We notice that and are both skewsymmetric time depending matrices that may be quite different.

REMARK 1.6: An easy computation in local coordinates for the case of the movement of a rigid body shows that the action of the skewsymmetric matrix on the position at time just amounts to the

vector product by the vortex vector (See [8] - [11] for more details).

The above particular case, well known by anybody studying the analytical mechanics of rigid bodies, can be generalized as follows. If is a manifold and is a lie group ( not acting necessarily on), let us consider maps or equivalently sections of the trivial (principal) bundle over

. If is a point of close to, then will provide a point close to

on. We may bring back to on by acting on with, either on the left or on the right, getting therefore a 1-form or with value in. As we also get if we set as a way to link with. When there is an action, we have and thus, a result leading through the first fundamental theorem of Lie to the equivalent formulas:

Introducing the induced bracket, we may define the curvature -form by the local formula (care again to the sign):

This definition can also be adapted to by using and we obtain from the second fundamental theorem of Lie:

THEOREM 1.7: There is a nonlinear gauge sequence:

Choosing “close” to, that is and linearizing as usual, we obtain the linear operator leading to (See [7] for more details):

COROLLARY 1.8: There is a linear gauge sequence:

which is the tensor product by of the Poincaré sequence.

It just remains to introduce the previous results into a variational framework. For this, we may consider a lagrangian on, that is an action where and to vary it. With

we may introduce with local coordinates

and we obtain that is in local coordinates. Then, setting, we get:

and therefore, after integration by part, the Euler-Lagrange (EL) equations [7] [12] [13] :

Such a linear operator for has non constant coefficients linearly depending on. However, setting, we get while, setting, we get the gauge transformation

. Setting with,

then becomes an infinitesimal gauge transformation. Finally, when with. Therefore, introducing such that, we get the divergence-like equations.

In 1954, at the birth of GT, the above notations were coming from electromagnetism with EM potential and EM field in the relativistic Maxwell theory [14] . Accordingly, (unit circle in the complex plane) was the only possibility to get a pure 1-form and a pure 2- form when. However, “surprisingly”, this result is not coherent at all with elasticity theory and, a fortiori with the analytical mechanics of rigid bodies where the Lagrangian is a quadratic expression of 1-forms as we saw, because the EM lagrangian is a quadratic expression of the EM field as a 2-form satisfying the first set of Maxwell equations. The dielectric constant and the magnetic constant are leading to the electric induction and the magnetic induction in the second set of Maxwell equations. In view of the existence of well known and quite useful field-matter couplings such as piezoelectricity and photoelasticity [13] [15] [16] , such a situation is contradictory as it should lead to put on equal footing 1-forms and 2-forms, contrary to any unifying mathematical scheme, but no other substitute could have been provided at that time, despite the tentatives of the brothers Eugene Cosserat (1866-1931) and Francois Cosserat (1852-1914) in 1909 [13] [16] - [18] or of Herman Weyl (1885-1955) in 1918 [13] [19] .

After this long introduction, the purpose of this paper will be to escape from such a contradiction by using new mathematical tools coming from the formal theory of systems of PD equations and Lie pseudogroups, exactly as we did in [20] for general relativity (GR). In particular, the titles of the three parts that follow will be quite similar to those of this reference though, of course, the contents will be different. The first part proves hat the name “curvature” given to has been quite misleading, the resulting confusion between translation and rotation being presented with humour in [21] through the chinese saying “to put Chang’s cap on Li’s head”. The second part explains why the Cosserat/Maxwell/Weyl (CMW) theory MUST be described by the Spencer sequence and NOT by the Janet sequence, with a SHIFT by one step contradicting the mathematical foundations of both GR and GT. The third part finally presents the Poincaré duality scheme of physics [12] by means of unexpected methods of homological algebra and algebraic analysis.

2. First Part: The Nonlinear Janet and Spencer Sequences

In 1890, Lie discovered that Lie groups of transformations were examples of Lie pseudogroups of transfor- mations along the following definition [7] [13] [22] -[24] :

DEFINITION 2.1: A Lie pseudogroup of transformations is a group of transformations solutions of a system of OD or PD equations such that, if and are two solutions, called finite transformations, that can be composed, then and are also solutions while is the identity solution denoted by and we shall set. In all the sequel we shall suppose that is transitive that is

From now on, we shall use the same notations and definitions as in [7] [16] [20] for jet bundles. In particular, we recall that, if is the q-jet bundle of with local coordinates for, , and, we may consider sections transforming like the sections

where both and are over the section of. The (nonlinear) Spencer operator just allows to distinguish a section from a section by introducing a kind of “difference” through the operator with local components

and more generally. If

and with source projection, we denote by the open sub-bundle locally defined by.

We also notice that an action provides a Lie pseudogroup by eliminating the parameters among the equations obtained by successive differentiations with respect to only when is large enough. The system of PD equations thus obtained may be quite nonlinear and of high order. Looking for transformations “close” to the identity, that is setting when is a small constant parameter and passing to the limit, we may linearize the above (nonlinear) system of finite

Lie equations in order to obtain a (linear) system of infinitesimal Lie equations

for vector fields. Such a system has the property that, if are two solutions, then is also a solution. Accordingly, the set of its solutions satisfies and can therefore be considered as the Lie algebra of.

GAUGING PROCEDURE REVISITED 2.2: Setting and,

we obtain because and the matrix involved has rank in the following commutative diagram:

Looking at the way a vector field and its derivatives are transformed under any while replacing by, we obtain:

and so on, a result leading to:

LEMMA 2.3: is associated with that is we can obtain a new section from any section and any section by the formula:

where the left member belongs to. Similarly is associated with.

In order to construct another nonlinear sequence, we need a few basic definitions on Lie groupoids and Lie algebroids that will become substitutes for Lie groups and Lie algebras. The first idea is to use the chain rule for derivatives whenever can be composed and to replace both and respectively by and in order to obtain the new section. This kind of “composition” law can be written in a pointwise symbolic way by introducing another copy of with local coordinates as follows:

We may also define and obtain similarly an “inversion” law.

DEFINITION 2.4: A fibered submanifold is called a system of finite Lie equations or a Lie groupoid of order if we have an induced source projection, target projection, composition, inversion and identity. In the sequel we shall only consider transitive Lie groupoids such that the map is an epimorphism. One can prove that the new system obtained by differentiating times all the defining equations of is a Lie groupoid of order.

Now, using the algebraic bracket, we may obtain by bilinearity a differential bracket on extending the bracket on:

which does not depend on the respective lifts and of and in. One can prove that his bracket on sections satisfies the Jacobi identity and we set:

DEFINITION 2.5: We say that a vector subbundle is a system of infinitesimal Lie equations or

a Lie algebroid if, that is to say. Such a definition can be tested by means of computer algebra.

EXAMPLE 2.6: With and evident notations, the components of at order zero, one and two are defined by the totally unusual successive formulas:

For affine transformations, and thus.

We may prolong the vertical infinitesimal transformations to the jet coordinates up to order in order to obtain:

where we have replaced by, each component beeing the “formal” derivative of the previous one. Replacing by as sections of over the target, we obtain a vertical vector field over

such that over the target. We may then use the Frobenius theorem in order to find a generating fundamental set of differential invariants up to order

which are such that by using the chain rule for derivatives whenever acting now on. Looking at the way the differential invariants are transformed between themselves under changes of source, we may define a natural bundle. Specializing the at we obtain the Lie form of and a section of. If we introduce the maximum number of formal derivatives that are linearly independent over the jets of strict order, any other formal derivative is a linear combination with coefficients functions of. Applying, we get a contradiction unless these coefficients are killed by and are thus functions of the fundamental set, a result leading to CC of the form. Finally, setting, we obtain a new natural bundle as a vector bundle over.

THEOREM 2.7: There exists a nonlinear Janet sequence associated with the Lie form of an involutive system of finite Lie equations:

where the kernel of the first operator is taken with respect to the section of while the kernel of the second operator is taken with respect to the zero section of the vector bundle over (Compare to [24] [25] ).

THEOREM 2.8: There is a first nonlinear Spencer sequence:

with. Moreover, setting, this sequence is locally exact if and there is an induced second nonlinear Spencer sequence (See next section for definitions):

where all the operators involved are involutive.

Proof: There is a canonical inclusion defined by and the composition

is a well defined section of over the section of like. The

difference is thus a section of over and we have already noticed that. For we get with:

We also obtain from Lemma 6.3 the useful formula allowing to determine inductively.

We refer to ( [7] , p 215) for the inductive proof of the local exactness, providing the only formulas that will be used later on and can be checked directly by the reader:

(1)

(2)

There is no need for double-arrows in this framework as the kernels are taken with respect to the zero section of the vector bundles involved. We finally notice that the main difference with the gauge sequence is that all the indices range from 1 to and that the condition amounts to because by assumption (See [7] [16] [23] for more details).

Q.E.D.

COROLLARY 2.9: There is a first restricted nonlinear Spencer sequence:

and an induced second restricted nonlinear Spencer sequence:

where all the operators involved are involutive and which is locally isomorphic to the corresponding gauge sequence for any Lie groups of transformations when is large enough. The action, which is essential in the Spencer sequence, disappears in the gauge sequence.

DEFINITION 2.10: A splitting of the short exact sequence is a map such that or equivalently a section of over and is called a -connection. Its curvature is defined by. We notice that is a connection with if and only if and connections cannot be used for describing fields because we must have. İn particular is the only existing symmetric connection for the Killing system.

REMARK 2.11: Rewriting the previous formulas with instead of we get:

(1*)

(2*)

When and though surprising it may look like, we find back exactly all the formulas presented by E. and F. Cosserat in ( [17] , p 123 and [26] ) (Compare to [25] ).

Finally, setting, we get

.

With, we get the gauge transformation as in the Introduction, thus ACTING ON THE FIELDS WHILE PRESERVING THE FIELD EQUATIONS. Setting with over the source, we obtain an infinitesimal gauge transformation of the form as in [7] [13] [16] . However, setting now and with over the target, we get. The same variation is obtained whenever with, a transformation which only depends on and is invertible if and only if [7] [13] . This result proves that is also associated with the groupoid defined by. With, we have the unusual formulas:

Accordingly, THE DUAL EQUATIONS WILL ONLY DEPEND ON THE LINEAR SPENCER OPERA- TOR. Moreover, in view of the two variational results obtained at the end of the Introduction, THE CMW EQUATIONS CANNOT COME FROM THE GAUGE SEQUENCE, contrary to what mechanicians still be- lieve after more than a century.

EXAMPLE 2.12: We have the formulas (Compare to [17] [19] , (76) p 289,(78) p 290):

(3)

(4)

Setting, we have.

EXAMPLE 2.13: (Projective transformations) With, the formal adjoint of the Spencer operator brings as many dual equations as the number of parameters (1 translation + 1 dilatation + 1 elation).

Cosserat/Weyl equations : (equivalent “momenta”).

3. Second Part: The Linear Janet and Spencer Sequences

It remains to understand how the shift by one step in the interpretation of the Spencer sequence is coherent with mechanics and electromagnetism both with their well known couplings [7] [13] [16] [20] . In a word, the problem we have to solve is to get a 2-form in from a 1-form in for a certain.

For this purpose, introducing the Spencer map defined by, we recall from [7] [20] [27] the definition of the Janet bundles

and the Spencer bundles

or with. When is an involutive system on, we have the following crucial commutative diagram with exact columns where each operator involved is first order apart from, generates the CC of the preceding one and is induced by the extension

of the Spencer operator. The upper sequence is the (second) linear Spencer sequence while the lower sequence is the linear Janet sequence [7] [28] and the sum does not depend on the system while the epimorphisms are induced by.

For later computations, the sequence can be described by the images, , leading to the identities:

(1**)

(2**)

We also recall that the linear Spencer sequence for a Lie group of transformations, which essentially depends on the action because infinitesimal generators are needed, is locally isomorphic to the linear gauge sequence which does not depend on the action any longer as it is the tensor product of the Poincaré sequence by the Lie algebra.

The main idea will be to introduce and compare the three Lie groups of transformations:

The Poincare group of transformations with parameters leading to the Killing system:

The Weyl group of transformations with parameters leading to the system:

The conformal group of transformations with 15 parameters leading to the conformal Killing system and to the corresponding Janet/Spencer diagram:

where one has to eliminate the arbitrary function and 1-form for finding sections, replacing the ordinary Lie derivative by the formal Lie derivative, that is replacing by when needed.

We shall use the inclusions in the tricky proof of the next crucial proposition:

PROPOSITION 3.1: The Spencer sequence for the conformal Lie pseudogroup projects onto the Poincare sequence with a shift by one step.

Proof: Using as a -connection and the fact that while set- ting with and

with, we obtain the following commutative and exact diagram:

We also obtain from the relations and the previous identities (1**) + (2**):

As and, the conformal Spencer sequence projects onto the sequence which finally projects with a shift by one step onto the Poincaré sequence by applying the Spencer map, because these two sequences are only made by first order involutive operators and are thus formally exact. The short exact sequence has already been used in [16] [20] for exhibiting the Ricci tensor and the above result brings for the first time a conformal link between electromagnetism and gravitation by using second order jets (See [7] [13] for more details).

The study of the nonlinear framework is similar. Indeed, using Remark 2.11 with, we get:

and we may finish as before as we have taken out the quadratic terms through the contraction.

Q.E.D.

This unification result, which may be considered as the ultimate “dream” of E. and F. Cosserat or H. Weyl, could not have been obtained before 1975 as it can only be produced by means of the (linear/nonlinear) Spencer sequences and NOT by means of the (linear/nonlinear) gauge sequences. We invite the reader to notice that it only depends on the Formulas (1), (2), (3), (4) and their respective (*) or (**) consequences.

4. Third Part: The Duality Scheme

A duality scheme, first introduced by Henri Poincaré (1854-1912) in [12] , namely a variational framework adapted to the Spencer sequence, could be achieved in local coordinates as we did for the gauge sequence at the end of the Introduction. We have indeed presented all the explicit formulas needed for this purpose and the reader will notice that it is difficult or even impossible to find them in [25] . However, it is much more important to relate this dual scheme to homological algebra [29] and algebraic analysis [30] [31] by using the comment done at the end of the Second Part which amounts to bring the nonlinear framework to the linear framework, a reason for which the stress equations of continuum mechanics are linear even for nonlinear elasticity [13] [16] [18] .

Let be a unitary ring, that is and even an integral domain, that is or. However, we shall not always assume that is commutative, that is may be different from in general for. We say that is a left module over if or a right module for if the operation of on is . Of course, is a left and right module over itself. We define the torsion submodule and is a torsion module if or a torsion-free module if. We denote by the set of morphisms such that. In particular because and we recall that a sequence of modules and maps is exact if the kernel of any map is equal to the image of the map preceding it. When is commutative, is again an -module for the law as we have . In the non-commutative case, things are much more complicate and we have:

LEMMA 4.1: Given and, then becomes a right module over for the law.

Proof: We just need to check the two relations:

Q.E.D.

DEFINITION 4.2: A module is said to be free if it is isomorphic to a (finite) power of called the rank of over and denoted by while the rank of a module is the rank of a maximum free submodule. In the sequel we shall only consider finitely presented modules, namely finitely generated modules defined by exact sequences of the type

where and are free modules of finite ranks. For any short exact sequence, we have. A module is called projective if there exists a free module and another (projective) module such that. By a projective (free) resolution of, we understand a long exact sequence

where are projective (free) modules, and is the canonical projection.

We now introduce the extension modules, using the notation and, for any morphism, we shall denote by the morphism which is such that . For this, we take out in order to obtain the deleted sequence

and apply in order to get the sequence.

PROPOSITION 4.3: The extension modules and do not depend on the resolution chosen and are torsion modules for.

Let be a differential field, that is a field with commuting derivations with such that and . Using an implicit summation on multi-indices, we may introduce the (noncommutative) ring of differential operators with elements such that and. We notice that can be generated by and. Now, if we introduce differential indeterminates, we may extend to for. Therefore, setting, we obtain by residue the differential module or -module. Introducing the two free differential modules, we obtain equivalently the free presentation. More generally, introducing the successive CC as in the preceding section, we may finally obtain the free resolution of, namely the exact sequence. In actual practice, we let act on the left on column vectors in the operator case and on the right on row vectors in the module case. Homological algebra has been created for finding intrinsic properties of modules not depending on their presentation or even on their resolution.

We now exhibit another approach by defining the formal adjoint of an operartor and an operator matrix:

DEFINITION 4.4:

from integration by part, where is a row vector of test functions and the usual contraction.

LEMMA 4.5: IIf, we may set and we have the identity:

PROPOSITION 4.6: If we have an operator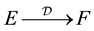, we obtain by duality an operator where is obtained from by inverting the transition matrix.

EXAMPLE 4.7: Let us revisit EM in the light of the preceding results when. First of all, we have in the sequence and the field equations are invariant under any local diffeomorphism. By duality, we get the sequence which is locally isomorphic (up to sign) to and the induction equations are thus also invariant under any. Indeed, using the last lemma and the identity, we have:

Accordingly, it is not correct to say that the conformal group is the biggest group of invariance of Maxwell equations as it is only the biggest group of invariance of the Minkowski constitutive laws in vacuum [14] . Finally, both sets of equations can be parametrized independently, the first by the potential, the second by the so- called pseudopotential (See [30] , p 492 for more details).

Now, with operational notations, let us consider the two differential sequences:

where generates all the CC of. Then but may not gene- rate all the CC of. Passing to the module framework, we just recognize the definition of. Now, exactly like we defined the differential module from, let us define the differential module from. Then does not depend on the presentation of [31] . More generally, changing the presentation of may change to but we have [30] [32] :

THEOREM 4.8: The modules and are projectively equivalent, that is one can find two projective modules and such that and we obtain therefore.

THEOREM 4.9: When is a left -module, then is also a left -module.

Proof: Let us define:

It is easy to check that in the operator sense and that is the standard bracket of vector fields. We finally get that is exactly the Spencer operator we used in the second part. In fact, is the projective limit of in a coherent way with jet theory [18] [19] [33] .

Q.E.D.

COROLLARY 4.10: if and are right -modules, then becomes a left - module.

Proof: We just need to set and conclude as before.

Q.E.D.

As is a bimodule, then is a right -module according to Lemma 4.1 and thus the module defined by the ker/coker sequence is in fact a right module.

THEOREM 4.11: We have the side changing procedure.

Proof: According to the above Corollary, we just need to prove that has a natural right module structure over. For this, if is a volume form with coefficient, we may set when. As is generated by and, we just need to check that the above formula has an intrinsic meaning for any. In that case, we check at once:

by introducing the Lie derivative of with respect to, along the intrinsic formula

where is the interior multiplication and is the exterior derivative of exterior forms. According to well known properties of the Lie derivative, we get:

Q.E.D.

REMARK 4.12: The above results provide a new light on duality in physics. Indeed, as the Poincaré se- quence is self-adjoint (up to sign) as a whole and the linear Spencer sequence for a Lie group of transformations is locally isomorphic to copies of that sequence, it follows from Proposition 4.3 that parametrizes in the dual of the Spencer sequence while parametrizes in the dual of the Janet sequence, a result highly not evident at first sight in view of the Janet/Spencer diagram for the conformal group of tranformations of space-time that we have presented because and are totally different operators.

5. Conclusion

The mathematical foundations of Gauge Theory (GT) leading to Yang-Mills equations are always presented in textbooks or papers without quoting/taking into account the fact that the group theoretical methods involved are exactly the same as the standard ones used in continuum mechanics, particularly in the analytical mechanics of rigid bodies and in hydrodynamics. Surprisingly, the lagrangians of GT are (quadratic) functions of the curvature 2-form while the lagrangians of mechanics are (quadratic or cubic) functions of the potential 1-form. Meanwhile, the corresponding variational principle leading to Euler-Lagrange equations is also shifted by one step in the use of the same gauge sequence. This situation is contradicting the well known field/matter couplings existing between elasticity and electromagnetism (piezzoelectricity, photoelasticity). In this paper, we prove that the mathematical foundations of GT are not coherent with jet theory and the Spencer sequence. Accordingly, they must be revisited within this new framework, that is when there is a Lie group of transformations consi- dered as a Lie pseudogroup, contrary to the situation existing in GT. Such a new approach, based on new mathematical tools not known by physicists, allows unifying electromagnetism and gravitation. Finally, the striking fact that the Cosserat/Maxwell/Weyl equations can be parametrized, contrary to Einstein equations, is shown to have quite deep roots in homological algebra through the use of extension modules and duality theory in the framework of algebraic analysis.

References