Journal of Modern Physics
Vol.5 No.3(2014), Article ID:42656,4 pages DOI:10.4236/jmp.2014.53016
Dipartimento di Fisica, Sezione Teorica, Università di Trieste and INFN, Sezione di Trieste, Italy
Email: euro@ts.infn.it, claudio@ts.infn.it
Copyright © 2014 Euro Spallucci, Claudio Verzegnassi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Euro Spallucci, Claudio Verzegnassi. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 22, 2013; revised November 26, 2013; accepted December 14, 2013
ABSTRACT
We compute in a theoretical quantum field theory framework the effects that a classic environment will have on an elementary one-fermion state, assumed for simplicity to be that of one electron, in the presence of a magnetic field. We consider its total energy and its spin angular momentum as relevant observables of the state. We show that the changes of these quantities produced by the combined environmental and magnetic effects can be expressed in a simple and compact form. We obtain expressions that only depend on the values of the external environment and magnetic fields, and on the special spin features of the free fermion state. We call these effects “fermion epigenetics” and try to motivate this definition discussing possible relevant analogies with the corresponding medical treatment of epigenetics in organic cells.
Keywords: Epigenetics; Quantum Field Theory; Dirac Equation
1. Introduction
The process of organic epigenetics is nowadays considered as a fundamental reaction for the possible positive consequence that it might generate on human health. In particular, a great amount of interest has been raised by the study of the effects that a weak magnetic field might have on the organic cell [1-3]. To completely define these effects, a reliable knowledge of the surrounding environment is also requested, and a detailed discussion is available in the medical literature [4].
From the point of view of physics, a fascinating possibility exists which would be summarized in the statement [5].
“The evolution of living systems is a continuation of that of the physical world.”
Accepting this statement, we have devoted a very recent paper [6] to the determination of the effects that a magnetic field would have on an elementary matter component, e.g. an electron, trying to derive possible analogies with the effects that would have been produced on the elementary organic cell component, i.e. the nucleus. The results of this study are, in our opinion, intriguing and one can find them discussed in detail in [7]. Here, we shall only summarize the main conclusions of our search, which starts from the initial observation that the complete description of the electron state can be given, in a theoretical quantum field theory framework, by the knowledge of four dependent, complex functions of space and time denoted by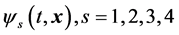 , which we called psinons. We introduced this definition to remark that, even if we use the technical tools of quantum field theory, we shall apply them to derive results that might be interpreted in a biological setting, thinking of the four complex components of
, which we called psinons. We introduced this definition to remark that, even if we use the technical tools of quantum field theory, we shall apply them to derive results that might be interpreted in a biological setting, thinking of the four complex components of 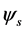 as the analogues of the four histones forming an “elementary” nucleus. Starting from these functions, one can build all the observable quantities of the electron, in particular, its total energy, its orbital and spin angular momentum. Our former investigation has been devoted to the determination of the effects that a classic magnetic field would produce on this quantity. In a quantum field theory approach, this study can be performed owing to the essential requests that 1) the four psinons obey the fundamental Dirac equation and 2) the laws of nature are invariant with respect to a local gauge transformation. Imposing the latter property (that requires the existence of the recently discovered Higgs boson) determines the form of the magnetic interaction with the electron in a simple universal way, denoted as the “minimal interaction”. Using these prescriptions, we have derived the expressions of the leading magnetic changes of the four psinons, which generate automatically the variations of all the physical observables. We have denoted this process as “fermion magnetic epigenetics” and discussed a number of possible analogies with the process of organic epigenetics. The whole discussion has assumed the existence of a classic magnetic field, but has ignored the possible relevance of the surrounding physical environment.
as the analogues of the four histones forming an “elementary” nucleus. Starting from these functions, one can build all the observable quantities of the electron, in particular, its total energy, its orbital and spin angular momentum. Our former investigation has been devoted to the determination of the effects that a classic magnetic field would produce on this quantity. In a quantum field theory approach, this study can be performed owing to the essential requests that 1) the four psinons obey the fundamental Dirac equation and 2) the laws of nature are invariant with respect to a local gauge transformation. Imposing the latter property (that requires the existence of the recently discovered Higgs boson) determines the form of the magnetic interaction with the electron in a simple universal way, denoted as the “minimal interaction”. Using these prescriptions, we have derived the expressions of the leading magnetic changes of the four psinons, which generate automatically the variations of all the physical observables. We have denoted this process as “fermion magnetic epigenetics” and discussed a number of possible analogies with the process of organic epigenetics. The whole discussion has assumed the existence of a classic magnetic field, but has ignored the possible relevance of the surrounding physical environment.
The aim of this paper is to consider the extra effects that would be produced by the presence of a surrounding environment, and by its modification of the “pure magnetic” effects considered in [7]. We have shown in [7] that for a weak intensity of the field, these effects can be very simply computed in a quantum field theory theoretical framework, assuming the minimal form of the electromagnetic interaction and the validity of the Dirac equation. The effects proceed via preliminary magnetic field induced, and modifications of the four-component spinor field. This generates consequent modifications of the various observable properties of the Fermion, which can always be simply expressed in terms of the four spinor field components. This search will be briefly, but completely, exposed in the next Section 2, which will be followed by a short final discussion of the main possible analogies with the existing, fascinating, medical search.
2. Combined Environmental-Magnetic Effects on an Elementary Fermion State
To pursue our investigation, we shall begin by writing the expressions of the total energy and of the components of the spin angular momentum 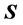 of a general free electron state. We have chosen these observables because, in our search of organic analogies, the energy would correspond to an “internal” property of the system, related to its possible space configuration, whilst the spin typically represents an “intrinsic”, space-independent property, which is common to all different fermions that obey Fermi-Dirac statistics. In terms of the four, complex, psinons
of a general free electron state. We have chosen these observables because, in our search of organic analogies, the energy would correspond to an “internal” property of the system, related to its possible space configuration, whilst the spin typically represents an “intrinsic”, space-independent property, which is common to all different fermions that obey Fermi-Dirac statistics. In terms of the four, complex, psinons 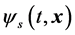 these expressions read:
these expressions read:
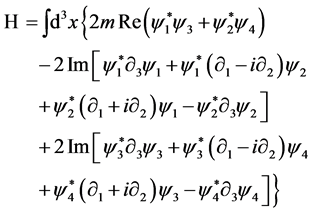 (1.1)
(1.1)
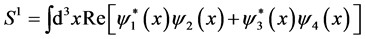 (1.2)
(1.2)
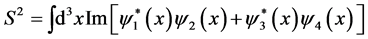 (1.3)
(1.3)
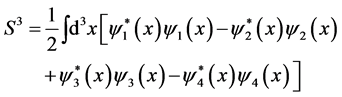 (1.4)
(1.4)
Equations (1.1), (1.22), (1.3) and (1.4) can be re-written in a way that will be more useful for the continuation of this paper. We will define a “spin current” density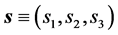 , where
, where
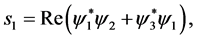 (1.5)
(1.5)
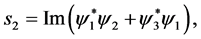 (1.6)
(1.6)
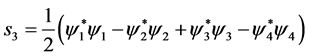 (1.7)
(1.7)
Thus, the general expression of the spin vector 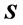 reads
reads
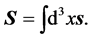 (1.8)
(1.8)
In our previous analysis, we have not concentrated on other properties of the chosen fermion state. For the purposes of this paper, we shall consider another feature of the system called “axial charge”,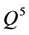 . The density of this new “charge” is the time component of the “axial current”, defined as the quantity
. The density of this new “charge” is the time component of the “axial current”, defined as the quantity
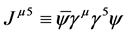 (1.9)
(1.9)
where 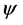 is the complete fermion field. Thus,
is the complete fermion field. Thus,
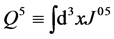 (1.10)
(1.10)
In terms of the four psinon fields, one easily derives that
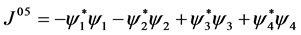 (1.11)
(1.11)
Quite generally, one can provide a physical meaning to the axial charge 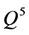 as follows. Notice that the axial current can be decomposed in the sum of two terms:
as follows. Notice that the axial current can be decomposed in the sum of two terms:
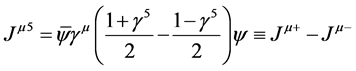 (1.12)
(1.12)
The two currents 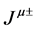 are generated by spinor components, or psinons in our case, with opposite spin orientation, i.e. opposite “chirality”, or “handedness”. It is worth to remind that in biology chirality represents the property of organic molecules that cannot be superimposed to their own mirror image. By comparing Equations (1.12) and (1.11) we see that the axial current density represents the difference between the current of right-handed and the current of left-handed psinons.
are generated by spinor components, or psinons in our case, with opposite spin orientation, i.e. opposite “chirality”, or “handedness”. It is worth to remind that in biology chirality represents the property of organic molecules that cannot be superimposed to their own mirror image. By comparing Equations (1.12) and (1.11) we see that the axial current density represents the difference between the current of right-handed and the current of left-handed psinons.
In this paper we want to consider the effects that would be produced on the previous free quantities by the simultaneous presence of a magnetic field and of some environment sourcing a classical electric field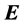 . Some remarkable examples of environmental electric fields are: the Earth electric static field; a low frequency domestic electric field; a high frequency cell phone network electric field [8]. We have neglected other kinds of environmental effects possibly due either to gravity or to nuclear forces. The first gravitational effects are too weak to be considered owing to the negligible mass of the considered electrons; the second kind of effects is due to forces that do not affect electrons. The electromagnetic effects thus appear to us to be the only relevant ones to be taken into account.
. Some remarkable examples of environmental electric fields are: the Earth electric static field; a low frequency domestic electric field; a high frequency cell phone network electric field [8]. We have neglected other kinds of environmental effects possibly due either to gravity or to nuclear forces. The first gravitational effects are too weak to be considered owing to the negligible mass of the considered electrons; the second kind of effects is due to forces that do not affect electrons. The electromagnetic effects thus appear to us to be the only relevant ones to be taken into account.
Here, we shall consider the simplest case of a timeindependent field. This means that one can properly derive the electric field as the gradient of a static Coulomb potential, 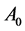 , from the Maxwell equation:
, from the Maxwell equation:
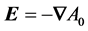 (1.13)
(1.13)
The same equations give a classic magnetic field 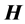 as the curl of a chosen time-independent vector potential
as the curl of a chosen time-independent vector potential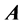 :
:
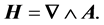 (1.14)
(1.14)
In conclusion, we shall treat a process in which the electron state is surrounded by a classic electric field, derived by a Coulomb potential 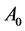 representing the environment. In this situation we imagine that a classic magnetic field
representing the environment. In this situation we imagine that a classic magnetic field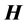 , derivable by a vector potential
, derivable by a vector potential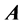 , is switched-on. In other words, we are considering the interaction of a quantum fermion field with a classical four-potential
, is switched-on. In other words, we are considering the interaction of a quantum fermion field with a classical four-potential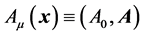 , representing an overall electromagnetic field. In the conventional quantum field theory approach, this interaction is completely described by the “minimal” prescription, which corresponds to the replacement in all the free quantities of the partial derivative
, representing an overall electromagnetic field. In the conventional quantum field theory approach, this interaction is completely described by the “minimal” prescription, which corresponds to the replacement in all the free quantities of the partial derivative 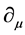 with the gauge “covariant” four momentum
with the gauge “covariant” four momentum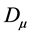 :
:
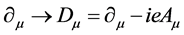 (1.15)
(1.15)
where 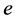 is the electron charge, conventionally chosen to be negative, i.e.
is the electron charge, conventionally chosen to be negative, i.e.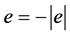 . Inposing the fermion fields to satisfy the Dirac equation leads to the overall changes, denoted by the symbol
. Inposing the fermion fields to satisfy the Dirac equation leads to the overall changes, denoted by the symbol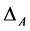 , of the four psinons already derived in [6], that we rewrite for completeness as follows:
, of the four psinons already derived in [6], that we rewrite for completeness as follows:
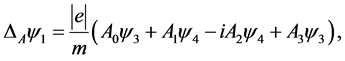 (1.16)
(1.16)
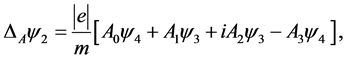 (1.17)
(1.17)
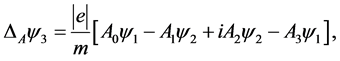 (1.18)
(1.18)
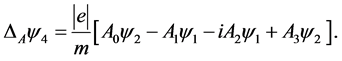 (1.19)
(1.19)
We are now ready to derive the changes of the considered free variables. This can be done by replacing in the relevant expressions the free psinons with the corrected ones, rewriting systematically
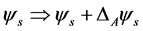 (1.20)
(1.20)
where, 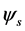 in the r.h.s. denotes, from now on, the free psinon.
in the r.h.s. denotes, from now on, the free psinon.
A last, but important, detail of our calculation is that we are going to consider only the combined effects of the mutual interaction between the environment and the magnetic field. In this spirit, we shall extract from all possible interaction terms among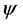 ,
, 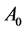 ,
, 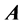 only those which are bi-linear in
only those which are bi-linear in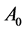 ,
, 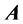 and neglect selfinteraction terms quadratic in the electric and magnetic potentials.
and neglect selfinteraction terms quadratic in the electric and magnetic potentials.
To derive the effects of the combined interaction, which we indicate again with the 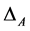 symbol, requires a long, but straightforward, calculation that we shall not report explicitly. At the end of this calculation, one finds the following results:
symbol, requires a long, but straightforward, calculation that we shall not report explicitly. At the end of this calculation, one finds the following results:
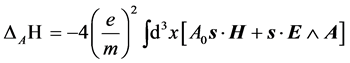 (1.21)
(1.21)
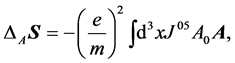 (1.22)
(1.22)
Euqations (1.21), (1.22) are the main result of this paper, and we shall spend a few final words to remark those features that appear to us particularly impressive. In particular:
1) In Euqation (1.21), the overall change is given by scalar products, where the free electron spin current is one of the components. The second component is given by the magnetic and electric fields and potentials. In other words, the overall effect for a given environment and magnetic field is determined by the spin density of the free electron.
2) In Equation (1.21), two terms appear. One of them, where the scalar product 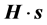 appears, has the same form that a classical contribution to the electron anomalous magnetic moment
appears, has the same form that a classical contribution to the electron anomalous magnetic moment 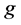 would have. In the conventional notation, the anomalous magnetic moment of a free electron would actually be drived from the expression of the magnetic Hamiltonian
would have. In the conventional notation, the anomalous magnetic moment of a free electron would actually be drived from the expression of the magnetic Hamiltonian
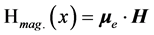 (1.23)
(1.23)
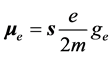 (1.24)
(1.24)
where 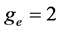 is the Landè factor. In this spirit, we can say that, as an effect of the environmental-magnetic interaction, the overall anomalous magnetic moment of the electron becomes
is the Landè factor. In this spirit, we can say that, as an effect of the environmental-magnetic interaction, the overall anomalous magnetic moment of the electron becomes
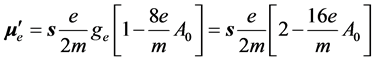 (1.25)
(1.25)
that can be interpreted as a correction to the value 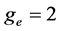 of the form
of the form
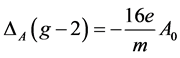 (1.26)
(1.26)
We will define this term as the 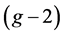 epigenetic effect. The second term has a characteristic and, to our knowledge, new form. Its special feature is to depend also on the relative orientation of the electric field with respect to the magnetic potential. This might have some relevance in possible practical applications.
epigenetic effect. The second term has a characteristic and, to our knowledge, new form. Its special feature is to depend also on the relative orientation of the electric field with respect to the magnetic potential. This might have some relevance in possible practical applications.
3) The spin changes are represented by an expression that depends on the product of the electric and magnetic potential and on the value of the axial current 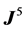 that we have introduced and discussed. Thus, again, the effect is fixed by a property of the electron spin, its spin orientation.
that we have introduced and discussed. Thus, again, the effect is fixed by a property of the electron spin, its spin orientation.
3. Conclusions
The main conclusion which could be drawn from our analysis is that all the considered changes of elementary matter components under the combined effect of a surrounding environment and of a magnetic field only depend on the spin properties of the free state (and on the intensity of the electric and magnetic fields). This conclusion is valid in the theoretical framework of quantum field that we adopted under the general and universal assumptions which are nowadays accepted.
In our search of analogies with the fascinating medical treatment of the epigenetic process, we would still propose the correspondence between 1) the electron energy and the space dependent properties of nucleus epigenome; 2) the electron intrinsic and space independent spin and the nucleus DNA.
Accepting our very personal proposal might lead to some more realistic check of its general properties in a proper medical experiment. A possibility that appears to us to be reasonably realistic is the following one. Looking at the Equation (1.21), we see that the “new” term (not of 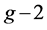 kind) contains the vector product
kind) contains the vector product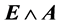 . The direction of
. The direction of 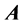 is identical to the direction of the chosen current
is identical to the direction of the chosen current 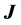 generating the magnetic field. Thus, since the direction of
generating the magnetic field. Thus, since the direction of 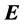 is known in the considered case, one can fix the direction of
is known in the considered case, one can fix the direction of 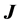 and choose it, for instance, parallel to the electric field. This choice makes the “new” effect vanish, and one remains with the term
and choose it, for instance, parallel to the electric field. This choice makes the “new” effect vanish, and one remains with the term 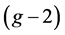 alone. Then one can rotate the current and make it orthogonal to the field
alone. Then one can rotate the current and make it orthogonal to the field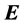 . This choice makes the “new” effect become maximum. One can measure the difference between the two observed energy shifts and verify that it exists.
. This choice makes the “new” effect become maximum. One can measure the difference between the two observed energy shifts and verify that it exists.
A last possibility to be considered, in our opinion, is the following one. If the magnetic field is sufficiently weak, more precise and much weaker than the electric field, its contribution to the overall effect might be negligibly small. In this case, the “new” term 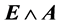 would be able to be described in a simple and elegant form that all the energy transfers in the environmental-magnetic situation. This appears to us the most relevant result of our research, for what concerns the possibility of a realistic experimental medical check. We are ready and willing to collaborate on these future plans which are fascinating in our opinion.
would be able to be described in a simple and elegant form that all the energy transfers in the environmental-magnetic situation. This appears to us the most relevant result of our research, for what concerns the possibility of a realistic experimental medical check. We are ready and willing to collaborate on these future plans which are fascinating in our opinion.
[1] REFERENCES
[2] C. Ventura, et al., FASEB Journal, Vol. 19, 2005, p. 155.
[3] C. Ventura, et al., Cell Transplant, Vol. 6, 2012, p. 1225.
[4] M. Biava, “Private Communication.”
[5] IARC Working Group on the Evaluation of Carcinogenic Risks to Humans, IARC Monographs on the Evaluation of Carcinogenic Risks to Humans, Vol. 80, 2002, pp. 1-395.
[6] A. Lima-de-Faria, “Evoluzione senza Selezione,” Nova Scripta Edizioni, Genova, 2003.
[7] C. Verzegnassi, Journal of Modern Physics, Vol. 4, 2013, p. 638. http://dx.doi.org/10.4236/jmp.2013.45092
[8] F. Burigana, E. Spallucci and C. Verzegnassi, Journal of Modern Physics, Vol. 4, 2013, pp. 1133-1138.
[9] F. Boffelli, “Private Communication.”

