Journal of Modern Physics
Vol.5 No.1(2014), Article ID:41969,7 pages DOI:10.4236/jmp.2014.51001
Relativistic Derivations of de Broglie and Planck-Einstein Equations
Department of Physics, Trento University, Povo, Italy
Email: log@science.unitn.it
Received October 20, 2013; revised November 23, 2013; accepted December 18, 2013
ABSTRACT
Special Relativity sets tight constraints on the form of the possible relations between the four-momentum of a particle and the wave four-vector. In fact, we demonstrate that there is just one way, according to Special Relativity, to relate the energy and the momentum of a corpuscle with the characteristics of a plane wave, frequency and wave vector, if the momentum has to flow in the same direction of the wave propagation: the laws must be of direct proportionality like de Broglie 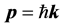 and Planck-Einstein
and Planck-Einstein  equations.
equations.
Keywords:Quantum Theory; Special Relativity; De Broglie Relation; Planck-Einstein Relation
1. Introduction
In the autumn of 1924, the French physicist Louis de Broglie submitted to the judgement of Sorbonne University in Paris, one of the most famous PhD theses in the history of physics [1]. His results, as he confessed several decades later, gathered the fruits of many solitary meditations on a conundrum of physics which had bothered him for a long time: the dual wave and particle nature of light. The dissertation brought together various notes already published mainly in the Comptes Rendus de l’Académie des Sciences [2-6].
In his thesis de Broglie suggests that the quanta of light had to be completely comparable to other known material particles. For instance, they had to have a rest mass different from zero, although very small1. Moreover, if the photons had to be put on the same conceptual framework of other particles, according to the French physicist, it was also possible to imagine that particles different from the photons could share the strange dual property of wave and corpuscle with the light. So the fundamental hypothesis of his dissertation was to consider true for all the particles, not only for the quanta of light, the Planck-Einstein law:
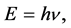 (1)
(1)
where  is a frequency and h is the Planck constant. But what was the physical origin of the frequency in the Planck-Einstein formula?
is a frequency and h is the Planck constant. But what was the physical origin of the frequency in the Planck-Einstein formula?
De Broglie initially imagines that the source of the frequency is related with some periodic phenomenon inside the particle [3]. He considers a particle with velocity v along the x axis in an inertial frame S. Assuming that the combination of the Planck-Einstein equation (1) for the photons and the relativistic energy of the particle,
 (2)
(2)
holds, he writes that in the rest frame S0 of the particle there must be:
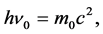 (3)
(3)
where 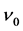 is the frequency of the supposed inner vibration. But de Broglie is immediately forced to face a problem. Because of the relativistic time dilation, an observer, for whom the particle is moving with velocity v, ascribes to the inner vibration a lower frequency
is the frequency of the supposed inner vibration. But de Broglie is immediately forced to face a problem. Because of the relativistic time dilation, an observer, for whom the particle is moving with velocity v, ascribes to the inner vibration a lower frequency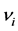 :
:
 (4)
(4)
However, comparing equation (1) with equation (2):
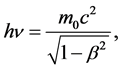 (5)
(5)
and considering the condition (3), we easily obtain the relativistic formula of transformation between frequencies
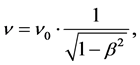 (6)
(6)
which is typically linked with a wave phenomenon: 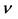 is the frequency of a wave in S, while
is the frequency of a wave in S, while 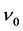 is now the frequency of such a wave in the frame S0.
is now the frequency of such a wave in the frame S0.
In order to resolve this difficulty, de Broglie assumes the existence of a “fictitious” wave associated with the particle [3] with frequency ![]() and phase velocity
and phase velocity
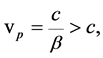 (7)
(7)
that is
![]() (8)
(8)
According to the French physicist, the wave was fictitious because, being its speed greater than the speed of light, it cannot transport energy2. In order to justify the assumption of equation (7), he shows that if the periodic inner phenomenon and the external wave with phase velocity in equation (7) are in phase at a given time, they will be always in phase; i.e. the particle moves within the wave maintaining its inner vibration in phase with the wave. De Broglie called that “law of the harmony of phases”.
His result, according to de Broglie, suggests that “any moving body could be accompanied by a wave, and it is impossible to disjoin the motion of the body from the wave propagation” [6]. Therefore, he assumes that  is the frequency of a plane wave which accompanies the particle, and that this frequency is the same which is in the Planck-Einstein equation.
is the frequency of a plane wave which accompanies the particle, and that this frequency is the same which is in the Planck-Einstein equation.
Let us recall the relativistic momentum of the particle:
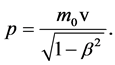 (9)
(9)
By comparing equation (9) with equation (5) and assuming that this holds in any frame, we can write the momentum in terms of the wave frequency:
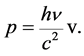 (10)
(10)
But from equation (8) we know that![]() , and remember that for a monochromatic wave the wavelength is
, and remember that for a monochromatic wave the wavelength is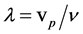 , from equation (10) we have the formula that made de Broglie famous:
, from equation (10) we have the formula that made de Broglie famous:
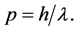 (11)
(11)
Equation (11) connects the module of the momentum p of a particle with the wavelength  of the associated plane wave through the Planck constant h. (For historical precision, we have to say that de Broglie expressly writes equation (11) only in the last chapter of his PhD thesis, in the form
of the associated plane wave through the Planck constant h. (For historical precision, we have to say that de Broglie expressly writes equation (11) only in the last chapter of his PhD thesis, in the form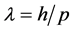 . In all his preceding works, including the treatment of the Bohr atom, he always reasons in terms of frequency.)
. In all his preceding works, including the treatment of the Bohr atom, he always reasons in terms of frequency.)
De Broglie’s prediction on the wave nature of the electron, the reason for his Nobel Prize, will be confirmed a few years later in the experiments of Davisson, Germer [14] and Thomson [15] on the diffraction of electrons by crystals. (For an introduction of the Thomson’s experiment and its optical analogy, see [16].)
Today just a few introductory textbooks to quantum theory describe the original way of de Broglie’s thinking. Some books contain simplified versions [17,18] or the successive de Broglie’s derivation with wave packets [19]; most of them simply cite equation (11) as a postulate, and its application in the deduction of the energy quantization in Bohr’s atom [20,21].
Perhaps, from the present perspective, many of de Broglie’s initial suppositions appear strange (but see [22]). However, rejecting entirely the reasoning of the French physicist, and ignoring completely the history of his formula, mean also missing the relativistic argument, which underlines from the beginning how quantum mechanics is related to Special Relativity (without having to wait for the Dirac equation, with his description of spin and prediction of antimatter). This is a pity, as the power to unify different descriptions of the phenomena is one of the more interesting sides of the physics.
In the next section we report an alternative deduction of the de Broglie relation obtained directly from the Lorentz transformations and the Planck-Einstein equation. In Section 3, following de Broglie and other authors [23-25], we show how Special Relativity puts constraints on the possible formulas that may connect energy and momentum of a particle with wavelength, frequency and wave amplitude. In particular we demonstrate that equations like de Broglie’s and Planck-Einstein’s are the only relations allowed by Special Relativity, once we assume that momentum and wave vector have the same direction.
2. De Broglie Relation from Special Relativity and Planck-Einstein Relation
For particles without rest mass 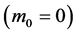 such as photons, deducing the de Broglie relation from the PlanckEinstein equation is straightforward. In fact, following Einstein [26-28], it is enough to consider the relativistic equation between momentum and energy:
such as photons, deducing the de Broglie relation from the PlanckEinstein equation is straightforward. In fact, following Einstein [26-28], it is enough to consider the relativistic equation between momentum and energy:
 (12)
(12)
Putting 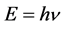 in equation (12) and recalling that
in equation (12) and recalling that  we quickly obtain equation (11).
we quickly obtain equation (11).
An elegant way to derive the de Broglie relation, for any massive or massless particle, can be achieved using directly the Lorentz transformations3. We put forward the following assumptions:
1.a: Each particle is associated with a wave phenomenon.
2.a: In every inertial frame the relation 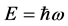 holds, where E is the energy of the particle,
holds, where E is the energy of the particle, 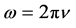 is the angular frequency of the associated wave in that frame and
is the angular frequency of the associated wave in that frame and 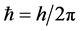 is a relativistically invariant constant.
is a relativistically invariant constant.
We want to show that:
Theorem a: According to Special Relativity and 1.a-2.a, between momentum and wave vector there is necessarily the relation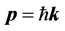 .
.
Let S and S’ be two inertial frames in relative motion. According to 2.a, we assume that in both frames the Planck-Einstein relation applies to any particle:
 (13)
(13)
We introduce, for the particle and the wave, the fourmomentum P and the wave four-vector K, respectively:
 (14)
(14)
where the wave vector k has modulus . We assume, for simplicity, that the frames S and S’ have parallel axes to each other and that at time
. We assume, for simplicity, that the frames S and S’ have parallel axes to each other and that at time  the origins O and O’ of the spatial coordinates coincide.
the origins O and O’ of the spatial coordinates coincide.
Moreover, we suppose S’ to move with respect to S with speed 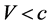 along the direction of the x axis, and the direction of the wave propagation to be along such axis (Figure 1).
along the direction of the x axis, and the direction of the wave propagation to be along such axis (Figure 1).
The Lorentz transformations for the four-momentum and the wave four-vector are
 (15)
(15)
where

Figure 1. Given a plane wave with wave vector k, we choose our inertial frame S with x axis coinciding with the direction of the wave vector, so that . The figure schematically shows some fronts of the plane wave. S’ is the inertial frame travelling with velocity V in comparison with S.
. The figure schematically shows some fronts of the plane wave. S’ is the inertial frame travelling with velocity V in comparison with S.
 (16)
(16)
Then we have
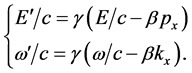 (17)
(17)
By multiplying the second of equations (17) by the Planck constant :
:
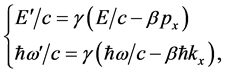 (18)
(18)
and by subtracting side by side the two equations (18):

![]() (19)
(19)
from which, because of equation (13), we get
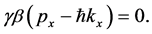 (20)
(20)
If we exclude the trivial condition in which the relative velocity V of the frames is zero (in such a case the factor  is also zero and the two systems S and S’ coincide), equation (20) is only satisfied with
is also zero and the two systems S and S’ coincide), equation (20) is only satisfied with
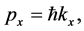 (21)
(21)
equivalent to the de Broglie equation for the x component of the momentum.
We point out as the just given demonstration, with the assumption 2.a, holds for particles of any mass, while de Broglie’s demonstration, starting from the relation (9), only holds for particles with nonzero rest mass.
Equation (21) can be easily generalized to other components of momentum and wave vector. In fact, consider a general orientation of the wave vector k with respect to the S frame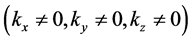 . We may use inertial frames S’y and S’z travelling with velocities along y and z with respect to S. Applying the correspondent relations (17) for S’y and S’z for the pairs of components
. We may use inertial frames S’y and S’z travelling with velocities along y and z with respect to S. Applying the correspondent relations (17) for S’y and S’z for the pairs of components ,
,  and
and ,
,  we get at once
we get at once 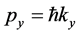 and
and .
.
3. De Broglie and Planck-Einstein Relations Together from Special Relativity
As already remarked by Einstein in one of his fundamental works of 1905, the energy of an electromagnetic radiation contained in a closed surface, and the frequency of the same radiation, change under the Lorentz transformations in the same way [30]. And as pointed out by Ashby and Miller [23], even the energy of a massless particle and the frequency of an electromagnetic wave change under the Lorentz transformations in the same way. According to Ashby and Miller that gives strong constraints on the possible forms that a relation between the energy of a photon and the frequency of a wave may have. In fact, these authors assume, ab absurdo, 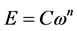 , where n is in general different from 1 and C is an invariant constant. They show that the Planck-Einstein relation, which is obtained with
, where n is in general different from 1 and C is an invariant constant. They show that the Planck-Einstein relation, which is obtained with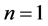 , is the only kind of dependence between energy and frequency which is relativistically invariant.
, is the only kind of dependence between energy and frequency which is relativistically invariant.
Therefore it would seem, from the developed reasoning in Section 2 and from the Ashby and Miller result, that, at least for the photons, both Planck-Einstein and de Broglie equations may follow from Special Relativity. Moreover it is also natural to wonder if a general constraint exists, which is valid for particles with any mass, for which the condition of relativistic invariance imposes the form of both Planck-Einstein and de Broglie relations.
As a matter of fact, here we intend to show that between the determinate four-momentum of a particle and the wave four-vector of a monochromatic wave there must be a condition of direct proportionality, if the velocity of the particle has the same direction of the associated wave propagation.
We assume from experience that every particle is in relation with a wave [31]. We make no assumptions about the specific nature of this wave, (still a controversial issue after almost a century [32]) or on the type of differential equation it may have: the d’Alembert wave equation, or Schrödinger’s, or Klein-Gordon’s, or Dirac’s, or more. We suppose only that a perturbation of an unclear kind, describable as a plane wave with definite wave number and frequency, is associated with the finite energy and momentum of a corpuscle.
We recall that in classical mechanics a plane wave possesses infinite total momentum and infinite total energy, and then we can only define for it a flux and a density of momentum, or a flux and a density of energy [33], so our assumption, that we could call “quantistic”, is in contrast with classical mechanics.
We consider as previously, for sake of simplicity, a plane wave of angular frequency 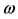 travelling with wave vector k along the x positive direction of an inertial frame S. All our results will be generalizable for k with a generic direction with respect to S following the way sets out at the end of Section 2.
travelling with wave vector k along the x positive direction of an inertial frame S. All our results will be generalizable for k with a generic direction with respect to S following the way sets out at the end of Section 2.
In S,  and because of the Lorentz transformations (15) of the wave four-vector, the y and z components of k will be always zero also in any other inertial reference S’. Therefore we will look for the expressions of E and
and because of the Lorentz transformations (15) of the wave four-vector, the y and z components of k will be always zero also in any other inertial reference S’. Therefore we will look for the expressions of E and 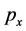 only as functions of
only as functions of 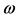 and
and . In fact, since we assume that no force acts on our system, the energy and the momentum depend neither on the spatial coordinate x nor on the time t. Let us denote with A a generic amplitude of the wave (without defining whether it is a scalar, a four-vector or other). We assume the following postulates:
. In fact, since we assume that no force acts on our system, the energy and the momentum depend neither on the spatial coordinate x nor on the time t. Let us denote with A a generic amplitude of the wave (without defining whether it is a scalar, a four-vector or other). We assume the following postulates:
1.b: Each particle is associated with a wave and it is impossible to disjoin the motion of the particle from its wave.
2.b: The finite energy and momentum of a free particle are associated with the characteristics of a monochromatic plane wave, amplitude, frequency and wave vector:
 (22)
(22)
3.b: The momentum of the particle flows in the same direction of the wave propagation.
We intend to show:
Theorem b: The only functions (22) allowed by Special Relativity and by 1.b - 3.b, are the relations of proportionality 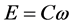 and
and , where C is a relativistic invariant.
, where C is a relativistic invariant.
For the development of Theorem b we need the following lemma:
Lemma: In the frame S0 where the momentum of the particle is zero,  the wave vector is zero as well,
the wave vector is zero as well,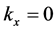 .
.
According to our assumptions, the momentum has to flow in the direction of the wave propagation, in conformity with what happens to the waves of classical mechanics. That is, for , if
, if 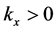 then it is also
then it is also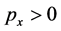 , if
, if  it must be
it must be :
:
 (23)
(23)
We require that such a condition holds in every inertial system S. Let S0 be the frame in which the momentum of the particle is zero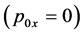 . The Lorentz transformations between the two inertial frames S and S0 for the components of the momentum and the wave vector are:
. The Lorentz transformations between the two inertial frames S and S0 for the components of the momentum and the wave vector are:
 (24)
(24)
where now we have represented in explicit form the dependence of β on the velocity 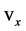 of S0, coincident with the rest frame of the particle (hence
of S0, coincident with the rest frame of the particle (hence  is also the velocity of the particle with respect to S). The sign of
is also the velocity of the particle with respect to S). The sign of  only depends on the sign of
only depends on the sign of . Therefore it follows from equations (24) that condition (23) is satisfied if, and only if, in S0 there is
. Therefore it follows from equations (24) that condition (23) is satisfied if, and only if, in S0 there is . Then:
. Then:
 (25)
(25)
So assuming that the momentum, i.e., the velocity of the particle, is always in the direction of the wave propagation implies the existence of a frame S0 where momentum and wave vector are both zero4.
Let us look for the velocity 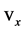 of the frame S0 as a function of
of the frame S0 as a function of 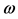 and
and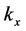 . Putting
. Putting  into the inverse of the second transformation in equations (24),
into the inverse of the second transformation in equations (24),
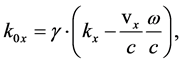 (26)
(26)
we get immediately:
 (27)
(27)
Remembering that the phase velocity is defined as , from equation (27 ) we have
, from equation (27 ) we have
![]() (28)
(28)
Equation (28) is exactly equivalent to equation (8), postulated by de Broglie in order to obtain the harmony of phases between the periodic inner phenomenon and the external wave.
Coming back to Theorem b, we consider the two invariants square moduli of the four-momentum and the wave four-vector:
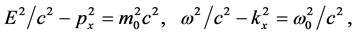 (29)
(29)
where 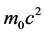 and
and  are, respectively, the energy E0 and the frequency in the frames where the momentum and the wave vector are zero. We study the four different possible cases:
are, respectively, the energy E0 and the frequency in the frames where the momentum and the wave vector are zero. We study the four different possible cases:
Case 1: 
We have, from the Lorentz transformations between S and S0 for the four-vectors P and K:
 (30)
(30)
Now, according to our Lemma, we assume that in the frame S0 we have 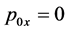 and
and . The previous equations become:
. The previous equations become:
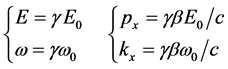 (31)
(31)
and by dividing side by side equations (31) we get:
 (32)
(32)
So, being the inertial frame S arbitrary, from the first of equations (32) we deduce that the ratio  has to be an invariant. Then we can introduce the invariant C:
has to be an invariant. Then we can introduce the invariant C:
 (33)
(33)
where C is for the initial hypotheses finite, positive and constant with respect to the space-time coordinates . By confronting equations (32) with equation (33), we directly have:
. By confronting equations (32) with equation (33), we directly have:
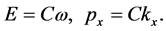 (34)
(34)
Identifying C with the Planck constant, we can recognize in equations (34), respectively, the Planck-Einstein and the de Broglie relations.
From the definition of C in relation (33), we see that
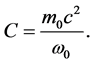 (35)
(35)
Therefore C does not explicitly depend on the amplitude, but may depend on the inertial mass of the particle and the invariant , the frequency in the frame where the wave is stationary. In general:
, the frequency in the frame where the wave is stationary. In general:
 (36)
(36)
However, if we require, according postulate 2.b and the first of equations (32), that in the limit 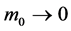 the invariant C is finite and different from zero, from relation (35) it must necessarily be also
the invariant C is finite and different from zero, from relation (35) it must necessarily be also  (we shall analyze the case
(we shall analyze the case  and
and  below). This claim implies the existence of a dependence between
below). This claim implies the existence of a dependence between  and
and ,
, . So, in such a circumstance, C can only depend on the mass,
. So, in such a circumstance, C can only depend on the mass, 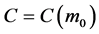 , and the invariant is constant for that particle. That is equivalent to assuming the inertial mass is the only invariant which plays a role in the problem.
, and the invariant is constant for that particle. That is equivalent to assuming the inertial mass is the only invariant which plays a role in the problem.
Finally, if we demand that C is independent of the mass, such as the Planck constant seems to be experimentally [34], we deduce easily from equation (35) that there must be , where
, where 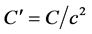 is an identical constant for every particle. Then the inertial mass is proportional to the frequency of a periodic phenomenon, as initially supposed by de Broglie.
is an identical constant for every particle. Then the inertial mass is proportional to the frequency of a periodic phenomenon, as initially supposed by de Broglie.
Case 2: 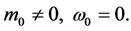
Now, in S0, we have 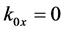 and
and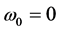 . So, from the Lorentz transformations (30), if
. So, from the Lorentz transformations (30), if 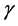 was finite in every frame S there would be
was finite in every frame S there would be 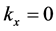 and
and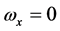 , a situation physically impossible for a wave.
, a situation physically impossible for a wave.
A way out is represented by allowing the factor  to be infinite. But this happens only for
to be infinite. But this happens only for , and in such a situation the frame S0 and the particle travel at the speed of light. In order to avoid the infinite energy of the particle we should assume
, and in such a situation the frame S0 and the particle travel at the speed of light. In order to avoid the infinite energy of the particle we should assume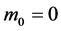 , in contradiction with the conditions of Case 2.
, in contradiction with the conditions of Case 2.
Case 3: 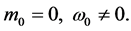
In this case, since , in S0 we have
, in S0 we have  and
and . Then, from the Lorentz transformations (30), for
. Then, from the Lorentz transformations (30), for 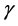 finite the energy of the particle would be zero in any frame; but this is a situation devoid of physical meaning as well. To preserve finite E we should assign to
finite the energy of the particle would be zero in any frame; but this is a situation devoid of physical meaning as well. To preserve finite E we should assign to 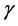 an infinite value considering, like the previous case,
an infinite value considering, like the previous case,  , the particle in motion at the speed of light. However, in order to maintain finite the wave vector
, the particle in motion at the speed of light. However, in order to maintain finite the wave vector , in such a circumstance it would be also necessary to suppose
, in such a circumstance it would be also necessary to suppose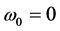 , in contradiction with the conditions of Case 3.
, in contradiction with the conditions of Case 3.
Case 4: 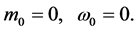
Let us consider the Lorentz transformations between two inertial frames S and S’ for the components of the four-momentum and the wave four-vector:
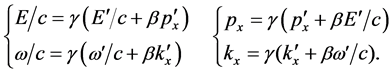 (37)
(37)
If we put 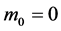 and
and  into the invariants (29), and we consider in accordance with our lemma, that
into the invariants (29), and we consider in accordance with our lemma, that  and
and  must have the same sign, we have5:
must have the same sign, we have5:
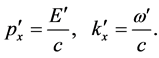 (38)
(38)
Inserting equations (38) into equations (37):
 (39)
(39)
we obtain, dividing side by side:
 (40)
(40)
Being primed and non-primed arbitrary inertial frames, from the first of relations (40), we deduce that the ratio 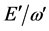 has to be an invariant. As above, we define the invariant
has to be an invariant. As above, we define the invariant
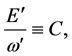 (41)
(41)
and from equations (40) we get again the Planck-Einstein and the de Broglie relations (34).
Summing up, the physically meaningful cases are Case 1 and Case 4. Case 1 corresponds to particles with inertial mass and waves with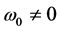 . This is the situation which is verified for fields with massive quanta. Case 4 corresponds instead to particles without inertial mass like photons, where the associated waves have
. This is the situation which is verified for fields with massive quanta. Case 4 corresponds instead to particles without inertial mass like photons, where the associated waves have , like the electromagnetic waves.
, like the electromagnetic waves.
4. Conclusions
We have shown that, once we assume the existence of a wave phenomenon with finite energy and momentum like a classical particle, and that the momentum fluxes along the same direction of the wave propagation, from Special Relativity follows that the four-momentum P and the wave four-vector K can be related just in one way, by a rule of direct proportionality:
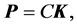
where C is an invariant under the Lorentz transformations.
Therefore, we have deduced de Broglie and PlanckEinstein relations for plane waves from more general assumptions than those usually considered. De Broglie uses the following hypotheses:
1) The rest energy of a particle 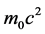 is proportional to a wave frequency
is proportional to a wave frequency :
:

where h is an invariant constant.
2) The relationship between phase velocity 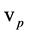 and particle velocity
and particle velocity  is
is

or 2ʹ) The frame in which the particle is at rest is the same frame in which the wave vector is zero,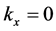 .
.
Assumptions 2) and 2ʹ) are equivalent, and de Broglie himself showed it [1]. However, we have also shown that, in order to deduce the proportionality between fourmomentum and wave four-vector, assumption 1) is not a necessary starting point. Moreover 2) and 2ʹ) can be replaced by another postulate:
2‴) The momentum always flows in the same direction of the wave propagation in every inertial frame.
The fact that the particle is at rest, that is , in the frame where
, in the frame where 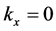 is a situation rather arbitrary, which de Broglie justifies with his phase harmony theorem. But as we have shown in our work, it follows from the quite natural and classical assumption that a wave and its momentum always travel in the same direction.
is a situation rather arbitrary, which de Broglie justifies with his phase harmony theorem. But as we have shown in our work, it follows from the quite natural and classical assumption that a wave and its momentum always travel in the same direction.
Our result shows that the relationship between Relativity and quantum physics is closer than usually thought6. It is also a meaningful example of the conditions that Special Relativity imposes to other theories, with Einstein’s words [36]: “the universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to the Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen system of inertia). This is a restricting principle for natural laws, comparable to the restricting principle of non-existence of the perpetuum mobile which underlies thermodynamics”.
Acknowledgements
This work has been supported by the EU-STREP Project QIBEC within the activities of the BEC center. QSTAR is the MPQ, IIT, LENS, UniFi joint center for Quantum Science and Technology in Arcetri.
REFERENCES
- L. de Broglie, “Recherches sur la Théorie des Quanta,” PhD Thesis, Masson, Paris, 1924.
- L. de Broglie, Journal de Physique, Vol. 3, 1922, pp. 422-428.
- L. de Broglie, Comptes Rendus de l’Académie des Sciences, Vol. 177, 1923, pp. 507-510.
- L. de Broglie, Comptes Rendus de l’Académie des Sciences, Vol. 177, 1923, pp. 548-550.
- L. de Broglie, Comptes Rendus de l’Académie des Sciences, Vol. 177, 1923, pp. 630-632.
- L. de Broglie, Philosophical Magazine, Vol. 47, 1924, pp. 446-458. http://dx.doi.org/10.1080/14786442408634378
- E. MacKinnon, American Journal of Physics, Vol. 44, 1976, pp. 1047-1055. http://dx.doi.org/10.1119/1.10583
- R. Schlegel, American Journal of Physics, Vol. 45, 1976, pp. 871-872. http://dx.doi.org/10.1119/1.11068
- E. MacKinnon, American Journal of Physics, Vol. 45, 1977, pp. 872-873. http://dx.doi.org/10.1119/1.11069
- F. Logiurato, Giornale di Fisica, Vol. LII, N 4, pp. 261-281. http://dx.doi.org/10.1393/gdf/i2011-10145-7
- R. Dugas, “History of Mechanics, Sec. 4, Part 5,” Routledge & Kegan Paul, London, 1957.
- M. Jammer, “The Conceptual Development of Quantum Mechanics, Sec. 5.3,” Mc Graw-Hill, New York, 1966.
- F. Logiurato, “De Broglie and Planck-Einstein Relations for Wave Packets in Special Relativity,” Unpublished.
- C. J. Davisson and L. H. Germer, Nature, Vol. 119, 1927, pp. 558-560. http://dx.doi.org/10.1038/119558a0
- G. P. Thomson, Proceedings of the Royal Society, Vol. 117, 1928, pp. 600-609. http://dx.doi.org/10.1098/rspa.1928.0022
- F. Logiurato, L. M. Gratton and S. Oss, “Optical Simulation of Debye-Scherrer Crystal Diffraction,” The Physics Teacher, Vol. 46, 2008, pp. 109-112. http://dx.doi.org/10.1119/1.2834534
- E. H. Wichmann, “Quantum Physics,” Berkeley Physics Course, Vol 4, McGraw-Hill, New York, 1971.
- A. P. French and E. F. Taylor, “An Introduction to Quantum Physics,” Norton & Company Inc, New York, 1978.
- D. Bohm, “Quantum Theory,” Prentice-Hall, Englewood Cliffs, 1951.
- S. Gasiorowicz, “Quantum Physics,” John Wiley & Sons, New York, 2003.
- D. Cassidy, G. Holton and J. Rutherford, “Understanding Physics,” Springer-Verlag, New York, 2002.
- P. Catillon, et al., Foundations of Physics, Vol. 38, 2008, pp. 659-664. http://dx.doi.org/10.1007/s10701-008-9225-1
- N. Ashby and S. Miller, “Principles of Modern Physics,” Holden-Day, San Francisco, 1970.
- I. S. Reed, IEE Proceedings A, Vol. 138, 1991, pp. 223- 236. http://dx.doi.org/10.1049/ip-a-3.1991.0031
- T. P. Jorgensen, International Journal of Theoretical Physics, Vol. 37, 1998, pp. 2763-2766. http://dx.doi.org/10.1023/A:1026689008592
- A. Einstein, “Quantentheorie der Strahlung,” Mitt. Ph. Ges. Zürich, Vol. 16, 1916, pp. 47-62.
- A. Einstein, Phys. Z., Vol. 18, 1917, pp. 121-128; R. Resnick, “Introduction to Special Relativity,” John Wiley & Sons, New York, 1968.
- C. Møller, “The Theory of Relativity,” Claredon Press, Oxford, 1955.
- L. de Broglie, “An Introduction to the Study of Wave Mechanics,” Methuen, London, 1930.
- A. Einstein, Annalen der Physik, Vol. 322, 1905, pp. 891- 921. http://dx.doi.org/10.1002/andp.19053221004; English translation in: H. A. Lorentz, et al., “The Principle of Relativity,” Methuen, London, 1923, pp. 35-65.
- R. P. Feynman, R. B. Leighton and M. Sands, “The Feynman Lectures on Physics,” Vol. 3, Addison-Wesley, Reading, 1989.
- F. Laloë, American Journal of Physics, Vol. 69, 2001, pp. 655-701. http://dx.doi.org/10.1119/1.1356698
- C. E. Elmore and M. A. Heald, “Physics of Waves,” McGraw-Hill, New York, 1969.
- A. D. Cronin, J. Schmiedmayer and D. E. Pritchard, Reviews of Modern Physics, Vol. 81, 2009, pp. 1051-1129. http://dx.doi.org/10.1103/RevModPhys.81.1051
- F. Logiurato and A. Smerzi, Journal of Modern Physics, Vol. 3, 2012, pp. 1802-1812. http://dx.doi.org/10.4236/jmp.2012.311225
- A. Einstein, “Autobiographical Notes,” In: P. A. Schilpp, Ed., Albert Einstein Philosopher-Scientist, MJF Books, New York, 1949, p. 57.
NOTES
1The development of de Broglie’s thought, even confining ourselves to his PhD thesis, is rather complex and not without contradictory points. In this introduction we only recall some of its fundamental aspects, referring to the literature [7-12] for the necessary details.
2For that reason, in a successive derivation of his equation, de Broglie regarded the velocity of the particle as the group velocity of a wave packet, this being always lower than the speed of light . We shall devote to wave packets, Relativity and de Broglie’s relation a next paper .
3For other proofs one can look at the cited Wichmann’s, French and Taylor’s books [17,18], and especially L. de Broglie’s .
4Alternatively, we can arrive at this conclusion from inequalities (23) by supposing  a continuous function.
a continuous function.
5Of course, we can also choose

For brevity, we study only one of the two possibilities, the final result being the same for both of them.
6About the connection between the postulates of quantum physics and Special Relativity, you can also read .

