Journal of Modern Physics
Vol.5 No.8(2014), Article
ID:46119,13
pages
DOI:10.4236/jmp.2014.58067
Physics in Discrete Spaces: On Space-Time Organization
Figure 1. The model of space we put forward in this essay. Here 18 cosmic bits (small circles: black for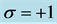 , white for
, white for ) are shared between 3 world points (large dotted circles) each comprised of
) are shared between 3 world points (large dotted circles) each comprised of 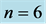 cosmic bits. Heavy lines are for binary negative (ferromagnetic) interactions
cosmic bits. Heavy lines are for binary negative (ferromagnetic) interactions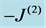 , dotted lines are for binary positive, anti-ferromagnetic, interactions
, dotted lines are for binary positive, anti-ferromagnetic, interactions 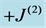 (only a part of these interactions are represented in the graph). This graph has no geometrical signification. The cosmic bits are only but elements of a set. The world points are subsets of this set.
(only a part of these interactions are represented in the graph). This graph has no geometrical signification. The cosmic bits are only but elements of a set. The world points are subsets of this set.
tions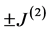 . It is therefore a random variable whose distribution
. It is therefore a random variable whose distribution  is Gaussian and given by
is Gaussian and given by
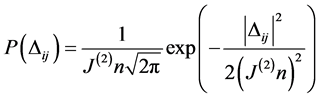 .
.
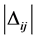 may be seen as a degree of proximity, the larger
may be seen as a degree of proximity, the larger 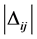 the closer i and j, but this interpretation has only a local topological signification and
the closer i and j, but this interpretation has only a local topological signification and 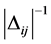 for example cannot be seen as a distance since no global topology, no geometry and no metrics have been defined so far.
for example cannot be seen as a distance since no global topology, no geometry and no metrics have been defined so far.
2.2. Statistical Properties
The Lagrangian of a world point writes
 .
.
In this expression, the Lagrangian  is limited to second order interactions because the fourth order interactions are completely negligible inside world points. Due to the interplay between the binary interactions
is limited to second order interactions because the fourth order interactions are completely negligible inside world points. Due to the interplay between the binary interactions  and the cosmic noise b the world points may be polarized. The polarization
and the cosmic noise b the world points may be polarized. The polarization 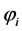 of a world point i comprised of n cosmic bits is defined as the thermal average
of a world point i comprised of n cosmic bits is defined as the thermal average 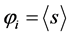 of the order parameter s:
of the order parameter s:
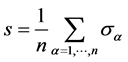 .
.
The statistical properties of a world point W are determined by using the mean field theory which consists in replacing the dynamic variables by their statistical averages. In general, the mean field theory is an approximation but when the connectivity of the elements of the system is high enough the mean field is an exact theory. This is the case for four dimensional Ising or Heisenberg magnets. This is also the case for world points due to their complete connectivity. The polarization ![]() is then the solution of a self consistent equation given by
is then the solution of a self consistent equation given by
 . (1)
. (1)
Here the binary interaction has been renormalized 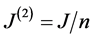 so as to make the Lagrangian
so as to make the Lagrangian 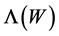 an extensive quantity. The polarization vanishes if
an extensive quantity. The polarization vanishes if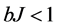 . This situation is called symmetric vacuum. It does not vanish if
. This situation is called symmetric vacuum. It does not vanish if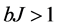 , and then vacuum is asymmetric.
, and then vacuum is asymmetric.
Another important property of mean field theories is the disappearance of fluctuations at least in the limit of infinitely large systems.
2.3. World Points Internal Spaces
We endow a world point with a (non-directly observable) organization by assuming that the polarization 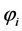 may be considered as the length
may be considered as the length 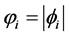 of a vector
of a vector ![]() in a d-dimensional abstract space called the internal space of W:
in a d-dimensional abstract space called the internal space of W:
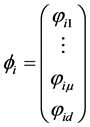 .
.
To give an analytical expression to the components 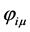 of vector
of vector ![]() we pose the following question: can a world point be considered as a set of d subsets (sub-world points so to speak) such that the system obtained by putting these d sub-world points together, reproduces the polarization of the world point as a whole?
we pose the following question: can a world point be considered as a set of d subsets (sub-world points so to speak) such that the system obtained by putting these d sub-world points together, reproduces the polarization of the world point as a whole?
To answer that question we must study more carefully the statistical mechanics of a world point made of d sub-world points. Let 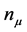 (with
(with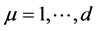 ),
), 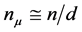 , be the number of cosmic bits associated with a sub world point
, be the number of cosmic bits associated with a sub world point  of W. The polarization components are given by the statistical averages of the d order parameters
of W. The polarization components are given by the statistical averages of the d order parameters 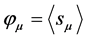 with
with
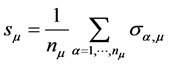 .
.
The calculation, a classical calculation in statistical mechanics, is given in Appendix 1. The polarizations 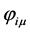 are obtained by minimizing the quantity
are obtained by minimizing the quantity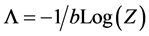 , somehow similar to a free energy. In the framework of a mean field theory
, somehow similar to a free energy. In the framework of a mean field theory 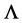 is given by
is given by
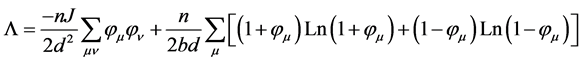 . (2)
. (2)
The polarizations are obtained by solving the set of d equations given by:  (the saddle point method). In the case where d = 1, that is to say if
(the saddle point method). In the case where d = 1, that is to say if
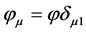 the free energy per bit reduces to
the free energy per bit reduces to
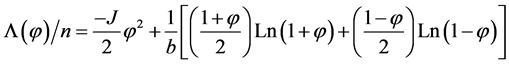 .
.
The condition 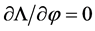 gives Equation (1).
gives Equation (1).
When b is large enough, 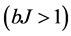 , the global polarization
, the global polarization ![]() does not vanish and it does not fluctuate. This no fluctuation property is also desirable for the components
does not vanish and it does not fluctuate. This no fluctuation property is also desirable for the components  to give to
to give to  the properties of a vector, but this is not guaranteed. To illustrate this point we use a good approximation for the solution of the self consistent Equation (1)
the properties of a vector, but this is not guaranteed. To illustrate this point we use a good approximation for the solution of the self consistent Equation (1)
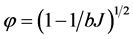
for . Let us take
. Let us take  for example. Then
for example. Then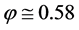 : Whereas a majority of CBs is oriented along
: Whereas a majority of CBs is oriented along , about 20% are oriented along
, about 20% are oriented along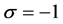 . Therefore if the world point is divided into d sub world points the order parameters
. Therefore if the world point is divided into d sub world points the order parameters 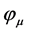 strongly depend on the way the sharing has been carried out. To cope with this difficulty we consider an isolated sub-world point
strongly depend on the way the sharing has been carried out. To cope with this difficulty we consider an isolated sub-world point . Its polarization
. Its polarization 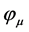 is given by the following self-consistent equation:
is given by the following self-consistent equation:
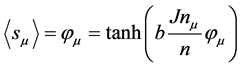 .
.
The order parameter does not vanish and does not fluctuate if
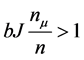
Therefore the polarization components 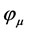 are well defined quantity if
are well defined quantity if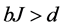 , the condition that we are looking for. This yields a highest value for d
, the condition that we are looking for. This yields a highest value for d
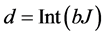 .
.
d is called the dimensionality of internal space. Our space is 4-dimensional. This implies that  , that is
, that is 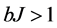 and the vacuum is asymmetric indeed.
and the vacuum is asymmetric indeed.
By expanding the logarithmic functions to second order in Equation (2) and by using the definition of polarization components, one has
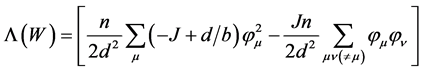 . (3)
. (3)
The expression (3) is rewritten along
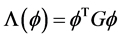 where G is a d-dimensional symmetric matrix whose elements are
where G is a d-dimensional symmetric matrix whose elements are
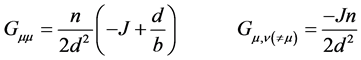 .
.
G is called the space-time generator. A more convenient form of G is its diagonal representation. The eigenvalues of G are solutions of the following equation:
 .
.
The diagonal representation identifies two and only two subspaces for G. The first one corresponds to the eigenvalue
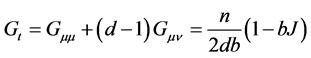 .
.
It is not degenerate. This subspace, of dimension 1 whatever d, will be called “time type dimension”. The other subspace corresponds to the eigenvalue
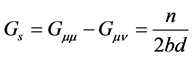 .
.
This subspace, of dimension d − 1, will be called “space type dimensions”.
2.4. Gauge Symmetry Invariance
Nothing determines the orientation of the internal space of a world point. Therefore physics must be insensitive to any reorientation of the internal space or to any permutation of its axes. This generates two sorts of gauge invariance symmetry. Let us consider the permutation invariance. Then G must transform according to direct sums of irreducible representations of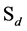 , the group of permutations of d objects. Let us for example consider four dimensional spaces. The permutation group
, the group of permutations of d objects. Let us for example consider four dimensional spaces. The permutation group  of four objects has
of four objects has  elements. Since
elements. Since  has 5 classes there are 5 irreducible representations that are
has 5 classes there are 5 irreducible representations that are
 with orders 1, 1, 2, 3 and 3 respectively [5] . The table of characters of these representations is given in Table1
with orders 1, 1, 2, 3 and 3 respectively [5] . The table of characters of these representations is given in Table1
The invariance of four dimensional matrices, such as G, under those transformations, requires the matrix to commute with the 24 matrices of permutations. An example of a permutation matrix is
 which is a four dimensional representation of the permutation
which is a four dimensional representation of the permutation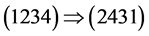 . Let
. Let 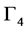 be this representation. Its characters are given in Table2
be this representation. Its characters are given in Table2
From these tables it is deduced that

a sum of two irreducible representations with dimensions 1 (time type dimension) and 3 (space type dimension) respectively.
The state 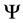 of the universe is now determined by a family of world point states
of the universe is now determined by a family of world point states 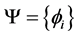 and the Langrangian
and the Langrangian 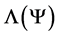 of the system becomes
of the system becomes
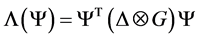 , (4)
, (4)
an expression that, via the Cartesian product, takes the global independence of internal spaces into account. The universe is now seen as a fibre bundle where ![]() forms the basis of the fibre bundle and G its fibres. If G is the same whatever the world point, the fibre bundle is trivial and we are dealing with flat spaces. If G is world point dependant, the fibre bundle is not trivial and we are dealing with general relativity.
forms the basis of the fibre bundle and G its fibres. If G is the same whatever the world point, the fibre bundle is trivial and we are dealing with flat spaces. If G is world point dependant, the fibre bundle is not trivial and we are dealing with general relativity.
3. Recovering the Space-Time Continuum
3.1. The Possible States of the Universe
The possible states 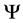 of the universe are obtained by minimizing the Lagrangian (4) under the constraint
of the universe are obtained by minimizing the Lagrangian (4) under the constraint 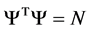 (N is the number of world points) that is by minimizing the expression
(N is the number of world points) that is by minimizing the expression
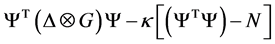
where ![]() is a Lagrange multiplier. The solution is an eigenvalue equation
is a Lagrange multiplier. The solution is an eigenvalue equation
 (5)
(5)
Table
Pierre Peretto Laboratory of Physics and Modelling of Condensed Matter, Grenoble, France Email: Pierre.peretto@lpmmc.cnrs.fr Copyright © 2014 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Received 6 October 2013; revised 5 November 2013; accepted 2 December 2013 ABSTRACT We see the whole universe as a collection of very simple binary physical systems. With this assumption, we put forward a detailed model of discrete spaces. Our own universe with its four dimensions, shared between one time-like dimension and three space-like dimensions, as well as the Minkowski metrics, are emerging properties of the model. Keywords:Space-Time Dimensions, Minkowski Metrics, Klein-Gordon Equation 1. A Model of Discrete Universe The natural phenomena are usually described in the framework of a four-dimensional space. This space has three equivalent space-like components, one time-like component and it is equipped with a Minkowski metrics. Space-time usually has an ontological status that it generally requires no further explanations. However, the numbers of dimensions (3 the number of space-like dimensions, and 1 the number of time-like dimensions) are numerical experimental data. If one considers that the general purpose of physics is to build theories that account for numerical experimental data, the construction of a theory of space-time is a necessity. In this essay, we put forward such a model and we explore some of its consequences. Any physical model rests upon a number of hypotheses and one can wonder what sort of hypotheses would form the basis of a relevant theory of space-time. We do not want to make any ad hoc hypothesis such as in string [1] , twister [2] or quantum loop gravity [3] theories for example. We even want the quantum or relativistic theories not to be prerequisites but to be consequences of the structure of space itself and to have no ontological status. The model that we propose here rests on three statements that we cannot reject without jeopardizing physics itself. We consider these three statements and their mathematical formalizations in turn. 1.1. The Universe Does Exist The first statement is simply that the universe does exist, that is, some information can be obtained on the universe through experimental observations. Information is the key word. As a matter of fact, since nothing else besides information is available on the nature of the universe, at least for materialist philosophers, one can assume that information itself constitutes the fabrics of the physical world. Information is measured in terms of an information unit or bit. A bit, here called a cosmic bit (CB), is the simplest physical object one can imagine. Accordingly, the first hypothesis of the model writes: Our universe as a whole is entirely made of a finite, countable, set of cosmic bits. The state The state We write 1.2. The Universe Is Not Disordered The second statement follows from the observation that the universe is not completely disordered and, therefore, that all possible states of the universe cannot be realized. As a consequence we must assume that there exists a functional of CBs states where Finally 1.3. The Universe Is Not Frozen The last statement follows from the observation that the states of the universe are never completely frozen, that is, order is not perfect. This implies that the CBs are subject to a degree of disorder whose amplitude is determined by a parameter b called “cosmic noise”. Space-time is then treated as an ordinary thermodynamic system analogous to e.g. a magnetic material, more precisely to a special sort of spin glass. It can be studied by using the tools of statistical mechanics. This is not a trivial assertion because statistical mechanics rests upon two fundamental hypotheses. The first one is the ergodic hypothesis, according to which temporal averages may be replaced by ensemble averages. Since the concept of time is not yet defined, only ensemble averages may be given a physical meaning, at least for the time being. Ergodicity is then a natural hypothesis and this makes it possible to derive the statistical properties of space from usual statistical physics techniques. In particular, according to statistical physics, the probability for space to be in a state and b the cosmic noise parameter. The second basic hypothesis of statistical mechanics is the existence of a reservoir that makes the noise b a well defined parameter. One may imagine that the total number of CBs is infinite and that To summarize, with these three statements, we put forward a thermodynamic model of space-time. This model is basically discrete. It introduces three, and only three, sorts of free parameters 2. World Points: The Cells of the Universe 2.1. Topological Properties The interplay between second order and fourth order interactions gives rise to clusters of cosmic bits called world (or physical) points. Let us consider a cluster W of n cosmic bits all connected to each over through negative (ferromagnetic) binary interactions Then, according to the majority rule, one has A world point is a cluster that minimizes its Lagrangian since there are about The following picture emerges: Space can be seen as a collection of world points i Table 2. Table of characters of Γ4. 3.2. Derivatives in Discrete Spaces To introduce the notion of derivatives in the context of discrete spaces one must introduce a square N-dimensional matrix D, namely the square root of One defines the increment or for each component of D may be seen as a differential operator because it is linear and it obeys the Leibniz formula. Let us consider two states that is On the other hand The second term vanishes because the elements of D are random The third term is a second order term. It may also be ignored and one has whence The parameters The first order derivative of The connection between D and the usual classical first order derivatives is more carefully studied in Appendix 2. Let us now consider second order derivatives. The second order increment of a scalar function or for each component of 3.3. Klein-Gordon Equation For trivial fibre bundles where the G matrix is the same whatever the world point, one entry of Equation (5) One introduces the coefficient By using the diagonal expression of G and the two parameters recognized a set of four Klein-Gordon equations. Let us write The metric tensor g is defined by Since bJ > 1 its that is The metrics is therefore Minkowskian. It would be Euclidian for The identification of Equation (6) with Equation (7) allows fundamental parameters to be expressed in terms of the basic parameters b, J and l* of the discrete space model. 1) The speed of light c is a universal dimensionless constant given by The speed of light diverges at the transition 2) The constant of Planck writes 3) Finally the mass m of the particle associated with the field The connection between the eigenvalue Equation (5) and the Klein-Gordon Equation (7) establishes the link between the discrete and the continuous descriptions of our universe. 4. Discussion and Conclusions The universe exists. The universe is globally ordered (it is not pure chaos). The universe shows some degree of disorder (it is not fully frozen). We present in this contribution a model of discrete universe fully and only based on these three very general statements. According to this model the universe is made of elementary physical systems called “cosmic bits”. The idea that the universe is made of bits is not new. Wheeler, for example, states that physics at large could be understood in terms of “It from bit” [6] . There is however a fundamental difference between his approach and ours. In the Wheeler approach the bits are to be understood as signals of information that are transmitted through some channel from an emitter to a receiver. The physical laws are the results of computations carried out on those bits by a huge sort of universal computer, a Turing machine for example, according to convenient programs. The physical world would be the result of these computations and the physicists would be the receivers. In our approach, there is no program and no programmer behind the stage. The bits are physical objects, not signals, that together constitute a system somehow similar to a ferromagnetic powder. The process that moves the bits is purely physical and determined by statistical physics. Moreover, in our approach time and space are treated on equal footing, in the spirit of relativity theory, and, therefore, this avoids the philosophical problems arising from the necessary existence of a clock driving the computer. Besides the three statements there is, a priori, no other prerequisites, no landscape, no metrics, no fields, no particles. Everything has to be rebuilt. The 4-dimensional time-space continuum has been recovered in this contribution but it remains to prove that the postulates of quantum theory or the Lagrangian of general relativity for example can also be recovered. These topics are outside the scope of the present discussion. As a matter of fact the model does not bring any essentially new results but it allows many concepts that are introduced in physical theories without justifications to be given a physical interpretation. Let us finish this paper by a list of these concepts. World point: this term has been introduced by Einstein to denote a point of the space-time continuum. In his context a world point is a mathematical point with zero dimension. Here a world point is a physical entity with a physical dimension l* Internal spaces: This notion is introduced in particles theory but is not given a physical interpretation. Here an internal space is the internal space of a world point that is the space spanned by all possible states Generator G: the Lagrangian of a world point i in state Gauge symmetry invariance: If G is invariant under the operations of a symmetry group the physical phenomena generated by G must be invariant under these operations, a property called. gauge symmetry invariance. Space-time generation: Minkowski metrics: the model generates a specific metrics with signature (−, +, +, +) that is the Minkowski metrics. It eliminates the ambiguity between the signatures (−, +, +, +) and (+, −, −, −) that are equivalent in special relativity. Finally, the appearance of the Klein-Gordon equation and the equivalence principle (in Appendix 2) strongly suggests that the quantum theory is, so to speak, cosubstantial with our model. Acknowledgements I would like to thank Pr. Roger Maynard for his helpful remarks and comments and Dr. Ana Cabral for her careful reading of this text. References Appendix 1 In this appendix, one computes the partition function of world points W. The Lagrangian of a world point W made of d sub-points with one has The partition function is By using the Stirling formula one obtains The realizable physical states are those that minimize F. Appendix 2 In this appendix one studies more carefully the connections between discrete and continuous derivatives The derivative When a computer is used for the calculation, the most accurate estimate of the derivative is obtained by using the smallest where f is described as a column vector with elements D and The second order derivative The operator Can the operator A second order derivative is a measurement of the curvature of f. We observe that 



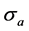 of a cosmic bit a,
of a cosmic bit a, 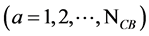 , is a binary variable
, is a binary variable 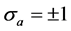 analogous to an Ising (classical) spin.
analogous to an Ising (classical) spin.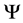 of the universe is determined by a family of CBs states
of the universe is determined by a family of CBs states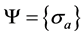 .
. as a
as a  -dimensional vector whose norm is
-dimensional vector whose norm is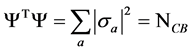 . In discrete spaces, if
. In discrete spaces, if 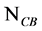 is finite as we assume it is, the states of the universe are necessarily normalized.
is finite as we assume it is, the states of the universe are necessarily normalized.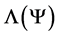 , called a Lagrangian, which is, at least approximately, minimized for the physically realizable states of the universe. The most general Lagrangian is written as an expansion over all possible clusters of CBs:
, called a Lagrangian, which is, at least approximately, minimized for the physically realizable states of the universe. The most general Lagrangian is written as an expansion over all possible clusters of CBs: .
.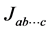 is an interaction parameter between the cosmic bits
is an interaction parameter between the cosmic bits 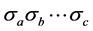 belonging to cluster
belonging to cluster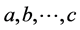 . Nothing determines the overall orientation of
. Nothing determines the overall orientation of 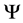 and therefore one must have
and therefore one must have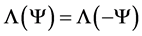 . This eliminates the odd terms of
. This eliminates the odd terms of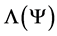 . In other ways, all CBs must be treated on equal footing which compels the amplitudes of interactions of same order to be identical. That is, for clusters implying a
. In other ways, all CBs must be treated on equal footing which compels the amplitudes of interactions of same order to be identical. That is, for clusters implying a ![]() number of CBs,
number of CBs, 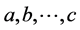 one has, for arbitrary
one has, for arbitrary 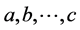
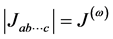 with
with ![]() an even number. For example all pairs ab are such that
an even number. For example all pairs ab are such that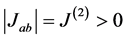 . It is assumed that the interaction amplitude
. It is assumed that the interaction amplitude 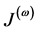 decreases very rapidly with the number
decreases very rapidly with the number ![]() of CBs, in particular
of CBs, in particular 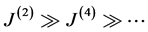 and we shall limit the expansion of
and we shall limit the expansion of 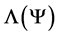 to clusters of 4 CBs. The signs of interactions remain to be determined. Since no knowledge exists,
to clusters of 4 CBs. The signs of interactions remain to be determined. Since no knowledge exists, 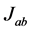 is taken as a random binary variable:
is taken as a random binary variable: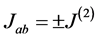 . Likewise
. Likewise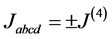 . Some correlations, however, possibly exist between the signs of second order interactions
. Some correlations, however, possibly exist between the signs of second order interactions 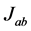 and those of fourth order interactions
and those of fourth order interactions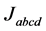 . In the present essay, it is assumed that the sign of
. In the present essay, it is assumed that the sign of 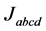 obeys a majority rule, that is
obeys a majority rule, that is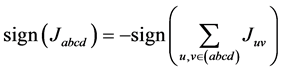 .
.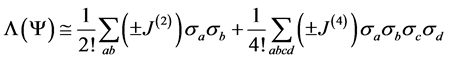 where the sign correlations are to be taken into account.
where the sign correlations are to be taken into account.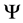 is given by the following Gibbs expression
is given by the following Gibbs expression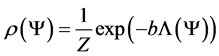 where Z is the partition function
where Z is the partition function
 , the number of CBs belonging to our own universe, is just a finite part of this set. Then the reservoir is made of the set of CBs not belonging to our universe.
, the number of CBs belonging to our own universe, is just a finite part of this set. Then the reservoir is made of the set of CBs not belonging to our universe. and
and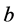 . In the model, everything of our familiar physics is, a priori, lost, no more space, no more time, no more fields, and no more particles. Everything has to be rebuilt. In the present article, we start the process with the construction of space and time. A first issue on this subject has already been published in a previous contribution [4] but here we develop the model in more detail.
. In the model, everything of our familiar physics is, a priori, lost, no more space, no more time, no more fields, and no more particles. Everything has to be rebuilt. In the present article, we start the process with the construction of space and time. A first issue on this subject has already been published in a previous contribution [4] but here we develop the model in more detail. .
.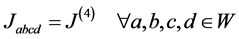 .
.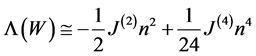
 pairs and
pairs and 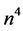 quartets of cosmic bits in a n cosmic bits system. That gives
quartets of cosmic bits in a n cosmic bits system. That gives . Since
. Since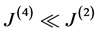 , n must be a very large number. Every cosmic bit of a world point W is a close neighbour of every cosmic bit of the same world point. Nothing distinguishes a cosmic bit of W from another cosmic bit of W and, therefore, the properties of the interior of W are not directly physically observable. However, some characteristics of the interior of W that we call generators may induce physical phenomena outside the world points and are physically observable. Space and time are the example that we consider in this contribution. Fields or particles are other examples that are not treated in this article. There are no possibilities for the building of such physical structures in mathematical points simply because there is no room for the notion of an inside in a mathematical point.
, n must be a very large number. Every cosmic bit of a world point W is a close neighbour of every cosmic bit of the same world point. Nothing distinguishes a cosmic bit of W from another cosmic bit of W and, therefore, the properties of the interior of W are not directly physically observable. However, some characteristics of the interior of W that we call generators may induce physical phenomena outside the world points and are physically observable. Space and time are the example that we consider in this contribution. Fields or particles are other examples that are not treated in this article. There are no possibilities for the building of such physical structures in mathematical points simply because there is no room for the notion of an inside in a mathematical point.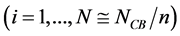 , comprised of n cosmic bits, whose robust states
, comprised of n cosmic bits, whose robust states ![]() are more or less loosely connected to each other through a random interaction
are more or less loosely connected to each other through a random interaction 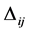 (see Figure 1). This interaction
(see Figure 1). This interaction 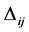 results from a sum of
results from a sum of 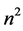 random binary interac-
random binary interac-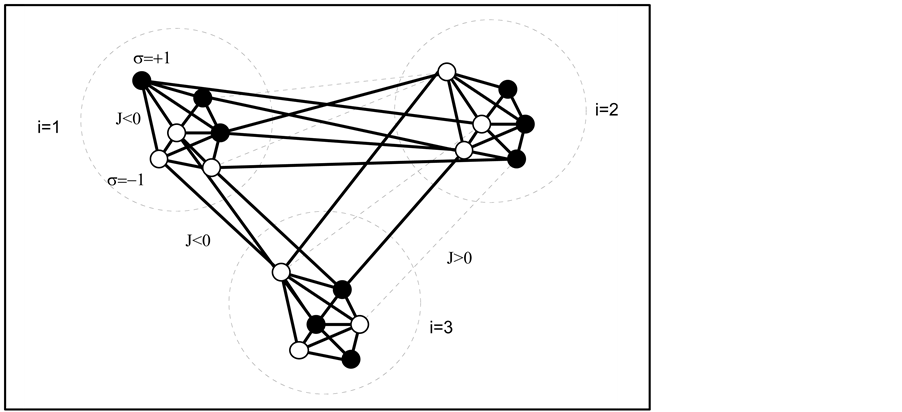 1. Table of characters of S4.
1. Table of characters of S4. ![]() that is
that is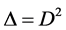 . Since the elements of
. Since the elements of ![]() are positive or negative D is, in general, a complex matrix.
are positive or negative D is, in general, a complex matrix.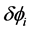 of a polarization
of a polarization ![]() of world point “i” by
of world point “i” by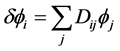 .
.
![]() . The first order derivative of
. The first order derivative of ![]() along the axis
along the axis  is then defined by
is then defined by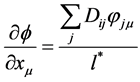 where l* is the smallest length that has a physically measurable meaning, that is the scale where the metrics is lost and also the scale where the distinction between the particles, be they fermions or bosons, disappears. Therefore l* should be the scale where super symmetry theories (Susy) come into play. Accordingly, the metric scale l* must be of the order of
where l* is the smallest length that has a physically measurable meaning, that is the scale where the metrics is lost and also the scale where the distinction between the particles, be they fermions or bosons, disappears. Therefore l* should be the scale where super symmetry theories (Susy) come into play. Accordingly, the metric scale l* must be of the order of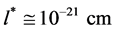 .
. and
and . One has
. One has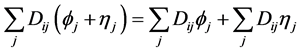
 and
and  is linear indeed.
is linear indeed. .
. .
.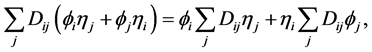
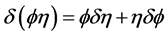 , the Leibniz formula.
, the Leibniz formula.![]() is a scalar field but physics generally deals with vector fields that are vectors of the internal spaces of world points. The components of a vector field
is a scalar field but physics generally deals with vector fields that are vectors of the internal spaces of world points. The components of a vector field  are given by
are given by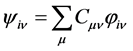
 are the components of vector
are the components of vector  and the increment of the
and the increment of the 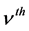 component is given by
component is given by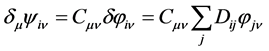 .
.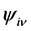 along the axis
along the axis 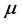 then writes
then writes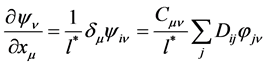 .
.![]() at world point “i” is
at world point “i” is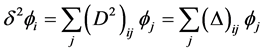
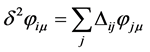
![]() . The second order derivative of
. The second order derivative of ![]() along the axis
along the axis  is given by
is given by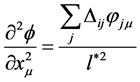 and the second order derivative of the vector field component
and the second order derivative of the vector field component 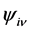 along axis
along axis 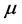 by
by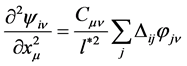 .
.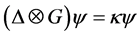 writes
writes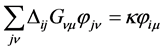 .
.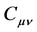 in both members of this equation and carries out the sum over index
in both members of this equation and carries out the sum over index .
.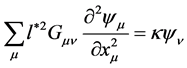 .
. and
and 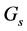 the final equation reads
the final equation reads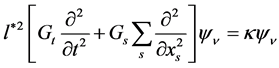 (6)
(6) .
.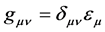 .
. elements associated with
elements associated with 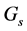 are
are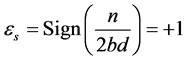 and its unique element associated with
and its unique element associated with 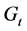 is
is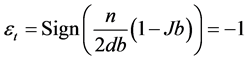
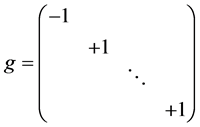 .
.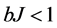 . It is worth pointing out that there is no more ambiguity on the sign of g (whereas relativistic mechanics does not distinguish between g and –g). The three dimensions of space and the unique dimension of time constitute a conformal space with dilatations factors given by
. It is worth pointing out that there is no more ambiguity on the sign of g (whereas relativistic mechanics does not distinguish between g and –g). The three dimensions of space and the unique dimension of time constitute a conformal space with dilatations factors given by  and
and 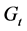 respectively. With
respectively. With 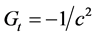 and
and 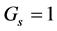 we recover the usual expression of the Klein-Gordon equation
we recover the usual expression of the Klein-Gordon equation . (7)
. (7)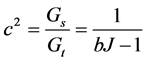 .
.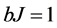 .
.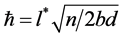 .
.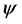 is given by
is given by 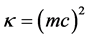 (provided that
(provided that ).
).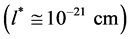 called the metric limit because the notion of a distance disappear into a world point. In his book “The Meaning of Relativity”, Einstein suggests that the difficulties he is facing in trying to unify gravity and electromagnetism could be possibly solved in discrete spaces [7] .
called the metric limit because the notion of a distance disappear into a world point. In his book “The Meaning of Relativity”, Einstein suggests that the difficulties he is facing in trying to unify gravity and electromagnetism could be possibly solved in discrete spaces [7] . of the world point.
of the world point.![]() writes
writes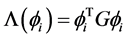 . G is a generator associated with i. All physical properties, fields, particles etc, are determined by G.
. G is a generator associated with i. All physical properties, fields, particles etc, are determined by G.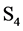 as the fundamental gauge invariance: nothing determines the orientation and the respective directions of the d axes of internal spaces. In particular any permutation of axes must leave physics unchanged. Therefore G must be invariant under the operations of the permutation group
as the fundamental gauge invariance: nothing determines the orientation and the respective directions of the d axes of internal spaces. In particular any permutation of axes must leave physics unchanged. Therefore G must be invariant under the operations of the permutation group 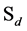 of d objects, that is
of d objects, that is 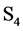 in our 4- dimensional space.
in our 4- dimensional space.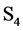 , we have seen, is of paramount importance because its irreducible representations generate the dimensions of the universe,
, we have seen, is of paramount importance because its irreducible representations generate the dimensions of the universe, 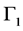 for the time-like dimension and
for the time-like dimension and 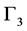 for the three space-like dimensions.
for the three space-like dimensions.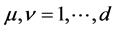 is given by
is given by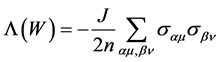 .
.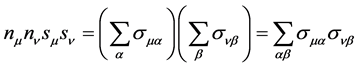
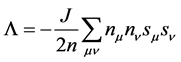 .
.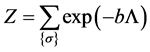 where the sum is over all possible configurations of the world point.
where the sum is over all possible configurations of the world point. .
. is a sum over all bits states for a given set of polarizations
is a sum over all bits states for a given set of polarizations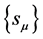 .
.  is purely combinatorial in nature. It is given by
is purely combinatorial in nature. It is given by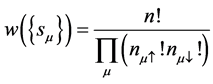 .
.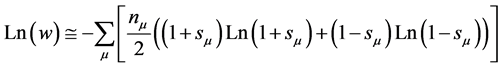 where a non-relevant constant has been skipped. The partition function reads:
where a non-relevant constant has been skipped. The partition function reads:
 a sum that, in the thermodynamic limit, reduces to one term where
a sum that, in the thermodynamic limit, reduces to one term where  (the so-called saddle point method). F, the free energy, is defined by
(the so-called saddle point method). F, the free energy, is defined by 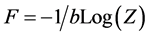 One has with
One has with 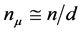
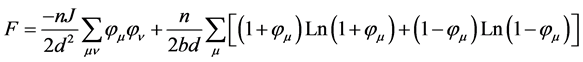 .
. of a continuous function
of a continuous function 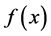 is defined in the limit
is defined in the limit  by
by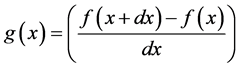 .
. that can be programmed. This value is given by the bit of the memory that controls the least significant digit of x. Let x* be this value. Then the variable x and the function
that can be programmed. This value is given by the bit of the memory that controls the least significant digit of x. Let x* be this value. Then the variable x and the function  are discrete:
are discrete: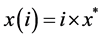 and
and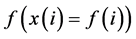 . The approximate value of the derivative is
. The approximate value of the derivative is that we can be written
that we can be written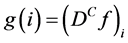
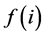 and
and 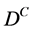 is a classical differential operator
is a classical differential operator .
.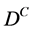 shows some similarities with the operator D that we have introduced in section III B. Any square matrix such as
shows some similarities with the operator D that we have introduced in section III B. Any square matrix such as ![]() can be expressed, according to the LDU theorem of Banachiewicz [8] , as a product of a lower triangular matrix L, a diagonal matrix A and an upper triangular matrix U. When the matrix is real, and symmetric, as is the case for
can be expressed, according to the LDU theorem of Banachiewicz [8] , as a product of a lower triangular matrix L, a diagonal matrix A and an upper triangular matrix U. When the matrix is real, and symmetric, as is the case for![]() , the two triangular matrices are each other conjugate:
, the two triangular matrices are each other conjugate: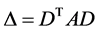 where D is a triangular (as
where D is a triangular (as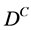 ) here a random triangular matrix, that is Dij = 0 for i < j. DT is the conjugate matrix and A is diagonal. Since
) here a random triangular matrix, that is Dij = 0 for i < j. DT is the conjugate matrix and A is diagonal. Since ![]() is real the diagonal matrix A can be absorbed in D and
is real the diagonal matrix A can be absorbed in D and  hence
hence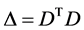 .
. are both triangular. Moreover they both obey the following conditions
are both triangular. Moreover they both obey the following conditions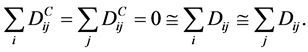
 , understood as the derivative of
, understood as the derivative of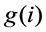 , is
, is .
.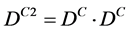 is therefore given by
is therefore given by .
.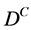 be considered a quantum operator? For an operator to be considered a quantum operator it is necessary that its representative matrix be hermitic which is not the case for
be considered a quantum operator? For an operator to be considered a quantum operator it is necessary that its representative matrix be hermitic which is not the case for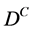 . Nevertheless the operator
. Nevertheless the operator , where
, where 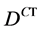 is the conjugate of
is the conjugate of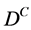 , is hermitic. We have
, is hermitic. We have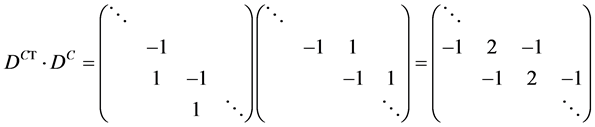 .
.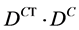 yields the good value of the curvature of f but the wrong sign. To correct this difficulty it is convenient to see
yields the good value of the curvature of f but the wrong sign. To correct this difficulty it is convenient to see ,
, 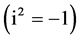 , rather than
, rather than 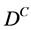 (and
(and 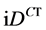 rather than
rather than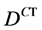 ) to be the convenient representation of a quantum derivation operator. In other words, the derivative D must correspond to the quantum operator
) to be the convenient representation of a quantum derivation operator. In other words, the derivative D must correspond to the quantum operator  or
or . This is the correspondence principle.
. This is the correspondence principle.
Journal Menu >>


