Journal of Modern Physics
Vol.4 No.12A(2013), Article ID:41320,5 pages DOI:10.4236/jmp.2013.412A1001
CC and NC Pion Production
1Departamento de F sica, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, Buenos Aires, Argentina 2Instituto de Fsica La Plata, CONICET, Buenos Aires, Argentina
3Departamento de F sica, Cinvestav, Mexico City, Mexico
Email: *mariano@fisica.unlp.edu.ar
Copyright © 2013 A. Mariano et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property A. Mariano et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 2, 2013; revised November 1, 2013; accepted November 28, 2013
Keywords: Neutrino Scattering; Pion Production; Neutrino Oscillation
ABSTRACT
The disappearance searching experiments 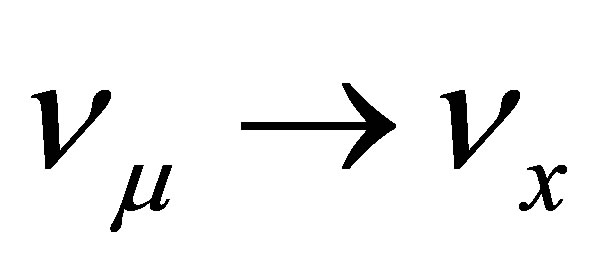 use charged current quasielastic (CCQE) reaction to detect an arriving neutrino and reconstruct its energy, while the CC1π+ production can mimic the CCQE signal process. In
use charged current quasielastic (CCQE) reaction to detect an arriving neutrino and reconstruct its energy, while the CC1π+ production can mimic the CCQE signal process. In 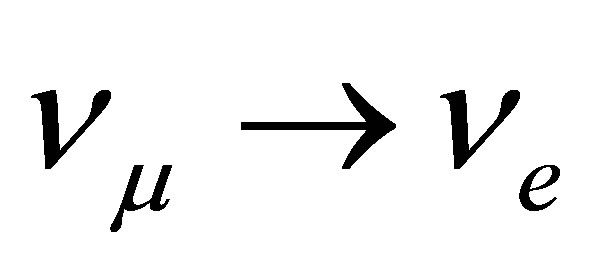 appearance experiments, the NC1π0 production process can lead to a fake
appearance experiments, the NC1π0 production process can lead to a fake  event by the impossibility for the detector of distinguish an arriving electron or a photon. Here we present a consistent model, from the point of view of the construction of the elemental amplitude, for the mentioned pion production background processes including bounding, smearing and final state interaction (FSI) effects in a single fashion. Results are comparable with more evolved approaches based on Monte Carlo simulations.
event by the impossibility for the detector of distinguish an arriving electron or a photon. Here we present a consistent model, from the point of view of the construction of the elemental amplitude, for the mentioned pion production background processes including bounding, smearing and final state interaction (FSI) effects in a single fashion. Results are comparable with more evolved approaches based on Monte Carlo simulations.
1. Introduction
Neutrino oscillation experiments search a distortion in the neutrino flux at a detector positioned far away (L) from the source. By comparing near and far neutrino energy spectra, one gains information about the oscillation probability
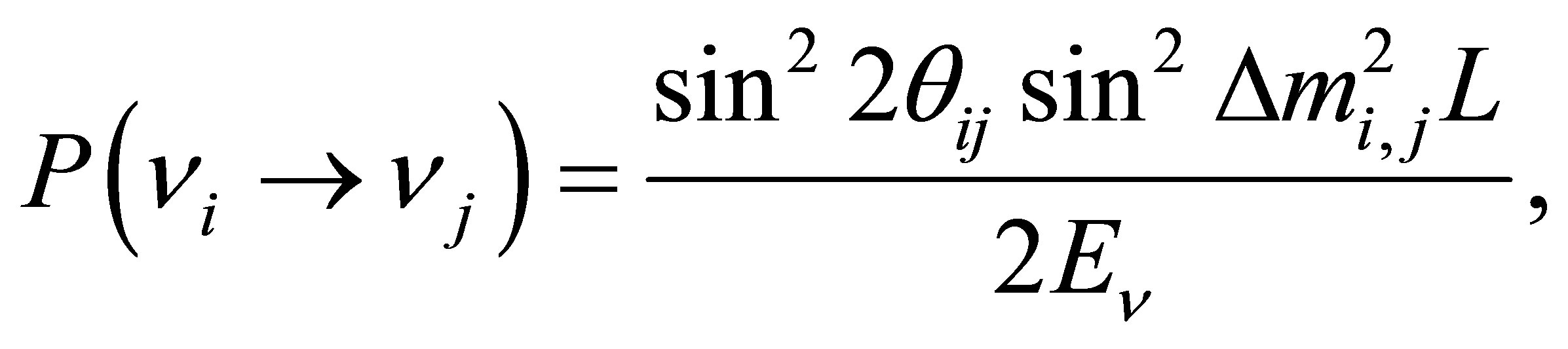
and then about the 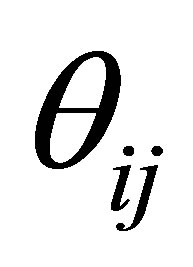 mixing angles and
mixing angles and  mass squared differences. New high quality data are becoming from MiniBoone, MINOS, NOMAD, MinerνA and SciBoone full dedicated to measure cross sections.
mass squared differences. New high quality data are becoming from MiniBoone, MINOS, NOMAD, MinerνA and SciBoone full dedicated to measure cross sections.
Disappearance searching experiments  use
use 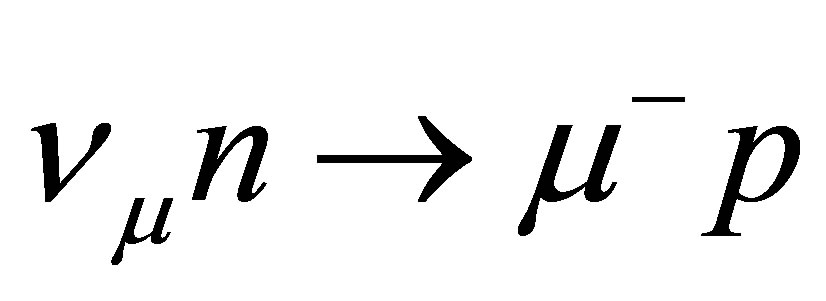 CCQE reaction to detect an arriving neutrino and reconstruct its energy.
CCQE reaction to detect an arriving neutrino and reconstruct its energy. 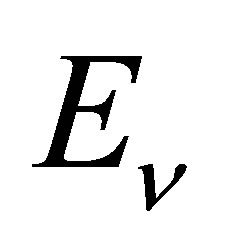 determination could be wrong for a fraction of CC1
determination could be wrong for a fraction of CC1 background events (20%)
background events (20%)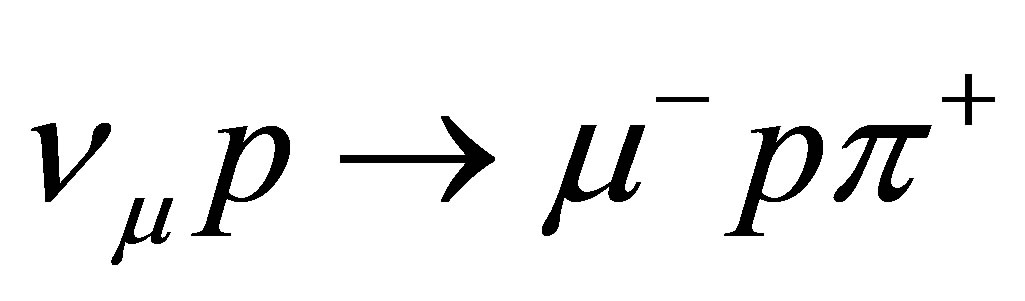 , that can mimic a CCQE one if the pion is absorbed in the target and/or not detected. In
, that can mimic a CCQE one if the pion is absorbed in the target and/or not detected. In 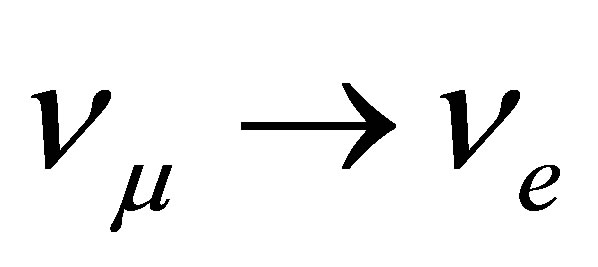 appearance experiment, one detects
appearance experiment, one detects 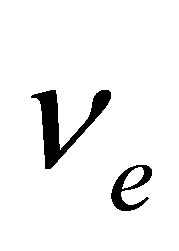 in an (almost)
in an (almost) 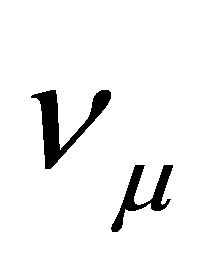 beam. Here the signal event
beam. Here the signal event  is dominated by a NC1π0
is dominated by a NC1π0 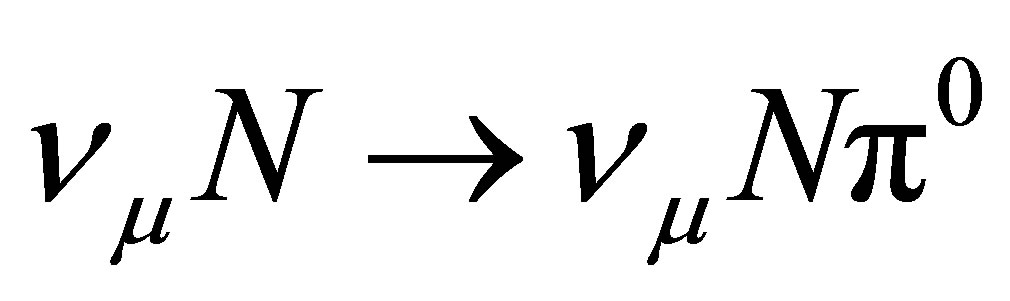 background, and the detector can not distinguish between
background, and the detector can not distinguish between 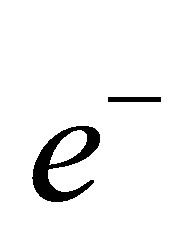 and
and  if one of both photons from the
if one of both photons from the 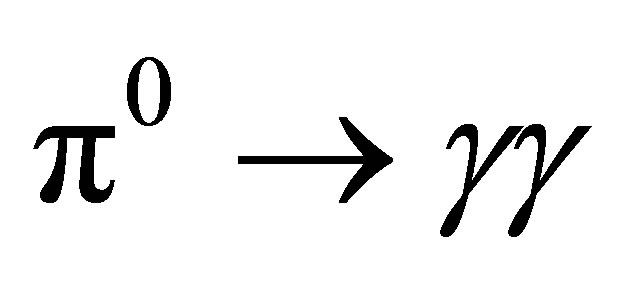 decay escapes. Then a precise knowledge of cross sections is a prerequisite in order to make simulations in event generators to substract fake 1π events in QE countings.
decay escapes. Then a precise knowledge of cross sections is a prerequisite in order to make simulations in event generators to substract fake 1π events in QE countings.
Several models have been developed over the last thirty years to evaluate these corresponding background elementary cross sections [1-4]. The scattering amplitude in all these models always contains a resonant term (R) in the 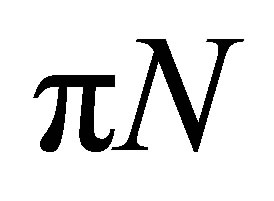 system, described by the
system, described by the  -pole contribution and (in some cases) by higher mass intermediate resonances, plus a nonresonant (B) term describing other processes (where the cross-
-pole contribution and (in some cases) by higher mass intermediate resonances, plus a nonresonant (B) term describing other processes (where the cross- contribution can also be included) leading to
contribution can also be included) leading to 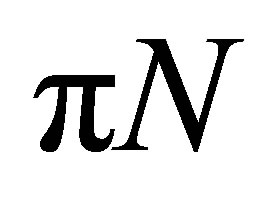 final states. The differences between all these models stem mainly from the treatment of the vertexes and the propagator used to describe the
final states. The differences between all these models stem mainly from the treatment of the vertexes and the propagator used to describe the  resonance and from the consideration (or not) of the nonresonant terms and its interference with the resonant contribution. Nuclear effects and FSI have been introduced by several works, where different nuclear models and event generators or simulations codes have been implemented in [5] (GiBUU) and [6,7].
resonance and from the consideration (or not) of the nonresonant terms and its interference with the resonant contribution. Nuclear effects and FSI have been introduced by several works, where different nuclear models and event generators or simulations codes have been implemented in [5] (GiBUU) and [6,7].
In this paper we reanalyze the elementary amplitude, bounding+ ground state correlations (GSC) effects, and FSI on the emerging nucleon (N) and pion , all what will be developed in the following sections.
, all what will be developed in the following sections.
2. Elementary Amplitude
For the 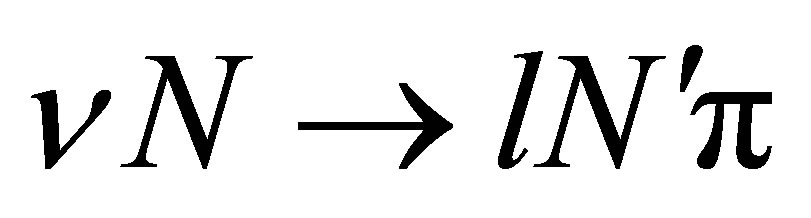 process the total cross section reads
process the total cross section reads
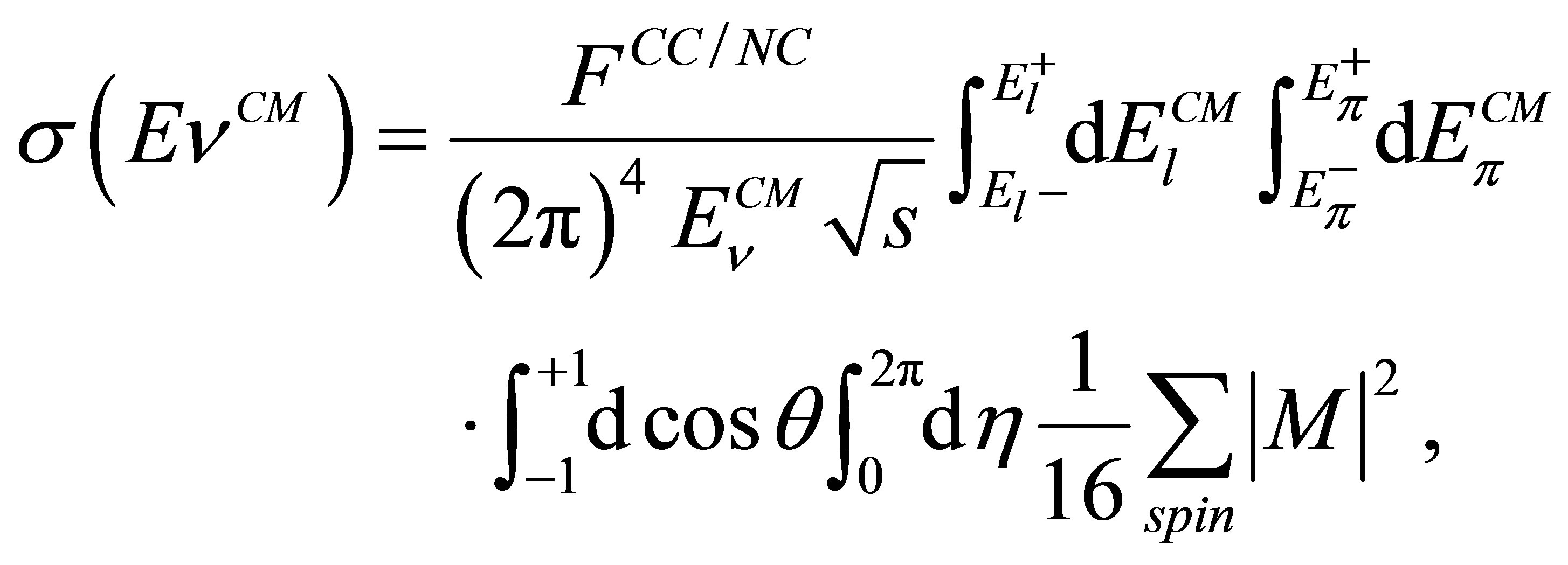 (1)
(1)
being 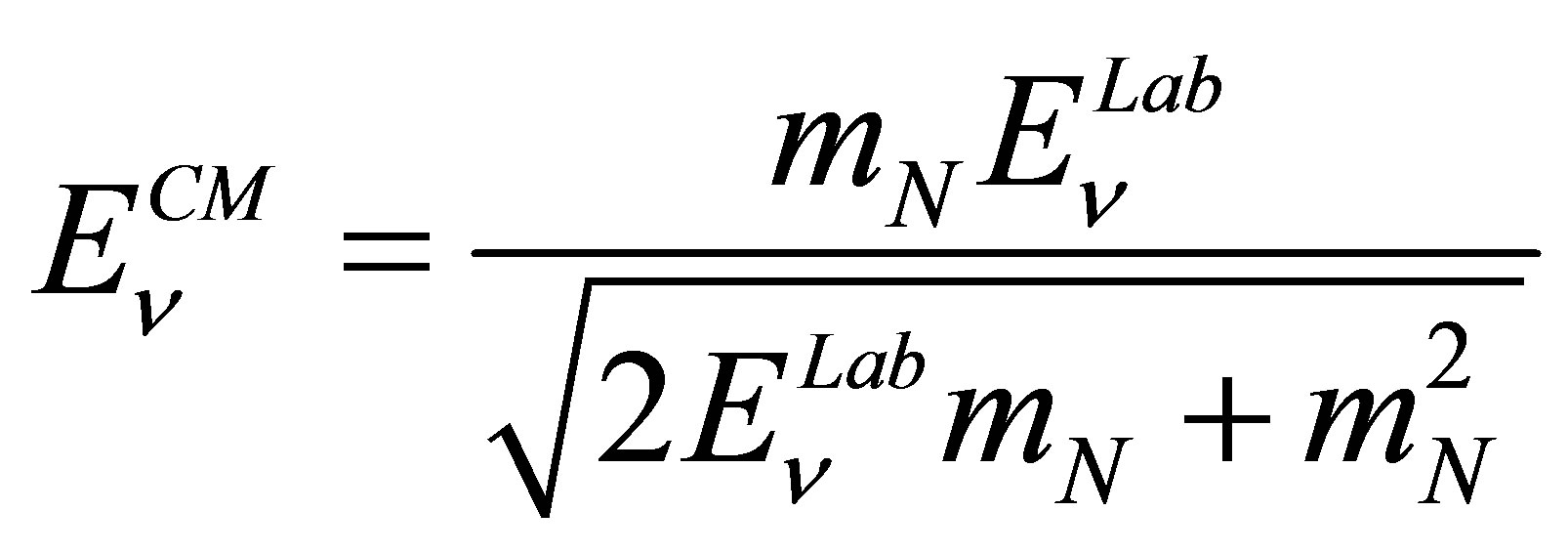 is the CM-Lab
is the CM-Lab 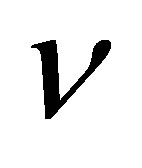 -energy relation,
-energy relation, 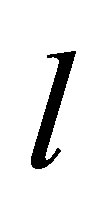 the merging lepton,
the merging lepton,  phasespace factors, and
phasespace factors, and
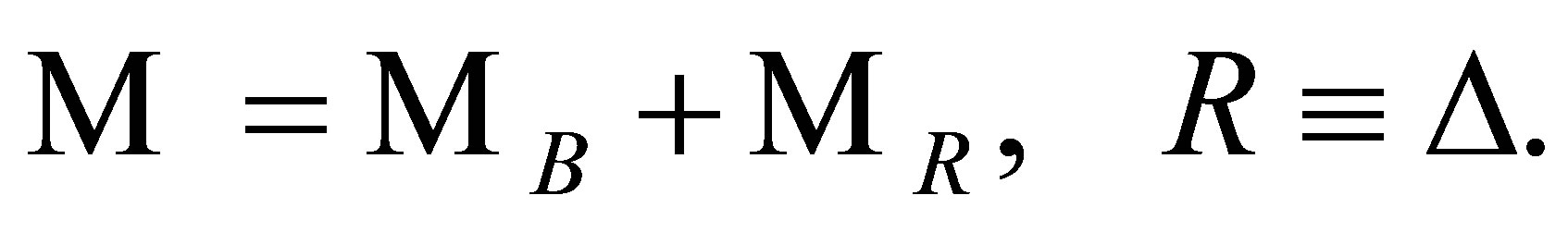 (2)
(2)
the amplitude where the contributions for the B amplitude are shown in the Figures 1(a)-(g), while for the R contribution is shown in the Figure 1(h).
The requirements on the hadronic part of the amplitude
 (3)
(3)
where 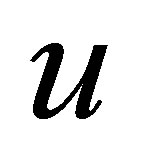 indicate the lepton and nucleon spinors, are: 1) Unitarity, violated with real B terms. It is possible an unitarization by introduction of experimental phase shifts
indicate the lepton and nucleon spinors, are: 1) Unitarity, violated with real B terms. It is possible an unitarization by introduction of experimental phase shifts
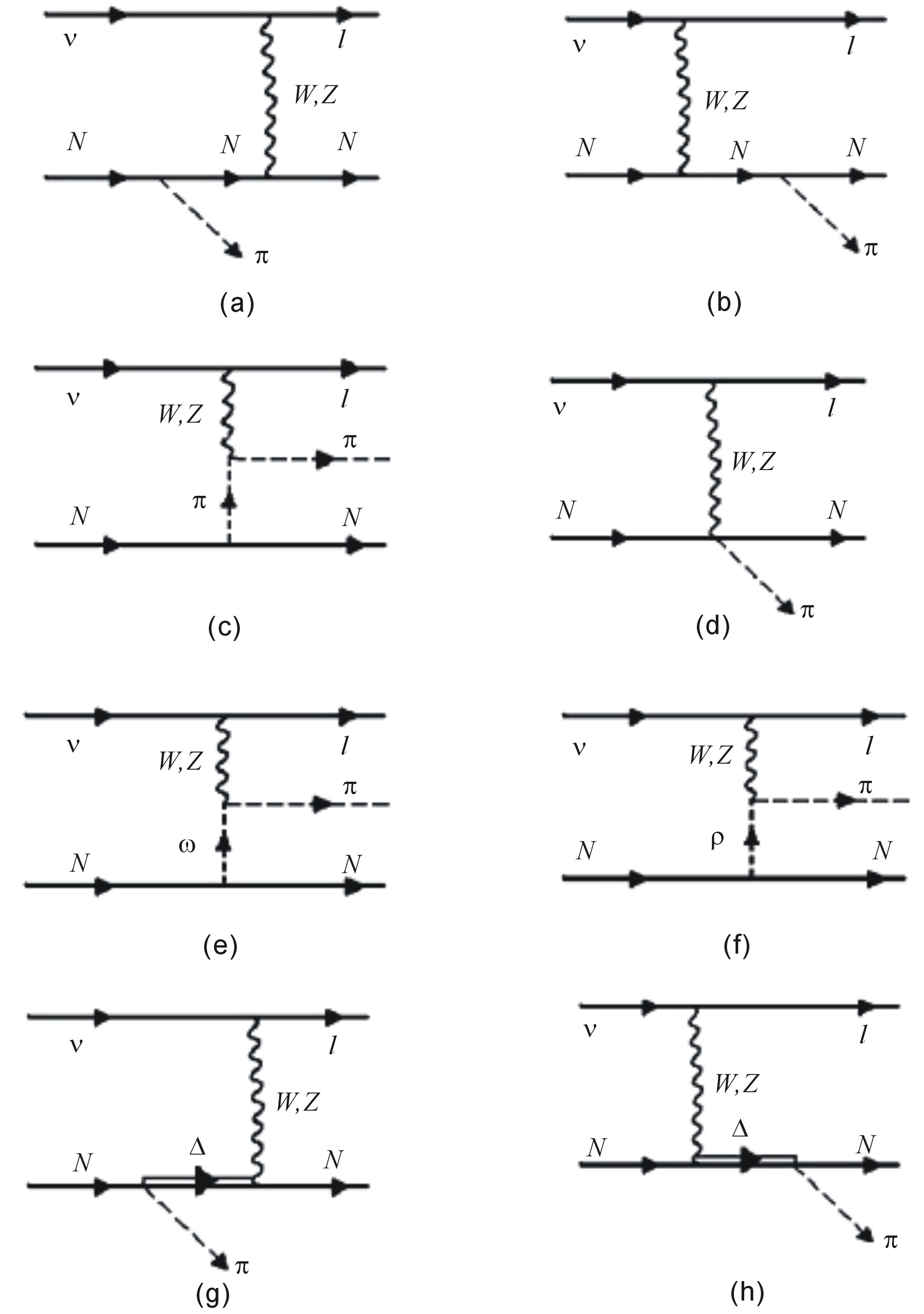
Figure 1. Different contributions to the amplitude.
and rescattering of the final 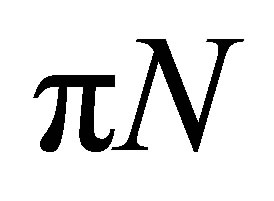 pair, but the effects are not so important as in photoproduction.
pair, but the effects are not so important as in photoproduction.
2) Vector amplitude should fulfill electromagnetic gauge invariance (GI)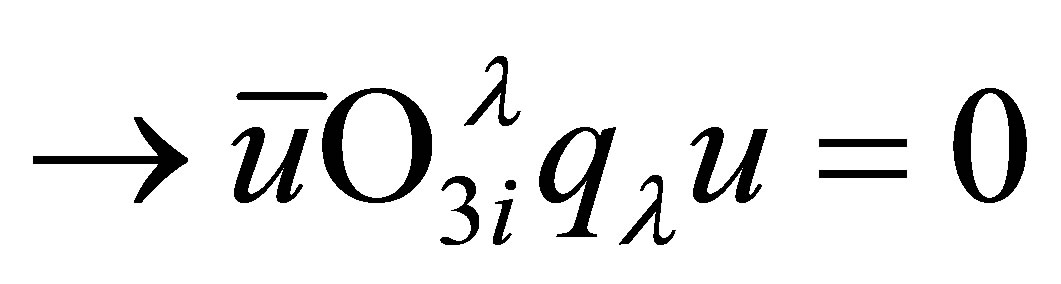 . In the B amplitude we must to have same vector FF (
. In the B amplitude we must to have same vector FF ( contribution is axial and the
contribution is axial and the  one is self-GI), while for R contributions GI must be fulfilled in presence of finite width effects.
one is self-GI), while for R contributions GI must be fulfilled in presence of finite width effects.
3) 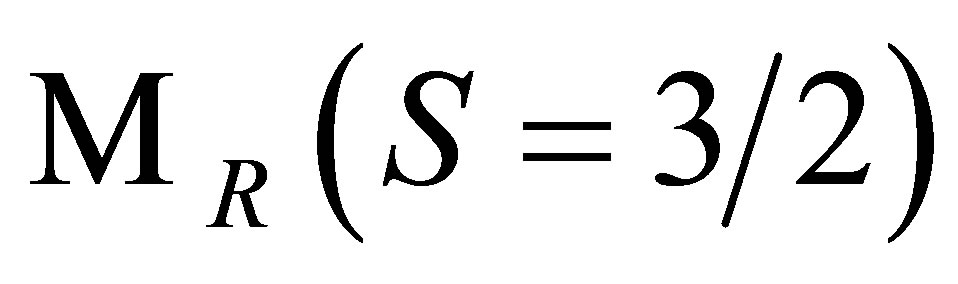 should be invariant under contact transformations (CT), which fixes the Feynman rules to built the amplitude [8], being the corresponding propagator (in the momentum space)
should be invariant under contact transformations (CT), which fixes the Feynman rules to built the amplitude [8], being the corresponding propagator (in the momentum space)
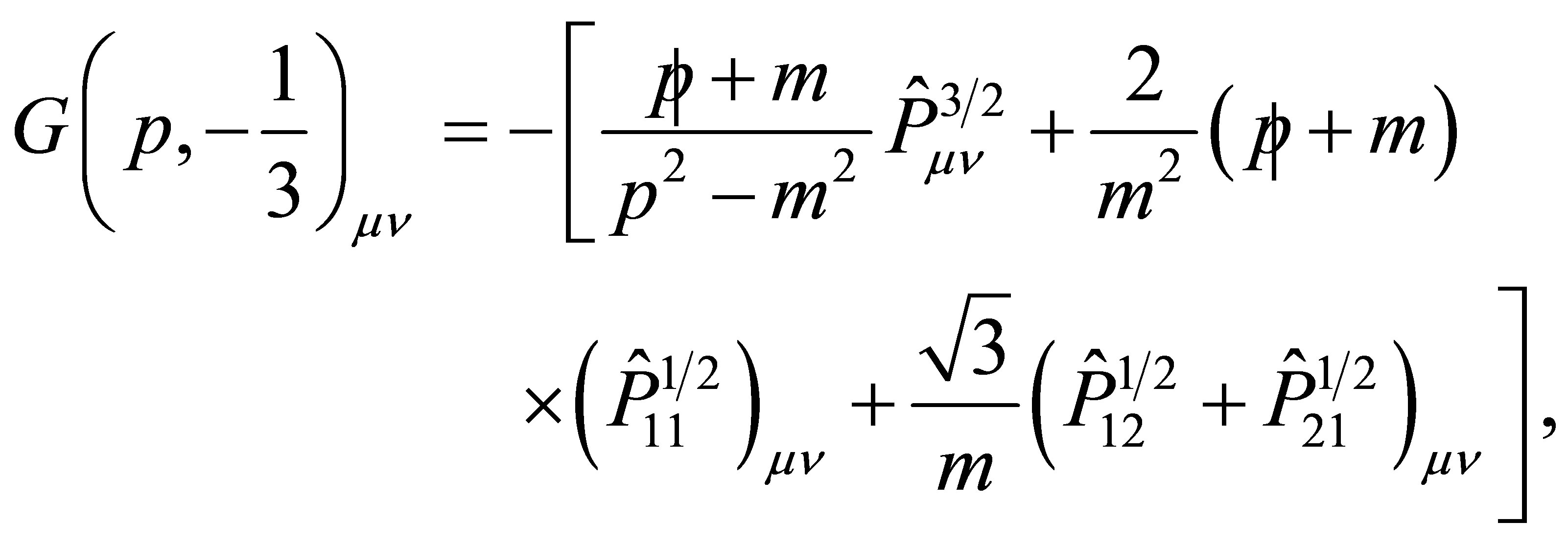
and a general vertex interaction
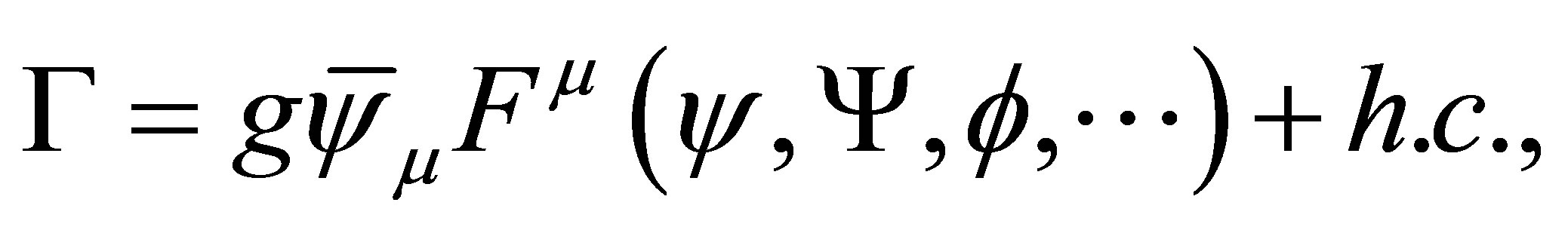 (4)
(4)
depending on the fields (nucleon, pion, photon, W-Z bosons, etc.) interacting with the  field
field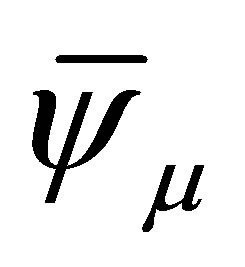 . We have introduced
. We have introduced  (defined in Ref. [9]) which projects on the
(defined in Ref. [9]) which projects on the  space. Unstableness of
space. Unstableness of  is included in the
is included in the  through a self-energy
through a self-energy 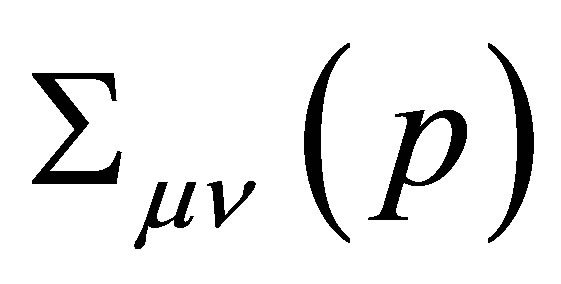 (one loop-corrections), which accounts an energy dependent width and vertex corrections to get GI. Alternatively, we make
(one loop-corrections), which accounts an energy dependent width and vertex corrections to get GI. Alternatively, we make , referred as complex mass scheme that results to be appropriated along the resonance region [10].
, referred as complex mass scheme that results to be appropriated along the resonance region [10].
3. Bounding + GSC + FSI
The bounding effects in the nucleus are introduced within the relativistic Hartree approximation (RHA) of QHD I where the exchange of 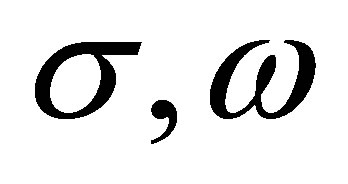 mesons is considered. The meson fields are approximated by their vacuum spectation (MFT), i.e. constant values, and within the RHA [11] the vacuum fluctuation corrections are added. The nucleon field is expanded as
mesons is considered. The meson fields are approximated by their vacuum spectation (MFT), i.e. constant values, and within the RHA [11] the vacuum fluctuation corrections are added. The nucleon field is expanded as
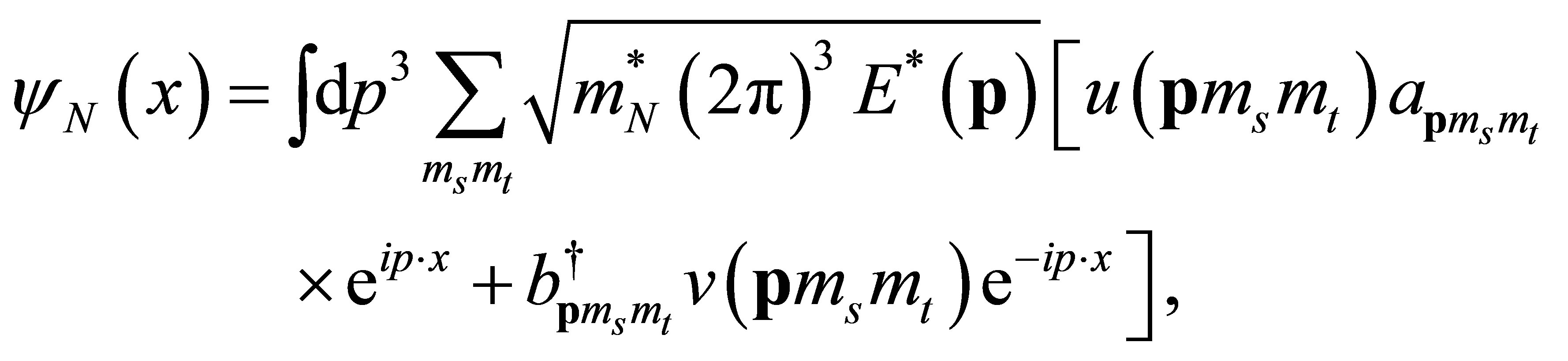 (5)
(5)
being the single particle spectrum
 (6)
(6)
where
 (7)
(7)
 is the effective mass acquired by the nucleon [11] through the scalar self-energy
is the effective mass acquired by the nucleon [11] through the scalar self-energy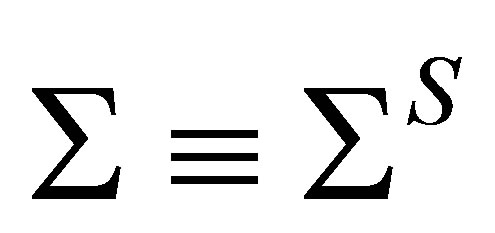 .
. 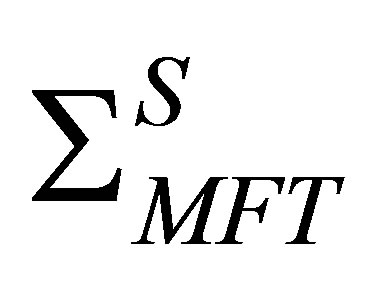 includes the tadpole diagram from Figure 2, retaining in its evaluation only the contribution from nucleons in the filled Fermi sea in the nucleon propagator (tick full lines).
includes the tadpole diagram from Figure 2, retaining in its evaluation only the contribution from nucleons in the filled Fermi sea in the nucleon propagator (tick full lines). 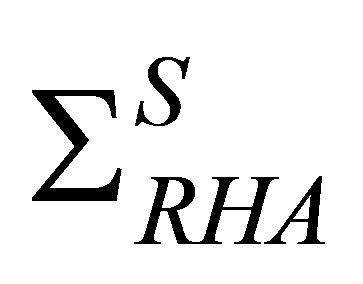 includes the same diagram but the full nucleon propagator (which encloses the contribution of the occupied negative-energy states) is used in the evaluation of the self-energy.
includes the same diagram but the full nucleon propagator (which encloses the contribution of the occupied negative-energy states) is used in the evaluation of the self-energy. 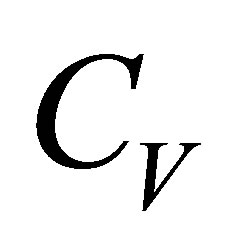 and
and 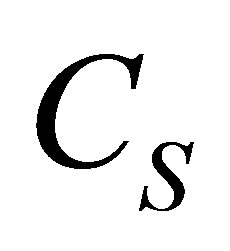 are fixed to reproduce the experimental binding energy per nucleon of -16 MeV at the Fermi momentum
are fixed to reproduce the experimental binding energy per nucleon of -16 MeV at the Fermi momentum 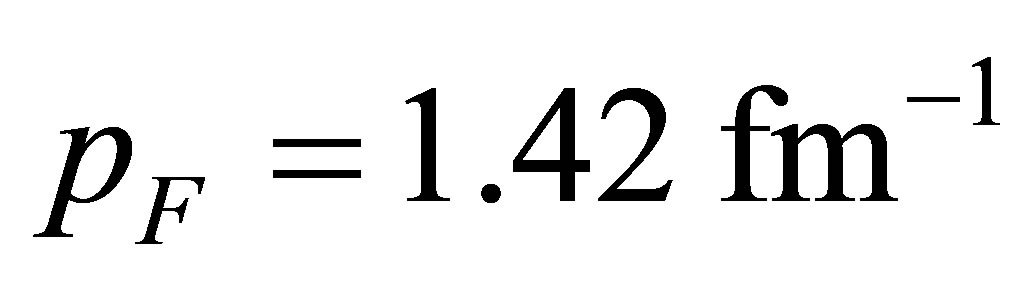 for the normal nuclear matter. For the
for the normal nuclear matter. For the  we assume the same scalar and vector self energies that for nucleon, approximation known as “universal couplings”. In the structure of the ground state, 2p2h + 4p4h states (p, h ≡ particle, hole) are included through perturbation theory in nuclear matter, from which a momentum distribution can be built as
we assume the same scalar and vector self energies that for nucleon, approximation known as “universal couplings”. In the structure of the ground state, 2p2h + 4p4h states (p, h ≡ particle, hole) are included through perturbation theory in nuclear matter, from which a momentum distribution can be built as
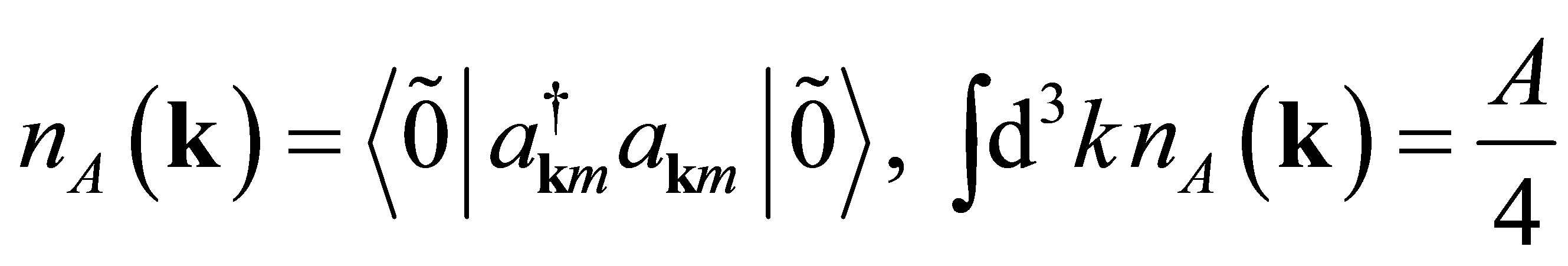
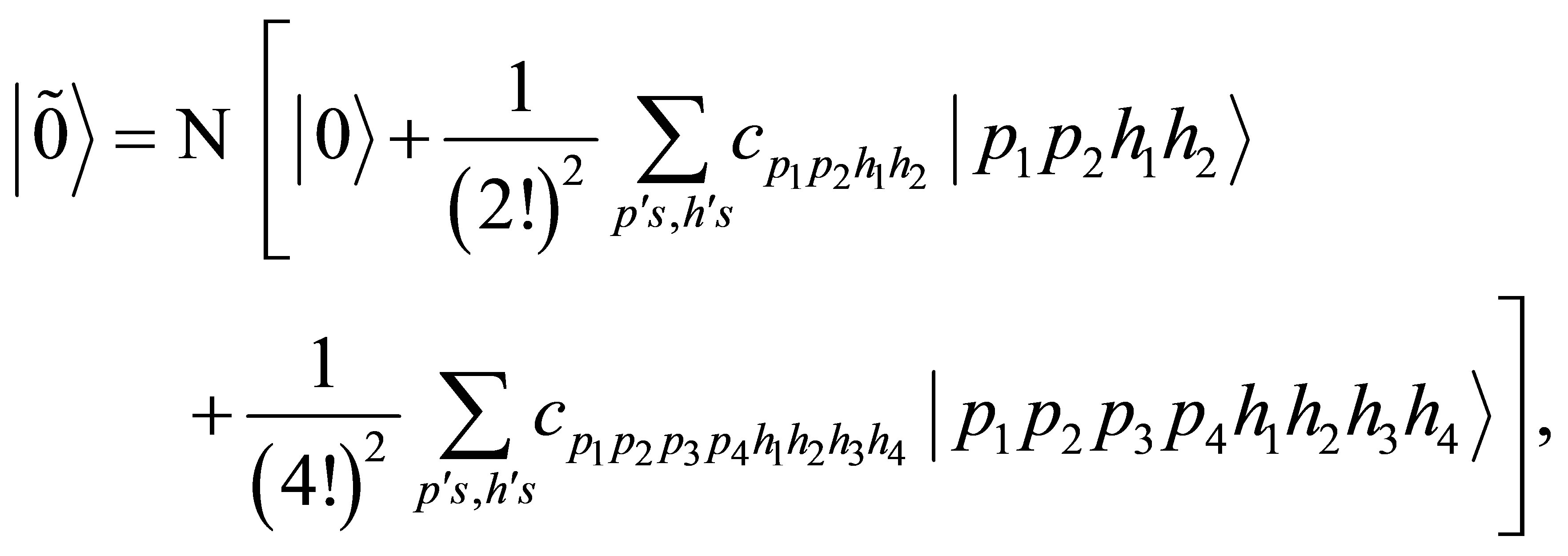
where
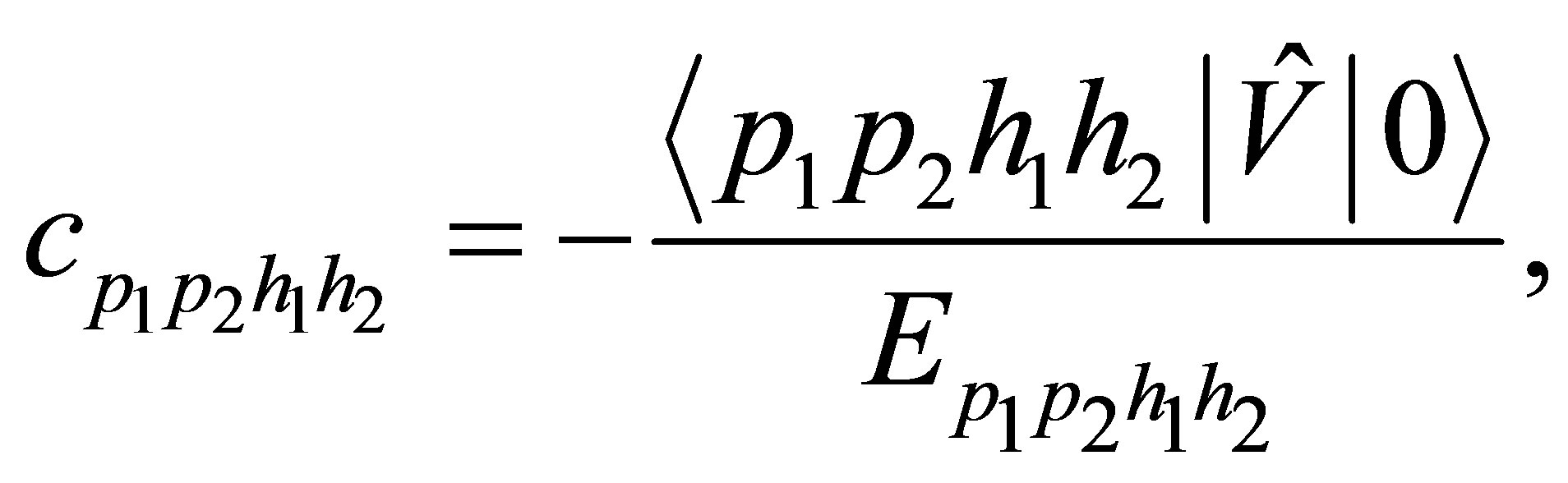
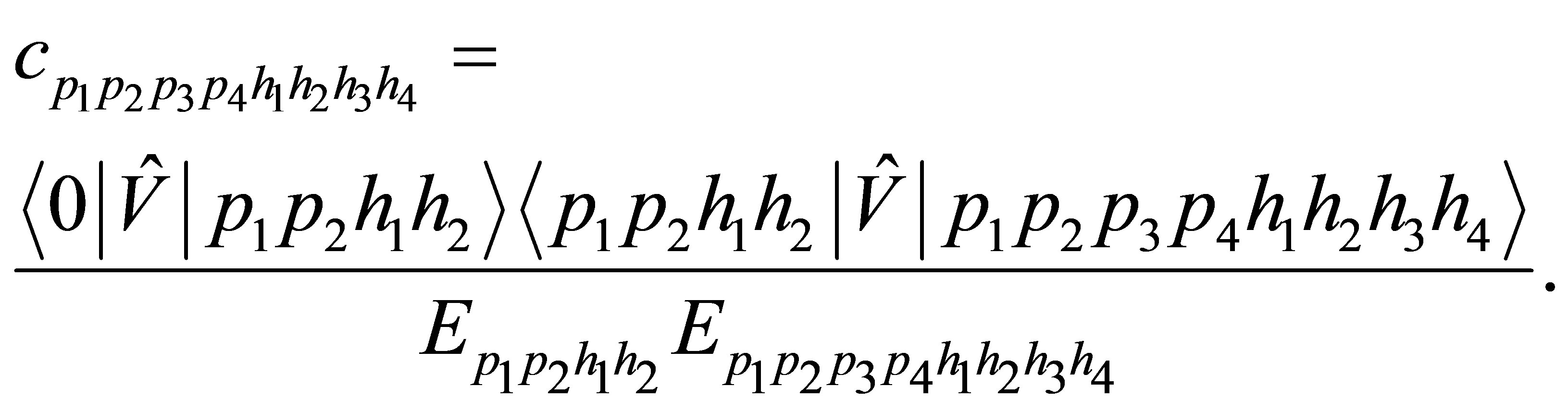
FSI on nucleons are taken (Toy model!) through the used effective fields within the RHA also for final N. While for pions we use the Eikonal approach in its simplest version [12], that is , where
, where
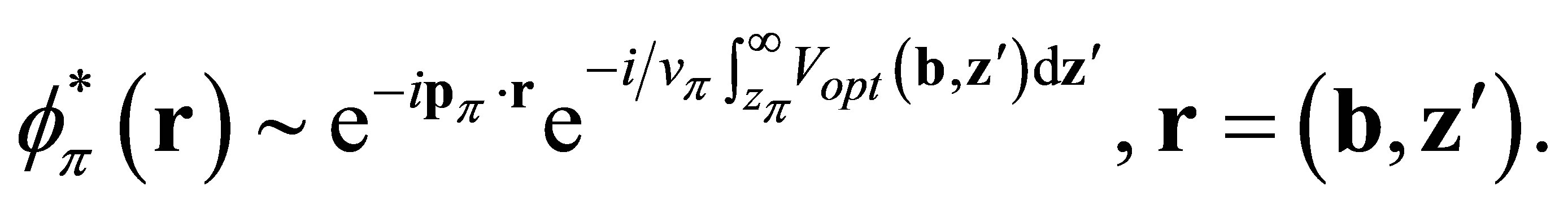 (8)
(8)
 (a) (b)
(a) (b)
Figure 2. (a) Tadpole diagram included in the MFT and RHA self-energies. (b) Tadpole exchange diagram that is added in order to get the relativistic Hartree Fock self-energy. The dashed lines indicate the propagator of the scalar (S) or vector meson (V) that interacts with a nucleon n (full lines).
Assuming a mean distance of trip for  in nucleus
in nucleus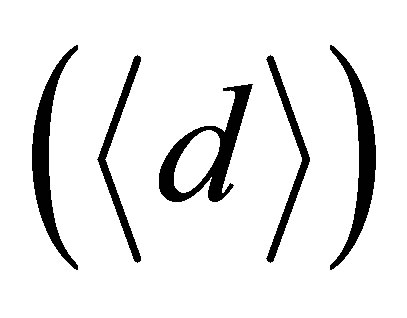 , constant nucleon density and the
, constant nucleon density and the  -h model for the
-h model for the  -optical potential, we get
-optical potential, we get
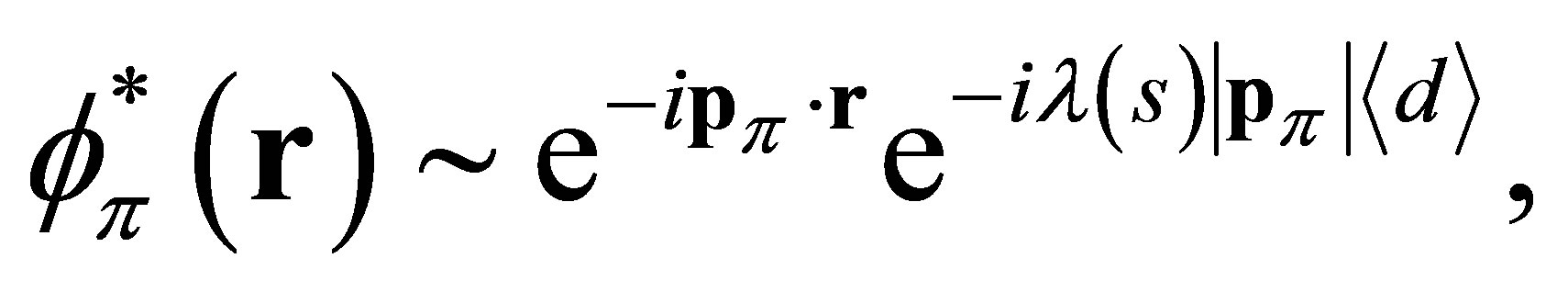
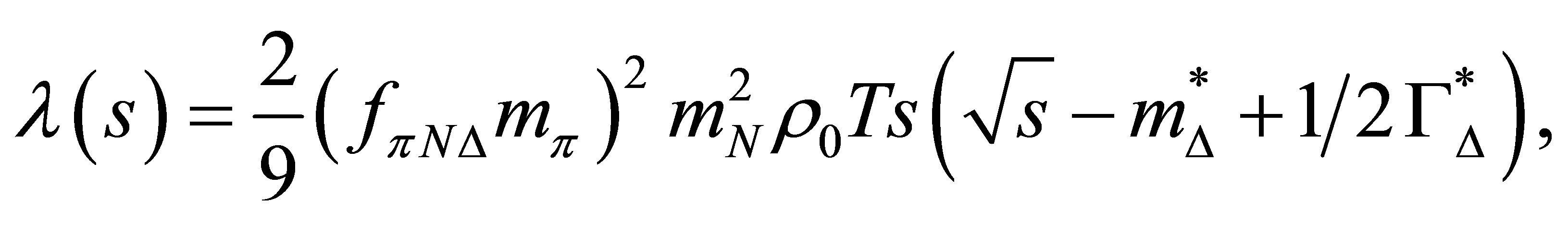
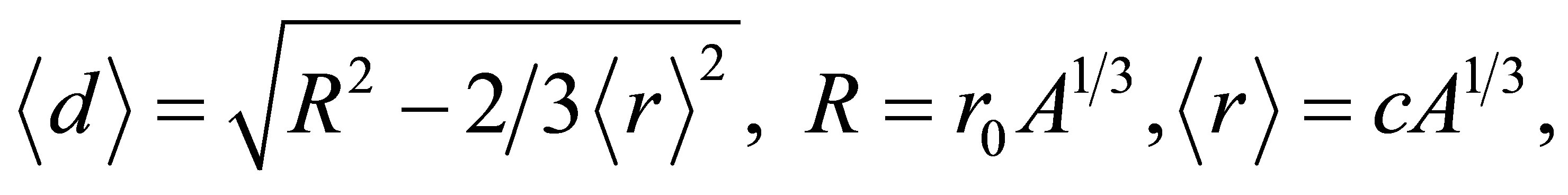
where 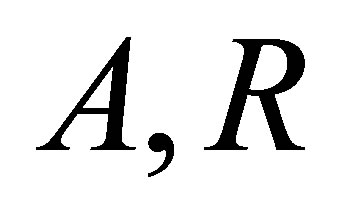 and
and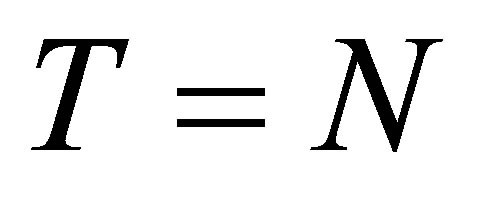 ,
,  are the mass number, radii and isospin factor of the nucleus respectively.
are the mass number, radii and isospin factor of the nucleus respectively.
4. Results and Conclusions
The different coupling constants presented in the B and R terms have been fixed by the fitting to the elastic 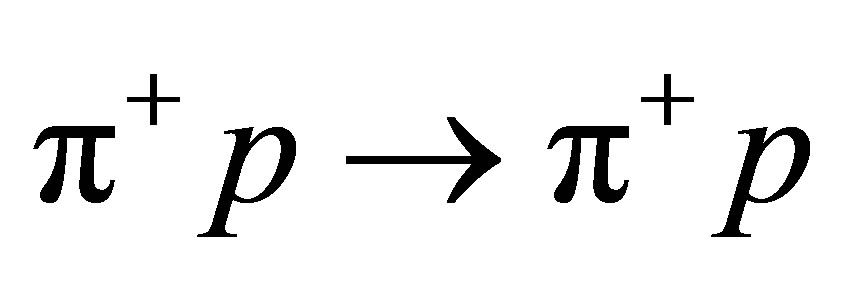 cross section data [13], to the
cross section data [13], to the 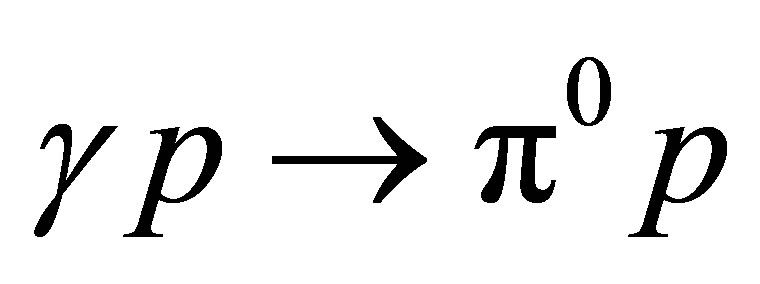 and
and 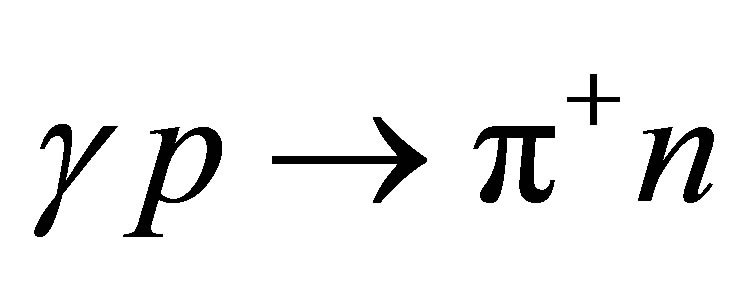 processes [14], and using the CVC hypotesis and a fitting to the differential cross section
processes [14], and using the CVC hypotesis and a fitting to the differential cross section
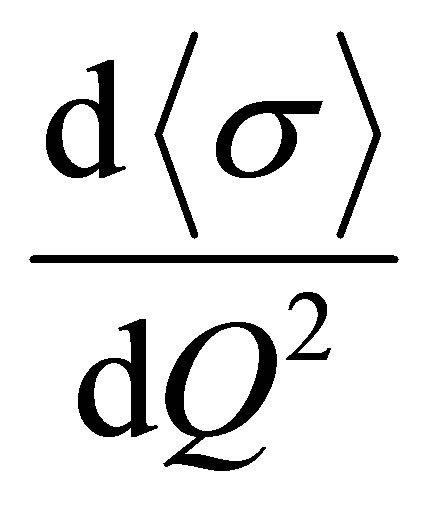 for the
for the  (ANL) data [15]. The results obtained for the background processes mentioned at the introduction are shown in Figures 3-5, where the different effects, bounding, smearing (GSC) and FSI are added gradually. In Figure 3 we show the total cross section for the
(ANL) data [15]. The results obtained for the background processes mentioned at the introduction are shown in Figures 3-5, where the different effects, bounding, smearing (GSC) and FSI are added gradually. In Figure 3 we show the total cross section for the 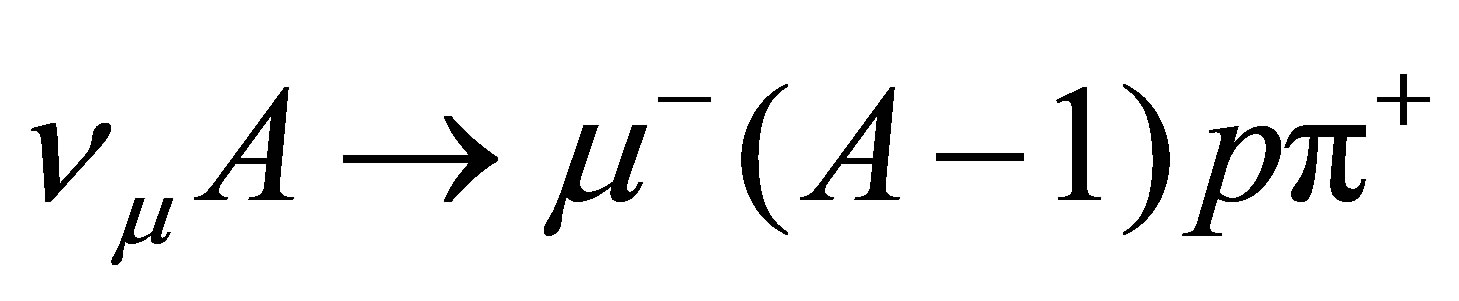 process where
process where 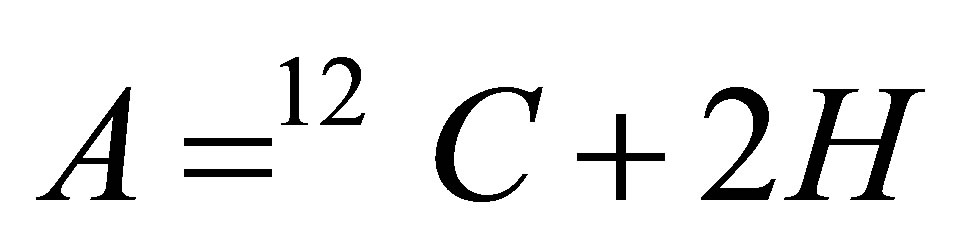 (mineral oil detector) and compare with the corresponding data of the MoniBooNE [16,17] experiment. Results corresponding to the
(mineral oil detector) and compare with the corresponding data of the MoniBooNE [16,17] experiment. Results corresponding to the 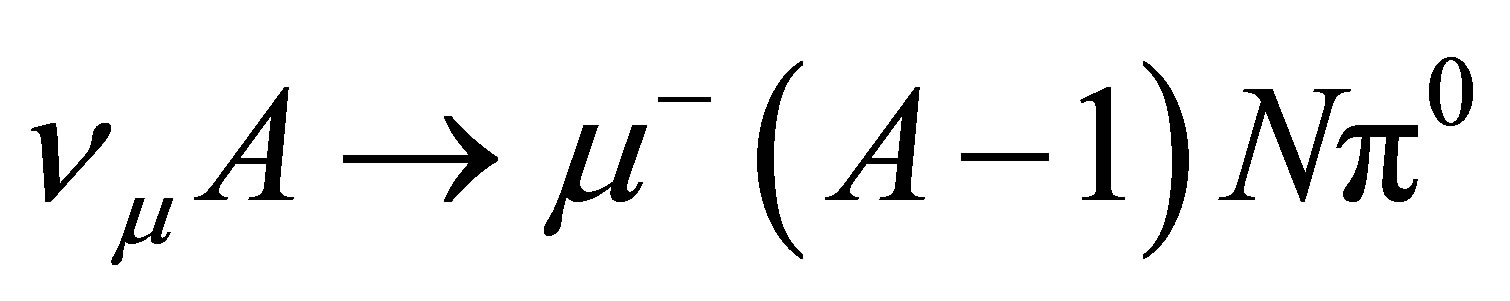 reaction are shown in Figure 4, and those for NC1
reaction are shown in Figure 4, and those for NC1 per nucleon in Figure 5.
per nucleon in Figure 5.
Calculations are  below MoniBooNE for CC 1π (comparable to the GiBUU Monte Carlo results) and
below MoniBooNE for CC 1π (comparable to the GiBUU Monte Carlo results) and 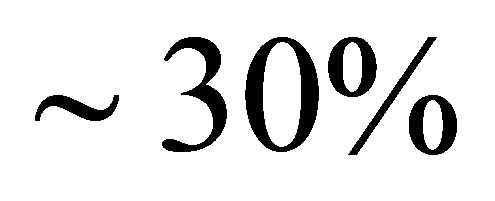 for NC
for NC  production. The FSI inclusion is very primitive, and perhaps an overvaluation of them is
production. The FSI inclusion is very primitive, and perhaps an overvaluation of them is

Figure 3. CC 1π+ calculation compared with MiniBooNE data [16].
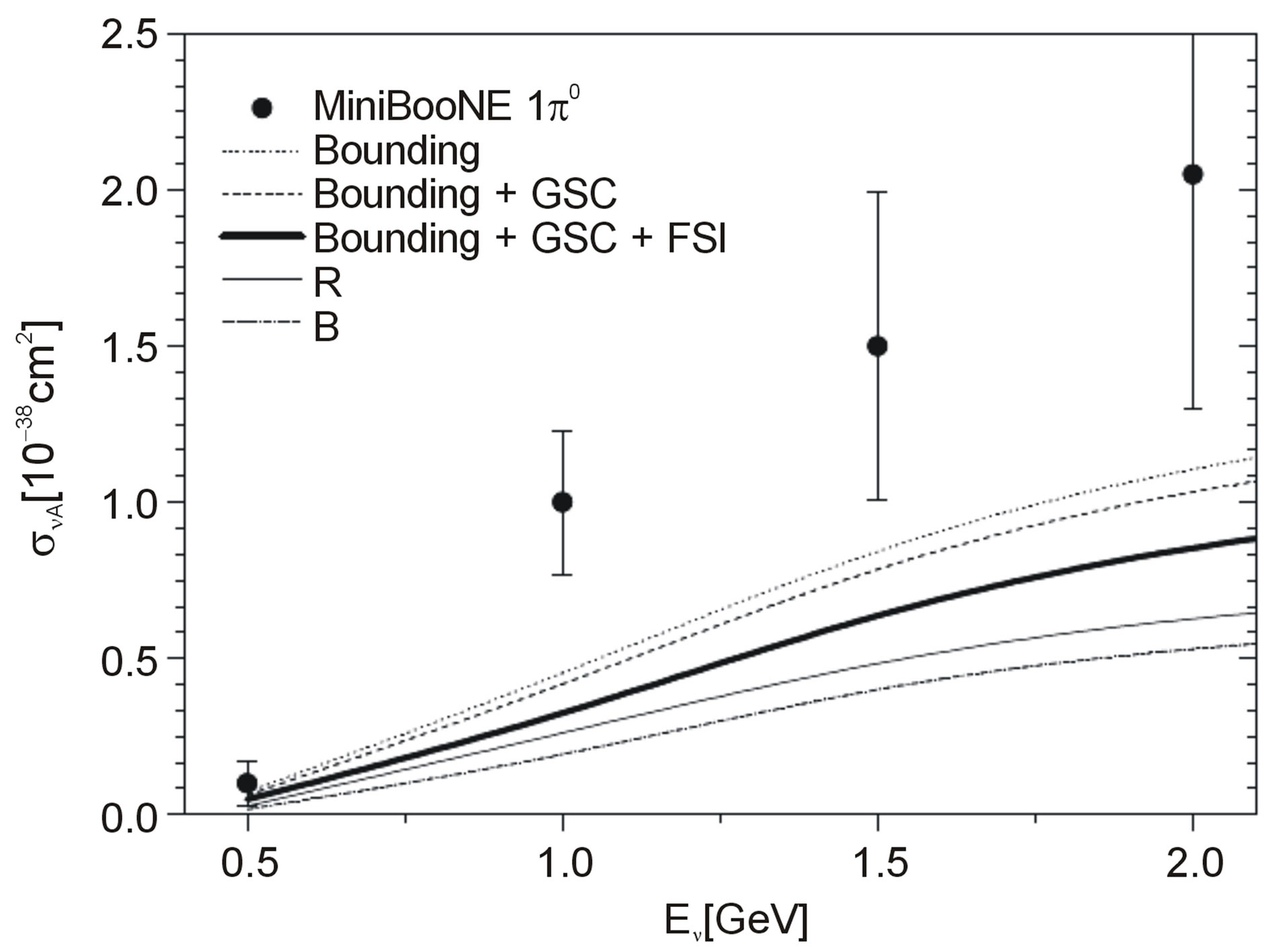
Figure 4. Idem for CC 1π0.

Figure 5. Idem for NC 1π0. Data form [17].
presented and should be improved. Nevertheless, it is noted that for example at  for MiniBooNE and ANL or BNL (without cuts), data
for MiniBooNE and ANL or BNL (without cuts), data 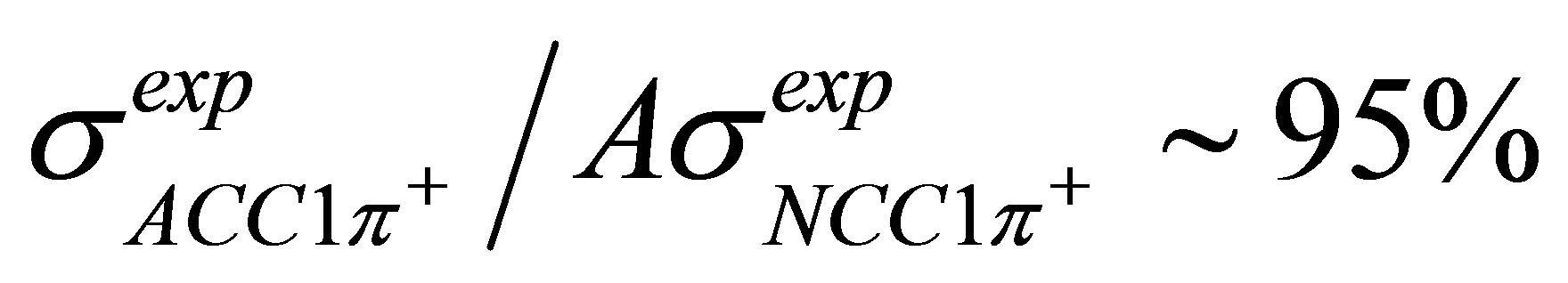 ,
,
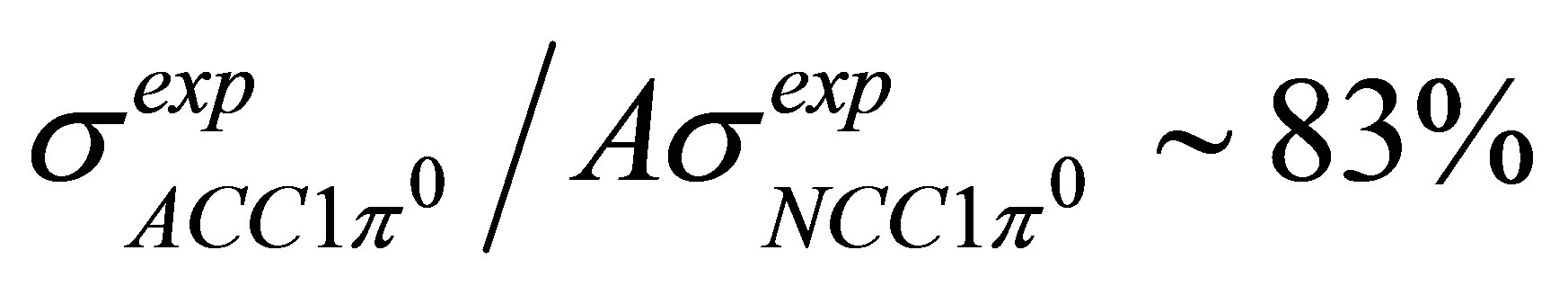 ,
,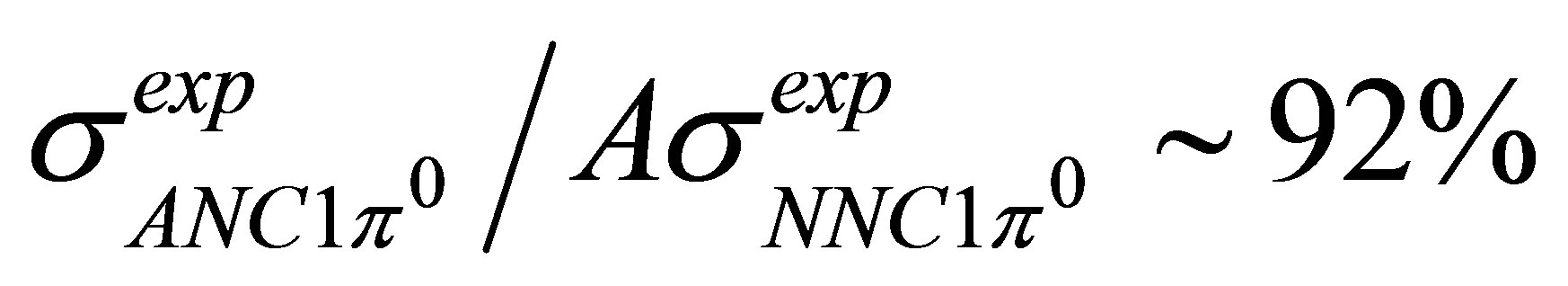 .
.
This seems to indicate that nuclear effects should be of much minor importance, or that another mechanism coming from nuclear effects should be considered, as 2p2h + 1π configurations generated by FSI added to the 1p1h + 1π considered here, and meson exchange currents contributions that are also capable of generating 2p2h + 1π acting on the nuclear ground state.
REFERENCES
- G. L. Fogli and G. Nardulli, Nuclear Physics B, Vol. 160, 1979, pp. 116-150. http://dx.doi.org/10.1016/0550-3213(79)90233-5
- T. Sato, D. Uno and T.-S. H. Lee, Physical Review C, Vol. 67, 2003, Article ID: 065201. http://dx.doi.org/10.1103/PhysRevC.67.065201
- E. Hernandez, J. Nieves and M. Valverde, Physical Review D, Vol. 76, 2007, Article ID: 033005. http://dx.doi.org/10.1103/PhysRevD.76.033005
- O. Lalakulich, T. Leitner, O. Buss and U. Mosel, Physical Review D, Vol. 82, 2010, Article ID: 093001. http://dx.doi.org/10.1103/PhysRevD.82.093001
- O. Lalakulich and U. Mosel, Pion Production in the MiniBooNE Experiment, Physical Review C, Vol. 87, 2013, Article ID: 014602. http://dx.doi.org/10.1103/PhysRevC.87.014602
- J. T. Sobczyk and J. Zmuda, Physical Review C, Vol. 87, 2013, Article ID: 065503. http://dx.doi.org/10.1103/PhysRevC.87.065503
- E. Hernandez, J. Nieves and M. J. Vacas, Physical Review D, 87, 2013, Article ID: 113009. http://dx.doi.org/10.1103/PhysRevD.87.113009
- M. El-Amiri, G. López Castro and J. Pestieau, Nuclear Physics A, Vol. 543, 1992, pp. 673-684. http://dx.doi.org/10.1016/0375-9474(92)90553-V
- F. de Jong and R. Malfliet, Physical Review C, Vol. 46, 1992, pp. 2567-2581. http://dx.doi.org/10.1103/PhysRevC.46.2567
- C. Barbero, A. Mariano and G. López Castro, Journal of Physics G: Nuclear and Particle Physics, Vol. 39, 2012, Article ID: 085011. http://dx.doi.org/10.1088/0954-3899/39/8/085011
- J. D. Walecka, “Theroretical Nuclear and Subnuclear Physics,” Part I, Oxford University Press, New York, 1995.
- C. Barbero, A. Mariano and S. B. Duarte, Physical Review C, Vol. 82, 2010, Article ID: 067305. http://dx.doi.org/10.1103/PhysRevC.82.067305
- G. López Castro and A. Mariano, Nuclear Physics A, Vol. 697, 2001, pp. 440-468.
- A. Mariano, Journal of Physics G: Nuclear and Particle Physics, Vol. 34, 2007, p. 1627.
- C. Barbero, G. López Castro and A. Mariano, Physics Letters B, Vol. 664, 2008, pp. 70-77. http://dx.doi.org/10.1016/j.physletb.2008.05.011
- A. A. Aguilar-Arevalo, et al., Physical Review D, Vol. 83, 2011, Article ID: 052007. http://dx.doi.org/10.1103/PhysRevD.83.052007
- A. A. Aguilar-Arevalo, et al., Physical Review D, Vol. 81, 2010, Article ID: 013005. http://dx.doi.org/10.1103/PhysRevD.81.013005
NOTES
*Corresponding author.

