Journal of Modern Physics
Vol. 4 No. 3A (2013) , Article ID: 29318 , 10 pages DOI:10.4236/jmp.2013.43A055
Functional N-Representability in 2-Matrix, 1-Matrix, and Density Functional Theories
1Prometheus Program, Senescyt, Quito, cuador
2Grupo Ecuatoriano para el Estudio Experimental y Teórico de Nanosistemas (GETNano), Universidad San Francisco de Quito (USFQ), Edificion Newton, Oficina N102C Diego de Robles y Vía Interoceánica, Quito, Ecuador
3Grupo de Química Computacional y Teórica (QCT-USFQ), Universidad San Francisco de Quito (USFQ), Diego de Robles y Vía Interoceánica, C.P. 17-1200-841, Quito, Ecuador
4Departamento de Física, Escuela Politécnica Nacional (EPN), Ladrón de Guevara E11-256, Quito, Ecuador
Email: *popluabe@yahoo.es
Received January 12, 2013; revised February 13, 2013; accepted February 21, 2013
Keywords: N-Representability; DFT; D1-Matrix Theory; D2-Matrix Theory
ABSTRACT
The N-representability conditions on the reduced second-order reduced density matrix (2-RDM), impose restrictions not only in the context of reduced density matrix theory (RDMT), but also on functionals advanced in one-matrix theory such as natural orbital functional theory (NOFT), and on functionals depending on the one-electron density such as those of density functional theory (DFT). We review some aspects of the applications of these N-representability conditions in these theories and present some conclusions.
1. Introduction
Due to the fact that the Hamiltonian for a many-electron system contains at most two-particle interactions, the energy can be written solely as a functional of the reduced second-order density matrix, 2-RDM. However, minimization of the energy expression without imposing conditions on this 2-RDM leads to values of the energy below the exact ground-state value. This was denoted by Coleman as the 2-matrix N-representability problem. It emerges because constraints on the 2-matrix are necessary in order to guarantee that it comes from an N-matrix, or equivalently, from an N-particle wave function.
There has been a long history of how Density Matrix Functional Theory, DMFT, has slowly evolved in the last almost five decades and how little by little, N-representability conditions for density matrices, in particular for the 2-RDM have been discovered. This efforts, of course, have been followed by the development of practical computational schemes leading to algorithms whose levels of efficiency are nowadays competitive with those of the usual quantum chemistry programs. In fact, the present situation of DMFT looks highly promising not only in view of this computational progress but mainly because of the recent discovery of complete N-representability conditions for the 2-RDM (for some recent reviews, see [1,2]).
An important issue having to do with RDMT (expressed in terms of the 2-RDM) is that the N-representabily conditions on the energy functional are the same as those on the 2-RDM. This comes about because the energy is the trace of a known two-particle operator and an unknown 2-RDM (see Equation (8)). However, when the energy is expressed in terms of the reduced first-order density matrix, 1-RDM, the energy functional has to be reconstructed in terms of the parameters that enter into the difinition of 1-RDM, namely, the occupation numbers 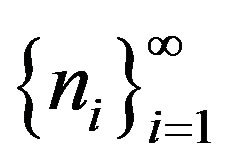 and the natural-spin orbitals
and the natural-spin orbitals . Although the
. Although the  -representability conditions on ensemble representable 1-RDM are known, the functional reconstructed in terms of
-representability conditions on ensemble representable 1-RDM are known, the functional reconstructed in terms of 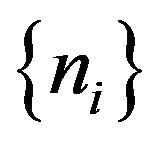 and
and 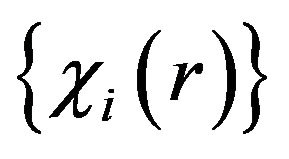 must obey the N-representability conditions of the 2-RDM. In other words, it is through this reconstruction of the 2-RDM in terms of the 1-RDM that the functionals in NOFT are generated. Thus, the reconstructed 2-RDM entering in these functionals must satisfy the same N-representability conditions as the unreconstructed 2-RDM.
must obey the N-representability conditions of the 2-RDM. In other words, it is through this reconstruction of the 2-RDM in terms of the 1-RDM that the functionals in NOFT are generated. Thus, the reconstructed 2-RDM entering in these functionals must satisfy the same N-representability conditions as the unreconstructed 2-RDM.
When the energy is represented as a functional of the one-particle density, again, although the N-representability conditions on the one-particle density are knownthe energy as a functional of the one-particle density must be obtained by a reconstruction of the 2-RDM in terms of the one-particle density. Thus, in density functional theory, DFT, there arises a functional N-representalility problem, namely, the requirement that the 2-RDM reconstructed in terms of the one particle density satisfy the same N-representabilty conditions as those imposed on the unreconstructed 2-RDM. Of course, these conditions in turn impose restrictions on the energy expressed as a functional of just the one-particle density.
The present article aims at putting in perspective the functional N-representability problem as related to the RDMT, NOFT and DFT approaches. In Section II, we briefly review RDMT with respect to the discovery of Nrepresentability conditions for the 2-RDM. In Section III, we review advances in NOFT, placing special attention to approaches that incorporate as a basic ingredient the 2-RDM N-representability conditions for the construction of the energy functionals. In Section IV, we examine how the N-representability conditions on the 2-RDM are implicit in the definition of the universal functional generated through constrained variation. We also comment on the application of these conditions in the development of DFT functionals. Finally we review works in DFT where the problem of N-reresentability of the functionals has been brought into focus. Finally, in Section V, we present some conclusions.
2. N-Representability in RDM Theory
Let us start by quoting Dirac’s statement of 1929 on the meaning of the Schrödinger equation for chemistry: “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed” [3]. And let us contrast it with a very recent one (2012) of Nakata et al.: “The goal [of chemistry] is to enable us to predict, understand, and control what happens when we mix substances. To do that, we usually do experiments, which can be explosive, poisonous, expensive, and unstable. This means that it is desirable to do chemistry without experiments. Fortunately, the basic equation of chemistry is known, and it is called the Schrödinger equation. [...] The reduced-density-matrix method is a promising nextgeneration electronic structure calculation method; it is equivalent to solving the Schrödinger equation for the ground state. The number of variables is the same as a four electron system and constant regardless of the number of electrons in the system. Many researchers have been hoping for a simpler method of doing quantum mechanical calculations and this one may be it” [2].
Apparently Dirac’s request for the development of approximate methods so that the Schrödinger equation becomes a predictive tool in chemistry is in its way to being fulfilled.
In order to succintly state the meaning of the N-representability problem in 2-RDM theory, consider the Hamiltonian for an N-electron system
 (1)
(1)
where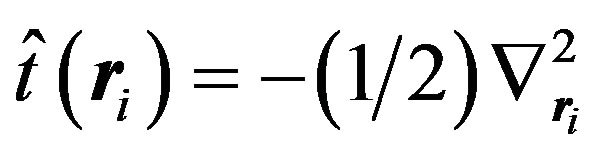 ,
, 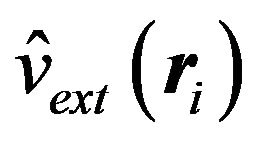 is the interaction of the
is the interaction of the  electron with the external field of nuclei and
electron with the external field of nuclei and 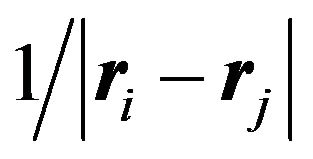 represents the electron-electron repulsion. The Hamiltonian can also be written in terms of the twoparticle operator
represents the electron-electron repulsion. The Hamiltonian can also be written in terms of the twoparticle operator  (where its dependence on the number of electrons,
(where its dependence on the number of electrons,  , is emphasized) as:
, is emphasized) as:
 (2)
(2)
where
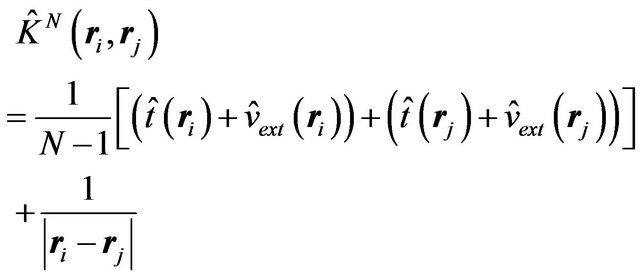 (3)
(3)
The energy corresponding to a normalized wave-function 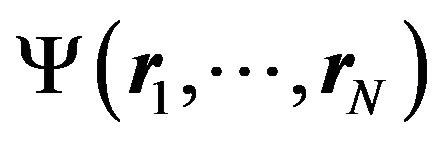 is:
is:
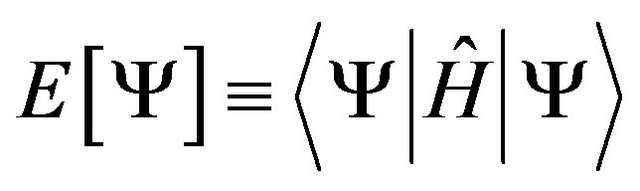 (4)
(4)
which in view of Equation (2) can be written as
 (5)
(5)
where 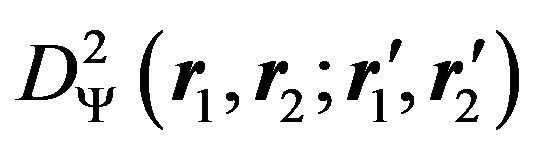 is the normalized reduced secondorder density matrix obtained from the wavefunction
is the normalized reduced secondorder density matrix obtained from the wavefunction :
:
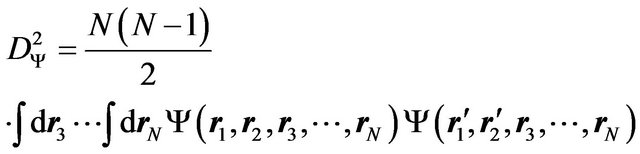 (6)
(6)
Thus, the ground state energy is obtained by minimizing this functional
 (7)
(7)
where  is the antisymmetric Hilbert space, or equivalently through
is the antisymmetric Hilbert space, or equivalently through
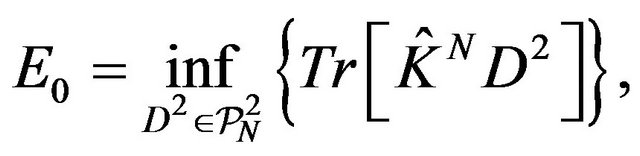 (8)
(8)
where  is the set of normalized N-representable 2-matrices. Hence, the N-representability problem in 2- RDM theory has to do with how to set up the necessary and sufficient intrinsic conditions for defining
is the set of normalized N-representable 2-matrices. Hence, the N-representability problem in 2- RDM theory has to do with how to set up the necessary and sufficient intrinsic conditions for defining  such that it is guaranteed that the 2-RDM
such that it is guaranteed that the 2-RDM 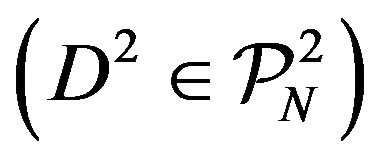 satisfies Equation (6).
satisfies Equation (6).
The development of 2-RDM theory may be separated in the following four stages. A first stage, which is marked by the studies of the properties of reduced density matrices carried out by Löwdin (1955) [4] and McWeeny (1960) [5] (based on the pioneering works of Dirac (1930, 1931) [6,7] and Husimi (1940) [8]); by the unsuccessful attempts to obtain the energy by direct variation of the 2-RDM undertaken by Mayer in 1955 [9] and Tredgold in 1957 [10]); by the recognition and formulation of the N-representability problem by Coleman in 1963 [11] (see also [12,13]) and by the construction of a formal solution to this problem by Garrod and Percus in 1964 [14] (for a comprehensive description and bibliography of this stage, see [15-17]).
The second stage is characterized by the reduction of the Schrödinger equation to a hierarchy of equations relating RDM of different orders (Cohen and Frishberg (1976) [18], Nakatsuji (1976) [19], Alcoba and Valdemoro [20]). This reduction has received the generic name of Contracted Schrödinger Equation, CSE. These CSEs have been derived both in their Hermitian and anti-Hermitian [21,22] versions. If the RDM which are connected through the CSE are N-representable then, according to Nakatsuji’s theorem [19], the CSE is equivalent to the Schrödinger equation. Harriman, however, pointed out to the difficulties of the CSE approach when the RDMs do not satisfy N-representability conditions [21].
For a number of years the CSE remained as a theoretical finding which had little possibility of being applied to solve the quantum many-body problem. However, an important development ocurred when Valdemoro et al. advanced a way to reconstruct the higher-order RDM in terms of lower-order ones [23,24]. This effort, certainly stimulated other developments such a those of Nakatsuji and collaborators and of Mazziotti [25-28]. These advances, once again, restored the high expectations that had been previously placed on methods based on RDMs. Moreover, through these works it became evident that the Nrepresentability conditions for the 2-RDM are intimately tied to the reconstruction of the 3- and 4-RDM in the context of the CSE formalism. As a result, the N-representability problem became a basic ingredient of the cumulant theory for RDM ensuing from these developments [27-31]. For some more recent applications and discussions of this approach, see Refs [32,33].
The third stage is related to the identification of the applied mathematical problem arising in the treatment of RDMs as semidefinite programming. This problem had certainly attracted the attention of mathematicians and engineers (see, for example the early work of Vandenberghe and Boyd [34] plus other more recent ones [35- 38]). Thus, useful tools already developed in applied mathematics were identified and adapted to the particular application at hand, namely, the direct optimization of the 2-RDM [39-47]. These efforts are still being extended to other domains of physics [48].
This third stage also comprises application of computer codes based on semidefinite programming to the actual calculation of the 2-RDM subject to N-representability conditions [49-51]. In fact, these mathematical and computational developments made it possible to systematically assesss the effect that the progressive inclusion of tighter  -representability conditions had on the energy [52-56]. This has lead to the possibility of approaching the accuracy of traditional and very exact quantum chemical calculations such as those based on the Coupled-Cluster method [57,58]. In fact, Nakata et al. [58] have obtained the following inequalities for the energies when the N-representability conditions are progressively included:
-representability conditions had on the energy [52-56]. This has lead to the possibility of approaching the accuracy of traditional and very exact quantum chemical calculations such as those based on the Coupled-Cluster method [57,58]. In fact, Nakata et al. [58] have obtained the following inequalities for the energies when the N-representability conditions are progressively included:
 (9)
(9)
In the above expression, the energies are characterized by the imposition of a set of N-representability conditions. For example, 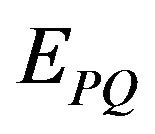 is the variational energy obtained when the conditions P and Q are imposed in the variation; similarly,
is the variational energy obtained when the conditions P and Q are imposed in the variation; similarly, 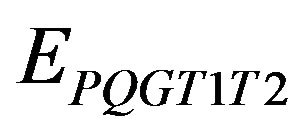 is the variational energy obtained under conditions
is the variational energy obtained under conditions  and
and . These variational energies give lower bounds because the variational 2-RDM are non-N-representable. However, the very interesting finding of these authors is that they progressively approach the upper-bound energy given by
. These variational energies give lower bounds because the variational 2-RDM are non-N-representable. However, the very interesting finding of these authors is that they progressively approach the upper-bound energy given by . Summing up, as in the variational upper bound calculations based on wave functions, where the accuracy is improved when the variational space is made larger, in the 2-RDM theory, the accuracy is also improved by imposition of more
. Summing up, as in the variational upper bound calculations based on wave functions, where the accuracy is improved when the variational space is made larger, in the 2-RDM theory, the accuracy is also improved by imposition of more  -representability conditions.
-representability conditions.
Finally, we are fathoming a fourth stage marked by important mathematical developments such as Mazziotti’s very recent discovery of complete N-representability conditions for the 2-RDM and higher order reduced density matrices [59,60]. No doubt, faster and more efficient computer codes will be developed to implement these new ideas. Thus, these recent developments, obviously place 2-RDM theory in a very bright perspective. To close this section, let us quote Mazziotti on these implications:
“The constructive solution of N-representability establishes 2-RDM theory as a fundamental theory for many particle quantum mechanics for particles with pairwise interactions. Lower bounds on the ground-state energy can be computed and improved systematically within the theory. While not all of the 2-RDM conditions will be imposed in practical calculations, a complete knowledge of the conditions their form and functions can be invaluable in devising and testing approximate N-representability conditions for different types of quantum systems and interactions” [60].
3. N-Representability in NOFT
The normalized reduced first-order density matrix or 1-RDM 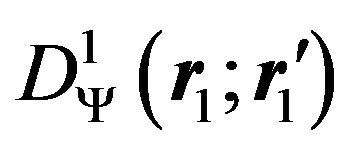 is defined by:
is defined by:
 (10)
(10)
The kinetic plus the external energy are linear functionals of the 1-RDM:
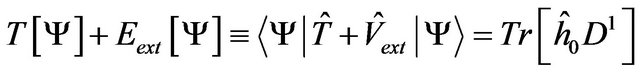 (11)
(11)
where . In view of Equation (11), the following functional of the 1-RDM can be defined: [61]
. In view of Equation (11), the following functional of the 1-RDM can be defined: [61]
 (12)
(12)
In this expression,  is the set containing the ensemble N-representability conditions on
is the set containing the ensemble N-representability conditions on , [11],
, [11],  is the highest eigenvalue of
is the highest eigenvalue of  and
and  is the unit matrix.
is the unit matrix.
Since 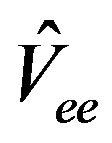 is a sum of 2-particle operators, we can rewrite the functional
is a sum of 2-particle operators, we can rewrite the functional
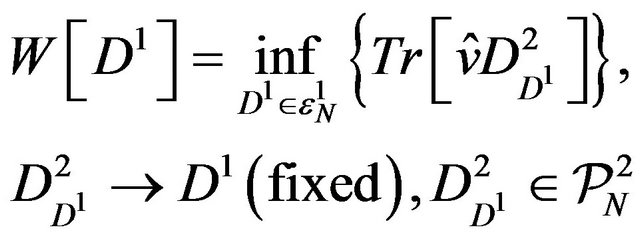 (13)
(13)
where 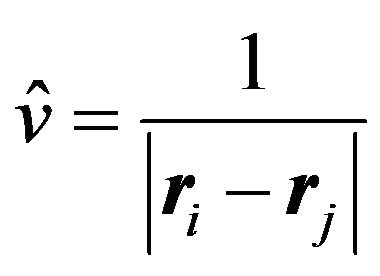
Thus, we see that once again, the N-representability conditions 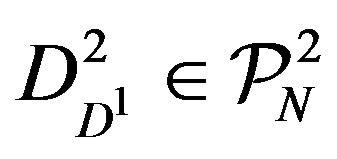 on the 2-RDMs that reduce to the given and fixed
on the 2-RDMs that reduce to the given and fixed 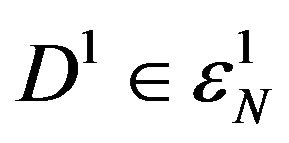 also appear here in the definition of the functional
also appear here in the definition of the functional  through Equation (13).
through Equation (13).
It is interesting to observe under the present perspective, i.e., bearing in mind the need to impose Nrepresentability conditions, that the initial works [62-65] attempting to obtain Euler-Lagrange equations of motion for the 1-RDM, when the 1-RDM is expressed in terms of the natural orbital expansion, namely,
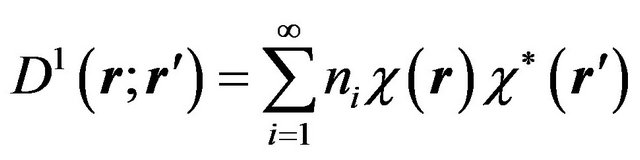 (14)
(14)
led to the paradoxical situation in which all partially occupied natural spin orbitals 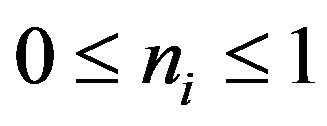 had to belong to the same degenerate eigenvalue of a natural orbital one-particle equation:
had to belong to the same degenerate eigenvalue of a natural orbital one-particle equation:
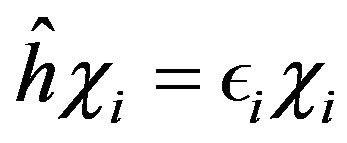 (15)
(15)
However, in the variational treatment of Nguyen-Dang, Ludeña and Tal where built-in N-representability conditions were included from the outset, this paradoxical results did not emerge [66-68].
A fairly complete historical account of the formulation and development of density matrix theory based on the 1-RDM can be found in the review article of Piris, 2007 [69].
The simplest case in which the energy can be expressed as a funtional of the 1-RDM is, of course, the Hartree-Fock approximation. The exchange term is just a functional of the occupied Hartree-Fock orbitals:

(16)
where 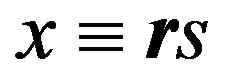 denotes both the spatial and spin coordinates. In terms of natural orbitals and their occupation numbers, a generalization of this expression, for the exchange-correlation functional is given by:
denotes both the spatial and spin coordinates. In terms of natural orbitals and their occupation numbers, a generalization of this expression, for the exchange-correlation functional is given by:

(17)
where 
Several approximations to the function 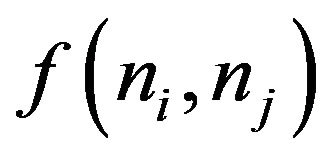 define different types of functionals such as those of Müller, [70] Goedecker-Umrigar, [71] Csanyi and Arias, [72] Buijse and Baerends, [73,74] Gritsenko-PernalBaerends, [75] Sharma et al., [76] and Lathiotakis et al. [77-80].
define different types of functionals such as those of Müller, [70] Goedecker-Umrigar, [71] Csanyi and Arias, [72] Buijse and Baerends, [73,74] Gritsenko-PernalBaerends, [75] Sharma et al., [76] and Lathiotakis et al. [77-80].
The mathematical characteristics of the Müller functional, taken as a paradigmatic example, has been extensively studied [81]. The accuracy of these approximate functionals has been assessed with respect to traditional quantum chemistry methods [78]. The lack of size consistency in these functionals has been recently analized. [80]
We have selected to discuss separately the approach of Piris et al., because although they present functionals based on occupation numbers and natural orbitals, their approach is different in that they systematically introduce N-representability conditions. Piris’ work is essentially based on the reconstruction of the 2-RDM by means of an explicit formulation of the cumulant expansion [27- 30]. The particular reconstruction functional for the twoparticle cumulant is presented in Ref. [82] and it is based on the introduction of some auxiliary matrices 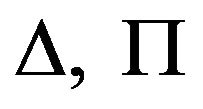 and
and , expressed in terms of natural orbitals and their occupation numbers. The matrix elements of these matrices are required to satisfy some necessary conditions for the N-representability of the 2-RDM [69, 83-87].
, expressed in terms of natural orbitals and their occupation numbers. The matrix elements of these matrices are required to satisfy some necessary conditions for the N-representability of the 2-RDM [69, 83-87].
Of course, progressive enforcement of these N-representability conditions plus some different ways of approximating the off-diagonal elements of the matrix  have led to the appearance of different versions of these functionals, generically denoted as Piris Natural Orbital Functional i, PNOFi. In general, the performance of these functionals is comparable to those of best quantum chemistry methods in the sense that chemical accuracy is being attained by the PNOFi, [78] in particular by PNOF5 [85].
have led to the appearance of different versions of these functionals, generically denoted as Piris Natural Orbital Functional i, PNOFi. In general, the performance of these functionals is comparable to those of best quantum chemistry methods in the sense that chemical accuracy is being attained by the PNOFi, [78] in particular by PNOF5 [85].
In a recent paper, Pernal [88] has shown that PNOF5 and the natural orbital functional corresponds to the antisymmetrized product of strongly orthogonal geminal theory if the expansion of geminals is limited to twodimensional subspaces. This result is remarkable in the sense that for the first time it is shown that top-down and bottom-up methods for generating density functionals are equivalent. The top-down method is represented by the reduction of an N-particle functional generated from an ansatz wave function such as the antisymmetrized product of strongly orthogonal geminals. In the bottom-up method a functional is generated by progressive inclusion of N-representability conditions. This example shows that perhaps the unity of quantum theory on many-particle systems can be attained by careful handling of topdown and bottom-up methods.
4. N-Representability in DFT
In the Hohenberg-Kohn-Sham version of density functional theory, HKS-DFT, there is a basic assertion concerning the existence of a universal functional , depending solely on the density which in the context of Levy’s constrained-search formulation of DFT is defined as [61]:
, depending solely on the density which in the context of Levy’s constrained-search formulation of DFT is defined as [61]:
 (18)
(18)
Note that in this case, the wavefunction 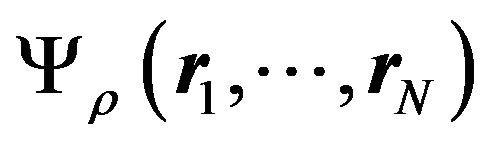 is any N-particle wavefunction in
is any N-particle wavefunction in  yielding the fixed density
yielding the fixed density . Now, introducing the two-particle operator
. Now, introducing the two-particle operator
 (19)
(19)
and using the same arguments as those used in deriving Equation (8), the above functional can be rewritten as [89]:
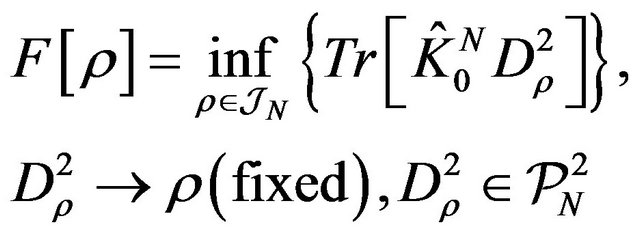 (20)
(20)
The striking similarity between Equations (8) and (20) where the latter is the definition of the exact functional 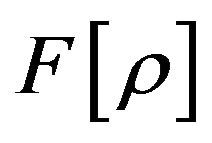 leads us to the conclusion that this exact functional is fully characterized only in terms of the N-representability conditions on the reduced 2-matrix.
leads us to the conclusion that this exact functional is fully characterized only in terms of the N-representability conditions on the reduced 2-matrix.
It has been generally assumed that there is no N-representablity problem in HKS-DFT as it was believed that only N-representable conditions on the one-particle densities were necessary. But, as shown by Gilbert [62] any 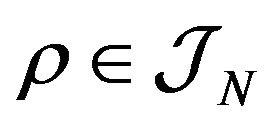 is N-representable. In fact, much more effort has been dedicated to solving the one-particle density v-representability problem. However, the existence of functional derivatives of the functionals
is N-representable. In fact, much more effort has been dedicated to solving the one-particle density v-representability problem. However, the existence of functional derivatives of the functionals , important for v-representability, is not related to the N-representability of this functional [89].
, important for v-representability, is not related to the N-representability of this functional [89].
By and large, the great majority of functional developments in DFT do not incorporate the N-representability conditions on approximate realizations of the functional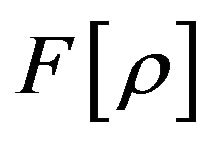 . Some early warnings pointing out that these conditions should be relevant are given in the works of Löwdin, McWeeny, Ludeña and Keller [90-92] as well as in the local-scaling transformation version of DFT, LST-DFT [93-96].
. Some early warnings pointing out that these conditions should be relevant are given in the works of Löwdin, McWeeny, Ludeña and Keller [90-92] as well as in the local-scaling transformation version of DFT, LST-DFT [93-96].
However, the current situation is that the N-representability of the exact and approximate  has been fully recognized as a true problem in HKS-DFT [89]. In fact, formal solutions (necessary and sufficient conditions) to the N-representability problem for
has been fully recognized as a true problem in HKS-DFT [89]. In fact, formal solutions (necessary and sufficient conditions) to the N-representability problem for 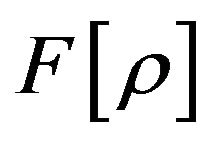 have been advanced by Ayers and Liu [97] and a more practical one through a variational principle for the exchange hole, by Ayers, Cuevas-Saavedra and Chakraborty [98]. However, aside from this formal recognition, there is little that has been done to impose N-representability on the construction of commonly used functionals.
have been advanced by Ayers and Liu [97] and a more practical one through a variational principle for the exchange hole, by Ayers, Cuevas-Saavedra and Chakraborty [98]. However, aside from this formal recognition, there is little that has been done to impose N-representability on the construction of commonly used functionals.
Imposition of N-representability conditions on DFT functionals is not merely an academic exercise. Its importance stems from the fact that, for example, the Nelectron self-interaction error is directly related to the non-N-representability of . Also, the lack of these conditions can affect the values of vibrational frequencies as well as of dipole moments [99].
. Also, the lack of these conditions can affect the values of vibrational frequencies as well as of dipole moments [99].
One of the most successful correlation functionals in DFT is the LYP functional developed by Lee, Yang and Parr [100]. This functional resulted from a reconstruction of the Colle-Salvetti functional, [101] which in turn came from an approximate 2-RDM formed by the product of the Hartree-Fock 2-RDM times a correlation factor. Through this reconstruction, the functional was expressed in terms of  and
and . Dependence on the Laplacian was later on eliminated by integration by parts [102]. Although it was suspected that this functional was not N-representable, the mathematical proof of this fact was presented by Morrison in 1993 [103]. Also, an analysis of this functional showed that it overcorrelated at high density but it did not account properly for long-range correlation [104]. Other approximations based on the Colle-Salvetti ansatz, such as the RagotCortona local correlation energy model, also suffer from non-N-representability [105].
. Dependence on the Laplacian was later on eliminated by integration by parts [102]. Although it was suspected that this functional was not N-representable, the mathematical proof of this fact was presented by Morrison in 1993 [103]. Also, an analysis of this functional showed that it overcorrelated at high density but it did not account properly for long-range correlation [104]. Other approximations based on the Colle-Salvetti ansatz, such as the RagotCortona local correlation energy model, also suffer from non-N-representability [105].
Corrections of long-range correlation by means of the introduction of “double-hybrid” functionals based on second-order Møller-Plesset perturbation theory, MP2, although quite adequate for producing reasonable values for the energy, also lead to difficulties for other variables, such as the dipole moments [99]. Again, the cause of this difficulties was traced to non-observance of N-representability conditions.
In summary, although N-representability of the DFT functionals is established as a solid mathematical fact, the actual development of functionals that satisfy these conditions has not been a general trend (we should mention, however, the exceptions cited above). This lack of compliance to these conditions not only is observed in functionals standing at all rungs of Joseph’s ladder but also in the more recent double hybrid functionals, etc.
5. Conclusions
The main purpose of reviewing from a unified perspective the somewhat disparate approaches embodied in 2- RDM, 1-RDM and DFT is to bring into focus a common problem: the N-representability conditions on the energy functionals. For a long time it had been assumed that there is no N-representability problem in DFT as all that is necessary is to enforce N-representability on the one particle densities. But, as discussed in Section 4 these conditions are trivially met by most trial densities. However, the N-representability problem of the energy functional in DFT has been finally been recognized as such and it stands nowadays on firm mathematical bases. In fact, the necessary and sufficient conditions guaranteeing the N-representability of DFT functionals are known. [97].
Also in the case of the 1-RDM theory, it has been assumed that there is no N-representability problem for the energy functional and that just the knowledge of the ensemble-N-representability conditions on the 1-RDM is sufficient. For this reason, most approximations examined in Section 3 have been determined either through heuristic considerations or by invoking reasonable physical arguments. Only in the case of the Piris functionals does one find a systematic application of the 2-RDM N-representability conditions in the construction of the 1-RDM functional.
Of course, the full-fledged application of these Nrepresentability conditions has been realized in the context of the 2-RDM theory. Obviously, in that case there is no need to actually construct a functional for the energy because the energy is a linear functional of the 2-RDM. In the cases of the 1-RDM theory and DFT, the functionals have to be constructed by reduction of the 2-RDM in terms of natural orbitals and their occupation numbers for the 1-RDM theory, and of the density (and other forms such as gradient, Laplacian of the density, etc.), in DFT.
A systematic construction of DFT energy functionals via a reconstruction of the 2-RDM has not been the usual way to develop these functionals. Of course, we should mention the early attempt of Colle-Salvetti of setting up a correlation functional based on the 2-RDM of the helium atom which, later on, was complemented by the reconstruction of Lee-Yang-Parr of this 2-RDM in terms of the density and its derivatives leading to the LYP correlation energy functional. Maybe it is time to devise systematic schemes for the reconstruction of 2-RDM in terms of the one-particle density (and its derivatives) taking care in applying N-representability conditions. Perhaps in this way one could incorporate the computational advantages of DFT to the strictness of a quantum mechanical approach based on the enforcement of the N-represent-ability conditions.
6. Aknowledgements
E.V.L. would like to express his gratefulness to Senescyt of Ecuador for giving him the opportunity to participate in the Prometheus Program. He also acknowledges the participation of his students in the DFT course he gave for GETNano during 2012 as the source of inspiration for the writing of the present review.
REFERENCES
- D. A. Mazziotti, “Two-Electron Reduced Density Matrix as the Basic Variable in Many-Electron Quantum Chemistry and Physics,” Chemical Review, Vol. 112, No. 1, 2012, pp. 244-262. doi:10.1021/cr2000493
- M. Nakata, M. Fukuda and K. Fujisawa, “Variational Approach to Electronic Structure Calculations on Second-Order Reduced Density Matrices and the N-Representability Problem,” Lecture Note Series, Vol. 9, 2012, pp. 1-32.
- P. A. M. Dirac, “Quantum Mechanics of Many Electron Systems,” Proceedings of the Royal Society A, Vol. 123, No. 792, 1929, pp. 714-735
- P.-O. Löwdin, “Quantum Theory of Many-Particle Systems I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction,” Physical Review, Vol. 97, No. 6, 1955, pp. 1474-1489. doi:10.1103/PhysRev.97.1474
- R. McWeeny, “Some Recent Advances en Density Matrix Theory,” Reviews of Modern Physics, Vol. 32, No. 2, 1960, pp. 335-369. doi:10.1103/RevModPhys.32.335
- P. A. M. Dirac, “Note on Exchange Phenomena in the Thomas Atom,” Proceedings of Cambridge Philosophy Society, Vol. 26, No. 3, 1930, pp. 376-385. doi:10.1017/S0305004100016108
- P. A. M. Dirac, “Note on the Interpretation of the Density Matrix in the Many-Electron Problem,” Proceedings of Cambridge Philosophical Society, Vol. 27, No. 2, 1931, pp. 240-243. doi:10.1017/S0305004100010343
- K. Husimi, “Some Formal Properties of the Density Matrix,” Proceedings of Physical Mathematical Society of Japan, Vol. 22, 1940, pp. 264-314.
- J. E. Mayer, “Electron Correlation,” Physical Review, Vol. 100, No. 6, 1955, pp. 1579-1586.
- R. H. Tredgold, “Density Matrix and the Many-Body Problem,” Physical Review, Vol. 105, No. 5, 1957, pp. 1421- 1423. doi:10.1103/PhysRev.105.1421
- A. J. Coleman, “Structure of Fermion Density Matrices,” Reviews of Modern Physics, Vol. 35, No. 3, 1963, pp. 668-687. doi:10.1103/RevModPhys.35.668
- A. J. Coleman, “The Convex Structure of Electrons,” International Journal of Quantum Chemistry, Vol. 11, No. 6, 1977, pp. 907-916. doi:10.1002/qua.560110604
- A. J. Coleman, “Reduced Density Operators and the NParticle Problem,” International Journal of Quantum Chemistry, Vol. 13, No. 1, 1978, pp. 67-82. doi:10.1002/qua.560130106
- C. Garrod and J. K. Percus, “Reduction of the N-Particle Variational Problem,” Journal of Mathematical Physics, Vol. 5, No. 12, 1964, pp. 1756-1776. doi:10.1063/1.1704098
- E. R. Davidson, “Reduced Density Matrices in Quantum Chemistry,” Academic Press, London, 1976.
- J. Cioslowski, “Many-Electron Densities and Reduced Density Matrices,” Kluwer, New York, 2000.
- A. J. Coleman and V. I. Yukalov, “Reduced Density Matrices: Coulson’s Challenge,” Springer-Verlag, New York, 2000. doi:10.1007/978-3-642-58304-9
- L. Cohen and C. Frishberg, “Hartree-Fock Density Matrix Equation,” Physical Review A, Vol. 13, No. 3, 1976, pp. 4234-4238. doi:10.1103/PhysRevA.13.927
- H. Nakatsuji, “Equation for the Direct Determination of the Density Matrix,” Physical Review A, Vol. 14, No. 1, 1976, pp. 41-50. doi:10.1103/PhysRevA.14.41
- D. R. Alcoba and C. Valdemoro, “Family of ModifiedContracted Schrodinger Equations,” Physical Review A, Vol. 64, No. 6, 2001, Article ID: 062105.
- J. E. Harriman, “Limitation on the Density-Equation Approach to Many-Electron Problems,” Physical Review A, Vol. 19, No. 5, 1979, pp. 1893-1895. doi:10.1103/PhysRevA.19.1893
- W. Kutzelnigg, “Generalized K-Particle Brillouin Conditions and Their Use for the Constructlon of Correlated Electronic Wavefunctions,” Chemical Physics Letters, Vol. 64, No. 2, 1979, pp. 383-387. doi:10.1016/0009-2614(79)80537-0
- C. Valdemoro, “Approximating the Second-Order Reduced Density Matrix in Terms of the First-Order One,” Physical Review A, Vol. 45, No. 7, 1992, pp. 4462-4467. doi:10.1103/PhysRevA.45.4462
- F. Colmenero and C. Valdemoro, “Approximating q-Order Reduced Density Matrices in Terms of the Lower-Order Ones. II. Applications,” Physical Review A, Vol. 47, No. 2, 1993, pp. 979-987. doi:10.1103/PhysRevA.47.979
- H. Nakatsuji and K. Yasuda, “Direct Determination of the Quantum-Mechanical Density Matrix Using the Density Equation,” Physical Review Letters, Vol. 76, No. 7, 1996, pp. 1039-1042. doi:10.1103/PhysRevLett.76.1039
- D. A. Mazziotti, “Contracted Schrödinger Equation: Determining Quantum Energies and Two-Particle Density Matrices without Wave Functions,” Physical Review A, Vol. 57, No. 7, 1998, pp. 4219-4243. doi:10.1103/PhysRevA.57.4219
- D. A. Mazziotti, “Approximate Solution for Electron Correlation through the Use of Schwinger Probes,” Chemical Physics Letters, Vol. 289, No. 6, 1998, pp. 419-427. doi:10.1016/S0009-2614(98)00470-9
- D. A. Mazziotti, “Complete Reconstruction of Reduced Density Matrices,” Chemical Physics Letters, Vol. 326, No. 3-4, 2000, pp. 212-218. doi:10.1016/S0009-2614(00)00773-9
- D. A. Mazziotti, “Pursuit of N-Representability for the Contracted Schrödinger Equation through Density-Matrix Reconstruction,” Physical Review A, Vol. 60, No. 5, 1999, pp. 3618-3626. doi:10.1103/PhysRevA.60.3618
- W. Kutzelnigg and D. Mukherjee, “Direct Determination of the Cumulants of the Reduced Density Matrices,” Chemical Physics Letters, Vol. 317, No. 6, 2000, pp. 567-574. doi:10.1016/S0009-2614(99)01410-4
- M. Nooijen, M. Wladyslawski and A. Hazra, “Cumulant Approach to the Direct Calculation of Reduced Density Matrices: A Critical Analysis,” Journal of Chemical Physics, Vol. 118, No. 11, 2003, pp. 4832-4848. doi:10.1063/1.1545779
- D. R. Alcoba and C. Valdemoro, “The Correlation Contracted Schrdinger Equation: An Accurate Solution of the G-Particle-Hole Hypervirial,” International Journal of Quantum Chemistry, Vol. 109, No. 14, 2009, pp. 3178- 3190. doi:10.1002/qua.21943
- D. A. Mazziotti, “Parametrization of the Two-Electron Reduced Density Matrix for Its Direct Calculation without the Many-Electron Wave Function: Generalizations and Applications,” Physical Review A, Vol. 81, No. 6, 2010, Article ID: 062515.
- L. Vandenbergue and S. Boyd. “Semidefinite Programming,” SIAM Review, Vol. 38, No. 1, 1996, pp. 49-50. doi:10.1137/1038003
- M. J. Todd, “Semidefinite Optimization,” Acta Numerals, Vol. 10, 2001, pp. 515-560. doi:10.1017/S0962492901000071
- E. A. Yildirim and M. J. Todd, “Sensitivity Analysis in Linear Programming and Semidefinite Programming Using Interior-Point Methods,” Mathematical Programming, Vol. 90, No. 2, 2001, pp. 229-261. doi:10.1007/PL00011423
- S. Boyd and L. Vandenberghe, “Convex Optimization,” Cambridge University Press, Cambridge, 2009.
- S. Pironio, M. Navascues and A. Acio, “Convergent Relaxations of Polynomial Optimization Problems with Noncommuting Variables,” SIAM Journal of Optimization, Vol. 20, No. 5, 2010, pp. 2157-2180. doi:10.1137/090760155
- M. Nakata, H. Nakatsuji, M. Ehara, M. Fukuda, K. Nakata and K. Fujisawa, “Variational Calculations of Fermion Second-Order Reduced Density Matrices by Semidefinite Programming Algorithm,” Journal of Chemical Physics, Vol. 114, No. 19, 2001, pp. 8282-8292. doi:10.1063/1.1360199
- D. A. Mazziotti and R. M. Erdahl, “Uncertainty Relations and Reduced Density Matrices: Mapping Many-Body Quantum Mechanics onto Four Particles,” Physical Review A, Vol. 63, No. 4, 2001, Article ID: 042113.
- S. Burer and R. D. C. Monteiro, “A Nonlinear Programming Algorithm for Solving Semidefinite Programs via Low-Rank Factorization,” Mathematical Programming, Vol. 95, 2003, pp. 329-357. doi:10.1007/s10107-002-0352-8
- D. A. Mazziotti, “Realization of Quantum Chemistry without Wave Functions through First-Order Semidefinite Programming,” Physical Review Letters, Vol. 93, No. 21, 2004, Article ID: 213001.
- D. A. Mazziotti, “Exactness of Wave Functions from TwoBody Exponential Transformations in Many-Body Quantum Theory,” Physical Review A, Vol. 69, No. 1, 2004, Article ID: 012507.
- M. Fukuda, B. J. Braams, M. Nakata, M. L. Overton, J. K. Percus, M. Yamashita and Z. Zhao, “Large-Scale Semidefinite Programs in Electronic Structure Calculation,” Mathematical Programming, Vol. 109, 2007, pp. 553-580. doi:10.1007/s10107-006-0027-y
- M. Fukuda, M. Nakata and M. Yamashita, “Semidefinite Programming: Formulations and Primal-Dual InteriorPoint Methods,” Advanced Chemical Physics, Vol. 134, 2007, pp. 103-118.
- M. Nakata, B. J. Braams, K. Fujisawa, M. Fukuda, J. K. Percus, M. Yamashita and Z. Zhao, “Variational Calculation of Second-Order Reduced Density Matrices by Strong N-Representability Conditions and an Accurate Semidefinite Programming Solver,” Journal of Chemical Physics, Vol. 128, No. 16, 2008, Article ID: 164113.
- M. Yamashita, K. Fujisawa, M. Fukuda, K. Nakata and M. Nakata, “Algorithm 925: Parallel Solver for Semidefinite Programming Problem Having Sparse Schur Complement Matrix,” ACM Transactions on Mathematical Software, Vol. 39, No. 1, 2012, pp. 1-22. doi:10.1145/2382585.2382591
- T. Baumgratz and M. B. Plenio, “Lower Bounds for Ground States of Condensed Matter Systems,” New Journal of Physics, Vol. 14, Article ID: 023027.
- D. A. Mazziotti, “Variational Minimisation of Atomic and Molecular Ground-State Energies via the Two-Particle Reduced Density Matrix,” Physical Review A, Vol. 65, No. 6, 2002, Article ID: 062511.
- D. A. Mazziotti, “Variational Method for Solving the Contracted Schrödinger Equation through a Projection of the N-Particle Power Method onto the Two-Particle Space,” Journal of Chemical Physics, Vol. 116, No. 4, 2002, pp. 1239-1249. doi:10.1063/1.1430257
- G. Guidofalvi and D. A. Mazziotti, “Boson Correlation Energies via Variational Minimization with the Two-Particle Reduced Density Matrix: Exact N-Representability Conditions for Harmonic Interactions,” Physical Review A, Vol. 69, No. 4, 2004, Article ID: 042511.
- K. Yasuda, “Uniqueness of the Solution of the Contracted Schrödinger Equation,” Physical Review A, Vol. 65, No. 5, 2002, Article ID: 052121.
- M. Nakata, M. Ehara and H. Nakatsuji, “Fundamental World of Quantum Chemistry,” Kluwer Academic Publishers, New York, 2003.
- D. A. Mazziotti, “Variational Two-Electron Reduced Density Matrix Theory for Many-Electron Atoms and Molecules: Implementation of the Spinand Symmetry-Adapted T2 Condition through First-Order Semidefinite Programming,” Physical Review A, Vol. 72, No. 3, 2005, Article ID: 032510.
- G. Guidofalvi and D. A. Mazziotti, “Computation of Quantum Phase Transitions by Reduced-Density-Matrix Mechanics,” Physical Review A, Vol. 74, No. 1, 2006, Article ID: 012501.
- D. R. Alcoba, C. Valdemoro, L. M. Tel and E. Pérez-Romero, “Controlling the Nand S-Representability of the Second-Order Reduced Density Matrix: The Doublet-State Case,” Physical Review A, Vol. 77, No. 4, 2008, Article ID: 042508.
- Z. Zhao, B. J. Braams, M. Fukuda, M. L. Overton and J. K. Percus, “The Reduced Density Matrix Method for Electronic Structure Calculations and the Role of Three-Index Representability,” Journal of Chemical Physics, Vol. 120, No. 5, 2004, pp. 2095-2125. doi:10.1063/1.1636721
- M. Nakata, B. J. Braams, K. Fujisawa, M. Fukuda, J. K. Percus, M. Yamashita and Z. Zhao, “Variational Calculation of Second-Order Reduced Density Matrices by Strong N-Representability Conditions and an Accurate Semidefinite Programming Solver,” Journal of Chemical Physics, Vol. 128, No. 16, 2008, Article ID: 164113.
- D. A. Mazziotti, “Structure of Fermionic Density Matrices: Complete N-Representability Conditions,” Physical Review Letters, Vol. 108, No. 26, 2012, Article ID: 263002.
- D. A. Mazziotti, “Significant Conditions for the Two-Electron Reduced Density Matrix from the Constructive Solution of N-Representability,” Physical Review A, Vol. 85, No. 6, 2012, Article ID: 062507.
- M. Levy, “Universal Variational Functionals of Electron Densities, First-Order Density Matrices, and Natural Spin-Orbitals and Solution of the V-Representability Problem,” Proceedings of National Academy Science of the USA, Vol. 76, No. 12, 1979, pp. 6062-6065. doi:10.1073/pnas.76.12.6062
- T. L. Gilbert, “Hohenberg-Kohn Theorem for Nonlocal Externai Potentiais,” Physical Review B, Vol. 12, No. 6, 1975, pp. 2111-2120. doi:10.1103/PhysRevB.12.2111
- R. A. Donnelly and R. G. Parr, “Elementary Properties of an Energy Functional of the First Order Reduced Density Matrix,” Journal of Chemical Physics, Vol. 69, No. 10, 1978, pp. 4431-4439. doi:10.1063/1.436433
- R. A. Donnelly, “On a Fundamental Difference between Energy Functionals Based on First and on Second Order Density Matrices,” Journal of Chemical Physics, Vol. 71, No. 7, 1979, pp. 2874-2879. doi:10.1063/1.438678
- S. M. Valone, “Consequences of Extending 1matrix Energy Functionals from Pure State Representable to All Ensemble Representable 1 Matrices,” Journal of Chemical Physics, Vol. 73, No. 3, 1980, pp. 1344-1349. doi:10.1063/1.440249
- T. T. Nguyen-Dang, E. V. Ludeña and Y. Tal, “Variation of the Energy Functional of the Reduced 1st-Order Density Operator,” Journal of Molecular Structures (Theochem), Vol. 120, 1985, pp. 247-264. doi:10.1016/0166-1280(85)85114-9
- E. V. Ludeña and A. Sierraalta, “Necessary Conditions for the Mapping of Gamma-into ρ,” Physical Review A, Vol. 32, No. 1, 1985, pp. 19-25. doi:10.1103/PhysRevA.32.19
- E. V. Ludeña, “Density Matrices and Density Functionals,” Reidel, Dordrecht, 1987. doi:10.1007/978-94-009-3855-7_15
- M. Piris, “Natural Orbital Functional Theory,” In: D. A. Mazziotti, Ed., Reduced Density-Matrix Mechanics with Applications to Many-Electron Atoms and Molecules, John Wiley and Sons, New York, 2007, p. 387. doi:10.1002/9780470106600.ch14
- A. M. K. Müller, “Explicit Approximate Relation between Reduced Twoand One-Particle Density Matrices,” Physical Letter A, Vol. 105, No. 9, 1984, pp. 446-452. doi:10.1016/0375-9601(84)91034-X
- S. Goedecker and C. J. Umrigar, “A Natural Orbital Functional for the Many-Electron Problem,” Physical Review Letters, Vol. 81, No. 4, 1998, pp. 866-870. doi:10.1103/PhysRevLett.81.866
- G. Csanyi and T. A. Arias, “Tensor Product Expansions for Correlation in Quantum Many-Body Systems,” Physical Review B, Vol. 61, No. 11, 2000, pp. 7348-7352. doi:10.1103/PhysRevB.61.7348
- E. J. Baerends, “Exact Exchange-Correlation Treatment of Dissociated H2 in Density Functional Theory,” Physical Review Letters, Vol. 87, No. 13, 2001, Article ID: 133004.
- M. A. Buijse and E. J. Baerends, “An Approximate Exchange-Correlation Hole Density as a Functional of the Natural Orbitals,” Molecular Physics, Vol. 100, No. 4, 2002, pp. 401-421. doi:10.1103/PhysRevB.61.7348
- O. Gritsenko, K. Pernal and E. J. Baerends, “An Improved Density Matrix Functional by Physically Motivated Repulsive Corrections,” Journal of Chemical Physics, Vol. 122, No. 20, 2005, Article ID: 204102.
- S. Sharma, J. K. Dowhurst, N. N. Lathiotakis and E. K. U. Gross, “Reduced Density Matrix Functional for Many Electron Systems,” Physical Review B, Vol. 78, No. 20, 2008, Article ID: 201103.
- N. N. Lathiotakis, N. Helbig and E. K. U. Gross, “Performance of One-Body Reduced Density-Matrix Functionals for the Homogeneous Electron Gas,” Physical Review B, Vol. 75, No. 19, 2007, Article ID: 195120.
- N. N. Lathiotakis and M. A. L. Marques, “Benchmark Calculations for Reduced Density-Matrix Functional Theory,” Journal of Chemical Physics, Vol. 128, No. 18, 2008, Article ID: 184103.
- N. N. Lathiotakis, N. Helbig, A. Zacarias and E. K. U. Gross, “A Functional of the One-Body-Reduced Density Matrix Derived from the Homogeneous Electron Gas: Performance for Finite Systems,” Journal of Chemical Physics, Vol. 130, No. 6, 2009, Article ID: 064109.
- N. N. Lathiotakis, N. I. Guidopoulos and N. Helbig, “Size Consistency of Explicit Functionals of the Natural Orbitals in Reduced Density Matrix Functional Theory,” Journal of Chemical Physics, Vol. 132, No. 8, 2010, Article ID: 084105.
- R. L. Frank, E. H. Lieb, R. Seiringer and H. Siedentrop, “Müller’s Exchange-Correlation Energy in Density-Matrix-Functional Theory,” Physical Review A, Vol. 76, No. 5, 2007, Article ID: 052517.
- M. Piris, “A New Approach for the Two-Electron Cumulant in Natural Orbital Functional Theory,” International Journal of Quantum Chemistry, Vol. 106, No. 5, 2006, pp. 1093-1104. doi:10.1002/qua.20858
- M. Piris, “Natural Orbital Functional Theory: Molecules and Polymers,” Recent Research Development of Quantum Chemistry, Vol. 4, 2004, pp. 1-26.
- M. Piris, J. M. Matxain, X. Lopez and J. M. Ugalde, “Communication: The Role of the Positivity N-Representability Conditions in Natural Orbital Functional Theory,” Journal of Chemical Physics, Vol. 133, No. 11, 2010, Article ID: 111101.
- M. Piris, X. Lopez, F. Ruizpérez, J. M. Matxain and J. M. Ugalde, “A Natural Orbital Functional for Multiconfigurational States,” Journal of Chemical Physics, Vol. 134, No. 16, 2011, Article ID: 164102.
- J. M. Matxain, M. Piris, J. Uranga, X. Lopez, G. Merino and J. M. Ugalde, “The Nature of Chemical Bonds from PNOF5 Calculations,” Chemical Physics, Vol. 13, No. 9, 2012, pp. 2297-2303. doi:10.1002/cphc.201200205
- M. Piris, “A Natural Orbital Functional Based on an Explicit Approach of the Two-Electron Cumulant,” International Journal of Quantum Chemistry, Vol. 113, No. 5, 2013, pp. 620-630. doi:10.1002/qua.24020
- K. Pernal, “The Equivalence of the Piris Natural Orbital Functional 5 (PNOF5) and the Antisymmetrized Product of Strongly Orthogonal Geminal Theory,” Computational and Theoretical Chemistry, Vol. 1003, 2013, pp. 127-129. doi:10.1016/j.comptc.2012.08.022
- E. V. Ludeña, F. Illas and A. Ramrez-Sols, “On the N-Representability and Universality of F[ρ] in the Hohenberg-Kohn-Sham Version of Density Functional Theory,” International Journal of Modern Physics, Vol. 22, No. 25-26, 2008, pp. 4642-4654. doi:10.1142/S0217979208050395
- P.-O. Löwdin, “Density Matrices and Density Functionals,” Reidel, Dordrecht, 1987. doi:10.1007/978-94-009-3855-7_3
- R. McWeeny, “Density-Functions and Density Functionals,” Philosophical Magazine Part B, Vol. 69, No. 5, 1994, pp. 727-735. doi:10.1080/01418639408240141
- E. V. Ludeña and J. Keller, “The Importance of PureState N-Representability in the Derivation of Extended Kohn-Sham Equations,” Advaced Quantum Chemistry, Vol. 21, 1990, pp. 46-67.
- E. S. Kryachko and E. V. Ludeña, “Formulation of N-Representable and V-Representable Density-Functional Theory,” Physical Review A, Vol. 43, No. 5, 1991, pp. 2179- 2193. doi:10.1103/PhysRevA.43.2179
- E. S. Kryachko and E. V. Ludeña, “The N-Representability Problem and the Local-Scaling Version of Density Functional Theory,” Condensed Matter Theories, Vol. 7, pp. 229-241. doi:10.1007/978-1-4615-3352-8_22
- E. V. Ludeña, V. V. Karasiev, A. Artemyev and D. Gó- mez, “Many-Electron Densities and Reduced Density Matrices,” Kluwer, New York, 2000. doi:10.1007/978-1-4615-4211-7_10
- O. Bokanowski, “New N-Representability Results Involving Symmetry and Application to the Density-Functional Theory Formalism,” Journal of Mathematical Chemistry, Vol. 26, No. 4, 1999, pp. 271-296. doi:10.1023/A:1019106516542
- P. W. Ayers and S. Liu, “Necessary and Sufficient Conditions for the N-Representability of Density Functionals,” Physical Review A, Vol. 75, No. 2, 2007, Article ID: 022514.
- P. W. Ayers, R. Cuevas-Saavedra and D. Chakraborty, “A Variational Principle for the Electron Density Using the Exchange Hole & Its Implications for N-Representability,” Physical Letters A, Vol. 376, No. 6-7, 2012, pp. 839- 844. doi:10.1016/j.physleta.2012.01.028
- W. Kurlancheek and M. Head-Gordon, “Violations of N-Representability from Spin-Unrestricted Orbitals in Møller-Plesset Perturbation Theory and Related DoubleHybrid Density Functional Theory,” Molecular Physics, Vol. 107, No. 8-12, 2009, pp. 1223-1232. doi:10.1080/00268970902835637
- C. Lee, W. Yang and R. G. Parr, “Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Elcetron Density,” Physical Review B, Vol. 37, No. 2, 1988, pp. 785-789. doi:10.1103/PhysRevB.37.785
- R. Colle and O. Salvetti, “Approximate Calculation of the Correlation Energy or the Closed Shells,” Theoretica Chimica Acta, Vol. 37, No. 4, 1975, pp. 329-334. doi:10.1007/BF01028401
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, “Results Obtained with the Correlation-Energy Density Functionals of Becke and Lee, Yang and Parr,” Chemical Physics Letters, Vol. 157, No. 3, 1989, pp. 200-206. doi:10.1016/0009-2614(89)87234-3
- R. C. Morrison, “The Non-N-Representability of the ColleSalvetti Second-Order Reduced Density Matrix,” International Journal of Quantum Chemistry, Vol. 46, No. 4, 1993, pp. 583-587. doi:10.1002/qua.560460406
- S. Caratzoulas, “Gaussian Resummation Approximation of the Reference Spin-Reduced Second-Order Density Matrix in the Colle-Salvetti Model for Electron Correlation,” Physical Review A, Vol. 63, No. 6, 2001, Article ID: 062506.
- S. Ragot, “Assessment of an Analytical Density Matrix Derived from a Modified Colle-Salvetti Approach to the Electron Gas,” Journal of Chemical Physics, Vol. 132, No. 6, 2010, Article ID: 064104.
NOTES
*Corresponding author.

