Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28565,7 pages DOI:10.4236/jmp.2013.43040
Thermal Electromagnetic Radiation of Rarefied Gas
Department of Physics, Samara State University, Samara, Russia
Email: volobuev47@yandex.ru
Received December 25, 2012; revised January 27, 2013; accepted February 7, 2013
Keywords: Rarefied Gas; Boltzmann Kinetic Equation; Electromagnetic Radiation; Laws of Atoms Distribution in the Velocities
ABSTRACT
The Boltzmann kinetic equation for rarefied radiating gas is found. It is shown, that process of radiation is defined by excitation of atoms at their collision, and also spontaneous radiation of quantums at transition of electrons to the basic power level and the compelled radiation of quantums at collision of the excited atoms. It is shown, that distributions on velocities of the excited and not excited atoms submit to various laws. Distinctions in laws of distribution of the excited and not excited atoms define power parameters of radiating gas, and also a share of radiating molecules in gas.
1. Introduction
The theory of the kinetic equations is rather widely applied to the analysis of various physical processes [1]. The interaction of molecules of rarefied gas in gas laser [2], particles in plasma, phonons in crystals, etc. have been successfully analyzed with the help of this theory. Most strict deduction of Maxwell distribution of ideal gas molecules by the speeds (or their kinetic energy) is carried out with the help of Boltzmann kinetic equation [3] on consideration of system of interacting atoms in a stationary condition. Boltzmann kinetic equation, first of all, reflects non-stationary process of interaction of particles among themselves, influence of this interaction on the establishment of corresponding distribution of molecules and influence on examined system of external factors.
The method of the kinetic equations with use of a principle of detailed equilibrium is applied also at research of transition of the atoms interacting with electromagnetic radiation, from one condition in another [3].
The theory of thermal radiation represents one of the most advanced physical theories. Actually this theory has begun development of quantum mechanics. The matter is that even before creation of quantum mechanics the formula for spectral density of energy of equilibrium thermal radiation, so-called Rayleigh-Jeans law has been found. The deduction of this law was based on the wave nature of light. Concentration of electromagnetic standing waves in a cavity has been found and multiplied on the average energy of a standing wave kT, where kBoltzmann constant, Т-absolute temperature [3].
In spite of the fact that the deduction of this law is completely transparent, it was in the absolute contradiction with experiment, showing, that the density of energy of electromagnetic radiation monotonously grows with increase in frequency. It has induced M. Planck to researches which have led him to Planck’s to well-known formula for radiation of absolutely black body and further to development of quantum statistics.
All events of this history were repeatedly discussed as in scientific, and scientific-popular literature.
We shall consider some questions of thermal radiation, on which researchers usually take insufficient attention.
2. Processes in the Gas, Resulting to Thermal Electromagnetic Radiation
There is interest to consider in more detail processes in the gas, resulting to thermal electromagnetic radiation.
In Figure 1 some constant volume of gas V which is heated up due to submission of heat Q is shown. It results in radiation by gas of quantums of electromagnetic energy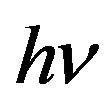 .
.
Let’s carry out the kinetic analysis of processes in the rarefied gas, resulting to electromagnetic radiation.
We shall assume gas the closed thermodynamic system which is taking place in equilibrium state. i.e. how many thermal energy Q gives in system, as much electromagnetic energy from it is radiated. Interaction external of molecules electrons in such gas occurs only at their collision.
Let’s consider probability of transition of electron in a molecule of gas from the top energy level on bottom. This probability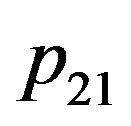 , it is similar to a method to Einstein [3], we shall divide into two parts, on the spontaneous
, it is similar to a method to Einstein [3], we shall divide into two parts, on the spontaneous
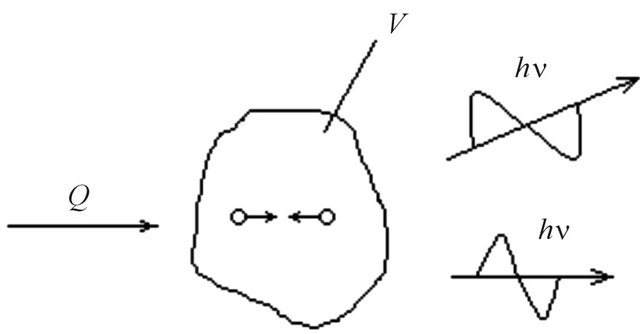
Figure 1. The volume of gas radiating at heating.
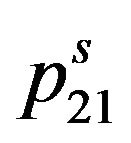 and compelled
and compelled 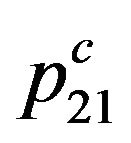 probabilities. We shall consider, that the compelled transition of electrons occurs only due to collision of molecules, Figure 2.
probabilities. We shall consider, that the compelled transition of electrons occurs only due to collision of molecules, Figure 2.
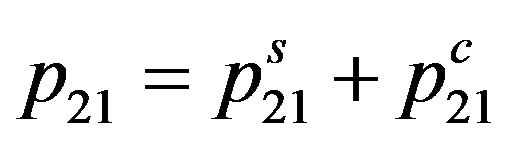 . (1)
. (1)
Let’s note, that as at spontaneous transition of electrons on the bottom energy level, and at compelled there is radiation of electromagnetic energy quantums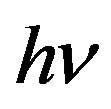 .
.
Using a principle of detailed balance and Boltzmann distribution, we have:
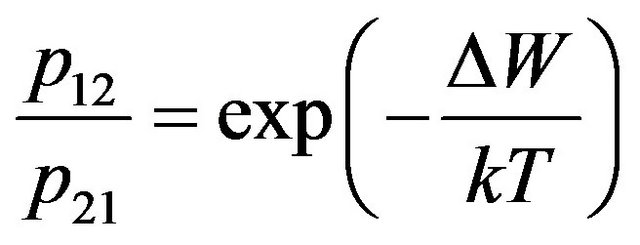 , (2)
, (2)
where 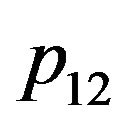 is probability of transition of electron on the top energy level at impact of molecules, Т-absolute temperature of gas. The value
is probability of transition of electron on the top energy level at impact of molecules, Т-absolute temperature of gas. The value 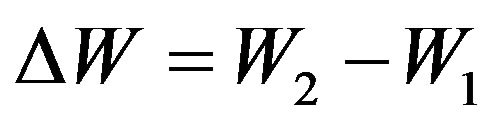 takes into account change of the energy condition of molecules at their collision, i.e. redistribution of kinetic energy of molecules and transitions of electrons in molecules from a level on a level.
takes into account change of the energy condition of molecules at their collision, i.e. redistribution of kinetic energy of molecules and transitions of electrons in molecules from a level on a level.
Substituting (1) in (2), and taking into account, that the probability of the compelled transition at collision of molecules with the bottom energy level on top is equal to probability of the compelled transition at collision of molecules with the top level on bottom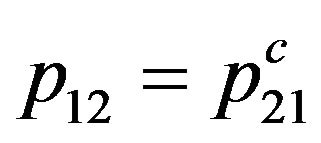 , we find:
, we find:
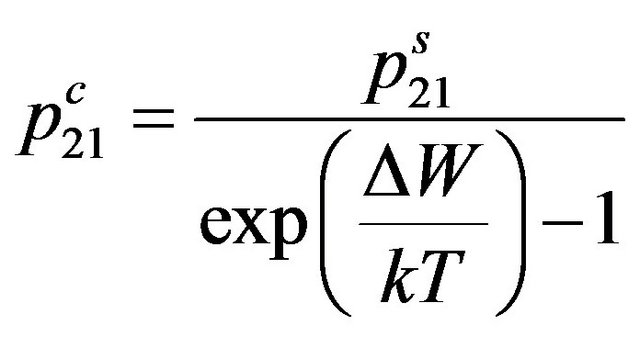 . (3)
. (3)
Change of the energy condition 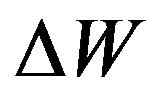 of molecule generally can take place or due to transfer of kinetic energy from one molecule to another at their collision, or due to supply of energy from the outside, or due to electromagnetic radiation of gas, or all these cases simultaneously took place.
of molecule generally can take place or due to transfer of kinetic energy from one molecule to another at their collision, or due to supply of energy from the outside, or due to electromagnetic radiation of gas, or all these cases simultaneously took place.
On the other hand at impact of molecules, in them there is a distribution of external electrons on their energy. This distribution, as well as Maxwell distribution, has thermal character. Since it results from collisions of molecules the internal electrons of molecules do not participate in occurrence of the given distribution.
The probability for electron to appear at a level 1, Figure 2, we shall accept equal p1, and at a level 2 equal p2. Taking into account the condition of normalization p1 +
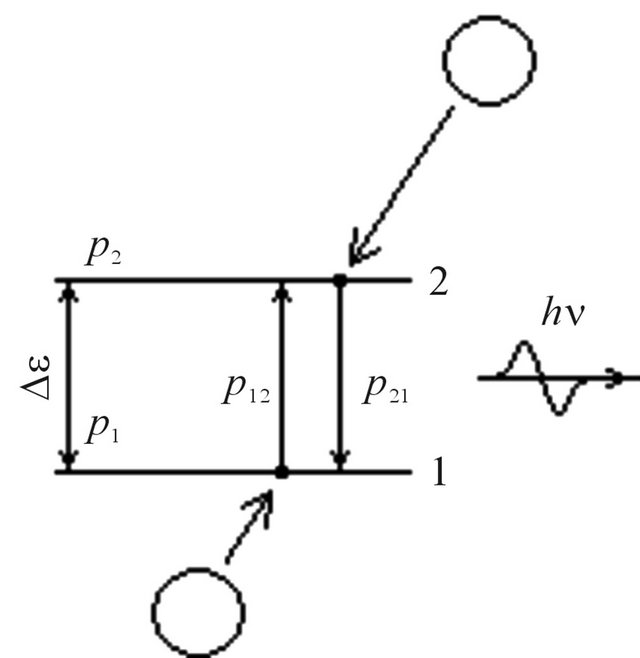
Figure 2. Excitation and the compelled radiation of molecules at their collisions.
p2 = 1 and Boltzmann distribution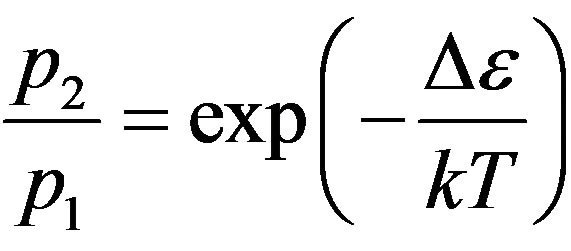 , we receive:
, we receive:
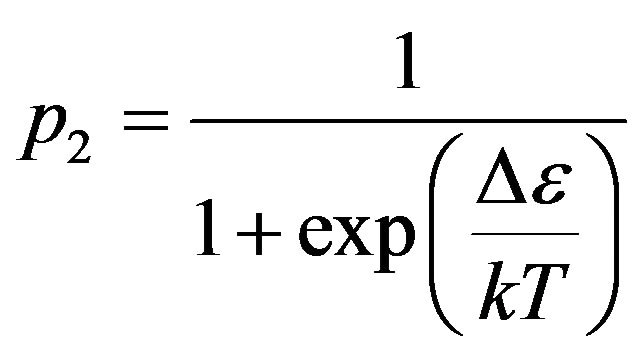 . (4)
. (4)
The value 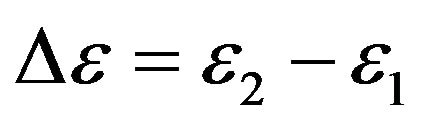 takes into account only difference of the electrons energy at energies levels 1 and 2.
takes into account only difference of the electrons energy at energies levels 1 and 2.
In the form of record the received formula is close to Fermi-Dirac [4] distribution, but not identical to it. As against Fermi-Dirac distribution, in the formula (4) value  is not excess of electron energy above Fermi’s level, and represents a difference of energies levels of external electrons to which they can transit at collision of molecules. Besides we shall noted, that at the deduction of distribution (4) Pauli principle was not used.
is not excess of electron energy above Fermi’s level, and represents a difference of energies levels of external electrons to which they can transit at collision of molecules. Besides we shall noted, that at the deduction of distribution (4) Pauli principle was not used.
The Maxwell distribution and distributions (3), (4) contradict each other since that there were distributions (3), (4) it is necessary, that impacts of molecules were not elastic, and to Maxwell distribution there correspond absolutely elastic impacts of molecules.
Besides distinction of forms of distributions (3) and (4), concerning as a whole to the same system to rarefied gas pays attention. Hence, distribution of molecules on energy or to velocities in examined gas system cannot be described by the uniform formula.
3. The Quantum Kinetic Equation of Radiating Rarefied Gas
To find out how molecules of gas should be distributed on energy in view of quantum processes, we shall consider kinetic Boltzmann equation as [3]:
 , (5)
, (5)
where f and f1 is the density of probabilities of molecules distribution in the velocities (or energy) for two molecules to have velocities before collision v and v1, and f2, f3-density of probabilities for the same molecules to have velocities after collision v2 and v3. Besides sizes vrel-relative speed of impacting molecules, s-effective section of interaction of particles, p1-impulse of examined impacting molecule,  -a solid angle in which particles scattered, in this case molecule a, after collision, Figure 3.
-a solid angle in which particles scattered, in this case molecule a, after collision, Figure 3.
The main lack of Boltzmann Equation (5) is the impossibility with the help of it to describe electromagnetic thermal radiation of gas. It is connected to the assumption of absolutely elastic impacts of gas molecules. We shall notice also, that this equation found before creation of quantum mechanics has no quantum character.
With the purpose of the account of not elastic process of collisions of molecules, finally, resulting in radiation of quantums of electromagnetic energy, and also translation of Boltzmann equation in quantum area, we modify the Equation (5).
Energy of a molecule represents the sum of kinetic energy of its movement and potential energy of excitation due to transition of electrons on higher energies levels
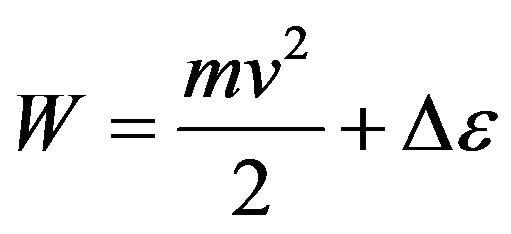 [5].
[5].
Let’s allocate in all volume of gas the relative share of molecules q (concerning corresponding interval of energy) which have energies W and W1. As a result of their collisions there are molecules with energies W2 and W3, which share too q. The number of collisions of molecules with energies W and W1 is proportional to product of probabilities ff1. But after the first collision the share of molecules with these energies will decrease due to occurrence of molecules with energies W2 and W3. Therefore the number of collisions will be proportional to reduction of a share of molecules with energies W and W1 due to increase in a share of molecules with energies W2 and W3, i.e. proportional to value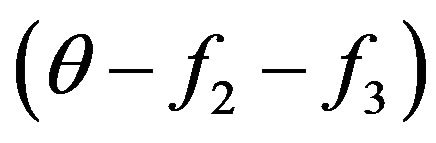 . Hence, Boltzmann kinetic Equation (5) for radiating gas gets a kind:
. Hence, Boltzmann kinetic Equation (5) for radiating gas gets a kind:
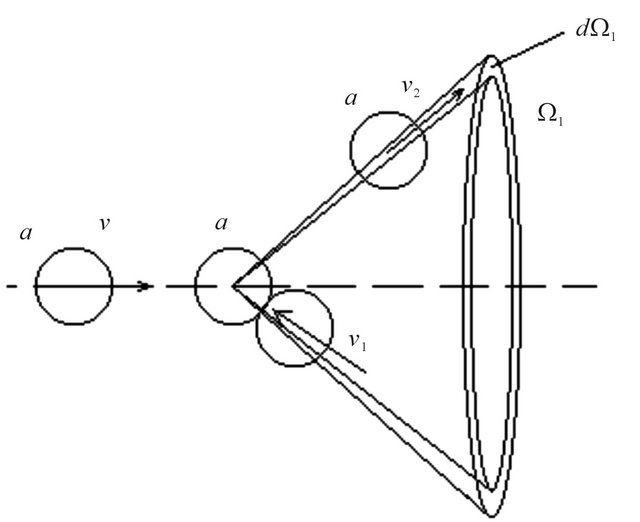
Figure 3. Scattering of molecule a after collision.
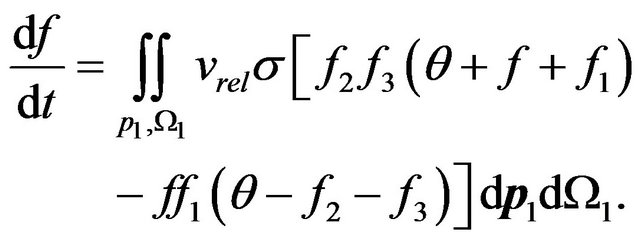 (6)
(6)
The value 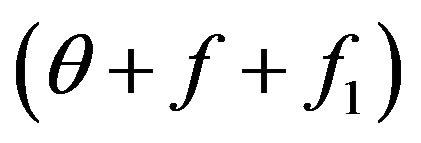 shows, that the share of molecules with energies W2 and W3 grows due to molecules which before collision had energies W and W1. In the Equation (6) as against (5) integral of collisions it is written down not only on the basis of balance of molecules before and after collision, but also dynamics of change of molecules shares is taken into account during the collisions, resulting to thermal electromagnetic radiation.
shows, that the share of molecules with energies W2 and W3 grows due to molecules which before collision had energies W and W1. In the Equation (6) as against (5) integral of collisions it is written down not only on the basis of balance of molecules before and after collision, but also dynamics of change of molecules shares is taken into account during the collisions, resulting to thermal electromagnetic radiation.
Let’s find stationary distributions of the molecules , submitting to the Equation (6). Stationary distributions of molecules arise in a case
, submitting to the Equation (6). Stationary distributions of molecules arise in a case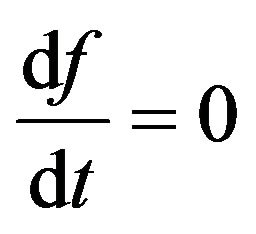 . Hence, from (6) we find:
. Hence, from (6) we find:
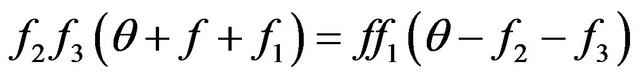 , (7)
, (7)
To the functional Equation (7) satisfy functions of distribution of type:
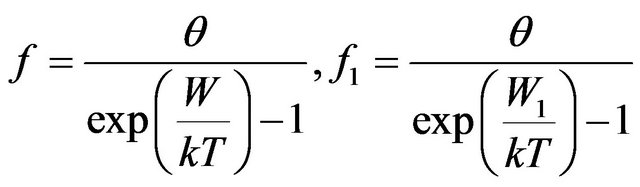 , (8)
, (8)
 . (9)
. (9)
Simply to show, that the Equation (7) will identically be transformed to a kind:
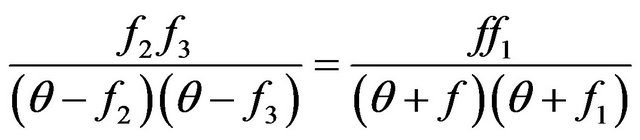 , (10)
, (10)
which decision, obviously, Functions (8) and (9) are.
Thus the law of energy conservation is carried out at not elastic collision of molecules:
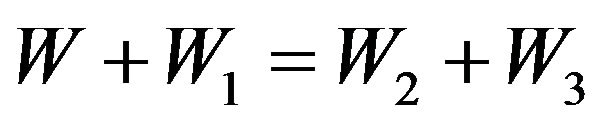 . (11)
. (11)
Substituting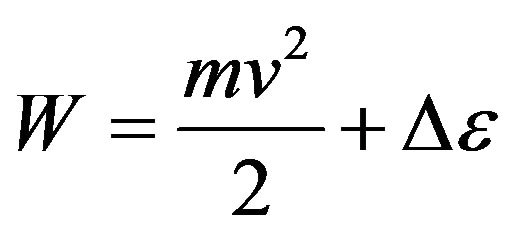 , we find:
, we find:
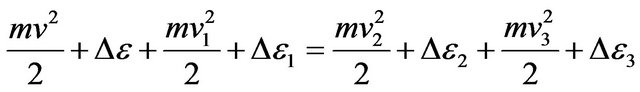 . (12)
. (12)
In the Formula (12) values 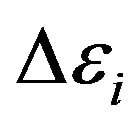 characterize change of molecules energy at transition of electrons from level on level. Thus this transition can be both compelled at impact, and spontaneous.
characterize change of molecules energy at transition of electrons from level on level. Thus this transition can be both compelled at impact, and spontaneous.
The kind of functions of molecules distribution at collision changes from the form (8) on the form (9) due to excitation of molecules. But after radiation by molecules of electromagnetic energy the kind of their function of distribution comes back to the form (8), Figure 4.

Figure 4. Oscillations of the distribution law of molecules at absorption of heat and radiation of quantums.
In figure it is marked, that is heat Q, submitted to isovolumetric heated up gas goes on change of internal energy of gas 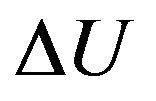 that results in change of the law of distribution of gas molecules at their excitation and to radiation of electromagnetic energy. Thus, not excited molecules have function of distribution (8), and excited-function of distribution (9). At gas simultaneously there are the molecules distributed under forms (8) and (9).
that results in change of the law of distribution of gas molecules at their excitation and to radiation of electromagnetic energy. Thus, not excited molecules have function of distribution (8), and excited-function of distribution (9). At gas simultaneously there are the molecules distributed under forms (8) and (9).
The kinetic Equation (6) has irreversible character on time that reflects the second law of thermodynamics. Really, collisions of molecules with energies W2 and W3 will not lead to molecules with energies W and W1. Mathematically, it is connected by that the left part of the difference in integral of collisions (6) is not symmetric of the right part, as against Boltzmann Equation (5). It is connected by that a fraction of molecules energy after their collision is irreversible lost due to radiation.
Thus, distribution of molecules in the velocities in case of their not elastic impacts cannot be described one function of distribution.
Distribution of molecules on energies in the given problem where it is examined not isolated, but closed isovolumetric molecules system submits to laws (8) and (9). Thus the given system of molecules there is can, both to be heated up from external source, and to emit electromagnetic thermal radiation. But the examined thermodynamic system of molecules is not open since change of it mass is excluded.
Concerning value q in the Equation (6) it is necessary to make the following explanations. In the kinetic Equation (6) interaction only molecules with energies W and W1 is examined. Before the first collision of molecules, information about resulting system of molecules with energies W2 and W3, for example, their relative shares in gas system, no. But at the first collision of molecules with energies W and W1 already there should be the information on relative shares of molecules with energies W2 and W3. Therefore the factor 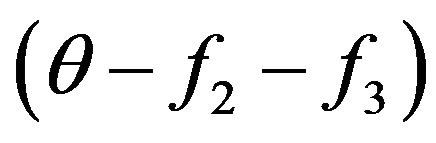 is used. Actually this factor before collision of molecules with energies W also W1 takes into account the information on the condition of molecules system with energies W2 and W3. From this point of view probably and a quantum explanation of a factor
is used. Actually this factor before collision of molecules with energies W also W1 takes into account the information on the condition of molecules system with energies W2 and W3. From this point of view probably and a quantum explanation of a factor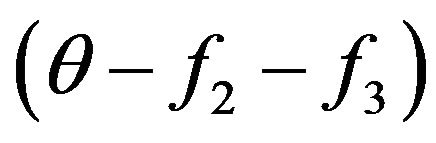 .
.
For the account of Pauli principle it is necessary to use the multiplier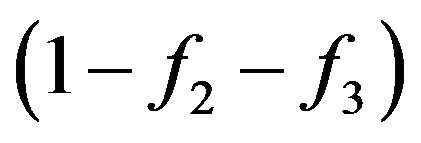 . The matter is that at collision of molecules, there is the interaction of their external electronic shells and Pauli’s principle starts to act. Due to this multiplier number of molecules transit in the filled conditions for which
. The matter is that at collision of molecules, there is the interaction of their external electronic shells and Pauli’s principle starts to act. Due to this multiplier number of molecules transit in the filled conditions for which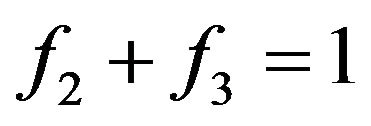 , it is equal to zero. i.e. collisions can result molecules only in yet not occupied conditions [1,6]. In other words, at fulfilment of a condition
, it is equal to zero. i.e. collisions can result molecules only in yet not occupied conditions [1,6]. In other words, at fulfilment of a condition 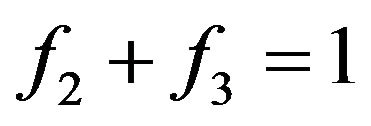 there can not be a molecule with energies W2 and W3. This position should be reflected in the Equation (6).
there can not be a molecule with energies W2 and W3. This position should be reflected in the Equation (6).
Thus, quantum consideration shows, that size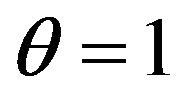 . It also means, that in rarefied gas, by consideration of collisions of molecules with energies W and W1 other molecules with others energies to consider there is no necessity and a relative share of molecules with these energies at anyone including the first collision, it is necessary to accept to equal one. From the quantum point of view the information on the condition of molecules with energies W2 and W3 is determined by Pauli’s principle. Therefore classical and quantum explanations of presence of the factor
. It also means, that in rarefied gas, by consideration of collisions of molecules with energies W and W1 other molecules with others energies to consider there is no necessity and a relative share of molecules with these energies at anyone including the first collision, it is necessary to accept to equal one. From the quantum point of view the information on the condition of molecules with energies W2 and W3 is determined by Pauli’s principle. Therefore classical and quantum explanations of presence of the factor 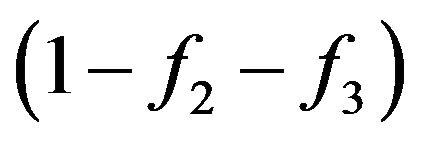 actually containing the information on the condition of system of interacting molecules after collision, it is equally correctly.
actually containing the information on the condition of system of interacting molecules after collision, it is equally correctly.
4. Distributions of Gas Molecules in the Velocities in Radiating Gas
Taking into account the duality of function of molecules distribution on energies, we shall estimate functions of distribution of molecules in the velocities. First we shall consider a case when the form of distribution corresponds (9), i.e. molecules are in the excited condition. The probability of a finding of a molecule energy W in phase volume 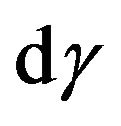 can be received under the formula:
can be received under the formula:
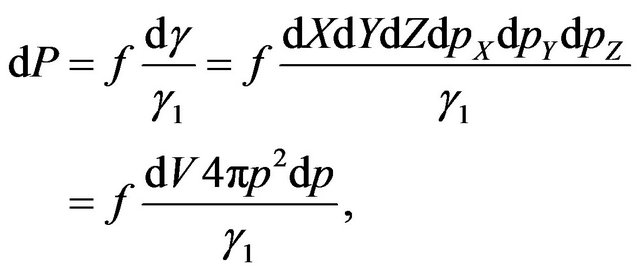 (13)
(13)
where 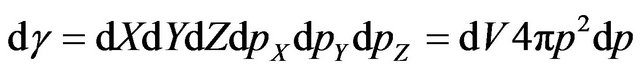 is element of phase volume,
is element of phase volume, 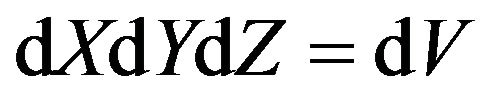 -the volume, falling one molecule in gas,
-the volume, falling one molecule in gas, 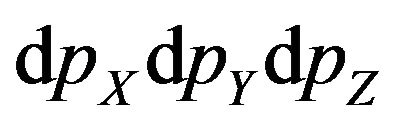 -product of components of molecule impulse, р-the module of molecule impulse,
-product of components of molecule impulse, р-the module of molecule impulse,  -phase volume falling one molecule. Function of distribution according to (9) is
-phase volume falling one molecule. Function of distribution according to (9) is .
.
In the Formula (13) integration executed of impulses on angles of spherical layer by thickness 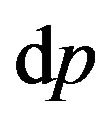 that is equivalent to replacement
that is equivalent to replacement 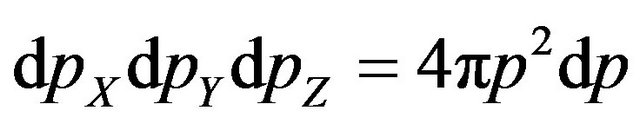 [4].
[4].
Transit in (13) from the impulse to velocity of molecule v, we shall find:
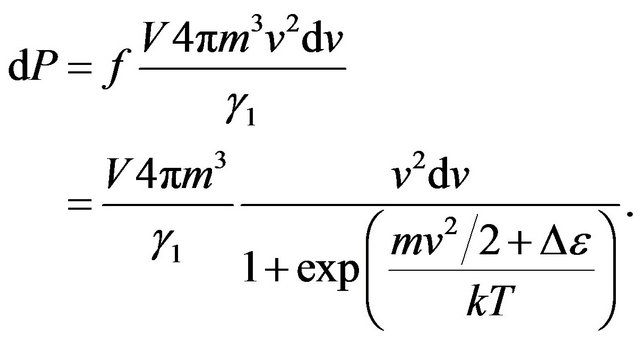 (14)
(14)
In the Formula (14) integration on volume of gas V is carried out.
Taking into account  where
where 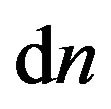 is number of molecules with a speed from v up to
is number of molecules with a speed from v up to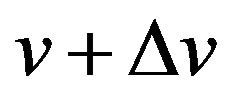 , and n the general number of molecules in volume V, from (14) we shall receive:
, and n the general number of molecules in volume V, from (14) we shall receive:
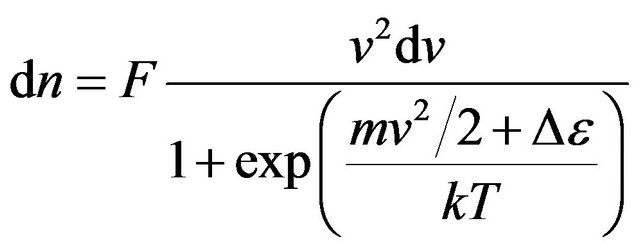 , (15)
, (15)
where the constant 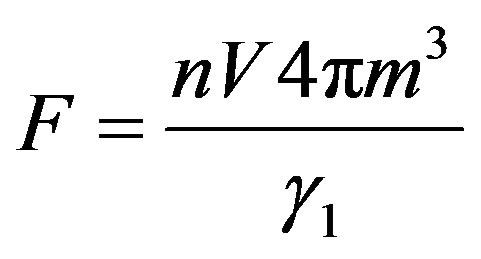 can be found from the condition of normalization:
can be found from the condition of normalization:
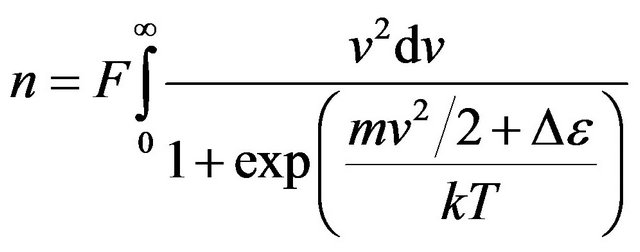 . (16)
. (16)
The integral (16) in elementary functions is not calculated.
The density of probability of molecules distribution in the velocities, using (15), looks like:
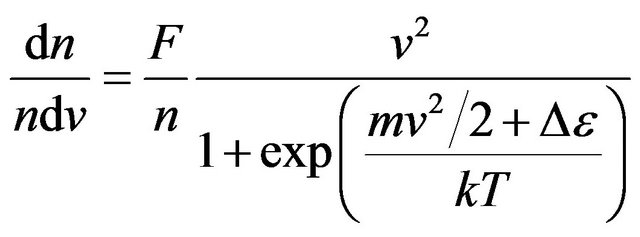 . (17)
. (17)
The value 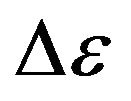 is change of molecules energy at transition of electrons from level on level depends on a kind of gas. For rarefied gas in atomic condition the spectrum of radiation is lined. And, on any length of wave at the certain temperature of gas the maximal energy is radiated. For example, in a spectrum of seen light at steam of mercury (in mercury-quartz lamps) the brightest green line with length of a wave
is change of molecules energy at transition of electrons from level on level depends on a kind of gas. For rarefied gas in atomic condition the spectrum of radiation is lined. And, on any length of wave at the certain temperature of gas the maximal energy is radiated. For example, in a spectrum of seen light at steam of mercury (in mercury-quartz lamps) the brightest green line with length of a wave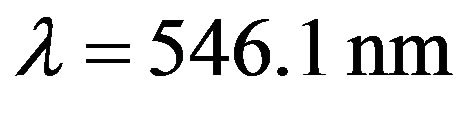 . Strictly speaking, the value
. Strictly speaking, the value 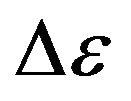 is necessary to calculate under the formula
is necessary to calculate under the formula 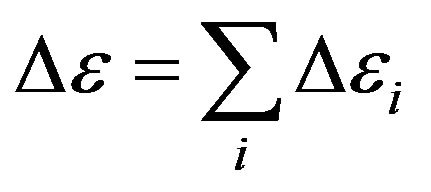 where summation executed on all possible energies transitions in a spectrum of gas. For the further analysis we shall assume, that radiation of rarefied gas monochromatic, occurs on one length of the wave corresponding to a maximum of energy of thermal equilibrium radiation of absolutely black body. Energy of electrons transition
where summation executed on all possible energies transitions in a spectrum of gas. For the further analysis we shall assume, that radiation of rarefied gas monochromatic, occurs on one length of the wave corresponding to a maximum of energy of thermal equilibrium radiation of absolutely black body. Energy of electrons transition 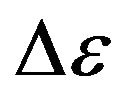 at which the maximum of energy of thermal radiation is observed, calculate from a ratio (the Wien’s law)
at which the maximum of energy of thermal radiation is observed, calculate from a ratio (the Wien’s law)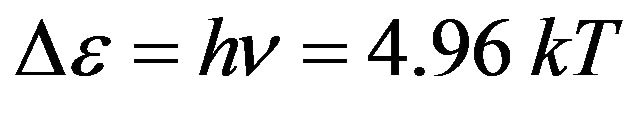 , [3].
, [3].
Let’s designate in (16) value . In result the Formula (16) it is possible to transform:
. In result the Formula (16) it is possible to transform:
 (18)
(18)
In the Formula (18) and lower all integrals are found by the numerical method.
Hence, value
 , (19)
, (19)
where constant a = 144.5. Size a and number p used for comparison of distribution (17) with Maxwell distribution [4]:
 . (20)
. (20)
Substituting (19) in (17), we find:
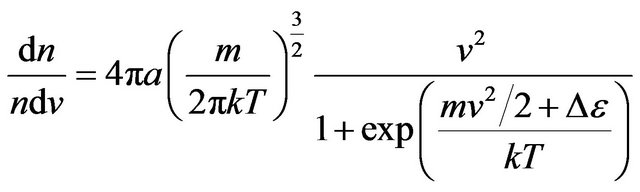 . (21)
. (21)
Distribution (21) actually depends on three variables: , and Т.
, and Т.
Let’s consider now a case of not excited molecules when function of distribution has the form (8).
Similarly (15) we shall write down:
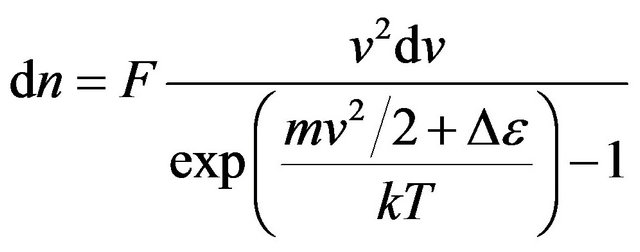 . (22)
. (22)
As before we accept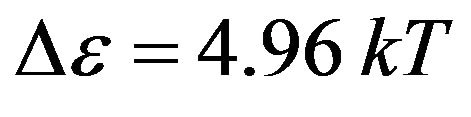 . Constant F we shall find from the condition of normalization:
. Constant F we shall find from the condition of normalization:
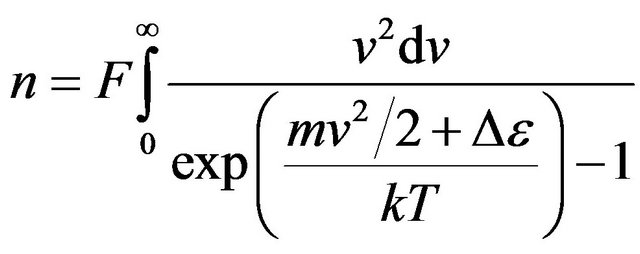 . (23)
. (23)
Hence:
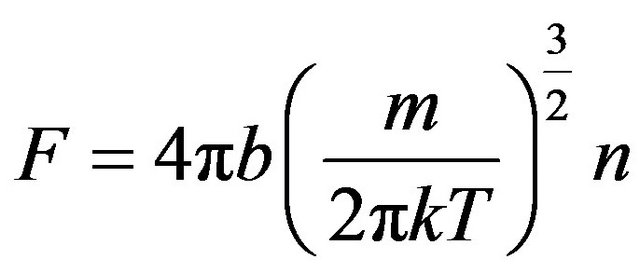 , (24)
, (24)
where b = 143.8.
Thus, distribution of not excited molecules looks like:
 . (25)
. (25)
In Figure 5 curves of functions of distribution which are described by Formulas (21), (25)-curve 1 are shown, and Maxwell distribution (20)-curve 2. The temperature of gas (air with equivalent molecular mass 29) is accepted equal T = 300 K.
From figure it is visible, that the difference between distributions (21) and (25) practically is absent. Distinction between them and Maxwell distribution does not exceed 1%. The curve of Maxwell distribution passes a little below the curves plotted under Formulas (21) and (25) only in areas of the most probable velocity of molecules.
Hence, for calculation of speeds of molecules and other statistical parameters of molecular radiating systems with the big accuracy it is possible to use Maxwell distribution.
Comparison of distributions (21) and (25) and Maxwell distributions shows, that Maxwell distribution (20) is some average distribution between (21) and (25).
That distributions of velocities of the excited and not excited molecules (21) and (25) are numerically practically identical, is defined by action of the law of quantity movement conservation of molecules 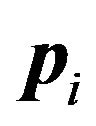 before and after collision which for differentials looks like:
before and after collision which for differentials looks like:
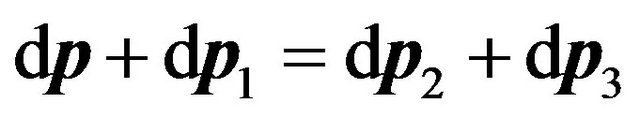 . (26)
. (26)
Concerning the law of conservation (26) the following
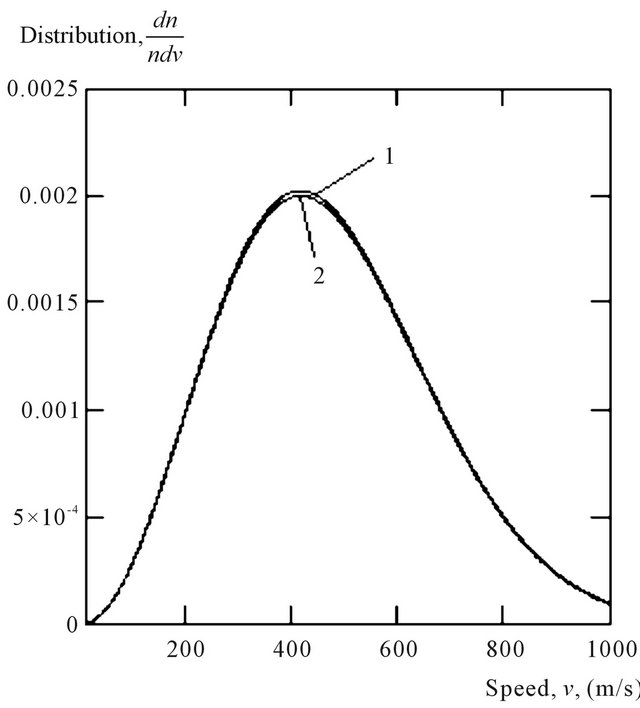
Figure 5. Distribution laws of molecules in the speeds in rarefied radiating gas.
is necessary remark. It is applicable and for a situation when in the condition of balance of system the left part reflects quantity of movement of particles leaving some phase volume at collision, and the right part quantity of movement of the particles passing at collision in this phase volume. The same can be attributed and to the law of conservation of energy (12).
From (26) it is received:
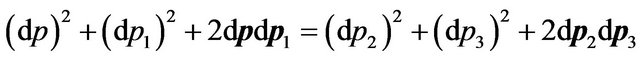 . (27)
. (27)
At interaction of molecules in the condition of balance, the quantity of molecules leaving and passing in the same phase volume is kept. Therefore it is possible to write, that  [3]. This equality is used at deduction of Boltzmann kinetic Equation (5). Hence, from (27) we have:
[3]. This equality is used at deduction of Boltzmann kinetic Equation (5). Hence, from (27) we have:
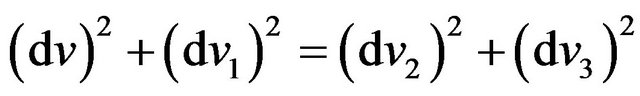 . (28)
. (28)
The ratio (28) shows that change of velocities of molecules 2 and 3 can occur only owing to change of velocities of molecules without index and 1, but not due to radiation by the excited molecules 2 and 3 of electromagnetic quantums. It also determines similarity (Figure 5) of distributions (21) and (25), despite of their various forms.
5. Energy Aspects of Rarefied Gas Radiation
Let’s find a share of energy which passes on radiation of gas.
The general energy of n gas molecules can be found under the formula:
 , (29)
, (29)
where the top sign attributes to the excited molecules, and bottom to not excited.
Using Formulas (15) and (22), we shall find:
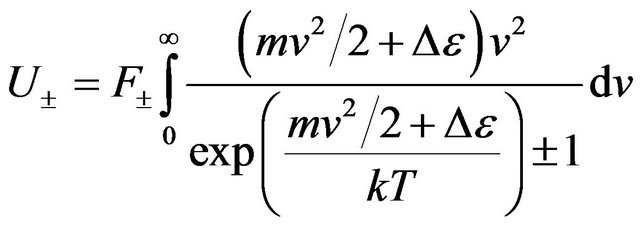 . (30)
. (30)
Carrying out separately integration for the excited and not excited molecules, we have:
 , (31)
, (31)
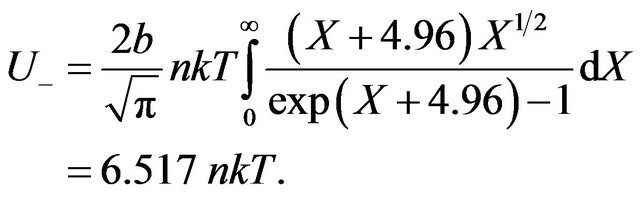 (32)
(32)
As before, it is made the substitution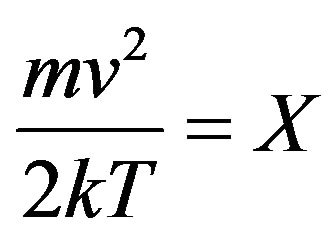 . Besides sizes of constants F from Formulas (19) and (24) are used.
. Besides sizes of constants F from Formulas (19) and (24) are used.
From (31) and (32) follows, that energy of radiating gas much more exceeds internal energy of ideal gas U = 1.5 nkT. It is connected by that the most fraction of energy Q passing in gas system transit on excitation of molecules. In condition of balance examined isovolumetric gas system, Figure 4, on radiation of gas is spent energy:
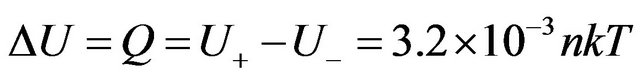 . (33)
. (33)
Let’s find, following [7], the energy of thermal radiation falling 1 quantum.
Using Bose-Einstein’s distribution for photon gas [4], we shall find volumetric density of energy of radiation:
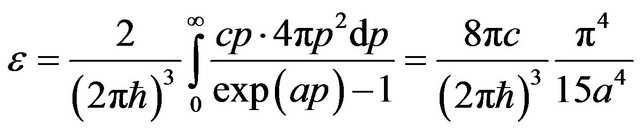 , (34)
, (34)
where р is the impulse of quantum, also it is designated .
.
Number of quantums in unit of volume equally:
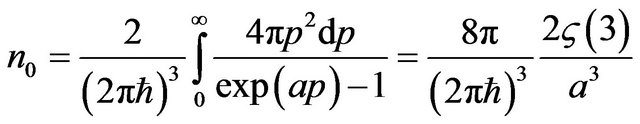 , (35)
, (35)
where 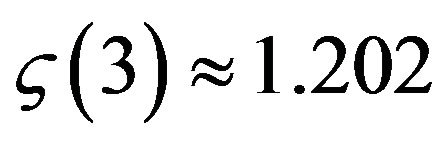 is dzeta-function of Riemann.
is dzeta-function of Riemann.
The average energy of thermal radiation falling 1 quantum is equal:
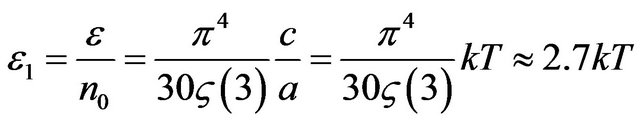 . (36)
. (36)
Let’s find quantity of simultaneously radiating molecules . Hence, simultaneously radiate only 0.118% of all gas molecules.
. Hence, simultaneously radiate only 0.118% of all gas molecules.
If to consider rarefied gas in the given thermodynamic system as the converter of thermal energy in energy of electromagnetic radiation on the basis of the carried out analysis it is possible to make the following conclusion. Energy of transition from the thermal form, for exampleby heating a vessel with gas, in energy of thermal radiation is very small part of the general internal energy of gas. That gas practically submits to Maxwell distribution testifies to it. If to use conditional efficiency of transformation of thermal energy into energy of radiation for gas system it makes:
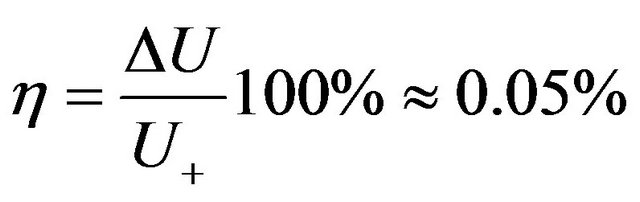 . (37)
. (37)
6. Conclusions
For calculation of the molecules velocities and other statistical parameters of molecular radiating systems with the big accuracy it is possible to use Maxwell distribution.
In spite of the fact that transitions of molecules at their collisions from one form of distribution in another practically do not influence distribution of molecules velocities, these transitions are determining in distribution of quantums of thermal radiation on their energies.
In ideal rarefied gas simultaneously radiate only 0.118% of all molecules.
REFERENCES
- E. M. Lifshits and L. P. Pitaevsky, “Physical Kinetics,” Fizmatlit, Moscow, 2002.
- V. P. Kochanov, “The Sated Two-Photon Absorption of Unifrequent Radiation in Gas Mediums,” Quantum Electronics, Vol. 42, No. 2, 2012, pp. 111-116. doi:10.1070/QE2012v042n02ABEH014766
- V. G. Levich, “Theoretic Physics Course,” Phismatgis, Moscow, 1962.
- A. N. Matveev, “Molecular Physics,” Higher School, Moscow, 1981.
- L. D. Landau and E. M. Lifshits, “Statistical Physics,” Science, Moscow, 1976.
- O. Madelung, “The Theory of a Solid Body,” Science, Moscow, 1980.
- J. B. Zeldovich and I. D. Novikov, “The Theory of Gravitation and Evolution of Stars,” Science, Moscow, 1971.

