Journal of Modern Physics
Vol.4 No.2(2013), Article ID:27697,13 pages DOI:10.4236/jmp.2013.42021
Natural Convection of Water-Based Nanofluids in a Square Enclosure with Non-Uniform Heating of the Bottom Wall
1Département de Physique, Faculté des Sciences de Tunis, Campus Universitaire, El-Manar, Tunisia
2Manufacturing Engineering Department, The Public Authority for Applied Education and Training, Shuweikh, Kuwait
Email: *nader_bc@yahoo.com
Received August 27, 2012; revised October 28, 2012; accepted November 21, 2012
Keywords: Natural Convection; Unsteady State; Nanofluids; Solid Volume Fraction; Heat Transfer Enhancement
ABSTRACT
In this paper, a numerical study of natural convection in a square enclosure with non-uniform temperature distribution maintained at the bottom wall and filled with nanofluids is carried out using different types of nanoparticles. The remaining walls of the enclosure are kept at a lower temperature. Calculations are performed for Rayleigh numbers in the range 5 × 103 ≤ Ra ≤ 106 and different solid volume fraction of nanoparticles 0 ≤ χ ≤ 0.2. An enhancement in heat transfer rate is observed with the increase of nanoparticles volume fraction for the whole range of Rayleigh numbers. It is also observed that the heat transfer enhancement strongly depends on the type of nanofluids. For Ra = 106, the pure water flow becomes unsteady. It is observed that the increase of the volume fraction of nanoparticles makes the flow return to steady state.
1. Introduction
Enhancement of heat transfer is an important goal in heat exchanger systems. Many different ways of heat transfer improvement such as placement of fins, use of porous media and others have been utilized. This is due to the fact that typical process or conventional base fluids have low thermal conductivities. An innovative way of heat transfer enhancement is the use of nano-particles of relatively higher thermal conductivities suspended in the base fluids (see Eastman et al. [1]). Keblinski et al. [2] reported on the possible mechanisms of enhancing thermal conductivity, and suggested that the size effect, the clustering of nano-particles and the surface adsorption could be the major reason of enhancement, while the Brownian motion of nanoparticles contributes much less than other factors. Wang and Peng [3] have studied experimentally the effective thermal conductivity of liquids with 25 nm SiO2 particle inclusions and observed the percolation pattern of particle clustering by scanning tunnel microscopic (STM) photos. It was believed that clustering could affect the enhancement prominently. Wang et al. [4] have used a fractal model for predicting the effective thermal conductivity of liquid with suspension of nano-particles and found that it predicts well the trend for variation of the effective thermal conductivity with dilute suspension of nanoparticles. Several other models have been proposed for calculating the effective apparent thermal conductivity of a solid-fluid system Hamilton and Crosser [5], Wasp [6], Maxwell-Garnett [7], Bruggeman [8] and Yu and Choi [9].
Several studies of convective heat transfer in nanofluids have been reported in recent years. Khanafer et al. [10] investigated the problem of buoyancy-driven heat transfer enhancement of nanofluids in a two-dimensional enclosure. Jang and Choi [11] studied free convection in a rectangular cavity (Benard convection) with nanofluids. Jou and Tzeng [12] reported a numerical study of the heat transfer performance of nanofluids inside two-dimensional rectangular enclosures. Their results indicated that increasing the volume fraction of nanoparticles produced a significant enhancement of the average rate of heat transfer. Santra et al. [13] conducted a study of heat transfer augmentation in a differentially heated square cavity using copper-water nanofluid using the models proposed by Maxwell-Garnett [7] and Bruggeman [8]. Their results show that the Bruggemann model [8] predicts higher heat transfer rates than the Maxwell-Garnett model [7]. Hwang et al. [14] have carried out a theoretical investigation of the thermal characteristics of natural convection of an alumina-based nanofluid in a rectangular cavity heated from below using Jang and Choi’s model [15] for predicting the effective thermal conductivity of nanofluids (and various models for predicting the effective viscosity). Wang et al. [16] investigated free convection heat transfer in horizontal and vertical rectangular cavities filled with nanofluids. Santra et al. [17] studied heat transfer characteristics of copper-water nanofluid in a differentially heated square cavity with different viscosity models. Ho et al. [18] reported a numerical simulation of natural convection of nanofluid in a square enclosure considering the effects due to uncertainties of viscosity and thermal conductivity. Oztop and Abu-Nada [19] studied heat transfer and fluid flow due to buoyancy forces in a partially heated enclosure using nanofluids with various types of nanoparticles. They found that the use of nanofluids caused heat transfer enhancement and that this enhancement is more pronounced at a low aspect ratio than at a high one. Aminossadati and Ghasemi [20] studied natural convection cooling of a localized heat source at the bottom of a nanofluid-filled enclosure. Ogut [21] investigated natural convection of water-based nanofluids in an inclined enclosure with a heat source using the expression for calculating the effective thermal conductivity of solid-liquid mixtures proposed by Yu and Choi [9]. Ghasemi and Aminossadati [22] considered periodic natural convection in a nanofluid-filled enclosure with oscillating heat flux.
Non-uniform heating of surfaces in buoyancy-driven flow in a cavity has significant effect of the flow and heat transfer characteristics and finds applications in various areas such as crystal growth in liquids, energy storage, geophysics, solar distillers and others. In a relatively recent study, Sarris et al. [23] reported that the sinusoidal wall temperature variation produced uniform melting of materials such as glass in their detailed study on the effect of sinusoidal top wall temperature variations in a natural convection within a square enclosure where the other walls are insulated. Corcione [24] studied natural convection in an air-filled rectangular enclosure heated from below and cooled from above for a variety of thermal boundary conditions at the side walls. Roy and Basak [25] studied numerically natural convection flows in a square cavity with non-uniformly (sinusoidal) heated wall(s) using the finite element method. The bottom wall and one vertical wall were heated (uniformly and nonuniformly) and the top wall was insulated while the other vertical wall was cooled by means of a constant temperature bath. Sathiyamoorthy et al. [26] investigated steady natural convection flows in a square cavity with linearly heated side wall(s). Natarajan et al. [27] investigated natural convection flows in a trapezoidal enclosure with uniform and non-uniform (sinusoidal) heating of bottom wall. Basak et al. [28] reported an analysis of mixed convection flows within a square cavity with uniform and non-uniform (sinusoidal) heating of bottom wall.
The objective of this work is to study natural convection in a square enclosure filled with a water-based nanofluid (water with Ag, Cu, Al2O3 or TiO2 nanoparticles) with non-uniform (sinusoidal) temperature distribution maintained at the bottom wall. An accurate finite volume scheme along with a multi-grid technique is devised for the purpose of solution of the governing equations.
2. Problem Formulation
Consider laminar natural convection of a water-based nanofluid in a square enclosure of side length L (Figure 1). The enclosure is heated from the bottom wall with a non-uniformly-distributed temperature such that
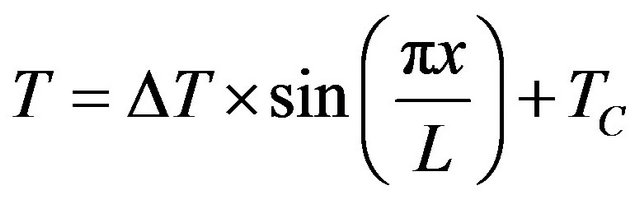 . The remaining walls are cooled at
. The remaining walls are cooled at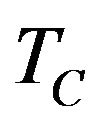 . The nanofluids used in the model development are assumed to be Newtonian and the flow is assumed incompressible. The nanoparticles are assumed to have uniform shape and size. Also, it is assumed that both the fluid phase (water) and nanoparticles (Ag, Cu, Al2O3 and TiO2) are in thermal equilibrium and they flow at the same velocity. The physical properties of the nanofluids are considered to be constant except the density variation in the body force term of the momentum equation which is determined based on the Boussinesq approximation. Under the above assumptions, the system of equations governing the two dimensional motion of a nanofluid in the enclosure can be written in dimensional form as
. The nanofluids used in the model development are assumed to be Newtonian and the flow is assumed incompressible. The nanoparticles are assumed to have uniform shape and size. Also, it is assumed that both the fluid phase (water) and nanoparticles (Ag, Cu, Al2O3 and TiO2) are in thermal equilibrium and they flow at the same velocity. The physical properties of the nanofluids are considered to be constant except the density variation in the body force term of the momentum equation which is determined based on the Boussinesq approximation. Under the above assumptions, the system of equations governing the two dimensional motion of a nanofluid in the enclosure can be written in dimensional form as
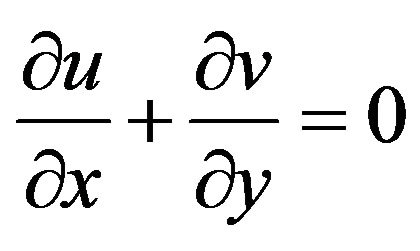 (1)
(1)
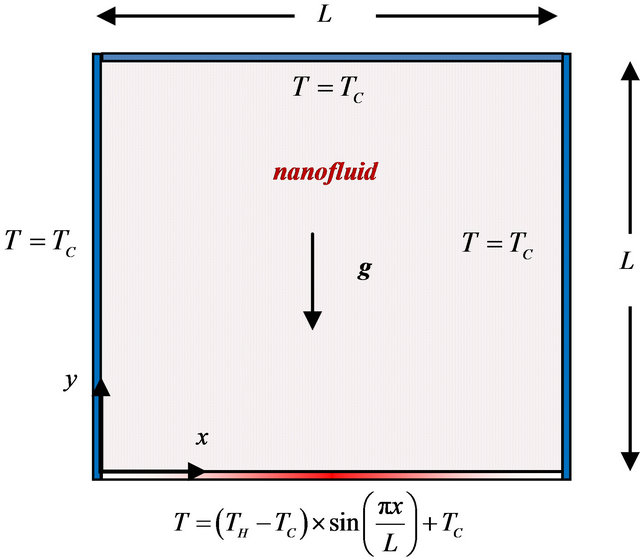
Figure 1. Physical model and coordinates.
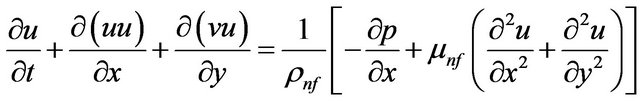 (2)
(2)
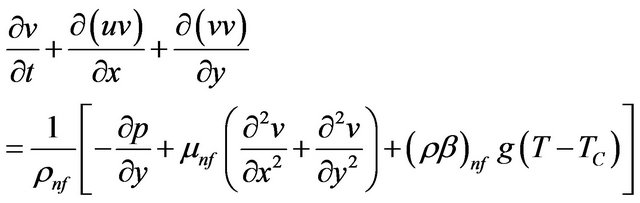 (3)
(3)
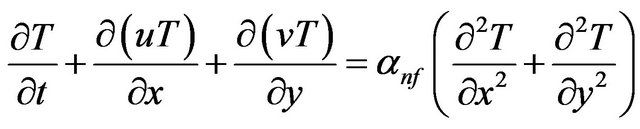 (4)
(4)
Here,  is the effective density of the nanofluid defined as:
is the effective density of the nanofluid defined as:
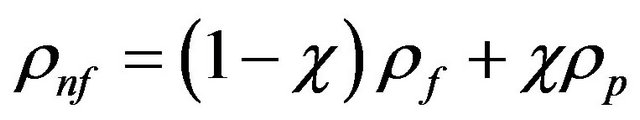 (5)
(5)
According to Brinkman’s formula [29], the effective dynamic viscosity of the nanofluid is expressed as:
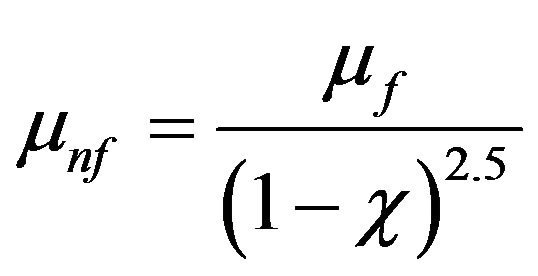 (6)
(6)
The thermal expansion coefficient of the nanofluid can be obtained by:
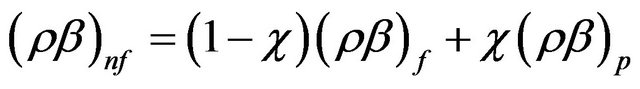 (7)
(7)
The thermal diffusivity of the nanofluid is given by:
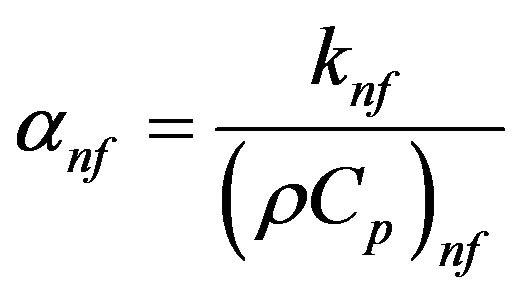 (8)
(8)
where 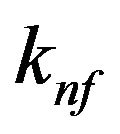 is the thermal conductivity of the nanofluid, which for spherical nanoparticles is given by Maxwell [30]:
is the thermal conductivity of the nanofluid, which for spherical nanoparticles is given by Maxwell [30]:
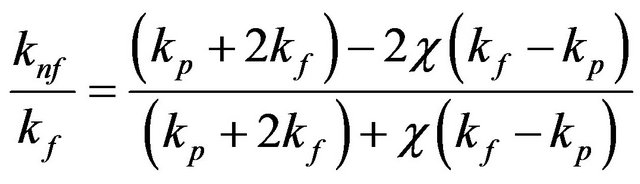 (9)
(9)
and where the heat capacitance of the nanofluid is given by:
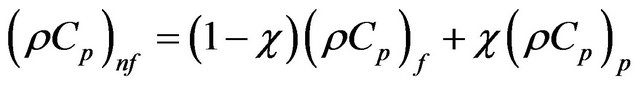 (10)
(10)
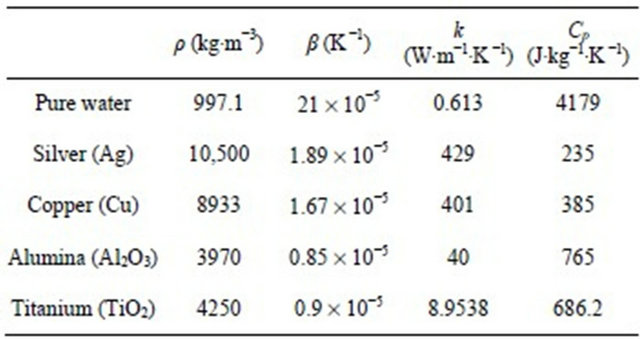
In the previous expressions, subscripts f and p are related to pure fluid and dispersed nanoparticles, respectively. The thermo-physical properties of the base fluid and the considered nanoparticles in this study are given in Table 1 as reported in [20].
In order to obtain non-dimensional equations, the following dimensionless parameters have been introduced:
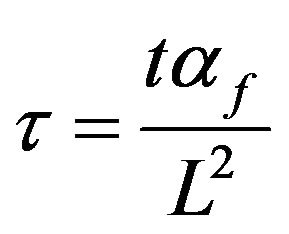 ,
, 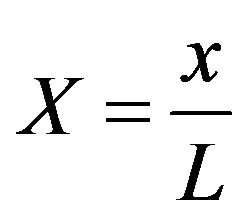 ,
, 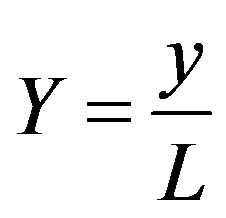 ,
, 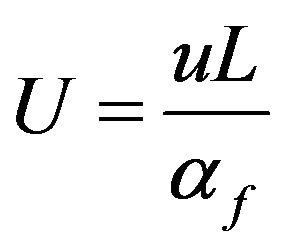 ,
, 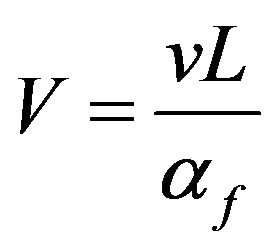 ,
, 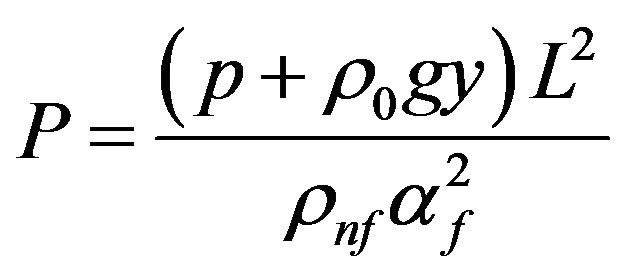 ,
, 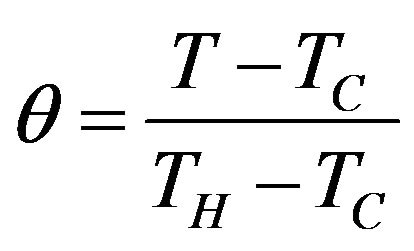
Table 1. Thermo-physical properties of water, silver, copper, alumina and titanium.
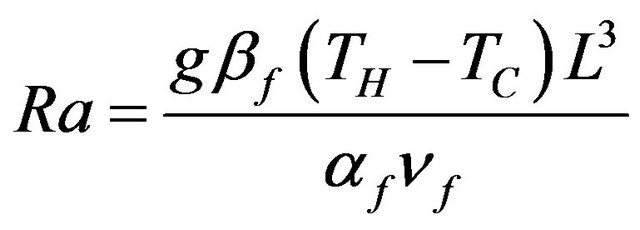 and
and
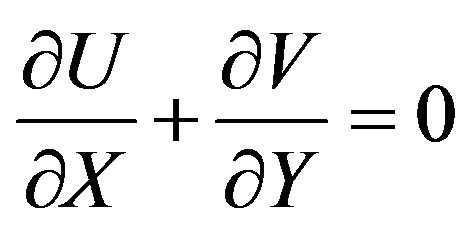 (11)
(11)
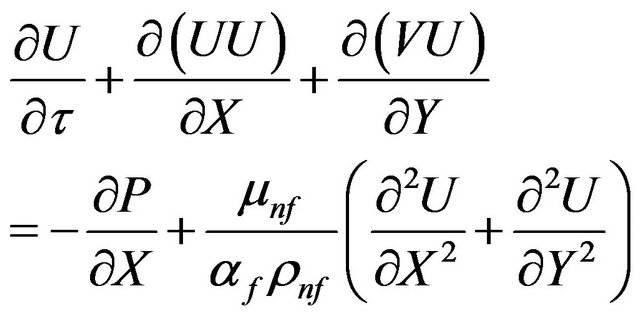 (12)
(12)
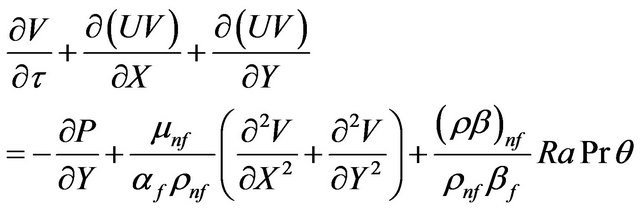 (13)
(13)
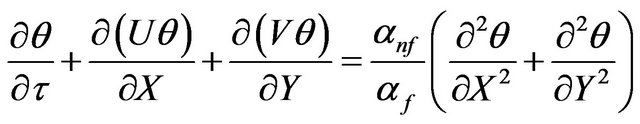 (14)
(14)
The enclosure boundary conditions consist of no-slip and no penetration walls, i.e., U = V = 0 on all four walls. The thermal boundary conditions on the bottom wall is such that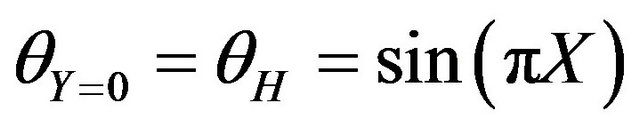 . The left and right vertical walls are at the cold temperature
. The left and right vertical walls are at the cold temperature 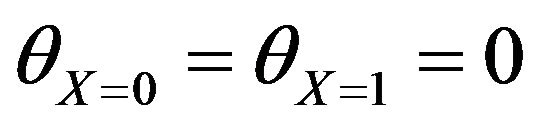 and the bottom wall at
and the bottom wall at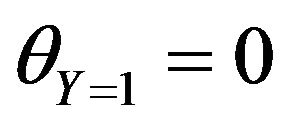 .
.
The local and averaged heat transfer rates at the bottom hot wall of the cavity are presented by means of the local and averaged Nusselt numbers, Nu and Num, which are, respectively, determined as follows:
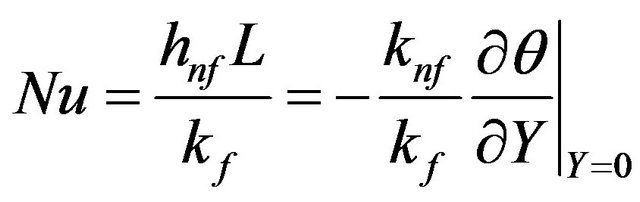 (15a)
(15a)
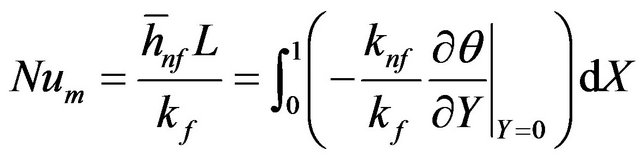 (15b)
(15b)
3. Numerical Method and Validation
The unsteady Navier-Stokes and energy equations are discretized using staggered, non-uniform control volumes. A projection method (Achdou and Guermond [31]) is used to couple the momentum and continuity equations. An intermediate velocity is first computed and later updated to comply with mass continuity. In the intermediate velocity field, the old pressure is used. A Poisson equation, with the divergence of the intermediate velocity field as the source term, is then solved to obtain the pressure correction and afterward the real velocity field.
A finite-volume method (Patankar [32]) is used to discretize the Navier-Stokes and energy equations. The advective terms are discretized using a QUICK third-order scheme proposed by Leonard [33] in the momentum equation and a second order central differencing one in the energy equation. The discretized momentum and energy equations are resolved using the red and black successive over relaxation method RBSOR (Leonard [34]), while the Poisson pressure correction equation is solved using a full multi-grid method as suggested by Ben Cheikh et al. [35]. The numerical method was implemented in a FORTRAN program.
3.1. Code Validation
Our code has been tested for natural convection fluid flows in differentially heated cavities and in RayleighBénard configuration and gave excellent results (see ref. [35,36]. In order to validate the nanofluid version, numerical calculations were carried on an uniform grid containing 80 × 80 nodes and for a test case considered recently by Aminossadati and Ghasemi [20]. It deals with a two-dimensional enclosure filled with nanofluids. A heat source is located on the bottom wall of the enclosure which is thermally insulated. The right and left vertical walls and the horizontal top wall of the enclosure are maintained at a low temperature TC. In order to validate our numerical results, we chose the case Pr = 6.2 (pure water), Ra = 105, χ = 0.1 and three different nanoparticles, i.e., Cu, Ag and Al2O3. Table 2 summarizes our obtained results with those of Aminossadati and Ghasemi [20]. Here, Num and 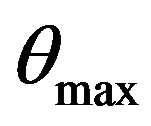 are the averaged Nusselt number through the hot source and the maximum value of temperature on the heated source, respectively. The relative errors in Num and
are the averaged Nusselt number through the hot source and the maximum value of temperature on the heated source, respectively. The relative errors in Num and 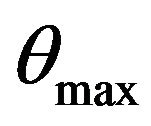 are denoted by
are denoted by 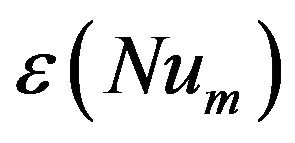 and
and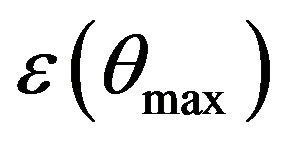 , respectively. Table 2 shows that our results do not exceed 1.0% of relative error, which is a good validation.
, respectively. Table 2 shows that our results do not exceed 1.0% of relative error, which is a good validation.
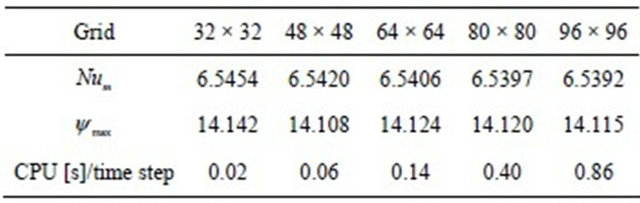
3.2. Grid Independence
In the present grid independence test, the Prandtl number is set to Pr = 6.2 (pure water). The nanoparticles are chosen to be copper (Cu) with a solid volume fraction χ = 0.1 and a Rayleigh number Ra = 105. Numerical computations have been carried on six different grid sizes, i.e., 32 × 32, 48 × 48, 64 × 64, 80 × 80 and 96 × 96 grid sizes. Table 3 regroups the values of the averaged Nusselt number through the hot wall and the maximum value of the stream function 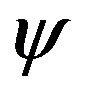 defined by
defined by 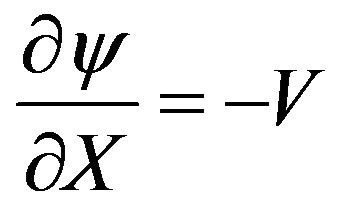 and
and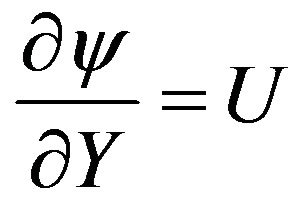 . We also report in Table 3 the CPU per time step for each grid size. Note that calculations were carried on a Pentium Dual-core processor. It is found that the difference between the results obtained for the 80 × 80 and the 96 × 96 grid size is less than 0.008% for the averaged Nusselt number and less than 0.035% for
. We also report in Table 3 the CPU per time step for each grid size. Note that calculations were carried on a Pentium Dual-core processor. It is found that the difference between the results obtained for the 80 × 80 and the 96 × 96 grid size is less than 0.008% for the averaged Nusselt number and less than 0.035% for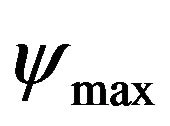 . In order to minimize the time cost of calculations, the 80 × 80 grid size was thus chosen for all of the following simulations.
. In order to minimize the time cost of calculations, the 80 × 80 grid size was thus chosen for all of the following simulations.
4. Results and Discussion
In this section, the nanofluid-filled enclosure is studied for a range of solid volume fraction 0% ≤ χ ≤ 20% and
Table 2. Comparison of our results with those of Aminossadati and Ghasemi [20].
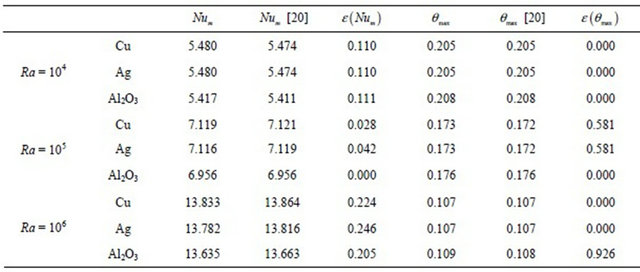
Table 3. Grid independency results for water-copper, Ra = 105 and χ = 0.1.
the Rayleigh number varies from 5 × 103 to 5 × 105. Four kinds of nanoparticles are envisaged, i.e., silver (Ag), copper (Cu), alumina (Al2O3) and titanium (TiO2). For all simulations the considered base fluid is water (Pr = 6.2). The dimensionless time step varies from ∆τ = 2 × 10−3 for Ra = 5 × 103 to ∆τ = 10−5 for Ra = 5 × 105. The steady state is considered as achieved according to the following criterion:
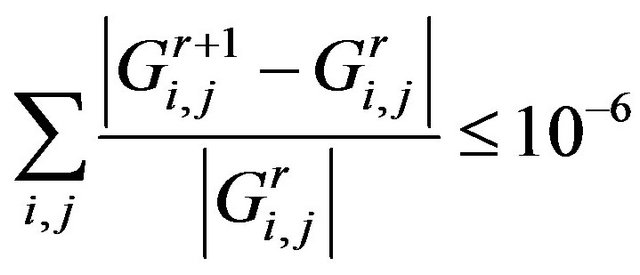 . (22)
. (22)
Here, G represents the variable U, V or θ, the superscript r refers to the iteration number and (i, j) refer to the space coordinates. Note that this criterion was only applied for Ra ≤ 5 × 105. At Ra = 106 where unsteady flow did not develop, the maximum dimensionless time to which the solution was continued was increased by up to 100% to ensure that unsteady flow did not in fact occur at larger dimensionless times. Note that this method is inspired from the one used by Oosthuizen and Paul [37]. For the smallest value of Ra, simulations started with a zero field as initial guess. Then, by increasing the Rayleigh number, the previous Rayleigh number is taken as the initial guess and so on.
4.1. Effect of Solid Volume Fraction
In this section, we consider the case where the cavity is filled with water and alumina particles. The solid volume fraction varies from 0% to 20%. It should be noted that tests were conducted for Ra = 106 and the flow then passes to an unsteady state with the appearance of several bifurcations. The results for Ra = 106 will be the subject of the next section.
In Figure 2, we present the streamlines (top) and isotherms (bottom) for 5 × 103 ≤ Ra ≤ 5 × 105, for the case of a water-Al2O3 nanofluid (- - - -) and pure water (——). The value of solid volume fraction is set to χ = 0.05. Figure 3 represents the same physical quantities but for a volume fraction value of χ = 0.2. Due to the temperature distribution imposed at the bottom wall and to the boundary conditions on vertical walls, we observe a symmetry behavior in both the streamlines and in the contour maps of the isotherms. We can see that whatever the Rayleigh number and value of solid volume fraction, the flow is mainly composed of two counter-rotating circulating cells. The maximum values of stream function 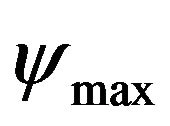 are reported in Table 4 according to the different cases. From Table 4, one can see that an increase in solid volume fraction generates a decrease in the values of
are reported in Table 4 according to the different cases. From Table 4, one can see that an increase in solid volume fraction generates a decrease in the values of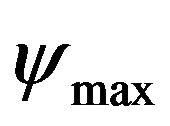 . The fluid is, therefore, moves slower in the enclosure in the presence of nanoparticles. Note that this phenomenon is not observed for Ra = 5 × 105 and the cases χ = 0.05 and χ = 0.1 for which the maximal intensities of the rotating cells increases by comparison to the case χ = 0. That means that for these combinations, the buoyancy force is greater than the inertia force due to the presence of nanoparticles.
. The fluid is, therefore, moves slower in the enclosure in the presence of nanoparticles. Note that this phenomenon is not observed for Ra = 5 × 105 and the cases χ = 0.05 and χ = 0.1 for which the maximal intensities of the rotating cells increases by comparison to the case χ = 0. That means that for these combinations, the buoyancy force is greater than the inertia force due to the presence of nanoparticles.
Figure 4 presents the vertical velocity profiles 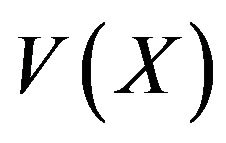 along the mid-section of the enclosure Y = 0.5 for different values of χ and is in good concordance with the fact that the nanofluid moves slower than a pure water. It is also observed that the reduction of velocity of the nanofluid is more accentuated for small values of Rayleigh number. Indeed, for Ra = 5 × 103, the deviation (relative to χ = 0) between the maximum values of velocity is
along the mid-section of the enclosure Y = 0.5 for different values of χ and is in good concordance with the fact that the nanofluid moves slower than a pure water. It is also observed that the reduction of velocity of the nanofluid is more accentuated for small values of Rayleigh number. Indeed, for Ra = 5 × 103, the deviation (relative to χ = 0) between the maximum values of velocity is 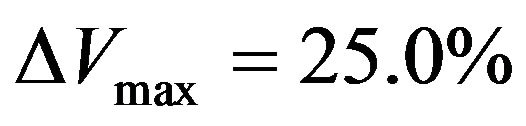 for
for 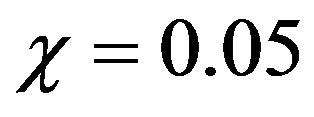 and
and 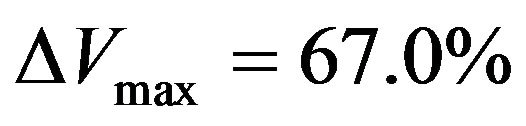 for χ = 0.2. By increasing the Rayleigh number, these deviations decrease. For Ra = 5 × 104 and Ra = 5 × 105 these deviations are
for χ = 0.2. By increasing the Rayleigh number, these deviations decrease. For Ra = 5 × 104 and Ra = 5 × 105 these deviations are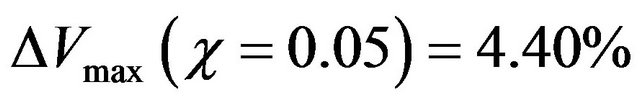 ,
, 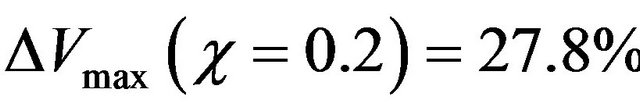 ,
, 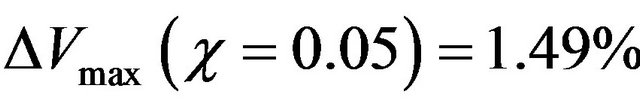 and
and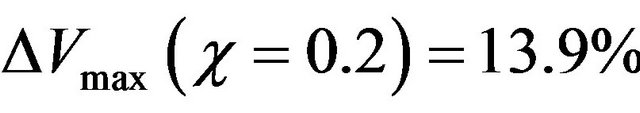 , respectively. As far as the temperature distribution is concerned, clear differences are observed in the isotherm contour plots compared to the case χ = 0. These differences are accentuated as the solid volume fraction increases. These differences mean that the presence of nanoparticles affect especially the heat transfer rate through the enclosure.
, respectively. As far as the temperature distribution is concerned, clear differences are observed in the isotherm contour plots compared to the case χ = 0. These differences are accentuated as the solid volume fraction increases. These differences mean that the presence of nanoparticles affect especially the heat transfer rate through the enclosure.
The heat transfer distribution through the hot wall is displayed in Figure 5 through the plotted lines of the local Nusselt number for different values of Ra. One can see that for all combinations of Ra and χ, the local Nusselt number behavior is symmetric with respect to the plane X = 0.5. For low Rayleigh numbers, (Ra = 5 × 103) and χ = 0, the transfer of heat through the hot wall is relatively low with a slight curvature at X = 0.5. This curvature is due to relatively higher intensity of the counterrotating cells represented by the highest value of 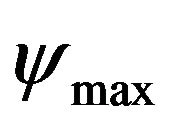 when χ = 0. When χ increases to χ = 0.2, the curvature at
when χ = 0. When χ increases to χ = 0.2, the curvature at
Table 4. Maximum values of stream function at different Rayleigh numbers and solid volume fractions for watercopper nanofluid.

Ra = 5 × 103 Ra = 5 × 104 Ra = 5 × 105

Figure 2. Streamlines (top) and isotherms (bottom) for the enclosure filled with water-alumina nanofluid, χ = 0.05 (- - - -) and pure water (——) at different Rayleigh numbers.
Ra = 5 × 103 Ra = 5 × 104 Ra = 5 × 105
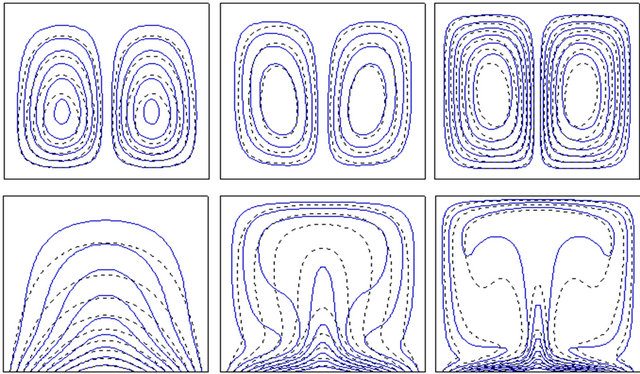
Figure 3. Streamlines (top) and isotherms (bottom) for the enclosure filled with water-alumina nanofluid, χ = 0.2 (- - - -) and pure water (——) at different Rayleigh numbers.
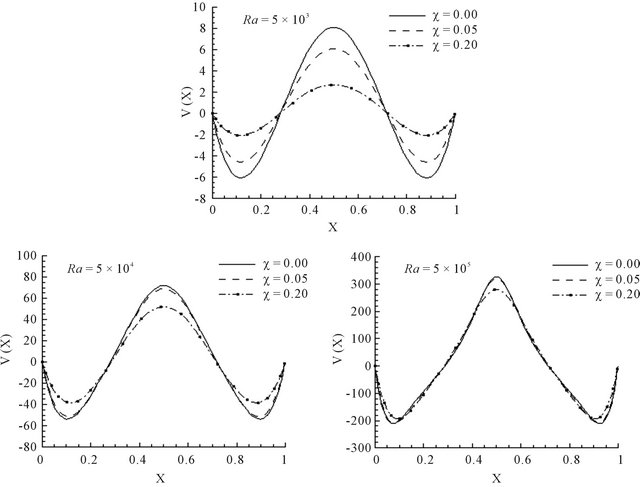
Figure 4. Vertical velocity profiles along the mid-plane for different Ra and solid volume fractions (Water-Al2O3).
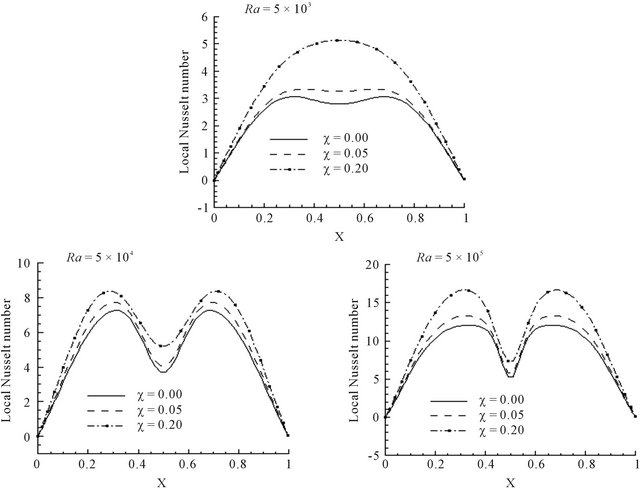
Figure 5. Local Nusselt number through the heated wall for different Ra and solid volume fractions (Water-Al2O3).
the center disappears because the fluid velocity decreases. The heat transfer in this case is maximum at X = 0.5 and is higher due to the presence of nanoparticles whose thermal conductivity is much greater than that of water. The same phenomena are observed almost on the curves related to Ra = 5 × 104 and Ra = 5 × 105 with a maximum heat transfer in the vicinity of X = 0.25 and X = 0.75. For example, for Ra = 5 × 104, the maximum Nusselt number value is Numax = 7.266 and is situated at both locations X = 0.314 and X = 0.686 for χ = 0. For χ = 0.2, Numax = 8.370 and is located at X = 0.295 and X = 0.705.
4.2. Effect of Type of Nanoparticle
In this part of the study, the solid volume fraction is fixed at 0.1 and three other solid nanoparticles, copper (Cu), silver (Ag), and titanium (TiO2) are studied. The physical properties of these metals are listed in Table 1.
In Figure 6, the profiles of velocity component 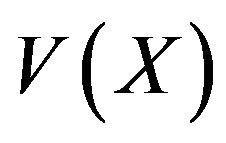 at Y = 0.5 for Ra = 5 × 104 are reported for Cu, Ag, TiO2 and Al2O3. It is observed that with nanoparticles of silver or copper, the velocity of fluid particles is higher than with nanoparticles of alumina or titanium. This fact should result in a heat transfer rate higher with nanoparticles of silver or copper than with nanoparticles of Al2O3 or TiO2. Indeed, as shown in Figure 7, the values of the averaged Nusselt number through the hot wall are higher when the nanofluid used is based on Ag or Cu nanoparticles. Figure 7 also shows that the averaged Nusselt number over the hot wall can be correlated by equations of the form:
at Y = 0.5 for Ra = 5 × 104 are reported for Cu, Ag, TiO2 and Al2O3. It is observed that with nanoparticles of silver or copper, the velocity of fluid particles is higher than with nanoparticles of alumina or titanium. This fact should result in a heat transfer rate higher with nanoparticles of silver or copper than with nanoparticles of Al2O3 or TiO2. Indeed, as shown in Figure 7, the values of the averaged Nusselt number through the hot wall are higher when the nanofluid used is based on Ag or Cu nanoparticles. Figure 7 also shows that the averaged Nusselt number over the hot wall can be correlated by equations of the form:
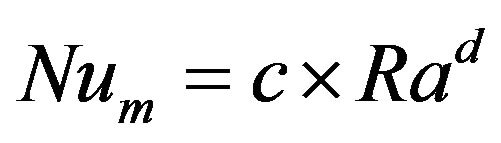 . (24)
. (24)
where the values of constant coefficients c and d corresponding to the different types of nanofluid are given in
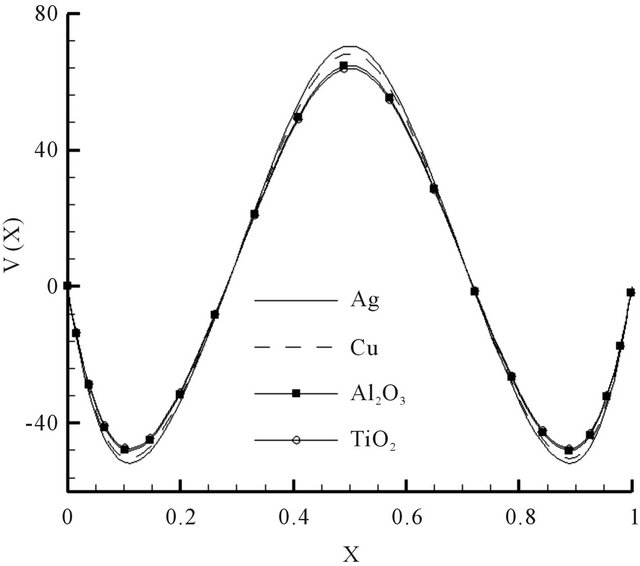
Figure 6. Vertical velocity profiles along the mid-plane for different nanofluids at Ra = 5 × 104 and χ = 0.1.
Table 5. Incidentally, the values of coefficients c and d were obtained using the same method as mentioned in the preceding paragraph for determining coefficients a and b.
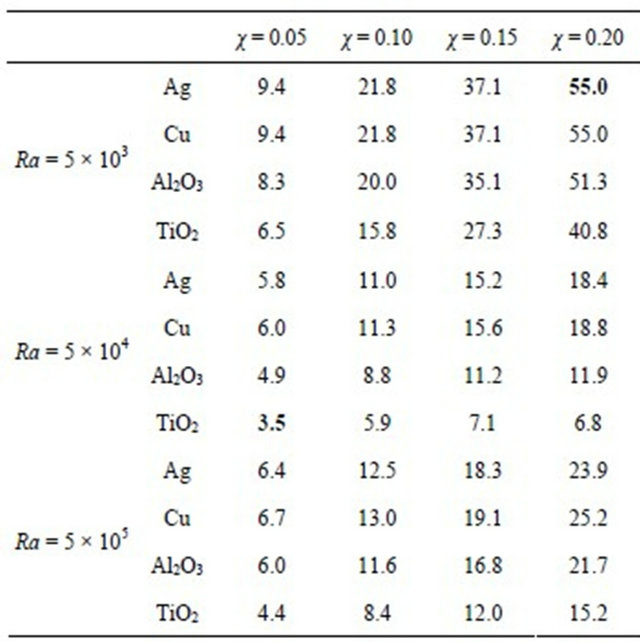
Finally, we conclude this study by presenting some benchmark results according to the mean Nusselt number reported in Table 6 and the percentage of heat transfer rate increase for different nanofluids with respect to pure water at different Rayleigh numbers and solid volume fractions in Table 7. It is noted that for 5 × 103 ≤ Ra ≤ 5 × 105, the maximum percentage increase in heat transfer rate is obtained for the combination (Ra = 5 × 103; χ = 0.2; water-Ag) with a gain of 55% and minimum for the combination (Ra = 5 × 104; χ = 0.05; water-TiO2) with a gain of 3.5%. Note that, the highest values of percentage increase in heat transfer are observed for low values of Rayleigh numbers and high values of solid volume fractions. This is due to the fact that for low Ra, the mechanism of heat transfer is mainly governed by conduction. However, good gains in heat transfer rate can also be obtained for higher Rayleigh number through the use of Nanofluids with appropriate percentage of solid volume fraction of nanoparticles.
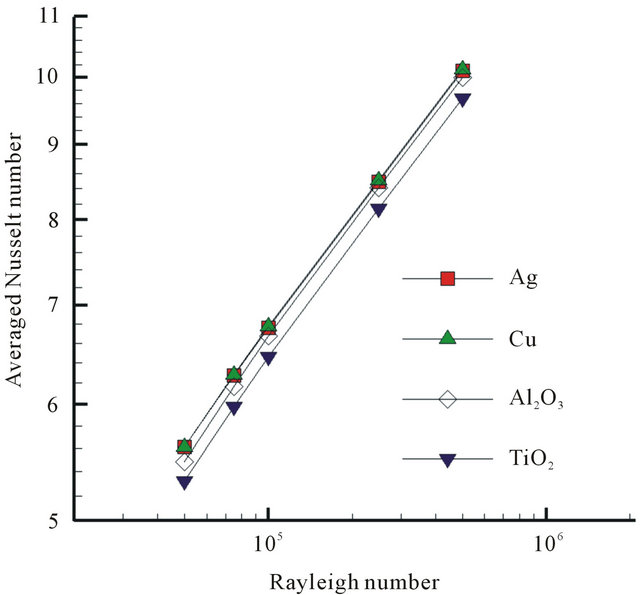
Figure 7. Averaged Nusselt number through the heated wall for different nanofluids at Ra = 5 × 104 and χ = 0.1.
Table 5. Values of coefficients c and d in the correlation Equation (24) according to different kinds of nanofluids.
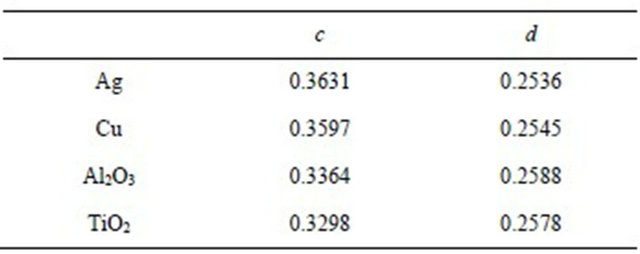
Table 6. Numerical values of mean Nusselt number through the heated wall.
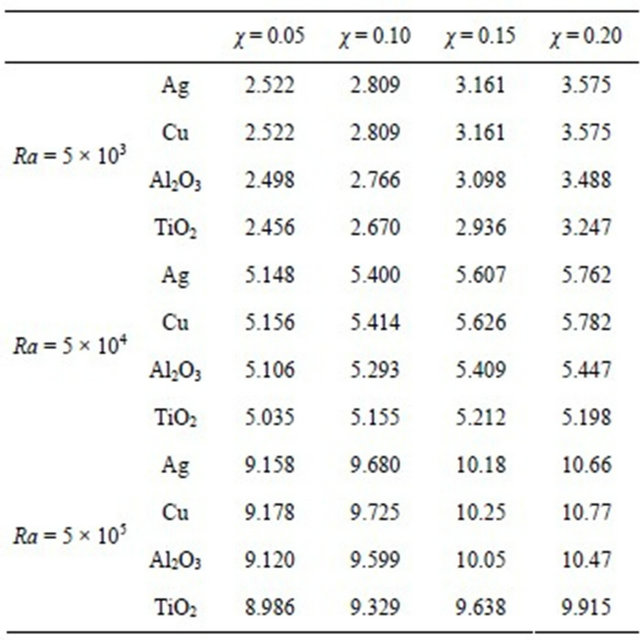
Table 7. Percentage of heat transfer rate increase for different nanofluids with respect to pure water at different Rayleigh numbers and solid volume fractions.
4.3. Results for Ra = 106
In this section, the Rayleigh number is fixed to Ra = 106 and three different fluids (pure water, water-Cu and water-TiO2) are considered. Figure 8 shows the average Nusselt number evolution related to pure water versus the dimensionless time. It is seen that for 0.1 ≤ t ≤ 0.4, the flow seems to be steady. For 0.6 ≤ t ≤ 1.4, a first bifurcation is observed. Indeed, the flow becomes unsteady with one single frequency. For t ≥ 1.5, a new bifurcation is observed and the flow becomes periodic and two frequencies may be observed. In order to ensure that a third bifurcation does not occur, a long time of integration up to ttot = 5 was used. After that, simulations were carried on for water-Cu and water-TiO2 with volume fractions in the range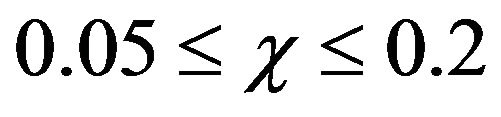 . The results are regrouped in Figure 9" target="_self"> Figure 9 by means of the average Nusselt number versus time. The four figures on the top are related to water-Cu and the bottom ones to water-TiO2. As a first observation, one can see that by increasing the value of the volume fraction, the flow becomes steady. Indeed, for the case water-Cu, the flow is unsteady for χ = 0.05 and χ = 0.1 but steady for χ ≥ 0.15. The same behaviors are seen for water-TiO2 combination. Here, the steadiness appears for χ ≥ 0.1. The average Nusselt number in time and space are reported in Table 8 for different volume fractions χ and both nano-fluids (water-Cu and water-TiO2).
. The results are regrouped in Figure 9" target="_self"> Figure 9 by means of the average Nusselt number versus time. The four figures on the top are related to water-Cu and the bottom ones to water-TiO2. As a first observation, one can see that by increasing the value of the volume fraction, the flow becomes steady. Indeed, for the case water-Cu, the flow is unsteady for χ = 0.05 and χ = 0.1 but steady for χ ≥ 0.15. The same behaviors are seen for water-TiO2 combination. Here, the steadiness appears for χ ≥ 0.1. The average Nusselt number in time and space are reported in Table 8 for different volume fractions χ and both nano-fluids (water-Cu and water-TiO2).
We would finally point out that the presented results in this section should be considered only qualitatively because we believe that when the flow becomes unsteady, three-dimensional effects cannot be neglected anymore and can affect quantitatively the global flow structures and hence, the values of the Nusselt number. However, the fact that the increase of volume fraction at a fixed Rayleigh number may change the flow from unsteady to steady state will probably remain the same in 3D simulations. Our next work is the extension to a three-dimensional study on the topic and comparisons between the 2D and 3D results.
5. Conclusions
This study focused on numerical modelling of natural convection in a square enclosure with non-uniform temperature distribution maintained at the bottom wall and filled with nanofluids using different types of nanoparticles. The remaining walls of the enclosure were kept at lower and equal temperatures. The finite volume method along with a multi-grid technique was used numerically investigate the effect of using different nanofluids on the flow structure and heat transfer rate in the enclosure. For 5 × 103 ≤ Ra ≤ 5 × 105 and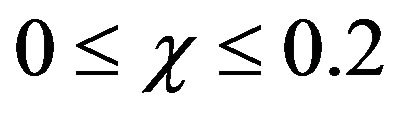 , the flow structure was characterized by two counter-rotating circulating cells for all type of nanofluids. For relatively moderate Rayleigh numbers, the intensity of these cells decreased with the increase of solid volume fraction. By increasing the value of Rayleigh number and keeping
, the flow structure was characterized by two counter-rotating circulating cells for all type of nanofluids. For relatively moderate Rayleigh numbers, the intensity of these cells decreased with the increase of solid volume fraction. By increasing the value of Rayleigh number and keeping
Table 8. Time averaged Nusselt number for different values of volume fractions and kinds of nanofluids for Ra = 106.
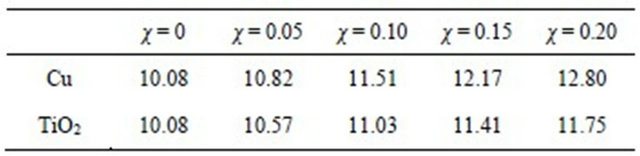
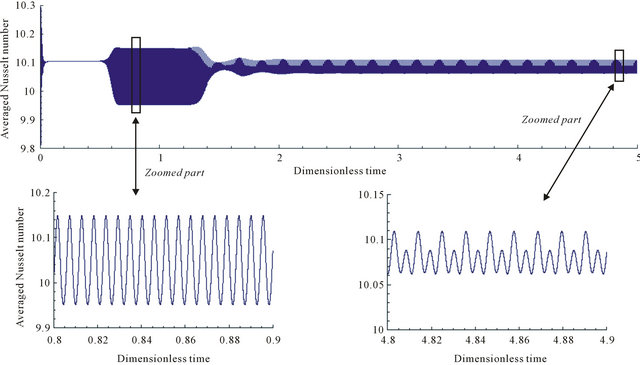
Figure 8. Time evolution of space averaged Nusselt number through the heated wall for pure water at Ra = 106.
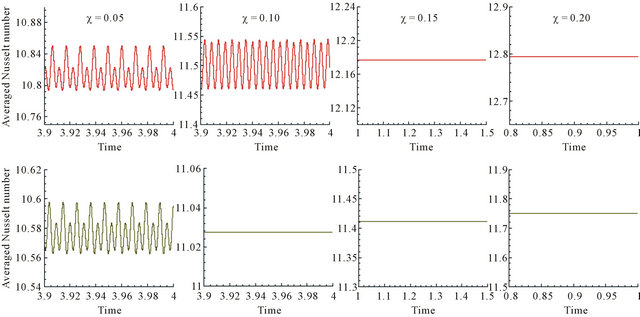
Figure 9. Localized time evolution of Nusselt number through the heated wall for Water-Cu (top) and Water-TiO2 (bottom) at Ra = 106.
other parameters fixed, the heat transfer was enhanced. Comparing the values of averaged Nusselt number obtained with pure water with other nanofluids, it was seen that for low Rayleigh numbers and high solid volume fractions, enhancements up to 55% could be reached. This percentage strongly depended on the type of nanofluids. Indeed, the highest heat transfer enhancements were obtained when using copper or silver nanoparticles. The lowest values of percentage increase in heat transfer were obtained with TiO2 nanoparticles but were not negligible as far. It reached 40.8% at high values of solid volume fractions and low Ra. For a higher Rayleigh number, i.e., Ra = 106, the pure water flow becomes unsteady. Several bifurcations were observed when changing the solid volume fractions values or the kind of the nanofluid used. Also, the increase of the volume fraction of nanoparticles made the flow return to steady state. This could be a good way to delay the transition to unsteadiness if needed. In the near future, this study will be extended for higher Rayleigh numbers, 3D studies and other types of base fluids and nanoparticles.
REFERENCES
- J. A. Eastman, U. S. Choi, S. Li, L. J. Thompson and S. Lee, “Enhanced Thermal Conductivity through the Development of Nanofluids,” In: S. Komarneni, J. C. Parker and H. J. Wollenberger, Eds., Nanophase and Nanocomposite Materials II. MRS, Materials Research Society, Pittsburg, 1997, pp. 3-11. doi:10.1016/S0017-9310(01)00175-2
- P. Keblinski, S. R. Phillpot, S. U.-S. Choi and J. A. Eastman, Mechanisms of Heat Flow in Suspensions of NanoSized Particles (Nanofluids),” International Journal of Heat Mass Transfer, Vol. 45, No. 4, 2002, pp. 855-863.
- B. X. Wang, H. Li and X. F. Peng, “Research on the Heat Conduction Enhancement for Liquid with Nanoparticles Suspensions, General Paper (G-1),” International Symposium on Thermal Science Engineering (TSE 2002), Beijing, 23-26 October 2002, pp. 23-26.
- B. X. Wang, L. P. Zhou and X. F. Peng, “A Fractal Model for Predicting the Effective Thermal Conductivity of Liquid with Suspension of Nanoparticles,” International Journal of Heat Mass Transfer, Vol. 46, No. 14, 2003, pp. 2665-2672. doi:10.1016/S0017-9310(03)00016-4
- R. L. Hamilton and O. K. Crosser, “Thermal Conductivity of Heterogeneous Two Component Systems,” Industrial & Engineering Chemistry Fundamentals, Vol. 1, No. 3, 1962, pp. 182-191.
- F. J. Wasp, “Solid-Liquid Flow Slurry Pipeline Transportation,” Translated Technical Publications, Berlin, 1977.
- J. C. Maxwell-Garnett, “Colours in Metal Glasses and in Metallic Films,” Philosophical Transactions the Royal Society A, Vol. 203, No. 359-371, 1904, pp. 385-420. doi:10.1098/rsta.1904.0024
- D. A. G. Bruggeman, “Berechnung Verschiedener Physikalischer Konstanten von Heterogenen Substanzen, I. Dielektrizitatskonstanten und Leitfahigkeiten der Mischkorper aus Isotropen Substanzen,” Annalen der Physik, Vol. 416, No. 7, 1935, pp. 636-679. doi:10.1002/andp.19354160705
- W. Yu and S. U. S. Choi, “The Role of Interfacial Layers in the Enhanced Thermal Conductivity of Nanofluids: A Renovated Maxwell Model,” Journal of Nanoparticle Research, Vol. 5, No. 1-2, 2003, pp. 167-171. doi:10.1023/A:1024438603801
- K. Khanafer, K. Vafai and M. Lightstone, “Buoyancy Driven Heat Transfer Enhancement in a Two-Dimensional Enclosure Utilizing Nanofluids,” International Journal of Heat Mass Transfer, Vol. 46, No. 19, 2003, pp. 3639-3653. doi:10.1016/S0017-9310(03)00156-X
- S. P. Jang and S. U. S. Choi, “Free Convection in a Rectangular Cavity (Benard Convection) with Nanofluids,” Proceedings of the IMECE, Anaheim, 13-19 November 2004, pp. 147-153.
- R. Y. Jou and S. C. Tzeng, “Numerical Research of Nature Convective Heat Transfer Enhancement Filled with Nanofluids in Rectangular Enclosures,” International Communications in Heat and Mass Transfer, Vol. 33, No. 6, 2006, pp. 727-736. doi:10.1016/j.icheatmasstransfer.2006.02.016
- A. K. Santra, S. Sen and N. Chakraborty, “Study of Heat Transfer Augmentation in a Differentially Heated Square Cavity Using Copper-Water Nanofluid,” International Journal of Thermal Sciences, Vol. 47, No. 9, 2008, pp. 1113-1122. doi:10.1016/j.ijthermalsci.2007.10.005
- K. S. Hwang, J. H. Lee and S. P. Jang, “Buoyancy-Driven Heat Transfer of Water-Based Al2O3 Nanofluids in a Rectangular Cavity,” International Journal of Heat and Mass Transfer, Vol. 50, No. 19-20, 2007, pp. 4003-4010. doi:10.1016/j.ijheatmasstransfer.2007.01.037
- S. P. Jang and S. U. S. Choi, “The Role of Brownian Motion in the Enhanced Thermal Conductivity of Nanofluids,” Applied Physics Letters, Vol. 84, No. 21, 2004, pp. 4316-4318. doi:10.1063/1.1756684
- X.-Q. Wang, A. S. Mujumdar and C. Yap, “Free Convection Heat Transfer in Horizontal and Vertical Rectangular Cavities Filled with Nanofluids,” International Heat Transfer Conference IHTC-13, Sydney, 13-18 August 2006, 12 p.
- A. K. Santra, S. Sen and N. Chakraborty, “Study of Heat Transfer Characteristics of Copper-Water Nanofluid in a Differentially Heated Square Cavity with Different Viscosity Models,” Journal of Enhanced Heat Transfer, Vol. 15, No. 4, 2008, pp. 273-287. doi:10.1615/JEnhHeatTransf.v15.i4.10
- C. J. Ho, M. W. Chen and Z. W. Li, “Numerical Simulation of Natural Convection of Nanofluid in a Square Enclosure: Effects Due to Uncertainties of Viscosity and Thermal Conductivity,” International Journal of Heat Mass Transfer, Vol. 51, No. 17-18, 2008, pp. 4506-4516. doi:10.1016/j.ijheatmasstransfer.2007.12.019
- H. F. Oztop and E. Abu-Nada, “Numerical Study of Natural Convection in Partially Heated Rectangular Enclosures Filled with Nanofluids,” International Journal of Heat and Fluid Flow, Vol. 29, No. 5, 2008, pp. 1326- 1336. doi:10.1016/j.ijheatfluidflow.2008.04.009
- S. M. Aminossadati and B. Ghasemi, “Natural Convection Cooling of a Localised Heat Source at the Bottom of a Nanofluid-Filled Enclosure,” European Journal of Mechanics B/Fluids, Vol. 28, No. 5, 2009, pp. 630-640. doi:10.1016/j.euromechflu.2009.05.006
- E. B. Ogut, “Natural Convection of Water-Based NanoFluids in an Inclined Enclosure with a Heat Source,” International Journal of Thermal Sciences, Vol. 48, No. 11, 2009, pp. 2063-2073. doi:10.1016/j.ijthermalsci.2009.03.014
- B. Ghasemi and S. M. Aminossadati, “Periodic Natural Convection in a Nanofluid-Filled Enclosure with Oscillating Heat Flux,” International Journal of Thermal Sciences, Vol. 49, No. 1, 2010, pp. 1-9. doi:10.1016/j.ijthermalsci.2009.07.020
- I. E. Sarris, I. Lekakis and N. S. Vlachos, “Natural Convection in a 2D Enclosure with Sinusoidal Upper Wall Temperature,” Numerical Heat Transfer, Part A, Vol. 42, No. 5, 2002, pp. 513-530. doi:10.1080/10407780290059675
- M. Corcione, “Effects of the Thermal Boundary Conditions at the Sidewalls upon Natural Convection in Rectangular Enclosures Heated from Below and Cooled from Above,” International Journal of Heat Mass Transfer, Vol. 42, No. 2, 2003, pp. 199-208.
- S. Roy and T. Basak, “Finite Element Analysis of Natural Convection Flows in a Square Cavity with Non-Uniformly Heated Wall(s),” International Journal of Engineering Science, Vol. 43, No. 8-9, 2005, pp. 668-680. doi:10.1016/j.ijengsci.2005.01.002
- M. Sathiyamoorthy, T. Basak, S. Roy and I. Pop, “Steady Natural Convection Flows in a Square Cavity with Linearly Heated Side Wall(s),” International Journal of Heat Mass Transfer, Vol. 50, No. 3-4, 2007, pp. 766-775. doi:10.1016/j.ijheatmasstransfer.2006.06.019
- E. Natarajan, T. Basak and S. Roy, “Natural Convection Flows in a Trapezoidal Enclosure with Uniform and Non-Uniform Heating of Bottom Wall,” International Journal of Heat Mass Transfer, Vol. 51, No. 3-4, 2008, pp. 747-756. doi:10.1016/j.ijheatmasstransfer.2007.04.027
- T. Basak, S. Roy, P. K. Sharma and I. Pop, “Analysis of Mixed Convection Flows within a Square Cavity with Uniform and Non-Uniform Heating of Bottom Wall,” International Journal of Thermal Sciences, Vol. 48, No. 5, 2009, pp. 891-912. doi:10.1016/j.ijthermalsci.2008.08.003
- H. C. Brinkman, “The Viscosity of Concentrated Suspensions and Solution,” Journal of Chemical Physics, Vol. 20, No. 4, 1952, pp. 571-581. doi:10.1063/1.1700493
- J. Maxwell, “A Treatise on Electricity and Magnetism,” 2nd Edition, Oxford University Press, Cambridge, 1904.
- Y. Achdou and J. L. Guermond, “Convergence Analysis of a Finite Element Projection Lagrange-Galerkin Method for the Incompressible Navier-Stokes Equations,” SIAM Journal on Numerical Analysis, Vol. 37, No. 3, 2000, pp. 799-826. doi:10.1137/S0036142996313580
- S. V. Patankar, “Numerical Heat Transfer and Fluid Flow,” McGraw-Hill, New York, 1980.
- B. P. Leonard, “A Stable and Accurate Convective Modelling Procedure Based on Quadratic Upstream Interpolation,” Computer Methods in Applied Mechanics and Engineering, Vol. 19, No. 1, 1979, pp. 59-98. doi:10.1016/0045-7825(79)90034-3
- B. P. Leonard, “Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods,” SIAM: Society for Industrial and Applied Mathematics, Philadelphia, 1994.
- N. B. Cheikh, B. B. Beya and T. Lili, “Benchmark Solution for Time-Dependent Natural Convection Flows with an Accelerated Full-Multigrid Method,” Numerical Heat Transfer. Part B Fundamentals, Vol. 52, No. 2, 2007, pp. 131-151.
- N. Ouertatani, N. B. Cheikh, B. B. Beya and T. Lili, “Numerical Simulation of Two-Dimensional Rayleigh-Bénard Convection in an Enclosure,” Comptes Rendus Mécanique, Vol. 336, No. 5, 2008, pp. 464-470. doi:10.1016/j.crme.2008.02.004
- P. H. Oosthuizen and J. T. Paul, “Natural Convection in a Rectangular Enclosure with Two Heated Sections on the Lower Surface,” International Journal of Heat and Fluid Flow, Vol. 26, No. 4, 2005, pp. 587-596.
Nomenclature
Cp specific heat, J∙kg−1∙K−1
g gravitational acceleration, m∙s−2
k thermal conductivity, W∙m−1∙K−1
L enclosure length, m Nu local Nusselt number Num average Nusselt number p pressure, Pa P dimensionless pressure Pr prandtl number, 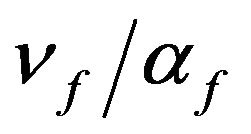
Ra Rayleigh number, 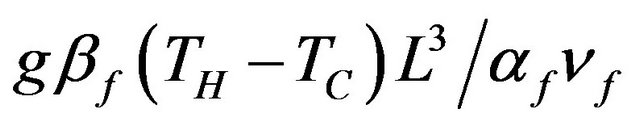
T temperature, K TC temperature of cold wall, K u, v velocity components in x, y directions, m∙s−1
U, V dimensionless velocity components x, y Cartesian coordinates, m X, Y dimensionless coordinates
Greek Symbols
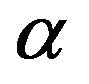 thermal diffusivity, m2∙s−1
thermal diffusivity, m2∙s−1
 volumetric thermal expansion coefficient, K−1
volumetric thermal expansion coefficient, K−1
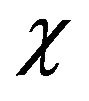 solid volume fraction
solid volume fraction
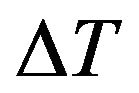 difference temperature,
difference temperature, 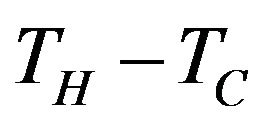
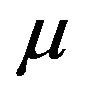 dynamic viscosity, N∙s∙m−2
dynamic viscosity, N∙s∙m−2
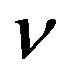 kinematic viscosity, m2∙s−1
kinematic viscosity, m2∙s−1
 non-dimensional temperature,
non-dimensional temperature, 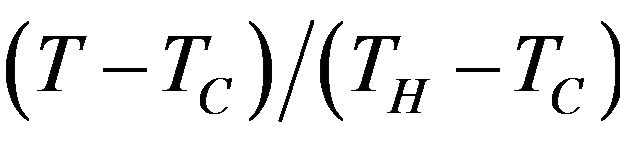
 density, kg∙m−3
density, kg∙m−3
Subscripts
C cold f pure fluid H hot nf nanofluid p nanoparticle
NOTES
*Corresponding author.

