Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23041,6 pages DOI:10.4236/jmp.2012.329144
Astrophysical Constraints on the Scale of Left-Right Symmetry in Inverse Seesaw Models
Department of Physics, Tezpur University, Tezpur, India
Email: dborah@tezu.ernet.in
Received July 1, 2012; revised August 9, 2012; accepted August 17, 2012
Keywords: PACS Numbers; 12.10.-g; 12.60.Jv; 11.27.+d
ABSTRACT
We revisit the recently studied supersymmetric gauged inverse seesaw model [1] to incorporate astrophysical constraints on lightest supersymmetric particle (LSP) lifetime such that LSP constitutes the dark matter of the Universe. The authors in [1] considered light sneutrino LSP that can play the role of inelastic dark matter (iDM) such that desired iDM mass splitting and tiny Majorana masses of neutrinos can have a common origin. Here we consider a generalized version of this model without any additional discrete symmetry. We point out that due to spontaneous R-parity 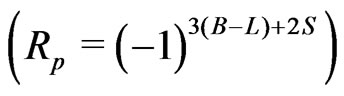 breaking in such generic supersymmetric gauged inverse seesaw models. LSP can not be perfectly stable but decays to standard model particles after non-renormalizable operators allowed by the gauge symmetry are introduced. We show that strong astrophysical constraints on LSP lifetime makes sneutrino dark matter more natural than standard neutralino dark matter. We also show that long-livedness of sneutrino dark matter constrains the left right symmetry breaking scale
breaking in such generic supersymmetric gauged inverse seesaw models. LSP can not be perfectly stable but decays to standard model particles after non-renormalizable operators allowed by the gauge symmetry are introduced. We show that strong astrophysical constraints on LSP lifetime makes sneutrino dark matter more natural than standard neutralino dark matter. We also show that long-livedness of sneutrino dark matter constrains the left right symmetry breaking scale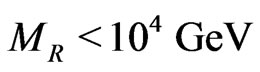 .
.
1. Introduction
Left-Right Symmetric Models (LRSM) [2-6] provide a framework within which spontaneous parity breaking as well as tiny neutrino masses [7-10] can be successfully implemented without reference to very high scale physics such as grand unification. Incorporating Supersymmetry (SUSY) into it comes with other advantages like providing a solution to the gauge hierarchy problem, and providing a Cold Dark Matter candidate which is the lightest supersymmetric particle (LSP). In Minimal Supersymmetric Standard Model (MSSM), the stability of LSP is guaranteed by R-parity, defined as 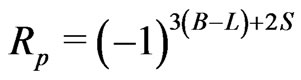 where
where 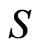 is the spin of the particle. This is a discrete symmetry put by hand in MSSM to keep the baryon number (B) and lepton number (L) violating terms away from the superpotential. In generic implementations of Left-Right symmetry, R-parity is a part of the gauge symmetry and hence not ad-hoc like in the MSSM. In one class of models [11-14], spontaneous parity breaking is achieved without breaking R-parity. This was not possible in minimal supersymmetric left right (SUSYLR) models where the only way to break parity is to consider spontaneous R-parity violation [15]. In minimal SUSYLR model parity,
is the spin of the particle. This is a discrete symmetry put by hand in MSSM to keep the baryon number (B) and lepton number (L) violating terms away from the superpotential. In generic implementations of Left-Right symmetry, R-parity is a part of the gauge symmetry and hence not ad-hoc like in the MSSM. In one class of models [11-14], spontaneous parity breaking is achieved without breaking R-parity. This was not possible in minimal supersymmetric left right (SUSYLR) models where the only way to break parity is to consider spontaneous R-parity violation [15]. In minimal SUSYLR model parity, 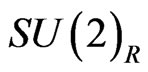 gauge symmetry as well as Rparity break simultaneously by the vacuum expectation value of right handed sneutrino.
gauge symmetry as well as Rparity break simultaneously by the vacuum expectation value of right handed sneutrino.
Here we study a different SUSYLR model which belong to a more general class of models where both R-parity and D-parity break spontaneously [16] by the vacuum expectation value (vev) of a Higgs field carying 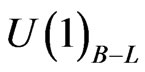 gauge charge
gauge charge 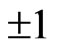 and hence odd under Rparity. Spontaneous R-parity breaking models have received lots of attention recently due to their rich phenomenology [17-19]. In such generic spontaneous Rparity breaking models, the scalar superpartner of righthanded neutrino acquire a non-zero vev which breaks
and hence odd under Rparity. Spontaneous R-parity breaking models have received lots of attention recently due to their rich phenomenology [17-19]. In such generic spontaneous Rparity breaking models, the scalar superpartner of righthanded neutrino acquire a non-zero vev which breaks 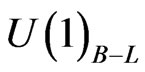 symmetry spontaneously. Such a scenario gives rise to tree level mixing between neutralinos and light neutrinos and hence the neutralino dark matter candidate is lost in such a model unless one talks about long lived gravitino dark matter. However the model we study in this letter, although breaks R-parity spontaneously, does not give rise to tree level mixing terms between LSP and standard model fermions. Thus we can have a dark matter candidate in such a model without introducing the least understood gravity sector into account. Recently right handed sneutrino dark matter in such a model was discussed in [1]. However, the authors in [1] (also in [20])
symmetry spontaneously. Such a scenario gives rise to tree level mixing between neutralinos and light neutrinos and hence the neutralino dark matter candidate is lost in such a model unless one talks about long lived gravitino dark matter. However the model we study in this letter, although breaks R-parity spontaneously, does not give rise to tree level mixing terms between LSP and standard model fermions. Thus we can have a dark matter candidate in such a model without introducing the least understood gravity sector into account. Recently right handed sneutrino dark matter in such a model was discussed in [1]. However, the authors in [1] (also in [20])
considered an additional discrete 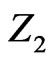 symmetry so as to guarantee a perfectly stable LSP. Here we consider a generalized version of this model without any additional symmetries apart from the gauge symmetry. We point out that LSP dark matter, although stable at the renormalizable level, decays after higher dimensional gauge invariant terms are introduced. The strength of such operators will be tightly constrained from the fact that LSP lifetime should be longer than the age of the Universe and large enough so as to agree with astrophysical observations of nearby galaxies and clusters [21]. Astrophysical constraints on such operators within the framework of MSSM was studied in [22]. Here we follow a similar analysis in our model and show that astrophysical constraints not only put an upper bound on the left-right symmetry breaking scale but also make the sneutrino dark matter more natural than standard neutralino dark matter. It is worth mentioning that constraints on the left-right symmetry breaking scale in such a model were derived recently in [23] from the requirement of successful gauge coupling unification and disappearance of transitory domain walls formed as a result of spontaneous discrete symmetry breaking.
symmetry so as to guarantee a perfectly stable LSP. Here we consider a generalized version of this model without any additional symmetries apart from the gauge symmetry. We point out that LSP dark matter, although stable at the renormalizable level, decays after higher dimensional gauge invariant terms are introduced. The strength of such operators will be tightly constrained from the fact that LSP lifetime should be longer than the age of the Universe and large enough so as to agree with astrophysical observations of nearby galaxies and clusters [21]. Astrophysical constraints on such operators within the framework of MSSM was studied in [22]. Here we follow a similar analysis in our model and show that astrophysical constraints not only put an upper bound on the left-right symmetry breaking scale but also make the sneutrino dark matter more natural than standard neutralino dark matter. It is worth mentioning that constraints on the left-right symmetry breaking scale in such a model were derived recently in [23] from the requirement of successful gauge coupling unification and disappearance of transitory domain walls formed as a result of spontaneous discrete symmetry breaking.
This letter is organized as follows. In Section 2 we briefly review the model. In Section 3 we discuss the higher dimensional operators in the model and astrophysical constraints. We summarise the constraints from gauge coupling unification and domain wall disappearance from our earlier work [23] in Section 4 and finally conclude in Section 5.
2. The Model
Spontaneous R-parity breaking can be achieved even without giving vev to the sneutrino fields. If the 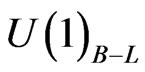 symmetry is broken by a Higgs field which has odd
symmetry is broken by a Higgs field which has odd 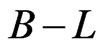 charge then R-parity is spontaneously broken. We call this model as Minimal Higgs Doublet (MHD) Model. The minimal such model [16,24] has the following particle content
charge then R-parity is spontaneously broken. We call this model as Minimal Higgs Doublet (MHD) Model. The minimal such model [16,24] has the following particle content
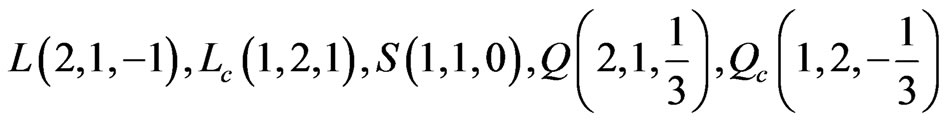
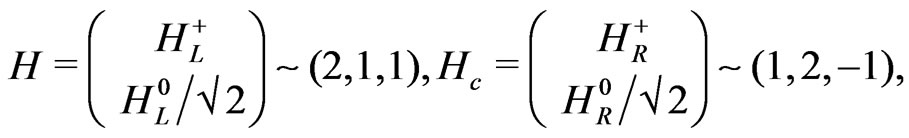
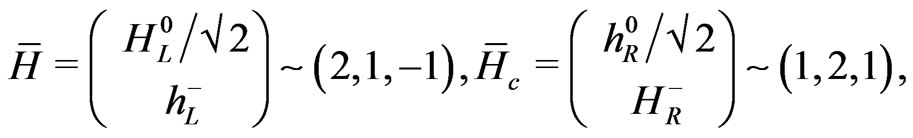
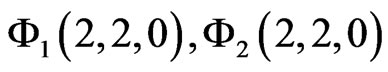
where the numbers in brackets correspond to the quantum numbers corresponding to
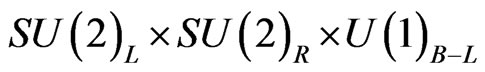 .
.
The symmetry breaking pattern is
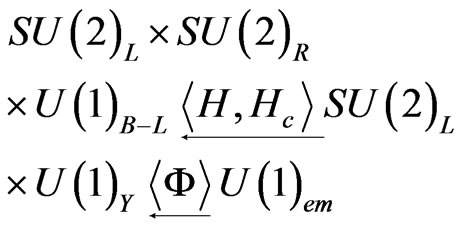 (1)
(1)
Neutrino masses arise naturally in this model by so called inverse seesaw mechanism by virtue of the presence of singlet superfields 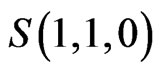 (one per generation). The renormalizable superpotential relevant for the spontaneous parity violation and neutrino mass is given as follows
(one per generation). The renormalizable superpotential relevant for the spontaneous parity violation and neutrino mass is given as follows
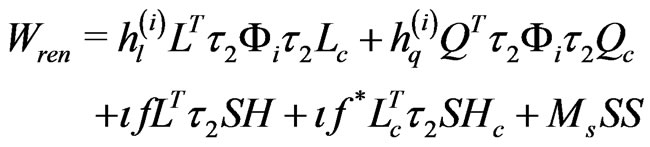
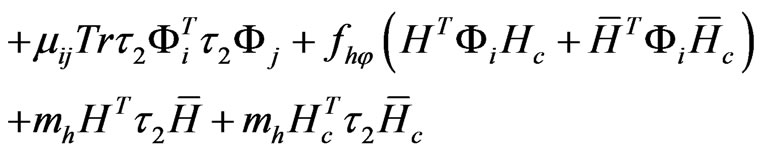 (2)
(2)
We denote the vev of the neutral components of 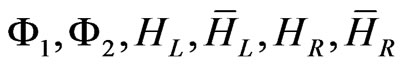 as
as
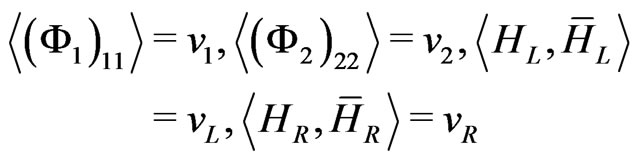
The neutrino mass matrix in the basis 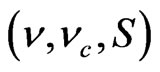 is given by
is given by
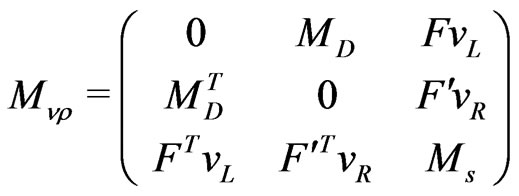 (3)
(3)
where
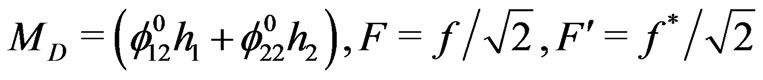 .
.
After orthogonalization we get the following expression for  mass
mass
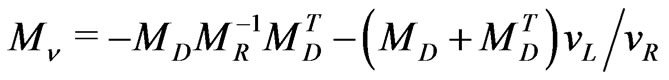 (4)
(4)
where
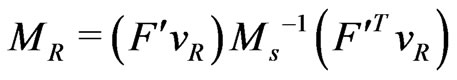 (5)
(5)
It should be noted from the neutrino mass matrix that these mass terms allow the mixing of an R-parity odd singlet fermion 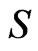 with an R-parity even neutrino. Note that the superpotential preserves R parity. The mild R parity violation occurring in the neutrino mass matrix should be understood as an accidental consequence of
with an R-parity even neutrino. Note that the superpotential preserves R parity. The mild R parity violation occurring in the neutrino mass matrix should be understood as an accidental consequence of 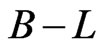 gauge symmetry breakdown.
gauge symmetry breakdown.
Neutrino mass can arise from type III seesaw mechanism [25] if we introduce fermionic triplets instead of singlets. However when we have a TeV scale intermediate 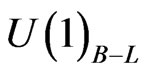 symmetry, the fermion triplets will spoil the gauge coupling unification [16,26] and hence fermion singlets will serve a better purpose in this case.
symmetry, the fermion triplets will spoil the gauge coupling unification [16,26] and hence fermion singlets will serve a better purpose in this case.
3. Non-Renormalizable Operators and Astrophysical Constraints
The authors of [22] considered explicit R-parity violating terms in the MSSM superpotential of the form 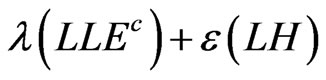 which lead to the decay of LSP dark matter candidate in the model. Similar analysis within the framework of grand unified theories can be found in [27,28]. We take the conservative lower bound
which lead to the decay of LSP dark matter candidate in the model. Similar analysis within the framework of grand unified theories can be found in [27,28]. We take the conservative lower bound 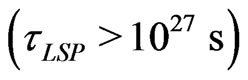 on LSP lifetime coming from the recent Fermi telescope observation of nearby galaxy and clusters [21].
on LSP lifetime coming from the recent Fermi telescope observation of nearby galaxy and clusters [21].
In the model we are studying, the effective terms in the superpotential leading to LSP decay can arise after introduing dimension four and dimension five operators as follows:
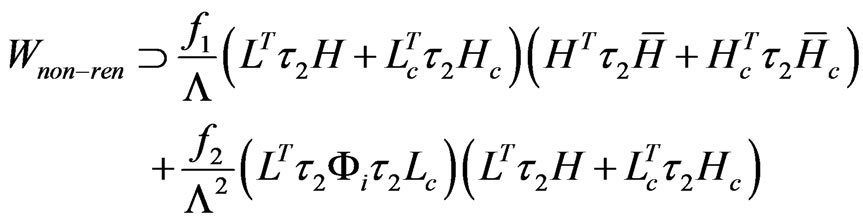
The first term give rise to terms like 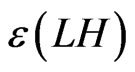 in the low energy effective theory after gauge symmetry is spontaneously broken. The strength of such a term is dictated by
in the low energy effective theory after gauge symmetry is spontaneously broken. The strength of such a term is dictated by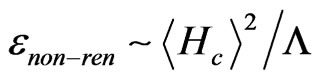 . Here
. Here 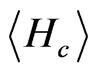 is the leftright symmetry breaking scale which has a lower bound of
is the leftright symmetry breaking scale which has a lower bound of 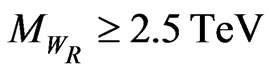 [29]. And, the cut-off scale
[29]. And, the cut-off scale  is the generic grand unified theory (GUT) scale
is the generic grand unified theory (GUT) scale 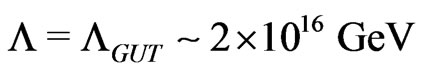 . Using these values and assuming generic order one dimensionless coefficients
. Using these values and assuming generic order one dimensionless coefficients , we have
, we have
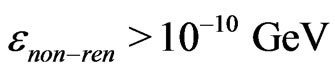 (6)
(6)
As shown in [22], the decay width of neutralino corresponding to a term 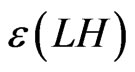 in the superpotential is given by
in the superpotential is given by
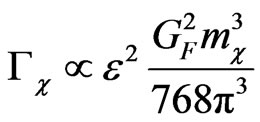 (7)
(7)
with constant of proportionality of order unity. Now, for generic neutralino dark matter with mass of the order of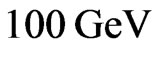 , the astrophysical constraint on LSP lifetime
, the astrophysical constraint on LSP lifetime 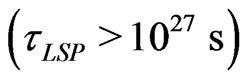 gives rise to
gives rise to
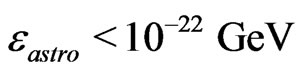 (8)
(8)
Clearly the astrophysical bound (8) does not agree with the strength of 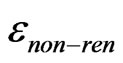 arising from generic nonrenormalizable operators in the theory. If we fine tune
arising from generic nonrenormalizable operators in the theory. If we fine tune 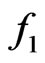 to be as small as electron Yukawa coupling
to be as small as electron Yukawa coupling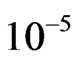 , then
, then 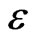 can be as small as
can be as small as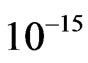 . But this lies around seven orders of magnitude above the upper bound set by astrophysical constraints (8). Thus, standard neutraino dark matter is very unlikely in these models unless we have unnatural fine tuning of the dimensionless coefficients in the non-renormalizable operators. It should be noticed that a term like
. But this lies around seven orders of magnitude above the upper bound set by astrophysical constraints (8). Thus, standard neutraino dark matter is very unlikely in these models unless we have unnatural fine tuning of the dimensionless coefficients in the non-renormalizable operators. It should be noticed that a term like 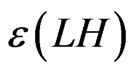 arise at tree level in generic spontaneous R-parity violating models with nonzero right handed sneutrino vev [17-19].
arise at tree level in generic spontaneous R-parity violating models with nonzero right handed sneutrino vev [17-19].
The second term in the non-renormalizable superpotential gives rise to an effective term of the form 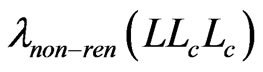 which opens the decay channel of sneutrino into two standard model fermions. The strength of such a term is given by
which opens the decay channel of sneutrino into two standard model fermions. The strength of such a term is given by 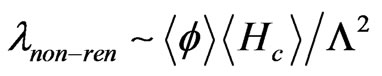 where
where 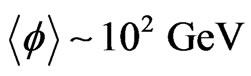 and
and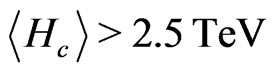 . For
. For 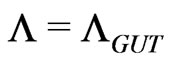 such a term is of strength
such a term is of strength
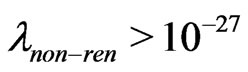 (9)
(9)
The decay width of a sneutrino to standard model fermion-antifermion pairs is given by
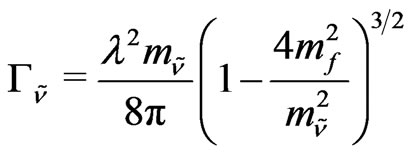 (10)
(10)
Now, for sneutrino LSP mass of the order of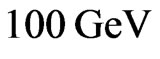 , the astrophysical constraint on LSP lifetime
, the astrophysical constraint on LSP lifetime 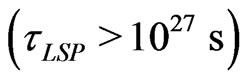 gives rise to
gives rise to
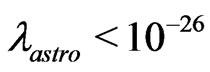 (11)
(11)
which agrees with the generic 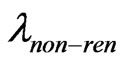 arising from the non-renormalizable operators in the theory (9). Thus sneutrino LSP in such a model can be a viable dark matter candidate provided it satisfies other relevant constraints of relic density, direct detection etc. Recently it was shown that such a right handed sneutrino dark matter (within the framework of a similar left right model) can satisfy relic density as well as direct detection constraints [1].
arising from the non-renormalizable operators in the theory (9). Thus sneutrino LSP in such a model can be a viable dark matter candidate provided it satisfies other relevant constraints of relic density, direct detection etc. Recently it was shown that such a right handed sneutrino dark matter (within the framework of a similar left right model) can satisfy relic density as well as direct detection constraints [1].
For right handed sneutrino dark matter to obey the relevant astrophysical constraints (11), the left right symmetry breaking scale should however have an upper bound. Requiring 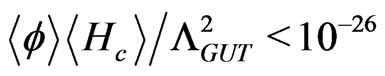 gives rise to a bound on the left-right symmetry breaking scale
gives rise to a bound on the left-right symmetry breaking scale
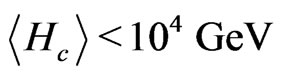 (12)
(12)
for generic GUT scale and order one dimensionless couplings. However, as studied in [16,23] and summarised in the next section, successful gauge coupling unification in such a minimal model puts a lower bound on left-right symmetry breaking scale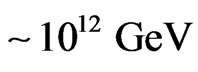 .
.
4. Constraints on MR from Unification and Domain Wall Disappearance
Similar to generic SUSYLR models, here also the intermediate symmetry breaking scales are constrained by demanding successful gauge coupling unification at a very high scale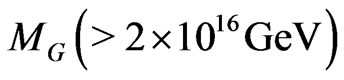 . The couplings of
. The couplings of 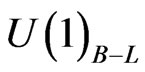 and
and 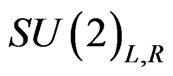 meet much before the allowed Unification scale if the intermediate symmetry breaking scale
meet much before the allowed Unification scale if the intermediate symmetry breaking scale 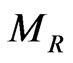 is lower than a certain value. For the minimal SUSYLR model with Higgs doublets, this lower bound on
is lower than a certain value. For the minimal SUSYLR model with Higgs doublets, this lower bound on 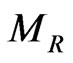 is found to be of the order of
is found to be of the order of 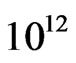 GeV. We also consider two additional heavy colored superfields so that the
GeV. We also consider two additional heavy colored superfields so that the 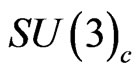 coupling meet the other two couplings at one point. They are denoted as
coupling meet the other two couplings at one point. They are denoted as 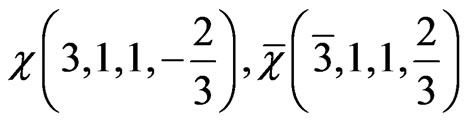 and can be accommodated within
and can be accommodated within  GUT theory in the representations
GUT theory in the representations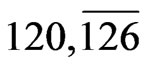 . Here we assume that the structure of the GUT theory is such that these fields survive the symmetry breaking and can be as light as the
. Here we assume that the structure of the GUT theory is such that these fields survive the symmetry breaking and can be as light as the 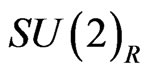 breaking scale. The resulting gauge coupling unification as shown in the Figure 1.
breaking scale. The resulting gauge coupling unification as shown in the Figure 1.
As discussed in details in [23], the succesful disappearance of domain walls in this model do not put any strict constraints on the left-right symmetry breaking scale and can be anywhere between a TeV scale and the Planck scale. Thus unification and domain wall disappearance constraints are compatible with each other. The discrepancy between the astrophysical limit 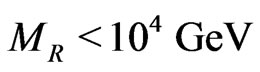 and the limit from successful unification
and the limit from successful unification 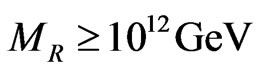
can be removed by including a parity odd singlet to our model. As studied in [16,26,30], such a framework allows even a TeV scale 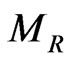 from the requirement of successful gauge coupling unification as can be seen from Figure 2. It should be noted that the authors of [1] indeed considered such a model with parity odd singlet which allows a TeV scale
from the requirement of successful gauge coupling unification as can be seen from Figure 2. It should be noted that the authors of [1] indeed considered such a model with parity odd singlet which allows a TeV scale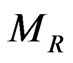 . Such TeV scale
. Such TeV scale  is not just a requirement from astrophysical constraints as we have found above, but these TeV scale gauge bosons also contribute to the dark matter annihilations [1] in the early universe producing the correct relic density at present.
is not just a requirement from astrophysical constraints as we have found above, but these TeV scale gauge bosons also contribute to the dark matter annihilations [1] in the early universe producing the correct relic density at present.
5. Results and Conclusions
We have discussed the issue of stability of LSP dark matter in a specific version of SUSYLR model with inverse seesaw mechanism of neutrino mass where both D-parity and R-parity are spontaneously broken. We point out that, although LSP is a stable particle in the renormalizable version of the model, it can decay into standard model fermions after the non-renormalizable terms are introduced. The requirement that LSP dark matter should be long lived so as to satisfy strict astrophysical and cosmological bounds constrains the strength of these higher dimensional operators suppressed by

Figure 1. Gauge coupling unification in minimal SUSYLR model with higgs doublets, 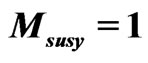 TeV,
TeV, 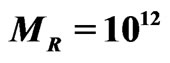 GeV,
GeV, 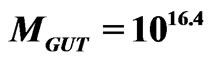 GeV. The figure is redrawn from [16,23].
GeV. The figure is redrawn from [16,23].
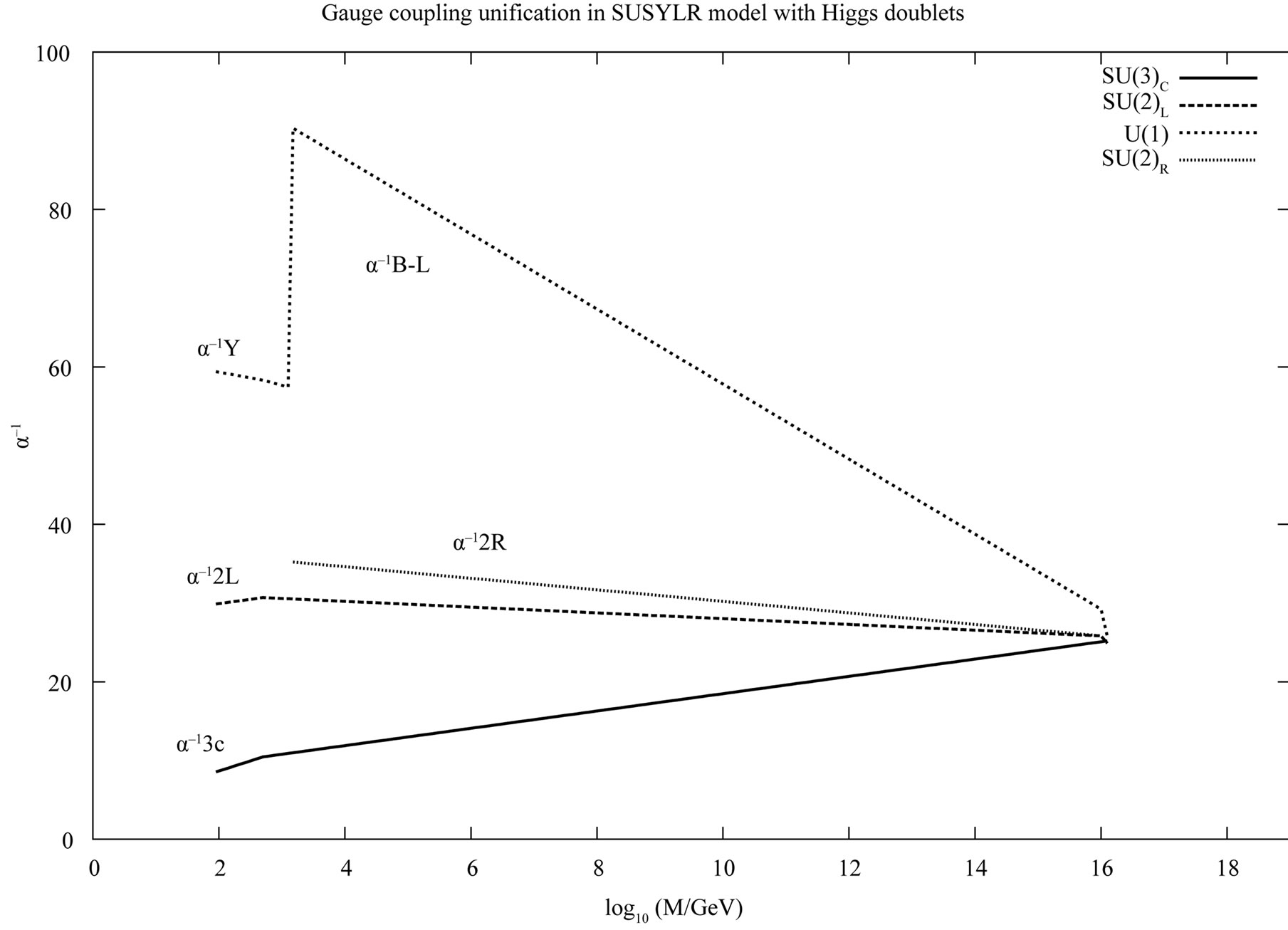
Figure 2. TeV scale 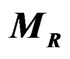 is possible with the introduction of parity odd singlets into the MHD model. The figure is redrawn from [16,26] with
is possible with the introduction of parity odd singlets into the MHD model. The figure is redrawn from [16,26] with 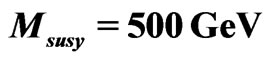 and
and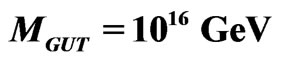 .
.
GUT scale. We point out that standard neutralino dark matter (decaying through dimension four operators in the superpotential) scenario is disfavored in this model unless one considers unnatural fine-tuning of the dimensionless coefficients in the higher dimensional operators. However, right handed sneutrino dark matter (decaying through dimension five operators in the superpotential) satisfy the astrophysical bounds more naturally and can be a viable dark matter candidate provided it satisfies other relevant constraints like relic density, direct detection etc.
Interestingly, the dimension five operators leading to sneutrino decay involve the left right symmetry breaking scale. The requirement that the strength of such an operator should be small enough to satisfy astrophysical bounds constrains the left right symmetry breaking scale. For generic GUT scale and order one dimensionless couplings, we find this bound to be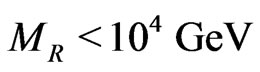 . However, as studied in [16,23], successful gauge coupling unification puts a lower bound
. However, as studied in [16,23], successful gauge coupling unification puts a lower bound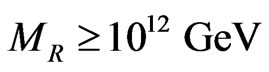 . The mismatch between these two bounds can be fixed by introducing a parity odd singlet [16,26,30] which allow
. The mismatch between these two bounds can be fixed by introducing a parity odd singlet [16,26,30] which allow 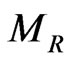 as low as a TeV from the requirement of successful gauge coupling unification. Such TeV scale gauge bosons, apart from satisfying the astrophysical constraints also opens up new dark matter annihilation channels [1] producing the correct relic density in the present Universe.
as low as a TeV from the requirement of successful gauge coupling unification. Such TeV scale gauge bosons, apart from satisfying the astrophysical constraints also opens up new dark matter annihilation channels [1] producing the correct relic density in the present Universe.
6. Acknowledgements
I would like to thank Prof Urjit A. Yajnik, IIT Bombay for useful comments and discussions.
REFERENCES
- H. An, P. B. Dev, Y. Cai and R. N. Mohapatra, “Sneutrino Dark Matter in Gauged Inverse Seesaw Models for Neutrinos,” Physical Review Letters, Vol. 108, 2012, Article ID: 081806. doi:10.1103/PhysRevLett.108.081806
- J. C. Pati and A. Salam, “Lepton Number as the Fourth Color,” Physical Review, Vol. D10, 1974, pp. 275-289.
- R. N. Mohapatra and J. C. Pati, “A Natural Left-Right Symmetry,” Physical Review, Vol. D11, 1975, pp. 2558- 2569.
- G. Senjanovic and R. N. Mohapatra, “Exact Left-Right Symmetry and Spontaneous Violation of Parity,” Physical Review, Vol. D12, 1975, pp. 1502-1513.
- R. N. Mohapatra and R. E. Marshak, “Local B-L Symmetry of Electroweak Interactions, Majorana Neutrinos and Neutron Oscillations,” Physical Review Letters, Vol. 44, 1980, pp. 1316-1319. doi:10.1103/PhysRevLett.44.1316
- N. G. Deshpande, J. F. Gunion, B. Kayser and F. I. Olness, “Left-Right Symmetric Electroweak Models with Triplet Higgs,” Physical Review, Vol. D44, 1991, pp. 837-858.
- S. Fukuda, et al., (Super-Kamiokande Collaboration), “Constraints on Neutrino Oscillations Using 1258 Days of Super-Kamiokande Solar Neutrino Data,” Physical Review Letters, Vol. 86, 2001, pp. 5656-5660. doi:10.1103/PhysRevLett.86.5656
- Q. R. Ahmad, et al., (SNO Collaboration), “Direct Evidence for Neutrino Flavor Transformation from Neutral Current Interactions in the Sudbury Neutrino Observatory,” Physical Review Letters, Vol. 89a, 2002, Article ID: 011301. doi:10.1103/PhysRevLett.89.011301
- Q. R. Ahmad, et al., (SNO Collaboration), “Measurement of Day and Night Neutrino Energy Spectra at SNO and Constraints on Neutrino Mixing Parameters,” Physical Review Letters, Vol. 89b, 2002, Article ID: 011302. doi:10.1103/PhysRevLett.89.011302
- J. N. Bahcall and C. Pena-Garay, “Solar Models and Solar Neutrino Oscillations,” New Journal of Physics, Vol. 6, 2005, pp. 63-79. doi:10.1088/1367-2630/6/1/063
- C. S. Aulakh, A. Melfo and G. Senjanovic, “Minimal Supersymmetric Left-Right Model,” Physical Review, Vol. D57, 1998, pp. 4174-4178.
- C. S. Aulakh, K. Benakli and G. Senjanovic, “Reconciling Supersymmetry and Left-Right Symmetry,” Physical Review Letters, Vol. 79, 1997, pp. 2188-2191. doi:10.1103/PhysRevLett.79.2188
- K. S. Babu and R. N. Mohapatra, “Minimal Supersymmetric Left-Right Model,” Physics Letters, Vol. B668, 2008, pp. 404-409.
- S. Patra, A. Sarkar, U. Sarkar and U. Yajnik, “Spontaneous Parity Violation in a Supersymmetric Left-Right Symmetric Model,” Physics Letters, Vol. B679, 2009, pp. 386-389.
- R. Kuchimanchi and R. N. Mohapatra, “No Parity Violation without R-Parity Violation,” Physical Review, Vol. D48, 1993, pp. 4352-4360.
- D. Borah, “Supersymmetric Left-Right Models with B-L Odd Higgs Doublets,” International Journal of Modern Physics, Vol. A26, 2011, pp. 1305-1326.
- P. F. Perez and S. Spinner, “Spontaneous R-Parity Breaking and Left-Right Symmetry,” Physics Letters, Vol. B673, 2009, pp. 251-254.
- V. Barger, P. F. Perez and S. Spinner, “Minimal Gauged U(1)(B-L) Model with Spontaneous R-Parity Violation,” Physical Review Letters, Vol. 102, 2009, Article ID: 181802. doi:10.1103/PhysRevLett.102.181802
- P. F. Perez and S. Spinner, “The Minimal Theory for RParity Violation at the LHC,” Journal of High Energy Physics, Vol. 2012, No. 4, 2012, pp. 118-155. doi:10.1007/JHEP04(2012)118
- P. S. B. Dev and R. N. Mohapatra, “Electroweak Symmetry Breaking and Proton Decay in SO(10) SUSY-GUT with TeV W(R),” Physical Review, Vol. D82, 2010, Article ID: 035014.
- L. Dugger, T. E. Jeltema and S. Profumo, “Constraints on Decaying Dark Matter from Fermi Observations of Nearby Galaxies and Clusters,” Journal of Cosmology and Astroparticle Physics, Vol. 1012, 2010, pp. 15-37.
- V. Berezinsky, A. S. Joshipura and J. W. F. Valle, “Gravitational Violation of R-Parity and Its Cosmological Signatures,” Physical Review, Vol. D57, 1998, pp. 147- 151.
- D. Borah and S. Mishra, “Spontaneous R-Parity Breaking, Left-Right Symmetry and Consistent Cosmology with Transitory Domain Walls,” Physical Review, Vol. D84, 2011, Article ID: 055008.
- D. Borah and S. Patra, “Type III Seesaw and Dark Matter in a Supersymmetric Left-Right Model,” arXiv:0910.0146.
- R. Foot, H. Lew, X. G. He and G. C. Joshi, “Seesaw Neutrino Masses Induced by a Triplet of Leptons,” Zeitschrift fur Physik, Vol. C44, 1989, p. 441.
- D. Borah, S. Patra and U. Sarkar, “TeV scale Left Right Symmetry with Spontaneous D-Parity Breaking,” Physical Review, Vol. D83, 2011, Article ID: 035007.
- A. Arvanitaki, et al., “Astrophysical Probes of Unification,” Physical Review, Vol. D79, 2009, Article ID: 105022.
- A. Arvanitaki, et al., “Decaying Dark Matter as a Probe of Unification and TeV Spectroscopy,” Physical Review, Vol. D80, 2009, Article ID: 055011.
- A. Maiezza, M. Nemevsek, F. Nesti and G. Senjanovic, “Left-Right Symmetry at LHC,” Physical Review, Vol. D82, 2010, Article ID: 055022.
- P. S. B. Dev and R. N. Mohapatra, “TeV Scale Inverse Seesaw in SO(10) and Leptonic Non-Unitarity Effects,” Physical Review, Vol. D81, 2010, Article ID: 013001.

