Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22621,8 pages DOI:10.4236/jmp.2012.39116
Dirac Hamiltonian with Imaginary Mass and Induced Helicity—Dependence by Indefinite Metric
1Department of Physics, Missouri University of Science and Technology, Rolla, USA 2Institute for Theoretical Physics, University of Heidelberg, Heidelberg, Germany
Email: ulj@mst.edu
Received June 27, 2012; revised July 29, 2012; accepted August 7, 2012
Keywords: Neutrinos; Particles; Tachyonos
ABSTRACT
It is of general theoretical interest to investigate the properties of superluminal matter wave equations for spin one-half particles. One can either enforce superluminal propagation by an explicit substitution of the real mass term for an imaginary mass, or one can use a matrix representation of the imaginary unit that multiplies the mass term. The latter leads to the tachyonic Dirac equation, while the equation obtained by the substitution m ® im in the Dirac equation is naturally referred to as the imaginary-mass Dirac equation. Both the tachyonic as well as the imaginary-mass Dirac Hamiltonians commute with the helicity operator. Both Hamiltonians are pseudo-Hermitian and also possess additional modified pseudo-Hermitian properties, leading to constraints on the resonance eigenvalues. Here, by an explicit calculation, we show that specific sum rules over the spectrum hold for the wave functions corresponding to the well-defined real energy eigenvalues and complex resonance and anti-resonance energies. In the quantized imaginary-mass Dirac field, one-particle states of right-handed helicity acquire a negative norm (“indefinite metric”) and can be excluded from the physical spectrum by a Gupta-Bleuler type condition.
1. Introduction and Overview
1.1. Theory and Experiment
The superluminal propagation of matter waves is a highly intriguing subject which is not without controversy. The subluminal (tardyonic) energy-momentum relation 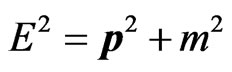 needs to be changed to the superluminal (tachyonic) dispersion relation
needs to be changed to the superluminal (tachyonic) dispersion relation . Recently, it has been argued that the tachyonic Dirac equation [1,2] provides for a convenient framework for the description of tachyonic particles; in this equation, the mass is multiplied by a matrix representation of the imaginary unit. Here, starting from the Dirac Hamiltonian, we explore a Dirac equation where the mass is explicitly multiplied by the imaginary unit and we find certain fundamental relations for the corresponding spin-1/2 field theory. We also explore certain algebraic properties of modified Dirac theories with an imaginary mass term, and pertaining consequences for the eigenvalue spectrum of the imaginary-mass Dirac Hamiltonian. The tachyonic formulation [3-8] of a fundamental field theory is the only one compatible with Lorentz invariance, and therefore, compatible with special relativity. We exclusively use this concept in the following and avoid any breaking of Lorentz invariance.
. Recently, it has been argued that the tachyonic Dirac equation [1,2] provides for a convenient framework for the description of tachyonic particles; in this equation, the mass is multiplied by a matrix representation of the imaginary unit. Here, starting from the Dirac Hamiltonian, we explore a Dirac equation where the mass is explicitly multiplied by the imaginary unit and we find certain fundamental relations for the corresponding spin-1/2 field theory. We also explore certain algebraic properties of modified Dirac theories with an imaginary mass term, and pertaining consequences for the eigenvalue spectrum of the imaginary-mass Dirac Hamiltonian. The tachyonic formulation [3-8] of a fundamental field theory is the only one compatible with Lorentz invariance, and therefore, compatible with special relativity. We exclusively use this concept in the following and avoid any breaking of Lorentz invariance.
According to the summary overview presented in Ref. [9], low-energy experiments have determined the neutrino mass square to be in the range of a few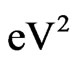 . The best estimate for the neutrino mass square has been determined as negative in all experiments [10-16], but the result has been consistent with a vanishing neutrino mass within experimental error bars. In direct measurements of the neutrino velocity [17-19], the best estimate derived from experimental data has been superluminal (
. The best estimate for the neutrino mass square has been determined as negative in all experiments [10-16], but the result has been consistent with a vanishing neutrino mass within experimental error bars. In direct measurements of the neutrino velocity [17-19], the best estimate derived from experimental data has been superluminal ( ), but again, consistent with the hypothesis
), but again, consistent with the hypothesis  within experimental error bars (see also Ref. [9] or Table 1 of Ref. [20]). The OPERA collaboration [21] has indicated a preliminary, revised result of
within experimental error bars (see also Ref. [9] or Table 1 of Ref. [20]). The OPERA collaboration [21] has indicated a preliminary, revised result of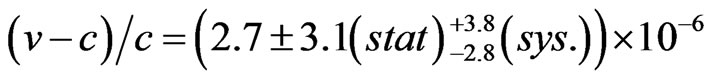 , which (just like all other available experimental results) neither excludes subluminal nor superluminal propagation.
, which (just like all other available experimental results) neither excludes subluminal nor superluminal propagation.
The neutrino is generally regarded as the most prominent candidate for a superluminal particle in the lowenergy domain [20,22-25]. However, the existence of conceivable superluminal particles in hitherto unexplored kinematic regions cannot be excluded, either; our study is of theoretical nature and not tied to a specific particle. It has recently been argued [1,2] that the tachyonic theory of spin-1/2 particles is easier to implement as compared to spinless particles, and we here continue this line of thought by analyzing a theory where the imaginary mass is used explicitly in the Dirac equation, rather than a matrix representation thereof. The latter has been used in Refs. [1,2,22,26,27]. We use natural units with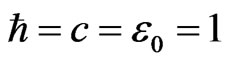 .
.
1.2. Theoretical Foundations
It is useful to recall that the subluminal (tardyonic) Dirac Hamiltonian 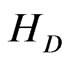 reads
reads
 (1)
(1)
Here, 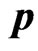 is the momentum operator. We use the Dirac matrices in the standard Dirac representation (
is the momentum operator. We use the Dirac matrices in the standard Dirac representation (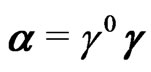 , and
, and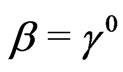 ),
),
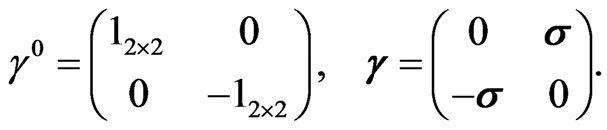 (2)
(2)
The Hamiltonian 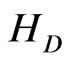 can be modified into a Hamiltonian describing superluminal (tachyonic) particles by the simple replacement
can be modified into a Hamiltonian describing superluminal (tachyonic) particles by the simple replacement 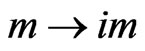 (see Ref. [28]), leading to the imaginary-mass Dirac Hamiltonian
(see Ref. [28]), leading to the imaginary-mass Dirac Hamiltonian
 (3)
(3)
Alternatively, one can choose a matrix representation of the imaginary unit, and write the tachyonic Dirac Hamiltonian [1,2,22,26,27] as
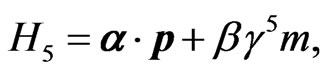 (4)
(4)
with 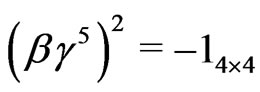 and
and
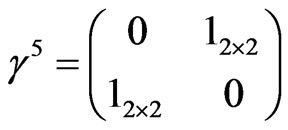 (5)
(5)
Both  and
and 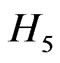 are pseudo-Hermitian, which implies that eigenvalues are either real or come in complexconjugate pairs,
are pseudo-Hermitian, which implies that eigenvalues are either real or come in complexconjugate pairs,  and
and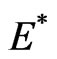 . Here, we also show that
. Here, we also show that 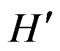 and
and 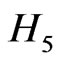 fulfill additional, modified pseudo-Hermiticity conditions (“quasi-pseudo-Hermiticity”), which allow us to further conclude that if
fulfill additional, modified pseudo-Hermiticity conditions (“quasi-pseudo-Hermiticity”), which allow us to further conclude that if 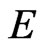 is a resonance eigenvalue, so is
is a resonance eigenvalue, so is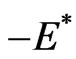 , and thus, the eigenvalues either come in (real) pairs
, and thus, the eigenvalues either come in (real) pairs 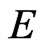 and
and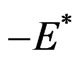 , or they occur in the rectangular complex configuration
, or they occur in the rectangular complex configuration ,
, 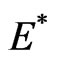 ,
, 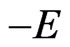 , and
, and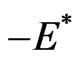 . The quantization of the imaginary-mass Dirac theory naturally leads to helicity-dependent anticommutators.
. The quantization of the imaginary-mass Dirac theory naturally leads to helicity-dependent anticommutators.
We proceed as follows. In Section 2, we derive a few algebraic properties of the Hamiltonians 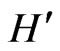 and
and 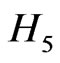 which determine the general properties of their spectra. The field theory defined by the Hamiltonian
which determine the general properties of their spectra. The field theory defined by the Hamiltonian 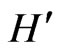 is quantized in Section 3. In Section 4, we analyze the Hamiltonian
is quantized in Section 3. In Section 4, we analyze the Hamiltonian 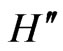 which is obtained from (3) by the replacement
which is obtained from (3) by the replacement . The quantization of the imaginary-mass Dirac theory is shown to yield rather interesting insight into helicity-dependent anticommutators. Conclusions are reserved for Section 5.
. The quantization of the imaginary-mass Dirac theory is shown to yield rather interesting insight into helicity-dependent anticommutators. Conclusions are reserved for Section 5.
2. Algebraic Properties and Eigenvalues
It is useful to derive a few algebraic properties of 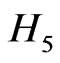 and
and 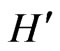 which determine the structure of the spectra of these Hamiltonians. We explicitly refer to the coordinatespace representations
which determine the structure of the spectra of these Hamiltonians. We explicitly refer to the coordinatespace representations 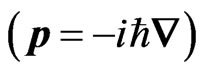
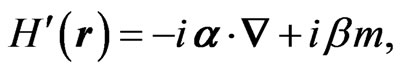 (6)
(6)
and
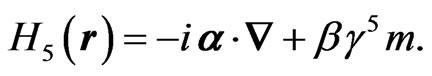 (7)
(7)
We use the following matrices,
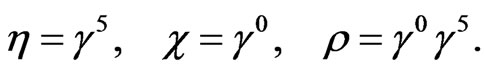 (8)
(8)
These fulfill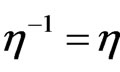 ,
, 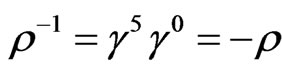 , and
, and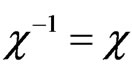 . By elementary calculation, we infer that
. By elementary calculation, we infer that
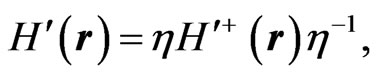 (9a)
(9a)
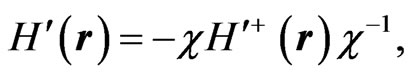 (9b)
(9b)
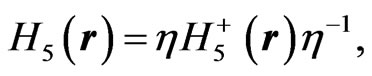 (9c)
(9c)
 (9d)
(9d)
where the superscript + denotes the Hermitian adjoint. The relations (9a) and (9c) imply the pseudo-Hermiticity of the Hamiltonians 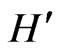 and
and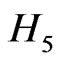 , respectively, in the sense of Refs. [29-38]. As shown in Refs. [1,29], for a pseudo-Hermitian Hamiltonian, if
, respectively, in the sense of Refs. [29-38]. As shown in Refs. [1,29], for a pseudo-Hermitian Hamiltonian, if 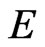 is a resonance eigenvalue, so is
is a resonance eigenvalue, so is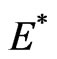 . Indeed, it has been shown in Ref. [2] that
. Indeed, it has been shown in Ref. [2] that 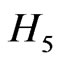 has both real eigenvalues (corresponding to plane-wave solutions of positive and negative energy), and also resonances and anti-resonances whose resonance energies are manifestly complex. The resonances correspond to evanescent waves whose wavelength is too long to support superluminal propagation; these waves therefore decay exponentially.
has both real eigenvalues (corresponding to plane-wave solutions of positive and negative energy), and also resonances and anti-resonances whose resonance energies are manifestly complex. The resonances correspond to evanescent waves whose wavelength is too long to support superluminal propagation; these waves therefore decay exponentially.
In comparison to the structure of Equations (9a) and (9c), the relations (9b) and (9d) feature an additional minus sign. They correspond to additional “quasi-pseudoHermitian” properties of 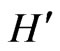 and
and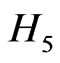 . These additional properties imply that if
. These additional properties imply that if 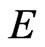 is a resonance eigenvalue, so is
is a resonance eigenvalue, so is . This can be shown as follows. Let
. This can be shown as follows. Let 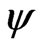 be an eigenfunction of a general Hamiltonian
be an eigenfunction of a general Hamiltonian 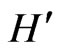 with eigenvalue
with eigenvalue . Then, because the spectrum of the Hermitian adjoint of an operator consists of the complex-conjugate eigenvalues, there exists a wavefunction
. Then, because the spectrum of the Hermitian adjoint of an operator consists of the complex-conjugate eigenvalues, there exists a wavefunction  with the property
with the property
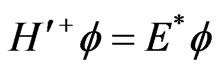 (10)
(10)
from which we infer that
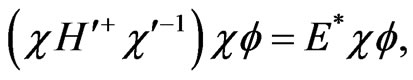 (11)
(11)
and so, in view of Equation (9b), we have 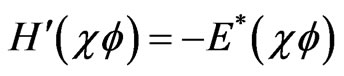 . So, if E is a resonance eigenvalue of
. So, if E is a resonance eigenvalue of , so is
, so is , with a corresponding eigenvector
, with a corresponding eigenvector . The same property is implied for
. The same property is implied for 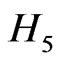 by Equation (9d). If E is real, then Equations (9b) and (9d) imply that energy eigenvalues come in pairs E and
by Equation (9d). If E is real, then Equations (9b) and (9d) imply that energy eigenvalues come in pairs E and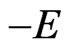 , whereas if they are manifestly complex, then they exhibit a rectangular configuration (in the complex plane) consisting of E,
, whereas if they are manifestly complex, then they exhibit a rectangular configuration (in the complex plane) consisting of E, 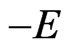 ,
, 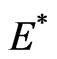 and
and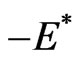 .
.
3. Quantization and Spin Sums
First, we observe that both 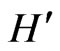 and
and 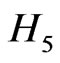 commute with the helicity operator,
commute with the helicity operator,
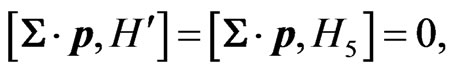 (12)
(12)
where
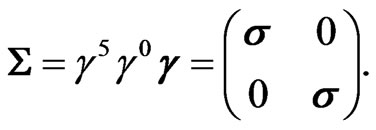 (13)
(13)
The quantization of the tachyonic theory defined by the Hamiltonian  has been discussed in Ref. [2]. Here, we are concerned with the Hamiltonian
has been discussed in Ref. [2]. Here, we are concerned with the Hamiltonian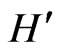 . The corresponding covariant form the imaginary-mass Dirac equation reads as
. The corresponding covariant form the imaginary-mass Dirac equation reads as
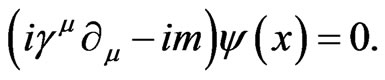 (14)
(14)
Of course, it could be argued that the solutions of the imaginary-mass Dirac equation can be written down immediately, by simply replacing 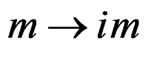 in the wellknown bispinor solutions of the ordinary Dirac equation, as given in Chapter 2 of Ref. [39]. However, this procedure does not lead to compact formulas when one tries to develop the formalism further. A brief, sketchy, illustrative remark is in order. According to Equation (2.40) of Ref. [39], the spin sum over the positive-energy states of the tardyonic (ordinary) Dirac equation leads to the expression
in the wellknown bispinor solutions of the ordinary Dirac equation, as given in Chapter 2 of Ref. [39]. However, this procedure does not lead to compact formulas when one tries to develop the formalism further. A brief, sketchy, illustrative remark is in order. According to Equation (2.40) of Ref. [39], the spin sum over the positive-energy states of the tardyonic (ordinary) Dirac equation leads to the expression
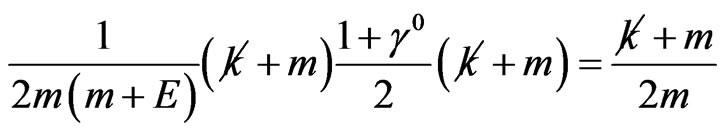 (15)
(15)
where the latter term is the projector onto positive-energy states. Here, 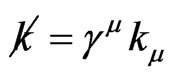 is the Feynman dagger. When replacing
is the Feynman dagger. When replacing 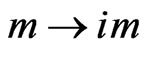 in the solution of the Dirac equation given in Equation (2.37) of Ref. [39], and performing the same spin sum over positive-energy solutions of the form
in the solution of the Dirac equation given in Equation (2.37) of Ref. [39], and performing the same spin sum over positive-energy solutions of the form 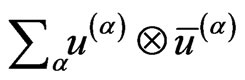 (using the notation of Ref. [39]), one has to replace
(using the notation of Ref. [39]), one has to replace 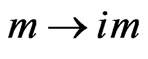 for the spinors and
for the spinors and 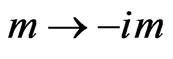 for the Dirac adjoint bispinors. But then,
for the Dirac adjoint bispinors. But then,
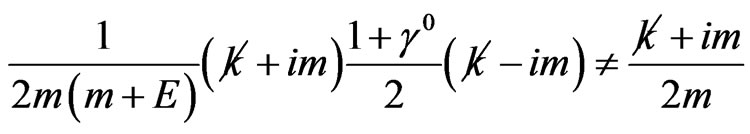 (16)
(16)
which is not equal to a compact projector form, as an elementary calculation shows. By contrast, compact formulas for sums over spins can be obtained in the helicity basis, as shown in the following.
For tachyonic particles, in analogy to the formalism developed in Ref. [2], it appears advantageous to use the helicity basis for the construction of the elementary solutions. We recall that the eigenfunctions of the operator 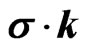 are given by
are given by
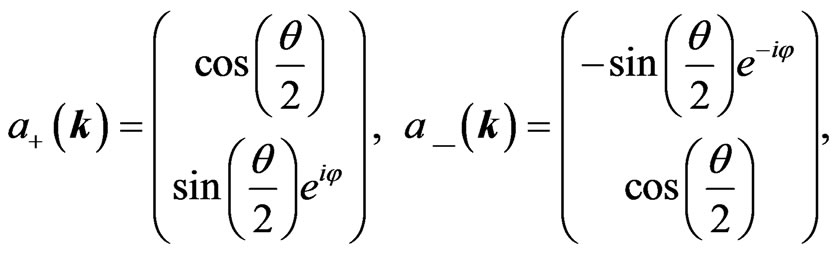 (17)
(17)
where  and
and 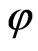 constitute the polar and azimuthal angles of the wave vector k, with
constitute the polar and azimuthal angles of the wave vector k, with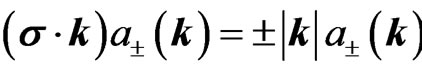 . We also recall the normalized positive-energy chirality and helicity eigenspinors of the massless Dirac equation as follows
. We also recall the normalized positive-energy chirality and helicity eigenspinors of the massless Dirac equation as follows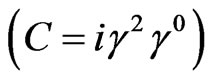 ,
,
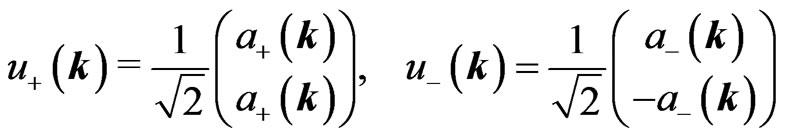 (18a)
(18a)
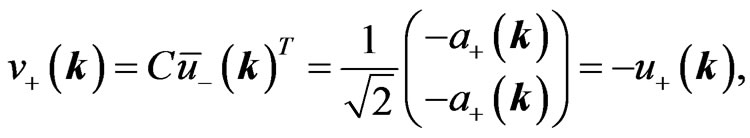 (18b)
(18b)
 (18c)
(18c)
Canonically, the subscripts 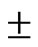 of the u and v spinors correspond to the chirality (eigenvalue of
of the u and v spinors correspond to the chirality (eigenvalue of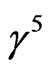 ), which (in the massless limit) is equal to helicity for positive-energy eigenstates, and equal to the negative of the chirality for negative-energy eigenstates. This is because the positiveand negative-energy solutions are multiplied by
), which (in the massless limit) is equal to helicity for positive-energy eigenstates, and equal to the negative of the chirality for negative-energy eigenstates. This is because the positiveand negative-energy solutions are multiplied by  and
and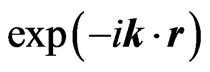 , respectively [see Equation (22)]. Using the relation
, respectively [see Equation (22)]. Using the relation
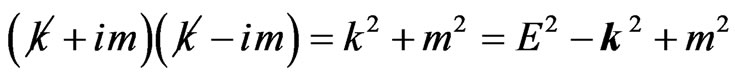 we find
we find
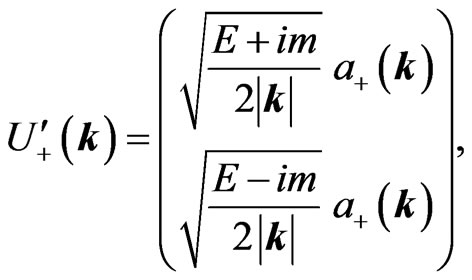 (19a)
(19a)
 (19b)
(19b)
The massless limit 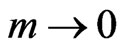
 is recovered as
is recovered as  and
and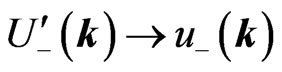 . The negativeenergy eigenstates of the imaginary-mass Dirac equation are given as
. The negativeenergy eigenstates of the imaginary-mass Dirac equation are given as
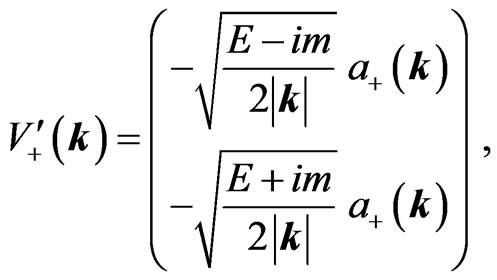 (20a)
(20a)
 (20b)
(20b)
In the massless limit, the solutions  and
and 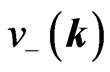 are recovered,
are recovered, 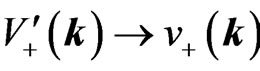 and
and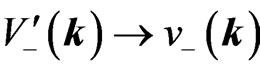 . The states are normalized with respect to the condition
. The states are normalized with respect to the condition
 (21)
(21)
The positiveand negative-energy solutions of the imaginary-mass Dirac equation are thus given as
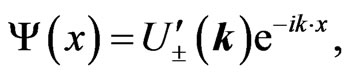 (22a)
(22a)
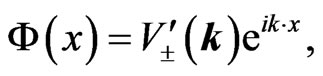 (22b)
(22b)
Here,  is a solution for positive energy, and
is a solution for positive energy, and  constitutes a solution for negative energy. All above formulas are valid for
constitutes a solution for negative energy. All above formulas are valid for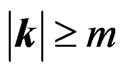 , so that
, so that 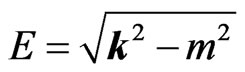 is real rather than complex. For
is real rather than complex. For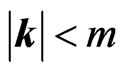 , one encounters resonances, which complete the spectrum. These are derived from Equations (19) and (20) by the identification
, one encounters resonances, which complete the spectrum. These are derived from Equations (19) and (20) by the identification
 (23a)
(23a)
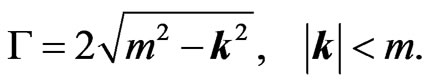 (23b)
(23b)
The Dirac adjoint is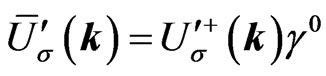 . By an elementary calculation, one shows that
. By an elementary calculation, one shows that
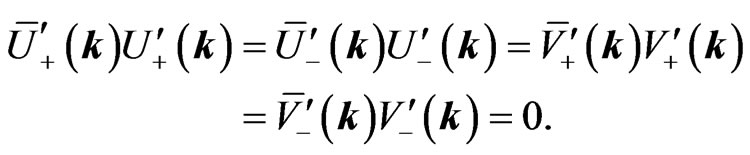
This can otherwise be seen as follows. One first realizes that the adjoint equation of 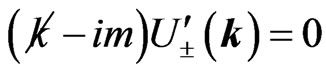 reads as
reads as , and so
, and so
 (24)
(24)
Here, we have used the adjoint equation for the “first”  and the original form of the imaginary-mass Dirac equation for the “second”
and the original form of the imaginary-mass Dirac equation for the “second”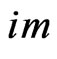 .
.
In analogy to Ref. [2], we define the 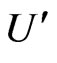 and
and  bispinors in the following normalization,
bispinors in the following normalization,
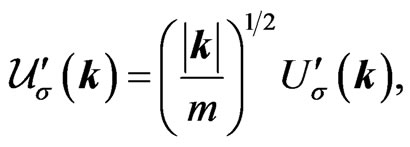 (25a)
(25a)
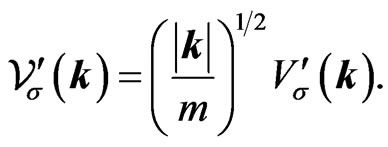 (25b)
(25b)
Under charge conjugation, the spinors transform as 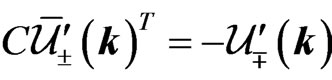 and
and . In analogy with Ref. [2], we write the field operator as
. In analogy with Ref. [2], we write the field operator as
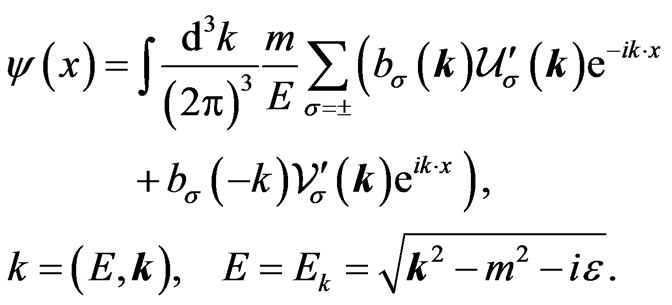 (26)
(26)
Note that the  prescription selects the resonances (as analytic continuations of the positive-energy solutions) and antiresonances (as analytic continuations of the negative-energy solutions). This ensures that the waves are evanescent in their respective propagation direction in time. The second term in the sum in Equation (26) describes the absorption of a negative-energy tachyonic particle that propagates backward in time; this process is of course equivalent to the emission of a positive-energy antiparticle propagating forward in time by the Feinberg-Sudarshan reinterpretation principle, as explained in Ref. [2]. Thus,
prescription selects the resonances (as analytic continuations of the positive-energy solutions) and antiresonances (as analytic continuations of the negative-energy solutions). This ensures that the waves are evanescent in their respective propagation direction in time. The second term in the sum in Equation (26) describes the absorption of a negative-energy tachyonic particle that propagates backward in time; this process is of course equivalent to the emission of a positive-energy antiparticle propagating forward in time by the Feinberg-Sudarshan reinterpretation principle, as explained in Ref. [2]. Thus,
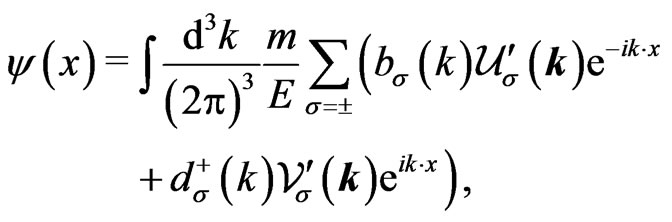 (27)
(27)
where 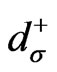 creates antiparticles. For the imaginary-mass formalism, we postulate the same anticommutators as in Ref. [2] for the tachyonic Dirac equation,
creates antiparticles. For the imaginary-mass formalism, we postulate the same anticommutators as in Ref. [2] for the tachyonic Dirac equation,
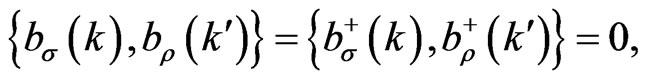 (28a)
(28a)
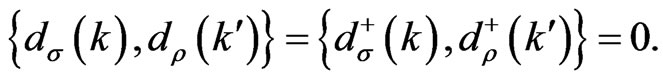 (28b)
(28b)
The nonvanishing anticommutators read as follows,
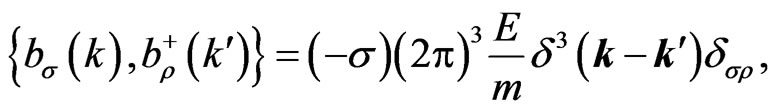 (29a)
(29a)
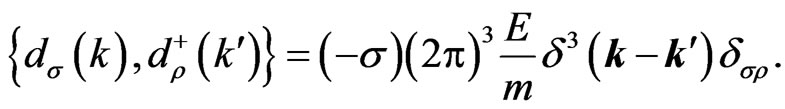 (29b)
(29b)
The σ-dependent anticommutator implies that the norm of the right-handed helicity (positive chirality) neutrino one-particle state is negative, and that the righthanded helicity particle state has negative norm and can be excluded from the physical spectrum if one imposes a Gupta-Bleuler type condition (according to Chapter 3 of Ref. [39]). Likewise, antiparticles described by the imaginary-mass formalism can only exist in the right-handed helicity state. The matrix-valued tachyonic field anticommutator reads as
 (30)
(30)
where 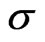 is the helicity (for positive-energy states) and the negative of the helicity (for negative-energy states) and
is the helicity (for positive-energy states) and the negative of the helicity (for negative-energy states) and  is the tensor product in bispinor space. The following two relations
is the tensor product in bispinor space. The following two relations
 (31a)
(31a)
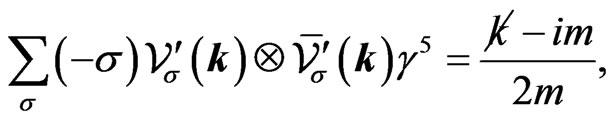 (31b)
(31b)
are analogous to those found for the bispinor solutions of the tachyonic Dirac described in Ref. [1]. Note that the factors 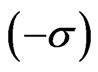 in these equations are due to the quantization conditions (28). Using Equation (31), we can derive the compact result,
in these equations are due to the quantization conditions (28). Using Equation (31), we can derive the compact result,
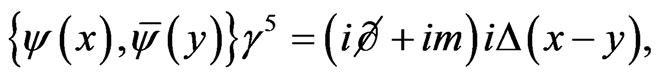 (32)
(32)
where  is the distribution encountered in Equations (3.55) and (3.56) of Ref. [39],
is the distribution encountered in Equations (3.55) and (3.56) of Ref. [39],
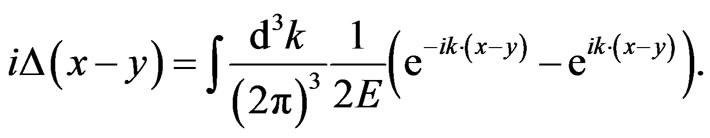 (33)
(33)
The equal-time anticommutator of the fields thus reads as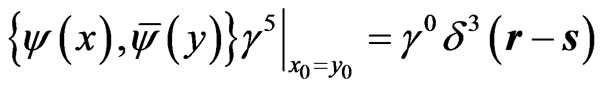 , with the full, unfiltered Dirac-δ function and
, with the full, unfiltered Dirac-δ function and 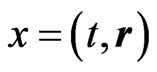 as well as
as well as 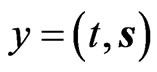 and the time
and the time . Furthermore, with the help of Equations (27) and (31), one obtains the propagator
. Furthermore, with the help of Equations (27) and (31), one obtains the propagator 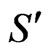 (time-ordered product),
(time-ordered product),
 (34a)
(34a)
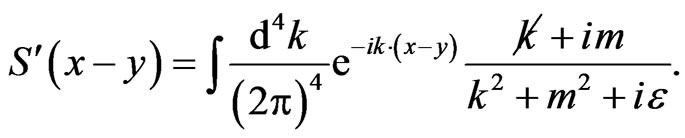 (34b)
(34b)
The chirality projectors are invariant under multiplication by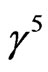 , in view of the relation
, in view of the relation  .
.
For consistency reasons, the imaginary-mass Dirac propagator should be connected with a Green function,
 (35)
(35)
where 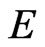 is the energy argument of the Green function and
is the energy argument of the Green function and 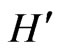 is the imaginary-mass Dirac Hamiltonian. In momentum space, we can replace
is the imaginary-mass Dirac Hamiltonian. In momentum space, we can replace 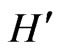 by
by . An elementary calculation then shows that
. An elementary calculation then shows that
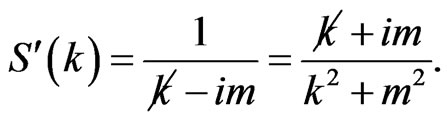 (36)
(36)
Introducing the 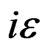 prescription as before, we find that
prescription as before, we find that
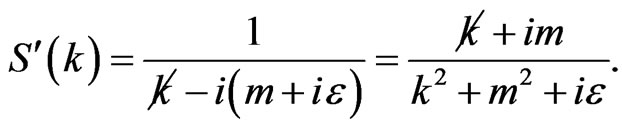 (37)
(37)
Having determined the propagator, let us briefly comment on the non-invariance of the imaginary-mass Dirac Hamiltonian under time reversal. Indeed, time reversal exchanges the inand out-states of a process. In the calculation of a cross section, one has to square an invariant amplitude, which also exchanges inand out-states, and leads to the occurrence of a propagator of the form
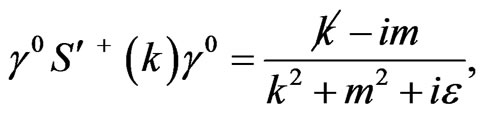 (38)
(38)
which is obtained from (37) under the replacement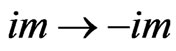 . In the time-reversed Hamiltonian, according to Ref. [40], the same replacement takes place. So, the non-invariance under time reversal of the imaginarymass Dirac equation does not necessarily lead to an inconsistent formalism within field theory.
. In the time-reversed Hamiltonian, according to Ref. [40], the same replacement takes place. So, the non-invariance under time reversal of the imaginarymass Dirac equation does not necessarily lead to an inconsistent formalism within field theory.
4. Inversion of the Mass Term
It is instructive to consider the Hamiltonian which is obtained from the imaginary-mass Dirac Hamiltonian in Equation (3) by the replacement , which amounts to an inversion of the sign of the mass term,
, which amounts to an inversion of the sign of the mass term,
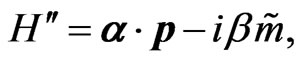 (39)
(39)
A preliminary remark is in order. Within  symmetric quantum mechanics [30-38], the one-dimensional quantum mechanical Hamiltonians
symmetric quantum mechanics [30-38], the one-dimensional quantum mechanical Hamiltonians 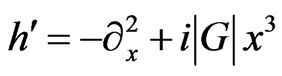 and
and 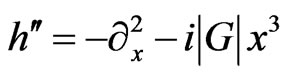 (with x being the coordinate) have been used as paradigmatic examples of an anharmonic (cubic) oscillator with imaginary coupling
(with x being the coordinate) have been used as paradigmatic examples of an anharmonic (cubic) oscillator with imaginary coupling . The Hamiltonians
. The Hamiltonians 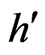 and
and 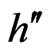 have the same spectrum [31,33,37,38], and moreover, the eigenvalues can be shown to be analytic functions in the complex G plane where
have the same spectrum [31,33,37,38], and moreover, the eigenvalues can be shown to be analytic functions in the complex G plane where , and the g plane has a branch cut along the negative real axis.
, and the g plane has a branch cut along the negative real axis.
As is to be expected, the Hamiltonians  and
and  have the same spectrum, because
have the same spectrum, because 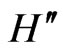 fulfills the same algebraic relations (9a) and (9b) as
fulfills the same algebraic relations (9a) and (9b) as . Moreover, the plane-wave eigenstates of
. Moreover, the plane-wave eigenstates of 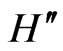 are solutions of the covariant equation
are solutions of the covariant equation
 (40)
(40)
where
 (41)
(41)
for positive-energy and negative-energy states, respectively. We find
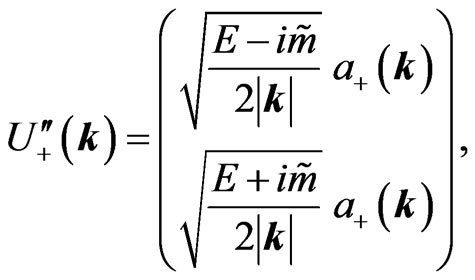 (42a)
(42a)
 (42b)
(42b)
The negative-energy eigenstates are given as
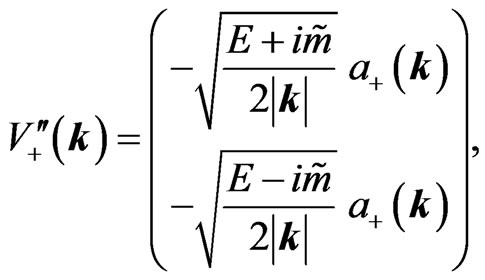 (43a)
(43a)
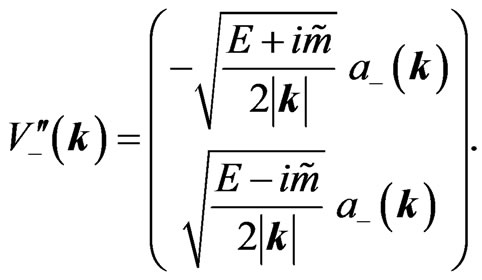 (43b)
(43b)
The states are normalized with respect to the condition
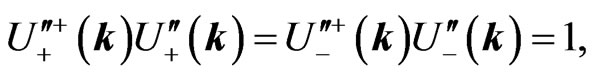 (44a)
(44a)
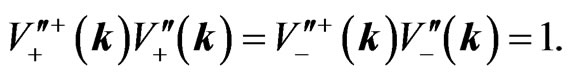 (44b)
(44b)
We normalize the  and
and 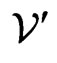 bispinors according to
bispinors according to
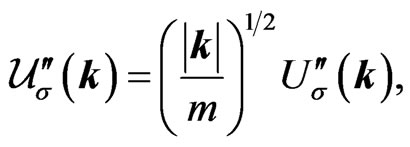 (45a)
(45a)
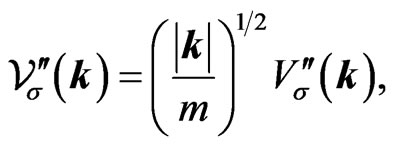 (45b)
(45b)
and obtain the following two relations,
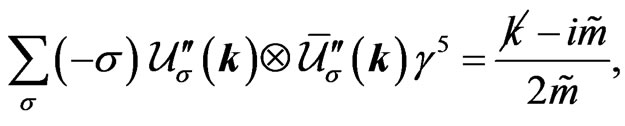 (46a)
(46a)
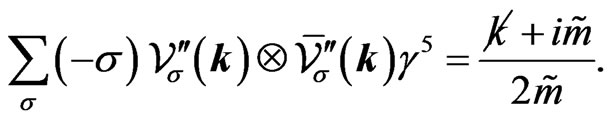 (46b)
(46b)
These are the analogues of Equations (31a) and (31b) and differ from Equations (31a) and (31b) by the replacement  in the numerator. However, in the denominator no change takes place, because the denominator is obtained as
in the numerator. However, in the denominator no change takes place, because the denominator is obtained as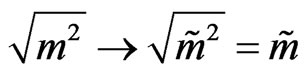 . The field operator is
. The field operator is
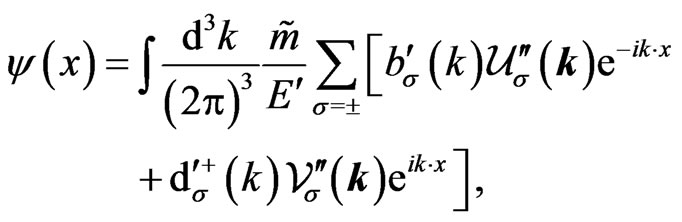 (47)
(47)
with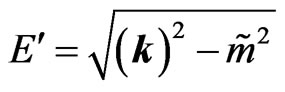 , and with an obvious identification of the field operators according to Equation (27). The nonvanishing anticommutators read as follows,
, and with an obvious identification of the field operators according to Equation (27). The nonvanishing anticommutators read as follows,
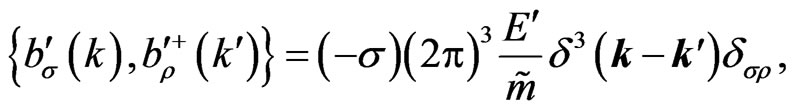 (48a)
(48a)
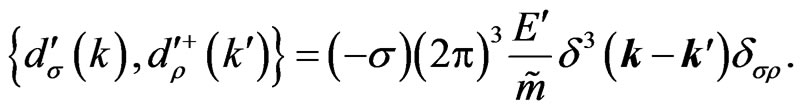 (48b)
(48b)
These imply that the inversion of the mass term does not change the fact that again, right-handed particle and left-handed antiparticle states acquire a negative norm. It is very instructive to clarify by an explicit, detailed calculation that the inversion of the mass term does not change the pattern by which helicity components are suppressed for particle and antiparticle states.
5. Conclusions
In the current work, we investigate the relativistic (tachyonic) quantum theory defined by the Hamiltonian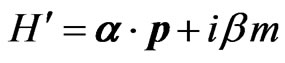 , which is obtained from the ordinary Dirac Hamiltonian by the simple replacement
, which is obtained from the ordinary Dirac Hamiltonian by the simple replacement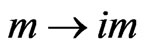 . In Section 2, we show that the Hamiltonian
. In Section 2, we show that the Hamiltonian 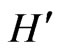 is pseudoHermitian and has an additional quasi-pseudo-Hermitian property given in Equation (9b). Eigenvalues come in a specific structure in the complex plane. Namely, if E is a resonance eigenvalue, so is
is pseudoHermitian and has an additional quasi-pseudo-Hermitian property given in Equation (9b). Eigenvalues come in a specific structure in the complex plane. Namely, if E is a resonance eigenvalue, so is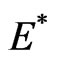 ,
,  , and
, and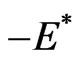 . This pattern is manifest in the spectrum calculated for the tachyonic Dirac Hamiltonian
. This pattern is manifest in the spectrum calculated for the tachyonic Dirac Hamiltonian 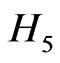 in Ref. [2] and in the spectrum of
in Ref. [2] and in the spectrum of 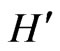 calculated here. Plane-wave solutions of the imaginary-mass Dirac equation are given in Equations (19) and (20).
calculated here. Plane-wave solutions of the imaginary-mass Dirac equation are given in Equations (19) and (20).
In Section 3, we complement recent work on the tachyonic Dirac Hamiltonian [2] and discuss the quantization of the spin one-half theory defined by the imaginary-mass Dirac Hamiltonian. We find helicity-dependent anticommutators as given in Equation (28). For both the imaginarymass as well as the tachyonic Dirac Hamiltonian, the oneparticle states of right-handed helicity acquire a negative norm and can be excluded from the physical spectrum by a Gupta-Bleuler type condition. Likewise, antiparticle states of left-handed helicity are excluded from the physical spectrum. Compact representations are found for the spin sums (31) which enter the field anticommutator and the propagator. In Section 4, we find that an inversion of the mass term does not change the fact that only left-handed helicity is allowed for particles described by a tachyonic generalization of the Dirac equation, and only right-handed helicity for antiparticles.
Obviously, the left-handedness of particle states and the right-handedness of antiparticles states imply that both the tachyonic Dirac equation as well as the imaginary-mass Dirac equation represent candidates for the description of neutrinos, if improved experimental techniques [10,18,19,41,42] finally allow us to decide if neutrinos propagate at superluminal or subluminal speeds, which would amount to deciding whether the neutrino mass square is positive or negative [9-16].
6. Acknowledgements
This work was supported by the NSF and by the National Institute of Standards and Technology (precision measurement grant). The author acknowledges helpful conversations with B. J. Wundt.
REFERENCE
[1] U. D. Jentschura and B. J. Wundt, “Pseudo-Hermitian Quantum Dynamics of Tachyonic Spin-1/2 Particles,” Journal of Physics A: Mathematical and Theoretical, e-print arXiv: 1110.4171, in Press.
[2] U. D. Jentschura and B. J. Wundt, “Localizability of Tachyonic Particles and Neutrinoless Double Beta Decay,” The European Physical Journal C—Particles and Fields, Vol. 72, No. 2, 2012, p. 1894. doi:10.1140/epjc/s10052-012-1894-4
[3] O. M. P. Bilaniuk, V. K. Deshpande and E. C. G. Sudarshan, “‘Meta’ Relativity,” American Journal of Physics, Vol. 30, No. 10, 1962, p. 718. doi:10.1119/1.1941773
[4] G. Feinberg, “Possibility of Faster-than-Light Particles,” Physical Review, Vol. 159, No. 5, 1967, p. 1089. doi:10.1103/PhysRev.159.1089
[5] M. E. Arons and E. C. G. Sudarshan, “Lorentz Invariance, Local Field Theory, and Faster-than-Light Particles,” Physical Review, Vol. 173, No. 5, 1968, p. 1622. doi:10.1103/PhysRev.173.1622
[6] J. Dhar and E. C. G. Sudarshan, “Quantum Field Theory of Interacting Tachyons,” Physical Review, Vol. 174, No. 5, 1968, p. 1808. doi:10.1103/PhysRev.174.1808
[7] O.-M. Bilaniuk and E. C. G. Sudarshan, “Causality and Space-Like Signals,” Nature, Vol. 223, 1969, pp. 386-387. doi:10.1038/223386b0
[8] G. Feinberg, “Lorentz Invariance of Tachyon Theories,” Physical Review D, Vol. 17, No. 6, 1978, p. 1651. doi:10.1103/PhysRevD.17.1651
[9] http://cupp.oulu.fi/neutrino/nd-mass.html
[10] R. G. H. Robertson, T. J. Bowles, G. J. Stephenson, D. L. Wark, J. F. Wilkerson and D. A. Knapp, “Limit on 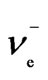 Mass from Observation of the β Decay of Molecular Tritium,” Physical Review Letters, Vol. 67, No. 8, 1991, p. 957. doi:10.1103/PhysRevLett.67.957
Mass from Observation of the β Decay of Molecular Tritium,” Physical Review Letters, Vol. 67, No. 8, 1991, p. 957. doi:10.1103/PhysRevLett.67.957
[11] K. Assamagan, et al., “Measurement of the Muon Momentum in Pion Decay at Rest Using a Surface Muon Beam,” Physical Letters B, Vol. 335, No. 2, 1994, pp. 231- 236. doi:10.1016/0370-2693(94)91419-2
[12] W. Stoeffl and D. J. Decman, “Anomalous Structure in the Beta Decay of Gaseous Molecular Tritium,” Physical Review Letters, Vol. 75, No. 18, 1995, p. 3237. doi:10.1103/PhysRevLett.75.3237
[13] K. Assamagan, et al., “Upper Limit of the Muon-Neutrino Mass and Charged-Pion Mass from Momentum Analysis of a Surface Muon Beam,” Physical Review D, Vol. 53, No. 11, 1996, p. 6065. doi:10.1103/PhysRevD.53.6065
[14] C. Weinheimer, B. Degen, A. Bleile, J. Bonn, L. Bornschein, O. Kazachenko, A. Kovalik and E. Otten, “High Precision Measurement of the Tritium Β Spectrum near Its Endpoint and upper Limit on the Neutrino Mass,” Physics Letters B, Vol. 460, No. 1-2, 1999, pp. 219-226. doi:10.1016/S0370-2693(99)00780-7
[15] V. M. Lobashev, et al., “Direct Search for Mass of Neutrino and Anomaly in the Tritium Beta-Spectrum,” Physics Letters B, Vol. 460, No. 1-2, 1999, pp. 227-235. doi:10.1016/S0370-2693(99)00781-9
[16] A. I. Belesev, et al., “Investigation of Space-Charge Effects in Gaseous Tritium as a Source of Distortions of the Beta Spectrum Observed in the Troitsk Neutrino-Mass Experiment,” Physics of Atomic Nuclei, Vol. 71, No. 3, 2008, pp. 427-436. doi:10.1134/S1063778808030046
[17] G. R. Kalbfleisch, N. Baggett, E. C. Fowler and J. Alspector, “Experimental Comparison of Neutrino, Antineutrino, and Muon Velocities,” Physical Review Letters, Vol. 43, No. 19, 1979, p. 1361. doi:10.1103/PhysRevLett.43.1361
[18] P. Adamson, et al., “Measurement of Neutrino Velocity with the MINOS Detectors and NuMI Neutrino Beam,” Physical Review D, Vol. 76, No. 7, 2007, p. 072005. doi:10.1103/PhysRevD.76.072005
[19] M. Antonello, et al., “ICARUS Collaboration, Measurement of the Neutrino Velocity with the ICARUS Detector at the CNGS Beam,” e-print arXiv: 1203.3433v3.
[20] J. Ciborowski, “Hypothesis of Tachyonic Neutrinos,” Acta Physica Polonica B, Vol. 29, No. 1-2, 1998, pp. 113- 121.
[21] M. Dracos, “On Behalf of the OPERA Collaboration, the Neutrino Velocity Measurement by OPERA Experiment,” The XXV International Conference on Neutrino Physics and Astrophysics, Kyoto, 3-9 June 2012, 15 p. http://regmedia.co.uk/2012/06/11/neutrinos_not_ftl_slides.pdf
[22] A. Chodos, A. I. Hauser and V. A. Kostelecky, “The Neutrino as a Tachyon,” Physics Letters B, Vol. 150, No. 6, 1985, pp. 431-435. doi:10.1016/0370-2693(85)90460-5
[23] A. Chodos, V. A. Kostelecky, R. Potting and E. Gates, “Null Experiments for Neutrino Masses,” Modern Physics Letters A, Vol. 7, No. 6, 1992, p. 467. doi:10.1142/S0217732392000422
[24] A. Chodos and V. A. Kostelecky, “Nuclear Null Tests for Spacelike Neutrinos,” Physics Letters B, Vol. 336, No. 3-4, 1994, pp. 295-302. doi:10.1016/0370-2693(94)90535-5
[25] J. Rembielinski, “Tachyons and Preferred Frames,” International Journal of Modern Physics A, Vol. 12, No. 9, 1997, p. 1677.
[26] T. Chang, “A New Dirac-Type Equation for Tachyonic Neutrinos,” e-print arXiv: hep-th/0011087.
[27] T. Chang, “Parity Violation and a Preferred Frame,” e-print arXiv: quant-ph/0204002.
[28] J. Bandukwala and D. Shay, “Theory of Free, Spin-$1/2$ Tachyons,” Physical Review D, Vol. 9, No. 4, 1974, p. 889. doi:10.1103/PhysRevD.9.889
[29] W. Pauli, “On Dirac’s New Method of Field Quantization,” Reviews of Modern Physics, Vol. 15, No. 3, 1943, p. 175. doi:10.1103/RevModPhys.15.175
[30] C. M. Bender and S. Boettcher, “Real Spectra in NonHermitian Hamiltonians Having PT Symmetry,” Physical Review Letters, Vol. 80, No. 24, 1998, p. 5243. doi:10.1103/PhysRevLett.80.5243
[31] C. M. Bender and G. V. Dunne, “Large-Order Perturbation Theory for a Non-Hermitian PT-Symmetric Hamiltonian,” Journal of Mathematical Physics, Vol. 40, No. 10, 1999, pp. 4616-4621. doi:10.1063/1.532991
[32] C. M. Bender, S. Boettcher and P. N. Meisinger, “PT-Symmetric Quantum Mechanics,” Journal of Mathematical Physics, Vol. 40, No. 5, 1999, pp. 2201-2229. doi:10.1063/1.532860
[33] C. M. Bender and E. J. Weniger, “Numerical Evidence That the Perturbation Expansion for a Non-Hermitian PT-Symmetric Hamiltonian Is Stieltjes,” Journal of Mathematical Physics, Vol. 42, No. 5, 2001, pp. 2167-2183. doi:10.1063/1.1362287
[34] C. M. Bender, D. C. Brody and H. F. Jones, “Complex Extension of Quantum Mechanics,” Physical Review Letters, Vol. 89, No. 27, 2002, Article ID: 270401. doi:10.1103/PhysRevLett.89.270401
[35] A. Mostafazadeh, “Pseudo-Hermiticity versus PT-Symmetry III: Equivalence of Pseudo-Hermiticity and the Presence of Antilinear Symmetries,” Journal of Mathematical Physics, Vol. 43, No. 8, 2002, pp. 3944-3951. doi:10.1063/1.1489072
[36] A. Mostafazadeh, “Pseudo-Hermiticity and Generalized PTand CPT-Symmetries,” Journal of Mathematical Physics, Vol. 44, No. 3, 2003, pp. 974-989. doi:10.1063/1.1539304
[37] U. D. Jentschura, A. Surzhykov and J. Zinn-Justin, “Unified Treatment of Even and Odd Anharmonic Oscillators of Arbitrary Degree,” Physical Review Letters, Vol. 102, No. 1, 2009, Article ID: 011601. doi:10.1103/PhysRevLett.102.011601
[38] U. D. Jentschura, A. Surzhykov and J. Zinn-Justin, “MultiInstantons and Exact Results III: Unification of Even and Odd Anharmonic Oscillators,” Annals of Physics, Vol. 325, No. 5, 2010, pp. 1135-1172. doi:10.1016/j.aop.2010.01.002
[39] C. Itzykson and J. B. Zuber, “Quantum Field Theory,” McGraw-Hill, New York, 1980.
[40] C. M. Bender, J. Brod, A. Refig and M. E. Reuter, “The C Operator in PT-Symmetric Quantum Theories,” Journal of Physics A: Mathematical and General, Vol. 37, No. 43, 2004, p. 10139. doi:10.1088/0305-4470/37/43/009
[41] R. M. Bionta, “Detection of a Rare Event on 23 February 1987 by the Neutrino Radiation Detector under Mont Blanc,” JETP Letters, Vol. 45, No. 10, 1987, pp. 593-595.
[42] T. Adam, et al., “OPERA Collaboration, Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” e-print arXiv: 1109.4897v4.

