Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21675,8 pages DOI:10.4236/jmp.2012.38087
Nonlinear Schroedinger Solitons in Massive Yang-Mills Theory and Partial Localization of Dirac Matter
Department of Physics, University of Athens, Athens, Greece
Email: fdiakono@phys.uoa.gr
Received April 20, 2012; revised May 25, 2012; accepted June 18, 2012
Keywords: Yang-Mills Solitons; Non-Linear Schroedinger Equation; Dirac Fermions; Localization
ABSTRACT
We investigate the classical dynamics of the massive SU(2) Yang-Mills field in the framework of multiple scale perturbation theory. We show analytically that there exists a subset of solutions having the form of a kink soliton, modulated by a plane wave, in a linear subspace transverse to the direction of free propagation. Subsequently, we explore how these solutions affect the dynamics of a Dirac field possessing an SU(2) charge. We find that this class of YangMills configurations, when regarded as an external field, leads to the localization of the fermion along a line in the transverse space. Our analysis reveals a mechanism for trapping SU(2) charged fermions in the presence of an external Yang-Mills field indicating the non-abelian analogue of Landau localization in electrodynamics.
1. Introduction
Over the last decades, the classical dynamics of YangMills (YM) field theory has been thoroughly investigated in the literature, both in Minkowski and in Euclidean space (see, e.g., [1] and references therein). The motivation for this study has been mainly the effort to understand the vacuum structure of non-abelian gauge theories like Quantum Chromodynamics (QCD). In a spatially homogeneous description, one can show that the YM classical dynamics possesses a chaotic component attributed to the nonlinear form of the YM self-interaction [1-6]. Generalizing to the case of inhomogeneous solutions, the conformal structure of the YM Lagrangian and the associated absence of a characteristic scale does not permit the presence of localized solutions [7], and complicated patterns with fractal characteristics may appear [8,9]. Recently, it has been argued that classical YangMills solutions may have impact on the properties of the quantum gauge fields. In particular, in [10-12], it was shown that periodic solutions of a special choice for the YM field configuration (Smilga’s choice [1]) after quantization lead to a description of the gauge field propagator compatible with the calculations performed in lattice gauge theories.
On the other hand, localized inhomogeneous solutions could permit a particle interpretation of the YM-field, which may be relevant for several applications where quasi-particles are involved. Such a scenario appears, for example, when the YM-field is coupled to a condensate, breaking spontaneously the underlying gauge symmetry, or when the YM-field itself condensates at particular thermodynamic conditions. In these cases the gauge field can acquire a mass introducing a scale in the YM-theory and bypassing the restrictions of the Coleman theorem [7]. This allows for spatially inhomogeneous localized classical solutions—at least at the level of an effective theory.
In the present work, we follow this line of thoughts trying to explore the space of classical solutions in massive SU(2) Yang-Mills theory. Our primary interest is to display the capacity of the theory in terms of possible classical dynamical behavior, as well as the influence of the choice for the YM-field initial configuration on this dynamics. In particular we will show that at a given combination of scales the classical Yang-Mills theory contains the non-linear Schrödinger equation regime. We start our considerations with a Langrangian describing the interaction of the Yang-Mills field with a scalar field. Then we assume, at the level of the Langrangian, that the scalar field is constant and we remain with a massive Yang-Mills theory. The effect of the spatio-temporal fluctuations of the scalar field is considered in [13]. As a next step, making a choice similar to Smilga’s [1] , we are able to construct within the framework of a multiscale perturbation theory a class of solutions which are localized along a line in the plane transverse to the momentum of the gauge field.
Furthermore, we study the dynamics of Dirac fields in the presence of such a gauge field configuration, considering the latter as an external classical field. We show that the Dirac field becomes bound in the subspace where the external gauge field is localized.
The paper is organized as follows: in section 2 we present the Lagrangian of the considered SU(2) YM field theory, we discuss the multiple scale approach used to solve the corresponding equations of motion and we obtain the associated solutions for the gauge field. We also give an interpretation of the involved parameters. In Section 3 we use the solution found in Section 2 as an external field for the Dirac dynamics of an SU(2)-charged matter field. Finally we end up, in section 4, with a summary and perspectives of our work.
2. Soliton-Like Solutions in the Massive Yang-Mills Dynamics
We start our analysis by considering the Lagrangian describing the interaction of the SU(2) Yang-Mills field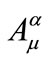 with a charged scalar field
with a charged scalar field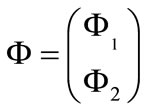 :
:
 (1)
(1)
where g is a dimensionless coupling and  is the self-interaction potential of the scalar field which we need not to specify more. We only assume that the potential possesses at least one stable equilibrium point. As usual, we use greek letters to denote the space-time components and latin letters to denote the Lie group components of the YM fields. For the SU(2) case
is the self-interaction potential of the scalar field which we need not to specify more. We only assume that the potential possesses at least one stable equilibrium point. As usual, we use greek letters to denote the space-time components and latin letters to denote the Lie group components of the YM fields. For the SU(2) case 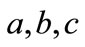 take the values 1, 2, 3. Let us now further assume that the scalar field is constant (independent of space-time) and equal to a value corresponding to a stable equilibrium point of V. Then the Lagrangian in Equation (1), up to the constant term
take the values 1, 2, 3. Let us now further assume that the scalar field is constant (independent of space-time) and equal to a value corresponding to a stable equilibrium point of V. Then the Lagrangian in Equation (1), up to the constant term 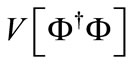 which can be neglected, becomes:
which can be neglected, becomes:
 (2)
(2)
where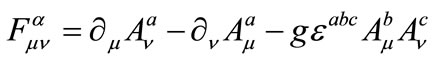 .
.
In Equation (2), 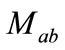 is the mass matrix of the YM field components which is diagonal in the group indices
is the mass matrix of the YM field components which is diagonal in the group indices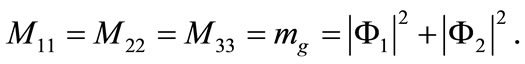 The corresponding evolution equations are given by:
The corresponding evolution equations are given by:
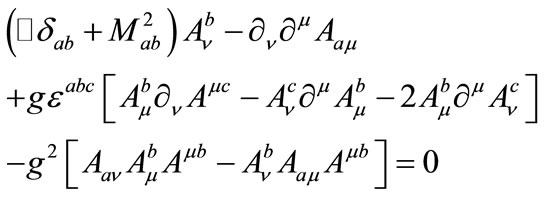 (3)
(3)
where 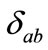 and
and 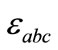 are the Kronecker delta and the full antisymmetric tensor in SU(2) space, respectively. We use the multiple-scale perturbation theory [14] to solve the nonlinear Equation (3): first, we introduce the new space-time independent variables,
are the Kronecker delta and the full antisymmetric tensor in SU(2) space, respectively. We use the multiple-scale perturbation theory [14] to solve the nonlinear Equation (3): first, we introduce the new space-time independent variables, 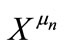 , as well as the partial derivatives thereof:
, as well as the partial derivatives thereof:
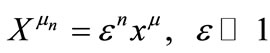
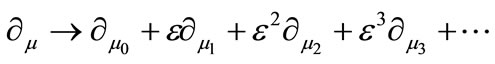 (4)
(4)
and we assume that the corresponding field variables are expanded into an asymptotic series of the form:
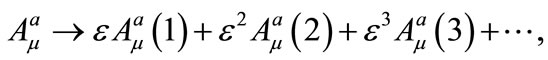 (5)
(5)
where 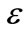 is a formal small parameter (connected to the kink soliton amplitude and inverse width—see below). Substituting the above expressions into the equations of motion, and equating coefficients of the same powers of
is a formal small parameter (connected to the kink soliton amplitude and inverse width—see below). Substituting the above expressions into the equations of motion, and equating coefficients of the same powers of , we obtain a set of equations from which
, we obtain a set of equations from which 
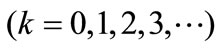 can be successively determined. Notice that each field
can be successively determined. Notice that each field 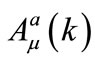 is to be determined so as to be bounded (nonsecular) at each stage of the perturbation.
is to be determined so as to be bounded (nonsecular) at each stage of the perturbation.
In order to solve the evolution equations arising at various orders in  one can make an appropriate choice for the gauge field components, allowing for their decoupling—at least in the lowest orders in the perturbation expansion. Here, we will use the following configuration for the gauge fields:
one can make an appropriate choice for the gauge field components, allowing for their decoupling—at least in the lowest orders in the perturbation expansion. Here, we will use the following configuration for the gauge fields:
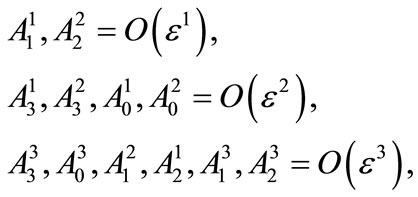 (6)
(6)
which allows us to decouple the corresponding equations of motion up to the order . This configuration is in fact a generalization of the Smilga’s choice [1] for spatial non-homogeneous fields (see Appendix A).
. This configuration is in fact a generalization of the Smilga’s choice [1] for spatial non-homogeneous fields (see Appendix A).
The resulting simplified equations for the component 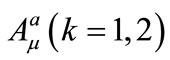 are given as follows:
are given as follows:
 (7)
(7)
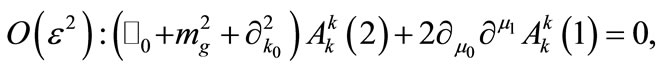 (8)
(8)
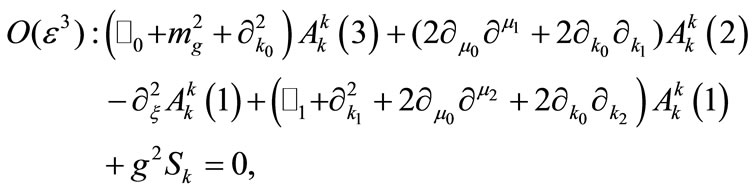 (9)
(9)
where we have used the notation:
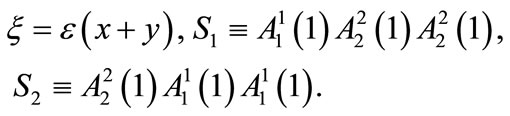
Here we should note that there is no summation over repeated latin indices in Equations (7)-(9). The equations of the remaining components are obtained in a similar way. Equation (9) still contains a coupling between 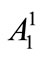 and
and , due to the nonlinear term, which can be resolved using the further assumption:
, due to the nonlinear term, which can be resolved using the further assumption: 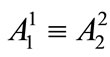 [1].
[1].
Equations (7)-(9) can be solved self-consistently, leading to the following equations satisfied by the unknown  component:
component:
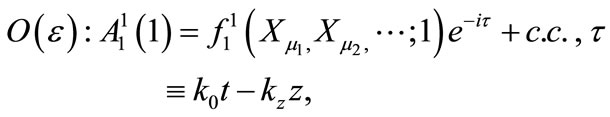 (10)
(10)
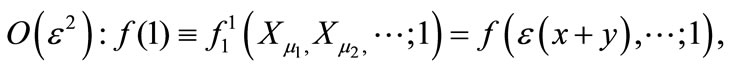 (11)
(11)
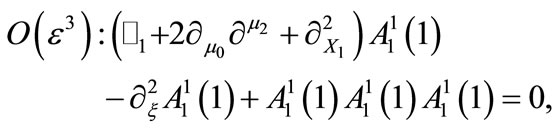 (12)
(12)
where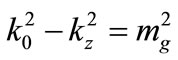 . After some simple algebraic manipulations, the nonlinear evolution equation (12) takes the usual form of a nonlinear Schroedinger (NLS) equation with a repulsive (self-defocusing) nonlinearity (due to
. After some simple algebraic manipulations, the nonlinear evolution equation (12) takes the usual form of a nonlinear Schroedinger (NLS) equation with a repulsive (self-defocusing) nonlinearity (due to 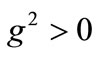 in the nonlinear term):
in the nonlinear term):
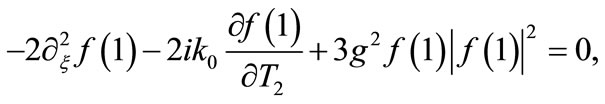 (13)
(13)
which has been studied extensively in various branches of physics and, especially, in nonlinear optics [15] and atomic Bose-Einstein condensates [16]. The above NLS equation possesses a stationary kink-type (alias “dark”) soliton solution [17], given by:
 (14)
(14)
where 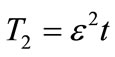 and
and . Details on the derivation of Equation (13) are provided in Appendix A.
. Details on the derivation of Equation (13) are provided in Appendix A.
In Figure 1 we show a plot of the solution (14) using the parameter values: a = 53 MeV, ε = 0.1, k0 = 550 MeV and F0 = 3.2 MeV1/2. It can be seen that the obtained form is characterized by a free propagation in z-direction and a kink-soliton profile in the ξ-direction, with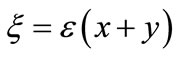 .
.
It is obvious that Equation (13), due to the presence of a first derivative in time, breaks the Lorentz invariance of the initial Lagrangian density; this is in accordance to the assumptions made to obtain the consistent solution (14) decomposing space-time in two inequivalent subspaces (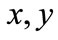 and
and ). This property is inevitably expected to hold for gauge field solutions varying over a finite space interval. Additionally, gauge invariance is violated from the very beginning due to the presence of the gauge field mass term. However, the validity of the solution (14) is restricted to specific space-time scales and, therefore, there is no apparent contradiction with first principles.
). This property is inevitably expected to hold for gauge field solutions varying over a finite space interval. Additionally, gauge invariance is violated from the very beginning due to the presence of the gauge field mass term. However, the validity of the solution (14) is restricted to specific space-time scales and, therefore, there is no apparent contradiction with first principles.
After suitable rescaling in order to introduce dimensionless quantities, we have checked the validity of the solution (14) through numerical integration of Equation (3). Adapting the choice (6) for the configuration of the gauge fields we concentrate on the equations of motion for the diagonal components 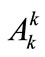 (
(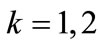 ). The results of our numerical treatment in 1 + 1 dimensions for
). The results of our numerical treatment in 1 + 1 dimensions for  is shown in the contour plot of Figure 2. Notice that
is shown in the contour plot of Figure 2. Notice that  holds for all considered times in accordance with our choice [1]. The solution (14) holds for more than 100 field oscillations indicating its remarkable stability and supporting the validity of our perturbative scheme.
holds for all considered times in accordance with our choice [1]. The solution (14) holds for more than 100 field oscillations indicating its remarkable stability and supporting the validity of our perturbative scheme.
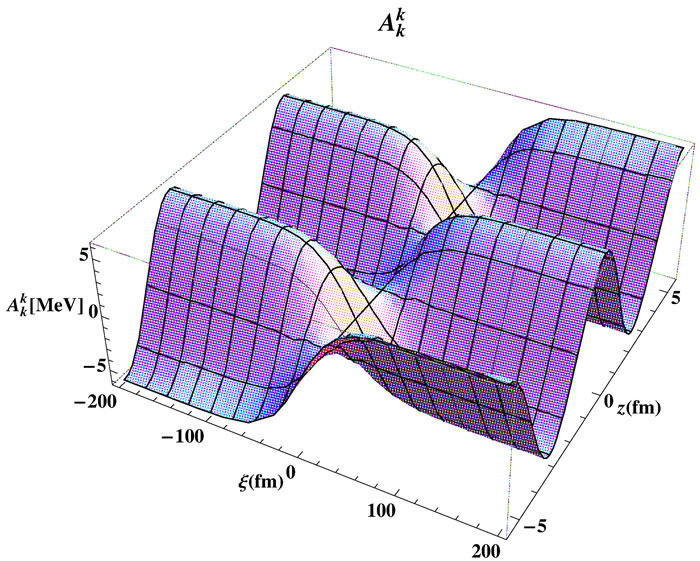
Figure 1. The kink-type solution of Equation (14) for the components of the SU(2) gauge field, using the parameter values: a = 53 MeV, ε = 0.1, k0 = 550 MeV and F0 = 3.2 MeV1/2.
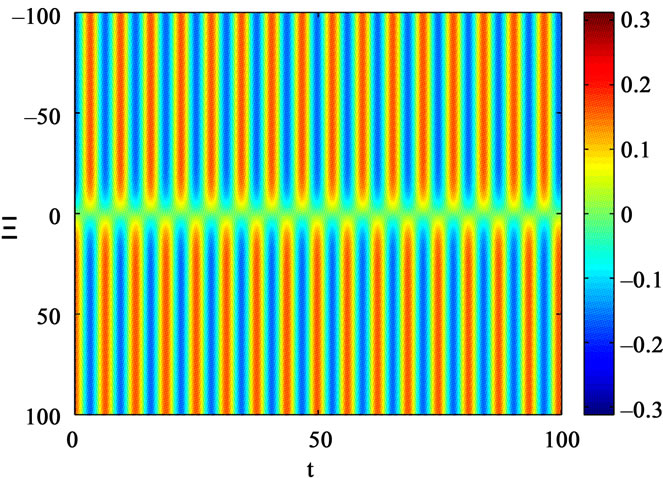
Figure 2. Contour plot of the numerical solution for  using as initial condition the analytically obtained form given by Equation (14). The length scale is
using as initial condition the analytically obtained form given by Equation (14). The length scale is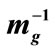 . We have also used ε = 0.1.
. We have also used ε = 0.1.
3. Partial Localization of Dirac Matter
In this section we will investigate the dynamics of an SU(2) charged Dirac field in the presence of an external gauge field which has the form found in Equation (14). The corresponding Dirac equation is written as follows:
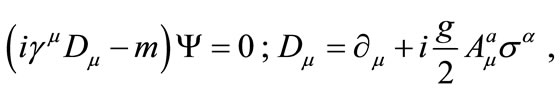 (15)
(15)
where  are the Pauli spin matrices,
are the Pauli spin matrices,  are the Dirac matrices, and
are the Dirac matrices, and
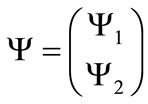
is the SU(2) doublet for the fermionic field. For the fermionic mass matrix 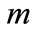 we assume a diagonal form with
we assume a diagonal form with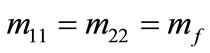 . Due to the non-abelian character of the gauge group, the equations describing the dynamics of the two charged fields
. Due to the non-abelian character of the gauge group, the equations describing the dynamics of the two charged fields  and
and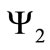 , after expanding (15) and substituting Equation (14) for the non-abelian gauge field, take the following coupled form:
, after expanding (15) and substituting Equation (14) for the non-abelian gauge field, take the following coupled form:
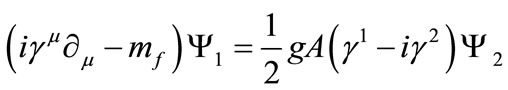 (16)
(16)
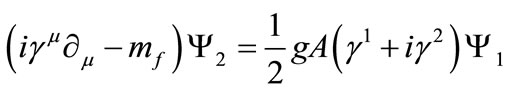 (17)
(17)
Taking into account that the expression (14) for the gauge field is non-covariant, it is consistent to consider the dynamics implied by Equations (16) and (17) in the nonrelativistic limit. For that purpose, it is necessary to write the bispinors 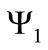 and
and 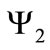 in terms of their components. In that regard, we introduce the following notation:
in terms of their components. In that regard, we introduce the following notation:
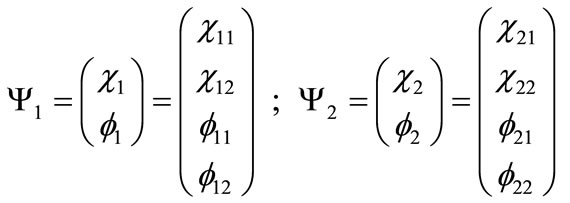 (18)
(18)
Applying the standard procedure [18] for obtaining the non-relativistic limit of Equations (16) and (17) (details of the calculations are given in Appendix B), we find the following set of coupled Schroedinger-type equations for the fermionic components 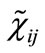
(where ):
):
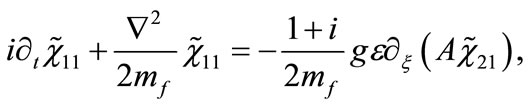 (19)
(19)
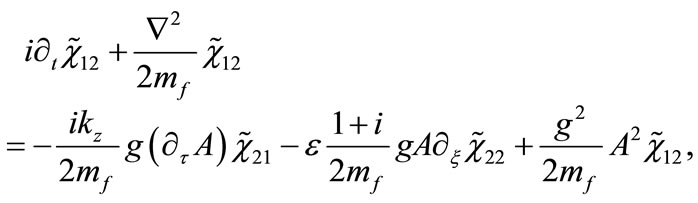 (20)
(20)
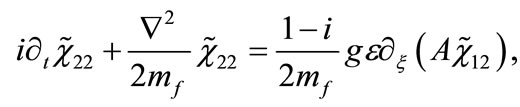 (21)
(21)
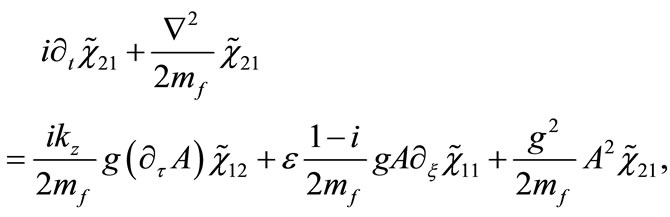 (22)
(22)
while 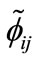 are determined through
are determined through 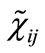 as follows:
as follows:
 (23)
(23)
 (24)
(24)
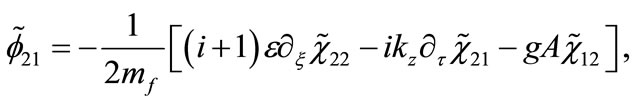 (25)
(25)
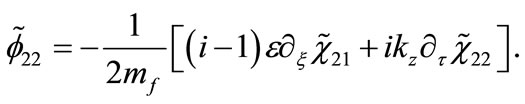 (26)
(26)
Equations (19)-(22) can be consistently reduced, using 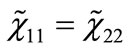 and
and 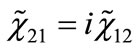 to the following two equations:
to the following two equations:
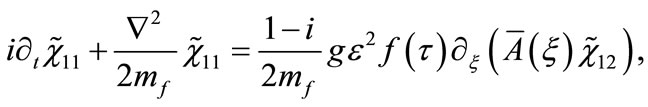 (27)
(27)
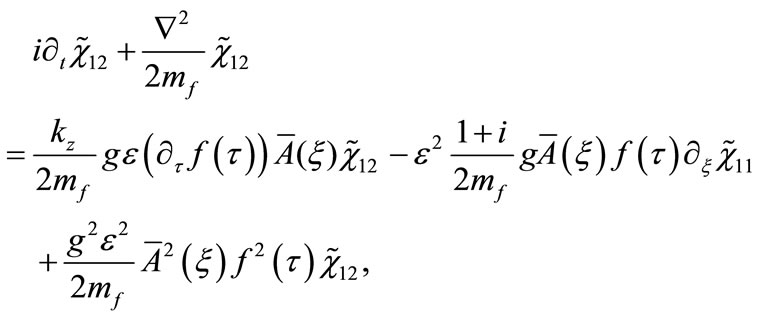 (28)
(28)
where 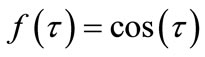 and
and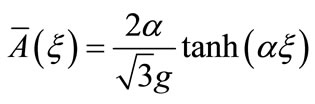 .
.
Without loss of generality we can choose 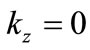 (using the rest frame of the massive gauge field as reference frame) to further simplify the above expressions. Furthermore, in order to allow for non-trivial dynamics in the fermionic field, the corresponding mass
(using the rest frame of the massive gauge field as reference frame) to further simplify the above expressions. Furthermore, in order to allow for non-trivial dynamics in the fermionic field, the corresponding mass 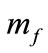 has to be small (of order
has to be small (of order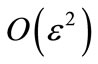 ) as compared to the gauge field mass. In this case, writing
) as compared to the gauge field mass. In this case, writing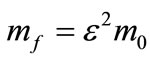 , we obtain the following system of two equations
, we obtain the following system of two equations
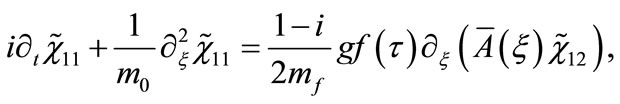 (29)
(29)
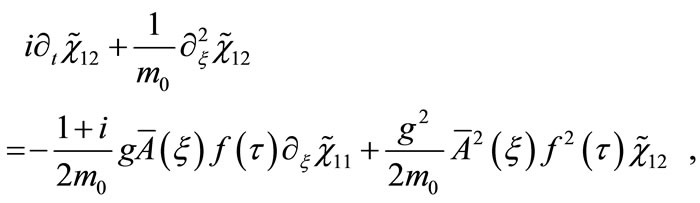 (30)
(30)
where 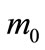 is a mass scale of the order of
is a mass scale of the order of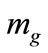 .
.
Let us now introduce the length scale 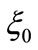 and the time scale
and the time scale 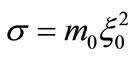 to express Equations (29) and (30) in a dimensionless form. In these units, the dimensionless frequency of the oscillating YM-field becomes:
to express Equations (29) and (30) in a dimensionless form. In these units, the dimensionless frequency of the oscillating YM-field becomes:
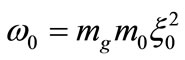 .
.
It also straightforward to define dimensionless variables 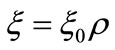 and
and . In these variables, we seek for solutions of the system (29) and (30) having the form:
. In these variables, we seek for solutions of the system (29) and (30) having the form:
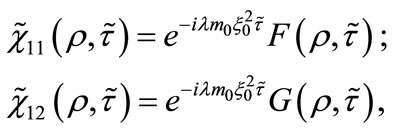 (31)
(31)
where F and G are slowly-varying functions of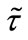 , while
, while  is the energy eigenvalue. In this limit, Equations (29) and (30) become:
is the energy eigenvalue. In this limit, Equations (29) and (30) become:
 (32)
(32)
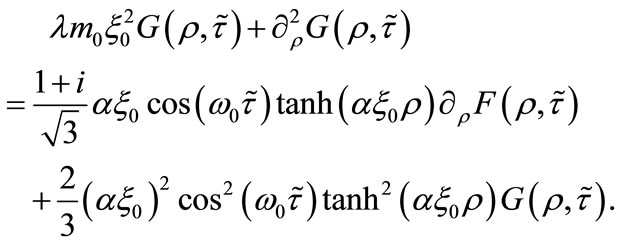 (33)
(33)
For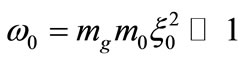 , Equations (32) and (33) can be integrated with respect to
, Equations (32) and (33) can be integrated with respect to 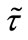 over a period
over a period 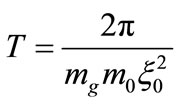
since in this time interval F and G are practically constant. Following this procedure, Equations (32) and (33) decouple and obtain the following form:
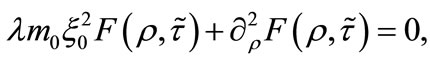 (34)
(34)
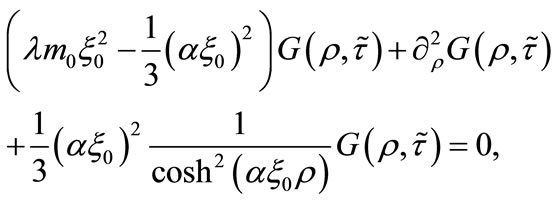 (35)
(35)
allowing as a solution a fermionic state which is bound in the  direction and has the form [19]:
direction and has the form [19]:
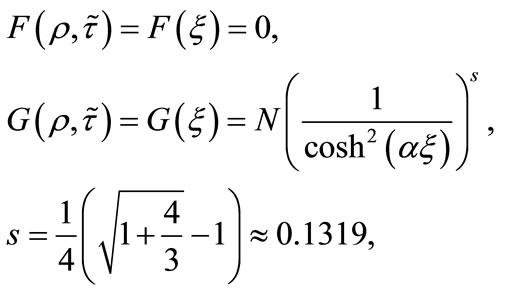 (36)
(36)
where N is a normalization constant. The state (36) resembles the Landau levels of a particle in an external magnetic field in quantum electrodynamics. In the YM case under consideration, the magnetic field is generated by the term proportional to 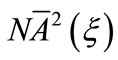 in Equation (30). The difference here is that we have a single level independently of the strength of the external Yang-Mills field. In addition, the Dirac particle is trapped only in the
in Equation (30). The difference here is that we have a single level independently of the strength of the external Yang-Mills field. In addition, the Dirac particle is trapped only in the 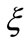 - direction, where the external field is also localized. It should be noticed that the condition
- direction, where the external field is also localized. It should be noticed that the condition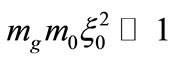 , necessary for the existence of the solution (36), can be justified by either using a large
, necessary for the existence of the solution (36), can be justified by either using a large  value or a large
value or a large 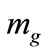 value (or both).
value (or both).
It is illuminating to give an example of the energy and length scales involved in this solution. Assuming a gauge field mass of 500 MeV and a much smaller fermionic mass i.e., of order of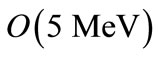 , we find that the SU(2) charged fermions are trapped in a region of radius of
, we find that the SU(2) charged fermions are trapped in a region of radius of 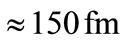 in the (x, y)-plane with energy eigenvalue
in the (x, y)-plane with energy eigenvalue 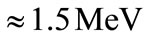 for an external field of amplitude
for an external field of amplitude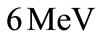 . It must be noted that for this choice of parameter values the non-relativistic approximation is valid within an error of 15% estimated by the relative magnitude of the first relativistic correction term. In Figure 3 we show the effective potential responsible for the trapping of the Dirac particle using the above mentioned parameter values. The dashed line indicates the energy
. It must be noted that for this choice of parameter values the non-relativistic approximation is valid within an error of 15% estimated by the relative magnitude of the first relativistic correction term. In Figure 3 we show the effective potential responsible for the trapping of the Dirac particle using the above mentioned parameter values. The dashed line indicates the energy 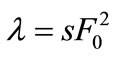 of the associated bound state in the ξ-space. The fact that this state is very close to the continuum threshold explains the absence of a second bound state. In Figure 4 we show the ξ-dependent wave function corresponding to the bound state displayed in Figure 3. The broad spatial extension of this state is attributed to the small exponent in Equation (36).
of the associated bound state in the ξ-space. The fact that this state is very close to the continuum threshold explains the absence of a second bound state. In Figure 4 we show the ξ-dependent wave function corresponding to the bound state displayed in Figure 3. The broad spatial extension of this state is attributed to the small exponent in Equation (36).

Figure 3. The effective potential responsible for the trapping of a Dirac particle with SU(2) charge emerging from the a time-dependent external Yang-Mills field of the type shown in Figure 1. The parameters values used are: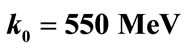 ,
,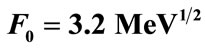 . The dashed line indicates the energy of the bound state.
. The dashed line indicates the energy of the bound state.

Figure 4. The ξ-dependent normalized wavefunction of the bound state shown in Figure 3 calculated using the same parameter values.
4. Conclusions and Discussion
We have investigated classical solutions of the SU(2) massive Yang-Mills equations in the framework of multiple scale perturbation theory. Due to the presence of the mass term, conformal symmetry is explicitly broken and the Coleman theorem does not apply [7]. Therefore, the YM dynamics in this case admit soliton-like solutions localized in a subspace of the transverse space.
Such solutions of the Yang-Mills field break both Lorentz and gauge invariance in higher orders of the perturbation expansion, in consistency with the presence of a mass term as well as the appearance of partial localization. Dirac fermions with non-vanishing SU(2) charge, when exposed in an external YM field having the form of these soliton-like solutions, become trapped in a similar way as electrons in a transverse magnetic field (Landau levels). However, the trapping of the SU(2) colored fermions is a pure dynamical effect occurring in the nonadiabatic limit of very fast oscillations of the external YM field, and occurs only along the (x + y)-direction.
Our analysis reveals a mechanism for the occurrence of localized fermionic states with SU(2) charge based on the interaction with a massive Yang-Mills field. The simplifying assumptions made in our approach (two non-vanishing equal components of the gauge field at the leading order) may restrict the profile of the found solutions allowing, on the other hand, for an analytical treatment. Despite this restriction, the main ingredients of the present study could be used as a guide to obtain more general inhomogeneous classical solutions of the massive SU(2) field. However, such a task is a subject for future investigations.
5. Acknowledgements
We thank N. G. Antoniou, E. G. Floratos and A. Tsapalis for helpful discussions. This work was partially supported by the Special Account for Research Grants of the University of Athens.
REFERENCES
- A. Smilga, “Lectures on Quantum Chromodynamics,” World Scientific, Singapore City, 2001. doi:10.1142/9789812810595
- S. G. Matinyan, G. K. Savvidy and N. G. Ter-ArutyunyanSavvidy, “Classical Yang—Mills Mechanics. Nonlinear Color Oscillations (in Russian),” Journal of Experimental and Theoretical Physics, Vol. 80, 1981, pp. 830-838.
- B. V. Chirikov and D. L. Shepelyanskii, “Stochastic Oscillations of Classical Yang-Mills Fields (in Russian),” Journal of Experimental and Theoretical Physics Letters, Vol. 34, No. 4, 1981, pp. 171-175.
- S. G. Matinyan, G. K. Savvidy and N. G. Ter-ArutyunyanSavvidy, “Stochasticity of Classical Yang-Mills Mechanics and Its Elimination by Using the Higgs Mechanism (in Russian),” Journal of Experimental and Theoretical Physics Letters, Vol. 34, No. 11, 1981, pp. 613- 616.
- S. G. Matinyan, “Dynamical Chaos of Nonabelian Gauge Fields (in Russian),” Fizika Elementarnykh Chastits I Atomnoya Yadra, Vol. 16, 1985, pp. 522-570.
- S. G. Matinyan, E. P. Prokhorenko and G. K. Savvidy, “Non-Integrability of Time Dependent Spherically Symmetric Yang-Mills Equations,” Nuclear Physics B, Vol. 258, No. 2, 1988, pp. 414-428. doi:10.1016/0550-3213(88)90273-8
- S. Coleman, “There Are No Classical Glueballs,” Communications in Mathematical Physics, Vol. 55, No. 2, 1977, pp. 113-116. doi:10.1007/BF01626513
- M. Wellner, “Evidence for a Yang-Mills Fractal,” Physical Review Letters, Vol. 68, No. 12, 1992, pp. 1811-1813. doi:10.1103/PhysRevLett.68.1811
- M. Wellner, “The Road to Fractals in a Yang-Mills System,” Physical Review E, Vol. 50, No. 2, 1994, pp. 780- 789. doi:10.1103/PhysRevE.50.780
- M. Frasca, “Strongly Coupled Quantum Field Theory,” Physical Review D, Vol. 73, No. 4, 2006, Article ID: 027701. doi:10.1103/PhysRevD.73.049902
- M. Frasca, “Infrared Gluon and Ghost Propagators,” Physics Letters B, Vol. 670, No. 1, 2008, pp. 73-77. doi:10.1016/j.physletb.2008.10.022
- M. Frasca, “Mapping a Massless Scalar Field Theory on a Yang-Mills Theory: Classical Case,” Modern Physics Letters A, Vol. 24, No. 30, 2009, pp. 2425-2432. doi:10.1142/S021773230903165X
- V. Achilleos, F. K. Diakonos, D. J. Frantzeskakis, G. C. Katsimiga, X. N. Maintas, C. E. Tsagkarakis and A. Tsapalis, “A Multi-Scale Perturbative Approach to SU(2)- Higgs Classical Dynamics: Stability of Nonlinear Plane Waves And Bounds of the Higgs Field Mass,” Physical Review D, Vol. 85, No. 2, Article ID: 027702. doi:10.1103/PhysRevD.85.027702
- A. Jeffrey and T. Kawahara, “Asymptotic Methods in Nonlinear Wave Theory,” Pitman, London, 1982.
- Yu. S. Kivshar and B. Luther-Davies, “Dark Optical Solitons: Physics and Applications,” Physics Reports, Vol. 298, No. 2-3, 1998, pp. 81-197. doi:10.1016/S0370-1573(97)00073-2
- D. J. Frantzeskakis, “Dark Solitons in Atomic Bose-Einstein Condensates: From Theory to Experiments,” Journal of Physics A-Mathematical and Theoretical, vol. 43, no. 21, 2010.
- V. E. Zakharov and A. B. Shabat, “Interaction between Solitons in a Stable Medium (in Russian),” Journal of Experimental and Theoretical Physics, Vol. 64, No. 5, 1973, pp. 1627-1639.
- J. D. Bjorken and S. D. Drell, “Relativistic Quantum Mechanics,” McGraw-Hill, New York, 1978.
- L. D. Landau and E. M. Lifshitz, “Quantum Mechanics,” Pergamon Press, Oxford, 1991.
Appendix A
Using the classification of the gauge fields in orders of  as stated in Equations (6), we can write the equations of motion for the components
as stated in Equations (6), we can write the equations of motion for the components ,
,  as follows:
as follows:
 (A1)
(A1)
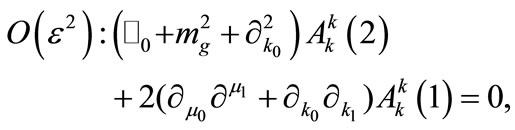 (A2)
(A2)
 (A3)
(A3)
where 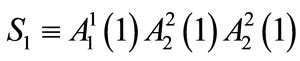 and
and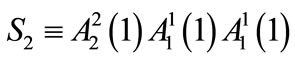 .
.
The non-diagonal equations, as well as the equations for the case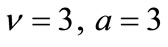 , are obtained in a similar way and their consistency with the choice in Equation (6) implies the following condition:
, are obtained in a similar way and their consistency with the choice in Equation (6) implies the following condition:
 (A4)
(A4)
for every . Thus, Equation (A3) becomes:
. Thus, Equation (A3) becomes:
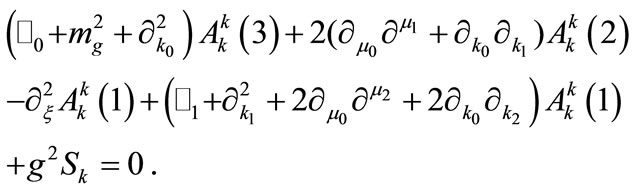 (A5)
(A5)
In Equation (A5) the fields 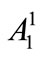 and
and 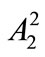 are still coupled due to the presence of the nonlinear term
are still coupled due to the presence of the nonlinear term ; nevertheless, we can readily resolve this problem by assuming that
; nevertheless, we can readily resolve this problem by assuming that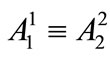 . Equation (A1) reveals the dependence on the normal scales
. Equation (A1) reveals the dependence on the normal scales 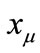 (in the first order of the perturbation expansion) of the gauge field, as it admits a harmonic solution for
(in the first order of the perturbation expansion) of the gauge field, as it admits a harmonic solution for 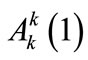 of the form:
of the form:
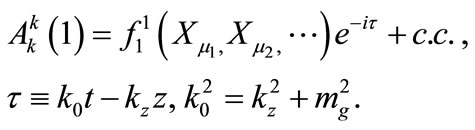 (A6)
(A6)
The function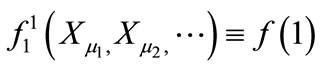 , which is for the moment an arbitrary complex function will be consistently determined by solving the equations arising at higher orders of
, which is for the moment an arbitrary complex function will be consistently determined by solving the equations arising at higher orders of .
.
Next, considering Equation (A2), it is clear that the homogenous part of the solution is similar to the one in Equation (A6), due to the fact that the linear operators in Equation (A2) and in Equation (A3) are identical. As a result, the term 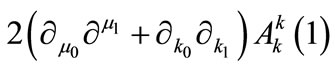 is secular, as
is secular, as  will contain terms of the form
will contain terms of the form .
.
The condition for nonsecularity, namely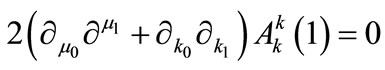 , leads to the following two equations [valid at order
, leads to the following two equations [valid at order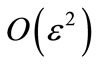 ]:
]:
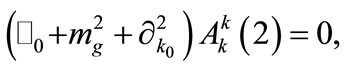 (A7)
(A7)
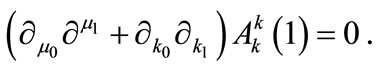 (A8)
(A8)
Since 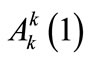 does not depend on x and y [cf. Equation (A6)], one has
does not depend on x and y [cf. Equation (A6)], one has 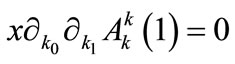 for
for 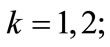 furthermore, the condition
furthermore, the condition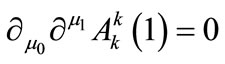 , introduces an important restriction for the function
, introduces an important restriction for the function  in Equation (A6): it is necessary to assume that
in Equation (A6): it is necessary to assume that
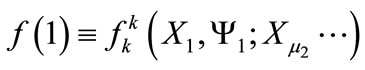
i.e., 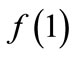 is independent of
is independent of 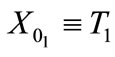 and
and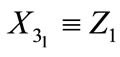 , a fact which sustains the decomposition of space-time in two inequivalent subspaces, as mentioned in Section 2.
, a fact which sustains the decomposition of space-time in two inequivalent subspaces, as mentioned in Section 2.
Finally, Equation (A5) decomposes in three independent equations. The first of them reads:
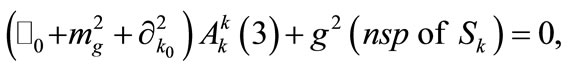 (A9)
(A9)
where “nsp” stands for the nonsecular part. The remaining two equations are found by eliminating all secular terms producing divergence of 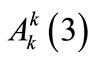 in Equation (A5). This way, we have:
in Equation (A5). This way, we have:
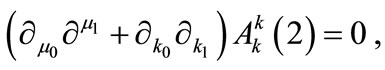 (A10)
(A10)
which is treated in the same way as Equation (A8) for the 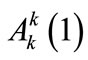 field, and
field, and
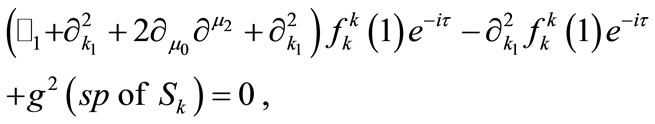 (A11)
(A11)
where “sp” stands for the secular part.
Our assumption that 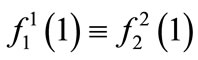 implies that
implies that
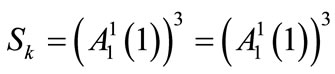
and, as a result, Equation (A11) should be of the same form for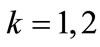 . This requirement is satisfied if
. This requirement is satisfied if
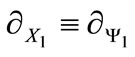 and
and 
Consequently, Equation (A11) is reduced to the form:
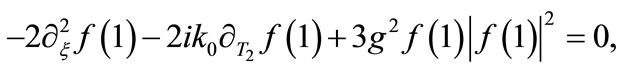 (A12)
(A12)
where 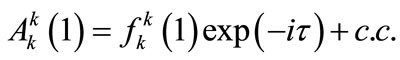
As far as Equation (A11) is concerned, it is important to note that the second term is the contribution of the non-diagonal terms [cf. Equations (A3) and (A4)]. Note that Equation (A12) is actually the NLS equation presented in Section 2 (see Equation (13)).
Appendix B
We start by rewriting Equations (16) and (17) in the following form:
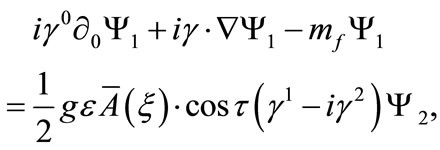 (B1)
(B1)
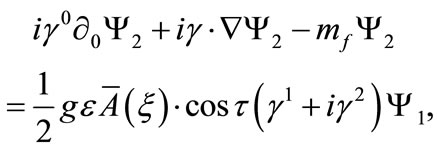 (B2)
(B2)
where 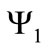 and
and 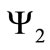 are the two components of the bispinor
are the two components of the bispinor  defined in Equation (18). In the following, we will apply the standard procedure [11] in order to obtain the non-relativistic limit of Equations (B1) and (B2). The necessity of this emerges by the violation of the covariance of the gauge field which we have imposed. Eventually, it is consistent to study the non-relativistic case.
defined in Equation (18). In the following, we will apply the standard procedure [11] in order to obtain the non-relativistic limit of Equations (B1) and (B2). The necessity of this emerges by the violation of the covariance of the gauge field which we have imposed. Eventually, it is consistent to study the non-relativistic case.
Taking into account that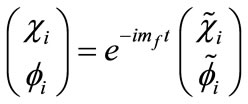 , for
, for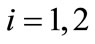 , Equation (B1) transforms into
, Equation (B1) transforms into
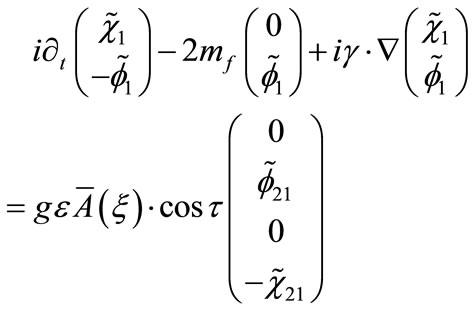 (B3)
(B3)
From Equation (B3) we obtain the following equations for the doublets  and
and  of the field
of the field :
:
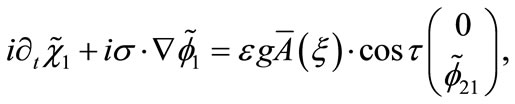 (B4)
(B4)
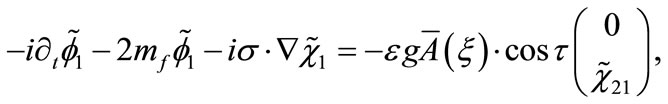 (B5)
(B5)
and similarly for the field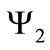 :
:
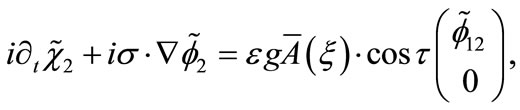 (B6)
(B6)
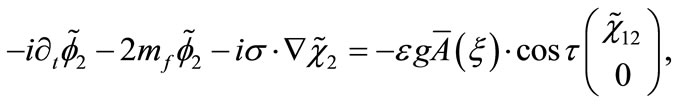 (B7)
(B7)
where 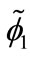 and
and 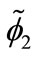 are slowly varying functions of timewhile
are slowly varying functions of timewhile 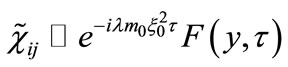 or
or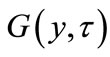 , with F, G being slowly varying functions of time as well, and
, with F, G being slowly varying functions of time as well, and . Using the relations
. Using the relations
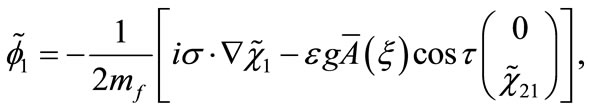 (B8)
(B8)
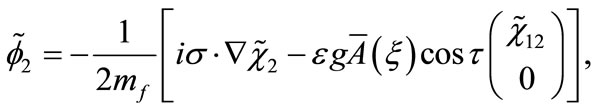 (B9)
(B9)
Εquation (B4) becomes
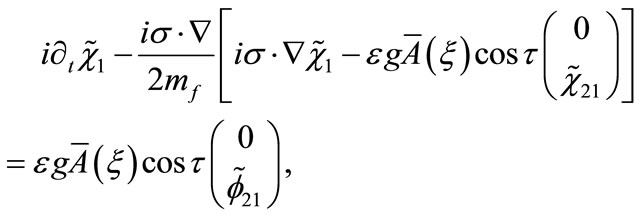
and since 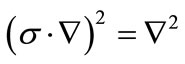 we have
we have
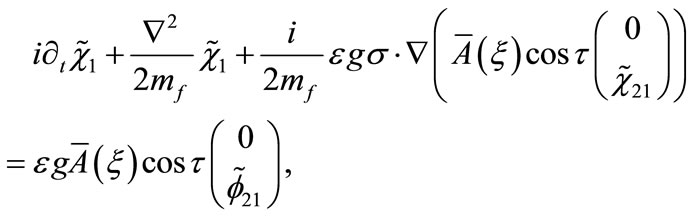 (B10)
(B10)
while 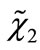 for the component, similarly we have
for the component, similarly we have
 (B11)
(B11)
where 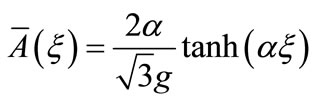 ,
,
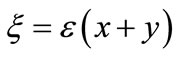 and
and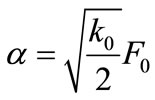 .
.
Finally, we expand Equations (B10) and (B11) in their components resulting in Equations (19)-(22) for the 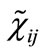 fields.
fields.

