Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40499,8 pages DOI:10.4236/jmp.2013.412191
New Statistical Methods for Systematizing the Nuclei Fission Fragments: Post-Scission Approach
Institute of Electron Physics, National Academy of Sciences of Ukraine, Uzhgorod, Ukraine
Email: nuclear@email.uz.ua, volodymyr.maslyuk@iep.org.ua
Copyright © 2013 V. T. Maslyuk et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 9, 2013; revised March 2, 2013; accepted April 11, 2013
Keywords: Fission; Fragments Yield; Ensemble; Thermodynamics; Post Scission Ordering; Mass/Charge Spectrum; Neutron Multiplicity; 236U
ABSTRACT
A new statistical method for systematizing the nuclei fission fragments, investigation of their mass and charge spectra and neutron fission parameters has been suggested. In proposed method, the mass and charge yields of nucleons are determined from the equilibrium conditions of the nuclear fragments post-fission ensemble. Here we consider protons and neutrons of different fragments as statistically non-equivalent. The abilities of the proposed statistical method for explanation of the U, Pa, Th, Ac and Ra post-fission fragments ordering and neutron emission function calculation have been demonstrated.
1. Introduction
It is known that the anisotropy of the nuclei fragments yields is common, but strongly expressed result of the atomic nuclear fission [1-4]. Information on characteristics of this phenomenon is important for understanding the nature of the internucleon forces, the roles of the shell effects and the magic nuclear numbers in the fission channels formation. At the same time, the studies of the mass and charge spectra of fission fragments (MCSFF) formation are important for a wide spectrum of applied approaches ranging from nuclear geochemistry, radioecology to nuclear power engineering and medicine.
The most significant features of the MCSFF are:
1) Symmetric (one-hump) or asymmetric (twoor threehumps) structure of the MCSFF;
2) MCSFF determined via the composition of the initial nucleus (the numbers of the protons and neutrons);
3) At the same excitation energy, the MCSFF weakly depends on the nucleus fission channel of (γ, f), (α, f), (f, f’), (n, f) or (p, f) [5];
4) Strong dependence on the excitation energy or nucleus temperature (T), namely, it becomes more symmetric with the rise of the T.
A number of theoretical approaches treat the problem of the nuclear fission based on the particles scattering theory, the change of the nucleus shapes and the profile of its potential energy, fission dynamics, formation of the mass channels, etc. Conditionally, they can be formally divided into four groups [6-12]:
Ÿ Statistical: the thermodynamics equilibrium state is valid before the atomic nucleus fission.
Ÿ Adiabatic: the nucleus deformation is smaller as compared to the nucleons motion.
Ÿ Empirical: the fission fragments yield modes tabulation etc.
Ÿ Computational: the methods implemented in the codes like ABLA, TALYS, etc.
Despite a big progress achieved with these methods in calculating the nuclear fission transformations, the traditional methods of the MCSFF investigation require a number of adjustable parameters such as effective viscosity, surface tension, level densities, etc.
Moreover, the investigation of the nuclear fission needs to take into account stochastic effects that are typical for small systems [13]. The ab initio calculations are also impossible because there is no sufficient knowledge on the nature of internuclear forces.
A series of experiments on the 1A GeV scale accelerators also confirmed the actuality of studies of the nuclear fission fragments ordering. First of all, it is well known that Darmstadt experiment (DE) [14] resulted in the complex form of the charge spectrum for 46 isotopes of U, Pa, Th, Ac and Ra photofission.
Then, the experiments on multifragmentation of heavy nuclei with the energies 1 - 10 MeV per nucleon showed the possibility to apply classical approaches of condensed and gaseous states of matter to nuclear subsystem and interpretation of nuclear fission in terms of phase transitions “liquid-gas” [15]. Such studies are related to a new approach named nuclear thermometry. It allows one to treat the transformation of the nuclear matter in terms of thermodynamics or chemical methods.
In our previous works [16,17], we suggested the statistical approach (color statistics), where the subject of the studies is the post-scission state of the nucleus derived from the thermal equilibrium condition of final nuclear fragments ensemble. This method allows using statistical thermodynamic methods to investigate the ordering of the nuclear fission fragments, see also [18]. The first result of using this approach was interpretation of the experimental data on the Xe and Kr isotope yields from light actinide fission [19].
In the present paper, other abilities of this method are demonstrated. The structure of the paper is as following: Section 2 is devoted to the explanation of the proposed statistical method; in Section 3 we present the results of nuclear fission characteristic calculations (MCSFF, neutron function) on the example of 236U and DE; Section 4 is the conclusive one.
2. Theory
In the proposed statistical method, the subject of investigation is not the pre-, or scission states of the initial nucleus, but a system of it fission fragments with very peculiar thermodynamical properties, their ordering and hierarchy. It is well known about specificity use of thermodynamics for small systems. Following paper [20], the concept of nuclear temperature T for a small nuclear system is valid in cases when the temperature fluctuation is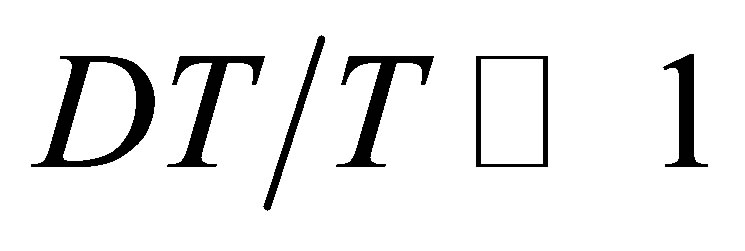 , where
, where
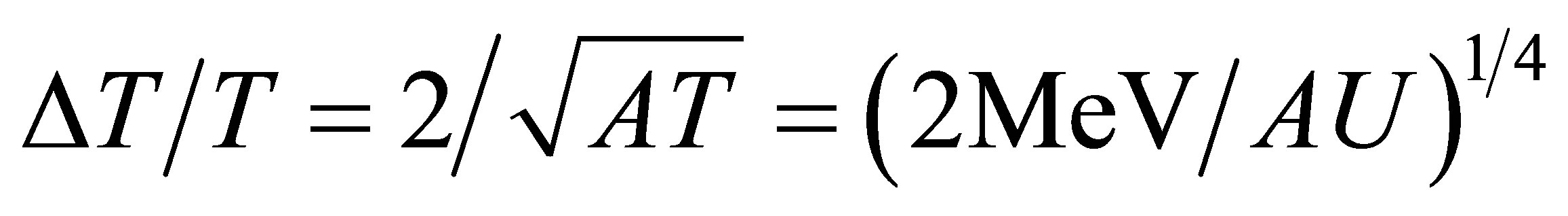
 .
.
Here U is an internal energy of nucleus, A is the atomic mass. Estimates show that the parameter T can be applied for nuclear systems with A ≥ 80.
2.1. Fission Fragments as a Thermodynamic Ensemble
We consider the scheme of the two-fragment fission and than must to realize all possible distribution of nucleons of initial nucleus by two fragments with their different atomic masses and the protons/neutrons ratio. Each such distribution creates the two-fragment clusters and the set of fragment clusters form a statistical ensemble.
In this case, the i-th cluster contains Zj,i protons and Aj,i - Zj,i neutrons in the j-th fragment, where j = 1.2, as well as ni fission neutrons. In general case, the following conservation conditions for all possible schemes of twofragment fission hold true
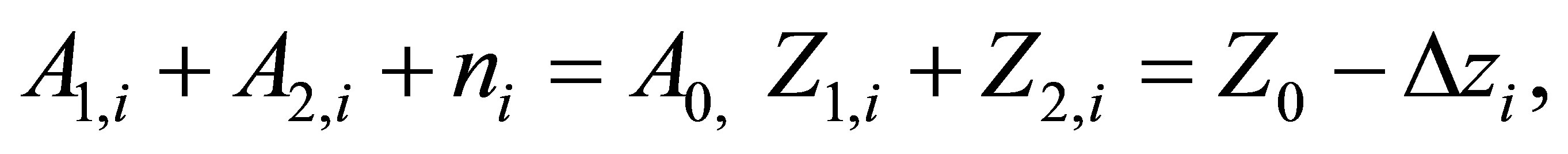 (1)
(1)
where Dzi is the number of b+ (at Dzi <0) or b− (Dzi >0) decays within a single nuclear cluster. Emission of nuclear particles plays an important role in the relaxation of the excitation of heavy-nuclei fission fragments and their approaching the islands of stability.
The thermodynamics parameters of the ensemble of two-fragment clusters are determined by the state of the initial nucleus. The initial nucleus determines the type of created statistical ensemble by considering the fluctuations of one set of the thermodynamics parameters and neglecting the other. In case of nuclear fission we assume the number of nucleons of all types in the two fragment clusters is constant, see (1) and only fluctuation of energy and volume is allowed. This leads to a canonical constant-pressure (P) ensemble. For example, in case of nuclear fusion as a result of the two nuclei interaction [18], the conception of Gibbs microcanonical ensemble can be proposed.
Since time and causality are not the parameters of the thermodynamic method the post scission evolution of fission fragments could be taken into account by the introduction of a sets of the ensembles of fragments clusters containing the nucleus restricted by their half-life T1/2. For all this ensembles we would assume that the equilibrium conditions are valid. The experiment, indeed, shows that the fragments separate at the scission point with an almost constant temperature [21].
2.2. The Thermodynamic Functions of the Fission Fragments Ensemble
Within the proposed approach, the problem of studying of fission fragments yields is reduced to the analysis of the equilibrium conditions for a canonical constantpressure ensemble. We must take into account that the еmission of fission neutrons decrease of the nucleus volume [22] and thus provides the PΔV work. The equilibrium parameters of the two-fragment clusters ensemble can be obtained from the condition of minimum of the Gibbs thermodynamic potential [23]:
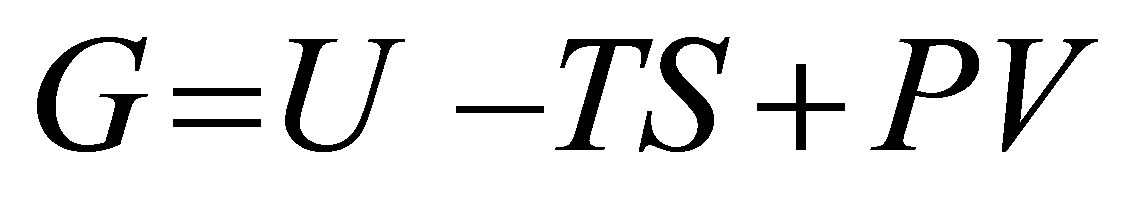 , (2)
, (2)
here T in MeV, U, initial or total energy consist from two major components, kinetic and potential energy. The kinetic energy is due to the motion of the system’s particles and is constant in our case because of constant temperature, T. The potential energy is associated with the static constituents of matter and for condensed nuclear matter as a nucleolus, U determined by binding energy of the two-fragment cluster and its spectrum  is an additive quantity with respect to the binding energy of fission fragments:
is an additive quantity with respect to the binding energy of fission fragments:
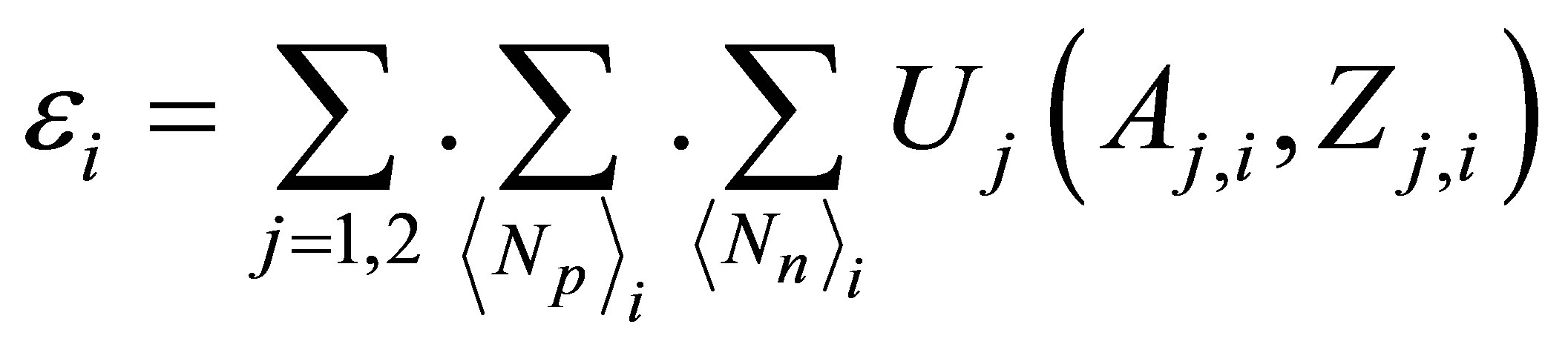 , (3)
, (3)
where Uj is the binding energy of the i-th fission fragment, j = 1, 2; the symbol 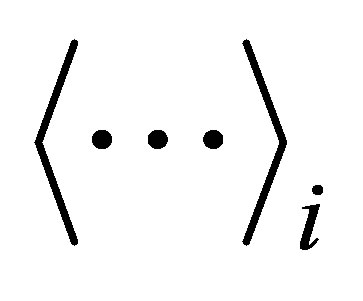 means that summation in (3) is taken over the i-th clusters containing two fission fragments with the numbers of protons
means that summation in (3) is taken over the i-th clusters containing two fission fragments with the numbers of protons 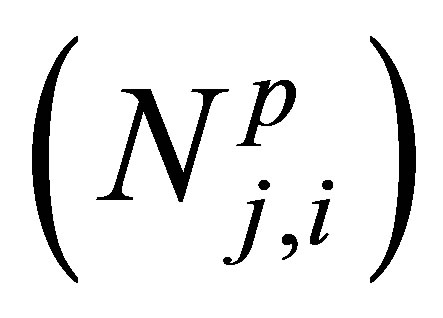 and neutrons
and neutrons 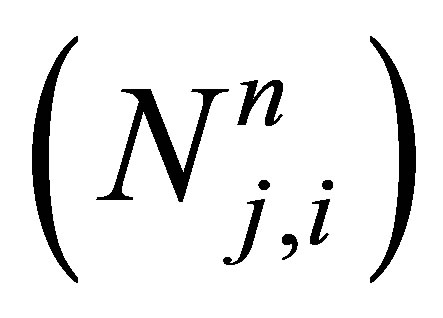 satisfying the following condition:
satisfying the following condition:
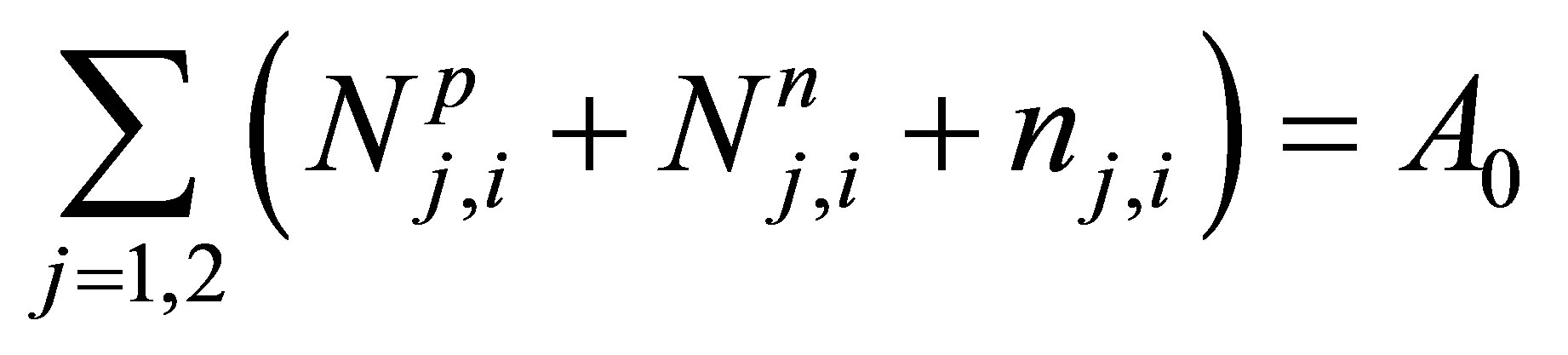 . (4)
. (4)
The configurational entropy Si introduced in (2) is determined by the degeneracy factor 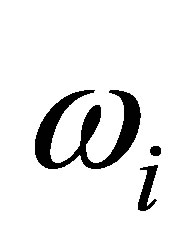 or number of states two-fragment cluster which have the same energy level ei and must take into account the statistical nonequivalence of nucleons with different specific binding energy in each of the fission fragments and fission neutrons,
or number of states two-fragment cluster which have the same energy level ei and must take into account the statistical nonequivalence of nucleons with different specific binding energy in each of the fission fragments and fission neutrons, 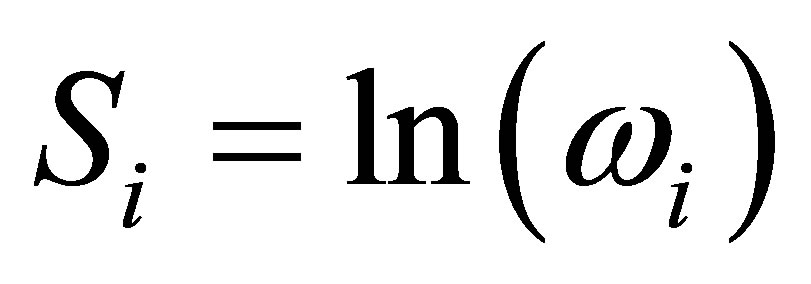 , where:
, where:
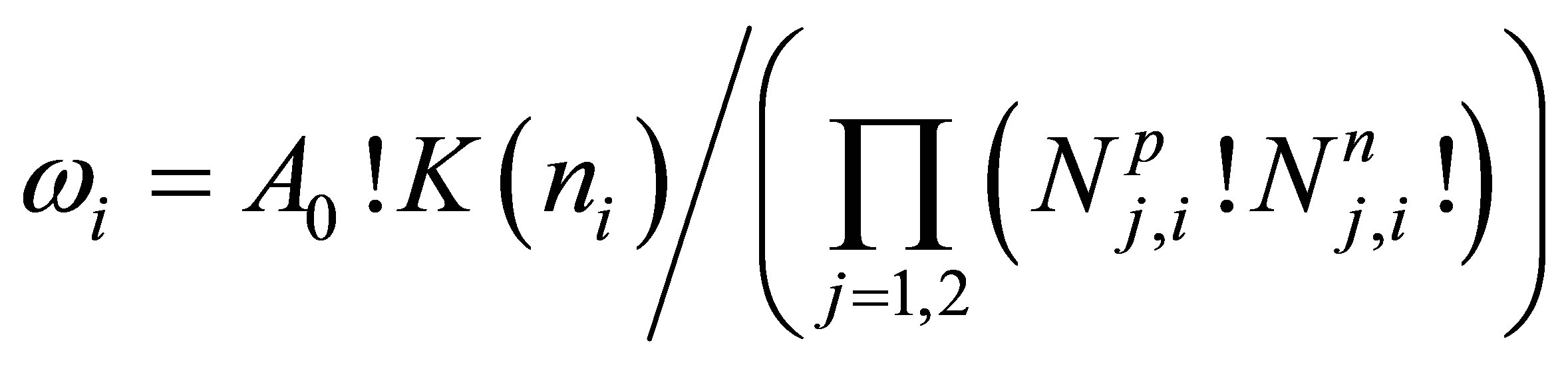 . (5)
. (5)
Here 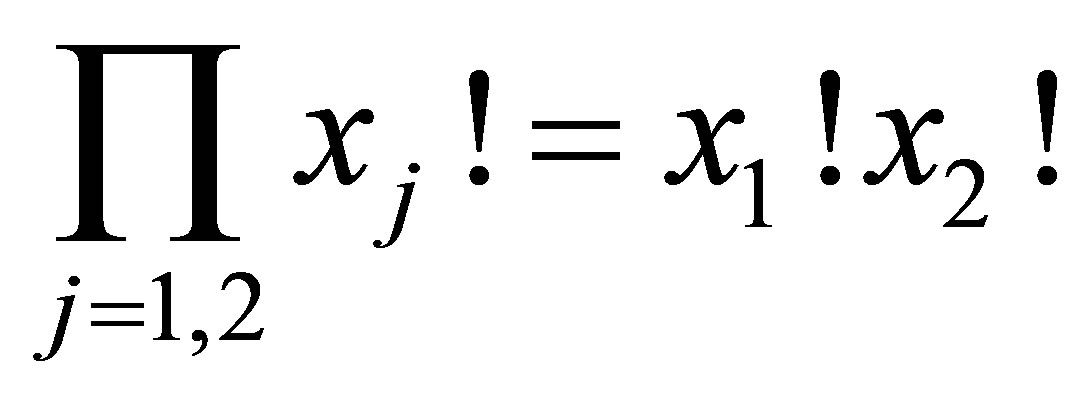 and
and 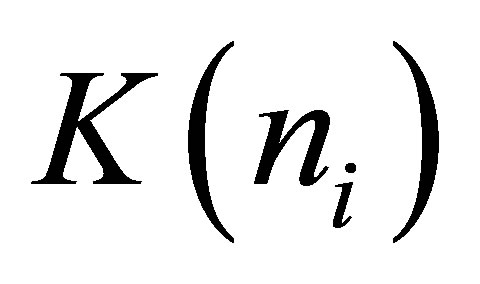 depend on the statistical equivalence of emitted neutrons,
depend on the statistical equivalence of emitted neutrons,
|
|
| Emitted neutrons are statistically equivalent. |
|
| Emitted neutrons are not statistically equivalent. | |
|
| Emitted neutrons are statistically equivalent within a single fragment, |
where 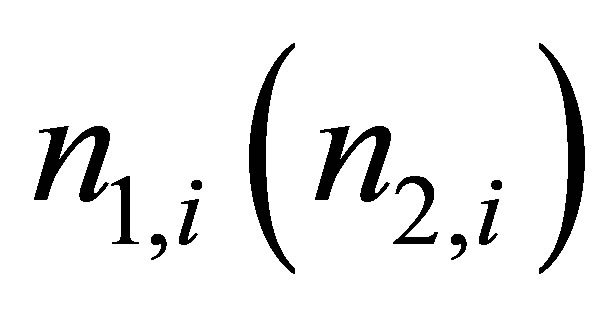 is the number of neutrons emitted from the first (second) fission fragments and the i-th cluster.
is the number of neutrons emitted from the first (second) fission fragments and the i-th cluster.
From the analysis of expression (5) we see that the entropy term in Equation (2) reaches maximum if 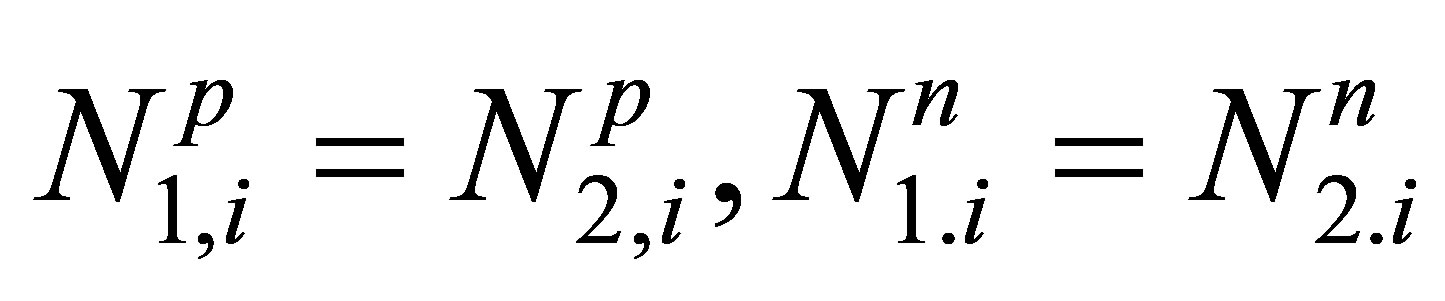 and is responsible for the symmetrization of the fission yields with the rise of the nuclear temperature Т.
and is responsible for the symmetrization of the fission yields with the rise of the nuclear temperature Т.
The isobaric distribution function, which describe the statistical properties of a system in thermodynamic equilibrium and represents a probability of finding a twofragment nuclear cluster in the i-th state of the ensemble with the energy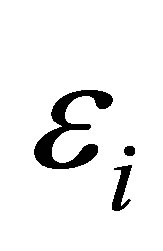 , can be expressed in the following way:
, can be expressed in the following way:
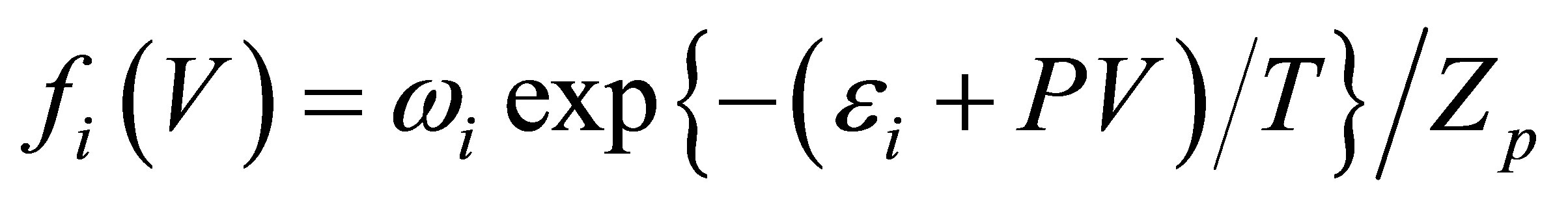 , (6)
, (6)
where the statistical sum Zp is defined as:
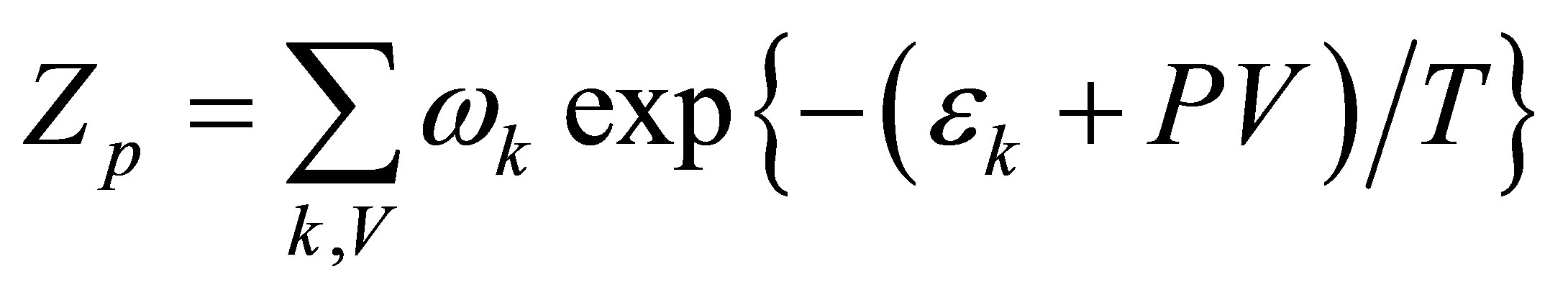 .
.
The set of Equations (2)-(6) is sufficient to study the observable characteristics of nuclear fission, including MCSFF.
3. The Statistical Properties of a Post-Scission Fragments Ensamble and Observable Characteristics of Nuclei Fission
The abilities of the proposed statistical method are demonstrated in the following calculations of the observable post-scission characteristics of nucleus fission, mainly on the example of 236U, which has the most complete nuclear-physical database [24,25]. The statistical fluctuations of the thermodynamics parameters typical for small nuclear systems were also taken into account.
First, we investigate the MCSFF yields. This was carried out using two sets of the ensembles of fragments clusters restricted by their half-life T1/2: the most complete database of possible fission fragments (from ultra short-lived to long-lived) and the same after exclusion the short-lived isotopes. The last case is capable for reconstructing the real experimental conditions of the MCSFF measurements.
Second, since the theory takes into account the presence of neutron fission in the two-fragment fission scheme, it is possible to calculate the number of equilibrium neutron as a function of the initial fragment mass n(А) and the total neutron multiplicity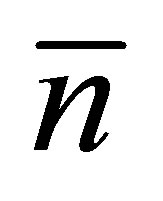 .
.
And, finally, we offer own interpretation the DE results [14] that demonstrated the symmetrical and asymmetrical structure of the light actinide nuclear charge spectra of the fragment fission.
3.1. MCSFF Post-Scission Characteristic and Their Temperatures Ordering
To study MCSFF and other experimentally observable parameters one has to start from Equation (5). Then, the distribution function 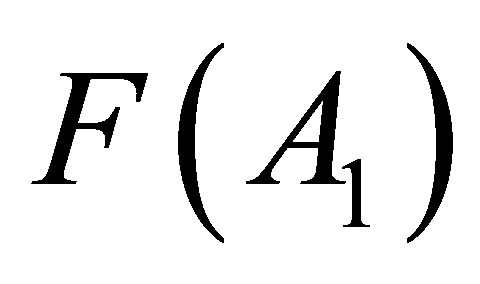 of a single fission fragment with mass A1, or the same,
of a single fission fragment with mass A1, or the same, 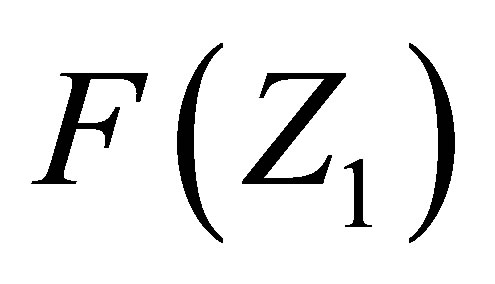 , with charge Z1 has to be obtained by a following procedure:
, with charge Z1 has to be obtained by a following procedure:
Ÿ Forming the whole ensemble of post-scission fragment clusters, using for nucleons conservation conditions (1), (3);
Ÿ The initial (not normalized) values 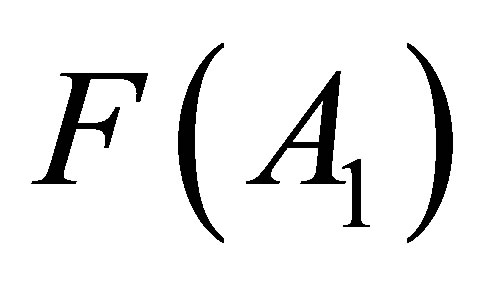 are obtained as the sum of probabilities of two-fragment cluster, containing the fission fragment with the mass A1, see Equation (5). This procedure is similar to the method of histograms and must includes cumulative chains;
are obtained as the sum of probabilities of two-fragment cluster, containing the fission fragment with the mass A1, see Equation (5). This procedure is similar to the method of histograms and must includes cumulative chains;
Ÿ The same procedure is valid for determination the initial values of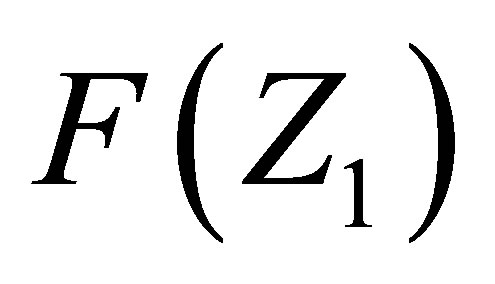 ;
;
Ÿ The Monte Carlo procedure must be applied to simulate the statistical fluctuations of the thermodynamical parameters of the fission fragments ensemble;
Ÿ The next step includes the normalization procedure and determination of the final values of 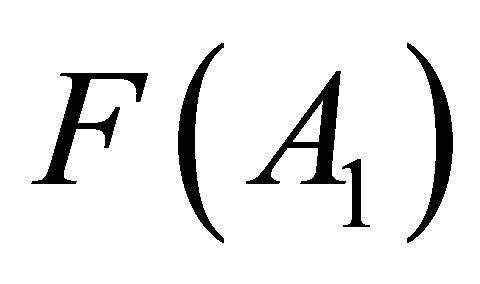 and
and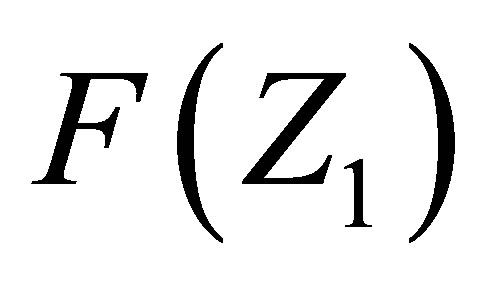 . These functions must satisfy the following normalization equations:
. These functions must satisfy the following normalization equations:
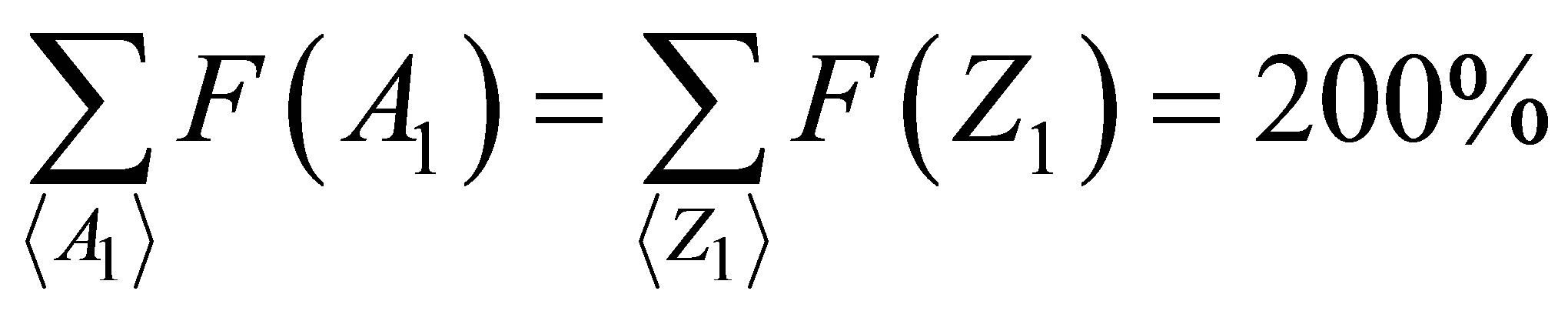 where
where  means the same as in (3).
means the same as in (3).
In the proposed statistical method, the isobaric term PV (see Equation (6)) was chosen in the form
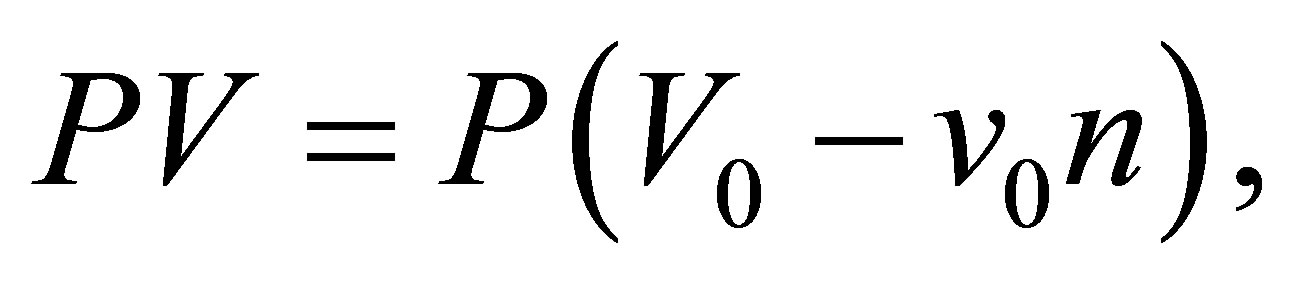
where 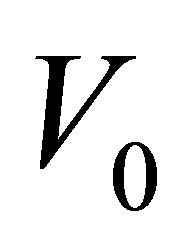 is the initial nucleus volume,
is the initial nucleus volume, 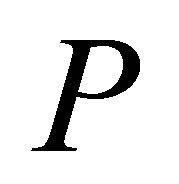 is the nucleon “gas” pressure and
is the nucleon “gas” pressure and 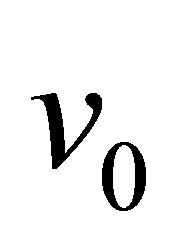 is the average volume related to a single fission neutron with total number of n. The isobaric constant
is the average volume related to a single fission neutron with total number of n. The isobaric constant 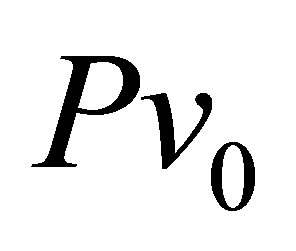 value was estimated within 4 - 5 МеV and was evaluated from the condition that the total fission neutron number
value was estimated within 4 - 5 МеV and was evaluated from the condition that the total fission neutron number 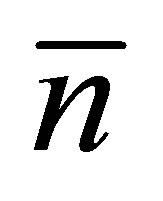 does not exceed 3 neutrons per fission (at Т ~ 0.5 МеV). Estimation shows that a
does not exceed 3 neutrons per fission (at Т ~ 0.5 МеV). Estimation shows that a 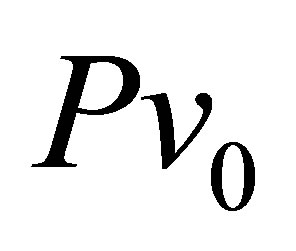 n value is less than 3% of the total U value in Equation (3).
n value is less than 3% of the total U value in Equation (3).
It should be noted that proposed statistical method contains no adjustable parameters, but only those that can be obtained from experiment. For instance, the temperature T can be defined by analyzing the evaporation spectra of the fission neutrons/protons or fission fragments (see [21,26,27] for more detail). The binding energies used in Equation (3) are tabulated in [28], their extrapolation (mass formula) is given, for example, in [29-31].
Since the theory does not allow taking into account the time evolution of ensembles of fragments clusters, an appropriate choice of nuclei sets 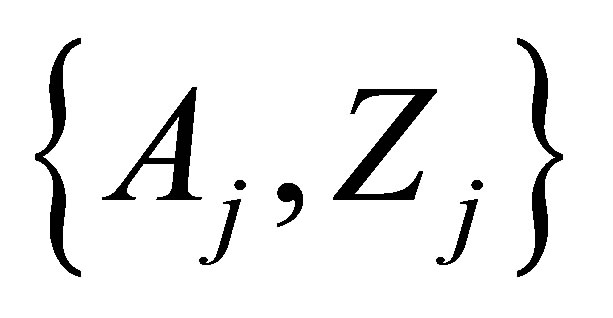 can be used for better fitting the calculated and experimental MCSFF data. To reconstruct the ideal and real experimental conditions of the MCSFF measurements one can use the ensembles of fragments clusters restricted by their halflife
can be used for better fitting the calculated and experimental MCSFF data. To reconstruct the ideal and real experimental conditions of the MCSFF measurements one can use the ensembles of fragments clusters restricted by their halflife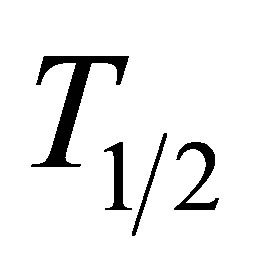 . Such ensembles are constructed on nuclei sets
. Such ensembles are constructed on nuclei sets 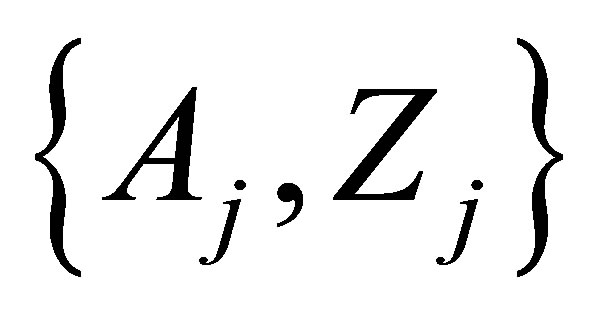 that satisfy conservation conditions (1), (4) and obtained by following way:
that satisfy conservation conditions (1), (4) and obtained by following way:
Ÿ The most complete sets 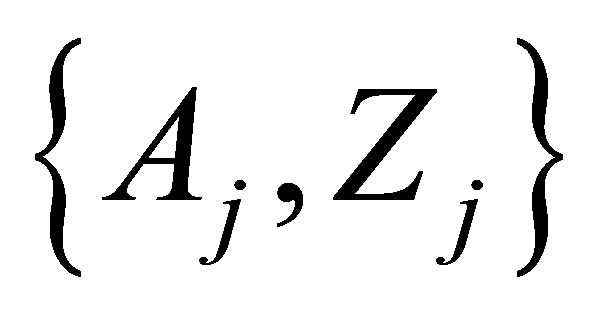 that contains all, from the ultra short-lived to long-lived and practically unobserved nucleons. The parameters of such sets as spectrum
that contains all, from the ultra short-lived to long-lived and practically unobserved nucleons. The parameters of such sets as spectrum  can be evaluated only on the basis of the mass formula [29-31];
can be evaluated only on the basis of the mass formula [29-31];
Ÿ The observable nuclei sets 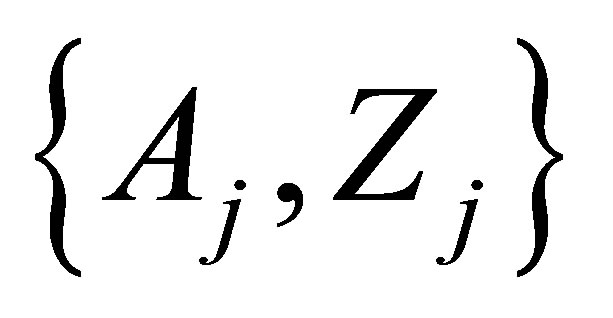 that contain observable and tabulated nucleus fragments, e.g. in Ref. [28];
that contain observable and tabulated nucleus fragments, e.g. in Ref. [28];
Ÿ The nuclei sets  containing no shortand ultra short-lived nuclei;
containing no shortand ultra short-lived nuclei;
Ÿ The same nuclei sets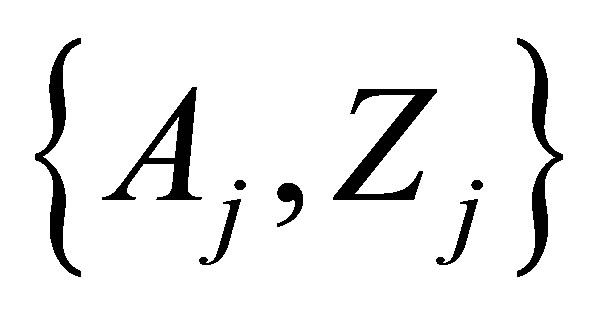 , but with taking into account the particle emission, such as neutrons or beta-particles.
, but with taking into account the particle emission, such as neutrons or beta-particles.
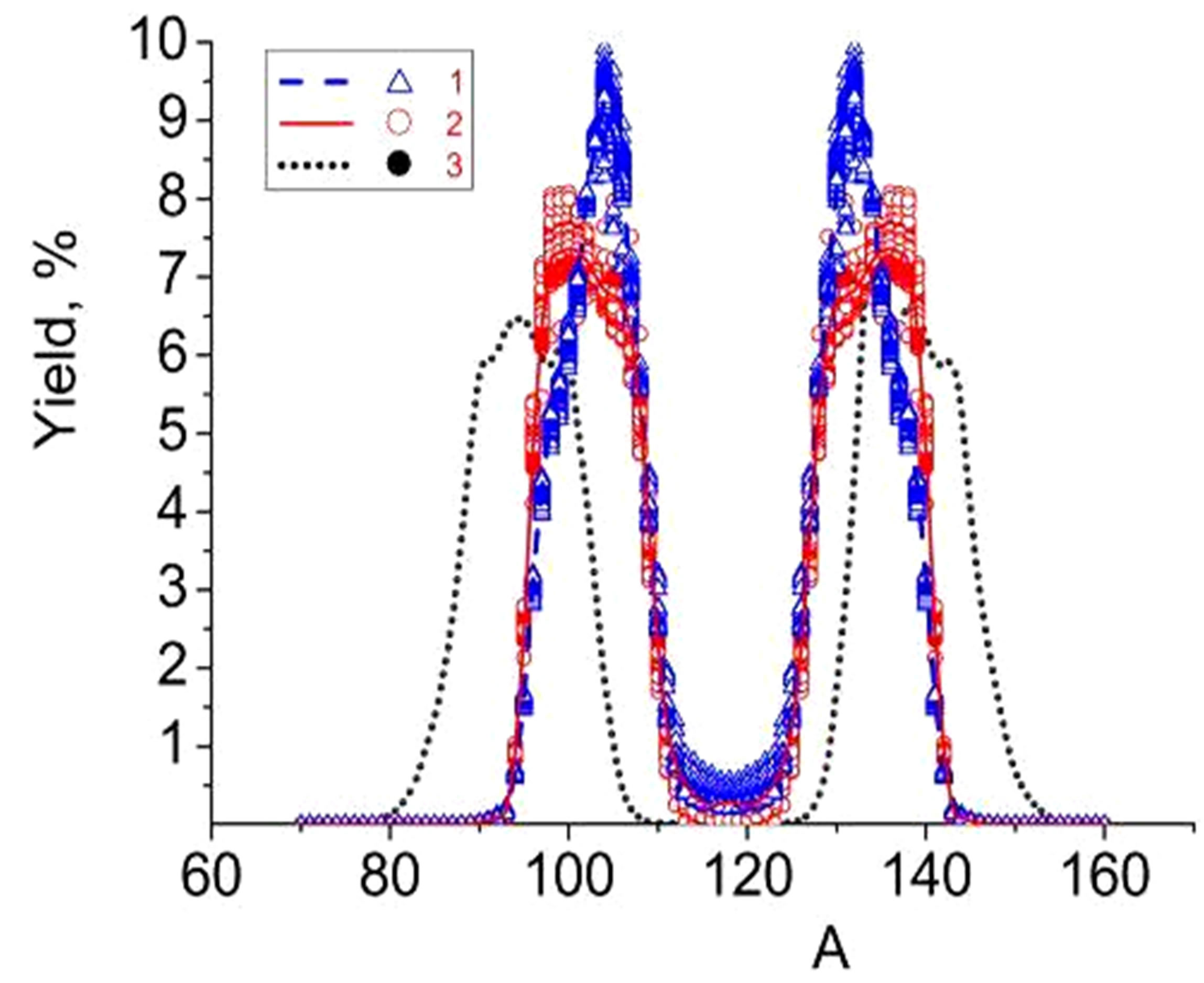
Figure 1 presents the experimental [25] and calculated MCSFF (yields) for the 236U. The theoretical curves were obtained for the two sets of the ensembles of fragments clusters, restricted by their half-life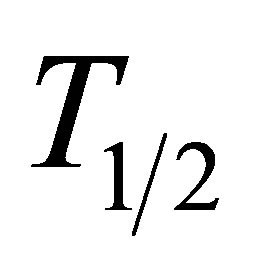 : the observable nuclei sets from database [28] for 1848 nuclei and the same after exclusion the short-lived isotopes with the half-life,
: the observable nuclei sets from database [28] for 1848 nuclei and the same after exclusion the short-lived isotopes with the half-life, 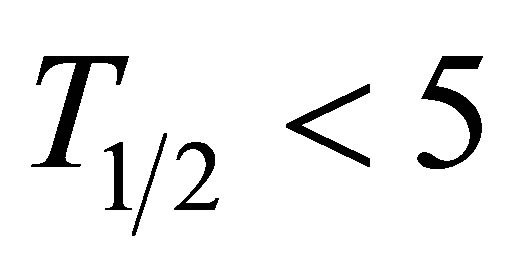 min.
min.
The following parameters were used in our calculations: Т = 0.5 МеV, the isobaric constant 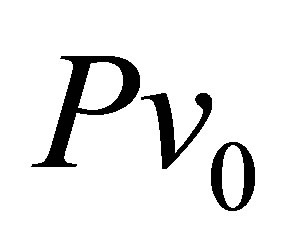 was equal to 4.5 МеV and the fluctuation range was up to 15% for all DТ,
was equal to 4.5 МеV and the fluctuation range was up to 15% for all DТ, 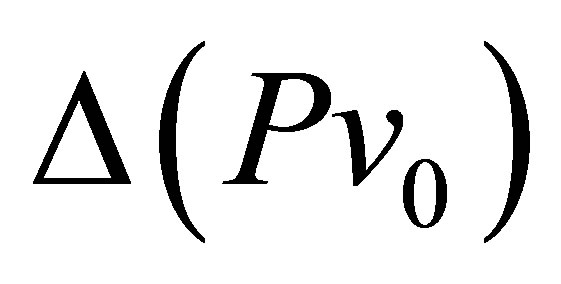 and for the neutron emission number
and for the neutron emission number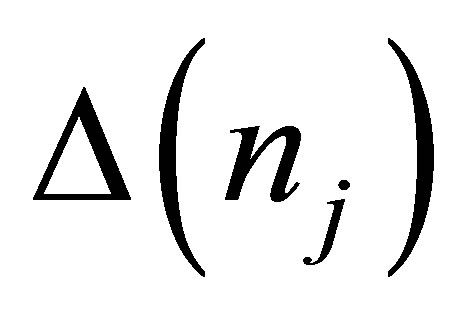 . The number of statistical events was 100 and the length of the cumulative chain was 10. The entropy term was calculated under the assumption that all emitted neutrons are statistically equivalent,
. The number of statistical events was 100 and the length of the cumulative chain was 10. The entropy term was calculated under the assumption that all emitted neutrons are statistically equivalent,
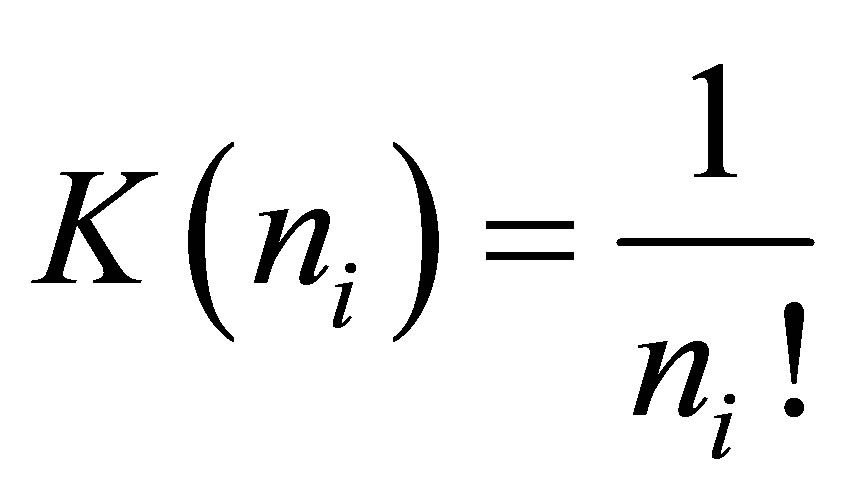 (see Equation (5)).
(see Equation (5)).
The second hump for heavier fragments in the theoretical mass spectra, Figure 1(a)) is related to a cluster, which contains heavy fragments in the vicinity of A2 = 132 or the nucleus with magic Z2 = 50 and N2 = 82. Our theoretical data cannot describe well the experimental mass spectrum in the vicinity of A1 = 90 and A2 = 140
 (a)
(a)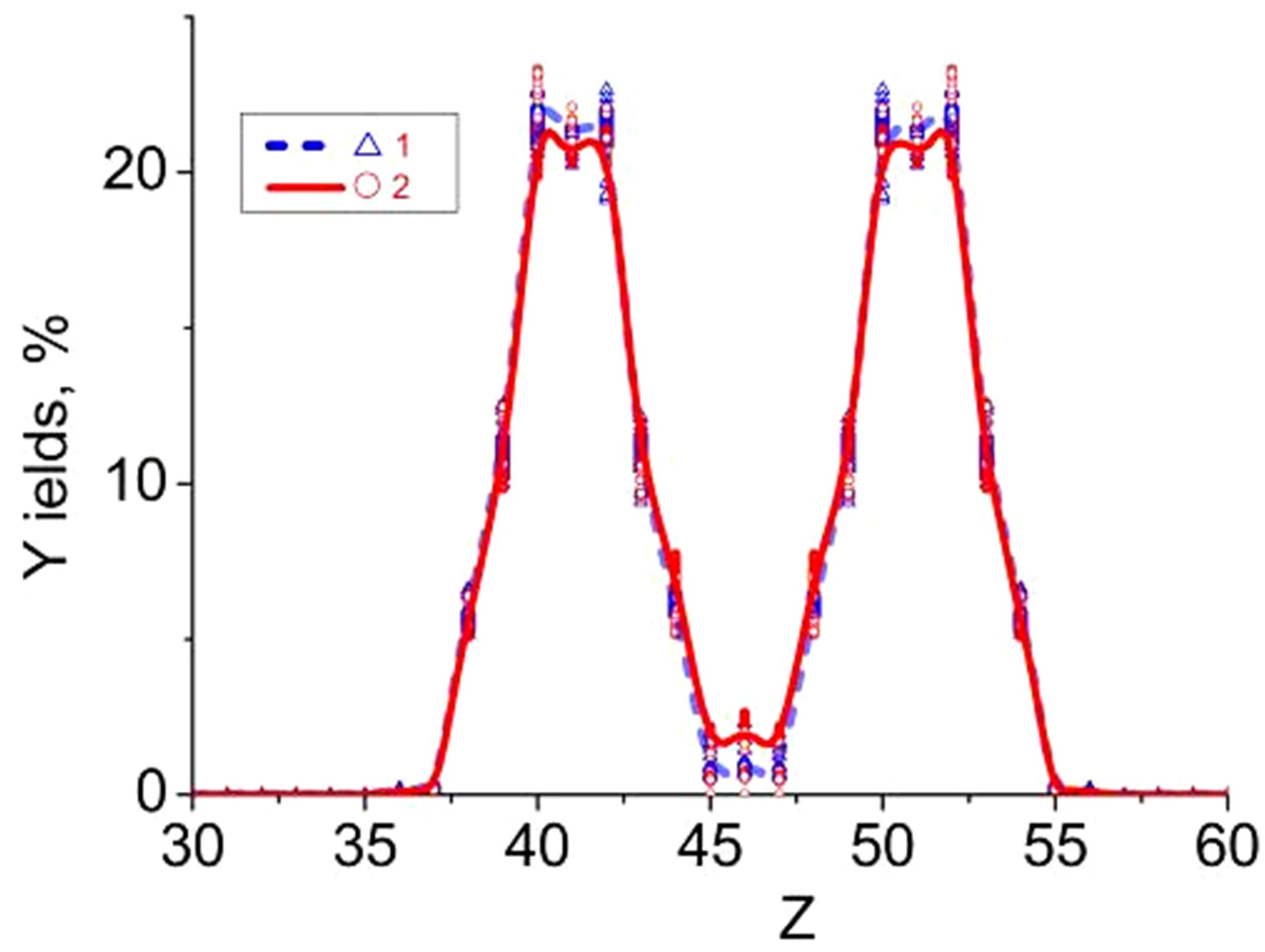 (b)
(b)
Figure 1. (Color online) Mass (a) and charge (b) spectra of the 236U fission fragments obtained by using database from Ref. [28] (triangles and dashes curves) and in case of neglecting the short-lived nucleons (Т1/2 < 5 min.) (circles and solid curves). The dotted curve in Figure 1(a) is related to the experimental fission fragment yields (spectrum) for the 236U: fission induced by the thermal neutrons, (nth, f) 235U [23].
for the mass fragment yields. It can be caused by the singular tendency of the isobaric distribution function for two-fragment cluster Equation (5) that may significantly affect the dependences F(A1) or F(Z1;) for single fragments.
Figure 1(b) shows the nuclear charge spectra 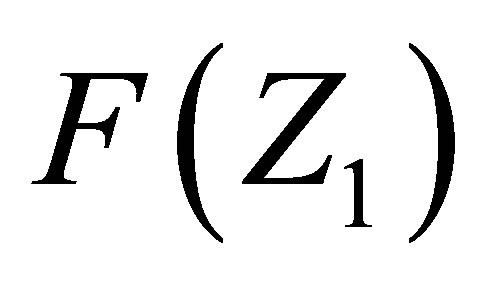 for the 236U fission fragments, normalized to 200%. The theoretical curves 1 and 2 are related to the same sets
for the 236U fission fragments, normalized to 200%. The theoretical curves 1 and 2 are related to the same sets 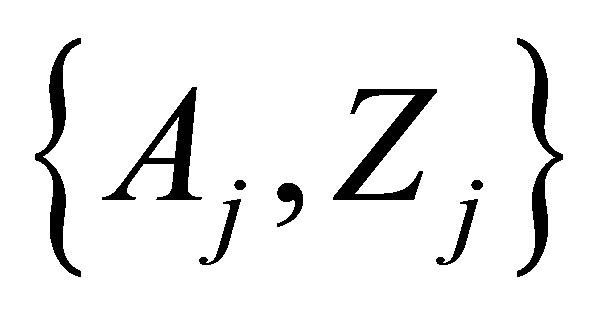 as for the mass spectra in Figure 1(a). Similarly to the previous case, one can see that the maximum of the charge spectra (cumulative yields) is formed by the fission fragments from the vicinity of a magic number, in particular, Z1 = 50, for heavy fragment. However the experimental charge spectrum [14] indicates the location of the maximum of heavy fragments yields in the vicinity of Z2 = 55. As in the previous case this could be caused by the singular tendency of the isobaric distribution function for two-fragment cluster Equation (5) or that the emissions of an b-particles was not being taken into account.
as for the mass spectra in Figure 1(a). Similarly to the previous case, one can see that the maximum of the charge spectra (cumulative yields) is formed by the fission fragments from the vicinity of a magic number, in particular, Z1 = 50, for heavy fragment. However the experimental charge spectrum [14] indicates the location of the maximum of heavy fragments yields in the vicinity of Z2 = 55. As in the previous case this could be caused by the singular tendency of the isobaric distribution function for two-fragment cluster Equation (5) or that the emissions of an b-particles was not being taken into account.
But in both cases in interpreting the MCSFF (yields) the better agreement between experimental and theoretical results are achieved when we used the nuclei sets 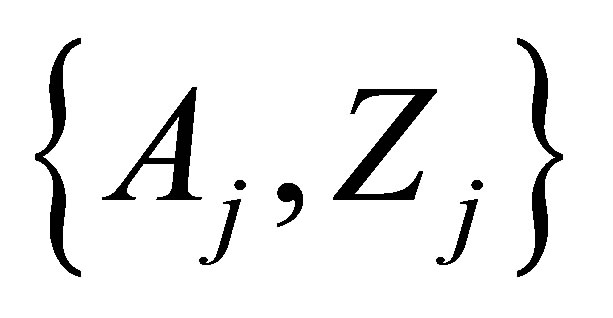 with long-lived nucleons and taking into account the post-scission nuclear particle emission. This shows the importance of experimental conditions in the MCSFF studies.
with long-lived nucleons and taking into account the post-scission nuclear particle emission. This shows the importance of experimental conditions in the MCSFF studies.
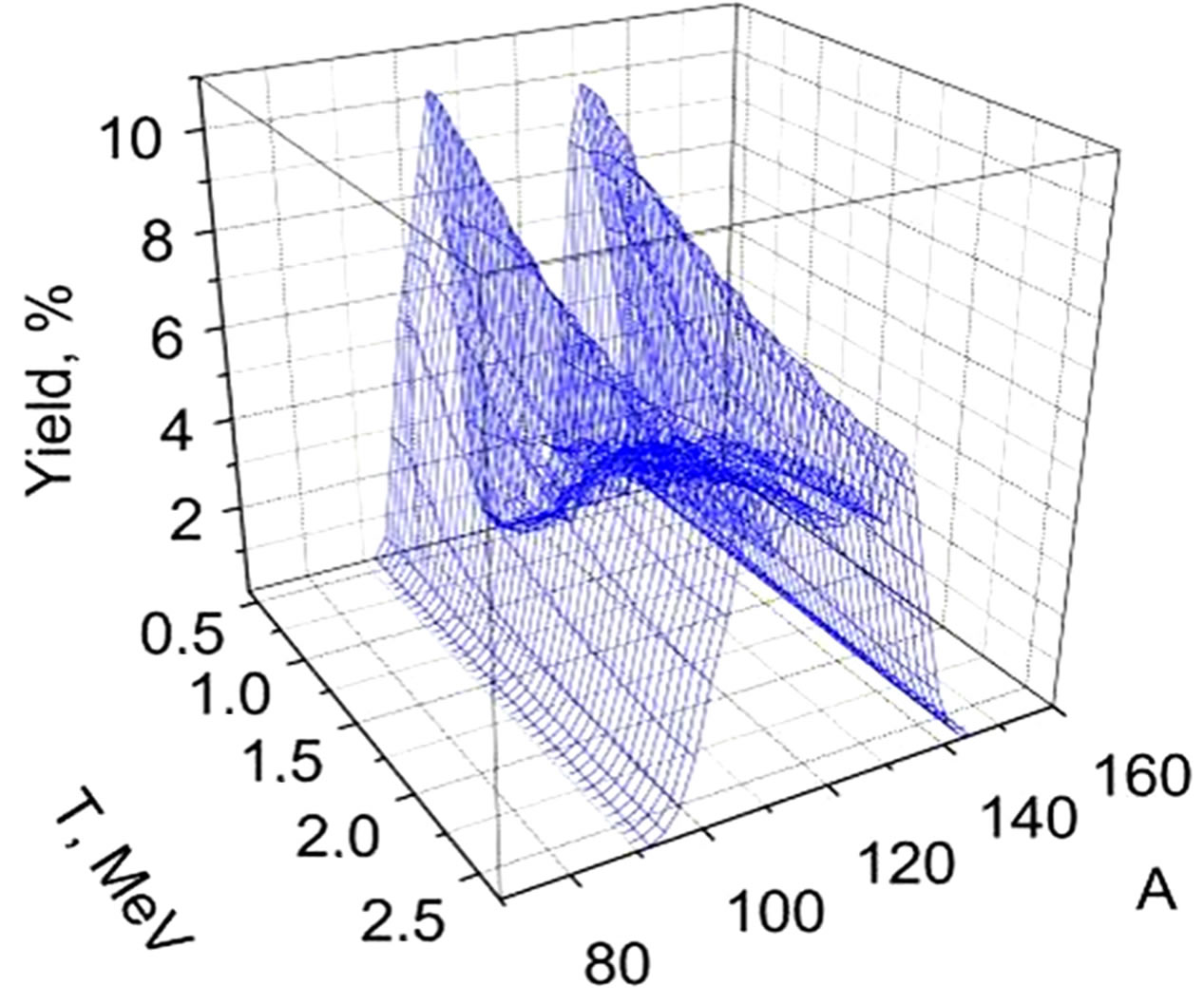
In Figure 2, the temperature evolution of the 236U MCSFF for 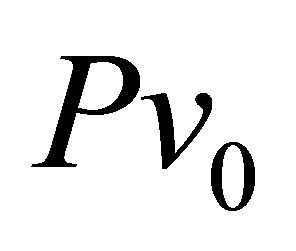 = 4.5 МеV on the basis of a most complete set of
= 4.5 МеV on the basis of a most complete set of 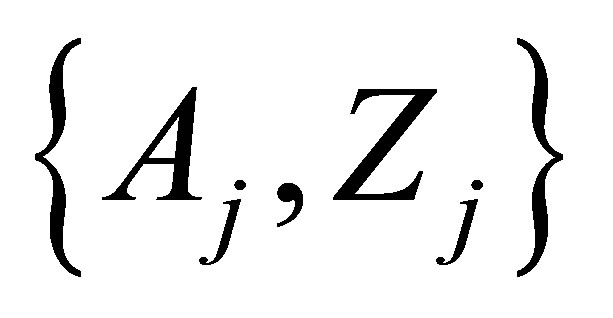 [28] is shown. The effect of
[28] is shown. The effect of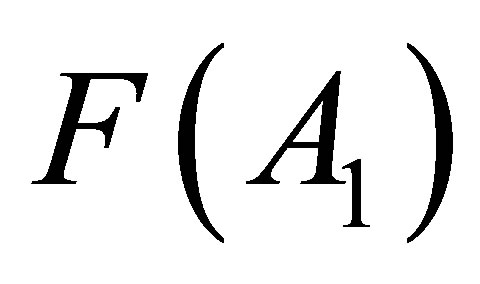 ,
, 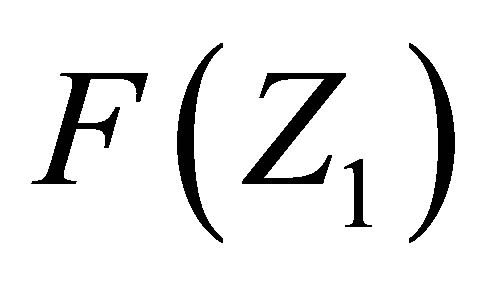 symmetrization with the rise of the nuclear temperature T can be explained by the influence of the entropic term in Equation (2), which reaches a maximum in case of symmetric fission, when A1 - A2 (Z1 - Z2).
symmetrization with the rise of the nuclear temperature T can be explained by the influence of the entropic term in Equation (2), which reaches a maximum in case of symmetric fission, when A1 - A2 (Z1 - Z2).
The theoretical results in Figure 2 show that the parameterization of the anisotropy of the nuclear mass (charge) spectra of the fission fragments is very promising for developing a new type of nuclear thermometers.
3.2. Neutron Emission Function for the 236U Fission Fragments
As was mentioned above the theory allows to calculate some observable neutron parameters: the total number of emitted neutrons as a function of the initial fragment mass (neutron emission function) 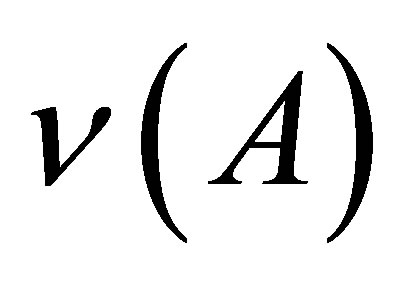 and total neutron emission number
and total neutron emission number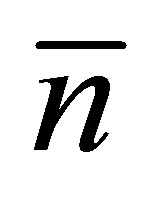 .
.
These functions are very important for neutron physics and numerous applications of neutron fluxes [32]. Among the factors that determine 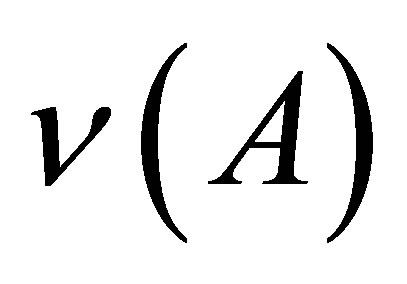 and
and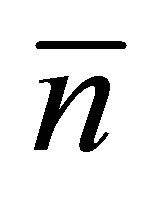 , the isotopic composition of the initial nucleus and its excitation energy or temperature T are the most important [33]. According to Equations (3) and (4), the emission of neu-
, the isotopic composition of the initial nucleus and its excitation energy or temperature T are the most important [33]. According to Equations (3) and (4), the emission of neu-
 (a)
(a)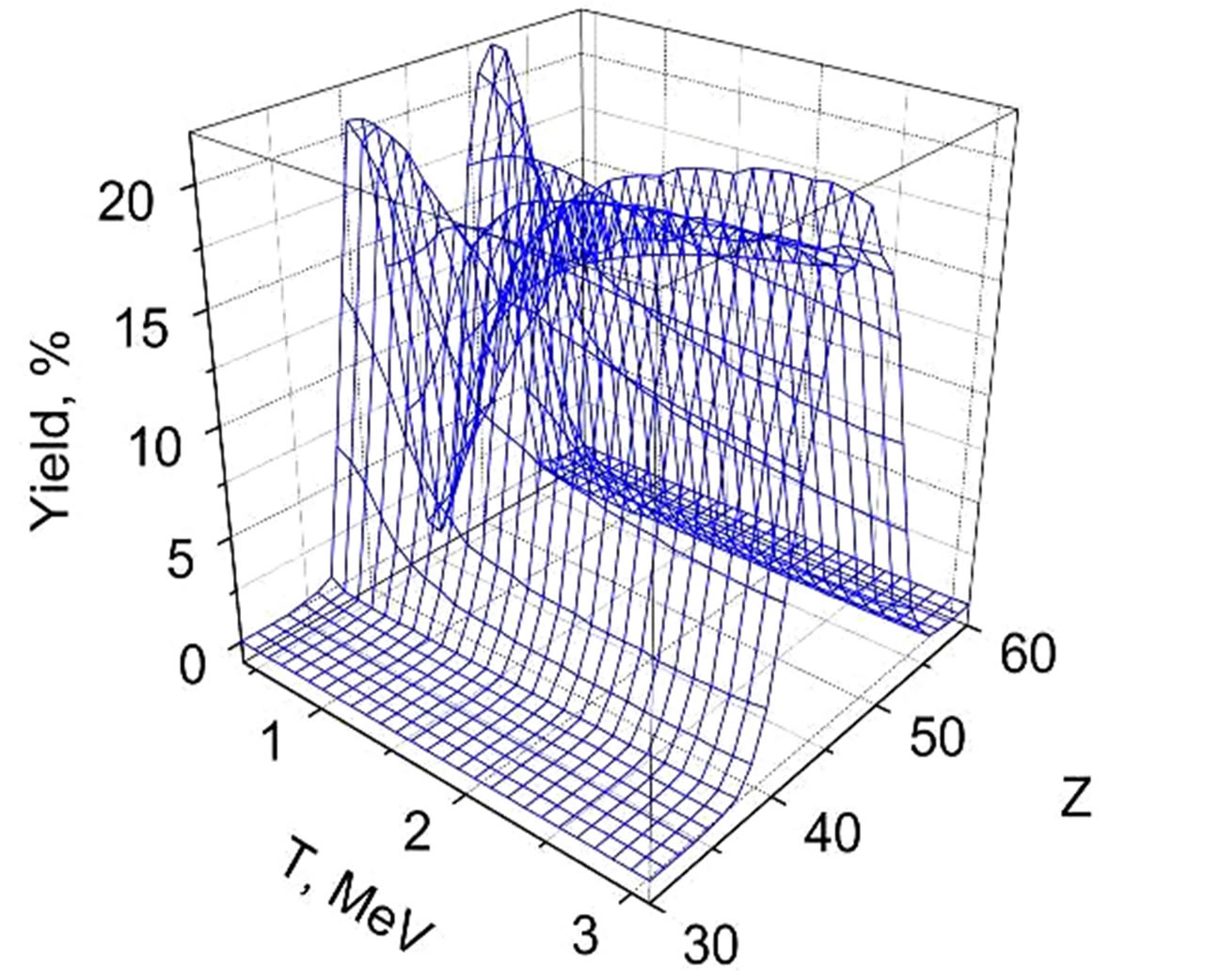 (b)
(b)
Figure 2. (Color online) Symmetrization of the nuclear mass (a) and charge (b) spectra with the temperature for the 236U fission fragments.
trons from fission fragments changes both the total binding energy of a two-fragment cluster and its entropic term.
The method of the 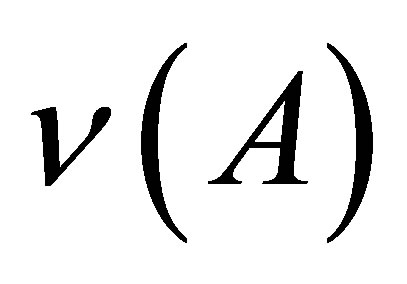 function calculation is based on determining the probability of realization (yield) of the two-fragment cluster that contains a preneutron fragment with mass A and the equilibrium number of neutrons n. Considering a cumulative yield of the fission fragments,
function calculation is based on determining the probability of realization (yield) of the two-fragment cluster that contains a preneutron fragment with mass A and the equilibrium number of neutrons n. Considering a cumulative yield of the fission fragments, 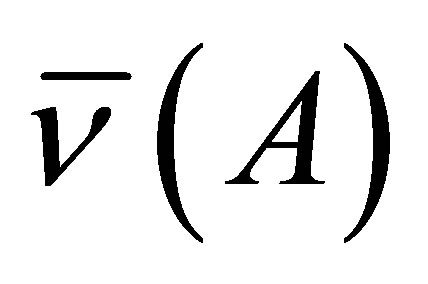 is equal to a mean value for all clusters containing the fragment with mass A from the cumulative chain:
is equal to a mean value for all clusters containing the fragment with mass A from the cumulative chain:
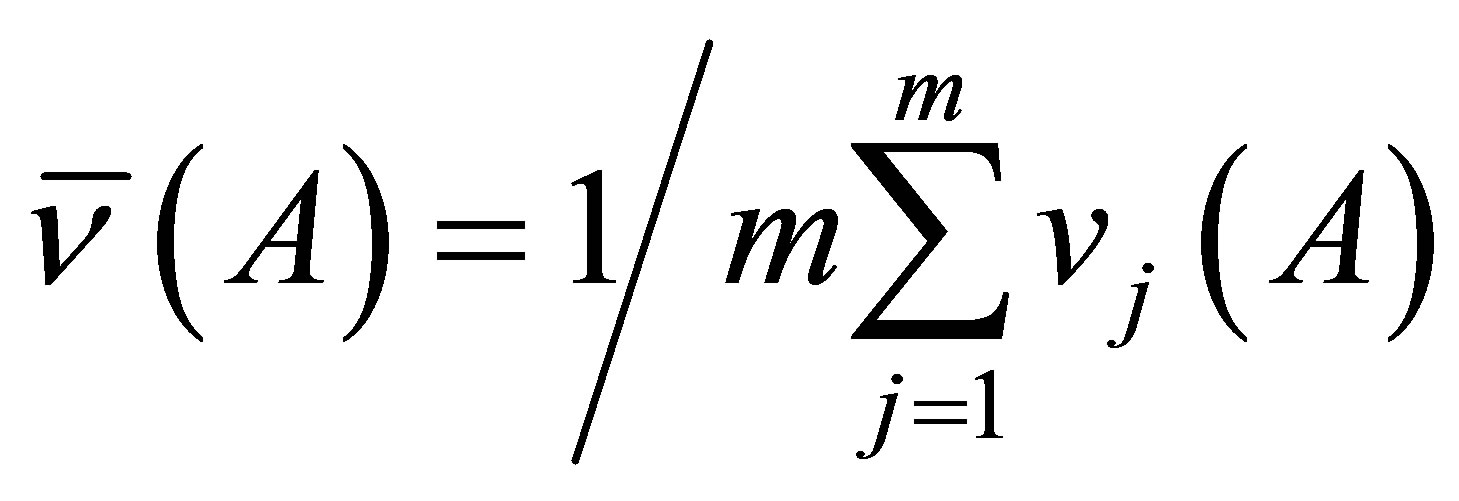 here m is the length of the cumulative chain that forms the yields of the fragments with the mass A. The total number of neutrons emitted in the act of nucleus fission
here m is the length of the cumulative chain that forms the yields of the fragments with the mass A. The total number of neutrons emitted in the act of nucleus fission 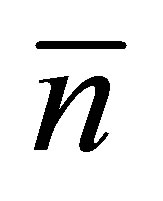 is calculated in a following way (normalization to 200% is used):
is calculated in a following way (normalization to 200% is used):
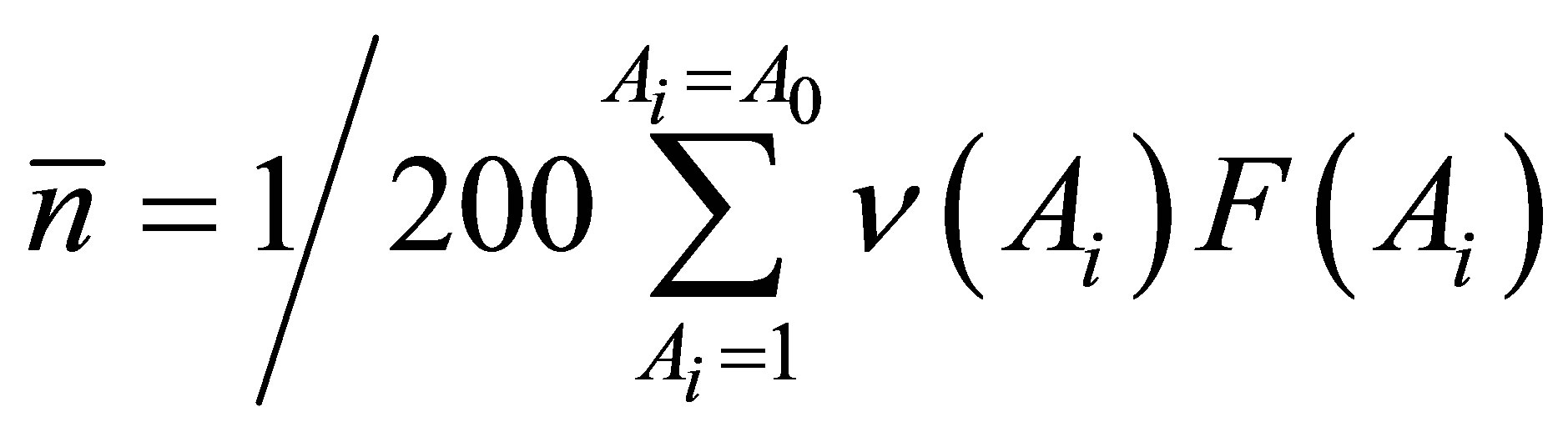 .
.
In Figure 3, the calculated and experimental [34] neutron emission functions for fission fragments of 236U are shown. As in previous cases the cumulative chain length was m = 10. The values of Т, 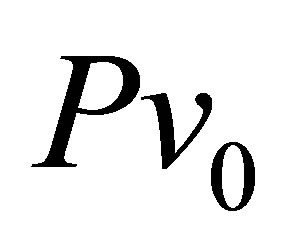 , their fluctuation var-
, their fluctuation var-
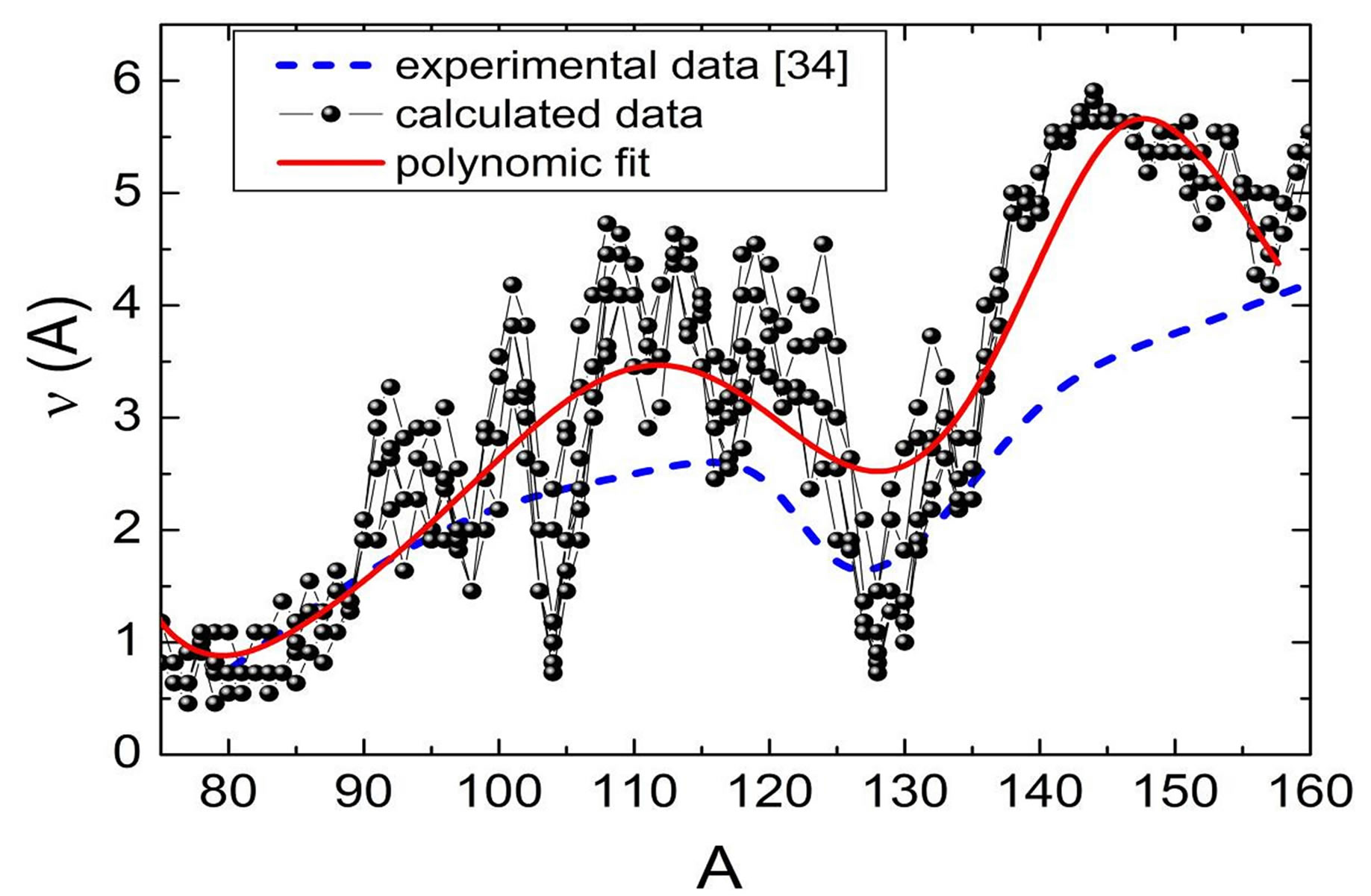
Figure 3. (Color online) The fission neutron yield is given as a function of the fusion fragment mass of 236U: dashed line corresponds to the experimental data [34], circles with line present the calculated data and the solid line is the polynomial fit of our data (see more detail in the text).
ies and the number of statistical events were the same as in the previous calculations described above. We obtained that the average value 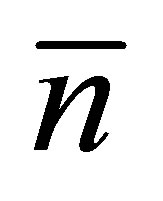 for such number of statistical events is 2.69 particles.
for such number of statistical events is 2.69 particles.
As one can see, the theoretical data agree well with the experiment. Moreover, the 9th order polynomial fit of our data (solid line in Figure 3) reproduces the known experimental “sawtooth”-curve of the neutron multiplicity, namely the peak about 115, minimum in vicinity of 128, the further growth in the range of 145 and decrease to 160. In addition, the proposed statistical method allows one to obtain the fine structure of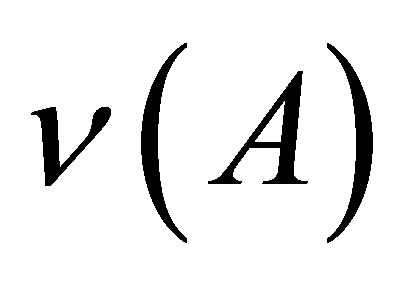 , like local minima at 98, 104, 117, 121, 128, 134, 158 and local maxima at 92, 101, 109, 114, 119, 124, 133, 144, 154.
, like local minima at 98, 104, 117, 121, 128, 134, 158 and local maxima at 92, 101, 109, 114, 119, 124, 133, 144, 154.
It should be noted that the experimental dependences 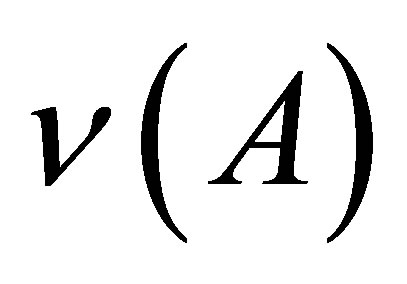 provide no data on such fine structure [34-38]. The fine structure might be caused by many factors as the presence of light and heavy fragments with the magic and near-magic numbers in the cluster, by the optimal proton/neutron ratio in the fragments or by the influence of the odd/even effects, etc.
provide no data on such fine structure [34-38]. The fine structure might be caused by many factors as the presence of light and heavy fragments with the magic and near-magic numbers in the cluster, by the optimal proton/neutron ratio in the fragments or by the influence of the odd/even effects, etc.
3.3. Calculation of the Nuclear Charge Spectrum of the U, Pa, Th and Ac Isotopes
The charge spectra of the U, Pa, Th and Ac isotopes were studied in the experiment with radioactive beams formed by the 238U fragmentation at the DESY Darmstadt heavyion synchrotron SIS (see [14,18,39] for experimental details). In particular, the charge spectra of the 230/234U, 223/232Pa, 220/229Th and 219/226Ac isotope series were investigated. They have different abilities of nuclear transformation because of the significant variations of their specific binding energy, e (fissionability parameter, Z2/A). Namely, for the U series it is 7.6209/7.6007 (36/36), for the Pa series it is 7.6519/7.5946 (37/35), for Th it is 7.6846/ 7.6349 (36/35) and for Ac it is 7.7006/7.6556 (36/35). These isotopes in the series also differ drastically by their half-live periods, for example, in the Th series—from 10−6 s to 7 × 103 years!
The experimental data (see Figure 4) indicate the different shapes of the charge spectra for the isotopes of the same chemical compound. In our method, the main features of the DE experiment can be explained by by letting the possibility of varying temperature T of the initial isotopes within 0.7 - 0.9 MeV at fixed values the set of basic model parameters: isobaric constants, 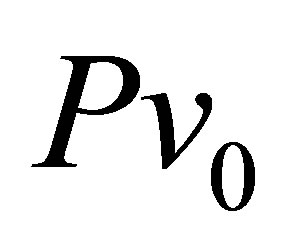 , the emitted neutrons number and the statistical fluctuation testing range. The variation of the temperature can be derived from the fact that the lighter initial isotopes of the U, Pa, Th and Ac series under the same fission conditions must be “hotter” than heavier. Really, the mass of difference of the isotopes in the same series varies up to 4%, and between the different elements within 7%.
, the emitted neutrons number and the statistical fluctuation testing range. The variation of the temperature can be derived from the fact that the lighter initial isotopes of the U, Pa, Th and Ac series under the same fission conditions must be “hotter” than heavier. Really, the mass of difference of the isotopes in the same series varies up to 4%, and between the different elements within 7%.
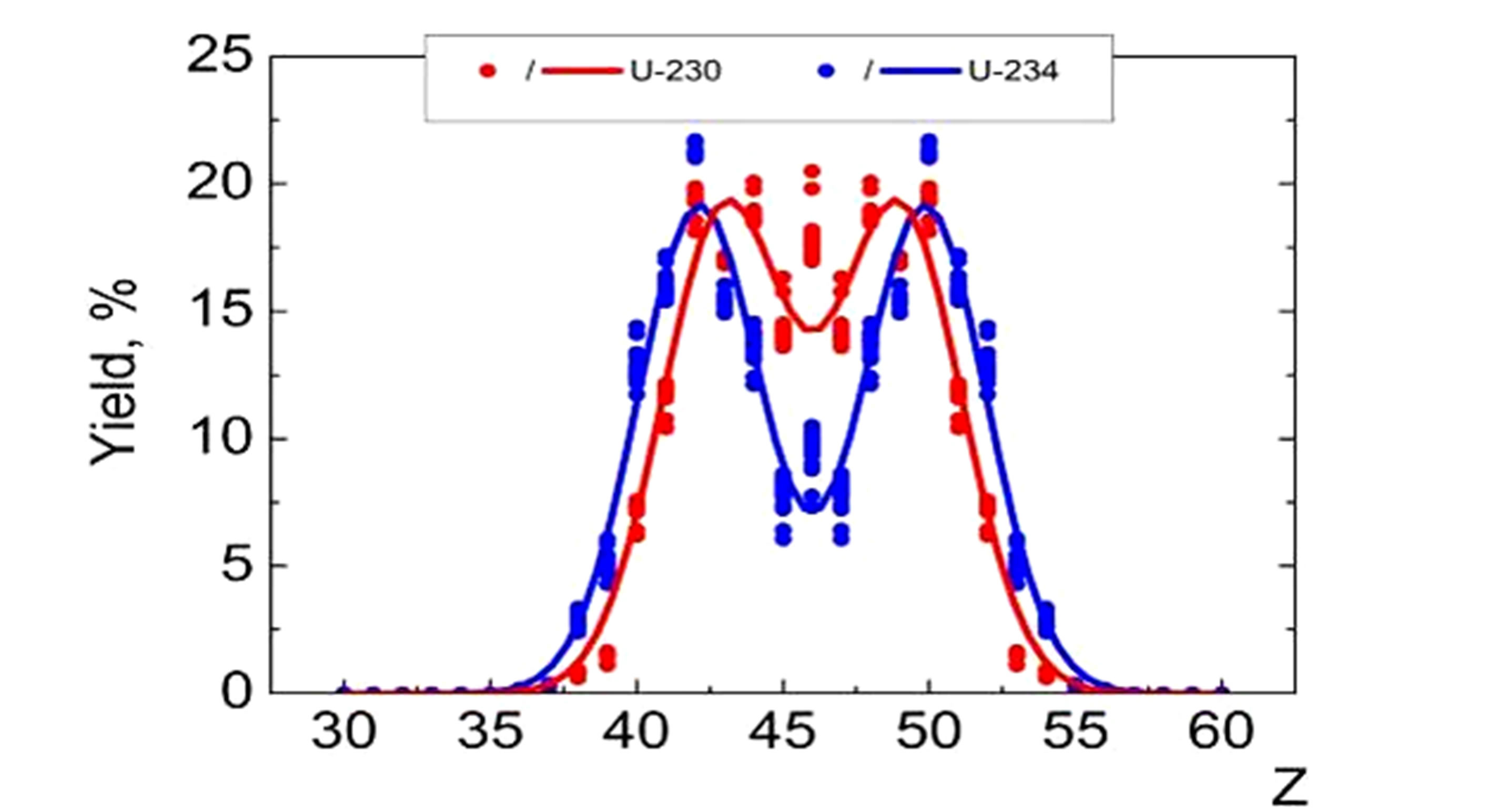
Our data are shown in Figure 5 for several outside (depleted/enriched by neutrons) isotopes in the U, Pa, Th and Ac series, see Figure 4. The spread of the theoretical data for the same proton number is caused by the statistical fluctuation of thermodynamical parameters. We fit the theoretical data with one, two and three Gaussian functions (solid lines in Figure 5) in order to emphasize their hump structure.
One can see that suggested method qualitatively reflects all the main experimentally observed structures of the nuclear-charge spectra. The U series demonstrates a strongly expressed two-hump structure. The Pa series exhibits the transition from oneto two-hump structure of the charge spectrum. The same trend we obtain for the isotopes of the Th series. However, we have also found a weakly expressed third-hump structure in the middle of the charge spectrum of 229Th (see Figure 5(c)). Finally, the three-hump structure is more expressed for the 226 isotope of the Ac series.
4. Conclusions
Thus, the statistical approach for the post-scission fragments ensembles is able to explain the main peculiarities of the nuclear fission observed characteristics. Despite
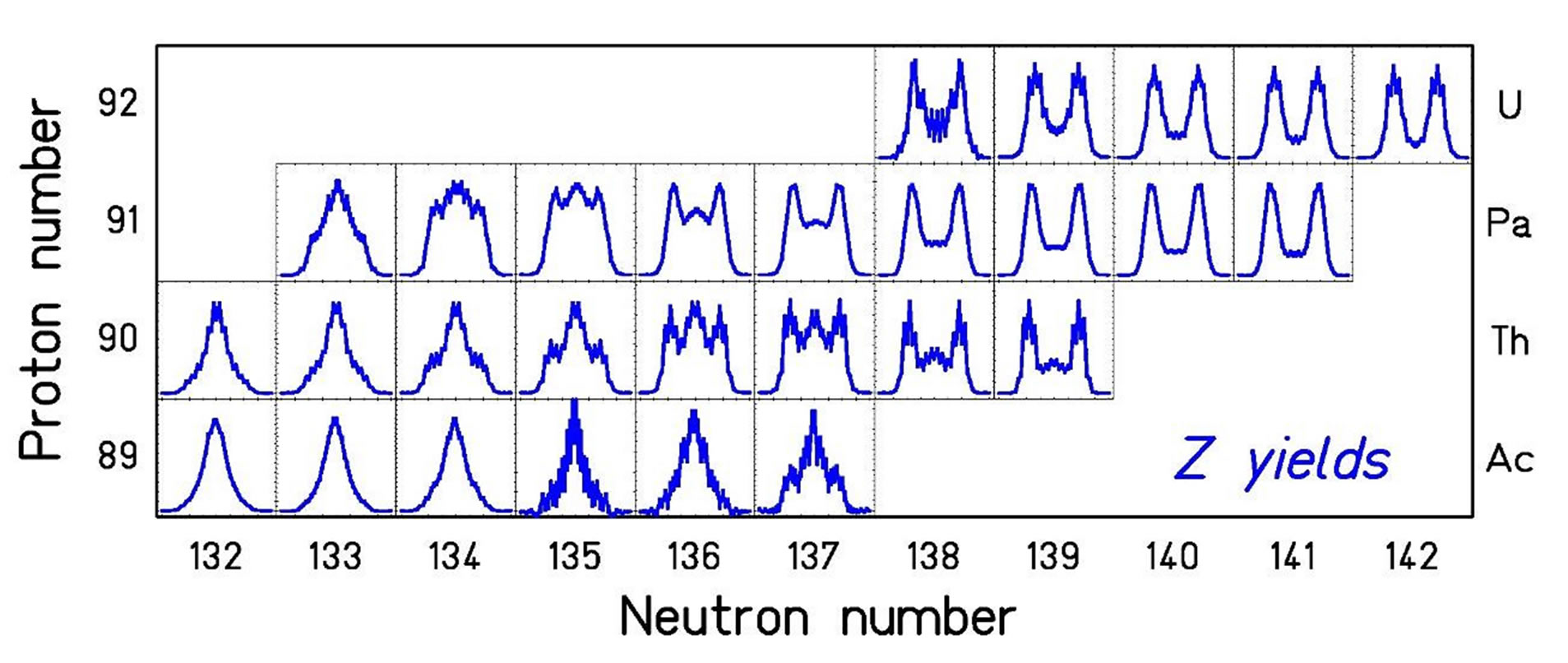
Figure 4. (Color online) Experimental fission-fragment nuclear-charge spectra of the U, Pa, Th, Ac isotopes, taken from [14].
 (a)
(a)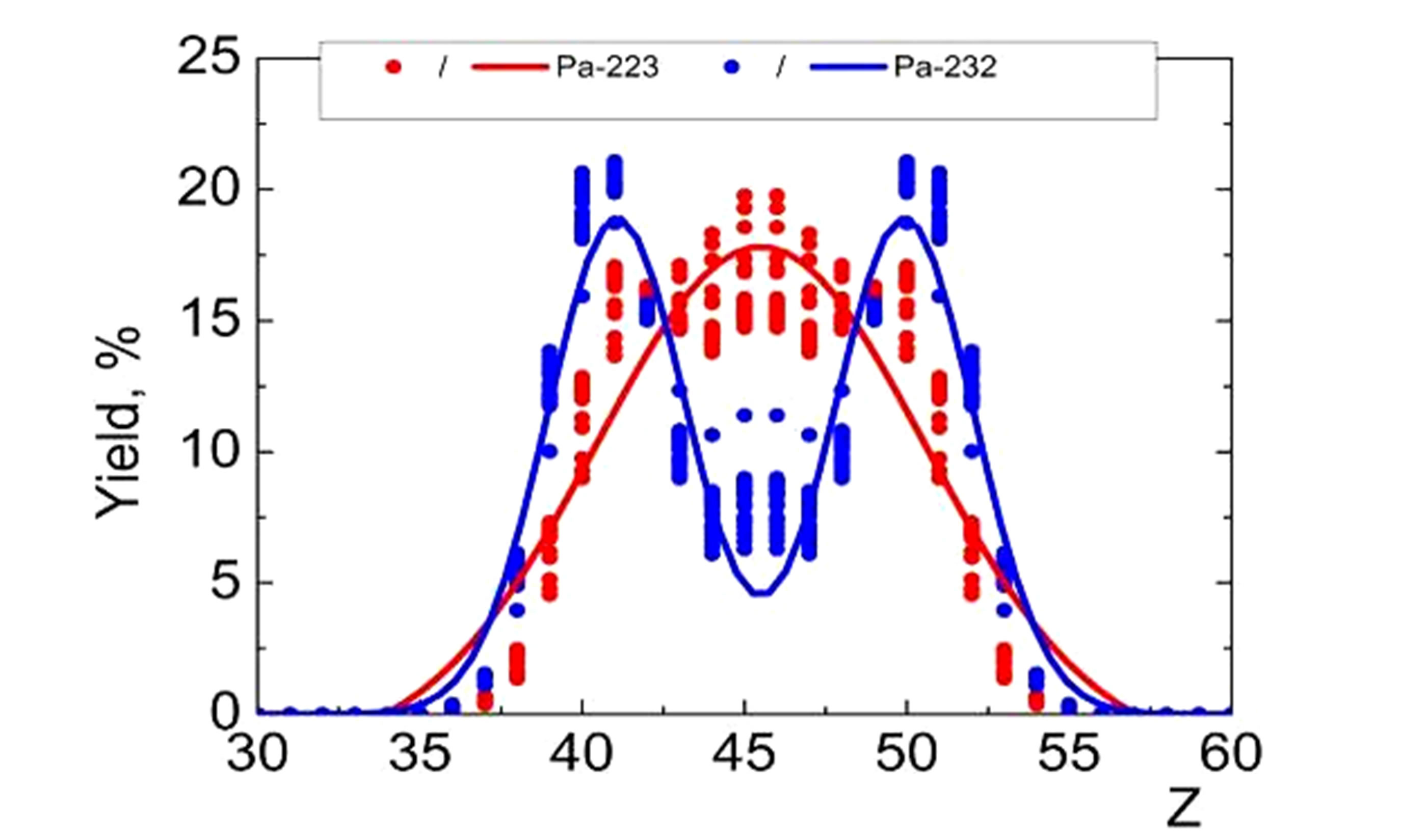 (b)
(b)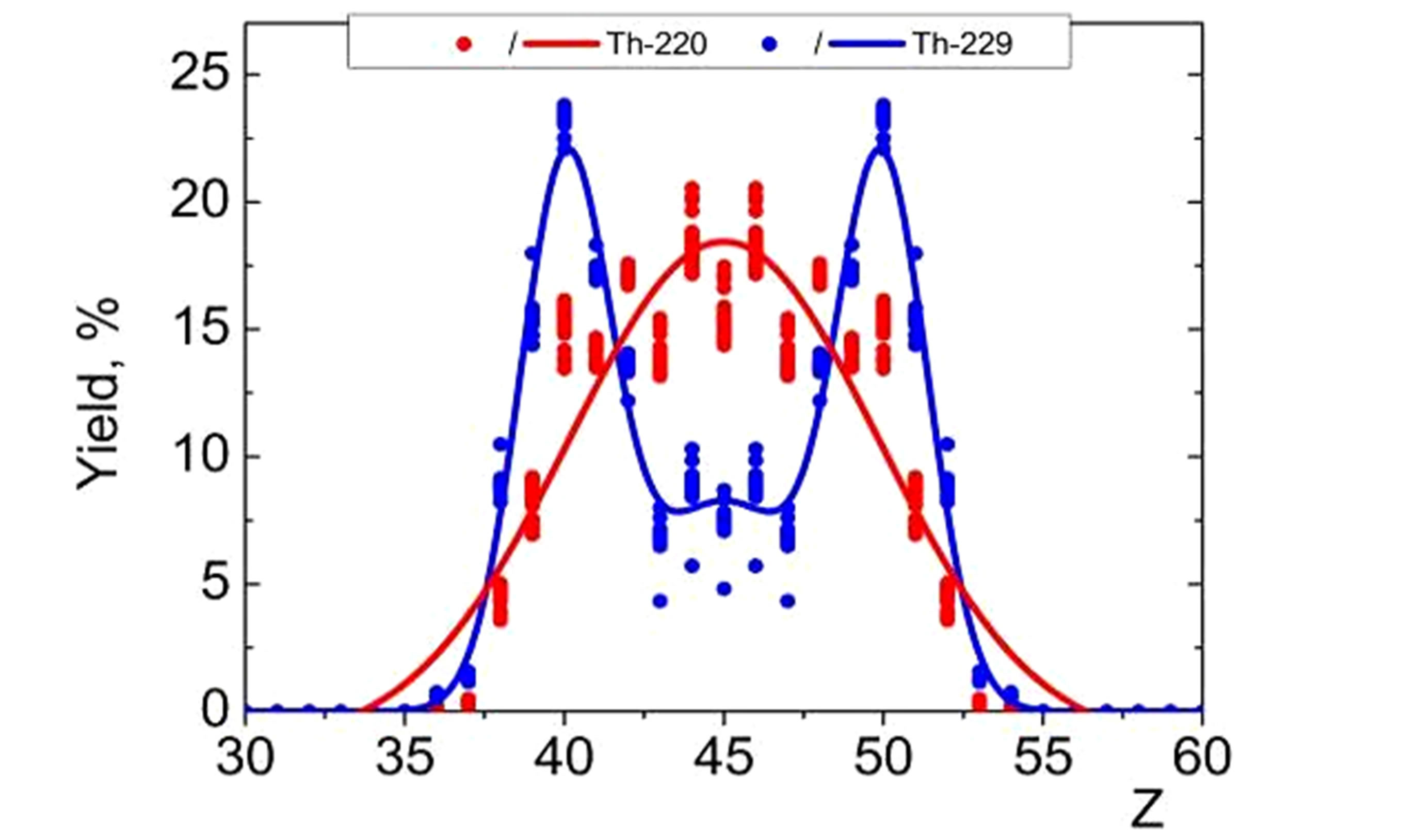 (c)
(c)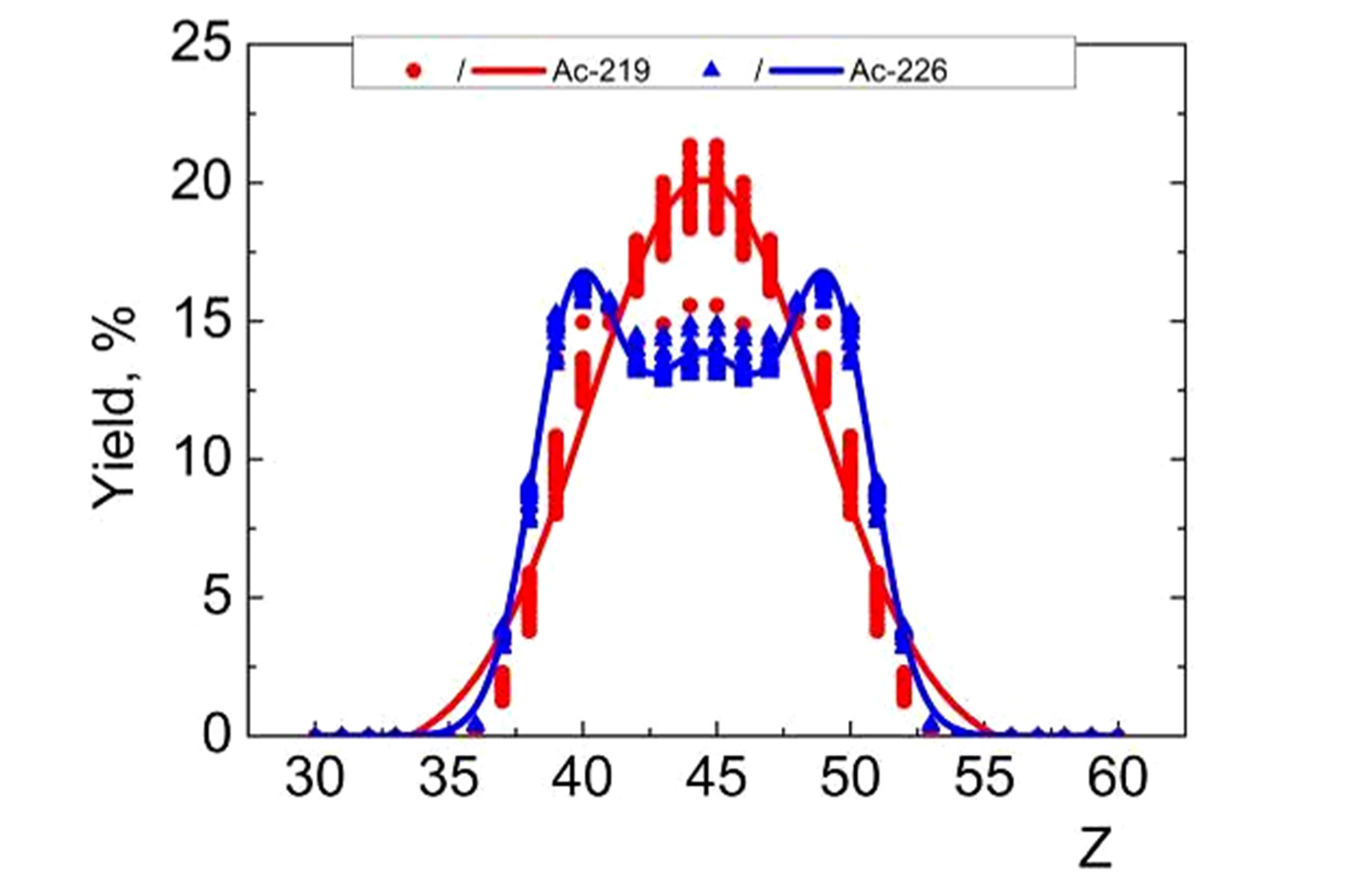 (d)
(d)
Figure 5. (Color online) The evaluated fission-fragment nuclear-charge spectra of the outside (depleted/enriched by neutrons) isotopes of the U → (a), Pa → (b), Th → (c), Ac → (d) series, see Figure 4.
a limited number of model parameters such as isobaric constant and cumulative chain length, the proposed statistical method can explain the principal features of the mass and charge fragments spectra, their anisotropy and symmetrization with the rise of temperature.
The method allows to estimate the validity of the MCSFF data obtained with different experimental methods such as gamma-, mass spectrometry with time-offlight mass data or the radiochemical one, e.g. with the verification of their possibilities in detecting the short-, ultraor long-lived nuclei.
We can also assume that taking into account the post-fission beta+ and beta− particles emission and statistical fluctuation of the binding energy will improve the analytic abilities of the proposed statistical method.
5. Acknowledgements
The authors are grateful to D. Symochko, V. Mazur, M. Stetc, O. Snigursky and V. V. Maslyuk for fruitful discussions and assistance. This work was carried out within the framework of the Program of informatization of the National Academy of Sciences of Ukraine and with the partial support of the Project X-5-7.
REFERENCES
- I. Halpern, Annual Review of Nuclear and Particle Science, Vol. 9, 1959, pp. 245-343. http://dx.doi.org/10.1146/annurev.ns.09.120159.001333
- N. I. Zaika, Y. V. Kibkalo, V. P. Tokarev and V. A. Shityuk, Soviet Journal of Nuclear Physics, Vol. 42, 1985, pp. 191-195.
- Yu. P. Gangrsky, B. Dalhsuren and B. N. Markov, “Fission Fragments of Nuclei,” Energoatomizdat, Moscow, 1986.
- Yu. V. Kibkalo, “Phenomenological Model for Fragment Mass and Charge Distribution in Actinide Nuclei Fission,” Fission Product Yield Data for the Transmutation of Minor Actinide Nuclear Waste, IAEA, Vienna, 2008, pp. 157-182. http://www-nds.iaea.org/publications/tecdocs/sti-pub-1286.pdf
- T. Ohtsuki, Y. Nagame, K. Tsukada, N. Shinohara, S. Baba, K. Hashimoto, I. Nishinaka, K. Sueki, Y. Hatsukawa, K. Hata, T. Sekine, I. Kanno, H. Ikezoe and H. Nakahara, Physical Review C (Nuclear Physics), Vol. 44, 1991, pp. 1405-1423. http://dx.doi.org/10.1103/PhysRevC.44.1405
- A. V. Ignatyuk, “Statistical Properties of Excited Atomic Nuclei,” Energoatomizdat, Moscow, 1983, p. 71.
- U. Brosa, S. Grossmann and A. Muller, Physics Reports, Vol. 197, 1990, pp. 167-262. http://dx.doi.org/10.1016/0370-1573(90)90114-H
- V. M. Strutinsky, Nuclear Physics A, Vol. 95, 1967, pp. 420-442. http://dx.doi.org/10.1016/0375-9474(67)90510-6
- P. Fong, Physical Review C, Vol. 17, 1978, pp. 1731- 1734. http://dx.doi.org/10.1103/PhysRevC.17.1731
- W. E. Swiatecky, Nuclear Physics A, Vol. 376, 1982, pp. 275-291. http://dx.doi.org/10.1016/0375-9474(82)90065-3
- B. Slavov, V. I. Dimitrov, K. Goeke, F. Gruemmer and P.-G. Reinhard, Nuclear Physics A, Vol. 454, 1986, p. 392. http://dx.doi.org/10.1016/0375-9474(86)90276-9
- A. C. Wahl, Atomic Data and Nuclear Data Tables, Vol. 39, 1988, pp. 1-156. http://dx.doi.org/10.1016/0092-640X(88)90016-2
- V. M. Kolomietz, Physical Review C (Nuclear Physics), Vol. 52, 1995, pp. 697-703. http://dx.doi.org/10.1103/PhysRevC.52.697
- K.-H. Schmidt, S. Steinhauser, C. Bockstiegel, A. Grewe, A. Heinz, A. R. Junghans, J. Benlliure, H.-G. Clerc, M. de Jong, J. Muller, M. Pfutzner and B. Voss, Nuclear Physics A, Vol. 665, 2000, pp. 221-267. http://dx.doi.org/10.1016/S0375-9474(99)00384-X
- Ph. Schewe, J. Riordon and B. Stein, Physics News, Vol. 572, 2002, pp. 35-38.
- V. Maslyuk, International Journal of Physics, Vol. 6, 2000, pp. 1-8.
- V. T. Maslyuk, O. A. Parlag and T. I. Marinets, Physics of Particles and Nuclei Letters, Vol. 4, 2007, pp. 78-84. http://dx.doi.org/10.1134/S1547477107010086
- K.-H. Schmidt and B. Jurado, Physical Review C, Vol. 83, 2011, Article ID: 014607.
- Yu. P. Gangrskii, V. I. Zhemenik, N. Yu. Maslova, G. V. Mishinsky, Yu. E. Penionzhkevich and O. Szöllös, Pis’ma Fiz. Elem. Chastits At. Yadra, Vol. 6, 2000, pp. 5-11.
- H. Feshbach, Physics Today, Vol. 12, 1987, pp. 9-12. http://dx.doi.org/10.1063/1.2820259
- U. Facchini, G. Pierini and E. Saettame, Energia Nucleare, Vol. 20, 1973, pp. 667-677.
- O. G. Sitenko and V. K. Tartakovs’kii, “Nuclear Theory,” Lebid’, Kiev, 2000.
- L. G. Girifalco, “Statistical Physics of Materials,” John Wiley & Sons, New York, 1973.
- A. J. Koning, T. Fukahori and A. Hasegawa, “Intern. Evaluation Cooperation: Intermediate Energy Data,” Rep. NEA/ WPEC-13, ECNRX-98-01413, 1998.
- T. J. Liu and Q. C. Liang, Communication of Nuclear Data Progress, IAEA, Vienna, 2000, pp. 105-119. http://www-nds.iaea.org/publications/indc/indc-cpr-0050.pdf
- A. M. Goryachev, V. A. Selivestrov and R. M. Umarov, Yadernaya Fizika, Vol. 57, 1994, pp. 815-819.
- A. Kolomietc, V. M. Kolomietz and S. Shlomo, Physical Review C, Vol. 55, 1997, pp. 1376-1379. http://dx.doi.org/10.1103/PhysRevC.55.1376
- G. Audi, A. H. Wapstra and C. Thibault, Nuclear Physics A, Vol. 729, 2003, pp. 337-676. http://dx.doi.org/10.1016/j.nuclphysa.2003.11.003
- P. Moller, J. P. Nix, W. D. Myers and W. J. Swiatecky, Atomic Data and Nuclear Data Tables, Vol. 59, 1995, pp. 185-381. http://dx.doi.org/10.1006/adnd.1995.1002
- N. Ghahramany, Sh. Gharaati and M. Ghanaatian, Pis’ma Fiz. Elem. Chastits At. Yadra, Vol. 8, 2011, pp. 169-181.
- P. Roy Chowdhury and D. N. Basu, Acta Physica Polonica B, Vol. 37, 2006, pp. 1833-1846.
- V. V. K. Mohindra, M. A. Vartolomei and A. McDonald, “Fission Chambers for CANDU® SDS Neutronic Trip Applications,” Proceedings of the 28th Annual Canadian Nuclear Society CNS 2007, Saint John, New Brunswick, 2007. https://www.thermo.com/eThermo/CMA/PDFs/Various/File_1719.pdf
- D. G. Madland, Acta Physica Hungarica A, Vol. 10, 2000, pp. 231-240.
- D. R. Nethaway and H. B. Levy, Physical Review B, Vol. 139, 1965, pp. 1505-1513. http://dx.doi.org/10.1103/PhysRev.139.B1505
- U. Brosa, Physical Review C, Vol. 32, 1985, pp. 1438- 1441. http://dx.doi.org/10.1103/PhysRevC.32.1438
- Y.-J. Chen and T.-J. Liu, Chinese Physics C, Vol. 35, 2011, pp. 343-348.
- V. Manea and A. Tudora, “Proceedings Scientific Workshop on Nuclear Fission Dynamics and the Emission of Prompt Neutrons and Gamma Rays,” In: F.-J. Hambsch and N. Carjan, Eds., Sinaia, 2010, p. 49.
- P. Talou, T. Kawano, J. E. Lynn, P. Moller, O. Bouland and M. B. Chadwick, Journal of the Korean Physical Society, Vol. 59, 2011, pp. 797-802. http://dx.doi.org/10.3938/jkps.59.797
- C. Schmitt, K.-H. Schmidt, A. Kelić, A. Heinz, B. Jurado and P. N. Nadtochy, Physical Review C, Vol. 81, 2010, Article ID: 064602. http://dx.doi.org/10.1103/PhysRevC.81.064602


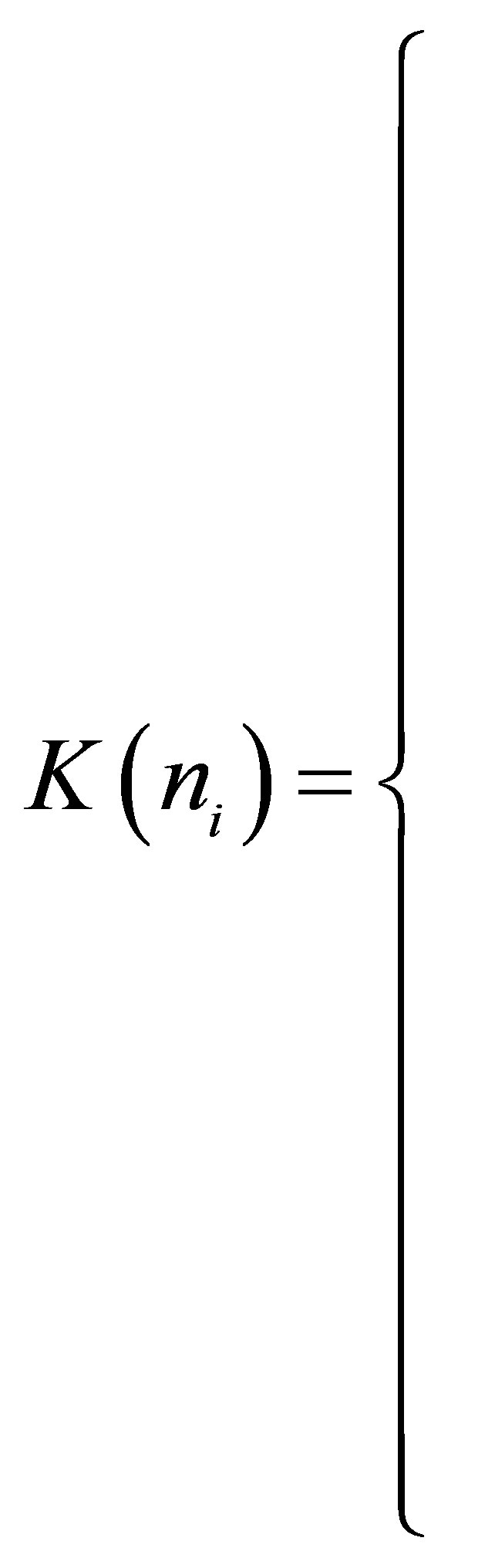
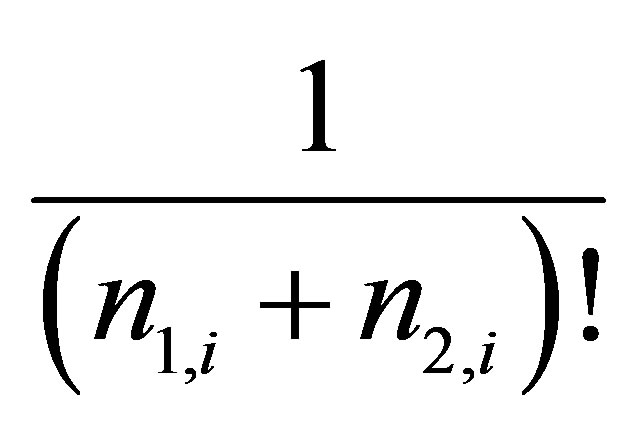
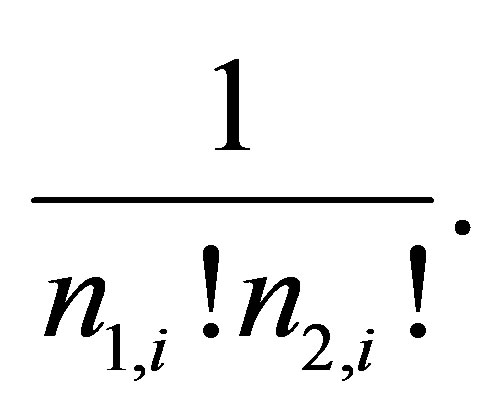
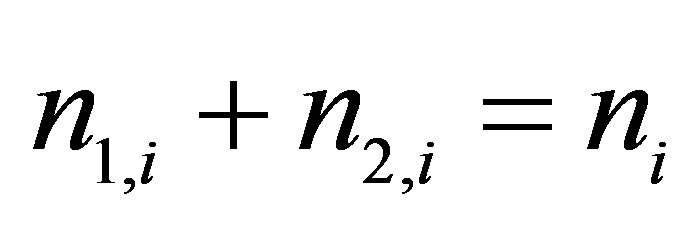 .
.