Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21071,4 pages DOI:10.4236/jmp.2012.37070
Variable Range Hopping in Hydrogenated Amorphous Silicon-Nickel Alloys
1Research Group ESNPS, Physics Department, Faculty of Sciences, University Ibn Zohr, Agadir, Morocco
2Laboratoire de Physique de la Matière Condensée, Département de Physique, Faculté des Sciences et Techniques de Mohammadia, Mohammedia, Morocco
3Laboratoire de Spectroscopie Hertzienne (LSH), Université des Sciences et Technologies de Lille I, Villeneuve d’Ascq, France
Email: *kaaouachi21@yahoo.fr
Received September 12, 2011; revised October 11, 2011; accepted November 12, 2011
Keywords: amorphous silicon-nickel alloys a-Si1–yNiy:H; variable range hopping conductivity; transport phenomenon; metal insulator transition
ABSTRACT
On the insulating side of the metal-insulator transition (MIT), the study of the effect of low Temperatures T on the electrical transport in amorphous silicon-nickel alloys a-Si1–yNiy:H exhibits that the electrical conductivity follows, at the beginning, the Efros-Shklovskii Variable Range Hopping regime (ES VRH) with T−1/2. This behaviour showed that long range electron-electron interaction reduces the Density of State of carriers (DOS) at the Fermi level and creates the Coulomb gap (CG). For T higher than a critical value of temperature TC, we obtained the Mott Variable Range Hopping regime with T−1/4, indicating that the DOS becomes almost constant in the vicinity of the Fermi level. The critical temperature TC decreases with nickel content in the alloys.
1. Introduction
Experimental results on resistivity in amorphous siliconnickel alloys a-Si1–yNiy:H at low temperature, have been analysed in the insulating side of the Metal-Insulator Transition (MIT). The resistivity measurements were obtained for the insulating samples, Si0.85Ni0.15:H and Si0.83Ni0.17:H, in the range of temperature 1 - 140 K.
The samples were prepared by radio-frequency sputtering from silicon target. The subtracts (Corning 7059 glass) were at room temperature during deposition and the sputtering gaz was a 90% Ar and 10% H2. The hydrogen was added to saturate silicon dangling bonds that might caused by the disorder.
Compositions of the samples were determined by energy dispersive analysis with x-rays (EDAX). Film thickness which were about 1 µm, were measured to an accuracy of 0.1 µm using a Talysurf stylus. The amorphous nature was demonstrated by electron diffraction measurements in a transmission electron microscope.
For the sample Si0.83Ni0.17:H, the electrical resistivity was measured using standard four-terminal AC techniques. However, this method gave rise to very long out of phase signal in the sample the most resistive (i.e., Si0.85Ni0.15:H), why the measurements were made using four-terminal DC technique .
It is known that the Variable Range Hopping (VRH) conductivity of the three dimensional disordered systems, was shown by Mott [1,2] to behave like Ln(σ)α(T/T0). This dependence was obtained by optimizing the hopping probability and assuming a slowly varying Density of State (DOS) in the vicinity of the Fermi level.
On the contrary, Efros and Shklovskii (ES) [3,4] have predicted that long range electron-electron interaction reduces the DOS at the Fermi level and creates a soft Coulomb Gap (CG), which takes the form N(E)α(E − EF)ν, with ν = 2. The existence of the CG leads to the ES VRH regime of the conductivity, which is written:
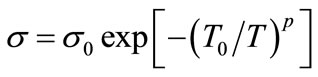 (1)
(1)
With p = (ν + 1)/(ν + 4) is an exponent that allows to conclude the profile of the DOS. In fact, Equation (1) remains quite universal since, when ν = 0, the DOS is constant and p = 0.25, corresponding to the Mott regime. But when ν = 2, the DOS varies in the vicinity of the Fermi level and p = 0.5 corresponding to ES VRH regime. The experimental situation has been confusing for some time, with both values of p being observed. Mott VRH and ES VRH regimes have been widely observed in many types of disordered materials [5-8].
Our aim in this paper is to characterize the DOS in vicinity of Fermi level in our samples by studying the proposed variable range hopping conduction at very low temperature.
2. Study of the Electrical Conductivity at Zero Magnetic Field
When the magnetic field B = 0 T, we used Zabrodskii et al. [9] method to determine which of the both VRH regimes is observed in the samples, Mott VRH regime or ES VRH regime.
Using Equation (1), Zabrodskii et al. [9] give the following function w(T) varying with temperature T as:
 (2)
(2)
where σ is the electrical conductivity (σ = 1/ρ). ρ is the electrical resistivity.
3. Results and Discussion
To highlight the regime that governs the electrical conductance, a plot of Ln(dLn(σ)/dLn(T)) versus Ln(T) is shown in Figure 1.
For sample Si0.85Ni0.15:H, we noticed that for values of temperature smaller than TC = 54 K the slope is very close to the value 0.5 indicating the existence of ES VRH conduction regime (p = 0.49). For T > TC, we observed a change of slope who becomes very close to the value 0.25 suggesting a crossover from ES VRH regime to the Mott VRH regime (p = 0.2).
For sample Si0.83Ni0.17:H, we have obtained the same behaviours. For T < TC (TC = 38 K), the slope is very close to the value 0.5 (p = 0.56) indicating the existence of ES VRH regime. For T > TC, the slope becomes very close to the value 0.25 (p = 0.22) corresponding to the Mott VRH regime.
For both samples, the values of Mott temperature TMott in Mott VRH regime, and Efros Shklovskii temperature TES in ES VRH regime were obtained by fitting the curves representing the experimental temperature dependence of the conductivity respectively for T < TC (ES VRH regime) and for T > TC (Mott VRH regime). These values were compared to those proposed by Rosenbaum et al. [10] (see Table 1).
 (3)
(3)
where TC is the critical value of temperature for which we observed the crossover from ES VRH regime to Mott VRH regime (change of slope in Figure 1).
In Table 1, we present the results of calculation of experimental and theoretical values of TC, TMott , TES, and the ratio TMott/TES. We noticed that for the sample Si0.85Ni0.15:H, the value of the ratio TMott/TES is comparable to that given by Rosenbaum [10], and theoretical value of TC is substantially equal to the experimental value. But for the sample Si0.83Ni0.17:H, the value of the ratio TMott/TES is roughly four times smaller than that given by Rosenbaum [10], and theoretical value of TC is almost ten times lower than the experimental value.
To confirm these results, the experimental values of the conductivity σi at different temperatures Ti were fitted to an expression given by Equation (1), using σ0 and T0 as adjustable parameters.
The fitting procedure was as follows: p was varied from 0.01 to 1 with a step of 0.01, for each value of pthe

Figure 1. Function w(T) versus Ln(T) in Equation (2) for samples (Si0.85Ni0.15:H and Si0.83Ni0.17:H).

Table 1. Results of calculation of experimental and theoretical values of TC, TMott, TES, and the ratio TMott/TES.
data were fitted to Equation (1), and σ0 and T0 were obtained by standard linear regression methods. The goodness of the fit was tested with the estimation of the percentage deviation Dev(%):
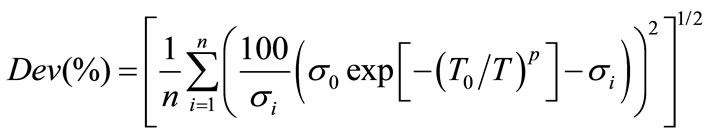 (4)
(4)
In Figures 2 and 3, we plot Dev(%) against the exponent p in Equation (1) for several ranges of temperature respectively for samples Si0.85Ni0.15:H and Si0.83Ni0.17:H.
For sample Si0.85Ni0.15:H, when T < TC (TC = 54 K) the minimum of Dev(%) is obtained for p = 0.54. This value is too close to 0.5 suggesting the existence of the ES VRH conduction regime in this range of temperature, and indicates that long range electron-electron interaction reduces the DOS at the Fermi level and creates a soft Coulomb Gap (CG). When T > TC, the minimum of

Figure 2. Percentage deviation Dev(%) versus exponent p in Equation (1) in all the range of temperature 1 - 140 K for sample Si0.85Ni0.15:H.

Figure 3. Percentage deviation Dev(%) versus exponent p in Equation (1) in all the range of temperature 1 - 140 K for sample Si0.83Ni0.17:H.
Dev(%) is obtained for p = 0.22. This value is too close to 0.25 indicating the existence of Mott VRH conduction regime. This suggests the slowly varying of the DOS at the Fermi level.
We noticed the same behaviours in the sample Si0.83Ni0.17:H depending on whether T > TC or T < TC. When T < TC (TC = 38 K) the minimum of Dev(%) is obtained for p = 0.55 indicating the existence of ES VRH conduction regime. When T > TC the minimum of Dev(%) is obtained for p = 0.23 showing the existence of Mott VRH conduction regime.
In this work, we have provided the crossover phenomenon from ES VRH regime (T < Tc) to Mott VRH regime (T > TC) in samples Si0.85Ni0.15:H and Si0.83Ni0.17:H. The VRH conduction depends essentially on the relative magnitude of the hopping energies of Mott ∆Mott, of ES ∆ES, and on CG ∆CG. The parameter p in Equation (1) is equal to 0.25 in the relatively high temperature limit, while at very low temperature, it is expected to be 0.5. Very close to the MIT, the CG becomes so narrow that the temperature range where the ES regime occurs cannot be reached and only the Mott regime is expected. Iqbal [11] et al. have observed the same behaviour in Si:(P,B) samples. In previous work [12] we have exhibited the crossover phenomenon from Mott VRH regime to ES VRH regime in presence of magnetic fields in n-type InP sample.
The physical signification of the relationship between the parameters (TES, TMott and TC) is that the crossover seen occurs when ∆Mott = ∆ES in the sample Si0.85Ni0.15:H. But we can not explicate the disagreement shown in the sample Si0.83Ni0.17:H.
In Figures 4 and 5, we have plotted Ln(ρ) versus temperature respectively for samples Si0.85Ni0.15:H and Si0.83Ni0.17:H. We notice that for low values of temperature (T < TC), the experimental resistivity follows the ES VRH regime whereas for higher values of temperature (T
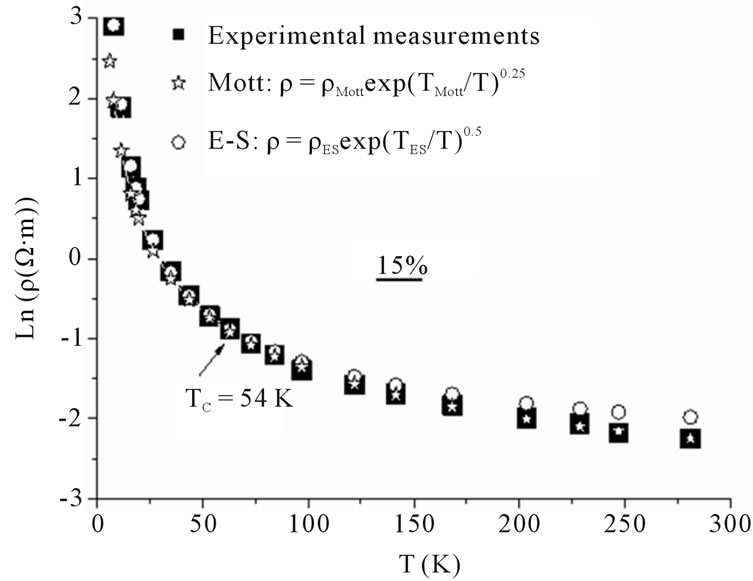
Figure 4. Ln(ρ) versus temperature for sample Si0.85Ni0.15:H.
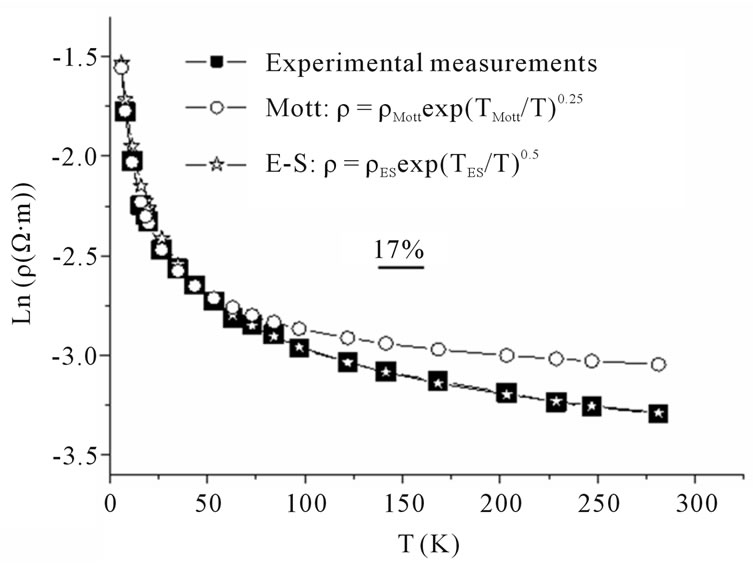
Figure 5. Ln(ρ) versus temperature for sample Si0.83Ni0.17:H.
> TC), electrical resistivity follows the Mott VRH regime.
In summary, our results shows the variable range hopping regime in both the samples Si0.85Ni0.15:H and Si0.83Ni0.17:H. The density of states is found to be characterized by Coulomb Gap at very low temperature and become constant above a critical temperature TC. The agreement with Rosenbaum predictions for the sample Si0.85Ni0.15:H indicates that the crossover Efros Shklovskii to Mott regime occurs when the relative magnitude of the hopping energies ∆Mott and ∆ES becomes comparables. While this property is not shown in the sample Si0.83Ni0.17:H.
4. Acknowledgements
We are grateful to Professor K. M. Abkemeier to have allowed us to use his experimental results on a-Si1–yNiy: H in our investigations.
REFERENCES
- N. F. Mott, “Conduction in Glasses Containing Transition Metal Ions,” Journal of Non-Crystalline Solids, Vol. 1, No. 1, 1968, pp. 1-17. doi:10.1016/0022-3093(68)90002-1
- N. F. Mott, “Metal-Insulator Transitions,” Taylor and Francis, London, 1974.
- B. I. Shklovskii and A. L. Efros, “Electronic Properties of Doped Semiconductors,” Springer, Berlin, 1984, pp. 191- 195.
- L. Efros and B. I. Shklovskii, “Coulomb Gap and LowTemperature Conductivity of Disordered Systems,” Journal of Physics C, Vol. 8, 1975, pp. L49-L51.
- A. El kaaouachi, A. Nafidi and G. Biskupski, “Positive and Negative Magnetoresistance on Both Sides of the Metal-Insulator Transition in Metallic n-Type InP,” Semiconductors Sciences and Technology, Vol. 18, 2003, pp. 69-74.
- R. Abdia, A. El kaaouachi, A. Nafidi and J. Himine, “Positive Magnetoresistance Behaviour in the Insulating Side of the Metal-Insulator Transition in CdSe,” Physica B: Condensed Matter, Vol. 373, No. 1, 2006, pp. 96-99. doi:10.1016/j.physb.2005.11.096
- A. El kaaouachi, R. Abdia and A. Nafidi, “Positive Magnetoresistance in the Variable Range Hopping Regime in CdSe, Physica E: Low-Dimensional Systems and Nanostructures,” Physica E, Vol. 32, 2006, pp. 419-421.
- R. Abdia, A. El kaaouachi, A. Nafidi, G. Biskupski and J. Hemine, “Variable Range Hopping Conductivity and Negative Magnetoresistance in n-Type InP Semiconductor,” Solid-State Electronics, Vol. 53, No. 5, 2009, pp. 469-472. doi:10.1016/j.sse.2009.02.002
- A. G. Zabrodskii and K. N. Zinoveva, “Low-Temperature Conductivity and Metal Insulator Transition in Compensate n-Ge,” Soviet Physics—JETP, Vol. 59, 1984, p. 425.
- R. Rosenbaum, “Crossover from Mott to Efros-Shklovskii Variable-Range Hopping Conductivity in InxOy,” Physical Review B, Vol. 44, 1991, pp. 3599-3603. doi:10.1103/PhysRevB.44.3599
- M. Iqbal, J. Galibert, J. Léotin, S. Askenazy, S. Waffenschmidt and J. Wosnitza, “Coulomb Gap Shrinkage in Compensated Si:(P,B) in High Magnetic Fields,” Physica B: Condensed Matter, Vol. 246-247, 1998, pp. 282-285. doi:10.1016/S0921-4526(97)00916-2
- A. El kaaouachi, R. Abdia, A. Nafidi and G. Biskupski, “Crossover Phenomenon for Variable Range Hopping Conduction and Positive Magnetoresistance in Insulating N-Type InP,” Journal of Annales de Chimie Sciences des Matériaux France, Vol. 33-34, 2008, pp. 357-364.
NOTES
*Corresponding author.

