Journal of Modern Physics
Vol.2 No.10(2011), Article ID:8046,5 pages DOI:10.4236/jmp.2011.210135
Oscillating Universe
Department Physik, Universität Paderborn, Paderborn, Germany
E-mail: lessner@phys.uni-paderborn.de
Received May 26, 2011; revised July 3, 2011; accepted July 18, 2011
Keywords: Origin of the Universe, Creation of Matter and Radiation, Cosmological Constant
ABSTRACT
It is pointed out that the inflationary flat Λ-CDM-model coming out from a big bang seems to be inconsistent. An alternative model based on previous work by the author is outlined. It starts with a geometrical phase transition in Minkowski space where the source of the gravitational field is a Higgs-like scalar field f. After the phase transition space-time is a contracting anti-deSitter space. Matter and radiation are created over a very long period of about 30 billion years from the gravitational energy. About 44 billion years after the phase transition the universe runs through a nonsingular minimum.
1. Introduction
In today’s cosmology the inflationary flat  -CDMmodel coming out from a big bang (standard model) is widely accepted as the best model of our universe. Although in this model most observations are well matched there are nevertheless some serious problems.
-CDMmodel coming out from a big bang (standard model) is widely accepted as the best model of our universe. Although in this model most observations are well matched there are nevertheless some serious problems.
Firstly: The big bang is out of physics and a source of some unsolved problems.
Secondly: The huge cosmological constant driving inflation must fall off within a tiny fraction of a second to the extremely small value we observe today where the inflaton field gives off its energy into reheating the matter. Up to now no consistent field theoretical model has been found to describe this process.
Thirdly: A positive cosmological constant according to 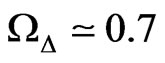 may explain the small deviation of the redshift-versus-distance relation from that for
may explain the small deviation of the redshift-versus-distance relation from that for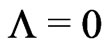 . On the other hand such a constant leads to problems in galaxy clusters. As shown in ref. [1] Einstein’s field equations with a cosmological constant yield in the weak field limit of slowly moving incoherent matter the modified gravitational law
. On the other hand such a constant leads to problems in galaxy clusters. As shown in ref. [1] Einstein’s field equations with a cosmological constant yield in the weak field limit of slowly moving incoherent matter the modified gravitational law
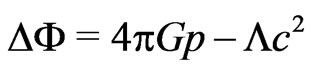 (1)
(1)
This leads to an additional force between two masses which increases linearly with the distance of the masses (repulsive for 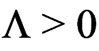 and attractive for
and attractive for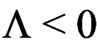 ). In refs.[1, 2] it has been shown that the masses and mean distances of galaxies in clusters have just such values that this additional force plays an important role. More precisely, in case of
). In refs.[1, 2] it has been shown that the masses and mean distances of galaxies in clusters have just such values that this additional force plays an important role. More precisely, in case of 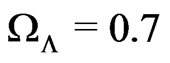 with
with 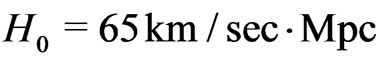 which means
which means 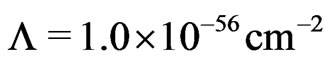 the repulsive forces between the galaxies are so strong that the clusters could not exist unless the content of uniformly distributed cold dark matter is greater than five times the content in the standard model. This, however, would close the universe and lead to an age problem. In other words, the standard model seems to be not consistent.
the repulsive forces between the galaxies are so strong that the clusters could not exist unless the content of uniformly distributed cold dark matter is greater than five times the content in the standard model. This, however, would close the universe and lead to an age problem. In other words, the standard model seems to be not consistent.
Fourthly: The standard scenario of galaxy formation is based on the paradigm of cold dark matter. Cold dark matter goes lumpy rather rapidly, and the lumps attract the baryonic matter. Latest observations, however, show that galaxies with their first star population have existed already some hundred million years after the big bang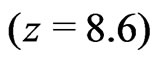 , and it seems to be questionable whether the cold dark matter scenario can explain this. Moreover, up to now this kind of matter has not been found.
, and it seems to be questionable whether the cold dark matter scenario can explain this. Moreover, up to now this kind of matter has not been found.
Finally: It is generally claimed that the peaks in the CMB correspond to acoustic oscillations in the photonbaryon plasma before recombination and that the positions of the peaks in the power spectrum favor definitively a flat universe. However, in ref.[3] it has been shown that this statement seems to be not correct. More precisely, the first peak in the power spectrum with multipole index 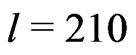 does not represent the fundamental acoustic oscillation, neither in a flat nor in an open universe. Thus the main argument for a flat universe, which is an outcome from inflation, seems to be not valid. In addition it should be noted that also the work by Bose and Grishchuck [4] queries the acoustic interpretation of the peaks.
does not represent the fundamental acoustic oscillation, neither in a flat nor in an open universe. Thus the main argument for a flat universe, which is an outcome from inflation, seems to be not valid. In addition it should be noted that also the work by Bose and Grishchuck [4] queries the acoustic interpretation of the peaks.
In recent years some efforts have been made to understand the big bang as a bouncing point of a cyclic universe. Ashtekar et al. [5] make use of loop quantum gravity to establish a nonsingular bounce in the quantum regime. The problem of this approach is the connection to the thermal history of the universe. Steinhardt and coworkers investigate the existence of a bouncing model in the regime of the Planckian scale (see the detailed list of references on his homepage). In the following article a model of an ever oscillating universe with a nonsingular bounce is outlined. There the bouncing point remains far from the Planckian scale.
2. An Ever Oscillating Universe without a Singularity
2.1. A Geometrical Phase Transition
The above problems are overcome in an ever oscillating universe without a singularity [2,6,7]. In this model the universe comes out from the Minkowski space by a geometrical phase transition in some distant past. This phase transition goes off in a Robertson-Walker spacetime where the source of the gravitational field is a real massless and selfinteracting minimally coupled scalar field 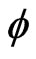 with a potential
with a potential
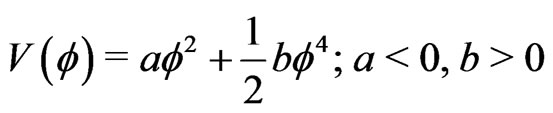 (2)
(2)
(see Figure 1).
The field equatons read
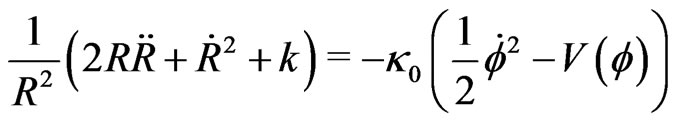 (3a)
(3a)
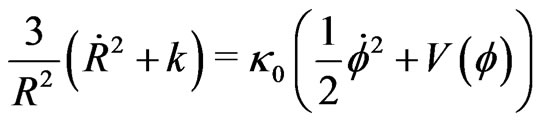 (3b)
(3b)
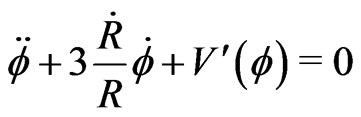 (3c)
(3c)
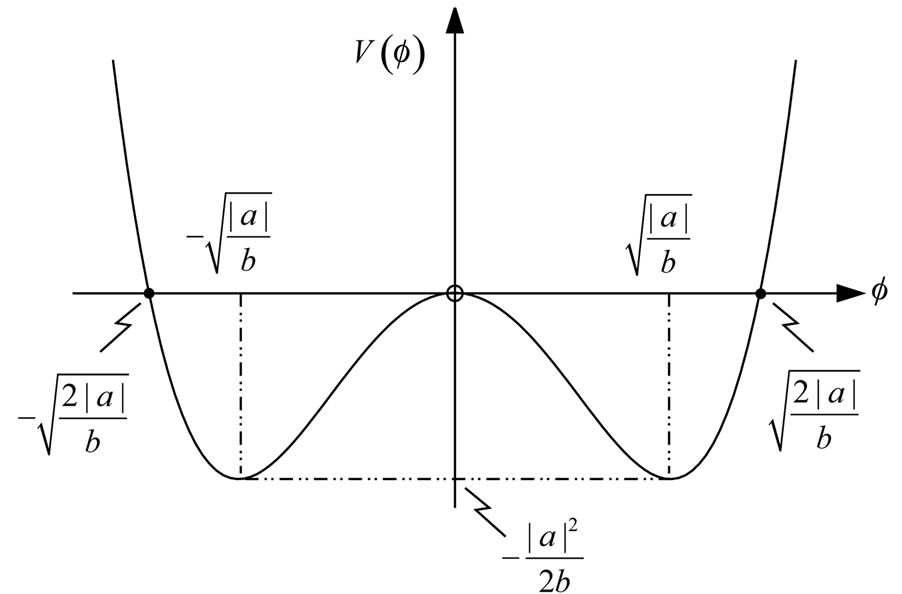
Figure 1. The potential V(f).
where a dot denotes the derivative with respect to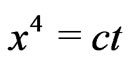 , the prime in Equation (3c) the derivative with respect to the argument and
, the prime in Equation (3c) the derivative with respect to the argument and 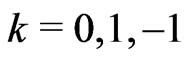 a flat, closed and open space respectively.
a flat, closed and open space respectively.
At the very beginning the universe is in the wrong unstable vacuum with 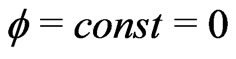 and
and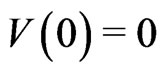 . As shown in ref.[2] space-time is then the Minkowski space
. As shown in ref.[2] space-time is then the Minkowski space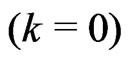 .
.
The selfinteraction of the scalar field lets the spacetime go over spontaneoulsy into the true stable vacuum with 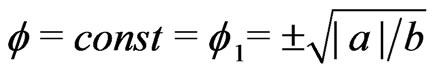 and
and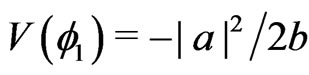 .
.
As shown in ref.[2] space-time is then an open 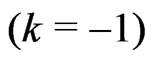 anti-deSitter space with the negative cosmological constant
anti-deSitter space with the negative cosmological constant
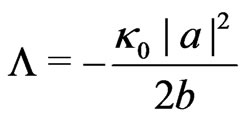 (4)
(4)
and
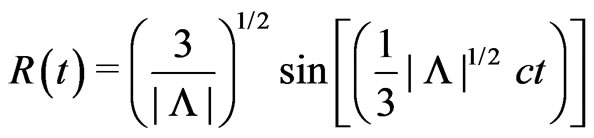 (5)
(5)
Furthermore, the constants a and b can be expressed by the constants 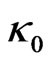 and
and  so that the potential (2) reads
so that the potential (2) reads
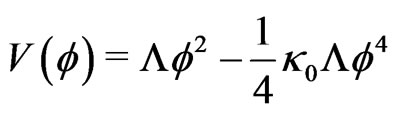 (6)
(6)
(see ref.[2]).
As shown in ref.[2] the total vanishing energy density ![]() is conserved in the geometrical phase transition, where
is conserved in the geometrical phase transition, where
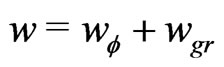 (7a)
(7a)
with
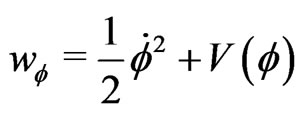 (7b)
(7b)
and
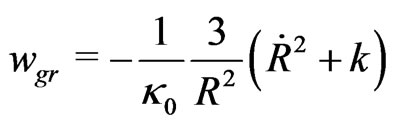 (7c)
(7c)
The purely gravitational energy density (7c) is due to Møllers energy-momentum complex [8] and some transformations given by Schmutzer [9] (see ref. [2]).
Any phase transition involves spontaneous symmetry breaking. In the above geometrical phase transition the symmetry 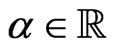
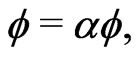 in the wrong vacuum is broken down to
in the wrong vacuum is broken down to 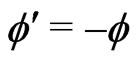 in the true vacuum, and the 10-parametric isometry of the Minkowski space is broken down to the 6-parametric isometry of the antideSitter space.
in the true vacuum, and the 10-parametric isometry of the Minkowski space is broken down to the 6-parametric isometry of the antideSitter space.
2.2. The Creation of Matter and Radiation
After the phase transition the anti-deSitter space starts to contract. However, this space-time can not be a model of our universe since it contains neither matter nor radiation. Hence, how did matter and radiation came into being?
In the contracting anti-deSitter space there is a natural energy source from which matter and radiation can be created. This source is the gravitational energy (7c) with 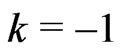 which is positive as long as
which is positive as long as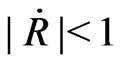 . In refs. [2, 7] a phenomenological model describing the creation of matter and radiation from this positive gravitational energy supply is presented. It is based on the fundamental law of energy conservation, that means that the sum of the gravitational energy density, the energy densities of created matter and radiation and the density
. In refs. [2, 7] a phenomenological model describing the creation of matter and radiation from this positive gravitational energy supply is presented. It is based on the fundamental law of energy conservation, that means that the sum of the gravitational energy density, the energy densities of created matter and radiation and the density 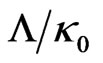 of dark energy is constantly zero as after the phase transition, hence
of dark energy is constantly zero as after the phase transition, hence
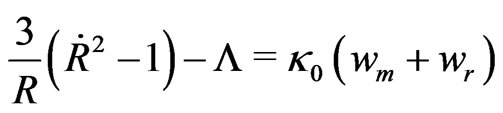 (8)
(8)
The creation of matter (index![]() ) and radiation (index
) and radiation (index ) is described by the two equations
) is described by the two equations
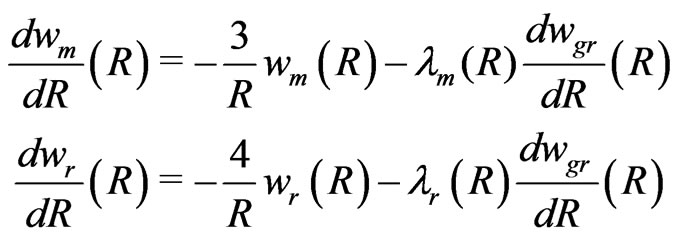 (9)
(9)
with phenomenological creation functions 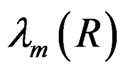 and
and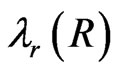 . The first terms on the right hand sides of these equations correspond to the conversation laws
. The first terms on the right hand sides of these equations correspond to the conversation laws 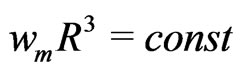 and
and 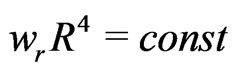 respectively. In these equations matter means normal matter with non-vanishing rest mass and infinite lifetime (protons, electrons, neutrinos) and possibly cold dark matter. However, in the following we exclude cold dark matter (see Section 1 and the discussion of a universe without cold dark matter and with a negative cosmological constant in Subsection 2.4).
respectively. In these equations matter means normal matter with non-vanishing rest mass and infinite lifetime (protons, electrons, neutrinos) and possibly cold dark matter. However, in the following we exclude cold dark matter (see Section 1 and the discussion of a universe without cold dark matter and with a negative cosmological constant in Subsection 2.4).
Equations (9) have been investigated in detail in refs.[2, 7] where in ref.[7] the solutions 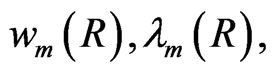
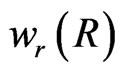 and
and 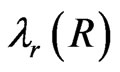 are calculated. It turns out that in a universe becoming later our universe with a present day density
are calculated. It turns out that in a universe becoming later our universe with a present day density 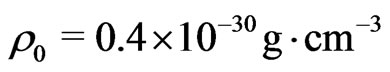 (purely baryonic, from big bang nucleosynthesis [10]), a Hubble parameter
(purely baryonic, from big bang nucleosynthesis [10]), a Hubble parameter 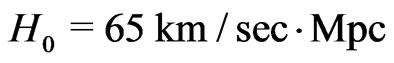 and a cosmological constant
and a cosmological constant
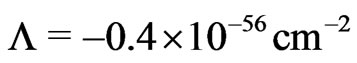 (10)
(10)
the maximal scale factor of the anti-deSitter space is 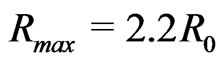 with
with 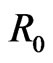 the present day scale factor. Furthermore, the creation functions
the present day scale factor. Furthermore, the creation functions 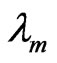 and
and 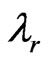 become zero at
become zero at . This can be interpreted as a smooth transition of the universe from the creation era to the conservation era at
. This can be interpreted as a smooth transition of the universe from the creation era to the conservation era at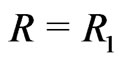 . And it seems to be obvious that this transition takes place when the gravitational energy density becomes zero, hence
. And it seems to be obvious that this transition takes place when the gravitational energy density becomes zero, hence
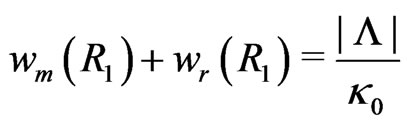 (11)
(11)
according to Equations (7c) and (8). Thus the energy content of the universe is determined by the two fundamental constants  and
and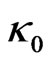 .
.
The period of the creation era is about 30 billion years, and in this extremely long time about one proton and one electron per cubic meter is created—an exceedingly small cross section!
2.3. The Hagedorn Phase and the Run through the Minimum
After the creation era the universe with its energy content (11) contracts further, and the question arises if it ends in a big crunch. It does not. In ref.[6] based on the ideas by Dehnen and Hönl [11] and Hagedorn’s theory of a hadron gas [12,13] it has been shown that the universe runs through a minimum with 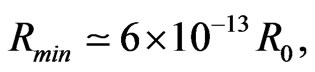
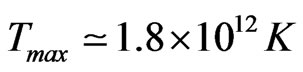 and a nucleon density
and a nucleon density 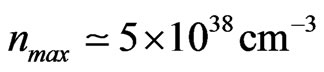 which is about four times the density of nucleons in atomic nuclei.
which is about four times the density of nucleons in atomic nuclei.
Recent investigations into the existence of a quarkgluon plasma (see ref.[14] and further references therein) show that Hagedorn’s hadron gas with its maximal temperature 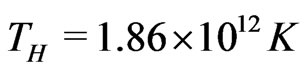 is not the final state of matter but the preliminary stage of a phase transition to a quark-gluon plasma. This phase transition begins when the hard cores of the strong nucleon interaction start to overlap. In ref.[6] it has been shown that just before this overlapping the energy density as well as the pressure in the contracting universe become negative due to the attractive strong interaction between the created nucleons. As a result the universe runs through a minimum.
is not the final state of matter but the preliminary stage of a phase transition to a quark-gluon plasma. This phase transition begins when the hard cores of the strong nucleon interaction start to overlap. In ref.[6] it has been shown that just before this overlapping the energy density as well as the pressure in the contracting universe become negative due to the attractive strong interaction between the created nucleons. As a result the universe runs through a minimum.
After the run through the minimum the universe expands and arrives after 44 billion years at its maximal extension because of the negative cosmological constant (10), then it contracts again, and so on: An open ever oscillating universe without a big bang.
2.4. Comparison with Observations
Is this cosmological model in agreement with observations?
1) What about cold dark matter?
Cold dark matter plays in the standard model a threefold role. Firstly, it yields a mechanism of structure formation (see Section 1), secondly it is assumed to hold together the galaxies in clusters, and thirdly one assumes that cold dark halos around galaxies explain the flat rotation curves.
Firstly: In ref. [15] (see also sect.6 in ref. [3]) a scenario of galaxy formation without cold dark matter is represented. It is based essentially on the fact that the baryonic neutral gas after recombination below 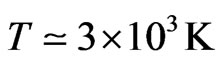 is an Einstein-Boltzmann gas running within the time down to
is an Einstein-Boltzmann gas running within the time down to 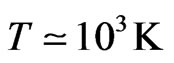 into a state very close to collision-dominated equilibrium. This state is characterized by extremely sharply bounded gas clouds although the anisotropies of the CMB are extremely small. These clouds have formed about 4 million years (!) after the big bang. Moreover, the mass spectrum of axially symmetric clouds agrees very well observations: The lower limit masses are spheres with
into a state very close to collision-dominated equilibrium. This state is characterized by extremely sharply bounded gas clouds although the anisotropies of the CMB are extremely small. These clouds have formed about 4 million years (!) after the big bang. Moreover, the mass spectrum of axially symmetric clouds agrees very well observations: The lower limit masses are spheres with 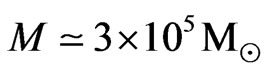 and the upper limit masses are extremely flat discs with
and the upper limit masses are extremely flat discs with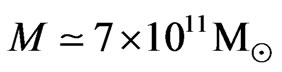 .
.
Secondly: In refs. [1,2] it has been shown that the additional attractive forces due to a negative cosmological constant (10) can completely replace cold dark matter in galaxy clusters.
Thirdly: A negative cosmological constant instead of cold dark matter can not explain the flat rotation curves in galaxies. These curves might have their origin in a very large baryonic halo. Indeed, in clusters a hot intergalactic plasma is known with a mass about five times the mass of luminous matter in the galaxies [16,17]. Hence the individual galaxies in clusters might be surrounded by a very large baryonic halo with a mass about five times their luminous mass.
So, maybe cold dark matter is not needed.
2) What about a negative cosmological constant?
Firstly: At first sight such a constant seems to contradict the observed small deviation of the redshiftversus-distance relation from that for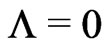 . However, for a present day density
. However, for a present day density 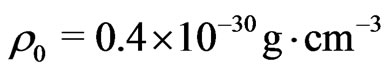 (purely baronic) and a Hubble parameter
(purely baronic) and a Hubble parameter 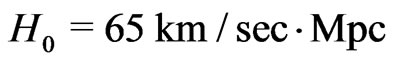 the redshift-versus-distance relation does for
the redshift-versus-distance relation does for 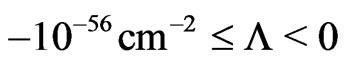 not deviate from that for
not deviate from that for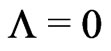 , at least up to
, at least up to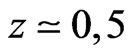 . Hence, if an alternative explanation for the deviation can be given in case of
. Hence, if an alternative explanation for the deviation can be given in case of 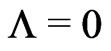 this explanation holds also in case of the cosmological constant (10). Up to now two explanations are possible: Evolution effects of the observed SNIasupernovae (see for example refs. [18,19]) and a very small amount of absorbing intercluster gas and dust. Maybe both effects combine.
this explanation holds also in case of the cosmological constant (10). Up to now two explanations are possible: Evolution effects of the observed SNIasupernovae (see for example refs. [18,19]) and a very small amount of absorbing intercluster gas and dust. Maybe both effects combine.
Secondly: A negative cosmological constant could lead to an age problem. This, however, is not true. With the above cosmological parameters and a cosmological constant (10) one finds 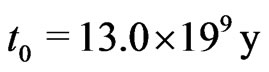 which is in agreement with the age of the oldest globular clusters according to the scenario of galaxy formation proposed in ref. [15].
which is in agreement with the age of the oldest globular clusters according to the scenario of galaxy formation proposed in ref. [15].
3) What about the origin of the small anisotropies in the CMB?
The run through the minimum is a giant collaps: As shown in ref. [6] the model looks like a big crunch universe about 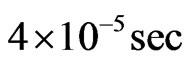 before the minimum and like a big bang universe the same time after the minimum. This gives rise to shock waves in the coupled photon-matter gas. They are smoothed out when the universe expands and are later the small anisotropies at the end of recombination.
before the minimum and like a big bang universe the same time after the minimum. This gives rise to shock waves in the coupled photon-matter gas. They are smoothed out when the universe expands and are later the small anisotropies at the end of recombination.
This, however, is only a qualitative picture which requires a quantitative analysis. Explaining the anisotropies in the CMB by classical shock waves instead of by quantum oscillations in an inflationary universe opens a new field in cosmology. A quantitative analysis of this new explanation is still to be found. However, if it comes true that the standard model is not consistent, an alternative model of our universe must be found, perhaps the model outlined in this article. And then shock waves in the bouncing point as an origin of the anisotropies in the CMB become important.
4) What about the nucleosynthesis?
The scenario represented in ref.[6] shows that (for 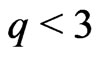 there) the model is for
there) the model is for 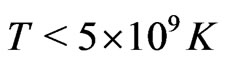 the radiation universe of the standard model with its well known nucleosynthesis.
the radiation universe of the standard model with its well known nucleosynthesis.
5) The model gives answers to some fundamental questions in cosmology.
Firstly: The universe is so isotropic because after the phase transition in Minkowski space the anti-deSitter space (protouniverse) with its gravitational energy density is completely isotropic. Matter and radiation are created from the positive content of the gravitational energy over an extremely long time of about 30 billion years. About 44 billion years after the phase transition the universe runs through a minimum without a singularity. So there is no horizon problem.
Secondly: The geometry of the universe is uniquely determined by the phase transition. The universe is open.
Thirdly: The extreme smallness of  is because of
is because of 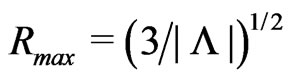 the reason why the universe is so big and so old.
the reason why the universe is so big and so old.
Finally: The cosmological constant appears in a new light. It is an independent natural constant like 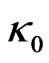 and plays a threefold role:
and plays a threefold role:
a)  and
and 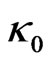 determine the potential
determine the potential  (Equation (6))
(Equation (6))
b)  determines the extension of the proto-universe (Equation (5)).
determines the extension of the proto-universe (Equation (5)).
c)  and
and 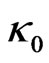 determine the energy content of matter and radiation in the universe (Equation (11)).
determine the energy content of matter and radiation in the universe (Equation (11)).
These are satisfying answers. Nevertheless, it should be noted that an explanation of the structure of the CMB, especially its scale invariance, is still to be found. Explaining this structure is a strong advantage of the inflationary standard model.
3. Conclusions
As any other cosmological model also the model outlined in this article raises some (new) problems.
Firstly: Similar to the inflaton field in the theory of inflation the origin of the scalar field 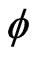 with its potential (2) is unclear. There is, however, a difference. The inflaton field is assumed to be created in the infinite temperature of the big bang, whereas the scalar field
with its potential (2) is unclear. There is, however, a difference. The inflaton field is assumed to be created in the infinite temperature of the big bang, whereas the scalar field 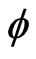 lies “sleeping” in its wrong vacuum state in the zero temperature Minkowski space. Anyway, in both cases the origin of the fields is a problem.
lies “sleeping” in its wrong vacuum state in the zero temperature Minkowski space. Anyway, in both cases the origin of the fields is a problem.
Secondly: How does the geometrical phase transition go off? Does it go off homogeneously (phase transition of second order) or inhomogeneously propagating from one or several seed regions (phase transition of first order)? In the first case we have one open universe, but a problem with causality since the space is infinite. In the second case we might have several finite but very huge bubbles of open universes with “Minkowski edge regions”, each separated from the other by space-like distances.
Thirdly: Can the phenomenological model (9) describing the creation of matter and radiation be derived from a quantum field theory of gravitation, matter and radiation in an anti-deSitter space? Unfortunately such a unified quantum field theory is a long way away.
Finally: Can the observed anisotropies in the CMB be derived from shock waves in the bouncing point?
REFERENCES
- G. Lessner, “Do We Really Need Cold Dark Matter?” General Relativity and Gravitation, Vol. 33, No. 5, 2001, pp. 757-765. doi:10.1023/A:1010243405209
- G. Lessner, “On the Origin of an Open Ever-Oscillating Universe,” Nuovo Cimento B, Vol. 117, 2002, pp. 219- 239.
- G. Lessner, “Are the Peaks in the Cosmic Microwave Background Really Acoustic?” General Relativity and Gravitation, Vol. 36, 2004, pp. 903-922. doi:10.1023/B:GERG.0000018081.11977.a3
- S. Bose and L. P. Grishchuk, “Observational Determination of Squeezing in Relic Gravitational Waves and Primordial Density Perturbations,” Physical Review D, Vol. 66, 2002, pp. 1-17.
- A. Ashtekar, T. Pawlowski and P. Singh, “Quantum Nature of the Big Bang,” Physical Review Letters, Vol. 96, 2006, pp. 1-4.
- G. Lessner, “An Open Ever-Oscillating Universe,” Nuovo Cimento B, Vol. 116, 2001, pp. 59-71.
- G. Lessner, “Oscillating Universe—An Alternative Approach in Cosmology,” Astrophysics and Space Science, Vol. 306, No. 4, 2006, pp. 249-257. doi:10.1007/s10509-006-9270-1
- C. Møller, “On the Localization of the Energy of a Physical System in the General Theory of Relativity,” Annals of Physics (N.Y.), Vol. 4, No. 4, 1958, pp. 347- 371.
- E. Schmutzer, “Relativistische Physik,” Teubner Verlagsgesellschaft, Leipzig, 1968,
- M. S. Turner and J. A. Tyson, “Cosmology at the Millenium,” Reviews of Modern Physics, Vol. 71, 1999, pp. 145-164. doi:10.1103/RevModPhys.71.S145
- H. Dehnen and H. Hönl, “The Influence of Strong Interactions on the Early Stages of the Universe,” Astrophysics and Space Science, Vol. 33, 1975, pp. 49-73. doi:10.1007/BF00646008
- R. Hagedorn, “Hadronic Matter Near Boiling Point,” Nuovo Cimento A, Vol. 56, No. 4, 1968, pp. 1027-1057. doi:10.1007/BF02751614
- R. Hagedorn, “Thermodynamics of Strong Interactions at High Energy and Its Consequences for Astrophysics,” Astronomy & Astrophysics, Vol. 5, 1970, pp. 184-205.
- P. Braun-Munzinger and J. Wambach, “Extreme Materie,” Physik Journal, Vol. 5, No. 10, 2006, pp. 41-47.
- G. Lessner, “Galaxy Formation—A Condensation Process just after Recombination,” Nuovo Cimento B, Vol. 113, No. 1, 1998, pp. 93-116.
- S. D. White, J. F. Navarro, A. E. Evrad and C. S. Frenk, “The Baryon Content of Galaxy Clusters—A Challenge to Cosmological Orthodoxy,” Nature, Vol. 366, No. 6454, 1993, pp. 429-433. doi:10.1038/366429a0
- N. A. Bahcall, “Clusters and Cosmology,” Physics Reports, Vol. 333-334, 2000, pp. 233-244. doi:10.1016/S0370-1573(00)00024-7
- A. Blanchard, “Cosmological Parameters: Where Are We?” Astrophysics and Space Science, Vol. 290, No. 1, 2004, pp. 135-148. doi:10.1023/B:ASTR.0000022169.31100.a4
- B. Leibundgut, “Are Type Ia Supernovae Standard Candles?” Astrophysics and Space Science, Vol. 290, No. 1-2, 2004, pp. 29-41. doi:10.1023/B:ASTR.0000022162.13380.39

