Applied Mathematics
Vol.09 No.01(2018), Article ID:81691,16 pages
10.4236/am.2018.91001
Uncertainty Principle and Bifurcations in the SU(2) Nonlinear Semiquantum Dynamics
Roberta Hansen1, Claudia M. Sarris1,2, Angelo Plastino3,4
1Department of Mathematics, Faculty of Engineering, University of Buenos Aires, Buenos Aires, Argentina
2Common Basic Cycle, Chair of Physics, University of Buenos Aires, Buenos Aires, Argentina
3Institute of Physics of La Plata, CCT-CONICET, National University of La Plata, La Plata, Argentina
4Physics Department and IFISC-CSIC, University of the Balearic Island, Palma de Mallorca, Spain
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 6, 2017; Accepted: January 8, 2018; Published: January 11, 2018
ABSTRACT
In this paper, a nonlinear semiquantum Hamiltonian associated to the special unitary group SU(2) Lie algebra is studied so as to analyze its dynamics. The treatment here applied allows for a reduction in: 1) the system’s dimension, as well as 2) the number of system’s parameters (to only three). We can now discern clear patterns in: 1) the complete characterization of the system’s fixed points and 2) their stability. It is shown that the parameter associated to the uncertainty principle, which constitutes a very strong constraint, is the key one in determining the presence of fixed points and bifurcation curves in the parameter’s space.
Keywords:
Semiquantum Dynamics, Uncertainty Principle, Fixed Points, Bifurcation Curves

1. Introduction
Semiquantum Dynamics (SD) may be used to describe systems in which quantum and classical degrees of freedom coexist. One finds in [1] an exhaustive compilation of physical phenomena and technological applications successfully modeled by SD. It is also possible to encounter situations in which SD is used to describe physical phenomena [2] [3] [4] [5] . A nonlinear semiquantum Hamiltonian associated to the SU(2) Lie algebra is very useful to model the problem of quantum confinement, which is of interest for nanotechnology and solid state physics. In particular, if the quantum subsystem is associated to the SU(2) Lie algebra generators , the uncertainty principle (UP) adopts a very simple form and turns out to be a motion invariant [6] .
In [7] , the authors consider the following semiquantum Hamiltonian
(1)
where and are quantum operators, the x and z components of a 1/2 spin particle, while q and p are canonical conjugated classical variables (position and momentum) that obey the Hamilton equations [5] [8] . B, C, m, D, and F are positive and constant parameters. The Hamiltonian given by Equation (1) represents a quantum 1/2 spin particle interacting with an external magnetic field [2] [7] (due to the term ). The particle is confined by the double well
potential , generated by a classical particle of mass m and it undergoes elastic reflections between the moving frontier, , of the double well potential. The term represents the classical kinetic energy. The clas-
sical and quantum variables are couple in non-linear fashion via the term, , being the coupling constant. In [7] , the authors concentrate on the likely presence of chaotic motion (semiquantum chaos) for special values of the coupling strength. The authors represent the trajectories for different initial conditions by stroboscopic plots, displaying regular and irregular dynamics. This Hamiltonian also may be reduced to the one in [2] (taking ). It also can be used to model the semiquantum differential equations of the spin-boson Hamiltonian of [9] (taking ). In [10] , the authors considered the simplest case of a spin-boson Hamiltonian, i.e., a two level system coupled to one oscillator degree of freedom, and made a posterior semiclassical approximation, to obtain a semiquantum Hamiltonian similar to that given by Equation (1).
We consider that, since the Hamiltonian of Equation (1) is able to model the quantum confinement phenomenon, its dynamics deserves an exhaustive analysis. In the present work, we purport to give a full description of its phase space taking into account that, in conservative systems like this one, the motion is fully determined by the amount and disposition of its fixed points. We make a complete characterization of them and determine their stability according to the system’s parameters values. In addition, we obtain the bifurcation curves which divide the phase space into the three different zones in which the fixed points are located, according to their stability. We present a dimensionless formulation, and because the uncertainty principle (UP) is an invariant of the motion for the nonlinear semiquantum Hamiltonians associated to the SU(2) Lie algebra [6] [11] , we make a change of variables that removes it as external strong constrain to the system’s motion equations. The UP provides then just an additional parameter in the concomitant new motion equations. We mention that, in [10] , a similar method is used for a coupled quasiparticle-oscillator system, which enables the authors to study the existence of fixed points and bifurcation curves, allowing for a formulation in canonically conjugate variables of the excitonic subsystem. In our case, the change of variables offers some advantages which are highlighted in describing our treatment and summarized in the conclusions.
2. Equations of Motion
If we consider the generators of the SU(2) Lie algebra, , it can be easily seen that they close a partial Lie algebra under commutation with the Hamiltonian of Equation (1), since the commutator of any with may be expressed as a linear superposition of these generators. The semiquantum equations of motion are obtained through the Maximum Entropy Approach (MEP), using the MEP density operator to evaluate the Hamiltonian’s mean value, which, in turn, plays the role of a Hamilton function so as to obtain the (evolution) differential equations of motion corresponding to the classical degrees of freedom q and p (the prescription given by the MEP, in order to find the density operator, is a standard procedure. The interested reader can consult [6] [12] [13] [14] to become familiar with the subject). The MEP density operator corresponds to a non-pure state given that it is constructed from a set of noncommuting observable (the generators of the SU(2) Lie algebra).
Following the prescription given in [6] [12] [13] , we obtain the equations of motion for the system given by Equation (1):
(2)
(3)
(4)
(5)
(6)
and they must obey the uncertainty relation [6] [11] which, for the SU(2) Lie algebra case, adopts the form [6] :
(7)
We will consider the whole range of values that the polarization vector can achieve in the interval , given that the generators of the SU(2) Lie algebra constitute a complete set of noncommuting observables. Thus, we are dealing with a non pure quantum state . Equation (7) defines the well-known Bloch sphere, whose “radius’’, , remains a constant of the motion while its possible values are determined by the initial conditions imposed on Equations (2)-(6). It is also taken into account that the system’s energy (evaluated via the non pure state density operator ) [6] [13] :
(8)
must remain a constant of motion during the whole temporal evolution [6] .
In order to find the fixed points it is convenient to express Equations (2)-(6), (7), and (8) in dimensionless form [15] , by defining new variables, and :
(9)
with
(10)
Accordingly, Equations (2)-(6) and (7) become:
(11)
(12)
(13)
(14)
(15)
(16)
and from Equation (8) the system’s energy reads:
(17)
3. The System’s Fixed Points
In order to determine the system’s fixed points we proceed, as usual, by equating (11)-(15) to zero. Note that the existence of them does not depend on the parameter , but only on the values of r and s. From Equation (13), there exist two situations: the cases and .
3.1. Case q* = 0
From in Equation (11), it follows . From in Equation (12), it follows . So, from Equation (16), we are led to . From in Equation (14), it follows . Therefore, in this case, one obtains
two fixed points, , where , and being the north and south pole of the dimensionless Bloch sphere.
3.2. Case q* 0
From Equations (11)-(15) it follows that these kinds of fixed points must fulfill:
(18)
so they adopt the appearance , and must obey the strong constraint given by Equation (16), the uncertainty principle, which in terms of , reads:
(19)
with , . Thus, are the roots of Equation (19), which should be tackled numerically. The system’s phase space, given by Equations (11)-(15), is five-dimensional. However, the Jacobian matrix at the fixed point must have, at least, one null eigenvalue, since the uncertainty condition of Equation (16) is an external constraint added to the equations of motion. This means that, in fact, the solutions lie on a 4D invariant manifold, .
Accordingly, we represent the quantum degrees of freedom, , in spherical coordinates:
(20)
with , , and we study the system’s fixed points by means of the four-dimensional variables, .
Using the relations:
(21)
we find:
(22)
The system of Equations (11)-(16) becomes now:
(23)
(24)
(25)
(26)
where means , and . The system’s energy given by Equation (17) becomes:
(27)
We claim that this change of variables (CV) offers some advantages:
1) The quantum variables and obey the relationship:
(28)
as if they were canonical spherical-conjugates, meanwhile the classical ones, q and p, obey, as usual, the Hamilton’s equations [6] [13] :
(29)
Thus, the fixed points of the system given by Equations (23)-(26), are the critical points of the energy function of Equation (27), since:
(30)
2) The uncertainty relation in Equation (16), now of the form , is incorporated into the new system’s equations in a natural way by reducing the system dimension and removing a superfluous null eigenvalue. One may speak of linearization of the original system at each fixed point.
3) Our CV provides a better characterization of the fixed points, since with this change we find a generic expression for them explicitly written in terms of the variable q. This fact facilitates the study of 1) the presence of bifurcations curves in the parameter’s space, and 2) the stability analysis of the fixed points.
To obtain the fixed points, , we equate (23)-(26) to zero. From in Equation (25), it follows that , and from in Equation (24), we are led to or , .
3.2.1. Case
From in Equation (23) and , it follows that:
(31)
so that:
(32)
Then, in this case, adopts the generic form . From Equation (32), , and . Since , then:
(33)
From in Equation (26) and one has:
(34)
and then:
(35)
Replacing Equation (33) into Equation (35), it follows that must be the solution of the following equation:
(36)
Since , the right side on Equation (36) is positive. Thus, the possible values of are restricted to the range . In each case, the amount of solutions will be obtained graphically by means of the intersection points of two curves, namely:
(37)
・ . Figure 1 depicts the intersection between the left branch of and . It is possible to see that for all , there is always a unique solution, , in the range of interest, and so a corresponding fixed point, , is obtained. Note also that this point does not bifurcate in the -parameter space.
・ . Here, we are looking for the intersection points of the right branch of and . The situations for different values of r and s are depicted in Figure 2, by considering r as a “fixed’’ parameter and s going down from to .
Figure 1. The graph of the functions g and the left branch of f of Equation (37) for
, showing the unique intersection point 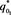 existing for
existing for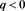 .
.




Figure 2. The graph of the functions g and the right branch of f of Equation (37) for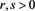 . The figures in the first column ((a)-(c)) depict the case where f is more convex than g at
. The figures in the first column ((a)-(c)) depict the case where f is more convex than g at  (
(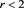 ); in the second column ((b)-(d)), g is more convex than f at
); in the second column ((b)-(d)), g is more convex than f at 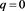 (
( ). (a) and (b) show the unique intersection point
). (a) and (b) show the unique intersection point 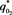 existing for
existing for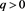 , when
, when . (c) there is no intersection point when
. (c) there is no intersection point when . (d) there are two intersection points,
. (d) there are two intersection points, 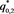 and
and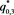 , when
, when


For


Decreasing the s value, the curves become tangent at




Thus, for 













This last scenario (











To find the relation 


From this, we obtain the relation between 

valid for



or, equivalently,

Replacing Equation (41) into Equation (40), we find the relation between 





or, equivalently:

Thus, as 


Note that the bifurcation curve 



3.2.2. Case
From 


Accordingly, in this case 




Replacing (33) into (47), it follows that 

Accordingly, in this case the possible values of 





Figure 3. The 


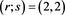



















Summing up, the amount of fixed points in the 
・
・
4. The Stability of the Fixed Points
The system given by Equation (1) (and then by Equation (27)) is conservative. Thus, the local behavior at the fixed point may be studied by considering the energy 






Definition 1. The instability index 
eigenvalues of the Hessian matrix of 

(whenever 

This is to say, k is the number of independent directions along which 







4.1. Obtaining the Index k of
From Equation (27) the Hessian matrix of 


Since 



where 

nant of the block

From Equation (26), 







and for


The eigenvalues 


guaranteeing 


Note that 



and using Equation (45), it follows that

From Equation (50), if






Then, from Equations (50), (54) and (55), 



Figure 4 and Figure 5 illustrate a case relative to the orange zone in Figure 3, for which the six fixed points coexist (
Table 1. The nondegenerate critical points 


Figure 4. The 










Figure 5. (a) The 






4.2. Note
The other two fixed points of the system, 




5. Conclusions
The dimensionless formulation of Equations (2)-(6), given by Equations (11)-(15), allows for reduction in the number of system’s parameters to three: r, s, and




The putative presence of chaotic dynamics in this system, for some 
Remark: by virtue of the SU(2) Lie algebra, the uncertainty principle becomes a constant of the motion. Thus, we claim that the methodology used in the present work applies even in the case in which the quantum subsystem of Equation (1) was nonlinear in the spin variables (as in the non-dissipative Hamiltonian case treated in [17] , which can be used to model a SQUID). Despite the nonlinearity in the quantum subsystem, the uncertainty principle would remain there a constant of the motion. This and other topics related to semiquantum dynamics will be part of future work.
Acknowledgements
The authors would like to thank the reviewers for their suggestions to improve the readability of the paper. C. Sarris dedicates this work to Professor Araceli Proto, in memoriam. This work was partially supported by Programación Cientfica UBACyT 2014-2017 (20020130200093BA GEF), Ministerio de Educación, Argentina.
Cite this paper
Hansen, R., Sarris, C.M. and Plastino, A. (2018) Uncertainty Principle and Bifurcations in the SU(2) Nonlinear Semiquantum Dynamics. Applied Mathematics, 9, 1-16. https://doi.org/10.4236/am.2018.91001
References
- 1. Porter, M.A. (2001) Nonadiabatic Dynamics in Semiquantal Physics. Reports on Progress in Physics, 64, 1165-1189. https://doi.org/10.1088/0034-4885/64/9/203
- 2. Ballentine, L.E. (2001) Is Semi-Quantum Chaos Real? Physical Review E, 63, Article ID: 056204. https://doi.org/10.1103/PhysRevE.63.056204
- 3. Cooper, F., Dawson, J.F., Meredith, D. and Shepard, H. (1994) Semiquantum Chaos. Physical Review Letters, 72, 1337-1340. https://doi.org/10.1103/PhysRevLett.72.1337
- 4. Blumel, R. and Esser, B. (1994) Quantum Chaos in the Born-Oppenheimer Approximation. Physical Review Letters, 72, 3658-3661. https://doi.org/10.1103/PhysRevLett.72.3658
- 5. Kowalski, A.M., Plastino, A. and Proto, A.N. (2002) Classical Limits. Physics Letters A, 297, 162-172. https://doi.org/10.1016/S0375-9601(02)00034-8
- 6. Sarris, C.M. and Proto, A.N. (2009) Information Entropy and Nonlinear Semiquantum Dynamics. International Journal of Bifurcation and Chaos, 19, 3473-3484. https://doi.org/10.1142/S0218127409024918
- 7. Ma, J. and Yuan, R.K. (1997) Semiquantum Chaos. Journal of the Physical Society of Japan, 66, 2302-2307. https://doi.org/10.1143/JPSJ.66.2302
- 8. Goldstein, H. (1950) Classical Mechanics. Addison-Wesley, Reading, MA.
- 9. Bonci, L., Roncaglia, R., West, B.W. and Grigolini, P. (1992) Semiclassical Chaos, the Uncertainty Principle, and Quantum Dissipation. Physical Review A, 45, 8490-8500. https://doi.org/10.1103/PhysRevA.45.8490
- 10. Schanz, H. and Esser, B. (1997) Mixed Quantum-Classical versus Full Quantum Dynamics: Coupled Quasiparticle-oscillator System. Physical Review A, 55, 3375-3387. https://doi.org/10.1103/PhysRevA.55.3375
- 11. Sarris, C.M., Caram, F. and Proto, A.N. (2004) The Uncertainty Principle as Invariant Motion for Time-dependent Hamiltonians. Physics Letters A, 324, 1-8. https://doi.org/10.1016/j.physleta.2004.02.036
- 12. Alhassid, Y. and Levine, R.D. (1977) Entropy and Chemical Change. III. The Maximal Entropy (Subject to Constraints) Procedure as a Dynamical Theory. The Journal of Chemical Physics, 67, 4321-4400. https://doi.org/10.1063/1.434578
- 13. Kowalski, A.M., Plastino, A. and Proto, A.N. (1997) A Semiclassical Statistical Model for Quantum Dissipation. Physica A, 236, 429-447. https://doi.org/10.1016/S0378-4371(96)00379-2
- 14. Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. Physical Review, 106, 620. https://doi.org/10.1103/PhysRev.106.620
- 15. Strogatz, S.H. (2000) Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry and Engineering. Perseus Publishing, Cambridge.
- 16. Velhurst, F. (1996) Nonlinear Differential Equations and Dynamical Systems. 2nd Ed., Springer-Verlag, Berlin, Heidelberg, New York.
- 17. Bonilla, L.L. and Guinea, F. (1992) Collapse of the Wave Packet and Chaos in a Model with Classical and Quantum Degrees of Freedom. Physical Review A, 45, 7718-7728. https://doi.org/10.1103/PhysRevA.45.7718











