ABSTRACT

In 2000, Wu and Gong [1] introduced the thought of the Henstock integrals of interval-valued functions and fuzzy-number-valued functions and obtained a number of their properties. The aim of this paper is to introduce the thought of the AP- Henstock integrals of interval-valued functions and fuzzy-number-valued functions which are extensions of [1] and investigate a number of their properties.

Keywords:

Fuzzy Numbers, AP-Henstock Integrals of Interval-Valued Functions, AP-Henstock Integrals of Fuzzy-Number-Valued Functions

1. Introduction

As it is well known, the Henstock integral for a real function was first defined by Henstock [2] in 1963. The Henstock integral is a lot of powerful and easier than the Lebesgue, Wiener and Richard Phillips Feynman integrals. Furthermore, it is also equal to the Denjoy and the Perron integrals [2] [3] . In 2016, Hamid and Elmuiz [4] introduced the concept of the Henstock-Stieltjes integrals of interval-valued functions and fuzzy-number-valued functions and discussed a number of their properties.

In this paper, we introduce the concept of the AP-Henstock integrals of interval-valued functions and fuzzy-number-valued functions and discuss some of their properties.

The paper is organized as follows. In Section 2, we have a tendency to provide the preliminary terminology used in this paper. Section 3 is dedicated to discussing the AP-Henstock integral of interval-valued functions. In Section 4, we introduce the AP- Henstock integral of fuzzy-number-valued functions. The last section provides conclusions.

2 Preliminaries

Let be a measurable set and let 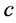be a real number. The density of at 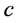is defined by

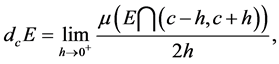(2.1)

provided the limit exists. The point 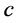is called a point of density o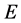f if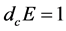. The set 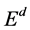represents the set of all points 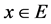such that is a point of density of.

A measurable set 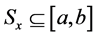is called an approximate neighborhood (br.ap-nbd) of 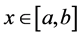if it containing 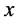as a point of density. We choose an ap-nbd 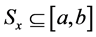for each 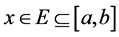and denote a choice on by. A tagged interval-point pair is said to be -fine if and.

A division is a finite collection of interval-point pairs, where are non-overlapping subintervals of. We say that is

1) a division of if;

2) -fine division of if and is -fine for all.

Definition 2.1. [2] [3] A real-valued function is said to be Henstock integrable to on if for every, there is a function such that for any -fine division of, we have

(2.2)

where the sum is understood to be over and we write, and.

Definition 2.2. [5] A function is AP-Henstock integrable if there exists a real number such that for each there is a choice such that

(2.3)

for each -fine division of. is called AP-Henstock integral of on, and we write.

Theorem 2.1. If and are AP-Henstock integrable on and almost everywhere on, then

(2.4)

Proof. The proof is similar to the Theorem 3.6 in [3] . W

3. The AP-Henstock Integral of Interval-Valued Functions

In this section, we shall give the definition of the AP-Henstock integrals of interval-valued functions and discuss some of their properties.

Definition 3.1. [1] Let

For, we define iff and, iff and, and, where

(3.1)

and

(3.2)

Define as the distance between intervals and.

Definition 3.2. [1] Let be an interval-valued function., for every there is a such that for any -fine division we have

(3.3)

then is said to be Henstock integrable over and write For brevity, we write

Definition 3.3. A interval-valued function is AP-Henstock integrable to, if for every there exists a choice on such that

(3.4)

whenever is a -fine division of, we write and

Theorem 3.1. If, then the integral value is unique.

Proof. Let integral value is not unique and let and . Let be given. Then there exists a choice on such that

(3.5)

(3.6)

whenever is a -fine division of.

Whence it follows from the Triangle Inequality that:

(3.7)

Since for there exists a choice on as above so W

Theorem 3.2. An interval-valued function if and only if and

(3.8)

Proof. Let, from Definition 3.3 there is a unique interval number with the property that for any there exists a choice on such that

(3.9)

whenever is a -fine division of. Since for we have

(3.10)

Hence whenever is a -fine division of. Thus and

(3.11)

Conversely, let. Then there exists with the property that given there exists a choice on such that

whenever is a -fine division of. We define then if is a -fine division of, we have

(3.12)

Hence is AP-Henstock integrable on. W

Theorem 3.3. If and Then and

(3.13)

Proof. If, then by Theorem 3.2. Hence

(1) If and then

(2) If and then

(3) If and (or and), then

Similarly, for four cases above we have

(3.14)

Hence by Theorem 3.2 and

(3.15)

W

Theorem 3.4. If and, then and

(3.16)

Proof. If and, then by Theorem 3.2 and. Hence and

Similarly, Hence by Theorem 3.2 and

(3.17)

W

Theorem 3.5. If nearly everywhere on and, then

(3.18)

Proof. Let nearly everywhere on and Then and, nearly everywhere on By Theorem 2.1 and Hence

(3.19)

by Theorem 3.2. W

Theorem 3.6. Let and is Lebesgue integrable on Then

(3.20)

Proof. By definition of distance,

(3.12)

W

4. The AP-Henstock Integral of Fuzzy-Number-Valued Functions

This section introduces the concept of the AP-Henstock integral of fuzzy-number- valued functions and investigates some of their properties.

Definition 4.1. [6] [7] [8] Let be a fuzzy subset on If for any and where then is called a fuzzy number. If is convex, normal, upper semi-continuous and has the compact support, we say that is a compact fuzzy number.

Let denote the set of all fuzzy numbers.

Definition 4.2. [6] Let, we define iff for all iff for any iff for any

For is called the distance between and

Lemma 4.1. [9] If a mapping satisfies when then

(4.1)

and

(4.2)

where

Definition 4.3. [1] Let. If the interval-valued function is Henstock integrable on for any then we say that is Henstock integrable on and the integral value is defined by

For brevity, we write

Definition 4.4. Let. If the interval-valued function is AP-Henstock integrable on for any then is called AP-Henstock integrable on and the integral value is defined by

We write

Theorem 4.1. then and

(4.3)

where

Proof. Let be defined by

Since and are increasing and decreasing on respectively, therefore, when we have on From Theorem 3.5 we have

(4.4)

From Theorem 3.2 and Lemma 4.1 we have

(4.5)

and for all where

W

Theorem 4.2. If and Then and

(4.6)

Proof. If, then the interval-valued function

and are AP-Henstock integrable on

for any and and . From Theorem 3.3 we have

and

for any.

Hence and

W

Theorem 4.3. If and, then and

(4.7)

Proof. If and, then the interval-valued function is AP-Henstock integrable on and for any

and and . From Theorem 3.4 we have and for any

. Hence and

W

Theorem 4.4. If nearly everywhere on and , then

(4.8)

Proof. If nearly everywhere on and, then

nearly everywhere on for any and and

are AP-Henstock integrable on for any and

and . From Theorem 3.5 we have for any. Hence

5. Conclusion

In this paper, we have a tendency to introduce the concept of the AP-Henstock integrals of interval-valued functions and fuzzy number-valued functions and investigate some properties of those integrals.

Cite this paper

Hamid, M.E., Elmuiz, A.H. and Sheima, M.E. (2016) On AP-Henstock Integrals of Interval-Valued Functions and Fuzzy-Number-Valued Func- tions. Applied Mathematics, 7, 2285-2295. http://dx.doi.org/10.4236/am.2016.718180

References