Applied Mathematics
Vol.07 No.15(2016), Article ID:70510,10 pages
10.4236/am.2016.715141
Clustering of the Values of a Response Variable and Simultaneous Covariate Selection Using a Stepwise Algorithm
Olivier Collignon1, Jean-Marie Monnez2,3,4
1Luxembourg Institute of Health, Strassen, Luxembourg
2Institut Elie Cartan de Lorraine, University de Lorraine, CNRS UMR 7502, Vandœuvre-lès-Nancy, France
3INRIA, Projet BIGS, Vandœuvre-lès-Nancy, France
4CIC-P, CHRU, University Hospital, Nancy, France
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 13, 2016; Accepted: September 9, 2016; Published: September 12, 2016
ABSTRACT
In supervised learning the number of values of a response variable can be very high. Grouping these values in a few clusters can be useful to perform accurate supervised classification analyses. On the other hand selecting relevant covariates is a crucial step to build robust and efficient prediction models. We propose in this paper an algorithm that simultaneously groups the values of a response variable into a limited number of clusters and selects stepwise the best covariates that discriminate this clustering. These objectives are achieved by alternate optimization of a user-defined model selection criterion. This process extends a former version of the algorithm to a more general framework. Moreover possible further developments are discussed in detail.
Keywords:
Classification, Variable Selection, Supervised Learning, Akaike Information Criterion, Wilks’ Lambda

1. Introduction
Regression and classification problems arise from various fields of application as medicine, social sciences, etc. The response variable can be continuous, as for instance blood pressure, or categorical with a potentially large number of levels, as a score of disease activity for example. In this article, we deal with the problem of prediction of a response variable, continuous or categorical, when an accurate predictive model cannot be satisfactorily developed, for instance when the 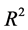 coefficient of a linear regression or the percentage of correct classification of a supervised classification model is too low. We propose then to group the values of the response variable into a limited number of clusters in order to improve the predictive performances of the model, as measured for instance by the
coefficient of a linear regression or the percentage of correct classification of a supervised classification model is too low. We propose then to group the values of the response variable into a limited number of clusters in order to improve the predictive performances of the model, as measured for instance by the 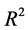 coefficient or the percentage of correct classification, evaluated via cross-validation or bootstrap internal validation [1] .
coefficient or the percentage of correct classification, evaluated via cross-validation or bootstrap internal validation [1] .
Consider two examples.
First, if the response variable is a level of rainfall, say in millimeters, one can en- counter a situation in which no model could accurately predict precisely the value of precipitations to fall using the available covariates, while another model, fitted with exactly the same covariates, could predict the level of rainfall to lie within a particular interval with a very low classification error rate.
Second, if the response variable is a disease severity score with a large number of ordered categories, like some scores of severity of peanut allergy [2] , it might be dif- ficult to build a model that satisfactorily predicts each of the categories, while some grouping of the initial categories could be more accurately predicted.
In addition to the clustering of the values of the response variable, the issue of covariate selection to include in the model has also to be solved concurrently in order to avoid overlearning and to improve classification given by the model describing the clustering.
This problem deals both with supervised and unsupervised classification. In model building covariate selection is a fundamental topic which has been widely adressed and is still of main interest [1] [3] [4] . In the unsupervised clustering setting, variable selec- tion is a matter to which some authors have also already contributed [5] - [8] . In this context statistical units are clustered solely regarding to explaining covariates since no response variable has to be accounted for. However, in order to address our problem, we have thus to deal with an additional constraint which is the variable to predict.
We already had to overcome these issues in a dataset we analyzed previously [9] . In order to clarify our objectives, recall briefly its framework. Peanut allergy is currently diagnosed in hospital during an open food challenge in which increasing doses of peanut extracts are administrated to the patient until an objective allergic reaction appears. The cumulative dose triggering the first clinical reaction is called eliciting dose. Since no effective treatment of peanut allergy is yet available, a diet adapted to the maximum tolerated dose of the patient is then initiated. Moreover, the open food challenge being a potentially harmful and costly procedure, our previous research aimed at discovering predictive covariates of the eliciting dose that can be measured via a non-invasive test, such as blood sampling, in order to further combine them within a discriminant analysis. However, the levels of dose investigated are fixed by the in- vestigator in the study protocol and the eliciting dose can therefore not be considered as a continuous endpoint nor analysed using a linear regression. Moreover the number of levels is large and in practice the number of patients reacting at a given dose can be very small, which renders an ordinal logistic regression disputable. In order to address this issue, an algorithm that simultaneously groups eliciting dose levels in a limited number of clusters and selects the most discriminant covariates was implemented. This algorithm processes in a forward fashion based on an alternative minimization of Wilks’ Lambda [10] . In our previous paper, the algorithm was applied on a dataset of 74 allergic patients in which 34 covariates were measured in order to predict their elicit- ing dose. Our method allowed identifying a clinically relevant cluster of levels of elicit- ing dose which could be predicted with encouraging performances using a small subset of covariates. Promising results were also achieved on simulated data [11] .
In this paper, we propose two generalizations of the latter version of our algorithm. First the algorithm was extended formally to the case where any model selection criterion can be used with the classifier of interest in addition to Wilks’ Lambda. For instance the Akaike Information Criterion (AIC) [12] can be used to allow using any classifier whose parameters are obtained by likelihood maximization, such as logistic regression [12] . Second we replaced forward selection with stepwise selection to allow removing covariates that could have become useless during the procedure.
The structure of the article is as follows. After the formulation of the problem and the definition of notations in Section 3, we present the new version of our algorithm in Section 4. Section 5 presents some technical discussions and future improvements of the algorithm. We finish by a conclusion.
2. Formulation of the Problem
Let 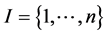 a sample. Let y be a continuous or categorical variable observed on the elements of I.
a sample. Let y be a continuous or categorical variable observed on the elements of I.
Let also 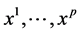 be p continuous or categorical covariates, all measured on I. The dataset consists then in the sample
be p continuous or categorical covariates, all measured on I. The dataset consists then in the sample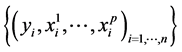 .
.
Denote by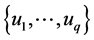 ,
,  , the q different values of y observed in the sample I and define the class
, the q different values of y observed in the sample I and define the class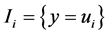 . When y is categorical, the values
. When y is categorical, the values  are its q levels. If y is continuous, q may equal n and the classes
are its q levels. If y is continuous, q may equal n and the classes 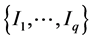 are then reduced to singletons.
are then reduced to singletons.
To address our problem, we propose in this article an algorithm to group the classes 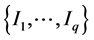 into a fixed limited number of clusters
into a fixed limited number of clusters 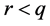 and to simultaneously select a subset of covariates among
and to simultaneously select a subset of covariates among 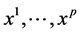 that best discriminates this clustering by optimizing a model selection criterion fixed a priori. A model to fit the data is then defined by:
that best discriminates this clustering by optimizing a model selection criterion fixed a priori. A model to fit the data is then defined by:
• a clustering  of
of 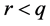 clusters to further gather the set of values
clusters to further gather the set of values 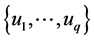 of y;
of y;
• a classifier;
• a subset of covariates of 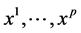 which are the most relevant ones to dis- criminate
which are the most relevant ones to dis- criminate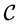 .
.
3. Details of the Algorithm
3.1. Principle
Select a classifier and a model selection criterion denoted Crit. Some model selection criteria are discussed in Section 3.3. Define now an algorithm of alternate optimization to address our problem.
3.1.1. First Algorithm
For every possible clustering of the classes

This first solution to address our problem could be computationally intensive when the numbers of possible clusterings and of covariates are too large.
3.1.2. Second Algorithm
In order to reduce the number of computations, we can proceed as follows. For a given clustering of the classes

3.1.3. Third Algorithm
When the number p of covariates is too large, in order to avoid exploring all subsets of covariates among the 
3.2. Algorithm
Fix the number 
We denote by Crit





Moreover we assume that a test statistic T is available to compare the criterion computed with two different models fitted with the same classifier and the same clustering but with two different subsets of covariates. This statistic will be used first to assess if adding a new covariate can improve significantly the discriminant power of the current model at level 

The algorithm processes as follows:
• Step 1:
1. determine the clustering 


2. select the covariate 




• Step 2:
1. determine the clustering 


2. select the covariate 




3. compute the T-to-remove of 



• ...
• Step k:
1. determine the clustering 


2. select the covariate 




3. compute the T-to-remove of all previously entered covariates 

• and so on...
• procedure stops if either no remaining covariate can improve the discriminant power of the model, i.e., if their T-to-enter p-value is greater than
Remark 1. Clustering inducing clusters with low frequencies can be ignored by setting an appropriate parameter if needed. Indeed a cluster containing too few obser- vations would be meaningless for further inference and results would be likely due to overfitting.
Remark 2. Note that when y is continuous or ordinal, its values can only be grouped into intervals, i.e. only consecutive values can be gathered together. These intervals are then built by selecting their upper bound. The number of possible clusterings at each
step of the algorithm is thus
of possible clusterings may be very large. It could be reduced by choosing an optimal clustering among a limited subset of candidate clusterings, defined for example using quantiles of the empirical distribution of y in I.
Remark 3. As in any regression or classification model, a categorical covariate would have to be replaced by dummy indicators if the number of levels is greater than two.
Remark 4. Note that removing part 3 in every step of the stepwise version of the algorithm gives the forward algorithm as studied in [9] .
Remark 5. The algorithm could be easily modified to allow the choices of two different test statistics when entering or removing a covariate.
Remark 6. In Step k.3, the last entered covariate cannot be removed unless
Remark 7. In Step k.3, the algorithm could be modified in order to remove not only the less relevant covariate but all covariates not meeting the criterion to stay in the model, i.e. with T-to-remove p-value greater than
3.3. Model Selection Criteria and Associated Test Statistic
We recall now some model selection criteria and the corresponding test statistics used in the algorithm.
3.3.1. Wilks’ Lambda
Wilks’ Lambda is defined as the ratio


covariance matrices computed using the covariates 


In order to evaluate the change in Wilks’ Lambda when the covariate 


clusters as the ratio


The use of Wilks’ Lambda is thus best suitable in case of homoscedasticity and normality of the response variable in the classes induced by its categories, even if the test above seems to be quite robust to small departures to those assumptions. In our framework these hypotheses are difficult to test in practice since the clustering might change at every step of the algorithm and thus the conditional distributions of the response variable as well. As such, homoscedasticity could hold for a given clustering but not for another.
3.3.2. Akaike Information Criterion
The Akaike Information Criterion (AIC) is used for a model whose parameters were estimated using the maximum of likelihood method, like for instance the logistic regression of 



In order to evaluate the change in AIC when the covariate 



3.3.3. Other Criteria
The algorithm can actually be used with any model selection criterion for which a statistical test of comparison between two models fitting the same response variable using different sets of covariates is available. For example, the area under the ROC curve (AUC), which is widely used in many diagnosis and prognosis studies, might be considered in the case of a binary response variable y. The ROC curve is defined by the set of the points with coordinates (1 − specificity, sensitivity) obtained from the classifier when the cut-off varies. A test on the difference between two AUC is given by DeLong in [13] .
4. Further Possible Developments of the Algorithm
4.1. Variable Selection
4.1.1. Backward Variable Selection
The algorithm was aimed at building parsimonious models. This is particularly relevant when the task of interest is prediction, for example when diagnosing a disease. This explains why the selection scheme was designed at first to process forward. In a framework where covariate elimination would be less essential, the algorithm could easily be converted to a backward selection mode. In some epidemiological studies for instance one is often interested in modelling the effects of risk factors on a disease rather than building a very sparse model for predictive purposes. In this context, we could thus adapt the algorithm in eliminating at each step the less informative covariate instead of adding the one optimizing the criterion.
4.1.2. Penalization Methods
As a first attempt we developed a stepwise scheme for the covariate selection step. The algorithm inherits thus all drawbacks of a stepwise covariate selection procedure [1] , as for example a propensity to keep useless covariates in the final model when candidate covariates are too numerous in regard to the informative ones. Penalization methods were suggested by several authors as a solution to sidestep these problems. In our context, the covariate inclusion step could be replaced by a penalized likelihood approach. If sparsity is needed, Tibshiranis’s LASSO is a valuable solution [14] . Note that several penalization functions have been defined, allowing use of different criteria:
4.2. Choice of the Number r of Clusters
When analyzing real-life data, the practitioner will have to fix the number r of clusters. An automated procedure to find the optimal number of clusters would be helpful. As a first attempt, one could simply vary r over a grid of values and keep the best result according to a specific criterion (via a resampling procedure as crossvalidation). The choice of r could be a compromise between the precision of the prediction, which increases if clusters are more numerous and less extensive, and the predictive accuracy of the classifier, which is expected to decrease when r increases. For instance, one can indeed expect the well-classification rates to be lower when using the algorithm with numerous clusters than with only two, since it seems more likely to fail classifying an observation correctly.
4.3. Nonlinear Covariates in Logistic Regression
We focused here on the case where a linear relationship exists between the covariates and the response variable when using logistic regression. This can be extended to a more general framework by including restricted cubic splines [16] or fractional poly- nomials [3] at the first step of the algorithm, i.e. when the optimal clustering is ob- tained with all candidate covariates. These new covariates could then be entered or removed afterwards as any other covariates while the algorithm processes. However, it could be difficult to choose an adequate transformation of the covariates since the shape of the link can potentially change with the clustering at each step of the algorithm.
4.4. Correlations
The case of high correlation between covariates was not treated. To address this issue, a first solution could be to eliminate the covariates that are strongly correlated to other covariates, and to keep the ones that are the most discriminant relatively to the response variable. Another solution would be to apply the algorithm on uncorrelated factors given by an appropriate factorial analysis like Principal Component Analysis. Also a Partial Least Square (PLS) approach could be integrated in order to take the y variable into account. This could be particularly interesting since several covariate selection techniques have been developed for PLS [17] .
4.5. Other Classifiers
As stated above, the algorithm can be applied with all available supervised learning methods. Mention among others Support Vector Machine [18] , which is a powerful classification method, especially in high dimension and for which penalizations tech- niques have already been developed [19] . For optimal use of the algorithm, other optimality criteria would have to be defined, like for instance the distance to the separating hyperplane in the case of SVM. Two different optimality criteria for cluster- ing and covariate selection could even be used.
5. Conclusion
In this article, we extended our previous version of the algorithm [9] to a more general framework where any model selection criterion for which a test of significance is available can be used in addition to Wilks’ Lambda and where forward covariate inclu- sion was replaced by stepwise selection. Of note, a version of the algorithm allowing the use of logistic regression with AIC as optimality criterion has already been coded and evaluated on two small datasets. Although the procedure achieved promising results (data not shown), larger and high dimensional datasets are required in order to pro- perly illustrate the algorithm. Besides, the same type of algorithm can be performed using a penalization method instead of stepwise selection. In conclusion this algorithm could be used in any situation where the values defined by a response variable need to be clustered in order to obtain a better predictive accuracy of a classifier using a limited number of covariates.
Acknowledgements
This work was funded by grant 602552 for the IDEAL project under the European Union FP7 programme and support from the programme is gratefully acknowledged.
Cite this paper
Collignon, O. and Monnez, J.-M. (2016) Clustering of the Values of a Response Variable and Simulta- neous Covariate Selection Using a Stepwise Algorithm. Applied Mathematics, 7, 1639- 1648. http://dx.doi.org/10.4236/am.2016.715141
References
- 1. Harrell, F.E. (2001) Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. Springer Verlag.
http://dx.doi.org/10.1007/978-1-4757-3462-1 - 2. Flinterman, A.E., Knol, E.F., Lencer, D.A., Bardina, L., den Hartog Jager, C.F., Lin, J., et al. (2008) Peanut Epitopes for IgE and IgG4 in Peanut-Sensitized Children in Relation to Severity of Peanut Allergy. Journal of Allergy and Clinical Immunology, 121, 737-743.
http://dx.doi.org/10.1016/j.jaci.2007.11.039 - 3. Sauerbrei, W., Royston, P. and Binder, H. (2007) Selection of Important Variables and Determination of Functional Form for Continuous Predictors in Multivariable Model Building. Statistics in Medicine, 26, 5512-5528.
http://dx.doi.org/10.1002/sim.3148 - 4. Fan, J.Q. and Lv, J.C. (2010) A Selective Overview of Variable Selection in High Dimensional Feature Space. Statistica Sinica, 20, 101.
- 5. Raftery, A.E. and Dean, N. (2006) Variable Selection for Model-Based Clustering. Journal of the American Statistical Association, 101, 168-178.
http://dx.doi.org/10.1198/016214506000000113 - 6. Fowlkes, E.B., Gnanadesikan, R. and Kettenring, J.R. (1988) Variable Selection in Clustering. Journal of Classification, 5, 205-228.
http://dx.doi.org/10.1007/BF01897164 - 7. Maugis, C., Celeux, G. and Martin-Magniette, M.L. (2009) Variable Selection for Clustering with Gaussian Mixture Models. Biometrics, 65, 701-709.
http://dx.doi.org/10.1111/j.1541-0420.2008.01160.x - 8. Andrews, J.L. and McNicholas, P.D. (2013) Variable Selection for Clustering and Classification. Journal of Classification, 31, 136-153.
http://dx.doi.org/10.1007/s00357-013-9139-2 - 9. Collignon, O., Monnez, J.M., Vallois, P., Codreanu, F., Renaudin, J.M., Kanny, G., et al. (2011) Discriminant Analyses of Peanut Allergy Severity Scores. Journal of Applied Statistics, 38, 1783-1799.
http://dx.doi.org/10.1080/02664763.2010.529878 - 10. Jennrich, R.I. and Sampson, P.F. (1960) Stepwise Discriminant Analysis. Mathematical Methods for Digital Computers.
- 11. Collignon, O. (2009) Recherche statistique de biomarqueurs du cancer et de l’allergie à l’arachide. PhD Thesis.
- 12. Hosmer, D.W. and Lemeshow, S. (2000) Applied Logistic Regression. Vol. 354, Wiley-Interscience.
http://dx.doi.org/10.1002/0471722146 - 13. DeLong, E.R., DeLong, D.M. and Clarke-Pearson, D.L. (1988) Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics, 44, 837-845.
http://dx.doi.org/10.2307/2531595 - 14. Tibshirani, R. (1996) Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society Series B (Methodological), 58, 267-288.
- 15. Zou, H. and Hastie, T. (2005) Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67, 301-320.
http://dx.doi.org/10.1111/j.1467-9868.2005.00503.x - 16. Gray, R.J. (1992) Flexible Methods for Analyzing Survival Data Using Splines, with Applications to Breast Cancer Prognosis. Journal of the American Statistical Association, 87, 942-951.
http://dx.doi.org/10.1080/01621459.1992.10476248 - 17. Liu, T.Y., Trinchera, L., Tenenhaus, A., Wei, D. and Hero, A.O. (2013) Globally Sparse PLS Regression. In: New Perspectives in Partial Least Squares and Related Methods, Springer, 117-127.
http://dx.doi.org/10.1007/978-1-4614-8283-3_7 - 18. Vapnik, V.N. (2000) The Nature of Statistical Learning Theory. Springer Verlag.
http://dx.doi.org/10.1007/978-1-4757-3264-1 - 19. Zhang, H.H., Ahn, J., Lin, X. and Park, C. (2006) Gene Selection Using Support Vector Machines with Non-Convex Penalty. Bioinformatics, 22, 88-95.
http://dx.doi.org/10.1093/bioinformatics/bti736

