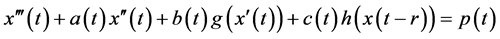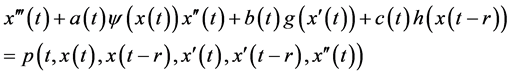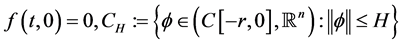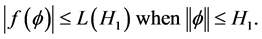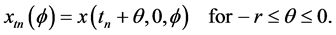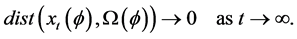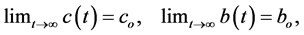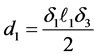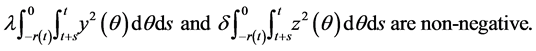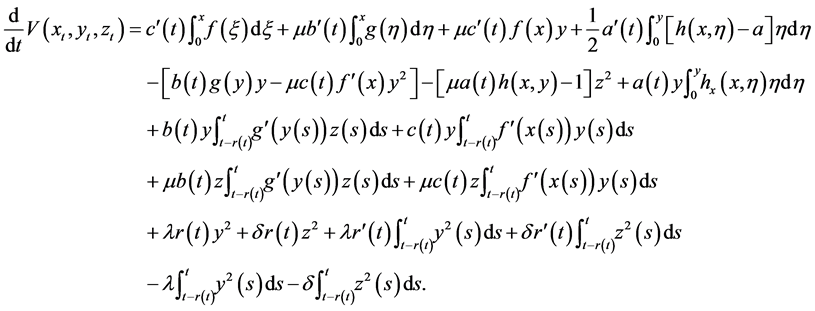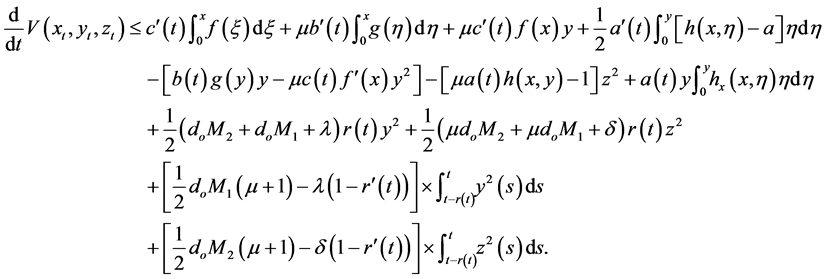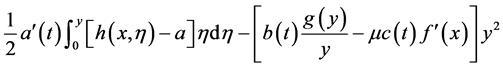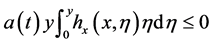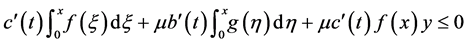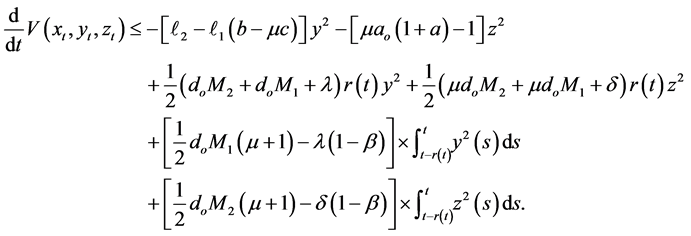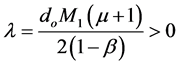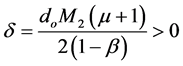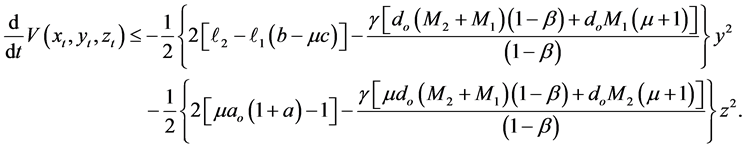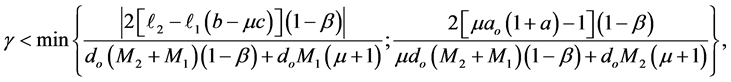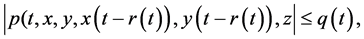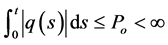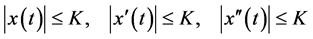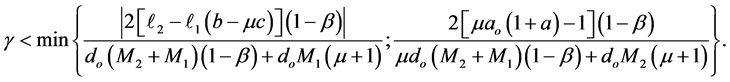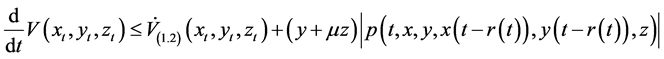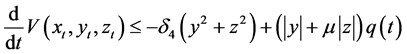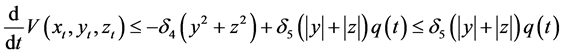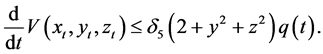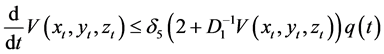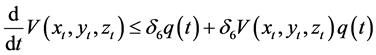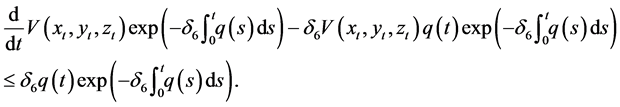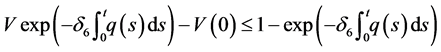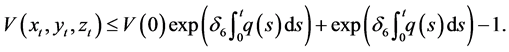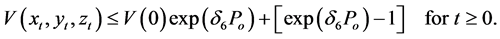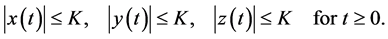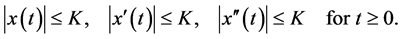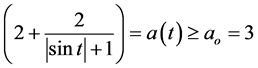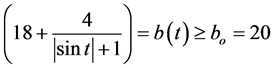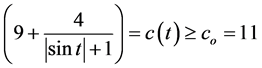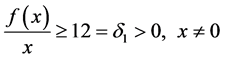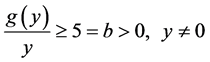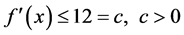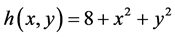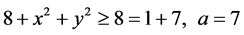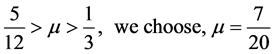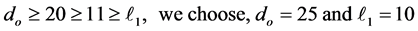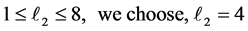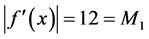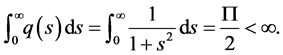Received 23 January 2016; accepted 21 March 2016; published 24 March 2016

ABSTRACT

In this paper, we study certain non-autonomous third order delay differential equations with continuous deviating argument and established sufficient conditions for the stability and boundedness of solutions of the equations. The conditions stated complement previously known results. Example is also given to illustrate the correctness and significance of the result obtained.

Keywords:

Asymptotic Stability, Boundedness, Lyapunov Functional, Delay Differential Equations, Third-Order Delay Differential Equations

1. Introduction

This paper considers the third order non-autonomous nonlinear delay differential

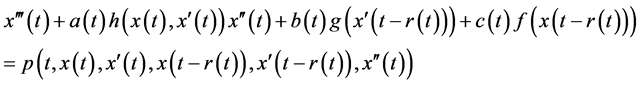(1.1)

or its equivalent system

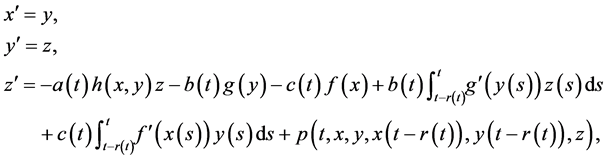(1.2)

where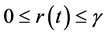, , 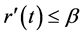, 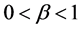β and 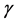are some positive constants, 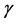will be determined later, 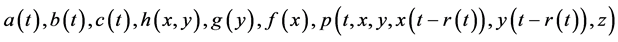, , 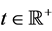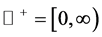are real valued functions continuous in their respective arguments on, , , , , and respectively and. Besides, it is supposed that the derivatives, are continuous for all x, y, with. In addition, it is also assumed that the functions, , and satisfy a Lipschitz condition in and z; throughout the paper, and are respectively abbreviated as x, y and z. Then the solutions of (1.1) are unique.

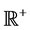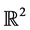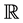
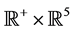
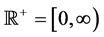
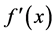
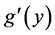
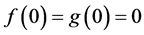
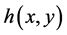
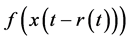
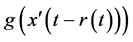
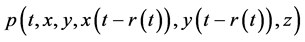
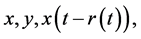
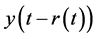
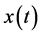
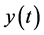
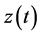
In applied science, some practical problems are associated with Equation (1.1) such as after effect, nonlinear oscillations, biological systems and equations with deviating arguments (see [1] - [3] ). It is well known that the stability of solutions plays a key role in characterizing the behavior of nonlinear delay differential equations. Stability is much more complicated for delay equations. Thus, it is worthwhile to continue to investigate the stability and boundedness of solutions of Equation (1.1) and its various forms.

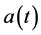
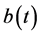
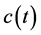
Equation of the form (1.1) in which, and are constants has been studied by several authors Sadek [4] [5] , Zhu [6] , Afuwape and Omeike [7] , Ademola and Aramowo [8] , Yao and Meng [9] , Tunc [3] and Ademola et al [10] to mention a few. They obtain the stability, uniform boundedness and uniform ultimate boundedness of solutions. In a sequence of results, Omeike [11] considers the following nonlinear delay differential equation of the third order, with a constant deviating argument r,

and established conditions for the stability and boundedness of solution when and while Tunc [12] considers a similar system with a constant deviating argument r of the form

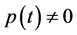
and obtains the conditions for its boundedness of solution.

Results obtained are now extended to non-autonomous delay differential Equation (1.1). Results obtained in this work are comparable in generality to the results of Sadek [7] on analogous third order differential equation which itself generalizes an analogous third-order results of Zhu [5] , and also complement existing results on third order delay differential equations. 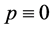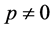We establish sufficient conditions for the stability (when) and boundedness (when) of solutions of Equation (1.1) which extend and improve the results of Omeike [11] and Tunc [12] . An example is given to illustrate the correctness and significance of the result obtained.

Now, we will state the stability criteria for the general non-autonomous delay differential system. We consider:

(1.3)

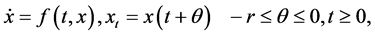
where 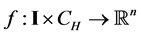is a continuous mapping,

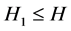
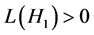
and for, there exists, with

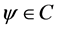
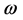
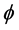
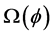
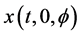
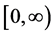
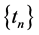
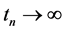
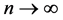
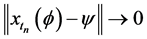
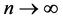
Definition 1.0.1 ( [8] ) An element is in the -limit set of, say, , if is defined on and there is a sequence, as, with as where

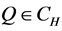
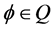
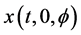
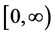
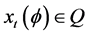
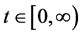
Definition 1.0.2 ( [8] [13] ) A set is an invariant set if for any, the solution of (1.2), , is defined on and for.

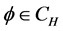
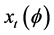
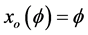
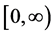
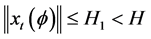
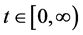
Lemma 1 ([8,13]) An element is such that the solution of (1.3) with is defined on and for, then is a non-empty, compact, invariant set and

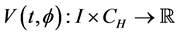
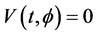
Lemma 2 ( [8] [13] ) Let be a continuous functional satisfying a local Lipschitz con- dition., and such that:

1) where, are wedges;

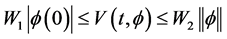
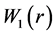
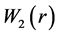
2) for

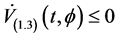
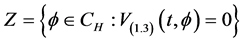
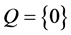
Then the zero solution of (1.3) is uniformly stable. If we define, then the zero solution of (1.3) is asymptotically stable provided that the largest invariant set in Z is.

The following will be our main stability result (when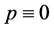) for (1.1).

2. Statement of Results

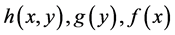
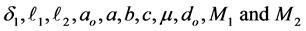
Theorem 1 In addition to the basic assumptions imposed on the functions a(t), b(t), c(t), and p, let us assume that there exist positive constants such that the following conditions are satisfied:

1);, ,;

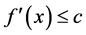
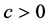
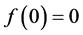
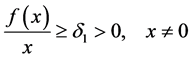
2);,;

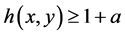
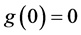
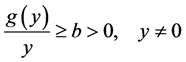
3); and;

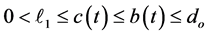
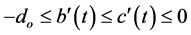
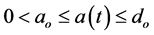
4); and, , for all x, y.

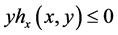
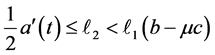
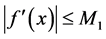
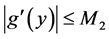
Then, the zero solution of system (1.2) is asymptotically stable, provided that

(2.1)

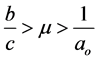
and

(2.2)

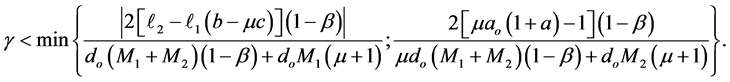
Proof

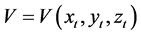
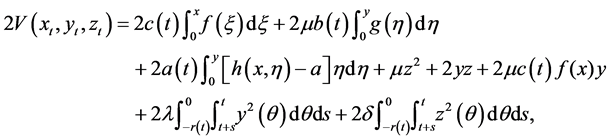
Our main tool is the following Lyapunov functional defined as

(2.3)

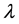
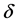
where and are positive constants which will be determined later.

We also assume that

where.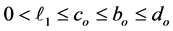

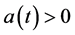
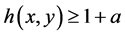
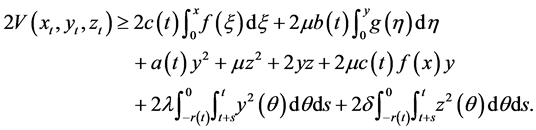
By the assumption and, from (2.3) we have

(2.4)

The Lyapunov functional (2.4) can be arranged in the form

(2.5)

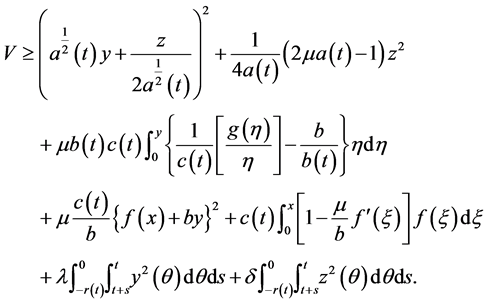
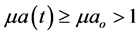
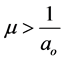
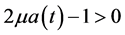
From Theorem 1, and which makes.

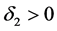
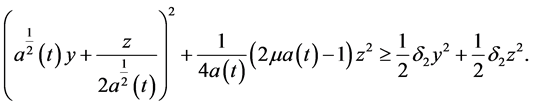
Thus, there is a such that

(2.6)

By (2) and (3) of Theorem 1, we have that the third term on the right in (2.5)

(2.7)

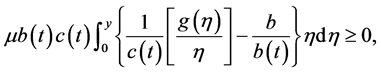
and next two terms give

(2.8)

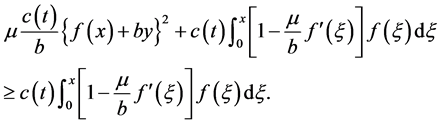
Using (2.6), (2.7) and (2.8) in (2.5), we have

(2.9)

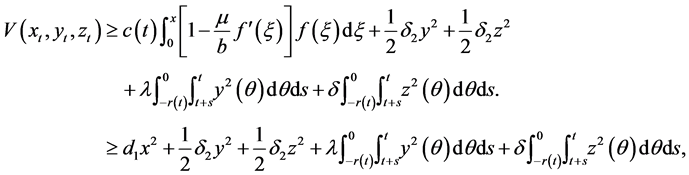
where

and integrals

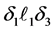
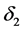
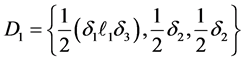
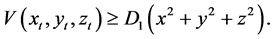
Thus, for some positive constants and, where small enough such that

(2.10)

For the time derivative of the Lyapunov functional (2.3), along a trajectory of the system (1.2), we have

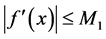
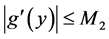
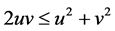
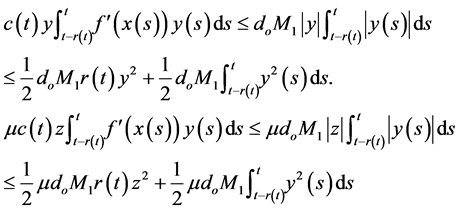
From (4) of Theorem 1, , and using, we have that

(2.11)

Similarly, we obtain

(2.12)

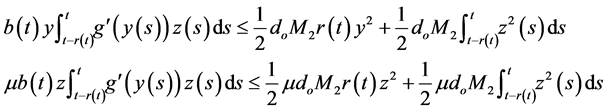
Thus,

If, then. If, we can rewrite the term as

(2.13)

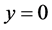
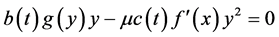
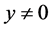
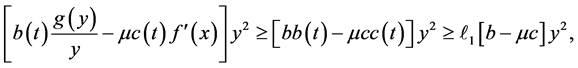
where by (3) of Theorem 1,.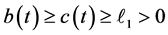

And by (1) and (2) of Theorem 1,

as

(2.14)

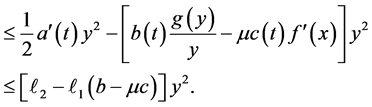
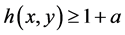
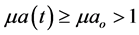
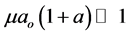
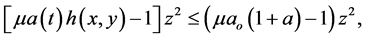
According to (2) of Theorem 1, and by (3), and certainly thus,

(2.15)

and by (3) and (4) of Theorem 1, we have that

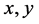
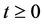
for all and.

Thus, from (2.11), (2.12), (2.13), (2.14) and (2.15), we have

If we choose

and

and using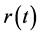, we obtain

Choosing

we have

(2.16)

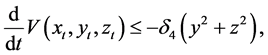
for some.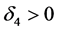

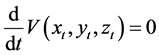
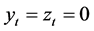
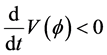
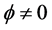
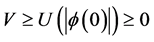
Finally, it follows that if and only if, for and for.

Thus, (2.10) and (2.16) and the last statement agreed with Lemma 2. This shows that the trivial solution of (1.1) is asymptotically stable.

Hence, the proof of the Theorem 1 is now complete.

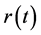
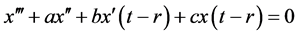
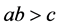
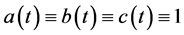
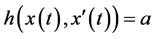
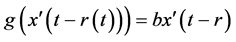
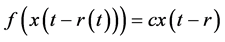
Remark 2.1 If is a constant and (1.1) is the constant co-efficient delay differential equation , then conditions (1)-(4) reduce to the Routh-Hurwitz conditions a > 0, c > 0 and. To show this we set and, and.

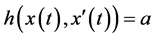
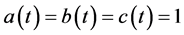
Remark 2.2 If and in (1.1), the non-autonomous Equation (1.1) reduces to the autonomous equation considered in Sadek [4] .

3. The Boundedness of Solution

Theorem 2 We assume that all the assumptions of Theorem 1 and

hold, where is a positive constant.

Then, there exists a finite positive constant K such that the solution 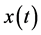of Equation (1.1) defined by the initial function

satisfies the inequalities

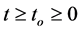
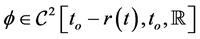
for all, where provided that

Proof of Theorem 2

As in Theorem 1, the proof of Theorem 2 depends on the scalar differentiable Lyapunov function 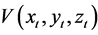defined in (2.3).

Since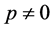, in (1.1).

In view of (2.16),

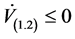
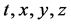
Since for all thus

Hence, it follows that

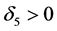
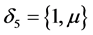
for a constant, where.

Making use of the inequalities 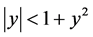and, it is clear that

By (2.10), we have,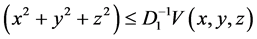

Hence,

or

where.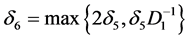

Multiplying each side of this inequality by the integrating factor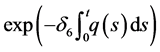, we get

Integrating each side of this inequality from 0 to t, we get, where,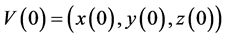

or

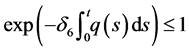
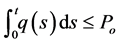
Since and using the fact that for all t, this implies

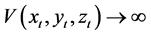
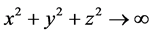
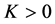
Now, since the right-hand side is a constant, and since as, it follows that there exist a such that

From the Equation (1.1) this implies

The proof of Theorem 2 is now complete.

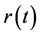
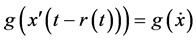
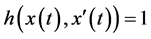
Remark 3.1 If is a constant, , and in (1.1), the result obtained reduces to Omeike [6] and a result of Tunc [10] .

4. Conclusions

The solutions of the third-order non-autonomous delay system are asymptotically stable and bounded according to the Lyapunov’s theory if the inequalities (2.1) and (2.2) are satisfied.

Example 3.1 We consider non-autonomous third-order delay differential equation

(3.1)

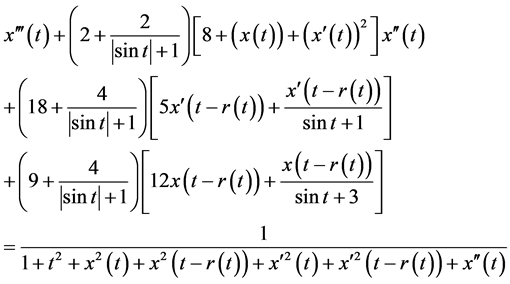
with equivalent system of (3.1) as:

(3.2)

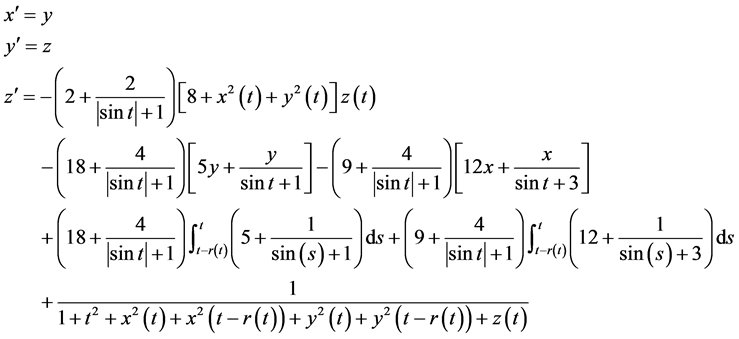
comparing (1.2) with (3.2), it is easy to see that

The function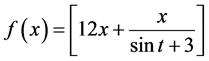, it is clear from the equation that

The function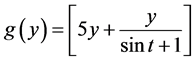, it is clear from the equation that

also,

Since

we have

It follows that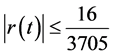, if the delay is increased beyond this range a limit cycle appear, followed even-

tually by a period-doubling cascade leading to chaos.

Finally,

and

Thus, all assumptions of Theorem 1 and Theorem 2 are held. That is, zero solution of Equation (1.1) is asymptotically stable and all the solutions of the same equation are bounded.

Cite this paper

Akinwale L.Olutimo,Daniel O.Adams, (2016) On the Stability and Boundedness of Solutions of Certain Non-Autonomous Delay Differential Equation of Third Order. Applied Mathematics,07,457-467. doi: 10.4236/am.2016.76041

References

NOTES

^*Corresponding author.