Received 20 January 2016; accepted 7 March 2016; published 10 March 2016

ABSTRACT

Fractal interpolation function (FIF) is a special type of continuous function which interpolates certain data set and the attractor of the Iterated Function System (IFS) corresponding to a data set is the graph of the FIF. Coalescence Hidden-variable Fractal Interpolation Function (CHFIF) is both self-affine and non self-affine in nature depending on the free variables and constrained free variables for a generalized IFS. In this article, graph directed iterated function system for a finite number of generalized data sets is considered and it is shown that the projection of the attractors on 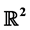is the graph of the CHFIFs interpolating the corresponding data sets.

Keywords:

Iterated Function System, Graph-Directed Iterated Function System, Fractal Interpolation Functions, Coalescence Hidden Variable FIFs

1. Introduction

The concept of fractal interpolation function (FIF) based on an iterated function system (IFS) as a fixed point of Hutchinson’s operator is introduced by Barnsley [1] [2] . The attractor of the IFS is the graph of a fractal function interpolating certain data set. These FIFs are generally self-affine in nature. The idea has been extended to a generalized data set in 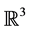such that the projection of the graph of the corresponding FIF onto 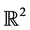pro- vides a non self-affine interpolation function namely Hidden variable FIFs for a given data set 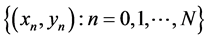[3] . Chand and Kapoor [4] , introduced the concept of Coalescence Hidden Variable FIFs which are both self-affine and non self-affine for generalized IFS. The extra degree of freedom is useful to adjust the shape and fractal dimension of the interpolation functions. For Coalescence Hidden Variable Fractal Interpolation Surfaces one can see [5] [6] . In [7] , Barnsley et al. proved existence of a differentiable FIF. The continuous but nowhere differentiable fractal function namely 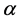-fractal interpolation function 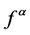is intro- duced by Navascues as perturbation of a continuous function f on a compact interval I of [8] . Interested reader can see for the theory and application of 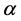-fractal interpolation function 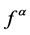which has been exten- sively explored by Navascues [9] -[12] .

In [13] , Deniz et al. considered graph-directed iterated function system (GDIFS) for finite number of data sets and proved the existence of fractal functions interpolating corresponding data sets with graphs as the attractors of the GDIFS.

In the present work, generalized GDIFS for generalized interpolation data sets in 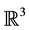is considered. Corre- sponding to the data sets, it is shown that there exist CHFIFs whose graphs are the projections of the attractors of the GDIFS on.

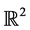2. Preliminaries

2.1. Iterated Function System

Let 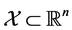and 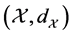be a complete metric space. Also assume,

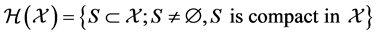with the Hausdorff metric 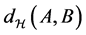defined as

, where for any two sets A, B in. The completeness of the metric space imply that is complete. For, let be continuous maps. Then is called an iterated function system (IFS). If the maps w_i’s are contractions, the set valued Hutchinson operator defined by, where is also contraction. The Banach fixed point theorem

ensures that there exists a unique set such that. The set G is called the

attractor associated with the IFS.

2.2. Fractal Interpolation Function

Let a set of interpolation points be given, where is a partition of the closed interval and,. Set for and. Let, be contraction homeomorphisms such that

(1)

for some. Furthermore, let, be given continuous functions such that

(2)

(3)

for all and for all and in, for some,. Define mappings, by

Then,

constitutes an IFS. Barnsley [1] proved that the IFS defined above has a unique attractor G where G is the graph of a continuous function which obeys for. This function f is called a fractal interpolation function (FIF) or simply fractal function and it is the unique function satisfying the following fixed point equation

The widely studied FIFs so far are defined by the iterated mappings

(4)

where the real constants and are determined by the condition (1) as

and q_i(x)’s are suitable continuous functions such that the conditions (2) and (3) hold. For each i, is a free parameter with and is called a vertical scaling factor of the transformation. Then the vector is called the scale vector of the IFS. If is taken as linear then the corresponding FIF is known as affine FIF (AFIF).

2.3. Coalescence FIF

To construct a Coalescence Hidden-variable Fractal Interpolation Function, a set of real parameters for are introduced and the generalized interpolation data is con- sidered. Then define the maps by

where are given in (4) and the functions such that satisfy the join-up conditions

Here are free variables with, and are constrained variables such that. Then the generalized IFS

has an attractor G such that. The attractor G is the graph of a

vector valued function such that for and . If, then the projection of the attractor G on is the graph of the function which satisfies and is of the form

also known as CHFIF corresponding to the data [4] .

2.4. Graph-Directed Iterated Function Systems

Let be a directed graph where V denote the set of vertices and E is the set of edges. For all, let denote the set of edges from u to v with elements where denotes the number of elements of. An iterated function system realizing the graph G is given by a collection of metric spaces with contraction mappings corresponding to the edge in the opposite direction of. An attractor (or invariant list) for such an iterated function system is a list of nonempty compact sets such that for all,

Then, is the graph directed iterated function system (GDIFS) realizing the graph G [14] [15] .

Example 1. An example of GDIFS may be seen in [13] [16] .

3. Graph Directed Coalescence FIF

In this section, for a finite number of data sets, generalized graph-directed iterated function system (GDIFS) is defined so that projection of each attractor on is the graph of a CHFIF which interpolates the corre- sponding data set and calls it as graph-directed coalescence hidden-variable fractal interpolation function (GDCHFIF). For simplicity, only two sets of data are considered. Let the two data sets be

where with

(5)

for all and. By introducing two sets of real parameters for and, consider the two generalized data sets

corresponding to and respectively. Also consider the directed graph with such that

To construct a generalized GDIFS associated with the data and realize the graph G, consider the functions defined as

(6)

such that

・

・

・

・

From each of the above conditions, the following can be derived respectively.

(7)

(8)

(9)

(10)

From the linear system of Equations (7)-(10) the constants, , , , and for, are determined as follows:

The following theorem shows that each map is contraction with respect to metric equivalent to the Euclidean metric and ensures the existence of attractors of generalized GDIFS.

Theorem 2. Let be the generalized GDIFS defined in (6) realizing the graph and associated with the data sets which satisfy (5). If, and are chosen such that for all and. Then there exists a metric on equivalent to the Euclidean metric such that the GDIFS is hyperbolic with respect to. In particular, there exist non empty compact sets such that

Proof. Proof follows in the similar lines of Theorem 2.1.1 of [17] and using the above condition (5). □

Following is the main result regarding existence of coalescence Hidden-variable FIFs for generalized GDIFS.

Theorem 3. Let be the attractors of the generalized GDIFS as in Theorem 2. Then is the graph of a vector valued continuous function such that for, for all. If then the projection of the attractors on is the graph of the continuous function known as CHFIF such that for,. That is

.

Proof. Consider the vector valued function spaces

with metrics

respectively, where denotes a norm on. Since and are complete metric spaces, is also a complete metric space where

Following are the affine maps,

Now define the mapping

where for,

and for,

Now using Equations (7)-(10) it is clear that,

Similarly, ,. It proves that T maps into itself. Since for each

, is continuous and therefore, is continuous on each subintervals.

For, using (7) it follows that.

For, using (8) it follows that.

For, using (7) and (8) it follows that since and.

Hence is continuous on I. Similarly it can be shown that is continuous on J. Consequently T is continuous.

To show that T is a contraction map on, let and. Now,

where and. Therefore

Similarly, it follows that

where and. Then

where and hence T is a contraction mapping. By Banach fixed point theorem, T possesses a unique fixed point, say.

Now, for,

For,

This shows that is the function which interpolates the data. Similarly, it can

be shown that is the function which interpolates the data. For and,

and

If F and H are the graphs of and respectively, then

The uniqueness of the attractor implies that and. That is and. Denoting and, result follows.

Example 4. Consider the data sets as

realizing the graph with, , , as in Figure 1. Take the first set of generalized data

and

corresponding to and respectively. Here for both the generalized data sets. Choose, , for all and. Then Figure 2 is the attractors of the corresponding generalized GDIFS.

Keeping the free variables and constrained variables same, Figure 3 is the attractors of the generalized GDIFS associated with the second set of generalized data

Take the third set of generalized data

and

corresponding to and respectively. For the generalized GDIFS with the free variables and constraints variables given in following Table 1, the attractors are given in Figure 4.

Cite this paper

Md. NasimAkhtar,M. Guru PremPrasad, (2016) Graph-Directed Coalescence Hidden Variable Fractal Interpolation Functions. Applied Mathematics,07,335-345. doi: 10.4236/am.2016.74031

References