Received 13 January 2016; accepted 21 February 2016; published 24 February 2016

ABSTRACT

In the paper, based on the data of Shanghai and Shenzhen 300 stock index in 2011, the 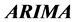model was established by using Eviews 6, and the historical trend of stock price was found out. The model was used to provide a reference for the investors.

Keywords:

Time Series, ARIMA, Stock Price Prediction

1. Introduction

Stock in the trading market as a trading object, with the same goods, has their own market and market prices. Because of the stock price to be affected by many factors such as company management, supply and demand, bank interest rate, public psychology and so on, it has a lot of uncertainty.

Shanghai and Shenzhen 300 index is a stock exchange in Shanghai and Shenzhen Stock Exchange in April 8, 2005 to reflect the overall trend of the stock market index A. Shanghai and Shenzhen 300 index sample covering the Shanghai and Shenzhen stock market around 60% of the market value, with good market representation and investment. The goal of Shanghai and Shenzhen 300 index is to reflect the profile and operation status of Chinese stock market stock price changes, and as the criteria for the evaluation of the investment performance, the index of investment and index derivative product innovation to provide basic conditions. So it is necessary for us to find a way to predict the stock price. In recent years, there have been papers investigating the problem (see [1] - [4] ). Time series analysis is a very good method [1] . Based on this, this paper in Shanghai and Shenzhen 300 stock index data as the basis, through time series analysis method established the Shanghai and Shenzhen 300 stock index prediction model, and the predictive effect was detected by Eviews 6.0 software [2] . Predictive results provide a reference to the decision-making of investors.

2. ARIMA Model

By 2011, the Shanghai and Shenzhen 300 stock index of 242 data (Due to the holidays, the stock market halted, some months of data is relatively few) as a time series analysis, a prediction model is established which is used in the modeling of 234 data and the prediction of the model is based on the following 8 data. Data comes from the financial research database (RESSETDB) (see Attached Table).

2.1. Data Preprocessing

The original data into a line chart was draw. A sequence of Y was written, as shown in Figure 1. Figure 1 shows that the data have a downward trend and there are no periodic fluctuations. The initial judgment of the sequence is a non stationary series.

In order to reduce the fluctuation of the sequence, the natural logarithm transformation of the original data is still showing obvious non-stationary, so it is necessary to carry on the differential operation to the data, until after the two order difference, the sequence is obviously smooth. The two order difference is shown in Figure 2.

2.2. Model Identification

Autocorrelation function and partial autocorrelation function are the most important tools for the identification of 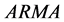model. In Eviews 6, the model identification and order determination are usually carried out using a sample of the autocorrelation and partial autocorrelation analysis. Draw autocorrelation and partial correlation diagram of the series as in Figure 3.

From Figure 3, when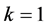, the autocorrelation coefficient is beyond the random range, when, the autocorrelation coefficients are all fall within the random interval. The autocorrelation function is truncated. In partial autocorrelation analysis, until the lag phase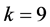, the partial autocorrelation coefficient of the sequence is clearly within the confidence interval. That sequence of partial autocorrelation function is tailing. Therefore, the sequence of Y can be established model.

2.3. Parameter Estimation

We can judge the type of time series model more accurately according to the principle of the model [1] . According to the principle can be calculated in Table 1, which takes,.

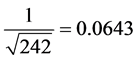From the table can be seen as the 1 step truncation, but after 6 steps are not censored, can think the tail, which belongs to 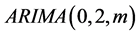model.

In order to determine the order number of the model, the, , 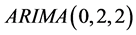model was established by using the least square method in Eviews 6. Now look at the different models under

Adjusted R², AIC, SC, such as Table 2.

In regression analysis, the requirement for the level of parameter t test is not so strict as the regression equation, and more is considered the whole fitting effect of the model. Adjusted R², AIC, SC are important criteria for the selection of models. And the three roots are within the unit circle, to meet the requirements. According to the standard function method, AIC, SC value reaches minimum is the best model order, so we choose model.

2.4. Model Test

We should further verify the suitability of the model, that is, the residual sequence of the model is tested by white noise. The use of Eviews software for the chi square test, the test results are shown in Figure 4.

In Figure 4, the last two columns for the chi square test, including with Q statistics and Adjoint probability of test. The sample size of the residual sequence is 240, and we take the maximum lag period is 15. From the figure, we can see the Q value 7.3636, and the probability that the first class error committed by the prob. column is 0.920. This shows that the residual sequence is independent of each other, test pass. That is, model through test.

3. Model Prediction

The model is suitable for the test, can be used for short-term prediction. In order to test the predictive effect of the model, we set aside the last 8 observations in December as the reference object. After the operation of the software, the result of the equation is obtained. The main contents are shown in Table 3.

The inverted root of the polynomial in Table 3 is in the unit circle, shows that the process is stable, and it is also reversible. We use the software to predict the last 8 values of the model. Use model in December of 2011 last eight group in Shanghai and Shenzhen 300 stock index data to predict, the predictive value and the real value, error, error ratio is shown in Table 4.

Experimental results show the absolute error of the model and the percentage of absolute error are controlled within a certain range. So the fitting effect of the model is good, and the predictive value is close to the actual value.

4. Conclusion

According to model, we got the last eight values in December. The error is controlled in less than 3% predicted value of stock buying and selling to make a short-term rational decision, for the risk of investing in stocks decrease will have a certain role. The research of this paper is limited to the establishment of the model of the stationary processing of the finite- and non-stationary data. Through the historical data of Shanghai and Shenzhen 300 stock index, it reveals the law of its change with time. Extending this law to the future, so as to predict the future of the Shanghai and Shenzhen 300 stock price index, the fitting effect is not perfect. However, the time series prediction model described by model in the financial, stock and other fields has its theoretical and practical significance. The stock price through the fitting and prediction, time series model has certain reference in the aspect of price volatility of the stock market. The result of fitting prediction

can represent the trend of stock price in a certain degree.

Fund

Qinghai Nationalities University Natural Science Foundation Item Number 2015XJZ03.

Cite this paper

Shichang Shen,Yue Shen, (2016) ARIMA Model in the Application of Shanghai and Shenzhen Stock Index. Applied Mathematics,07,171-176. doi: 10.4236/am.2016.73016

References