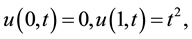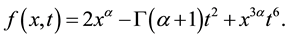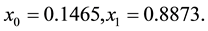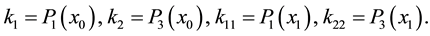Applied Mathematics
Vol.06 No.13(2015), Article ID:61584,7 pages
10.4236/am.2015.613190
Approximate Solution of Non-Linear Fractional Klein-Gordon Equation Using Spectral Collocation Method
Rubayyi T. Alqahtani
Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 1 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
In this paper, we implement the spectral collocation method with the help of the Legendre polynomials for solving the non-linear Fractional (Caputo sense) Klein-Gordon Equation (FKGE). We present an approximate formula of the fractional derivative. The Legendre collocation method is used to reduce FKGE to the solution of system of ODEs which is solved by using finite difference method. The results of applying the proposed method to the non-linear FKGE show the simplicity and the efficiency of the proposed method.
Keywords:
Fractional Klein-Gordon Equation, Legendre Spectral Method

1. Introduction
The theory of fractional calculus is initiated by Leibniz, Liouville, Riemann, Grunwald and Letnikov and since then has been found many applications in science and engineering. Finding accurate and efficient method for solving fractional differential equations has been an active research subject. Finding the exact solution for most of these equations is not an easy task, thus analytical and numerical methods must be used.
The Klein-Gordon equation plays a significant role in mathematical physics and many scientific applications such as solid-state physics, nonlinear optics, and quantum field theory [1] . The equation has attracted much attention in studying solitons and condensed matter physics, in investigating the interaction of solitons in a collisionless plasma and the recurrence of initial states, and in examining the nonlinear wave equations [2] . Wazwaz has obtained the various exact traveling wave solutions such as compactons, solitons and periodic solutions by using the tanh method [1] . The study of numerical solutions of the Klein-Gordon equation has been investigated considerably in the last few years. In the previous studies, the most papers have carried out different spatial discretization of the equation ([2] [3] ).
In this work, we apply spectral collocation method (with the help of Legendre polynomials) to obtain the numerical solution of the non-linear FKGE of the form
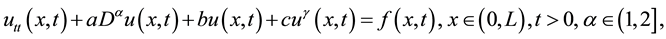 (1)
(1)
where  denotes the Caputo fractional derivative of order
denotes the Caputo fractional derivative of order 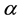 with respect to x,
with respect to x,  is unknown function, and
is unknown function, and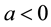 ,
, 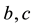 and
and 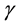 are known constants with
are known constants with ,
,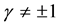 .
.
We consider the initial conditions and the boundary conditions as follows:
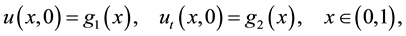 (2)
(2)
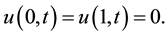 (3)
(3)
The existence and the uniqueness of the solution of Equations (1)-(3) are given in ([2] -[4] ).
For more details about the fractional calculus see ([5] -[8] ) and for more details about the Legendre collocation method see ([9] -[18] ).
2. An Approximate Formula of the Fractional Derivative
The well-known Legendre polynomials are defined on the interval 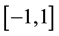 and can be determined with the aid of the following recurrence formula [19]
and can be determined with the aid of the following recurrence formula [19]
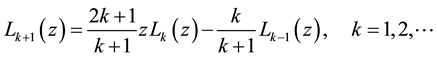
In order to use these polynomials on the interval 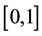 we define the so called shifted Legendre polynomials by introducing the change of variable
we define the so called shifted Legendre polynomials by introducing the change of variable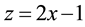 . Let the shifted Legendre polynomials
. Let the shifted Legendre polynomials 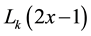


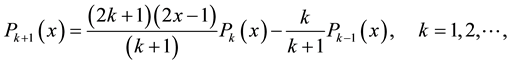
where 

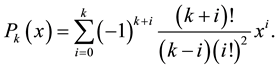
The function
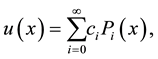
where the coefficients 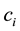
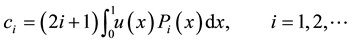
In practice, only the first 
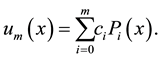
Theorem 1 [14] .
Let 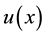
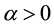
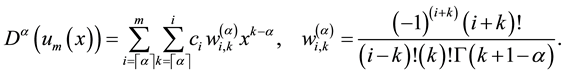
Theorem 2 [14] .
The error 
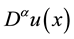

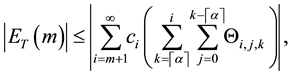
where
3. Numerical Implementation
Example 1.
Consider the fractional-order cubically nonlinear Klein-Gordon problem
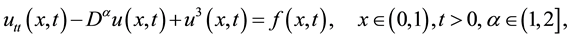
with the initial and boundary conditions 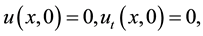
where the source term 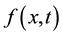
The exact solution of this problem is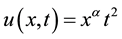
In order to use the proposed method, we approximate 
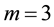
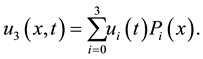
From Equation (11) and Theorem 1 we have

We now collocate Equation (13) at 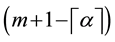
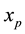
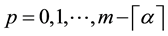
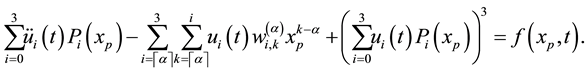
For suitable collocation points we use roots of shifted Legendre polynomial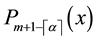
In this case, the roots 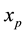

Also, by substituting Equation (12) in the boundary conditions we can find
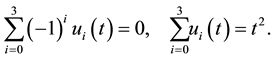
By using Equation (14) and Equation (15) we obtain the following non-linear system of ODEs:
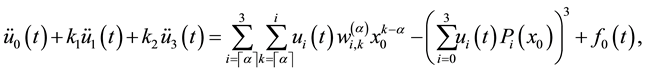
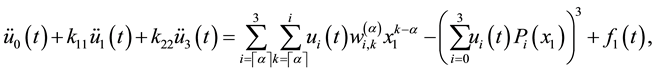

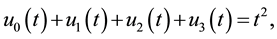
where
Now, to use FDM [20] for solving the system (16)-(19), we will use the following notations: 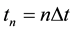
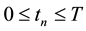

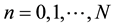

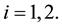
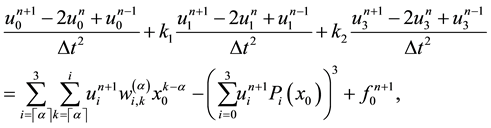
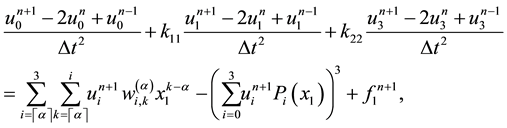
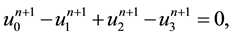
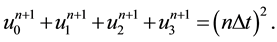
This system presents the numerical scheme of the proposed problem and is non-linear system of algebraic equations, and by solving this system yields the numerical solution of the non-linear FKGE (11).
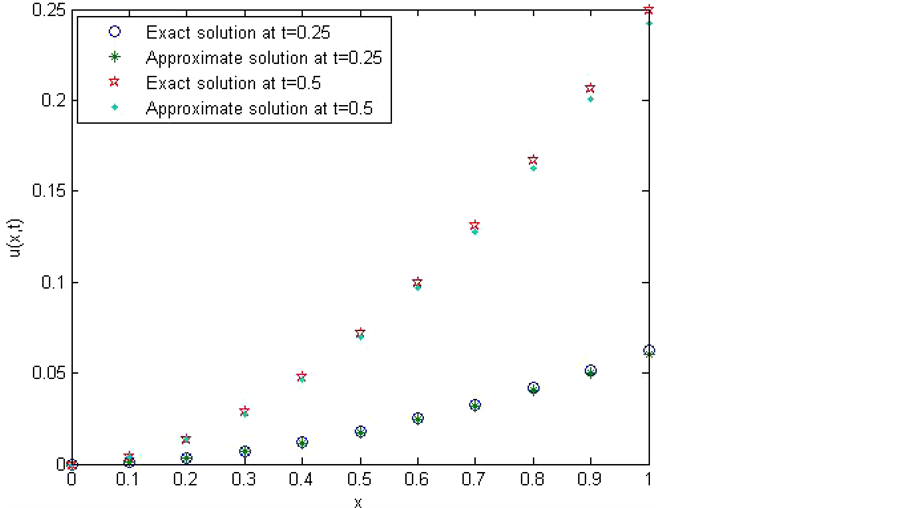
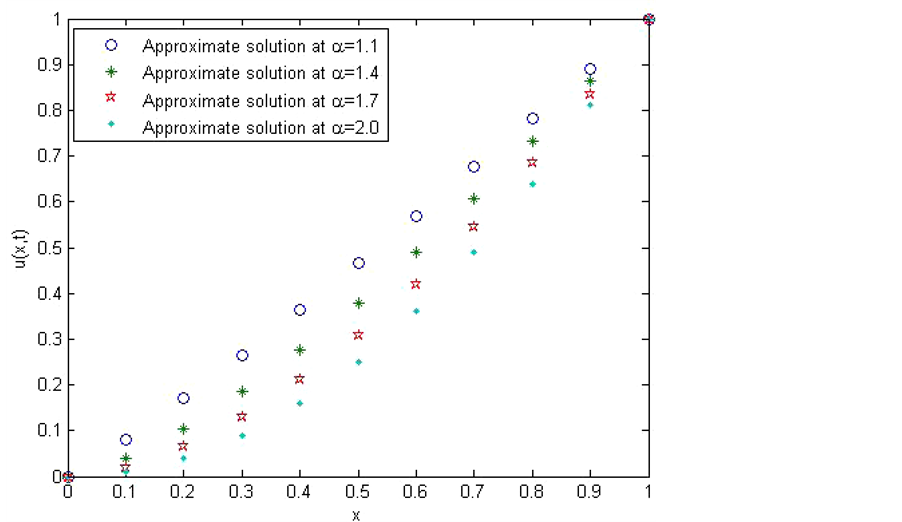
The obtained numerical results by means of the proposed method are shown in Table 1 and Figure 1 and Figure 2. In Table 1, the absolute errors between the exact solution 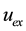

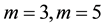

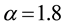
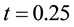
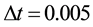
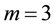

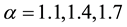
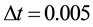
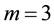
Example 2.
Consider the fractional cubically non-linear Klein-Gordon problem:
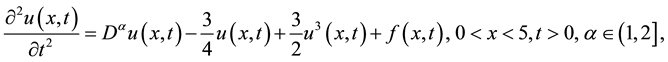
with the following initial and boundary conditions:
Table 1. The absolute error between the exact and approximate solutions at
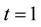
Figure 1. The exact and approximate solutions at 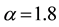
Figure 2. The approximate solution at 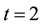

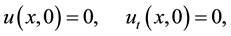

where the source term 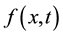
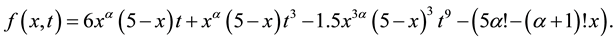
The exact solution of this problem is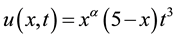
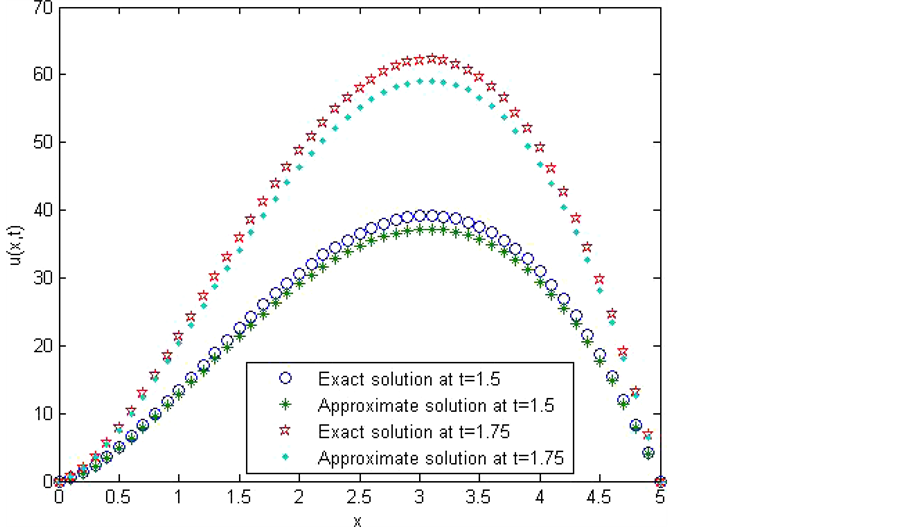
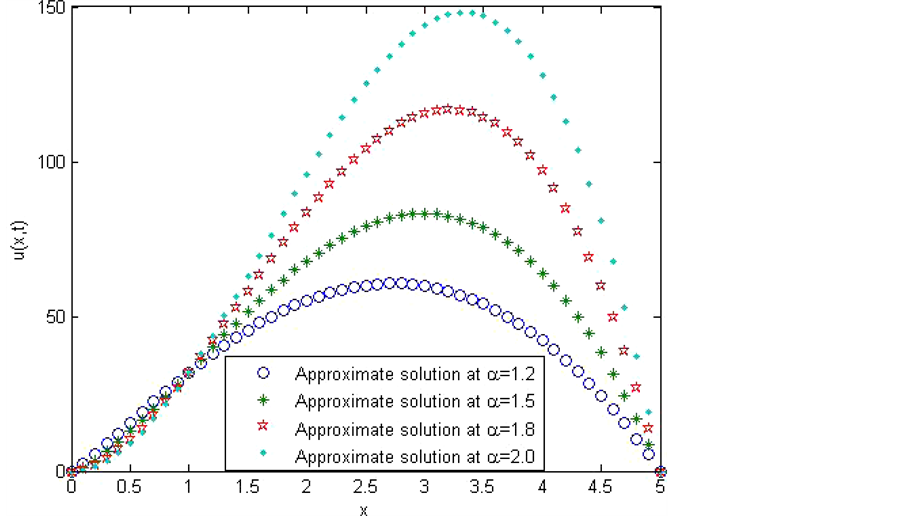
The obtained numerical results by means of the proposed method are shown in Figure 3 and Figure 4. In Figure 3, we presented comparison between the exact solution and the approximate solution using the proposed method at 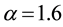
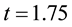
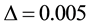
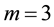
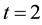
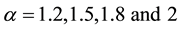
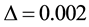

Figure 3. The exact and approximate solutions at 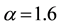
Figure 4. The approximate solution at 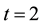
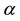
4. Conclusion and Remarks
We have implemented Legendre spectral method for solving the non-linear FKGE. The proposed method gives excellent results when it is applied to FKGE. Absolute error by the method decreases while increasing iterations or level of resolution or both, as shown in Figures 1-4. It is evident that the overall errors can be made smaller by adding new terms from the series (8). Comparisons are made between approximate solutions and exact solutions to illustrate the validity and the great potential of the technique.
Acknowledgements
We thank the editor and the referee for their comments.
Cite this paper
Rubayyi T.Alqahtani, (2015) Approximate Solution of Non-Linear Fractional Klein-Gordon Equation Using Spectral Collocation Method. Applied Mathematics,06,2175-2181. doi: 10.4236/am.2015.613190
References
- 1. Wazwaz, A.M. (2006) Compacton Solitons and Periodic Solutions for Some Forms of Nonlinear Klein-Gordon Equations. Chaos, Solitons and Fractals, 28, 1005-1013.
http://dx.doi.org/10.1016/j.chaos.2005.08.145 - 2. El-Sayed, S.M. (2003) The Decomposition Method for Studying the Klein-Gordon Equation. Chaos, Solitons and Fractals, 18, 1026-1030.
http://dx.doi.org/10.1016/S0960-0779(02)00647-1 - 3. Yusufoglu, E. (2008) The Variational Iteration Method for Studying the Klein-Gordon Equation. Applied Mathematics Letters, 21, 669-674.
http://dx.doi.org/10.1016/j.aml.2007.07.023 - 4. El-Sayed, A.M.A., Elsaid, A. and Hammad, D. (2012) A Reliable Treatment of Homotopy Perturbation Method for Solving the Nonlinear Klein-Gordon Equation of Arbitrary (Fractional) Orders. Journal of Applied Mathematics, 2012, 1-13.
http://dx.doi.org/10.1155/2012/581481 - 5. Doha, E.H., Bhrawy, A.H. and Ezz-Eldien, S.S. (2011) A Chebyshev Spectral Method Based on Operational Matrix for Initial and Boundary Value Problems of Fractional Order. Computers and Mathematics with Applications, 62, 2364- 2373.
http://dx.doi.org/10.1016/j.camwa.2011.07.024 - 6. El-Sayed, A.M.A., Elsaid, A., El-Kalla, I.L. and Hammad, D. (2012) A Homotopy Perturbation Technique for Solving Partial Differential Equations of Fractional Order in Finite Domains. Applied Mathematics and Computation, 218, 8329-8340.
http://dx.doi.org/10.1016/j.amc.2012.01.057 - 7. Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus. Academic Press, New York.
- 8. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, New York.
- 9. Khader, M.M. (2011) On the Numerical Solutions for the Fractional Diffusion Equation. Communications in Nonlinear Science and Numerical Simulations, 16, 2535-2542.
http://dx.doi.org/10.1016/j.cnsns.2010.09.007 - 10. Khader, M.M. (2015) An Efficient Approximate Method for Solving Fractional Variational Problems. Applied Mathematical Modelling, 39, 1643-1649.
http://dx.doi.org/10.1016/j.apm.2014.09.012 - 11. Khader, M.M. (2015) Fractional Chebyshev Finite Difference Method for Solving the Fractional-Order Delay BVPs. International Journal of Computational Methods, 12, Article ID: 1550033.
http://dx.doi.org/10.1142/s0219876215500334 - 12. Khader, M.M. (2014) On the Numerical Solution and Convergence Study for System of Non-Linear Fractional Diffusion Equations. Canadian Journal of Physics, 92, 1658-1666.
http://dx.doi.org/10.1139/cjp-2013-0464 - 13. Khader, M.M., Sweilam, N.H. and Mahdy, A.M.S. (2011) An Efficient Numerical Method for Solving the Fractional Diffusion Equation. Journal of Applied Mathematics and Bioinformatics, 1, 1-12.
- 14. Khader, M.M. and Hendy, A.S. (2012) The Approximate and Exact Solutions of the Fractional-Order Delay Differential Equations Using Legendre Pseudo-Spectral Method. International Journal of Pure and Applied Mathematics, 74, 287-297.
- 15. Sweilam, N.H., Khader, M.M. and Al-Bar, R.F. (2007) Numerical Studies for a Multi-Order Fractional Differential Equation. Physics Letters A, 371, 26-33.
http://dx.doi.org/10.1016/j.physleta.2007.06.016 - 16. Sweilam, N.H. and Khader, M.M. (2010) A Chebyshev Pseudo-Spectral Method for Solving Fractional Integro-Diffe- rential Equations. ANZIAM, 51, 464-475.
http://dx.doi.org/10.1017/S1446181110000830 - 17. Sweilam, N.H., Khader, M.M. and Nagy, A.M. (2011) Numerical Solution of Two-Sided Space-Fractional Wave Equation Using Finite Difference Method. Journal of Computational and Applied Mathematics, 235, 2832-2841.
http://dx.doi.org/10.1016/j.cam.2010.12.002 - 18. Sweilam, N.H., Khader, M.M. and Mahdy, A.M.S. (2012) Crank-Nicolson Finite Difference Method for Solving Time-Fractional Diffusion Equation. Journal of Fractional Calculus and Applications, 2, 1-9.
- 19. Bell, W.W. (1968) Special Functions for Scientists and Engineers. Great Britain, Butler and Tanner Ltd, Frome and London.
- 20. Smith, G.D. (1965) Numerical Solution of Partial Differential Equations. Oxford University Press, Oxford.