Applied Mathematics
Vol.06 No.09(2015), Article ID:58602,10 pages
10.4236/am.2015.69134
New Extension of Unified Family of Apostol-Type Polynomials and Numbers
Beih El-Sayed El-Desouky, Rabab Sabry Gomaa
Department of Mathematics, Mansoura University, Mansoura, Egypt
Email: b_desouky@yahoo.com, dr.rsg12@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 May 2015; accepted 1 August 2015; published 5 August 2015
ABSTRACT
The purpose of this paper is to introduce and investigate new unification of unified family of Apostol-type polynomials and numbers based on results given in [1] [2] . Also, we derive some properties for these polynomials and obtain some relationships between the Jacobi polynomials, Laguerre polynomials, Hermite polynomials, Stirling numbers and some other types of generalized polynomials.
Keywords:
Euler, Bernoulli and Genocchi Polynomials, Stirling Numbers, Laguerre Polynomials, Hermite Polynomials

1. Introduction
The generalized Bernoulli polynomials 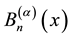 of order
of order 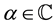 and the generalized Euler polynomials are defined by (see [3] ):
and the generalized Euler polynomials are defined by (see [3] ):
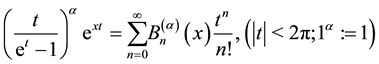 (1.1)
(1.1)
and
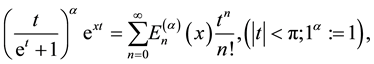 (1.2)
(1.2)
where 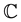 denotes the set of complex numbers.
denotes the set of complex numbers.
Recently, Luo and Srivastava [4] introduced the generalized Apostol-Bernoulli polynomials 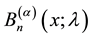 and the generalized Apostol-Euler polynomials
and the generalized Apostol-Euler polynomials 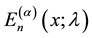 as follows.
as follows.
Definition 1.1. (Luo and Srivastava [4] ) The generalized Apostol-Bernoulli polynomials 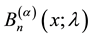 of order
of order 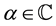 are defined by the generating function
are defined by the generating function
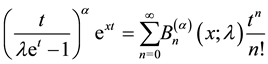
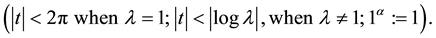 (1.3)
(1.3)
Definition 1.2. (Luo [5] ) The generalized Apostol-Euler polynomials 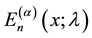 of order
of order 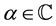 are defined by the generating function
are defined by the generating function
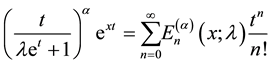
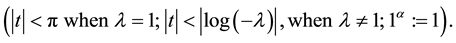 (1.4)
(1.4)
Natalini and Bernardini [6] defined the new generalization of Bernoulli polynomials in the following definition.
Definition 1.3. The generalized Bernoulli polynomials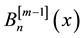 ,
, 


Recently, Tremblay et al. [7] investigated a new class of generalized Apostol-Bernoulli polynomial as follows.
Definition 1.4. The generalized Apostol-Bernoulli polynomials 




Also, Sirvastava et al. [1] introduced a new interesting class of Apostol-Bernoulli polynomials that are closely related to the new class that we present in this paper. They investigated the following form.
Definition 1.5. Let 




This sequel to the work by Sirvastava et al. [2] introduced and investigated a similar generalization of the family of Euler polynomials defined as follows.
Definition 1.6. Let 




It is easy to see that setting 


In Section 2, we introduce the new extension of unified family of Apostol-type polynomials and numbers that are defined in [9] . Also, we determine relations between some results given in [1] [3] [7] [10] [11] and our results. Moreover, we introduce some new identities for polynomials defined in [9] . In Section 3, we give some basic properties of the new unification of Apostol-type polynomials and numbers. Finally in Section 4, we introduce some relationships between the new unification of Apostol-type polynomials and other known polynomials.
2. Unification of Multiparameter Apostol-Type Polynomials and Numbers
Definition 2.1. Let





where 
Remark 2.1. If we set 

The generating function in (2.1) gives many types of polynomials as special cases, for example, see Table 1.
Remark 2.2. From NO. 13 in Table 1 and ([9] , Table 1), we can obtain the polynomials and the numbers given in [12] -[16] .
3. Some Basic Properties for the Polynomial
Theorem 3.1. Let 



Proof. For the first equation, from (2.1)
using Cauchy product rule, we can easily obtain (3.1).
For the second Equation (3.2), from (2.1)
Table 1. Special cases.
Equating the coefficient of 
Corollary 3.1. If 


Theorem 3.2. The following identity holds true, when 


Proof. From (2.1)
Hence, we can easily obtain (3.5).
Remark 3.1. If we put


where 
Theorem 3.3. The unification of Apostol-type numbers satisfy

Proof. When 
Using Cauchy product rule, we obtain (3.6).
Theorem 3.4. The following relationship holds true

where 



Proof. Starting with (2.1), we get
Using Cauchy product rule on the right hand side of the last equation and equating the coefficients of 
Using No. 13 in Table 1, we obtain Nörlund’s results, see [17] and Carlitz’s generalizations, see [18] by our approach in Theorem 3.5 and Theorem 3.6 as follows
Theorem 3.5. For


Proof. For the first equation and starting with (2.1), we get
Equating the coefficients of 
For the second equation and starting with (2.1), we get
then, we have
Equating coefficients of 
Theorem 3.6. For 



Proof. For the first equation and starting with (2.1), we get
Equating the coefficients of 
Also, It is not difficult to prove (3.11).
4. Some Relations between 
In this section, we give some relationships between the polynomials 
Theorem 4.1. For



between the new unification of Apostol-type polynomials and generalized Stirling numbers of second kind, see [19] .
Proof. Using (3.4) and from definition of generalized Stirling numbers of second kind, we easily obtain (4.1).
Theorem 4.2. For



between the new unification of Apostol-type polynomials and Stirling numbers of second kind.
Proof. Using (3.4) and from definition of Stirling numbers of second kind (see [20] ), we easily obtain (4.2).
Theorem 4.3. The relationship

holds between the new unification of multiparameter Apostol-type polynomials and generalized Laguerre polynomials (see [7] , No. (3), Table 1).
Proof. From (3.4) and substitute
then we get (4.3).
Theorem 4.4. For

holds between the new unification of Apostol-type polynomials and Jacobi polynomials (see [21] , p. 49, Equation (35)).
Proof. From (3.4) and substitute
then we get (4.4).
Theorem 4.5. The relationship

holds between the new unification of Apostol-type polynomials and Hermite polynomials (see [7] , No. (1) Table 1).
Proof. From (3.4) and substitute
then we get (4.5).
Theorem 4.6. When












between the new unified family of generalized Apostol-Euler, Bernoulli and Genocchi polynomials, and

Proof. From [9] , Equation (2.1),
Equating the coefficients of 
Using No. 13 in Table 1 (see [9] ) and the definition of the unified Bernstein and Bleimann-Butzer-Hahn basis (see [23] ),

where


Theorem 4.7. For 

between the unified Bernstein and Bleimann-Butzer-Hahn basis, the new unified family of generalized Apostol-Bernoulli, Euler and Genocchi polynomials (see [9] ) and generalized Stirling numbers of first kind (see [19] ).
Proof. From (2.1) and (4.7) and with some elementary calculation, we easily obtain (4.8).
Cite this paper
Beih El-SayedEl-Desouky,Rabab SabryGomaa, (2015) New Extension of Unified Family Apostol-Type of Polynomials and Numbers. Applied Mathematics,06,1495-1505. doi: 10.4236/am.2015.69134
References
- 1. Srivastava, H.M., Garg, M. and Choudhary, S. (2010) A New Generalization of the Bernoulli and Related Polynomials, Russian. Journal of Mathematical Physics, 17, 251-261.
http://dx.doi.org/10.1134/S1061920810020093 - 2. Srivastava, H.M., Garg, M. and Choudhary, S. (2011) Some New Families of Generalized Euler and Genocchi Polynomials. Taiwanese Journal of Mathematics, 15, 283-305.
- 3. Srivastava, H.M. and Pintér, á. (2004) Remarks on Some Relationships between the Bernoulli and Euler Polynomials. Applied Mathematics Letters, 17, 375-380.
http://dx.doi.org/10.1016/S0893-9659(04)90077-8 - 4. Luo, Q.-M. and Srivastava, H.M. (2005) Some Generalizations of the Apostol Bernoulli and Apostol Euler Polynomials. Journal of Mathematical Analysis and Applications, 308, 290-302.
http://dx.doi.org/10.1016/j.jmaa.2005.01.020 - 5. Luo, Q.-M. (2006) Apostol-Euler Polynomials of Higher Order and Gaussian Hypergeometric Functions. Taiwanese Journal of Mathematics, 10, 917-925.
- 6. Natalini, P. and Bernardini, A. (2003) A Generalization of the Bernoulli Polynomials. Journal of Applied Mathematics, 153-163.
http://dx.doi.org/10.1155/s1110757x03204101 - 7. Tremblay, R., Gaboury, S. and Fugère, B.-J. (2011) A New Class of Generalized Apostol-Bernoulli Polynomials and Some Analogues of the Srivastava-Pintér Addition Theorem. Applied Mathematics Letters, 24, 1888-1893.
http://dx.doi.org/10.1016/j.aml.2011.05.012 - 8. Luo, Q.-M., Guo, B.-N., Qui, F. and Debnath, L. (2003) Generalizations of Bernoulli Numbers and Polynomials. International Journal of Mathematics and Mathematical Sciences, 59, 3769-3776.
http://dx.doi.org/10.1155/S0161171203112070 - 9. El-Desouky, B.S. and Gomaa, R.S. (2014) A New Unified Family of Generalized Apostol-Euler, Bernoulli and Genocchi Polynomials. Applied Mathematics and Computation, 247, 695-702.
http://dx.doi.org/10.1016/j.amc.2014.09.002 - 10. Kurt, B. (2010) A Further Generalization of Bernoulli Polynomials and on 2D-Bernoulli Polynomials . Applied Mathematical Sciences, 47, 2315-2322.
- 11. Kurt, B. (2013) Some Relationships between the Generalized Apostol-Bernoulli and Apostol-Euler Polynomials. Turkish Journal of Analysis and Number Theory, 1, 54-58.
- 12. Ozden, H. and Simsek, Y. (2014) Modification and Unification of the Apostol-Type Numbers and Polynomials and Their Applications. Applied Mathematics and Computation, 235, 338-351.
http://dx.doi.org/10.1016/j.amc.2014.03.004 - 13. Apostol, T.M. (1951) On the Lerch Zeta Function. Pacific Journal of Mathematics, 1, 161-167.
http://dx.doi.org/10.2140/pjm.1951.1.161 - 14. Dere, R., Simsek, Y. and Srivastava, H.M. (2013) A Unified Presentation of Three Families of Generalized Apostol Type Polynomials Based upon the Theory of the Umbral Calculus and the Umbral Algebra. Journal of Number Theory, 133, 3245-3263.
http://dx.doi.org/10.1016/j.jnt.2013.03.004 - 15. Karande, B.K. and Thakare, N.K. (1975) On the Unification of Bernoulli and Euler Polynomials. Indian Journal of Pure and Applied Mathematics, 6, 98-107.
- 16. Luo, Q.-M. (2004) On the Apostol Bernoulli Polynomials. Central European Journal of Mathematics, 2, 509-515.
http://dx.doi.org/10.2478/BF02475959 - 17. Nörlund, N.E. (1924) Vörlesunge über differezerechnung. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-50824-0 - 18. Carlitz, L. (1962) Some Generalized Multiplication Formulae for the Bernoulli Polynomials and Related Functions. Monatshefte für Mathematik, 66, 1-8.
- 19. Comtet, L. (1972) Nombers de Stirling generaux et fonctions symetriques. Comptes Rendus de l’Académie des Sciences (Series A), 275, 747-750.
- 20. Gould, H.W. (1960) Stirling Number Representation Problems. Proceedings of the American Mathematical Society, 11, 447-451.
http://dx.doi.org/10.1090/S0002-9939-1960-0114767-8 - 21. Srivastava, H.M. and Choi, J. (2001) Series Associated with the Zeta and Related Functions. Kluwer Academic, Dordrecht.
http://dx.doi.org/10.1007/978-94-015-9672-5 - 22. Charalambides, C.A. (2005) Generalized Stirling and Lah Numbers. In: Charalambides, C.A., Ed., Combinatorial Methods in Discrete Distributions, John Wiley & Sons, Inc., Hoboken, 121-158.
- 23. özarslan, M.A. and Bozer, M. (2013) Unified Bernstein and Bleimann-Butzer-Hahn Basis and Its Properties. Advances in Difference Equations, 2013, 55.
http://dx.doi.org/10.1186/1687-1847-2013-55



































