Received 22 March 2015; accepted 14 June 2015; published 17 June 2015

ABSTRACT

Cell as elastic rod behavior model is proposed to describe its contractile activity. The model takes into account the result of the transduction of external influences, which is resulting in the formation of internal deformation, and evaluates the mobility and/or the tension in the muscle cells under the external influence.

Keywords:

Mathematical Modeling, Cell Mechanosensitivity, Muscle Cell

1. Introduction

Mechanical properties of both living and nonliving objects appear in its reaction against external action, mainly mechanical. Living cell like every system in external mechanical field stays in tense. External physical signals transformation results in corresponding cell response. Consequently, changes in external field lead to mechanical tension change in cell and deformations arise.

Interaction between cell and external mechanical field still remains one of the modern cell biophysics unsolved problems, due to the fact that determination of cell mechanosensor is an extremely difficult task. At the same time the need to solve this problem is necessary for different tissue cells protection methods development under changes of the external mechanical conditions, for example, during spaceflight, especially long-term spaceflight.

Special interest in mechanical properties study represent cells can change their own mechanical parameters in response to external influence by contractile-relaxation cycle initiation specific to muscle cells-myocytes. We supposed earlier the mechanosensor, being the most general for different cell types, to be connected to submembrane cytoskeleton [1] -[3] . We proposed a model capable to measure deformations arising in muscle cell membrane, after gravitation force was changed [4] . It allows us to suggest completely different mechanotransduction pathways in muscle cell.

On the other hand, muscle cells have specific structure, advanced cytoskeleton, which takes most of cell volume and forms a contractile apparatus. Taking into consideration these muscle cells features and contractile apparatus important role in mechanical tension generation, muscle cell mechanosensor may be connected with its contractile apparatus, for example with M-line [5] . Contractile apparatus formed with strictly aligned myofibrils, consisted from actin and myosin threads. Because of these threads strictly parallel displacement, their slide occurs in a same direction, and thus a huge tension occurs in a cell. Cell diameter is negligible in comparison with its length, this ratio is about 100 - 1000. For this reason one can consider a muscle cell as cylindrical body.

At present time the most powerful tool for different organisms functioning theoretical research is mathematical modeling in terms of continuum mechanics. With the help of equations and relations from this theory one can formulate a closed system of equations. Their solution allows us to study deformable media behavior and to obtain information about its state and motion.

2. Setting up the Problem in Cell Biomechanics

Let’s consider a cell like a structure with continuously distributed mass. To describe processes inside we use a system of equation for Cosserat’s continuum [6] :

, , , ,

,

(1)

,,

,,

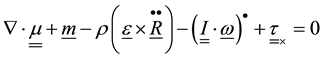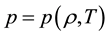
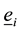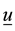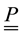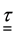where―Hamilton’s operator in reference configuration, and,―basis in reference and current configuration correspondingly,―radius-vector in reference configuration,―radius-vector in current configuration,―displacement vector,―rotation tensor,?deformation tensor,―moment strain,―stress tensor,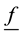―external bulk force,―density,―eccentricity vector,―moment tensor,―external moment,―Inertia tensor,―angular velocity,―symmetrical stress tensor,―deformation gradient,―free energy per volume unit in reference configuration,―temperature. Single underlining designates vector, double means tensor.

Cauchy boundary conditions are given by:,

Let’s transform the system above according to biomechanic medium specific features.

The system given depicts both continuous medium static and dynamic behavior, as it takes into consideration inertia parameters: mass, eccentricity, inertia tensor. This values describes mass distribution in the system. Eccentricity vector specifies mass center displacement in relation to pole. But we can place mass center into one point without detriment to generality. In this case. Moreover we will assume an inertia members contribution to be negligible. It arises from the fact that mass center is also an inertia center, hence, and the only remained inertia parameter is mass.

An external bulk moment action results in cell torsion. It means that every cross section appears to be turned by some angle relatively underlaying one. Lateral surface generatrixes becomes helix. The situation described is possible for different materials, but it can’t take place in a biological structure, like a living cell. It’s impossible because it will likely lead to dramatic deformations and possibly to ruptures in cytoplasmic membrane crucial for cell existing and functioning. For this reason we pose, external moments don’t acts on the modeled medium.

One should note that direct physical influence on biological structures are rather light. Mostly their action is mediated by internal signaling systems. For this reason, to simplify calculations we can take. However, during experimental study appears an external forces, which cannot be neglected.

In this case, the balance equation form is significantly simplified:

(2)

(3)

Despite a small magnitude of external influence on cell biomechanical parameters, mechanical signal transduction results in significant intracellular changes and forming an internal deformation (intracellular compartments structural changes). These deformations in turn generate motion, contractile activity. For this influence to be stated completely, we need knowledge about every mechanical parameter regulation pathways inside a cell. Data collected at present time are insufficient for this task. Nevertheless there are models depicted a mobility generation kinetic rather profound. Their essence is a chemical reaction kinetic of subcellular structures interaction analysis.

In this paper, during cell biomechanics consideration we only postulate a final result of all chemical interactions aimed at motion generation. Obviously, this result is some internal deformation causes internal tension arise and subcellular structures mutual displacement change. Parameters of “internal deformation” (for its ma-

thematical designation we will use tensor) may be obtained from both kinetic models and experimental data.

In this case the free energy becomes a function of not only known deformation tensor and temperature, but

also of tensor:.

Complexity of explicit determination internal deformations tensor leads us to another problem: free energy explicit determination. However, if we take internal deformation small (this assumption corresponds to experiments), then free energy might be stated as a square form. Then after differentiation we obtain:

(4)

Without loss of generality we can take a reference configuration strainless, i.e.,.

So, the cell biomechanics closed system of equations with Cauchy boundary conditions is given by:

, (5)

where, ,―displacement;―stiffness bending tensor (has only 3 components,

specifying bending in 3 different planes, since there are no external moments inducing torsion),?stretching and shift stiffness tensor,―crosstalk stiffness tensor (specifying very rare situations when different interactions influence each other);―thermal expansion coefficient, ,―temperature in a reference configuration;―density,―viscous resistance coefficient;―internal deformation tensor, specifying motility generation mechanism; and―correspondingly surface force and moment,―external bulk force.

3. Muscle Cell Contractile Activity Mathematical Modeling

Taking into account muscle cell structural features (see Introduction), one can consider a myocyte as a thin long cylindrical body. This assumption allows us to apply special methods of rods mechanic to describe the cell.

Cell biomechanics system of equation may be significantly simplified, in the same way we’ve done it with such system for rods, basing on continuum mechanics. We will consider motion in regard to stationary Cartesian coordinate system (OXYZ). For angle orientation being established we associate orthogonal trihedron with each particle of considerable biomechanical system, at the same time without loss of generality we can pose a tangential axis unit coordinate vector. Similar to rods theory we introduce one material coordinate s. Motion is described by dependent radius-vector on time and rotation tensor for every particle.

For example, radius-vector may be given by:

(6)

where:, , what in details means:.

At the same time vector specifies a relative length change.

In mechanics conventionally transversal shifts is concerned in cases, when we consider a short thick rod. Considerable cell structures are thin long bodies, for this reason we can neglect transversal shifts. Moreover, muscle filaments motions are aligned, in the case of transversal shift a myofibrilla and sole myocyte structure would be broken and they won’t function.

All mentioned above leads us to some modification of geometrical relations. We will consider a Kirchhoff model, where stretching and compression are allowed, but transversal shift is forbidden. Vector we can express in form, and without transversal shift.

Consequently:

(7)

where specifies a strain per unit length.

According with, and then one of geometrical equations trans-

forms from to:.

Crosstalk tensor, being present in definitive equations specifies very rare situations when different interaction influence each other. However its contribution should be proved by experimental data, showing bending-torsion and stretching-compression stiffness change.

Problem setting up for muscle cell derived from such formulation in cell biomechanics is given by:

, (8)

where.

Initial and boundary conditions are:

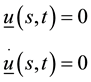
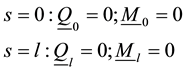
Or, if we fix one end:,.

Thus we have a muscle cell spatial motion description problem formulation as a result of contractile activity.

4. Problem Solution

For the problem stated to be solved we’ll use a variational procedure, formulating the problem statement as variational principle in a following way [7] :

(9)

where.

Let’s take into consideration forces and moments expressions, variation formulas, initial and boundary conditions obtained above. The problem formulation will be given by:

,,

,,

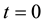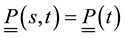
where, ,.

Rotation tensor explicit form is unknown, but it is obviously a function of rotation angle. Conse-

quently, ,. Rotation tensor and displacement

are connected by constraint equation. According to Kantorovich method [6] we can approximate either, or and express remained function through constrain equation. Then:

or

,

where n―degrees of freedom number;―prescribed functions задаваемые функции,―unknown independent variable values.

We have:

,,,,

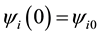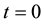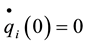
where,or, ,

, , ,;,―temperature

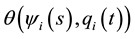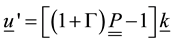in reference configuration,―thermal expansion coefficient;―viscous resistance coefficient, , where―medium shear viscosity.

The should be found for myocyte stretching compression analysis. Muscle fibers structure causes all myofibrils to be aligned, and as a result stretching-compression is allowed only in one direction. And there is no any muscle bending, only stretching or compression. According to physics, , so do stiffness tensors,. Besides, we can consider a myocyte as unidirectorial system. Then we pose:

We will calculate displacement as:.

For muscle cells we have correspondingly:

(10)

,,,

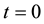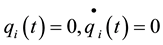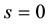where―temperature change,―thermal expansion coefficient;―medium shear viscosity.

Taking into account preconceived idea about motion, we will take and stretching and compression occur along OZ. Then we obtain:

(11)

In the case when stiffness coefficient depends on both coordinate and time, equation solving seems to be difficult.

Let’s assume the stiffness coefficient b does not depend on time. Then we can express from equation:

where g(t):, ,;, ,

Solution is derived from zero initial conditions:.

Then:

(12)

where.

So, for muscle cell we obtain:

where―internal deformation given, and leading to contraction-relaxation initiation,―external force (e.g. gravity), b―stretching-compression stiffness coefficient,―temperature change,―thermal expansion coefficient,―medium shear viscosity,―density distribution, l―muscle fiber length.

5. Discussion

Mechanosensitivity problem still remains to be one of the least studied. Most complicated case is one that deals with gravity change, since its magnitude, proportional to cell mass, is extremely small. Even more complex situation is possible when gravity magnitude is constant, but its direction varies. However for cells inside tissue such gravity vector change induces a number of nerve activity level change processes (for soleus muscle) or hydrostatic pressure redistribution (for cardiomyocytes). For this reason cell mechanosensor determination is extremely difficult task.

Extracellular matrix, membrane proteins, ion-channels components, cytoskeletal structures, intracellular structures could be considered as mechanosensors. It was shown that the strengthened force applying to neuron or smooth muscle cell culture via extracellular matrix results in microtubes polymerization increase [8] [9] . Integrins in this case might be considered as mechanosensors, since they form links with different extracelluar matrix proteins (e.g. fibronectin and vitronectin) and comprise a primary mechanotransduction site. Moreover tensin, alpha-actinin and filamin could bind integrins and submembrane cytoskeleton, since they have affinity domains for both integrins and actin [10] . Cell membrane mechanical stretching, for example, using patch-clump technology change mechanosensitive ion channels cation-transport activity as a result of conformation changes in either lipid bilayer [11] [12] or the very channel gate domain [13] . Plant cell reorientation in a gravity field results in calcium flow change within 25 seconds, arguing of calcium channels to be mechanosensitive [14] . External mechanic tension leads to calcium leakages from broken bone matrix [15] . External force field may be transducted to microtubes resulting in its breach, depolymerization and signaling pathways initiation [16] .

One of the most useful ways for on-cell influence significance estimation is mathematical modeling. In this paper we propose a living cell as biomechanical medium mathematical model, built on Cosserat’s system of equations. Such model allows us to evaluate cell response to both direct and transducted external mechanical conditions change.

Since muscle cells have specific structure we suggest developing such approach for all filamentic objects. Most of earlier crated models pay attention primarily on muscle cell internal processes kinetic, inducing contractile mechanism. In our method, we focused on cell level mechanics. At the same time internal deformations may be given by kinetic models. Obtained solution allows us to find given internal deformation and stretching- compression stiffness coefficient b experimentally.

Acknowledgements

The financial support of the Russian Fond of the Basic Research (RFBR grant 13-04-00755-a) and Program of Presidium of Russian Academy of Sciences “Molecular and Cell Biology” is greatly acknowledged.

References