Applied Mathematics
Vol.06 No.03(2015), Article ID:54371,8 pages
10.4236/am.2015.63042
Regular Elements of the Complete Semigroups
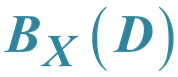 of Binary Relations of the Class
of Binary Relations of the Class

Nino Tsinaridze, Shota Makharadze
Department of Mathematics, Faculty of Mathematics, Physics and Computer Sciences, Shota Rustaveli Batumi State University, Batumi, Georgia
Email: ninocinaridze@mail.ru, shota_59@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 10 February 2015; accepted 28 February 2015; published 3 March 2015

ABSTRACT
As we know if
 is a complete
is a complete
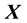 -semilattice of unions then semigroup
-semilattice of unions then semigroup
 possesses a right unit iff
possesses a right unit iff
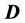 is an
is an
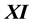 -semilattice of unions. The investigation of those
-semilattice of unions. The investigation of those
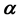 -idempotent and regular elements of semigroups
-idempotent and regular elements of semigroups
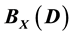 requires an investigation of
requires an investigation of
 -subsemilattices of semilattice
-subsemilattices of semilattice
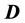 for which
for which . Because the semilattice
. Because the semilattice
 of the class
of the class
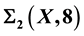 are not always
are not always
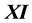 -semilattices, there is a need of full description for those idempotent and regular elements when
-semilattices, there is a need of full description for those idempotent and regular elements when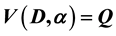 . For the case where
. For the case where
 is a finite set we derive formulas by calculating the numbers of such regular elements and right units for which
is a finite set we derive formulas by calculating the numbers of such regular elements and right units for which
Keywords:
Semilattice, Semigroup, Binary Relation
1. Introduction
In this paper we characterize the elements of the class




Let














Let

















Let





Let

In general, a representation of a binary relation


Note that for a quasinormal representation of a binary relation


a)


b)

Let










In [1] [2] they show that




A complete



(a)


(b)






Let









Let











In the sequel these equalities will be called formal.
It is proved that if the elements of the semilattice


meters







It is proved that under the mapping


The one-to-one mapping




Is fulfilled for each nonempty subset






(a)
(b)




Lemma 1.1. Let






unit of that semigroup (see ( [1] , Lemma 12.1.2), ( [2] , Lemma 12.1.2)).
Theorem 1.1. Let




mapping of the set



mappings




Theorem 1.2. Let





















(a)


(b)


(c)



Theorem 1.3. Let





2. Results
Let




The semilattice



Let



is a mapping of the semilattice




here the elements





Theorem 2.1. Let



Proof. Let





Figure 1. Diagram of
We have






If










Of the other hand, if




The Theorem is proved.
Lemma 2.1. Let


Proof. The given Lemma immediately follows from the formal equalities (2) of the semilattice
The lemma is proved.
Lemma 2.2. Let


is the largest right unit of the semigroup
Proof. By preposition and from Theorem 2.1 follows that


is the largest right unit of the semigroup
The lemma is proved.
Lemma 2.3. Let



where









Proof. It is easy to see, that the set


Figure 2. Diagram of Q’.
By Statement b) of the Theorem 1.2 follows that the following conditions are true:
i.e., the inclusions

i.e.,













Therefore the following conditions are hold:
The lemma is proved.
Definition 2.1. Assume that







It is easy to see the number


Theorem 2.2. Let







Proof. Assume that

where


Let













We are going to find properties of the maps




1)






2)






3)







Preposition we have that











4)







Preposition we have that











5)






Therefore for every binary relation


Let



are such mappings, which satisfying the conditions:











Now we define a map



Now let


and satisfying the conditions:
From this and by Lemma 2.3 we have that
Therefore for every binary relation


By Theorem 1.1 the number of the mappings

(see ( [1] , Corollary 1.18.1), ( [2] , Corollary 1.18.1)).
The number of ordered system

(see ( [1] , Theorem 6.3.5), ( [2] , Theorem 6.3.5)).
The theorem is proved.
Corollary 2.1. Let




Proof: This corollary immediately follows from Theorem 2.2 and from the ( [1] , Theorem 6.3.7) or ( [2] , Theorem 6.3.7).
The corollary is proved.
Cite this paper
NinoTsinaridze,ShotaMakharadze, (2015) Regular Elements of the Complete Semigroups BX(D) of Binary Relations of the Class∑2(X,8). Applied Mathematics,06,447-455. doi: 10.4236/am.2015.63042
References
- 1. Diasamidze, Ya. and Makharadze, Sh. (2013) Complete Semigroups of Binary Relations. Monograph. Kriter, Turkey, 1-520.
- 2. Diasamidze, Ya. and Makharadze, Sh. (2010) Complete Semigroups of Binary Relations. Monograph. M., Sputnik+, 657 p. (In Russian)
- 3. Lyapin, E.S. (1960) Semigroups. Fizmatgiz, Moscow. (In Russian)
- 4. Diasamidze, Ya., Makharadze, Sh. and Rokva, N. (2008) On XI-Semilattices of Union. Bull. Georg. Nation. Acad. Sci., 2, 16-24.
- 5. Diasamidze, Ya.I. (2003) Complete Semigroups of Binary Relations. Journal of Mathematical Sciences, 117, 4271-4319.
- 6. Diasamidze, Ya., Makharadze, Sh. and Diasamidze, Il. (2008) Idempotents and Regular Elements of Complete Semigroups of Binary Relations. Journal of Mathematical Sciences, 153, 481-499.
- 7. Diasamidze, Ya. (2009) The Properties of Right Units of Semigroups Belonging to Some Classes of Complete Semigroups of Binary Relations. Proceedings of A. Razmadze Mathematical Institute, 150, 51-70.






























