Applied Mathematics
Vol.5 No.8(2014), Article ID:45235,9 pages DOI:10.4236/am.2014.58103
Positive Periodic Solution for a Two-Species Predator-Prey System
Meiyu Cao, Xiaoping Li*, Xiangjun Dai
Science College, Hunan Agricultural University, Changsha, China
Email: *lxpiii168@aliyun.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 March 2014; revised 1 April 2014; accepted 8 April 2014
ABSTRACT
A two-species predator-prey system with time delay in a two-patch environment is investigated. By using a continuation theorem based on coincidence degree theory, we obtain some sufficient conditions for the existence of periodic solution for the system.
Keywords:Predator-Prey System, Diffusion, Periodic Solution, Coincidence Degree

1. Introduction
Dynamical systems generated by predator-prey models have long been the topic of research interest of many biomathematical scholars, and there have been vast studies to investigate the dynamics of predator-prey models, see e.g., Refs. [1] -[12] and references therein. In 1975, Beddington [13] and DeAngelis [14] proposed the predator-prey system with the Beddington-DeAngelis functional response as follows.
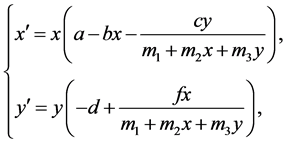 (1.1)
(1.1)
In the last years, some experts have studied the system [15] -[21] . Recently, Li and Takeuchi [22] proposed the following model with both Beddington-DeAngelis functional response and density dependent predator
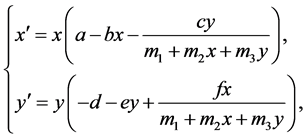 (1.2)
(1.2)
and discussed the dynamic behaviors of the model. In this paper, we consider the following nonautonomous two-species predator-prey system with diffusion and time delays.
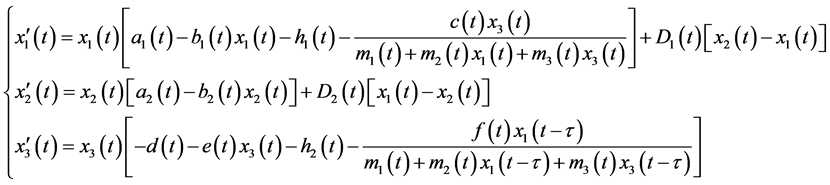 (1.3)
(1.3)
where 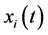 represents the prey population in the ith patch
represents the prey population in the ith patch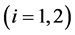 , and
, and  represents the predator population.
represents the predator population. 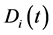 denotes the dispersal rate of the prey in the ith patch
denotes the dispersal rate of the prey in the ith patch . We always make the following fundamental assumptions for system (1.3):
. We always make the following fundamental assumptions for system (1.3):  is positive constant and
is positive constant and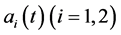 ,
, 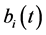 ,
,  ,
, 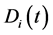 ,
, 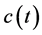 ,
, 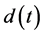 ,
, 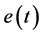 ,
,  ,
, 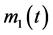 ,
, 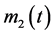 ,
, 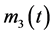 re positive continuous
re positive continuous  -periodic functions.
-periodic functions.
The main purpose of this paper is, by using the coincidence degree theory to derive the sufficient conditions for the existence of periodic solution of (1.3).
2. Preliminaries
The method to be used in this paper involves the applications of the continuation theorem of coincidence degree. we shall use some concepts and results from the book by Gaines and Mawhin [23] .
Let X, Z be real Banach spaces, 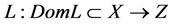 be a linear mapping, and
be a linear mapping, and 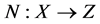 be a continuous mapping. The mapping L is called a Fredholm mapping of index zero if
be a continuous mapping. The mapping L is called a Fredholm mapping of index zero if
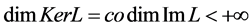
and 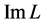 is closed in Z. If L is a Fredholm mapping of index zero and there exist continuous projectors
is closed in Z. If L is a Fredholm mapping of index zero and there exist continuous projectors 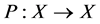 and
and 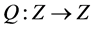 such that
such that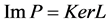 ,
, 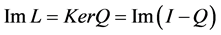 , then the restriction LP of L to
, then the restriction LP of L to  is invertible. Denote the inverse of LP by
is invertible. Denote the inverse of LP by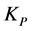 . If
. If  is an open bounded subset of X, the mapping N will be called L-compact on
is an open bounded subset of X, the mapping N will be called L-compact on 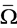 if
if 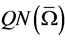 is bounded and
is bounded and 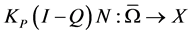 is compact. Since
is compact. Since 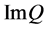 is isomorphic to
is isomorphic to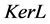 , there exists isomorphism
, there exists isomorphism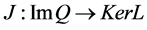 .
.
Lemma 2.1 (Continuation theorem [23] ) Let  be an open bounded set, L be a Fredholm mapping of index zero and N be L-compact on
be an open bounded set, L be a Fredholm mapping of index zero and N be L-compact on . Assume 1) for each
. Assume 1) for each 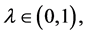
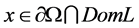 ,
, ;
;
2) for each 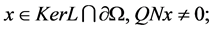
3) 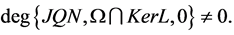
Then  has at least one solution in
has at least one solution in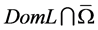 .
.
Throughout this paper, we adopt the notations ,
, 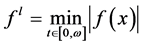 ,
, 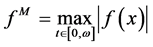 where
where 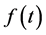 is an
is an  -periodic continuous function.
-periodic continuous function.
3. Main Result
Theorem 3.1 Assume that 1)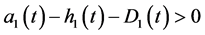 ;
;
2)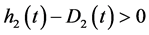 ;
;
3) ;
;
4)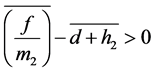 .
.
Then system (1.3) has at least one positive  -periodic solution.
-periodic solution.
Proof. Let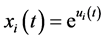 ,
,  ,
, 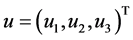 ,
, 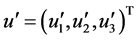 ,
, 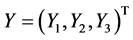 then (1.3) can be rewritten as follows:
then (1.3) can be rewritten as follows:
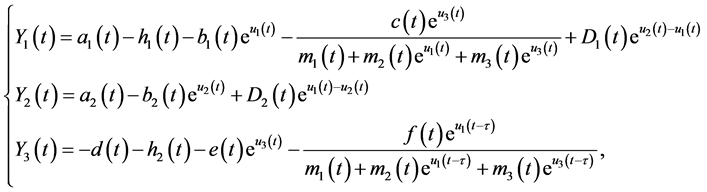 (3.1)
(3.1)
where all function are defined as ones in system (1.3). It is easy to know that if (3.1) has one  -periodic solution
-periodic solution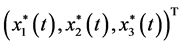 , then
, then 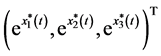 is a positive
is a positive 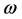 -periodic solution of system (1.3) Therefore, to complete the proof , it suffices to show that system (3.1) has one
-periodic solution of system (1.3) Therefore, to complete the proof , it suffices to show that system (3.1) has one  -periodic solution.
-periodic solution.
Take  and
and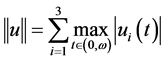 , then X and Z are Banach space with the norm
, then X and Z are Banach space with the norm .
.
Set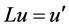 ,
,  ,
,  ,
,  ,
,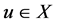 . Obviously,
. Obviously, 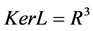 ,
,
 is closed in Z and
is closed in Z and . Therefore, L is a Fredholm mapping of index zero. Through an easy computation we find that the inverse
. Therefore, L is a Fredholm mapping of index zero. Through an easy computation we find that the inverse  of
of  has the form
has the form
 ,
,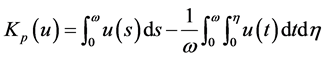 . Clearly, QN and
. Clearly, QN and  are continuous. By using Arzela-Ascoli theorem, it is not difficult to prove that
are continuous. By using Arzela-Ascoli theorem, it is not difficult to prove that 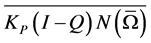 is compact for any open bounded set
is compact for any open bounded set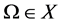 . Moreover,
. Moreover, 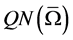 is bounded. Therefore, N is L-compact on
is bounded. Therefore, N is L-compact on  with any open bounded set
with any open bounded set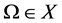 .
.
Corresponding to the operator equation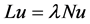 ,
,  , we have
, we have
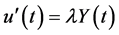 . (3.2)
. (3.2)
Suppose that 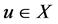 is a solution of (3.2) for an appropriate
is a solution of (3.2) for an appropriate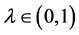 . Integrating (3.2) over the interval
. Integrating (3.2) over the interval 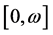 leads to
leads to
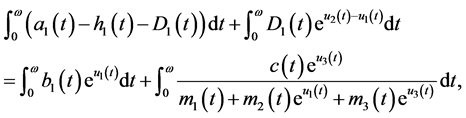 (3.3)
(3.3)
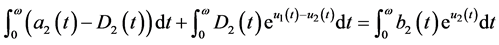 , (3.4)
, (3.4)
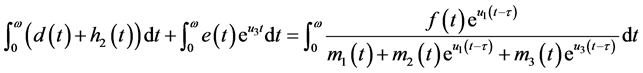 . (3.5)
. (3.5)
From (3.2)-(3.5), we have
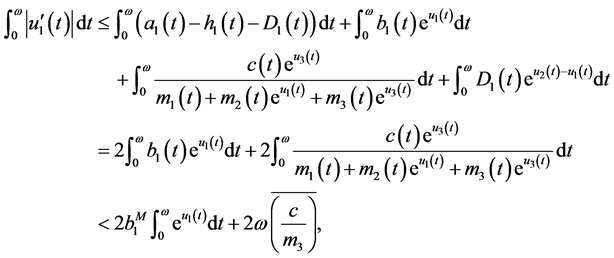 (3.6)
(3.6)
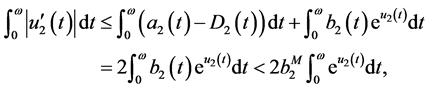 (3.7)
(3.7)
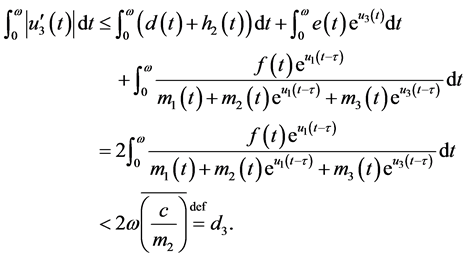 (3.8)
(3.8)
Multiplying the first equation of (3.2) by 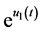 and integrating over
and integrating over 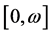 gives.
gives.
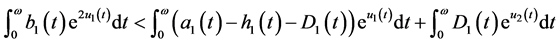 which implies
which implies
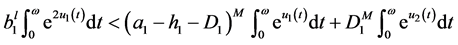 (3.9)
(3.9)
By using the inequalities
 .
.
It follows from (3.9) that
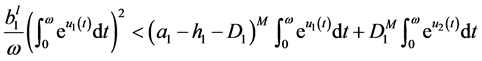 , (3.10)
, (3.10)
This yields
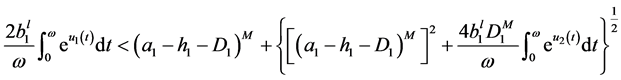 . (3.11)
. (3.11)
By using the inequalities
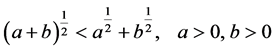 .
.
It follows from (3.10) that
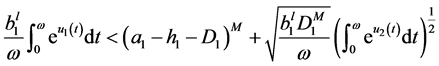 . (3.12)
. (3.12)
Multiplying the second equation of (3.2) by  and integrating over
and integrating over , similarly, we can obtain
, similarly, we can obtain
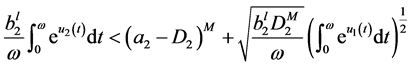 . (3.13)
. (3.13)
Substitute (3.13) to (3.12), which leads to
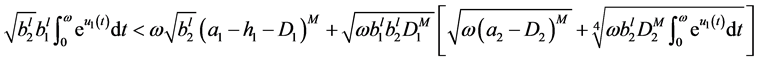
So, there exist a positive constant  such that
such that
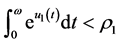 . (3.14)
. (3.14)
It follows from (3.13) and (3.14) that there exist a positive constant 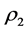 such that
such that
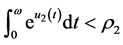 . (3.15)
. (3.15)
Substitute (3.14), (3.15) to (3.6) and (3.7), which leads to
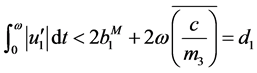 , (3.16)
, (3.16)
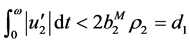 . (3.17)
. (3.17)
From (3.3) we have
 (3.18)
(3.18)
From (3.4) we have
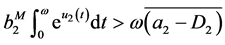 . (3.19)
. (3.19)
It follows from (3.14), (3.15), (3.18) and (3.19) that there exist  such that
such that
 , (3.20)
, (3.20)
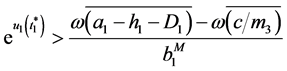 , (3.21)
, (3.21)
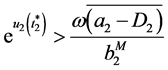 . (3.22)
. (3.22)
From (3.16), (3.17) and (3.20)-(3.22) we have
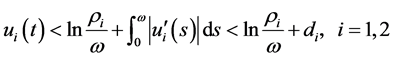 ,
,
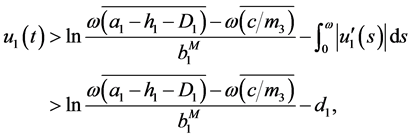
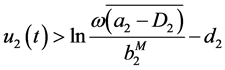 .
.
So, for 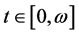 we have
we have
 , (3.23)
, (3.23)
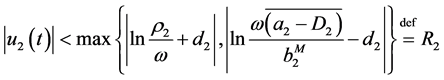 . (3.24)
. (3.24)
From (3.5) we have
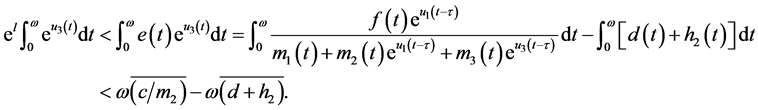
So, there exist 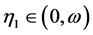 such that
such that
 . (3.25)
. (3.25)
From (3.5) we also have
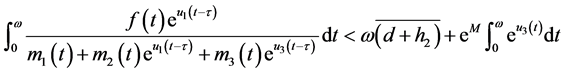 . (3.26)
. (3.26)
It follows from (3.26) that there exist  such that
such that
 .
.
So
 . (3.27)
. (3.27)
It follows from (3.8), (3.25) and (3.27) that for 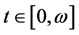 we have
we have
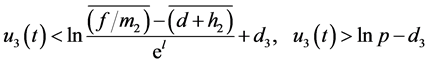 .
.
So 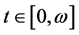 we have
we have
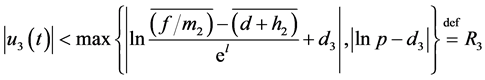 .
.
Clearly, 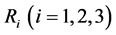 are independent of
are independent of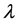 . On other hand, we consider the following algebraic equation
. On other hand, we consider the following algebraic equation
 (3.28)
(3.28)
Take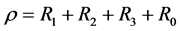 , where
, where 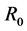 is large enough such that the solution
is large enough such that the solution 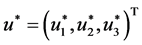 of (3.28) satisfies
of (3.28) satisfies
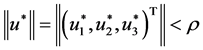 .
.
Let , then
, then  satisfies the condition (1) in Lemma 2.1. When
satisfies the condition (1) in Lemma 2.1. When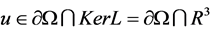 , u is a constant vector in R3 and
, u is a constant vector in R3 and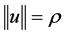 . It follows from the definition of
. It follows from the definition of 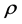 that
that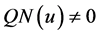 , so the condition (2) in Lemma 2.1 is satisfied. In order to verify the condition (3) in Lemma 2.1, we define
, so the condition (2) in Lemma 2.1 is satisfied. In order to verify the condition (3) in Lemma 2.1, we define 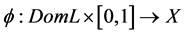 by
by
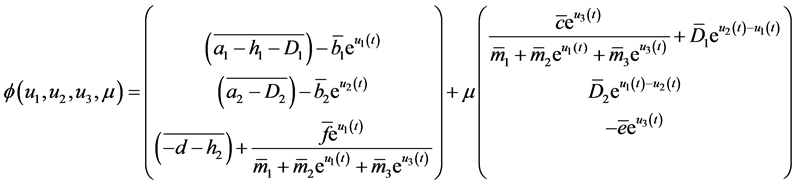 where
where 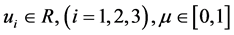 is a parameter. When
is a parameter. When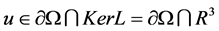 , u is a constant vector in
, u is a constant vector in 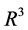 and
and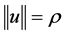 . It is easy to obtain that
. It is easy to obtain that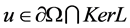 , then
, then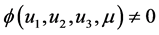 . So,
. So, 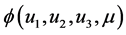 is a Homotopy mapping, due to homogoy invariance theorem of topology degree, we have
is a Homotopy mapping, due to homogoy invariance theorem of topology degree, we have
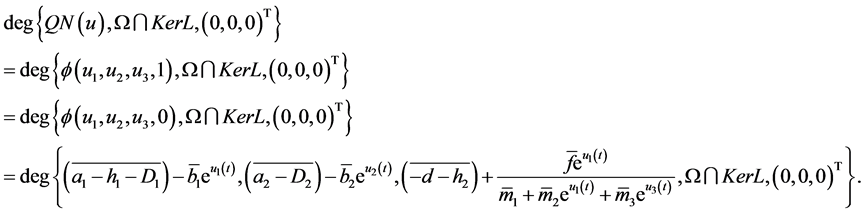
It is not difficult to see that the following algebraic equation
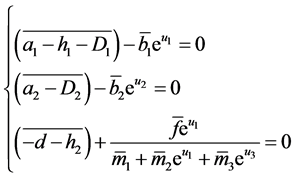
has a unique solution
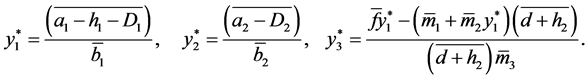
Thus

By now we have proved the condition (3) in Lemma 2.1. This completes the proof of Theorem 3.1.
References
- Freedman, H.I. (1980) Mathematical Models in Population Ecology. Marcel Dekker, New York.
- Sugie, J. (1998) Two-Parameter Bifurcation System of Ivlev Type. Journal of Mathematical Analysis and Applications, 217, 349-371. http://dx.doi.org/10.1006/jmaa.1997.5700
- Ardito, A. and Ricciardi, P. (1995) Lyapunov Functions for a Generalized Gause-Type Model. Journal of Mathematical Biology, 33, 816-828. http://dx.doi.org/10.1007/BF00187283
- Hassel, M.P. (1978) The Dynamics of Arthropod Predator-Prey Systems. Princeton University Press, Princeton.
- Hwang, T.W. (1999) Predator-Prey System. Journal of Mathematical Analysis and Applications, 238, 179-195. http://dx.doi.org/10.1006/jmaa.1999.6520
- Hsu, S.B., Hwang, T.W. and Kuang, Y. (2001) Global Analysis of the Michaelis-Menten Type Ratio-Dependent Predator-Prey. Journal of Mathematical Biology, 42, 489-506. http://dx.doi.org/10.1007/s002850100079
- Kot, M. (2001) Elements of Mathematical Biology. Cambridge University Press, Cambridge.
- Kuang, Y. and Freedman, H.I. (1988) Uniqueness of Limit Cycles in Gause-Type Predator-Prey Systems. Mathematical Biosciences, 88, 67-84. http://dx.doi.org/10.1016/0025-5564(88)90049-1
- Kooij, R.E. and Zegeling, A. (1996) A Predator-Prey Model with Ivlev’s Functional Response. Journal of Mathematical Analysis and Applications, 198, 473-489. http://dx.doi.org/10.1006/jmaa.1996.0093
- Liu, X.X. and Lou, Y.J. (2010) Global Dynamics of a Predator-Prey Model. Journal of Mathematical Analysis and Applications, 371, 323-340. http://dx.doi.org/10.1016/j.jmaa.2010.05.037
- Xiao, D.M., Li, W.X. and Han, M.A. (2006) Dynamics in Ratio-Dependent Predator-Prey Model with Predator Harvesting. Journal of Mathematical Analysis and Applications, 324, 14-29. http://dx.doi.org/10.1016/j.jmaa.2005.11.048
- Xiao, D. and Zhang, Z.D. (2003) On the Uniqueness and Nonexistence of Limit Cycles for Predator-Prey Systems. Nonlinearity, 16, 1185-1201. http://dx.doi.org/10.1088/0951-7715/16/3/321
- Beddington, J.R. (1975) Mutual Interference between Parasites or Predators and Its Effect on Searching Efficiency. Journal of Animal Ecology, 3, 331-340. http://dx.doi.org/10.2307/3866
- DeAngelis, D.L., Goldstein, R.A. and O’Neil, R.V. (1975) A Model for Trophic Interaction. Ecology, 4, 881-892. http://dx.doi.org/10.2307/1936298
- Cantrell, R.S. and Cosner, C. (2001) On the Dynamics of Predator-Prey Models with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 257, 206-222. http://dx.doi.org/10.1006/jmaa.2000.7343
- Chen, F., Chen, Y. and Shi, J. (2008) Stability of the Boundary Solution of a Nonautonomous Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 344, 1057- 1067. http://dx.doi.org/10.1016/j.jmaa.2008.03.050
- Cui, J. and Takeuchi, Y. (2006) Permanence, Extinction and Periodic Solution of Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 317, 464-474. http://dx.doi.org/10.1016/j.jmaa.2005.10.011
- Dimitrov, D.T. and Kojouharov, H.V. (2005) Complete Mathematical Analysis of Predator-Prey System with Linear Prey Growth and Beddington-DeAngelis Functional Response. Applied Mathematics and Computation, 162, 523-538. http://dx.doi.org/10.1016/j.amc.2003.12.106
- Fan, M. and Kuang, Y. (2004) Dynamics of a Nonautonomous Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 295, 15-39. http://dx.doi.org/10.1016/j.jmaa.2004.02.038
- Hwang, T.W. (2003) Global Analysis of the Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 281, 395-401. http://dx.doi.org/10.1016/S0022-247X(02)00395-5
- Liu, S. and Beretta, E. (2006) A Stage-Structured Predator-Prey Model of Beddington-DeAngelis Type. SIAM Journal on Applied Mathematics, 66, 1101-1129. http://dx.doi.org/10.1137/050630003
- Li, H.Y. and Takeuchi, Y. (2011) Dynamics of the Density Dependent Predator-Prey System with Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 374, 644-654. http://dx.doi.org/10.1016/j.jmaa.2010.08.029
NOTES

*Corresponding author.

