Applied Mathematics
Vol.5 No.15(2014), Article
ID:48486,10
pages
DOI:10.4236/am.2014.515211
Relationships among Three Multiplicities of a Differential Operator’s Eigenvalue
Shouzhong Fu, Zhong Wang*
School of Mathematics and Statistics, Zhaoqing University, Guangdong, China
Email: szfu@zqu.edu.cn, *kyczwang@zqu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 May 2014; revised 30 June 2014; accepted 14 July 2014
ABSTRACT
In this paper, the algebraic, geometric and analytic multiplicities of an eigenvalue for linear differential operators are defined and classified. The relationships among three multiplicities of an eigenvalue of the linear differential operator are given, and a fundamental fact that the algebraic, geometric and analytic multiplicities for any eigenvalue of self-adjoint differential operators are equal is proven.
Keywords:Differential Operators, Eigenvalue, Algebraic Multiplicities, Geometric Multiplicities, Analytic Multiplicities

1. Introduction
The study of spectral problems for linear ordinary differential equations (more generally, quasi-differential equations, to be abbreviated as QDE) originated from a series of seminal papers of Sturm and Liouville in [1] -[3] , while the singular case started with the celebrated work of Weyl in 1910 introducing the limit-point (LP) and limit-circle (LC) dichotomy [4] . Another important milestone in this area is the Glazman-Krein-Naimark (GKN) theorem [5] in 1950, see also [6] for generalizations (which will be included in the theorem). This theorem gives a one-to-one correspondence between the self-adjoint differential operators in a Hilbert function space representing a given QDE and the unitary isometries on an appropriate finite-dimensional subspace (or equivalently, certain Lagrange subspaces of some finite dimensional quotient space, see [7] ). In both regular case and singular case, the GKN theorem also yields a characterization of the self-adjoint operators in terms of linear complex boundary conditions (BC). So, the spectral problem of a linear ordinary differential equation (QDE) with boundary conditions maybe turn to study it of a linear ordinary differential operator [5] [8] [9] . It is well-known that the investigation of different self-adjoint extensions of symmetric operators and the estimation of the location and multiplicity of their point spectra are among fundamental mathematical problems arising in any quantum mechanical model ([10] , Chapter VIII, Section 11). While the eigenvalues of a linear ordinary differential operator were studied, three kinds of multiplicity (analytic multiplicity, geometric multiplicity and algebraic multiplicity) of an eigenvalue were defined and accompanied. Three kinds of multiplicity are often confused in some paper, and a problem how about the relationships among three kinds of multiplicity of an eigenvalue has arisen.
The differential equation
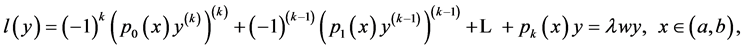 (1.1)
(1.1)
with boundary conditions
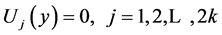 (1.2)
(1.2)
will be studied in present paper, where 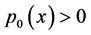 and
and 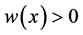 a.e. on
a.e. on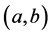 , the functions
, the functions 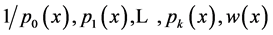 are real-valued, measurable over
are real-valued, measurable over 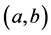 and Lebesgue integrable on all compact subset of
and Lebesgue integrable on all compact subset of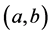 .
.
The endpoint ![]() is said to be regular if
is said to be regular if ![]() and each of the functions
and each of the functions  is integrable in every interval
is integrable in every interval ; otherwise
; otherwise ![]() is said to be singular. Similar definitions apply to endpoint
is said to be singular. Similar definitions apply to endpoint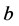 . The differential expression
. The differential expression  is said to be regular if it is regular at both endpoints, and otherwise is said to be singular.
is said to be regular if it is regular at both endpoints, and otherwise is said to be singular.
We assume throughout that (1.1) is regular, and the functions 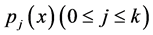 are sufficiently smooth and Lebesgue integrable on
are sufficiently smooth and Lebesgue integrable on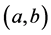 , then the boundary conditions may be written as
, then the boundary conditions may be written as :
:
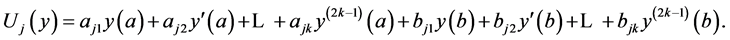
In the regular case, the GKN characterization of self-adjointness in terms of the complex boundary conditions can be simply expressed as the algebraic equation
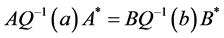 (1.3)
(1.3)
and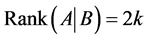 , where
, where 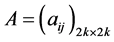 and
and 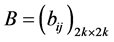 which come from the coefficient matrix
which come from the coefficient matrix
 of the boundary conditions are
of the boundary conditions are 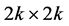 complex matrices, while
complex matrices, while 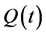 is a fixed matrix for Lagrange bilinear form
is a fixed matrix for Lagrange bilinear form 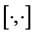 of differential expression
of differential expression 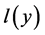 in (1.1).
in (1.1).
Let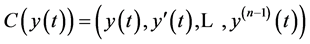 , and
, and 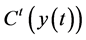 be the transpose of
be the transpose of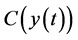 , then, for
, then, for
 (the domain of maximal operator generated by
(the domain of maximal operator generated by ),
),
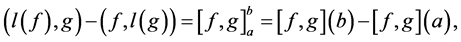
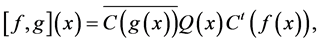
and following results are true (see [5] [6] [8] ):
1)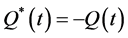 ;
;
2)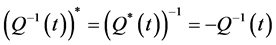 .
.
It is well-known that the spectrum of such a problem consists of an infinite number of real eigenvalues and has no finite accumulation point. The eigenvalues are precisely the zeros of an entire function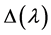 , called the characteristic function of the problem. The analytic multiplicity of an eigenvalue is the order of the eigenvalue as a zero of
, called the characteristic function of the problem. The analytic multiplicity of an eigenvalue is the order of the eigenvalue as a zero of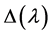 , the geometric multiplicity of an eigenvalue is the number of linearly independent eigenfunctions for the eigenvalue, and the algebraic multiplicity of an eigenvalue is the dimension of its root subspace (a subspace is spanned by the eigenvectors and its associated vectors).
, the geometric multiplicity of an eigenvalue is the number of linearly independent eigenfunctions for the eigenvalue, and the algebraic multiplicity of an eigenvalue is the dimension of its root subspace (a subspace is spanned by the eigenvectors and its associated vectors).
The analytic multiplicity of an eigenvalue gives the maximum number of new eigenvalues into which the original eigenvalue can split when the spectral problem involved. So, it is natural to use the analytic multiplicity to count eigenvalues, and the analytic multiplicity plays an important role in the study of the dependence of the eigenvalues of a spectral problem on the differential equation boundary value problem (see, for example, [5] [11] -[14] ). The geometric multiplicity is always defined and is more widely used in spectral theory (see [4] [5] [8] -[10] [15] ). However, the algebraic multiplicities and associated vectors (functions) of an eigenvector (eigenfunction) are used for the completeness of eigenvectors (eigenfunctions) of non self-adjoint operators (see [15] - [17] ). Therefore, it is of fundamental interest to compare the three multiplicities of an eigenvalue for differential operators.
Naimark studied the relationship between the algebraic and analytic multiplicities of an eigenvalue of highorder linear differential operators in [5] , and obtained the equivalence of the algebraic and analytic multiplicities of an eigenvalue of high-order linear differential Equation (1.1) with linear boundary conditions (1.2). From then, the relationships among the three multiplicities have been payed a good deal of attentions, and have had a strong appeal to studying.
Over the last decades, the fact that the analytic and geometric multiplicities of an eigenvalue of self-adjoint Sturm-Liouville problems are equal has been solved ([5] [11] -[14] [18] -[22] ). Sturm-Liouville problems (SLP) are differential equation:
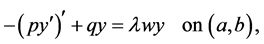 (1.4)
(1.4)
with boundary conditions
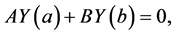 (1.5)
(1.5)
where  a.e. on
a.e. on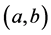 ,
, 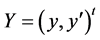 ,
,  and
and  are
are  matrices,
matrices,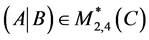 .
.
For the regular SLP, i.e. both endpoint ![]() and
and  are regular
are regular , the problem (1.4)-(1.5) is a self-adjiont SLP if the coefficients matrixes in (1.5) satisfy (1.3) and
, the problem (1.4)-(1.5) is a self-adjiont SLP if the coefficients matrixes in (1.5) satisfy (1.3) and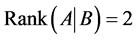 .
.
The equality of the analytic and geometric multiplicities in the case of separated boundary conditions (BC) was proved in [13] , while the case of coupled BC’s was settled in [18] . The equality of the two multiplicities in the case of singular self-adjoint SLP with LC non-oscillatory end points was shown in [19] using a regularization; the equality in the case of all singular self-adjoint SLP with LC end points was recently established in [21] , based on the equality of the regular self-adjoint SLP and certain regular approximations.
The proof in [18] uses some sophisticated identities involving 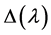 (the function
(the function 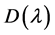 in [18] differs from
in [18] differs from  by a constant) and certain values of a fundamental set of solutions of (1.4). It seems to us that it is very hard to find similar identities for a higher order QDE by this way.
by a constant) and certain values of a fundamental set of solutions of (1.4). It seems to us that it is very hard to find similar identities for a higher order QDE by this way.
The basic idea of proof in [19] is as follows: for any eigenvalue 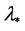 of geometric multiplicity 1, they can give a smooth curve in the space
of geometric multiplicity 1, they can give a smooth curve in the space 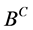 of self-adjoint BC through the BC
of self-adjoint BC through the BC 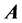 involved such that the composition of
involved such that the composition of 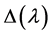 with a continuous eigenvalue branch through
with a continuous eigenvalue branch through 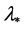 has a non-zero derivative along the curve at
has a non-zero derivative along the curve at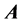 , which then implies that
, which then implies that 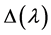 has a non-zero derivative at
has a non-zero derivative at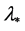 . Here, a continuous eigenvalue branch through
. Here, a continuous eigenvalue branch through 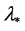 means a continuous function defined on a neighborhood O of A in
means a continuous function defined on a neighborhood O of A in  such that its value at A equals
such that its value at A equals  and its value at each BC
and its value at each BC  is an eigenvalue for
is an eigenvalue for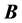 .
.
In [22] , we generalized the proof in [19] , and gave a new and unified proof of the equality between the analytic and geometric multiplicities of any eigenvalue of self-adjoint SLP in the regular case based on the geometric classifications of self-adjoint BC.
The classifications of self-adjoint BC about higher order differential operator are more complicated in geometric [7] , and it seems rather complicated to find similar identities for a higher order QDE by the same method in [22] . Recently, this result was generalized to the higher order differential equations with self-adjoint boundary conditions in [23] , but the proof was not easy.
In order to classify three multiplicities of an eigenvalue for linear differential operators, to obtain the relationships among three multiplicities, and to have a short and non-technical presentation so that the main idea of the general proof can be made transparent, we only give the general proof for regular self-adjoint QDE in this paper. For arbitrary self-adjoint nth-order QDE in singular end points with defect index n, the proof is basically the same (with only obvious minor changes), but the introduction of the self-adjoint BC and the definition of the characteristic function are more involved (see, for example, [7] or [24] ).
It is the main purpose, therefore, in the present work, to give the definitions of three kinds of multiplicities of an eigenvalue for linear differential operators and the relationships among them. In Section 2, we give the definitions of the geometric and algebraic multiplicities and the relationship between them. The definition of the analytic multiplicity for an eigenvalue of linear differential operators and the relationship between its analytic and algebraic multiplicities is given in Section 3. In last section, we have the equalities among three multiplicities of an eigenvalue for a self-adjoint linear differential operator.
2. Geometric and Algebraic Multiplicities
The definitions of the geometric and algebraic multiplicities for an eigenvalue of a linear operator are from [15] . Recall that a complex number 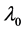 is called an eigenvalue of linear operator
is called an eigenvalue of linear operator ![]() if there exists a non-zero element
if there exists a non-zero element 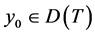 such that
such that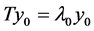 ; in this case,
; in this case, 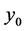 is called an eigenfunction of
is called an eigenfunction of ![]() for
for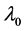 . The eigenfunctions for
. The eigenfunctions for  span a subspace of
span a subspace of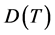 ,
, 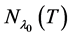 , called the eigenspace for
, called the eigenspace for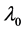 ; and the geometric multiplicity of
; and the geometric multiplicity of 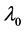 is the dimension of its eigenspace, denoted by
is the dimension of its eigenspace, denoted by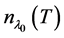 , i.e.
, i.e.

A non-zero element  is called a root vector of
is called a root vector of ![]() for a complex number
for a complex number 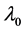 if
if 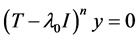 for some
for some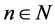 . In this case,
. In this case, 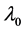 must be an eigenvalue. Together with the vector
must be an eigenvalue. Together with the vector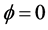 , the root vectors of
, the root vectors of 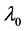 span a linear subspace of
span a linear subspace of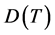 ,
, 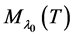 , called the root lineal for
, called the root lineal for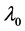 ; and the algebraic multiplicity of
; and the algebraic multiplicity of 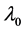 is the dimension of its root lineal, denoted by
is the dimension of its root lineal, denoted by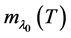 , i.e.
, i.e.
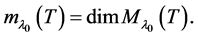
If an element 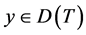 is not an eigenvector for
is not an eigenvector for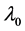 , then it is a root vector for
, then it is a root vector for  if and only if there is a
if and only if there is a 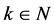 such that
such that 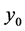 is an eigenvector for
is an eigenvector for  provided
provided 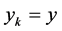 and
and  for
for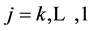 . A root vector is called an associated vector (or adjoint vector) if it is not an eigenvector. The theory of associated functions (vectors) of differential operator was originated by Keldysh [16] .
. A root vector is called an associated vector (or adjoint vector) if it is not an eigenvector. The theory of associated functions (vectors) of differential operator was originated by Keldysh [16] .
In general, the system of eigenvectors and associated vectors of ![]() is not complete in Hilbert space
is not complete in Hilbert space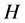 . From the definition of the algebraic multiplicities and geometric multiplicity of an eigenvalue of linear operator T in H, the eigenvectors of
. From the definition of the algebraic multiplicities and geometric multiplicity of an eigenvalue of linear operator T in H, the eigenvectors of 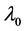 belong to root lineal of
belong to root lineal of 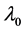 (i.e.
(i.e. 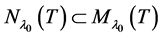 ), so, we have the following result:
), so, we have the following result:
Theorem 2.1. The geometric multiplicity of any eigenvalue of linear operator ![]() in Hilbert space does not exceed its algebraic multiplicity. i.e.
in Hilbert space does not exceed its algebraic multiplicity. i.e.
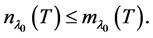 (2.1)
(2.1)
In general, the algebraic multiplicity is grater than the geometric multiplicity of an eigenvalue of operators. For example.
Example 2.2. We consider an operator  in
in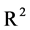 ,
,
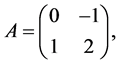 (2.2)
(2.2)
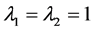 are eigenvalues of operator
are eigenvalues of operator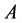 ,
, 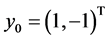 is an eigenvector for the eigenvalue
is an eigenvector for the eigenvalue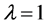 , and the eigenspace
, and the eigenspace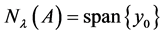 . So, the geometric multiplicity of the eigenvalue
. So, the geometric multiplicity of the eigenvalue 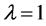 is equal to 1, i.e.
is equal to 1, i.e.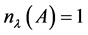 . But,
. But, 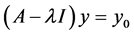 have solutions
have solutions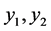 , where
, where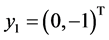 ,
, 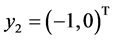 , the associated vector of
, the associated vector of 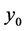 is
is 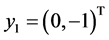 or
or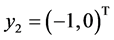 , and the root lineal
, and the root lineal 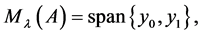 or
or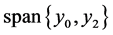 . Thus, the algebraic multiplicity of eigenvalue
. Thus, the algebraic multiplicity of eigenvalue 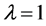 is equal to 2, i.e.
is equal to 2, i.e.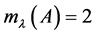 .
.
Example 2.3. We consider the differential equation
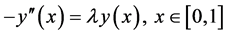 (2.3)
(2.3)
with boundary conditions
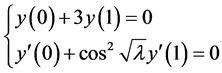 (2.4)
(2.4)
in Hilbert space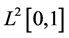 . After simple calculation,
. After simple calculation, 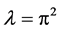 is an eigenvalue of boundary problem (1.3)-(1.4),
is an eigenvalue of boundary problem (1.3)-(1.4), 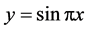 is corresponding eigenvector, and the eigenspace of
is corresponding eigenvector, and the eigenspace of 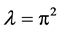 is
is . So, the geometric multiplicity of eigenvalue
. So, the geometric multiplicity of eigenvalue 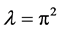 is equal to 1, i.e.
is equal to 1, i.e. . But,
. But, 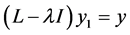 have solutions
have solutions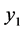 , where
, where
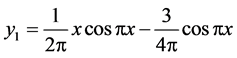 , but
, but 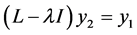 has not any solutions, the associated vector of
has not any solutions, the associated vector of ![]() is
is 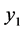 and the root lineal
and the root lineal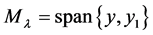 . Thus, the algebraic multiplicity of eigenvalue
. Thus, the algebraic multiplicity of eigenvalue  is equal to 2, i.e.
is equal to 2, i.e.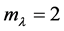 .
.
If ![]() is a spacial operator in Hilbert space
is a spacial operator in Hilbert space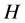 , then the geometric multiplicity of any eigenvalues of linear operator
, then the geometric multiplicity of any eigenvalues of linear operator ![]() maybe equal to its algebraic multiplicity, such as:
maybe equal to its algebraic multiplicity, such as:
Theorem 2.4. If ![]() is a self-adjoint operator in Hilbert space
is a self-adjoint operator in Hilbert space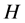 , then the geometric multiplicity of any eigenvalues of linear operator
, then the geometric multiplicity of any eigenvalues of linear operator ![]() is equal to its algebraic multiplicity.
is equal to its algebraic multiplicity.
Proof: We only need to prove that the eigenspace for an eigenvalue ![]() of operator
of operator ![]() is equal to the root lineal of
is equal to the root lineal of![]() .
.
From the definitions of eigenspace and root lineal of the eigenvalue![]() , we have
, we have
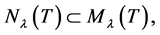
where 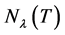 and
and 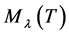 represent the eigenspace and the root lineal of
represent the eigenspace and the root lineal of![]() ,
, ![]() is an (isolated) eigenvalue of
is an (isolated) eigenvalue of![]() , i.e.
, i.e.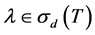 .
.
If 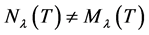
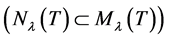 , then there exist a associated function
, then there exist a associated function 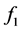 (
(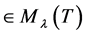 ,
, ) and an eigenfunction
) and an eigenfunction 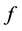 (
( ,
, ), such that
), such that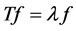 , and
, and .
.
From the last equation, we have
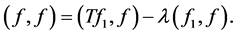 (2.5)
(2.5)
By self-adjointness of operator![]() , the eigenvalue
, the eigenvalue ![]() is a real number, and
is a real number, and 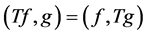 for any
for any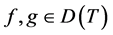 . Then,
. Then,
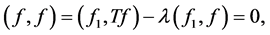 (2.6)
(2.6)
and there is a contradictory to the fact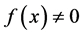 . Therefore,
. Therefore,
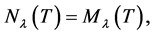 (2.7)
(2.7)
and the proof is complete. □
3. Analytic and Algebraic Multiplicities
We also introduce some notations here and review some basic facts about the problem of differential Equation (1.1) with boundary conditions (1.2). Let  be the fundamental solution of (1.1) satisfying
be the fundamental solution of (1.1) satisfying
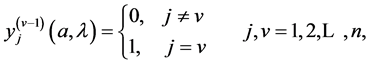 (3.1)
(3.1)
and 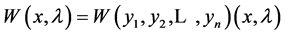 denote the Wronskian of (1.1) with respect to
denote the Wronskian of (1.1) with respect to 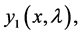
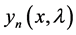
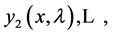 , then
, then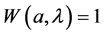 . The determinant of matrix
. The determinant of matrix  is denoted by
is denoted by , i.e.
, i.e.
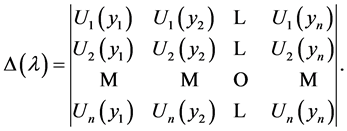 (3.2)
(3.2)
Theorem 3.1. The 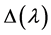 is an entire function of
is an entire function of![]() , and a complex number
, and a complex number ![]() is an eigenvalue of the boundary value problem consisting of (1.1) and (1.2) if and only if
is an eigenvalue of the boundary value problem consisting of (1.1) and (1.2) if and only if
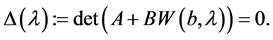 (3.3)
(3.3)
Proof: Simply calculate or see [8] and [5] .
The entire function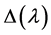 , unique up to a non-zero constant multiple, is called the characteristic function for the boundary value problem consisting of (1.1) and (1.2). The analytic multiplicity of an isolated eigenvalue is the order of the eigenvalue as a zero of
, unique up to a non-zero constant multiple, is called the characteristic function for the boundary value problem consisting of (1.1) and (1.2). The analytic multiplicity of an isolated eigenvalue is the order of the eigenvalue as a zero of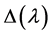 , denoted by
, denoted by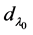 .
.
From the definition of analytic multiplicity, only the eigenvalues of boundary value problems have analytic multiplicity. In general, the analytic multiplicity isn’t equal to the other multiplicities for an eigenvalue of some boundary value problems.
Example 3.2. We still study the boundary value problem (2.3)-(2.4) in Example 2.3. The characteristic function 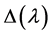 for the boundary value problem (2.3) and (2.4) can be easily obtained after calculating.
for the boundary value problem (2.3) and (2.4) can be easily obtained after calculating.
 (3.4)
(3.4)
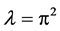 is a 3-order zero of the
is a 3-order zero of the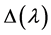 , so, the analytic multiplicity of the eigenvalue
, so, the analytic multiplicity of the eigenvalue 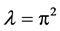 is 3.
is 3.
With the results in Example 2.3, we have proven that the geometric multiplicity, algebraic multiplicity and analytic multiplicity of the eigenvalue 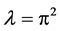 of boundary value problem (1.3)-(1.4) are 1, 2 and 3, and
of boundary value problem (1.3)-(1.4) are 1, 2 and 3, and 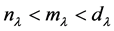 for the eigenvalue
for the eigenvalue 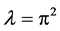 of boundary value problem (1.3)-(1.4).
of boundary value problem (1.3)-(1.4).
But the linear differential Equation (1.1) with linear boundary conditions (1.2), Naimark had the following theorem in [5] (Chapter: ).
).
Theorem 3.3. The analytic multiplicity of any eigenvalues of the boundary value problem consisting of (1.1) and (1.2) is equal to its algebraic multiplicity. i.e.
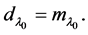 (3.5)
(3.5)
The algebraic multiplicity of an eigenvalue of self-adjoint SLP factually is the analytic multiplicity in [11] - [14] , because the authors realized that the equivalence of the algebraic and analytic multiplicities for any eigenvalues of self-adjoint SLP is a foundational fact.
4. Equalities among Three Multiplicities of an Eigenvalue of Self-Adjoint Differential Operators
In this section, we first collect some basic statements about higher order differential operator (especially, the self-adjoint differential operator with high-order), and then prove the equalities among analytic, algebraic and geometric multiplicities.
For any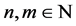 , we use
, we use 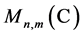 to denote the vector space of
to denote the vector space of ![]() matrices with complex entries and
matrices with complex entries and 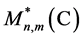 its open subset consisting of the elements with the maximum rank
its open subset consisting of the elements with the maximum rank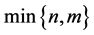 .
. 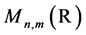 and
and 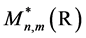 are defined similarly. When a capital Latin or Greek letter stands for a matrix, the entries of the matrix will be denoted by the corresponding lower case letter with two indices. If
are defined similarly. When a capital Latin or Greek letter stands for a matrix, the entries of the matrix will be denoted by the corresponding lower case letter with two indices. If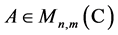 , then
, then 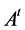 and
and 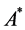 are the transpose and the complex conjugate transpose of
are the transpose and the complex conjugate transpose of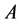 , respectively. The general linear group
, respectively. The general linear group 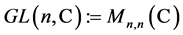 is a complex Lie group under the matrix multiplication, while the special linear group
is a complex Lie group under the matrix multiplication, while the special linear group 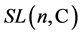 consists of all elements of
consists of all elements of 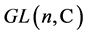 with determinant 1 and is a Lie subgroup of
with determinant 1 and is a Lie subgroup of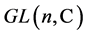 .
. 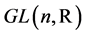 and
and 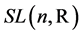 are defined similarly. Let
are defined similarly. Let ![]() be an open interval, bounded or unbounded. Assume that
be an open interval, bounded or unbounded. Assume that ![]() is one of the spaces
is one of the spaces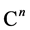 ,
, 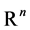 ,
, 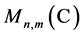 and
and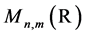 . We denote by
. We denote by 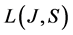 the space of Lebesgue integrable S-valued functions on
the space of Lebesgue integrable S-valued functions on![]() , and
, and 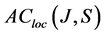 the space of S-valued functions which are absolutely continuous on all compact subintervals of
the space of S-valued functions which are absolutely continuous on all compact subintervals of![]() .
.
For the rest of this paper, we use 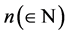 to denote a fixed number satisfying
to denote a fixed number satisfying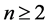 , and
, and 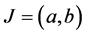 with
with
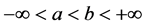 . When
. When ![]() is even
is even 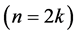 and
and ![]() is finite interval, there is a special case of the QDE (1.1). This special case was studied by Naimark [5] and Weidman [9] .
is finite interval, there is a special case of the QDE (1.1). This special case was studied by Naimark [5] and Weidman [9] .
For any 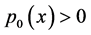 and
and  a.e. on
a.e. on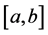 ,
, 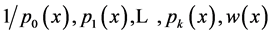 are integrable over
are integrable over
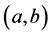 , and
, and  are
are 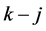
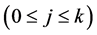 times continuous differentiable function on
times continuous differentiable function on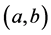 ,
,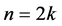 . We define
. We define
 (4.1)
(4.1)
then 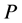 also belongs to
also belongs to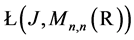 . Let
. Let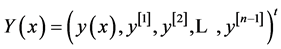 , the quasi-derivatives of
, the quasi-derivatives of ![]() associated with
associated with  are given by
are given by
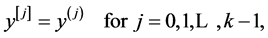

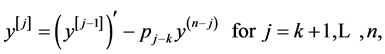
and
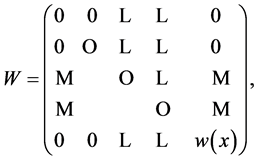
then, ordinary differential Equation (1.1) is equivalent quasi differential equation (QDE)
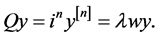 (4.2)
(4.2)
Thus,  and
and 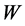 can be used as the coefficient matrix of (4.2), (4.2) is equivalent to its matrix form
can be used as the coefficient matrix of (4.2), (4.2) is equivalent to its matrix form
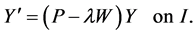 (4.3)
(4.3)
The quasi-differential expression in ![]() associated with
associated with 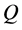 for
for 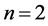 or
or 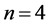 or
or 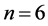 are of special interest:
are of special interest:
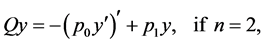
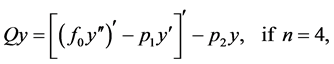
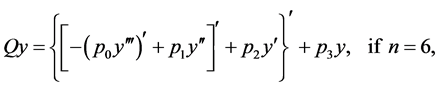
while, in general,  is equal to
is equal to
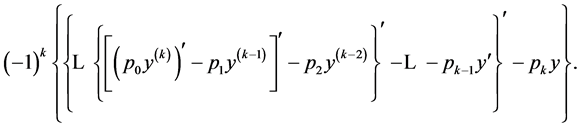
We now turn to the BVP consisting of the general QDE (1.2) and a (linear two-point) BC defined by
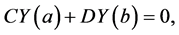 (4.4)
(4.4)
where 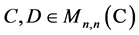 such that
such that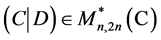 . Note that equivalent linear algebraic equations of the form (1.2) define the same BC. Each value of
. Note that equivalent linear algebraic equations of the form (1.2) define the same BC. Each value of ![]() for which the QDE (4.2) has a nontrivial solution satisfying the BC (1.4) is called an eigenvalue of the BVP consisting of (4.2) and (4.4), and a solution to this problem is called an eigenfunction for this eigenvalue.
for which the QDE (4.2) has a nontrivial solution satisfying the BC (1.4) is called an eigenvalue of the BVP consisting of (4.2) and (4.4), and a solution to this problem is called an eigenfunction for this eigenvalue.
Since (4.2) has exactly ![]() linearly independent solutions, the geometric multiplicity of any eigenvalue is an integer not smaller than 1 and not greater than
linearly independent solutions, the geometric multiplicity of any eigenvalue is an integer not smaller than 1 and not greater than![]() .
.
Theorem 4.1. A number 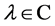 is an eigenvalue of the boundary value problem consisting of (4.2) and (4.4) if and only if
is an eigenvalue of the boundary value problem consisting of (4.2) and (4.4) if and only if
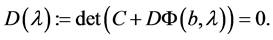 (4.5)
(4.5)
where 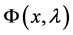 is the fundamental solution of (1.3) satisfying
is the fundamental solution of (1.3) satisfying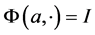 ,
, 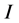 is the identity matrix.
is the identity matrix.
Proof: Simply calculate or see [7] . □
Theorem 4.2. 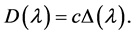
Proof: From the definition of quasi-derives of ![]() associated with
associated with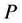 , we have
, we have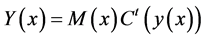 , where
, where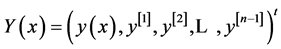 ,
, 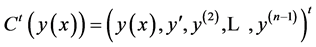 , and
, and
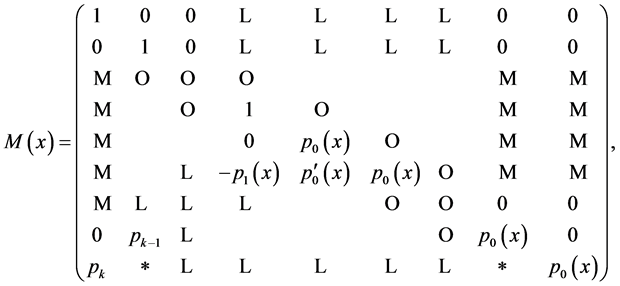 (4.6)
(4.6)
is a inverse matrix function on  because of
because of 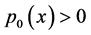 over
over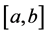 . Let
. Let 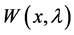 denote the Wronskian of (1.1) with respect to
denote the Wronskian of (1.1) with respect to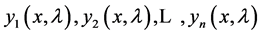 ,
, 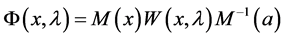 , then
, then 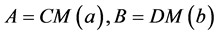 , and
, and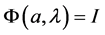 . Thus,
. Thus, 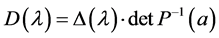 and
and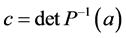 . So, the equality in this theorem was proved.
. So, the equality in this theorem was proved.
A coefficient matrix 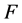 is said to be symmetric if
is said to be symmetric if
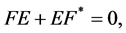 (4.7)
(4.7)
where
 (4.8)
(4.8)
The boundary condition (1.4) is said to be self-adjoint if  and
and
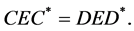 (4.9)
(4.9)
Theorem 4.3. The differential operator ![]() associated with (1.1) and (1.2) (or (4.2) and (4.4)) is a self-adjoint operator if the boundary conditions (1.2) (or (4.4)) satisfy (1.3) and
associated with (1.1) and (1.2) (or (4.2) and (4.4)) is a self-adjoint operator if the boundary conditions (1.2) (or (4.4)) satisfy (1.3) and 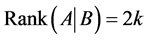 (or is self-adjoint).
(or is self-adjoint).
Proof: See [7] . □
Theorem 4.4. The analytic, algebraic and geometric multiplicity of any eigenvalue for a self-adjoint differential operator associated with (1.1) and (1.2) (or (4.2) and (4.4)) are equal.
Proof: From Theorem 2.4 and Theorem 3.3, we get the conclusion immediately. □
Corollary 4.5. The analytic, algebraic and geometric multiplicity of any eigenvalue of the differential operator L associated with (1.1) and (1.2) (or (4.2) and (4.4)) are equality when the coefficient matrixes A and B satisfy (1.3) (or  and
and  satisfy (4.9)), and equal to the multiplicities of the eigenvalue as a zero point of
satisfy (4.9)), and equal to the multiplicities of the eigenvalue as a zero point of  in (3.3) (or
in (3.3) (or  in (4.5)).
in (4.5)).
Example 4.6. We consider the differential equation
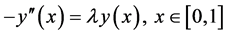 (4.10)
(4.10)
with boundary conditions
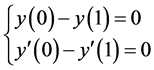 (4.11)
(4.11)
in Hilbert space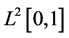 . After simple calculation,
. After simple calculation, 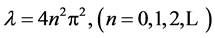 are eigenvalues of boundary problem (4.10)-(4.11),
are eigenvalues of boundary problem (4.10)-(4.11),  and
and 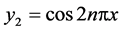 are corresponding eigenvectors for
are corresponding eigenvectors for , and the eigenspace of
, and the eigenspace of 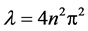 is
is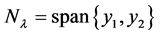 . So, the geometric multiplicity of eigenvalue
. So, the geometric multiplicity of eigenvalue 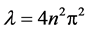 is equal to 2, i.e.
is equal to 2, i.e.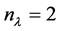 . Boundary problem (4.10)-(4.11) is a self-adjoint problem because of boundary conditions (4.11) satisfying (4.9), so, the algebraic multiplicity of eigenvalue
. Boundary problem (4.10)-(4.11) is a self-adjoint problem because of boundary conditions (4.11) satisfying (4.9), so, the algebraic multiplicity of eigenvalue 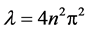 is also equal to 2, i.e.
is also equal to 2, i.e.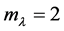 . We also have that
. We also have that
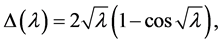 (4.12)
(4.12)
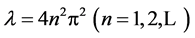 are 2-order zero of the
are 2-order zero of the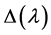 , so, the analytic multiplicity of the eigenvalue
, so, the analytic multiplicity of the eigenvalue 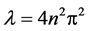 is 2, i.e.
is 2, i.e.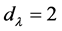 . Thus, the analytic, algebraic and geometric multiplicity of any eigenvalue
. Thus, the analytic, algebraic and geometric multiplicity of any eigenvalue 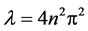 for boundary problem (4.10)-(4.11) are equal to 2, i.e.
for boundary problem (4.10)-(4.11) are equal to 2, i.e.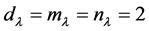 .
.
Funding
Work partially supported by the National Nature Science Foundation (11171295).
References
- Liouville, J. and Sturm, J.C.F. (1837) Extrait d’une méemoire sur le développement des fonctions en serie. Journal de Mathématiques Pures et Appliquées, 2, 220-223.
- Sturm, J.C.F. (1836) Mémoire sur les équations différentielles linéaires du second ordre. Journal de Mathématiques Pures et Appliquées, 1, 106-186.
- Sturm, J.C.F. (1837) Mémoire sur une classe d’équations différentielles partielles. Journal de Mathématiques Pures et Appliquées, 2, 373-444.
- Weyl, H. (1910) üeber gewöhnliche differentialgleichungen mit singularitäten und die zugehörigen entwichlungen willkürlicher funktionen. Mathematische Annalen, 68, 220-269. http://dx.doi.org/10.1007/BF01474161
- Naimark, M.A. (1968) Linear Differential Operators. Ungar, New York.
- Everitt, W.N. and Markus, L. (1997) The Glazman-Krein-Naimark Theorem for Ordinary Differential Operators, New Results in Operator Theory and Its Applications. Operator Theory: Advances and Applications, 98, 118-130.
- Cao, X. and Wu, H. (2004) Geomtric Aspects of High-Order Eigenvalue Problems I. Structures on Spaces of Boundary Conditions. International Journal of Mathematics and Mathematical Sciences, 13, 647-678.http://dx.doi.org/10.1155/S0161171204303522
- Coddington, E. and Levinson, N. (1955) Theory of Ordinary Differential Equations. McGraw-Hill, New York.
- Weidmann, J. (1987) Spectral Theory of Ordinary Differential Operator, Lecture Notes in Mathematics, Vl 1258. Springer-Verlag, Berlin.
- Reed, M. and Simon, B. (1972) Methods of Modern Mathematical Physics I. Functional Analysis. Academic Press, Waltham.
- Kong, Q., Wu, H. and Zettl, A. (1997) Dependence of Eigenvalues on the Problem. Mathematische Nachrichten, 188, 173-201. http://dx.doi.org/10.1002/mana.19971880111
- Kong, Q., Wu, H. and Zettl, A. (1999) Dependence of the n-th Sturm-Liouville Eigenvalue on the Problem. Journal of Differential Equations, 156, 328-354. http://dx.doi.org/10.1006/jdeq.1998.3613
- Kong, Q., Wu, H. and Zettl, A. (2000) Geometric Aspects of Sturm-Liouville Problems, I. Structures on Spaces of Boundary Conditions. Proceedings of the Royal Society of Edinburgh Section A, 130, 561-589.
- Zettl, A. (2005) Sturm-Liouville Theory. Mathematical Surveys and Monographs, Volume 121. American Mathematical Society.
- Gohberg, I.C. and Krein, M.G. (1969) Introduction to the Theory of Linear Non-Self-Adjoint Operator. Translation of Mathematical Monographs 18, American Mathematical Society, Providence.
- Keldysh, M.V. (1951) On Eigenvalues and Eigenfunctions of Some Classes of Non Self-Adjoint Equations. Doklady Akademii Nauk SSSR, 77, 11-14.
- Marcenko, V.A. (1963) Expansion in Eigenfuctions of Non-Self-Adjoint Singular Differential Operators of Second Order. American Mathematical Society Translations, 25, 77-130.
- Eastham, M., Kong, Q., Wu, H. and Zettl, A. (1999) Inequalities among Eigenvalues of Sturm-Liouville Problems. Journal of Inequalities and Applications, 3, 25-43.
- Kong, Q., Wu, H. and Zettl, A. (1999) Inequalities among Eigenvalues of Singular Sturm-Liouville Problems. Dynamic Systems and Applications, 8, 517-531.
- Kong, Q., Wu, H. and Zettl, A. (2001) Sturm-Liouville Problems with Finite Spectrum. Journal of Mathematical Analysis and Applications, 263, 748-762. http://dx.doi.org/10.1006/jmaa.2001.7661
- Kong, Q., Wu, H. and Zettl, A. (2004) Multiplicity of Sturm-Liouville Eigenvalues. Journal of Computational and Applied Mathematics, 171, 291-309. http://dx.doi.org/10.1016/j.cam.2004.01.036
- Wang, Z. and Wu, H. (2005) Equality of Multiplicities of a Sturm-Liouville Eigenvalue. Journal of Mathematical Analysis and Applications, 306, 540-547. http://dx.doi.org/10.1016/j.jmaa.2004.10.041
- Shi, D. and Huang, Z. (2010) Relationship of Multiplicities of a High-Order Ordinary Differential Operator Eigenvalue. Acta Mathematica Sinica, Chinese Series, 53, 763-772.
- Wang, Z. and Wu, H. (2009) Sturm-Liouville Problems with Limit-Circle End Points. Pacific Journal of Applied Mathematics, 1, 421-447.
NOTES

*Corresponding author.

