Applied Mathematics
Vol.5 No.7(2014), Article ID:44795,6 pages DOI:10.4236/am.2014.57098
Coefficient Estimates for a Certain General Subclass of Analytic and Bi-Univalent Functions
Nanjundan Magesh1, Jagadeesan Yamini2
1Post-Graduate and Research Department of Mathematics, Government Arts College for Men, Krishnagiri, India
2Department of Mathematics, Govt First Grade College, Bangalore, India
Email: nmagi_2000@yahoo.co.in, yaminibalaji@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 January 2014; revised 13 February 2014; accepted 20 February 2014
Abstract
Motivated and stimulated especially by the work of Xu et al. [1] , in this paper, we introduce and discuss an interesting subclass 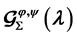 of analytic and bi-univalent functions defined in the open unit disc
of analytic and bi-univalent functions defined in the open unit disc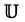 . Further, we find estimates on the coefficients
. Further, we find estimates on the coefficients 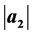 and
and 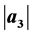 for functions in this subclass. Many relevant connections with known or new results are pointed out.
for functions in this subclass. Many relevant connections with known or new results are pointed out.
Keywords:Analytic Functions, Univalent Functions, Bi-Univalent Functions, Bi-Starlike Functions

1. Introduction
Let 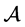 denote the class of functions of the form
denote the class of functions of the form
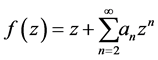 (1.1)
(1.1)
which are analytic in the open unit disc 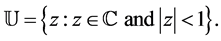 Further, by
Further, by  we shall denote the class of all functions in
we shall denote the class of all functions in 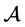 which are univalent in
which are univalent in  Some of the important and well-investigated subclasses of the univalent function class
Some of the important and well-investigated subclasses of the univalent function class 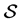 include (for example) the class
include (for example) the class 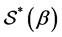 of starlike functions of order
of starlike functions of order 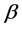
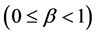 in
in 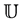 and the class
and the class 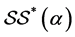 of strongly starlike functions of order
of strongly starlike functions of order 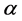
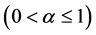 in
in 
It is well known that every function 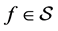 has an inverse
has an inverse 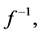 defined by
defined by
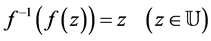
and
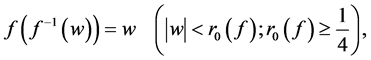
where
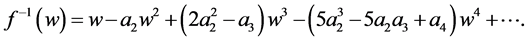 (1.2)
(1.2)
A function 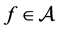 is said to be bi-univalent in
is said to be bi-univalent in 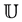 if both
if both 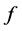 and
and 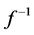 are univalent in
are univalent in 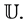 We denote by
We denote by 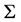 the class of all bi-univalent functions in
the class of all bi-univalent functions in 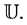 For a brief history and interesting examples of functions in the class
For a brief history and interesting examples of functions in the class 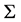 see [2] and the references therein.
see [2] and the references therein.
In fact, the study of the coefficient problems involving bi-univalent functions was revived recently by Srivastava et al. [2] . Various subclasses of the bi-univalent function class 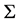 were introduced and non-sharp estimates on the first two Taylor-Maclaurin coefficients
were introduced and non-sharp estimates on the first two Taylor-Maclaurin coefficients 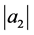 and
and 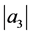 of functions in these subclasses were found in several recent investigations (see, for example, [3] -[13] ). The aforecited all these papers on the subject were motivated by the pioneering work of Srivastava et al. [2] . But the coefficient problem for each of the following Taylor-Maclaurin coefficients
of functions in these subclasses were found in several recent investigations (see, for example, [3] -[13] ). The aforecited all these papers on the subject were motivated by the pioneering work of Srivastava et al. [2] . But the coefficient problem for each of the following Taylor-Maclaurin coefficients 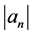 (
(
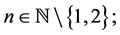 ) is still an open problem.
) is still an open problem.
Motivated by the aforecited works (especially [1] ), we introduce the following subclass 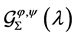 of the analytic function class
of the analytic function class 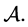
Definition 1 Let 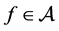 and the functions
and the functions 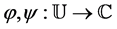 be so constrained that
be so constrained that

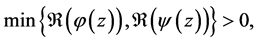 and
and  We say that
We say that 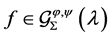 if the following conditions are satisfied:
if the following conditions are satisfied: 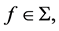
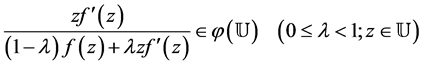 (1.3)
(1.3)
and
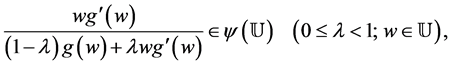 (1.4)
(1.4)
where the function 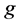 is the extension of
is the extension of 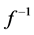 to
to 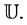
We note that, for the different choices of the functions 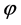 and
and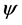 , we get interesting known and new subclasses of the analytic function class
, we get interesting known and new subclasses of the analytic function class 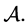 For example, if we set
For example, if we set
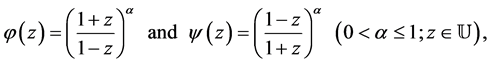
in the class 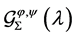 then we have
then we have 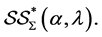 Also,
Also, 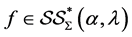 if the following conditions are satisfied:
if the following conditions are satisfied:
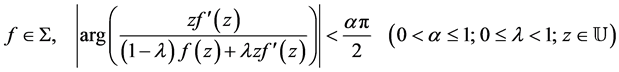
and
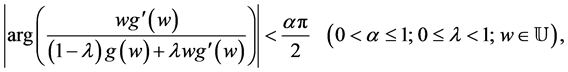
where 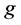 is the extension of
is the extension of 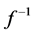 to
to 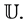
Similarly, if we let
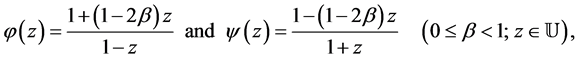
in the class 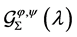 then we get
then we get  Further, we say that
Further, we say that 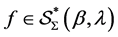 if the following conditions are satisfied:
if the following conditions are satisfied:
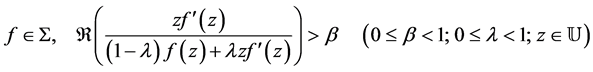
and
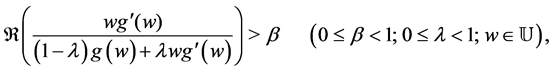
where 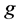 is the extension of
is the extension of 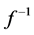 to
to 
The classes 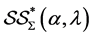 and
and 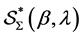 were introduced and studied by Murugusundaramoorthy et al. [12] , Definition 1.1 and Definition 1.2]. The classes
were introduced and studied by Murugusundaramoorthy et al. [12] , Definition 1.1 and Definition 1.2]. The classes 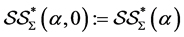 and
and 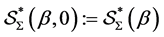 are strongly bi-starlike functions of order
are strongly bi-starlike functions of order 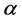 and bi-starlike functions of order
and bi-starlike functions of order 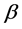 respectively. The classes
respectively. The classes 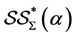 and
and 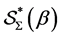 were introduced and studied by Brannan and Taha [14] , Definition 1.1 and Definition 1.2]. In addition, we note that,
were introduced and studied by Brannan and Taha [14] , Definition 1.1 and Definition 1.2]. In addition, we note that, 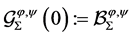 was introduced and studied by Bulut [4] , Definition 3].
was introduced and studied by Bulut [4] , Definition 3].
Motivated and stimulated by Bulut [4] and Xu et al. [1] (also [10] ), in this paper, we introduce a new subclass 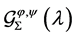 and obtain the estimates on the coefficients
and obtain the estimates on the coefficients 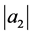 and
and 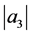 for functions in aforementioned class, employing the techniques used earlier by Xu et al. [1] .
for functions in aforementioned class, employing the techniques used earlier by Xu et al. [1] .
2. A Set of General Coefficient Estimates
In this section we state and prove our general results involving the bi-univalent function class 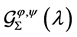 given by Definition 1.
given by Definition 1.
Theorem 1 Let 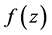 be of the form (1.1). If
be of the form (1.1). If 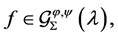 then
then
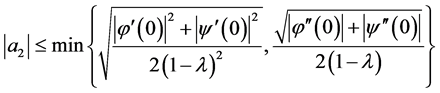 (1.5)
(1.5)
and
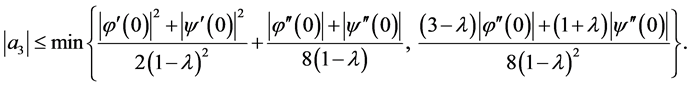 (1.6)
(1.6)
Proof 1 Since 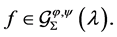 From (1.3) and (1.4), we have,
From (1.3) and (1.4), we have,
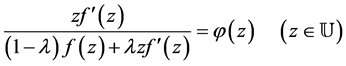
and
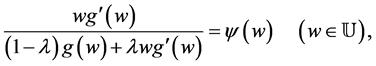
where
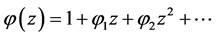
and
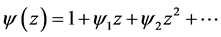
satisfy the conditions of Definition 1. Now, upon equating the coefficients of 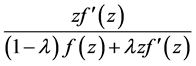 with those of
with those of 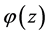 and the coefficients of
and the coefficients of 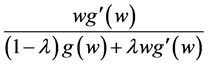 with those of
with those of , we get
, we get
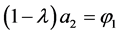 (1.7)
(1.7)
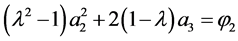 (1.8)
(1.8)
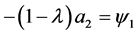 (1.9)
(1.9)
and
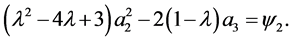 (1.10)
(1.10)
From (1.7) and (1.9), we get
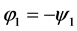 (1.11)
(1.11)
and
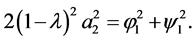 (1.12)
(1.12)
From (1.8) and (1.10), we obtain
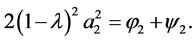 (1.13)
(1.13)
Therefore, we find from (1.12) and (1.13) that
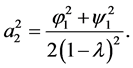 (1.14)
(1.14)
and
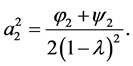 (1.15)
(1.15)
Since 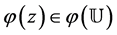 and
and 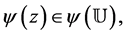 we immediately have
we immediately have
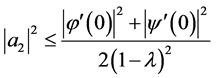
and
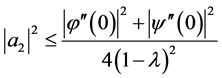
respectively. So we get the desired estimate on 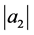 as asserted in (1.5).
as asserted in (1.5).
Next, in order to find the bound on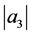 , by subtracting (1.10) from (1.8), we get
, by subtracting (1.10) from (1.8), we get
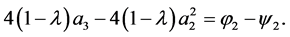 (1.16)
(1.16)
Upon substituting the values of 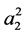 from (1.14) and (1.15) into (1.16), we have
from (1.14) and (1.15) into (1.16), we have
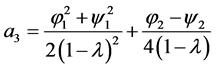
and
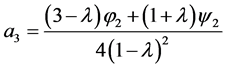
respectively. Since 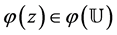 and
and 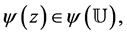 we readily get
we readily get

and
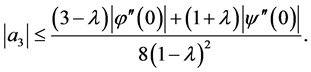
This completes the proof of Theorem 1.
If we choose
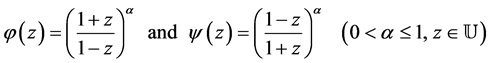
in Theorem 1, we have the following corollary.
Corollary 1 Let 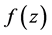 be of the form (1.1) and in the class
be of the form (1.1) and in the class 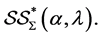 Then
Then
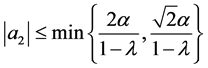
and
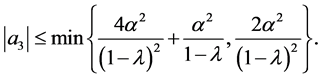
If we set
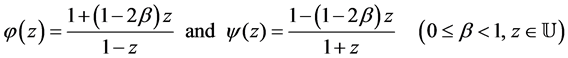
in Theorem 1, we readily have the following corollary.
Corollary 2 Let 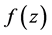 be of the form (1.1) and in the class
be of the form (1.1) and in the class 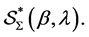 Then
Then
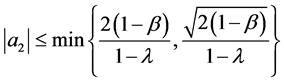
and
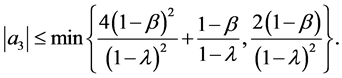
Remark 1 The estimates on the coefficients 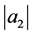 and
and 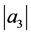 of Corollaries 1 and 2 are improvement of the estimates obtained in [10] , Theorems 4 and 5]. Taking
of Corollaries 1 and 2 are improvement of the estimates obtained in [10] , Theorems 4 and 5]. Taking 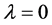 in Corollaries 1 and 2, the estimates on the coefficients
in Corollaries 1 and 2, the estimates on the coefficients 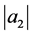 and
and 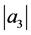 are improvement of the estimates in [14] , Theorems 2.1 and 4.1]. When
are improvement of the estimates in [14] , Theorems 2.1 and 4.1]. When 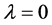 the results discussed in this article reduce to results in [4] . Similarly, various other interesting corollaries and consequences of our main result can be derived by choosing different
the results discussed in this article reduce to results in [4] . Similarly, various other interesting corollaries and consequences of our main result can be derived by choosing different 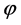 and
and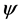 .
.
Acknowledgements
The authors would like to record their sincere thanks to the referees for their valuable suggestions.
Funding
The work is supported by UGC, under the grant F.MRP-3977/11 (MRP/UGC-SERO) of the first author.
References
- Xu, Q.-H., Gui, Y.-C. and Srivastava, H.M. (2012) Coefficient Estimates for a Certain Subclass of Analytic and Bi-Univalent Functions. Applied Mathematics Letters, 25, 990-994.
- Srivastava, H.M., Mishra, A.K. and Gochhayat, P. (2010) Certain Subclasses of Analytic and Bi-Univalent Functions. Applied Mathematics Letters, 23, 1188-1192.
- Ali, R.M., Lee, S.K., Ravichandran, V. and Supramanian, S. (2012) Coefficient Estimates for Bi-Univalent Ma-Minda Starlike and Convex Functions. Applied Mathematics Letters, 25, 344-351.
- Bulut, S. (2013) Coefficient Estimates for a Class of Analytic and Bi-Univalent Functions. Novi Sad Journal of Mathematics, 43, 59-65.
- Çağlar, M., Orhan, H. and Yağmur, N. (2012) Coefficient Bounds for New Subclasses of Bi-Univalent Functions. FILOMAT, 27, 1165-1171.
- Frasin, B.A. and Aouf, M.K. (2011) New Subclasses of Bi-Univalent Functions. Applied Mathematics Letters, 24, 1569-1573.
- Hayami, T. and Owa, S. (2012) Coefficient Bounds for Bi-Univalent Functions. Pan American Mathematical Journal, 22, 15-26.
- Li, X.-F. and Wang, A.-P. (2012) Two New Subclasses of Bi-Univalent Functions. International Mathematical Forum, 7, 1495-1504.
- Magesh, N., Rosy, T. and Varma, S. (2013) Coefficient Estimate Problem for a New Subclass of Biunivalent Functions. Journal of Complex Analysis, 2013, Article ID: 474231, 3 Pages.
- Murugusundaramoorthy, G., Magesh, N. and Prameela, V. (2013) Coefficient Bounds for Certain Subclasses of Bi-Univalent Functions. Abstract and Applied Analysis, 2013, Article ID: 573017, 3 Pages.
- Srivastava, H.M., Bulut, S., Çağlar, M. and Yağmur, N. (2013) Coefficient Estimates for a General Subclass of Analytic and Bi-Univalent Functions. FILOMAT, 27, 831-842.
- Srivastava, H.M., Murugusundaramoorthy, G. and Magesh, N. (2013) On Certain Subclasses of Bi-Univalent Functions Associated with Hohlov Operator. Global J. Math. Anal, 1, 67-73.
- Xu, Q.-H., Xiao, H.-G. and Srivastava, H. M. (2012) A Certain General Subclass of Analytic and Bi-Univalent Functions and Associated Coefficient Estimate Problems. Applied Mathematics and Computation, 218, 11461-11465.
- Brannan, D.A. and Taha, T.S. (1986) On Some Classes of Bi-Univalent Functions. Studia Universitatis Babeş-Bolyai. Mathematica, 31, 70-77.

