Applied Mathematics
Vol.4 No.10C(2013), Article ID:37488,6 pages DOI:10.4236/am.2013.410A3001
Solutions of the Dirac Equation with Gravitational plus Exponential Potential
Department of Pure and Applied Chemistry, University of Calabar, Calabar, Nigeria
Email: *iserom2001@yahoo.com
Copyright © 2013 Benedict Iserom Ita, Alexander Immaanyikwa Ikeuba. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 14, 2013; revised August 14, 2013; accepted August 21, 2013
Keywords: Dirac Equation; Alhaidari Formalism; Gravitational Potential; Exponential Potential; Nikiforov-Uvarov Method
ABSTRACT
The solutions of the Alhaidari formalism of the Dirac equation for the gravitational plus exponential potential have been presented using the parametric Nikiforov-Uvarov method. The energy eigenvalues and the corresponding un-normalized eigenfunctions are obtained in terms of Laguerre polynomials.
1. Introduction
The bound state solutions of the Dirac equation are only possible for some potentials of physical interest [1-5]. These solutions could be exact or approximate and they nornally contain all the necessary information for the quantum system. Quite recently, several authors have tried to solve the problem of obtaining exact or approximate solutions of the Dirac equation for a number of special potentials using different methods [6-20]. Some of these potentials are known to play very important roles in many fields of Physics such as Molecular Physics, Solid State and Chemical Physics [21]. When a particle is in a strong potential field, the relativistic effects must be considered, leading to the relativistic quantum mechanical description of such a particle [22-26]. In the relativistic limit, the particle’s motions are very often described using either the Klien-Gordon (KG) equation or the Dirac equation depending on the spin character of the particle [23,24]. The spin-zero particles like the mesons are satisfactorily described by the KG equation while the spin-half particles such as the electrons are described by the Dirac equation. It is therefore of interest in nuclear and high energy physics to obtain exact solutions of the KG and Dirac equations.
The purpose of the present work is to present the solution of the Alhaidari formalism of the Dirac equation [25] with the gravitational plus exponential potential (GEP) of the form:
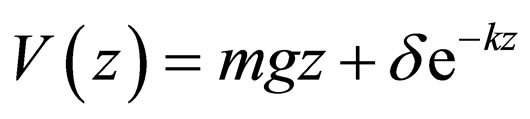 (1)
(1)
where 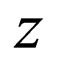 is the displacement,
is the displacement, 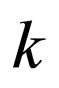 is the momentum,
is the momentum, ![]() is the mass,
is the mass, ![]() is gravitational acceleration and δ is an adjustable parameter. The GEP could be used to calculate the energy of a body falling under gravity from quantum mechanical point of view. Berberan-Santos et al. [22] have studied the motion of a particle in a gravitational field using the GEP without the exponential term. They obtained the classical and quantum mechanical position probability distribution function for the particle. Also quite recently, Ita and Ikeuba [27] have obtained the bound state solutions of the Klein-Gordon equation for the GEP using the parametric NU method. However, not much has been achieved in the area of solving the Dirac equation with GEP in the literature.
is gravitational acceleration and δ is an adjustable parameter. The GEP could be used to calculate the energy of a body falling under gravity from quantum mechanical point of view. Berberan-Santos et al. [22] have studied the motion of a particle in a gravitational field using the GEP without the exponential term. They obtained the classical and quantum mechanical position probability distribution function for the particle. Also quite recently, Ita and Ikeuba [27] have obtained the bound state solutions of the Klein-Gordon equation for the GEP using the parametric NU method. However, not much has been achieved in the area of solving the Dirac equation with GEP in the literature.
2. The Dirac Equation
The Dirac equation for the lower and upper spinor components can be written as [25]:
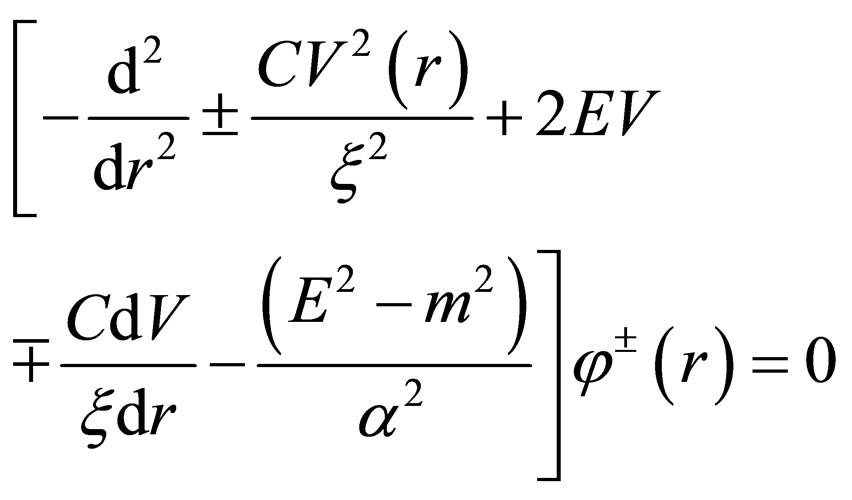 (2)
(2)
where ![]() is the rest mass,
is the rest mass,  is the relativistic energy, and
is the relativistic energy, and 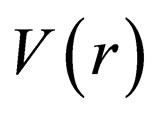 is the vector potential.
is the vector potential.
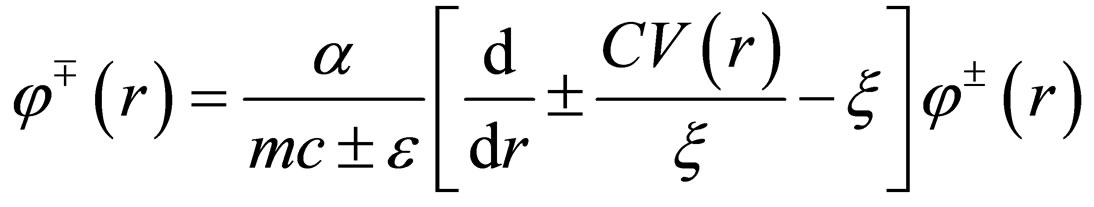 (3)
(3)
where 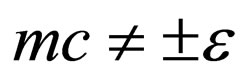 and
and  is a real parameter. The “
is a real parameter. The “![]() ” designate the upper and lower components respectively.
” designate the upper and lower components respectively.
3. The Nikiforov-Uvarov Method
The Nikiforov-Uvarov (NU) method is based on the solutions of a generalized second-order linear differential equation with special orthogonal functions [28]. The Schrodinger equation of the type as:
 (4)
(4)
can be solved by this method. This can be done by transforming Equation (2) into an equation of hypergeometric type with appropriate coordinate transformation 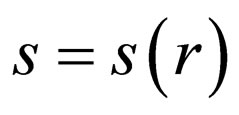 to get
to get
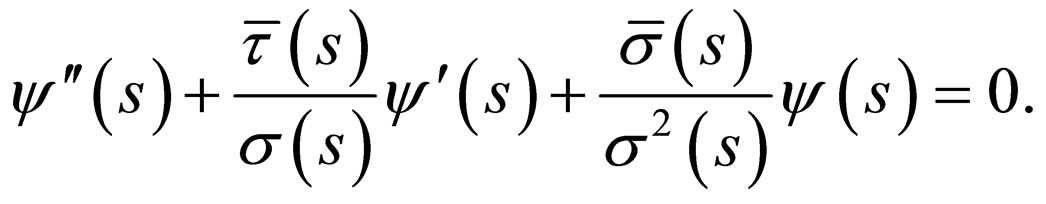 (5)
(5)
To find the exact solution to Equation (3), we write 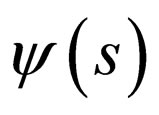 as
as
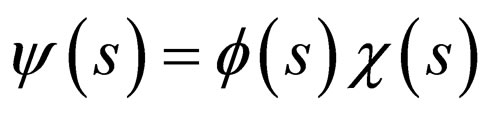 . (6)
. (6)
Substitution of Equation (6) into Equation (5) yields Equation (7) of hypergeometric type as
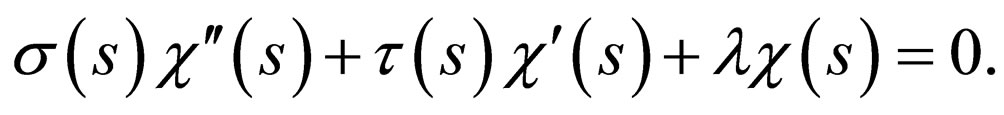 (7)
(7)
In Equation (6), the wave function 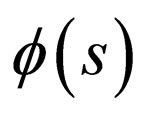 is defined as the logarithmic derivative [29]
is defined as the logarithmic derivative [29]
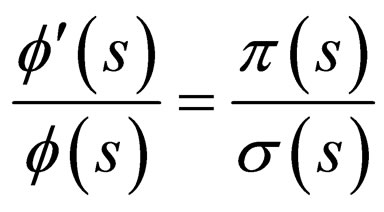 (8)
(8)
with 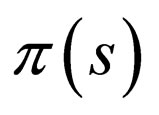 being at most first order polynomials. Also, the hypergeometric-type functions in Equation (7) for a fixed integer
being at most first order polynomials. Also, the hypergeometric-type functions in Equation (7) for a fixed integer ![]() is given by the Rodrigue relation as
is given by the Rodrigue relation as
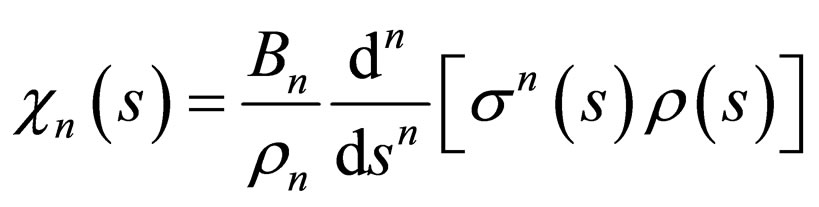 (9)
(9)
where 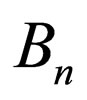 is the normalization constant and the weight function
is the normalization constant and the weight function  must satisfy the condition
must satisfy the condition
 (10)
(10)
with
 (11)
(11)
In order to accomplish the condition imposed on the weight function  it is necessary that the polynomial
it is necessary that the polynomial 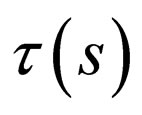 be equal to zero at some point of an interval
be equal to zero at some point of an interval 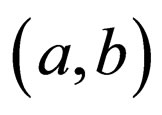 and its derivative at this interval at
and its derivative at this interval at 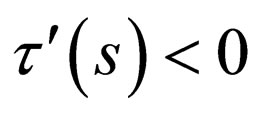 will be negative [30]. That is
will be negative [30]. That is
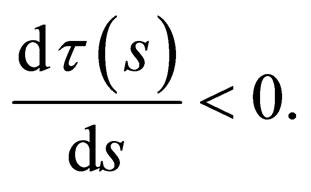 (12)
(12)
The function  and the parameter
and the parameter ![]() required for the NU method are then defined as [31]
required for the NU method are then defined as [31]
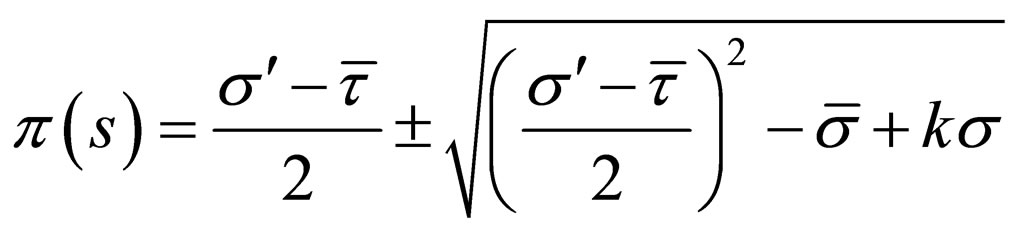 . (13)
. (13)
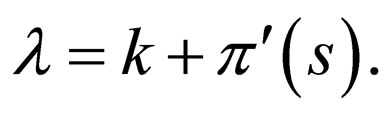 (14)
(14)
The values in Equation (13) are possible to evaluate if the expression under the square-root be square of polynomials. This is possible if and only if its discriminant is zero. Therefore, the new eigenvalue equation becomes [29]
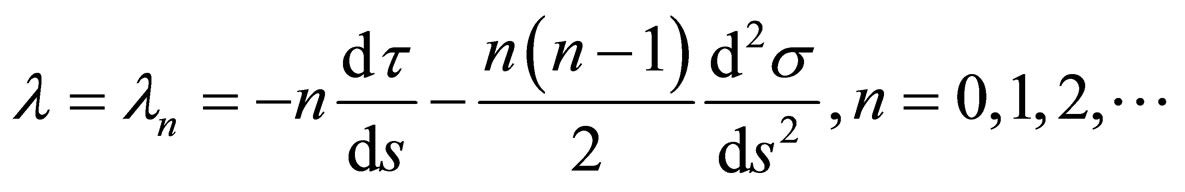 (15)
(15)
A comparison between Equations (14) and (15) yields the energy eigenvalues.
Secondly, the parametric generalization of the NU method is expressed by the generalized hypergeometric-type equation [32]
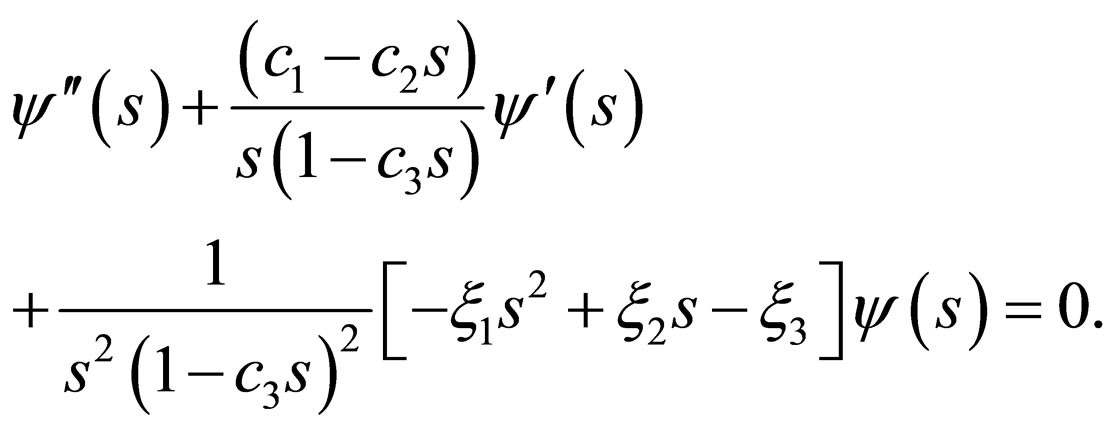 (16)
(16)
Equation (16) is solved by comparing it with Equation (5) and the following polynomials are obtained:
 (17)
(17)
Now, substituting Equation (17) into Equation (13) gives
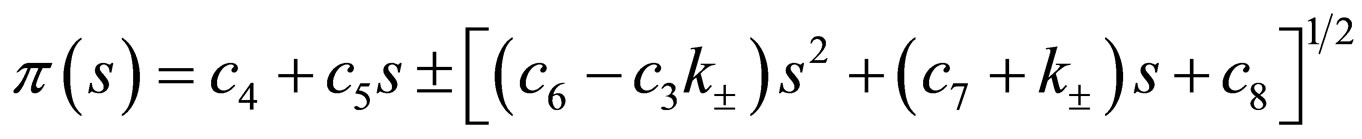 (18)
(18)
where
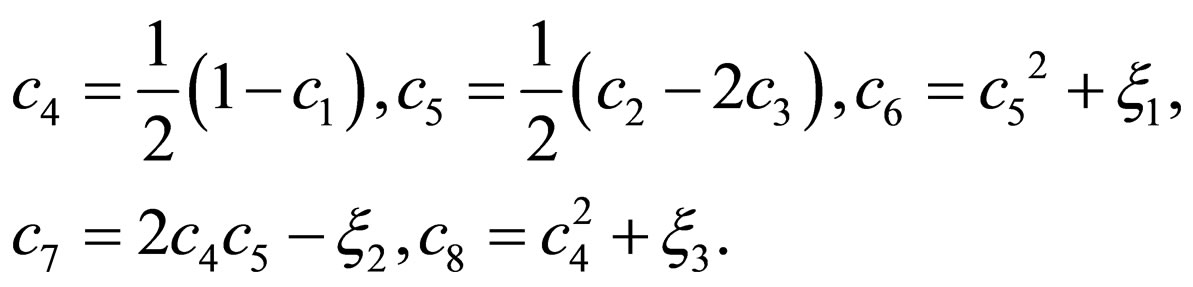 (19)
(19)
The resulting value of  in Equation (18) is obtained from the condition that the function under the square-root should be square of a polynomial and we get
in Equation (18) is obtained from the condition that the function under the square-root should be square of a polynomial and we get
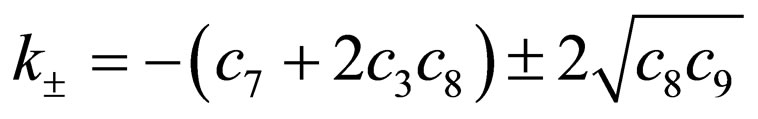 (20)
(20)
where
 (21)
(21)
The new 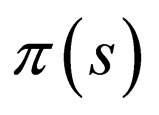 for
for 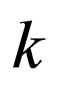 becomes
becomes
 (22)
(22)
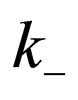 value becomes
value becomes
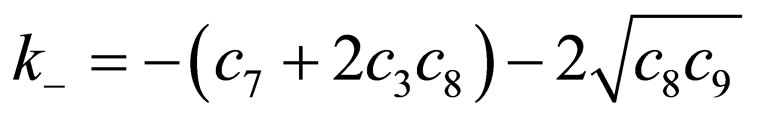 . (23)
. (23)
Using Equation (11), we obtain
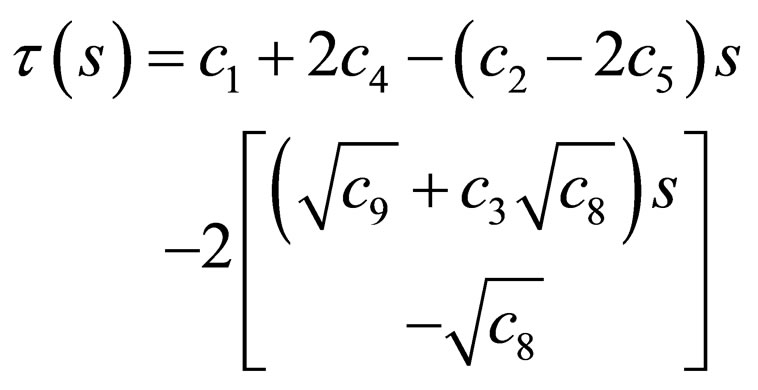 (24)
(24)
The physical condition for the bound state solution is 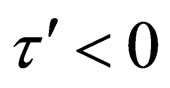 and thus
and thus
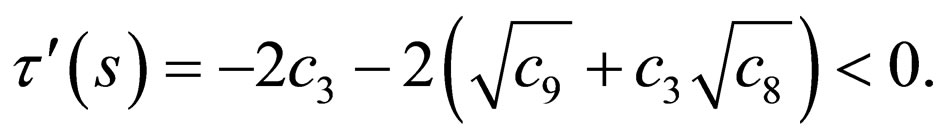 (25)
(25)
With the aid of Equations (12) and (13), we obtain the energy equation as
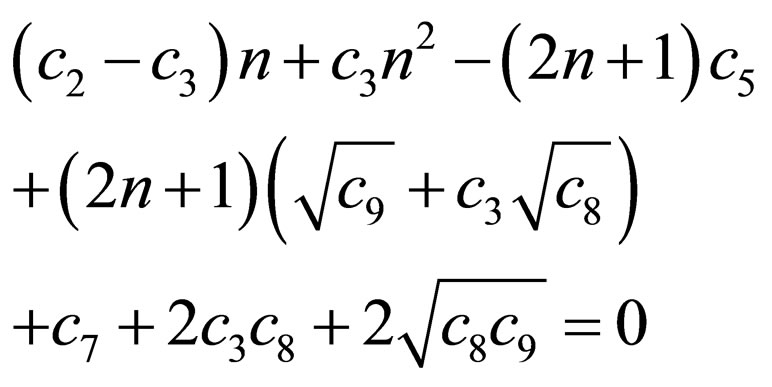 (26)
(26)
The weight function 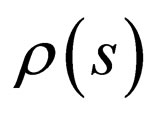 is obtained from Equation (10) as
is obtained from Equation (10) as
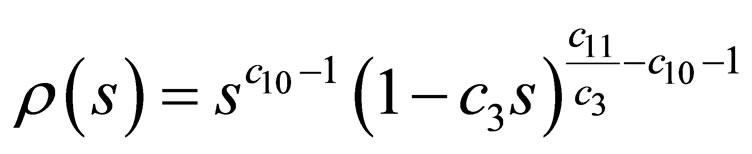 (27)
(27)
And together with Equation (9), we have
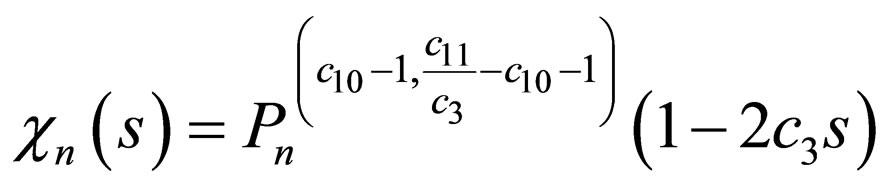 (28)
(28)
where
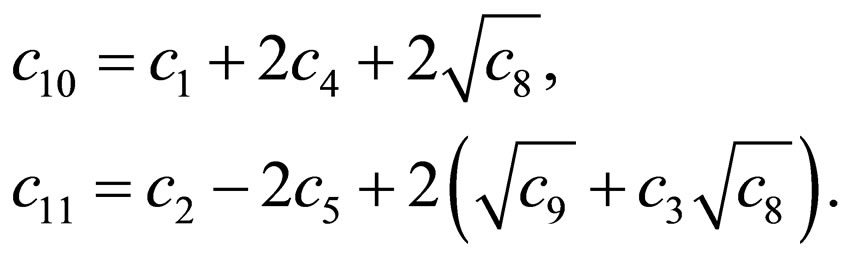 (29)
(29)
 are the Jacobi polynomials. The second part of the wave function is obtained from Equation (6) as
are the Jacobi polynomials. The second part of the wave function is obtained from Equation (6) as
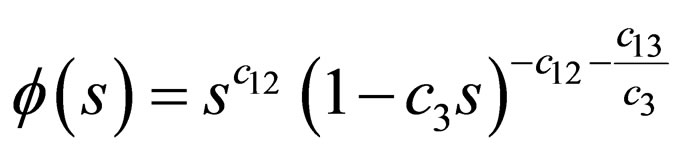 (30)
(30)
where
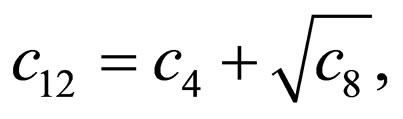
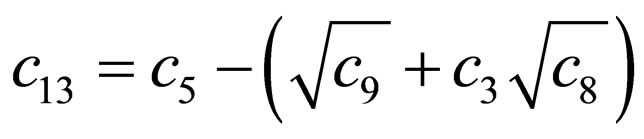 . (31)
. (31)
Thus the total wave function becomes
 (32)
(32)
where Nn is the normalization constant.
4. Solutions of the Dirac Equation
The potential in Equation (1) can be written as
 . (33)
. (33)
where . We can also write Equation (33) as
. We can also write Equation (33) as
 . (34)
. (34)
On arranging Equation (34) we get our working potential as
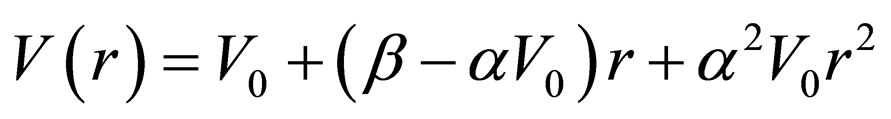 . (35)
. (35)
The potential of Equation (35) can be used to solve various quantum mechanical equations including the Schrodinger equation (SE), Klein-Gordon equation (KG) and Dirac equation using the NU method for their exact solutions. Writing Equation (32) with the GEP we get
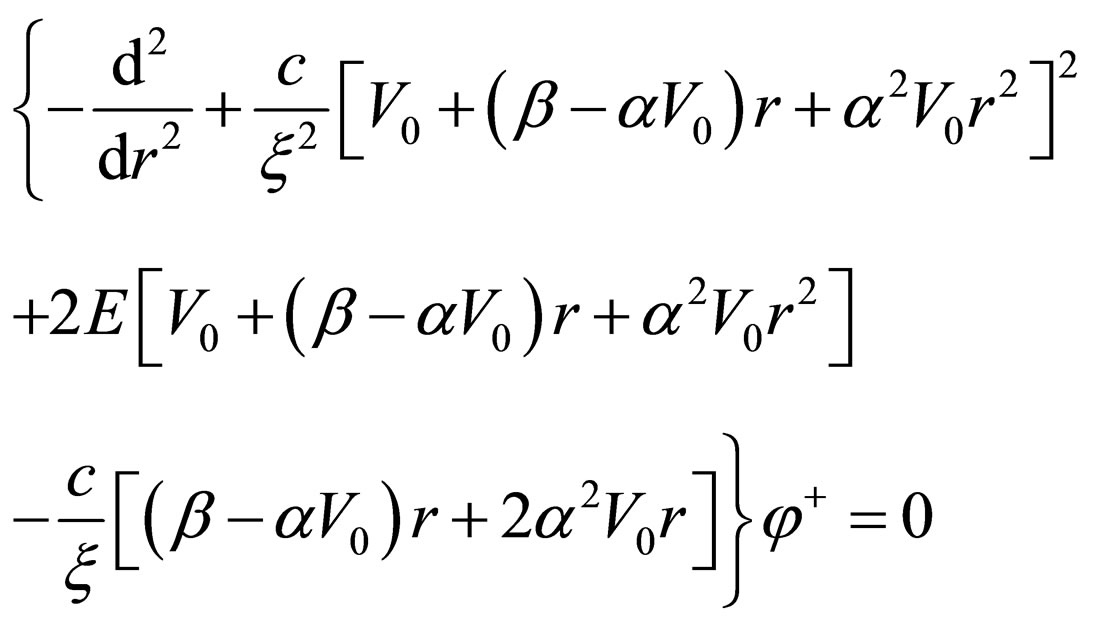 . (36)
. (36)
Ignoring all terms of the form 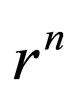 with
with 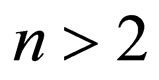 in Equation (36) as these will not affect the physics of the calculations, we write Equation (36) as
in Equation (36) as these will not affect the physics of the calculations, we write Equation (36) as
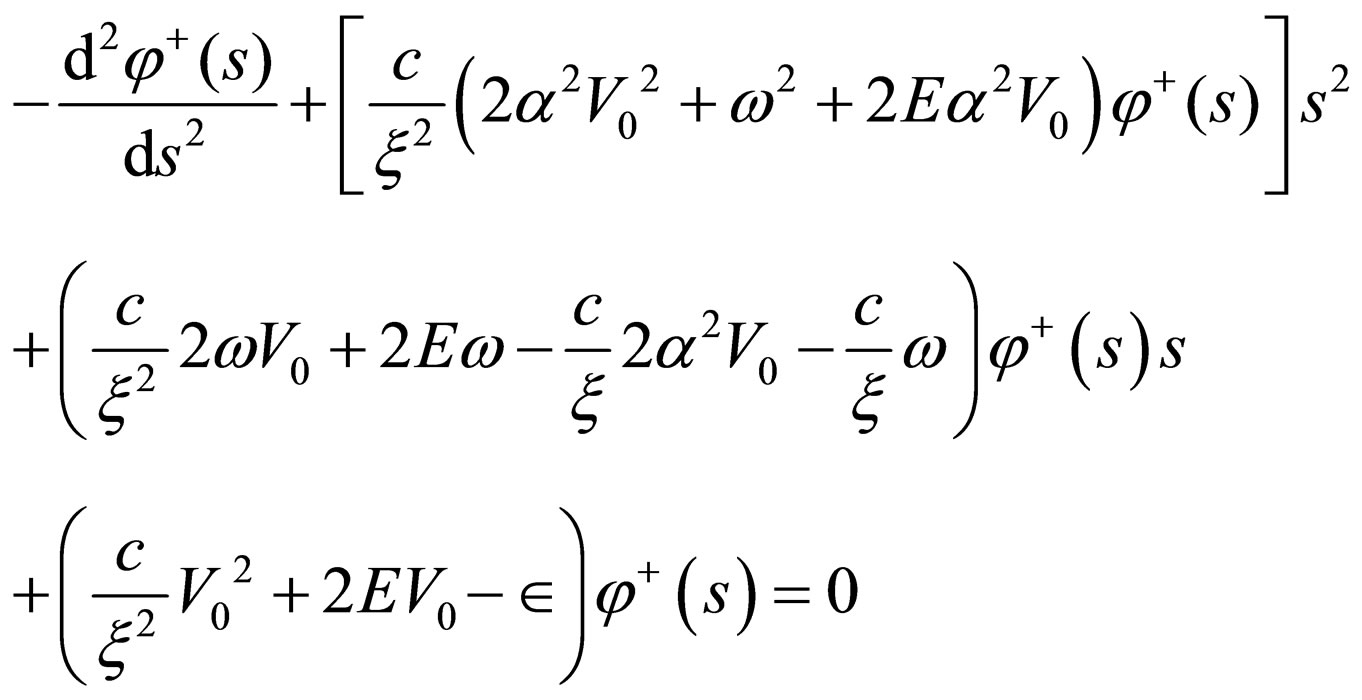 (37)
(37)
where we have used  and
and ![]() transformation in Equation (36).
transformation in Equation (36).
Comparing Equation (37) with Equation (16) yields the following parameters
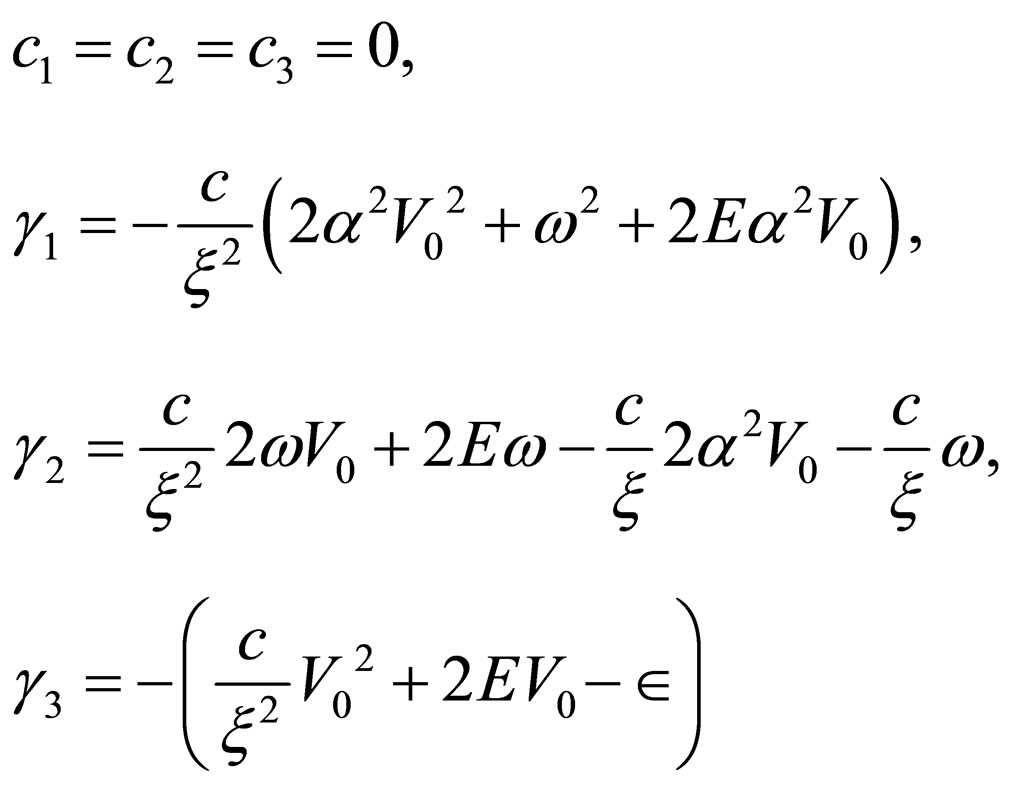 (38)
(38)
Other coefficients are determined as
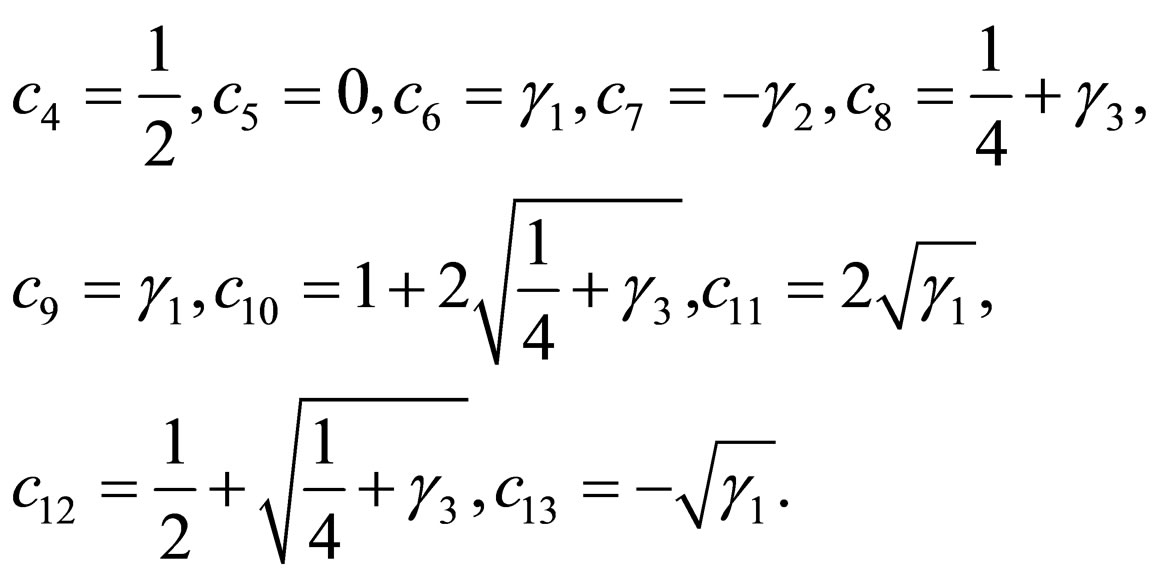 (39)
(39)
From Equation (16)
 (40)
(40)
From Equation (18)
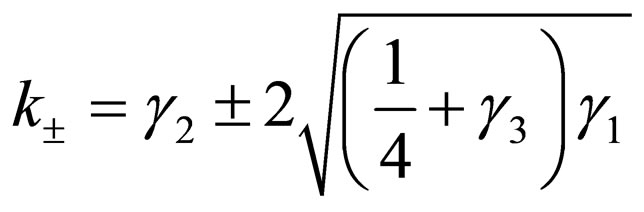 . (41)
. (41)
From Equation (22)
 . (42)
. (42)
The negative derivative of Equation (42) then becomes
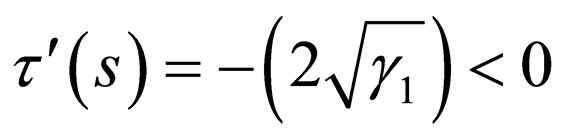 . (43)
. (43)
The new  for the NU method is chosen as
for the NU method is chosen as
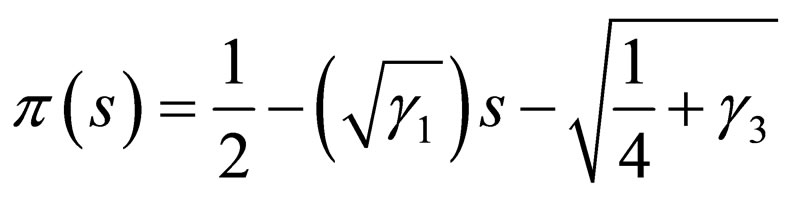 . (44)
. (44)
For
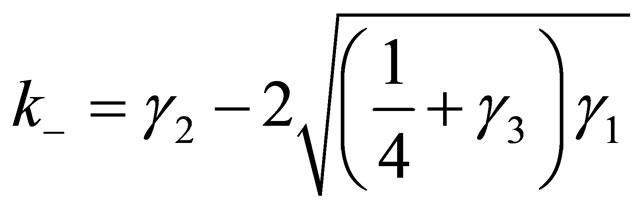 . (45)
. (45)
Now using Equations (24), (38) and (39) we obtain the energy spectrum of the GEP as
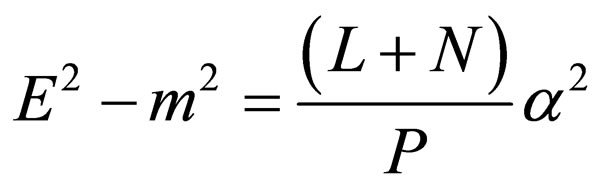 (46)
(46)
where
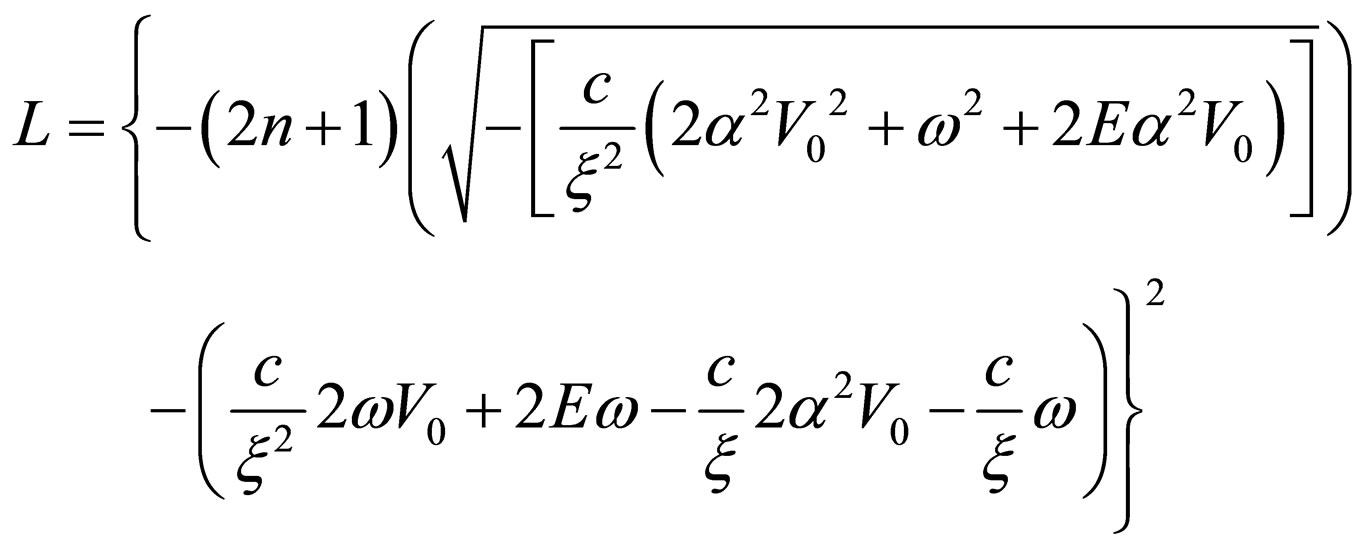 (47)
(47)
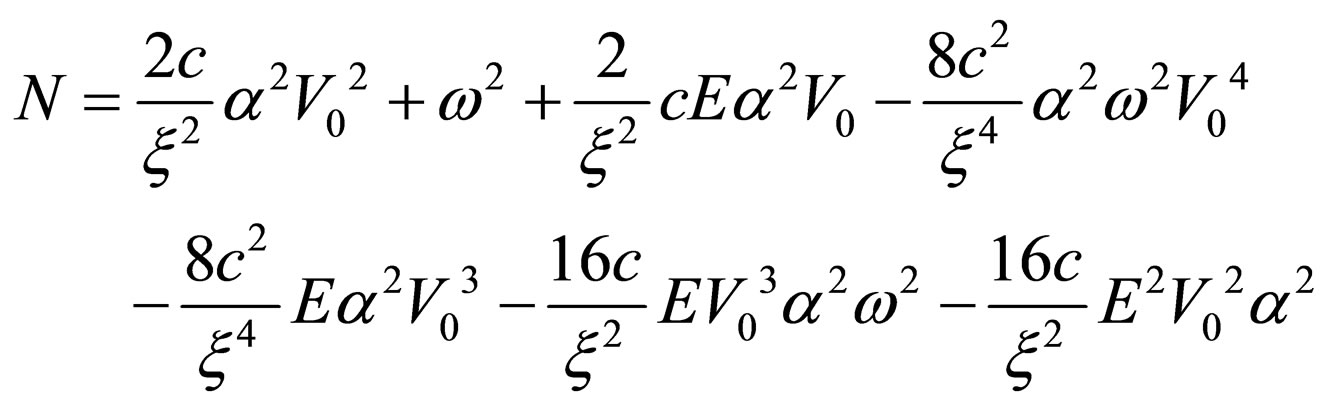 (48)
(48)
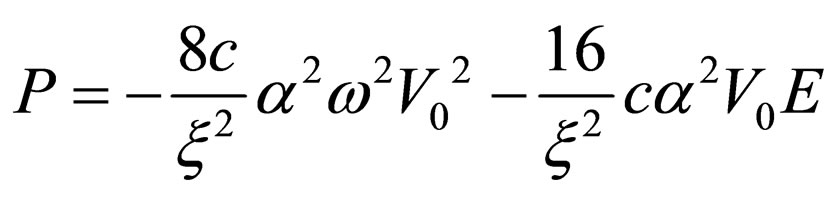 . (49)
. (49)
The weight function  is obtained from Equation (25) and the parameters of Equation (39) as
is obtained from Equation (25) and the parameters of Equation (39) as
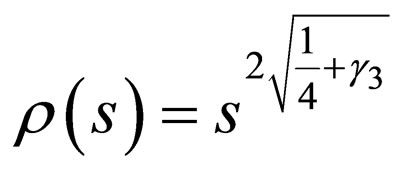 (50)
(50)
and using Equation (26) we get the wavefunction χn(s) as
 (51)
(51)
where 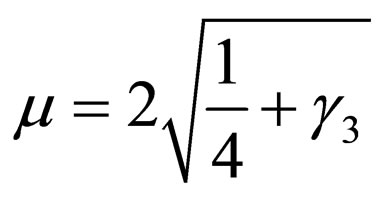 and
and 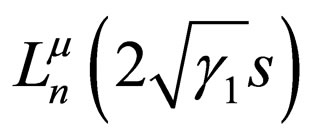 is the Laguerre polynomial. From Equation (28) the wave function is
is the Laguerre polynomial. From Equation (28) the wave function is
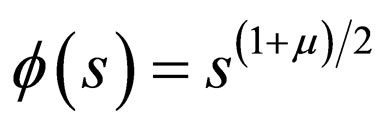 . (52)
. (52)
The unnormalized wave function is then obtained from Equation (30) as
 (53)
(53)
where 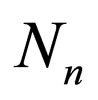 is the normalization constant.
is the normalization constant.
In addition, the corresponding lower-spinor wave function is
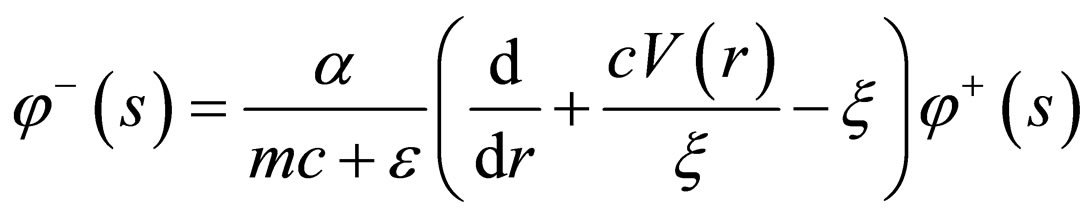 . (54)
. (54)
5. Conclusion
In summary, we have obtained the energy eigenvalues and the corresponding un-normalized wavefunction using the parametric NU method for the Dirac equation with the gravitational plus exponential potential.
6. Acknowledgements
The authors wish to acknowledge Dr. A. N. Ikot of the Department of Physics, University of Uyo in Nigeria for some useful discussions during the preparation of this paper.
REFERENCES
- M. K. Bahar and F. Yasuk, “Fermionic Particles with Position-Dependent Mass in the Presence of Inversely Quadratic Yukawa Potential and Tensor Interaction,” Pramana Journal of Physics, Vol. 80, No. 2, 2013, pp. 187-197. http://dx.doi.org/10.1007/s12043-012-0483-2
- A. N. Ikot and E. Maghsoodi, “Relativistic Spin and Pseudospin Symmetries of Inversely Quadratic YukawaLike plus Mobius Square Potentials Including a Coulomb-Like Tensor Interaction,” Few-Body Systems, 2013. http://dx.doi.org/10.1007/s00601-013-0701-6
- K. V. Koshelev, “Another Method to Solve Dirac’s OneElectron Equation Numerically,” arXiv:0811.3912v1 [Physics.gen-ph], 2008.
- H. Eleuch and H. Bahlouli, “Analytical Solution to the Dirac Equation in 3 + 1 Space-Time Dimensions,” Applied Mathematics and Information Science, Vol. 6, 2012, pp. 153-156.
- H. Nakashima and H. Nakatsuji, “Relativistic Free Complement Method for Correctly Solving the Dirac Equation with the Applications to Hydrogen Isoelectronic Atoms,” Theoretical Chemistry Account, Vol. 129, No. 3-5, 2011, pp. 567-574. http://dx.doi.org/10.1007/s00214-011-0899-7
- M. Eshghi, “Relativistic Problem by Choosing Spatially-Dependent Mass Coupled With Tensor Potential,” World Applied Sciences Journal, Vol. 6, No. 3, 2012, pp. 415-420.
- M. Hamzavi, A. A. Rajabi and H. Hassanabi, “Exact Pseudospin Symmetry Solution of the Dirac Equation for Spatially-Dependent Mass Coulomb Potential Including Coulomb-Like Tensor Interaction via Asymptotic Iteration Method,” Physics Letters A, Vol. 374, No. 42, pp. 4303-4307. http://dx.doi.org/10.1016/j.physleta.2010.08.065
- M. Eshghi and H. Mehraban, “Eigen Spectra for q-Deformed Hyperbolic Scarf Potential Including a CoulombLike Tensor Interaction,” Journal of Scientific Research, Vol. 3, No. 2, 2011, pp. 239-247.
- H. Akcay and C. Tezcan, “Exact Solutions of the Dirac Equation with Harmonic Oscillator Potential Including a Coulomb-Like Tensor Interaction,” International Journal of Modern Physics C, Vol. 20, No. 6, 2010, pp. 931-940. http://dx.doi.org/10.1142/S0129183109014084
- H. Akcay, “Dirac Equation with Scalar and Vector Quadratic Potentials and Coulomb-Like Tensor Potential,” Physics Letters A, Vol. 373, No. 6, 2009, pp. 616-620. http://dx.doi.org/10.1016/j.physleta.2008.12.029
- M. Hamzavi, H. Hassanabadi and A. A. Rajabi, “Approximate Pseudospin Solutions of the Dirac Equation with the Eckart Potential Including a Coulomb-Like Tensor Potential,” International Journal of Theoretical Physics, Vol. 50, No. 2, 2011, pp. 454-464. http://dx.doi.org/10.1007/s10773-010-0552-6
- O. Aydogdu and R. Sever, “Exact Pseduspin Symmetric Solution of the Dirac Equation for Pseudoharmonic Potential in the Presence of Tensor Potential,” Few-Body Systems, vol. 47, No. 3, 2010, pp. 193-200. http://dx.doi.org/10.1007/s00601-010-0085-9
- S. M. Ikhdair and R. Sever, “Approximate Bound State Solutions of Dirac Equation with Hulthen Potential Including Coulomb-Like Tensor Potential,” Applied Mathematics and Communication, Vol. 216, No. 3, 2010, pp. 911-923. http://dx.doi.org/10.1016/j.amc.2010.01.104
- D. Agboola, “Dirac Equation with Spin Symmetry for Modified Poschl-Teller Potential in D Dimensions,” Pramana journal of Physics, Vol. 76, No. 6, 2011, pp. 875-885.
- S. D. Bosanac, “Solution of Dirac Equation for a Step Potential and Klein Paradox,” Journal of Physics A: Mathematics and Theory, Vol. 40, No. 30, 2007, pp. 8991- 9001. http://dx.doi.org/10.1088/1751-8113/40/30/021
- M. Hamzavi and M. Amirfakhrian, “Dirac Equation for a Spherically Pseudoharmonic Oscillatory Ring-Shaped Potential,” International Journal of Physical Sciences, Vol. 6, No. 15, 2011, pp. 3803-3807.
- C. Berkdemir and Y. F. Cheng, “On the Exact Solutions of the Dirac Equation with a Novel Angle-Dependent Potential,” Physica Scripta, Vol. 79, No. 3, 2009, pp. 035003-035010. http://dx.doi.org/10.1088/0031-8949/79/03/035003
- C. Y. Chen, “Exact Solutions of the Dirac Equation with Scalar and Vector Hartmann Potentials,” Physics Letters A, Vol. 339, No. 3-5, 2005, pp. 283-287. http://dx.doi.org/10.1016/j.physleta.2005.03.031
- F. Zhou, Y. Wu and J. Y. Guo,” Solutions of the Dirac Equation for Makarov Potential with Pseudospin Symmetry,” Communications in Theoretical Physics, Vol. 52, No. 5, 2009, pp. 813-816. http://dx.doi.org/10.1088/0253-6102/52/5/09
- E. Maghsoodi, H. Hassanabadi and S. Zarrinkamar, “Exact Solutions of the Dirac Equation with Poschl-Teller Double-Ring Shaped Coulomb Potential via the Nikiforov-Uvarov Method,” Chinese Physics B, Vol. 22, No. 3, 2013, pp. 030302-1-030302-5.
- I. O. Akpan, A. D. Antia and A. N. Ikot, “Bound State Solutions of the Klein-Gordon Equation with q-Deformed Equal Scalar and Vector Eckart Potential Using a Newly Improved Approximation Scheme,” High Energy Physics, Vol. 2012, 2012, Article ID: 798209. http://dx.doi.org/10.5402/2012/798209
- M. N. Berberan-Santos, E. N. Bodunov and L. Pogliani, “Classical and Quantum Study of the Motion of a Particle in a Gravitational Field,” Journal of Mathematical Chemistry, Vol. 37, No. 2, 2005, pp. 101-105. http://dx.doi.org/10.1007/s10910-004-1443-y
- K. J. Oyewumi and C. O. Akoshile, “Bound State Solutions of the Dirac-Rosen-Morse Potential with Spin and Pseudospin Symmetry,” European Physics Journal A, Vol. 45, No. 3, 2010, pp. 311-318. http://dx.doi.org/10.1140/epja/i2010-11007-0
- W. A. Yahaya, K. J. Oyewumi, C. O. Akoshile and T. T. Ibrahim, “Bound State Solutions of the Relativistic Dirac Equation with Equal Scalar and Vector Eckart Potential Using Nikiforov-Uvarov Method,” Journal of Vectorial Relativity, Vol. 3, 2010, pp. 27-34.
- A. D. Alhaidari, H. Bahlouli and A. Al-Hasan, “Dirac and Klein-Gordon Equations with Equal Scalar and Vector Potentials,” Physics Letters A, Vol. 349, No. 1-4, 2006, pp. 87-96. http://dx.doi.org/10.1016/j.physleta.2005.09.008
- C. Berkdemir, A. Berkdemir and R. Sever, “Systematic Approach to the Exact Solution of the Dirac Equation for a Special Form of Woods-Saxon Potential,” Physics A: Mathematics and General, Vol. 39, No. 43, 2006, pp. 13455-13470. http://dx.doi.org/10.1088/0305-4470/39/43/005
- B. I. Ita and A. I. Ikeuba, “Solutions of the Klein-Gordon Equation with Quantum Mechanical Gravitational Potential,” Open Journal of Microphysics, Accepted for Publication, 2013.
- A. F. Nikiforov and A. B. Uvarov, “Special functions of Mathematical Physics,” Birkhauser, Basle, 1988. http://dx.doi.org/10.1007/978-1-4757-1595-8
- M. Hamzavi and A. A. Rajabi, “Exact S-Wave Solution of the Trigonometric Poschl-Teller Potential,” International Journal of Quantum Chemistry, Vol. 112, No. 6, 2012, pp. 1592-1597. http://dx.doi.org/10.1002/qua.23166
- S. M. Ikhdair and R. Sever, “Exact Solution of the KleinGordon Equation for the PT-Symmetric Generalized WoodsSaxon Potential by the Nikiforov-Uvarov Method,” Annalen der Physik, Vol. 16, No. 3, 2007, pp. 218-232.
- N. Candemir, “Pseudospin Symmetry in Trigonometric Poschl-Teller Potential,” International Journal of Modern Physics E, Vol. 21, No. 6, 2010, Article ID: 1250060.
- A. N. Ikot, “Solution of Dirac Equation with Generalized Hylleraas Potential,” Communications in Theoretical Physics, Vol. 59, No. 3, 2013, pp. 268-272. http://dx.doi.org/10.1088/0253-6102/59/3/04
NOTES
*Corresponding author.

