ABSTRACT

In this paper, the existence and uniqueness of solution systems for some binary nonlinear operator equations are discussed by using cone and partial order theory and monotone iteration theory, and the iterative sequences which converge to solution of operator equations and error estimates for iterative sequences are also given. Some corresponding results are improved and generalized. Finally, the applications of our results are given.

1. Introduction

In recent years, more and more scholars have studied binary operator equations and have obtained many conclusions, such as references [1-3] etc. In this paper, we will discuss solutions for ordinal symmetric contraction operator and obtain some general conclusions; some corresponding results of references [4,5] are improved and generalized. Finally, we apply our conclusions to two point boundary value problems with two degree superlinear ordinary differential equations.

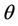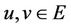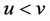In the following, let E always be a real Banach space which is partially ordered by a cone P, P be normal cone of E, N is normal constant of P, partial order ≤ is determined by P, denotes zero element of E. For and, let

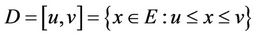
denotes an ordering interval of E.

The concepts of normal cone and partially order, mixed monotone operator, coupled solutions of operator equations etc. see [6].

Definition 1.1. Let 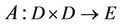be binary operator, A is said to be L-ordering symmetric contraction operator if there exists a bounded linear operator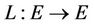, which its spectral radius 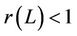such that

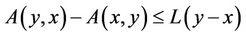
for any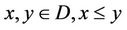, where L is called contraction operator of A.

2. Main Results

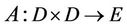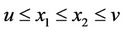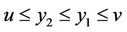Theorem 2.1. Let be L-ordering symmetric contraction operator, and there exists a, for any, such that

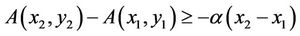. (1)

If condition

(H₁) ;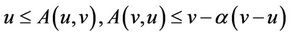

or

(H₂)

holds, then the following statements hold:

(C₁) 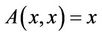has a unique solution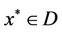, and for any coupled solution 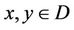such that;

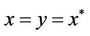(C₂) For any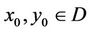, we make up symmetric iterative sequences

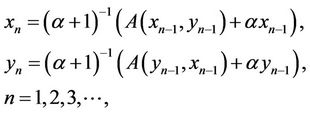(2)

then

and for any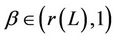, there exists a natural numbers m, if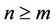, we get error estimates for iterative sequences (2):

.

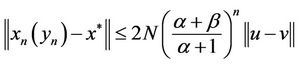Proof. Set

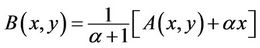if condition (H₁) or (H₂) holds, then it is obvious

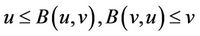by (1), we easily prove that 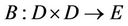is mixed monotone operator, and for any 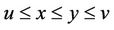such that

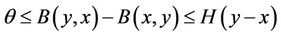where

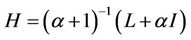
is a bounded linear operator, I is identical operator.

By the mathematical induction, we easily prove that

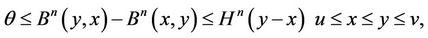
where

.

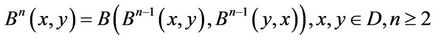By the character of normal cone P, we implies

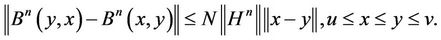
For any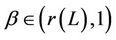, since

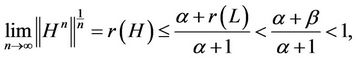
so there exists a natural numbers m, if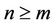, such that

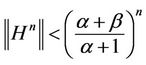
and constant.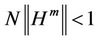

Considering mixed monotone operator 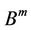and constant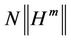, by Theorem 3 in reference [3], then we know 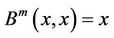has an unique solution, and for any coupled solution 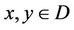such that

.

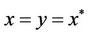From

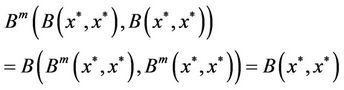
and uniqueness of solutions with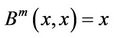, then we have 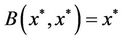and.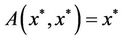

We take note of that 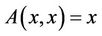and 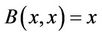have same coupled solution, therefore coupled solution for 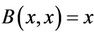must be coupled solution for x, consequently, (C₁) has been proved.

Considering that iterative sequence (2) and set iterative sequences:

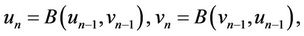
where 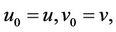it is obvious that

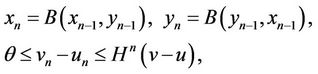
by the mathematical induction and character of mixed monotone of B, then

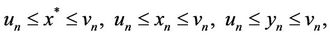
hence

moreover, if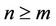, we get

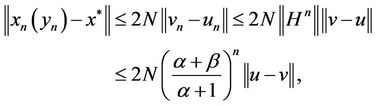
consequently,.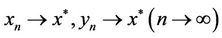

Remark 1. When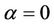, Theorem 1 in [4] is a special case of this paper Theorem 2.1 under condition (H₁) or (H₂).

Corollary 2.1. Let 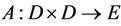be L-ordering symmetric contraction operator, if there exists a 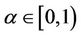such that A satisfies condition of Theorem 2.1, then (C₁), (C₂) hold and the following statements holds:

(C₃) For any 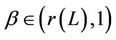and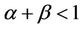, we make up iterative sequences

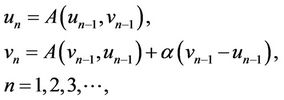(3)

or

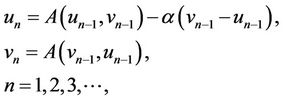(4)

where 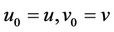thus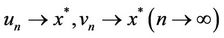, and there exists a natural numbers m, if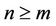, we have error estimates for iterative sequences (3) or (4):

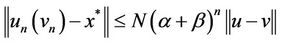. (5)

Proof. By the character of mixed monotone of A, then (1) and (C₁), (C₂) [in (1), (C₂) where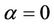] hold. In the following, we will prove (C₃).

Consider iterative sequence (3), since

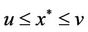so we get

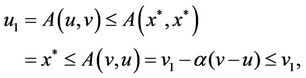
by the mathematical induction, we easily prove

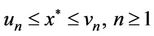
hence

It is clear

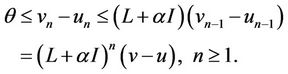
For any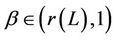, , 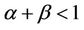since

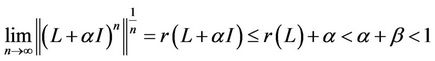thus there exists a natural numbers m, if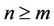, such that

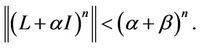
Moreover,

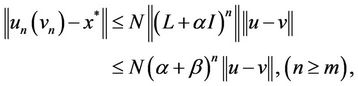
consequently, ,.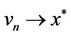

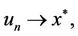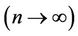Similarly, we can prove (4).

Theorem 2.2. Let 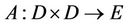be L-ordering symmetric contraction operator, if there exists a 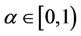such that

then the following statements holds:

(C₄) Operator equation

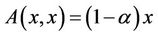
has an unique of solution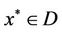, and for its any coupled solution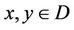, such that;

(C₅) For any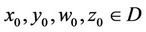, we make up symmetric iterative sequence

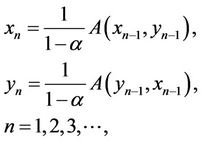(6)

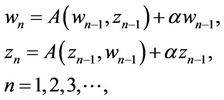(7)

then

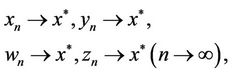
and that for any 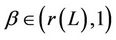and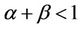, there exists a natural numbers m, if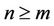, then we have error estimates for iterative sequences (6) and (7) respectively:

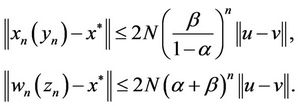(8)

Proof. Set

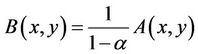
or

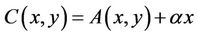we can prove this theorem imitate proof of Theorem 2.1, over.

Similarly, we can prove following theorems.

Theorem 2.3. Let 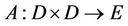be L-ordering symmetric contraction operator, if there exists a 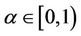such that

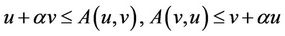then the following statements holds:

(C₆) Equation

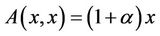
has an unique solution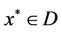, and for any coupled solution 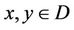such that;

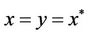(C₇) For any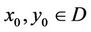, we make up symmetric iterative sequence

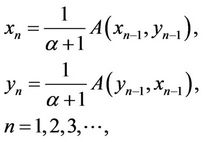(9)

then that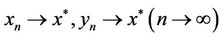, moreover, 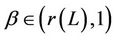, there exist natural number m, if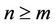, then we have error estimates for iterative sequence (9):

;

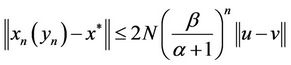(C₈) For any 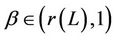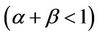, , 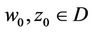we make up symmetry iterative sequence

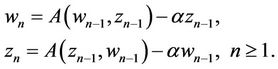
Then

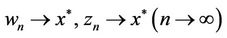and there exists a natural numbers m, if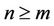, we have error estimates for iterative sequence (8).

Remark 2. When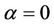, Corollary 2 in [4] is a special case of this paper Theorem 2.1 - 2.3.

Remark 3. The contraction constant of operator in [5] is expand into the contraction operator of this paper.

Remark 4. Operator A of this paper does not need character of mixed monotone as operator in [6].

3. Application

We consider that two point boundary value problems for two degree super linear ordinary differential equations

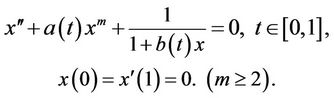(10)

Let 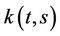be Green function with boundary value problem (7), that is

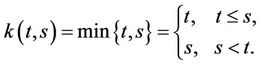
then that the solution with boundary value problem (7) and solution for nonlinear integral equation with type of Hammerstein

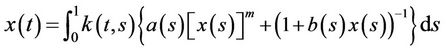(11)

is equivalent, where

.

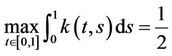Theorem 3.1. Let 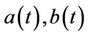are nonnegative continuous function in

.

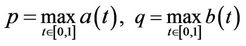If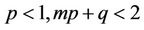, then boundary value problem (7) have an unique solution 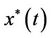such that

;

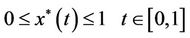Moreover, for any initial function 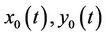such that

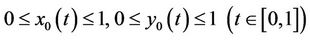we make up iterative sequence

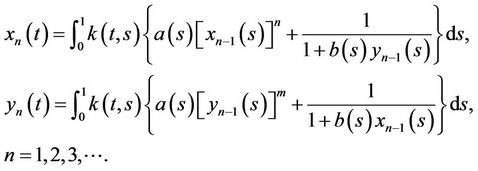
Then, uniform convergence to 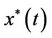on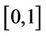, and we have error estimates

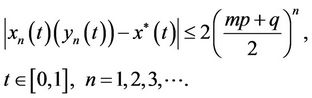
Proof. Let

,

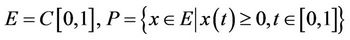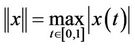denote norm of E, then that E has become Banach space, P is normal cone of E and its normal constant N = 1. It is obvious that integral Equation (8) is transformed to operator equation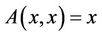, where

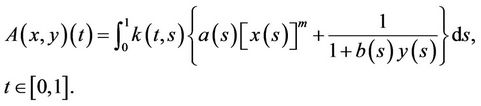
Set

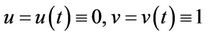then 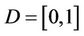denote ordering interval of E, 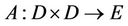is mixed monotone operator ,and

.

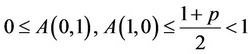Set

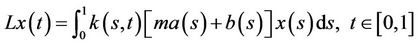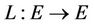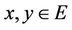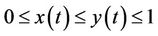then is bounded linear operator, its spectral radius and for any, such that 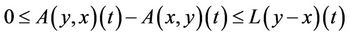that is, A is L-ordering symmetric contraction operator, by Theorem 2.1 (where), then Theorem 3.1 has be proved.

4. Acknowledgements

Supported by the Natural Science Foundation of Henan under Grant 122300410425; the NSF of Henan Education Bureau (2000110019); Supported by the NSF of Shangqiu (200211125).

REFERENCES