Applied Mathematics
Vol.4 No.10B(2013), Article ID:37454,14 pages DOI:10.4236/am.2013.410A2001
Optimal Vaccination Strategies in an SIR Epidemic Model with Time Scales
1School of Mathematics, University of Nairobi, Nairobi, Kenya
2TU Munich, Centre of Mathematical Science, Munich, Germany
3School of Mathematics, University of Nairobi, Nairobi, Kenya
Email: nelsonowuor@gmail.com, johannes.mueller@mytum.de, moindi@uonbi.ac.ke
Copyright © 2013 Onyango Nelson Owuor et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 31, 2013; revised June 30, 2013; accepted July 7, 2013
Keywords: Singular Perturbation Theory; Optimization; Vaccination Strategies
ABSTRACT
Childhood related diseases such as measles are characterised by short periodic outbreaks lasting about 2 weeks. This means therefore that the timescale at which such diseases operate is much shorter than the time scale of the human population dynamics. We analyse a compartmental model of the SIR type with periodic coefficients and different time scales for 1) disease dynamics and 2) human population dynamics. Interest is to determine the optimal vaccination strategy for such diseases. In a model with time scales, Singular Perturbation theory is used to determine stability condition for the disease free state. The stability condition is here referred to as instantaneous stability condition, and implies vaccination is done only when an instantaneous threshold condition is met. We make a comparison of disease control using the instantaneous condition to two other scenarios: one where vaccination is done constantly over time (constant vaccination strategy) and another where vaccination is done when a periodic threshold condition is satisfied (orbital stability from Floquet theory). Results show that when time scales of the disease and human population match, we see a difference in the performance of the vaccination strategies and above all, both the two threshold strategies outperform a constant vaccination strategy.
1. Introduction
Childhood related diseases such measles have an infective period lasting two weeks on average [1]. This is in sharp contrast to human population dynamics, as the human lifespan is on the average 50 - 60 years for the developing countries and higher for developed countries. Most modeling work involving an analysis of childhood diseases using epidemiological models of the SIR type do not however, take into consideration the possibility of different time scales for such diseases vis a vis the human population dynamics or human resident times, for instance, students in school have an average of 6 months to one year resident time in school, time which they are in contact that can lead to higher spread of disease.
We analyze SIR model with periodic vaccination and contact rates, but more importantly, with different time scales for disease and population dynamics. Periodicity is a common phenomenon for childhood diseases, due to the periodic nature of contacts as a result of school terms or even weather conditions. Weather affects the spread of diseases or disease vectors in different ways. High incidences have been reported for measles at the onset of rainy seasons [2].
In a previous publication, we solely considered the SIR model as a system of ODE with periodic coefficients. We made no reference to time scales, in which case, we used Floquét theory and did orbital stability analysis of the disease free periodic orbit. We shall refer to the results from Floquét theory as “orbital stability analysis” results, where the stability threshold condition is an average quantity over one complete vaccination period.
Analysis for ODE systems with time scales is done using singular perturbation theory. The stability threshold we obtained from singular perturbation theory gives an instantaneous function, unlike in the orbital case which gives an average condition over the whole period of vaccination. In this respect, we refer to the stability results of singular perturbation as “instantaneous stability analysis.”
Optimal vaccination strategies is being studied widely especially due to the challenges of few resources for the developing world, or even for better management of vaccination doses in the developed world [3-7]. A special case referred to as pulse vaccination strategy (PVS) has been addressed by authors such as Shulgin (e.g. [8]), d’Onofrio (e.g. [9]) among others. The concept of PVS addresses the idea of vaccination days. Authors such as Shulgin have compared PVS to the case of constant vaccination strategy (CVS) where vaccination doses are spread randomly over time. The conjecture is that vaccination days enable better management of vaccination doses and allows immune booster for initial vaccine failures. Furthermore, the theory of optimal control for age structured models has also been studied in among others, [10,11].
In all these cases, the idea is to seek which vaccination strategies offer effective control of diseases with minimum costs. In so doing, key assumptions that make the model more realistic need to be taken into consideration. We make effort to study optimal vaccination strategy under such assumptions such as periodicity and different time scales for childhood related diseases.
The paper is organized as follows: In Section 2, we introduce the model, its assumptions and the parameters. In Section 3, a brief overview of result from orbital stability analysis is given for the model defined in Section 2, for which no reference to time scales is made. In Section 4, we introduce the time scales. It turns out that the time scales are not clearly separated as required in the theory of singular perturbation, prompting a suitable transformation of the original model. Stability results of a disease free orbit along a defined “slow manifold” is done to obtain the required threshold condition for stability. We use the threshold condition to define the optimal control problem. In Section 5, we introduce the set of functions called the susceptible population profiles in which we seek optimal solutions and by the properties of this set, we show that optimal solutions exist. We further characterize a candidate optimal control solution from this set of optimal solutions. In Section 6, we conduct simulations using measles related parameters and compare the results of orbital stability and instantaneous stability.
2. Model and Assumptions
We consider a large population that is well mixed like the children of several large schools located close together. The following parameters are used:
1) Contact rate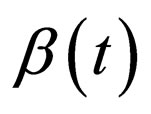 : for
: for 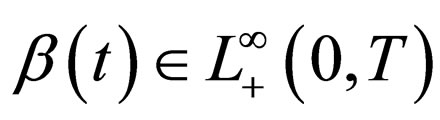 (the class of non-negative
(the class of non-negative 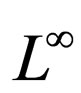 functions) and is also assumed to be bounded away from zero,
functions) and is also assumed to be bounded away from zero,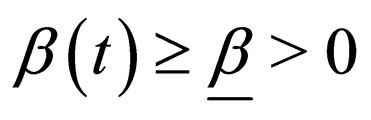 ;
;
2) Vaccination rate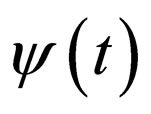 : for
: for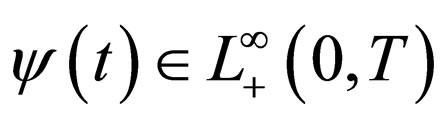 ;
;
3) The influx rate into the population, ;
;
4) 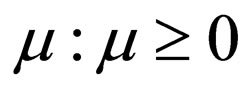 is the exit rate (which may be rather related to the exit from the population compartment under consideration than to mortality);
is the exit rate (which may be rather related to the exit from the population compartment under consideration than to mortality);
5) 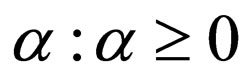 the recovery rate;
the recovery rate;
6) For comparison of the model with time scales that we hope to analyse in this paper and the previous periodically driven model, we shall maintain the feature of periodicity of the coefficients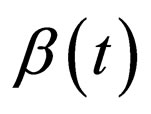 , periodic with period
, periodic with period 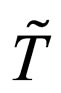 and vaccination rate
and vaccination rate 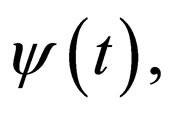 periodic with period
periodic with period 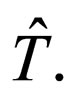 However we adopt a common time period T such that
However we adopt a common time period T such that
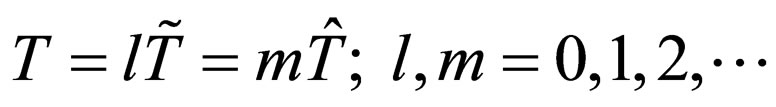 .
.
The SIR-model reads,
 (1)
(1)
We require that given a number of vaccination doses, the uninfected solution is stable against disease outbreak. We considered the stability analysis for model (1), which is a periodically driven ODE system, using Floquét theory. Implicitly, the time scale for both disease and human population dynamics was assumed the same. We shall introduce time scales in model (1) and use singular perturbation theory for analyzing ODE systems with different time scales [12-14]. The theory of model (1) was considered in a preceding paper [15].
The total population 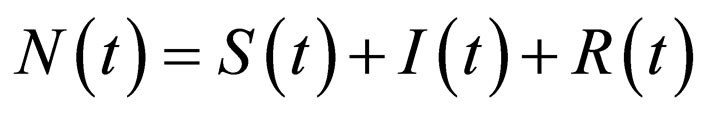 is governed by the differential equation,
is governed by the differential equation,
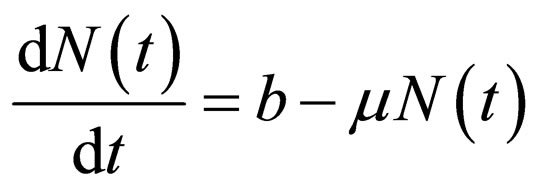 (2)
(2)
and thus,
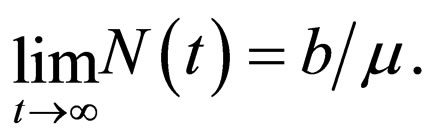 (3)
(3)
Proposition 1 For  a unique solution
a unique solution 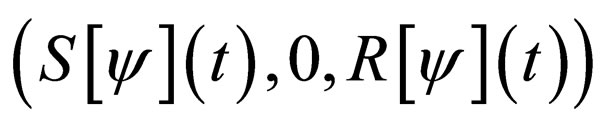 to the SIR model (1). Furthermore, even for periodic coefficients, the model (1) is well posed.
to the SIR model (1). Furthermore, even for periodic coefficients, the model (1) is well posed.
Proof. Well possedness of a standard SIR model has been extensively studied. For periodic driven system that we make reference to in this paper, refer to [15]. In Section 4, we make further comments on the well possedness of this model when time scales are introduced, on the invariant manifold □
□
3. Overview of the Model without Time Scales
In [15], we assumed that the parameters 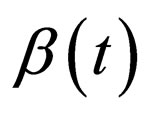 and
and 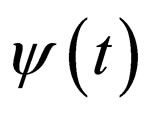 are periodic. Via Floquét theory, we obtained the threshold for stability of the disease free solution, that is, in the presence of vaccination, there is no epidemic outbreak if
are periodic. Via Floquét theory, we obtained the threshold for stability of the disease free solution, that is, in the presence of vaccination, there is no epidemic outbreak if 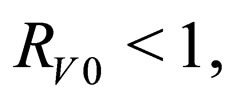 where
where
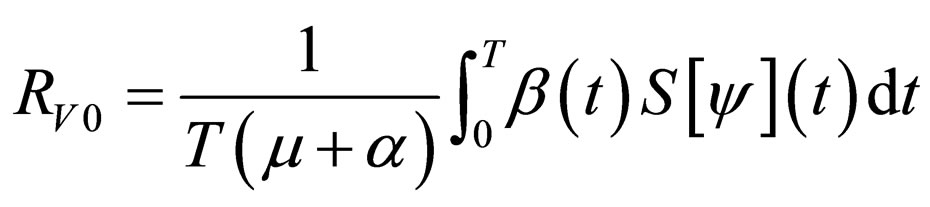 (4)
(4)
Further, we assumed that vaccination targets the susceptible population only. The vaccination coverage is therefore defined by the product of the vaccination rate and the size of susceptible population.
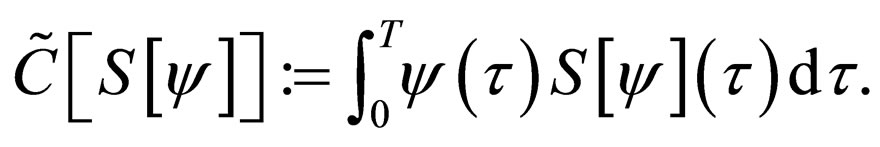
Define 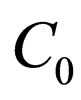 as the maximum amount of vaccination doeses available. We assume that the vaccination costs are subject to a constraint
as the maximum amount of vaccination doeses available. We assume that the vaccination costs are subject to a constraint 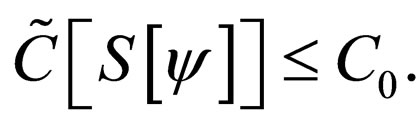 This leads to formulation of an optimal control problem of the form.
This leads to formulation of an optimal control problem of the form.
Problem 1 For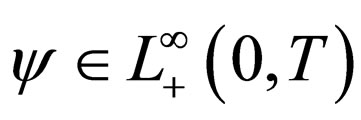 , find the vaccination schedule that minimizes
, find the vaccination schedule that minimizes
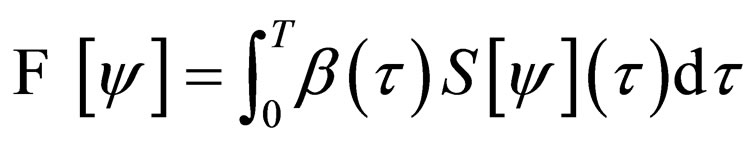
defined from the  under the cost constraint
under the cost constraint  and the susceptible population is governed by the differential equation,
and the susceptible population is governed by the differential equation,
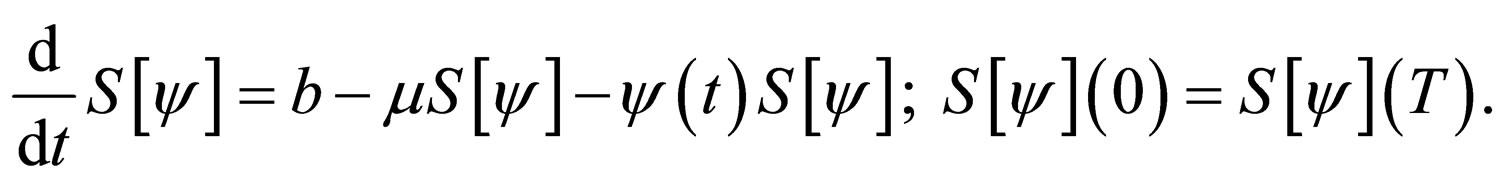
We sought solutions of the optimal control problem 3 in the set of susceptible population profiles
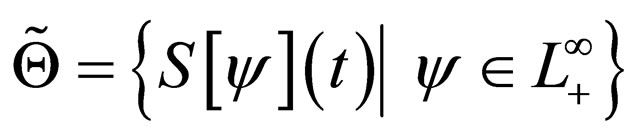
rather than in the set 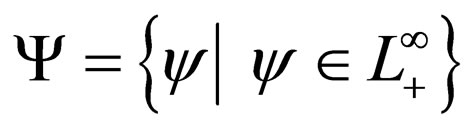 as would be the case in classical optimal control theory. This assumption was based on the fact that the disease affects the susceptible population and we can understand much about the progression of the disease by studying the susceptible population [16]. An optimal vaccination strategy ensures that the number of susceptible individuals in a population is small, if not zero and on the other hand, the number of immune individuals should be large.
as would be the case in classical optimal control theory. This assumption was based on the fact that the disease affects the susceptible population and we can understand much about the progression of the disease by studying the susceptible population [16]. An optimal vaccination strategy ensures that the number of susceptible individuals in a population is small, if not zero and on the other hand, the number of immune individuals should be large.
There could be infinitely many optimal solutions in  that satisfy the ODE and the cost constraint. We characterize one such solution, that belongs to the closure of the set
that satisfy the ODE and the cost constraint. We characterize one such solution, that belongs to the closure of the set  and corresponds to the minimum of the functional
and corresponds to the minimum of the functional
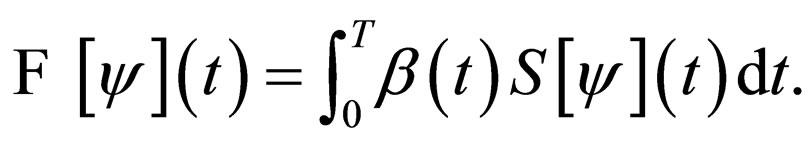
After some considerations, the problem of minimizing the functional 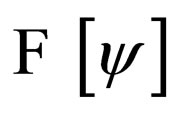 was reformulated into a problem of maximizing the functional
was reformulated into a problem of maximizing the functional
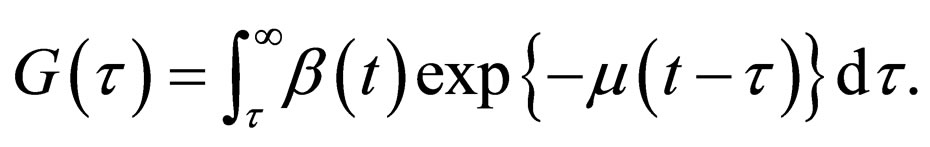 (5)
(5)
4. Introducing Time Scales
Consider a disease which is quite infectious but has a short infective period in comparison with the the human life span. This assumption holds for cases like measles that have a short infective period of two to four weeks. Thus, to seek to express the different time scales, we modify model (1) by introducing a parameter 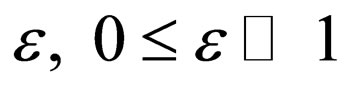 with a view to making the disease dynamics faster via disease related parameters
with a view to making the disease dynamics faster via disease related parameters 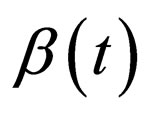 and
and 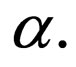
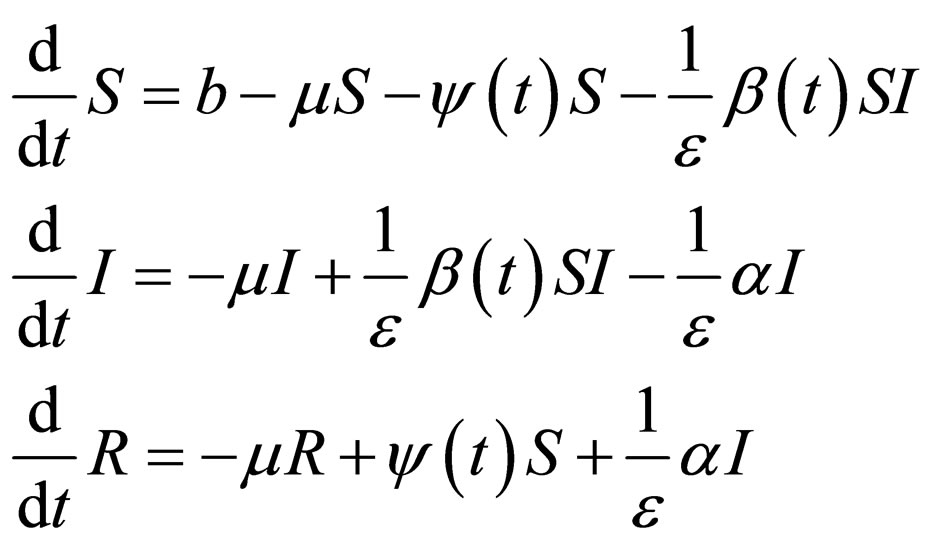 (6)
(6)
We want to know under what conditions an epidemic is possible in this scenario. We seek stability of disease free state for the model (6), via singular perturbation theory. The theory however requires clearly separated time scales and an autonomous equation.
To obtain an autonomous system, we first augment the state space with a variable 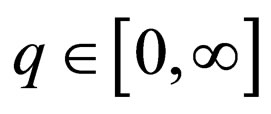 and obtain
and obtain
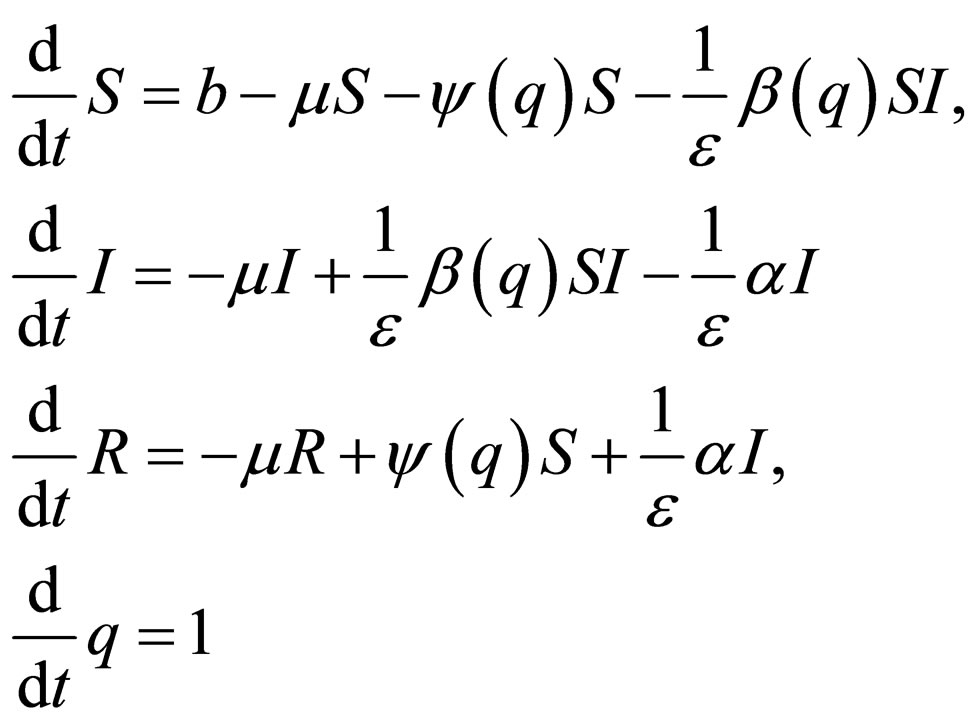 (7)
(7)
The time scale of (7) is the time scale of the population dynamics. If we transform time to the fast time scale of the disease, using 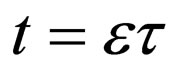 and dropping the equation for R since
and dropping the equation for R since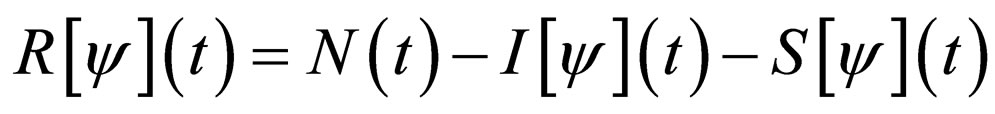 , we get,
, we get,
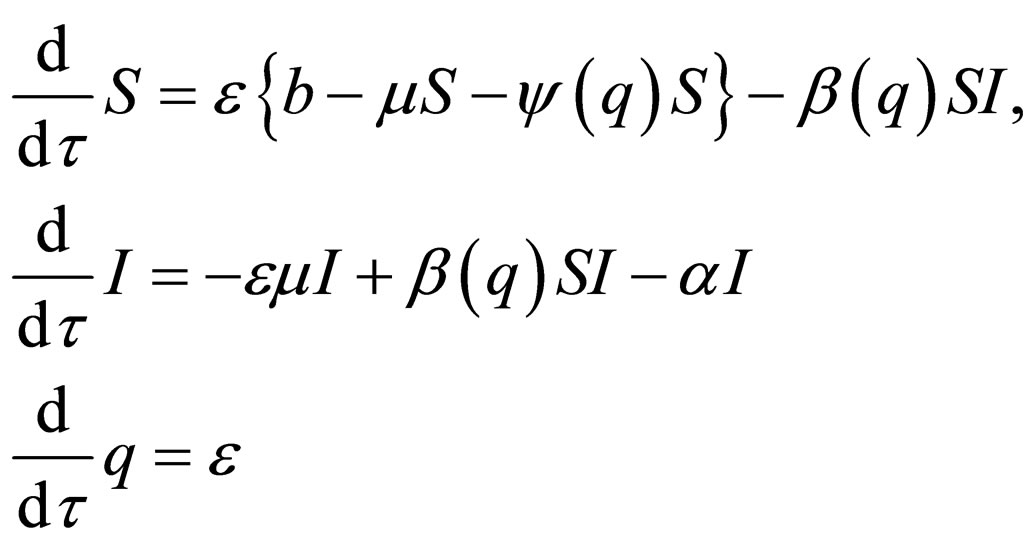 (8)
(8)
Taking  (8) becomes an SIR-model without population dynamics whose phase plane is fibred by the curves,
(8) becomes an SIR-model without population dynamics whose phase plane is fibred by the curves,
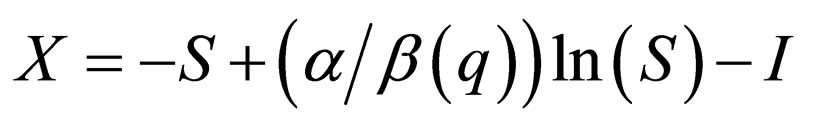 (9)
(9)
Remark 1 The attempt to have a perfect fast-slow system (in the context of singular perturbation theory) leads to a deeper examination of the function X. Note that X defines a constant on a fast system. We could heuristically define 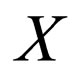 as a variable, a slow variable in the context of Singular perturbation theory. Hence we choose to transform the system
as a variable, a slow variable in the context of Singular perturbation theory. Hence we choose to transform the system 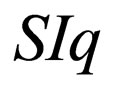 to
to 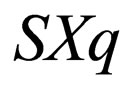 with X and S as the slow and fast variables respectively. The result is a distinct fast-slow system.
with X and S as the slow and fast variables respectively. The result is a distinct fast-slow system.
4.1. Distinct Time Scales
The system (7) mixes the slow time scales of population dynamics/vaccination with the fast time scale of the epidemic. In order to apply singular perturbation theory, we separate the time scales explicitly using a transformation of variables. The system (7) leads to the slow system,
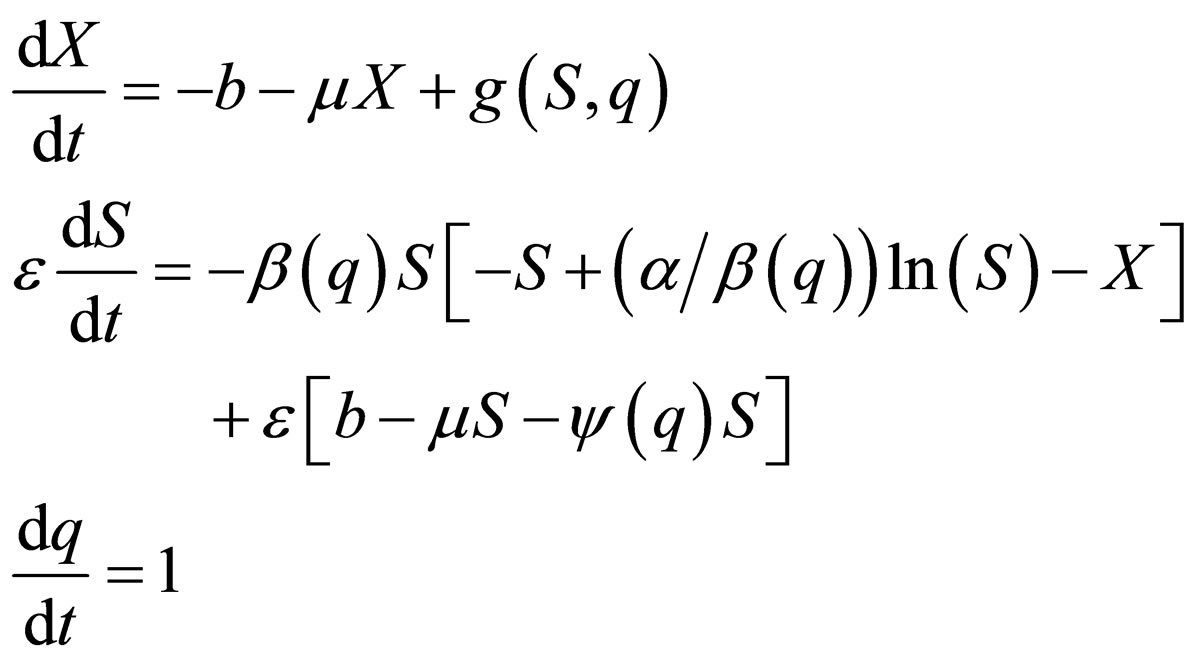 (10)
(10)
where
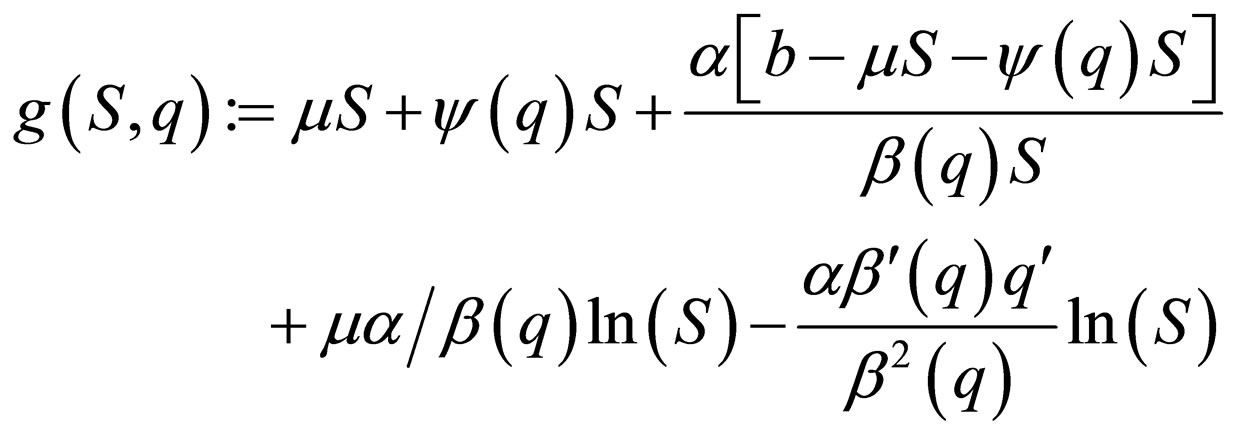
Let 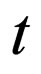 represent the slow time,
represent the slow time, 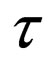 represent the fast time and
represent the fast time and 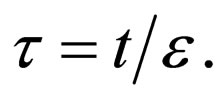 The fast system reads,
The fast system reads,
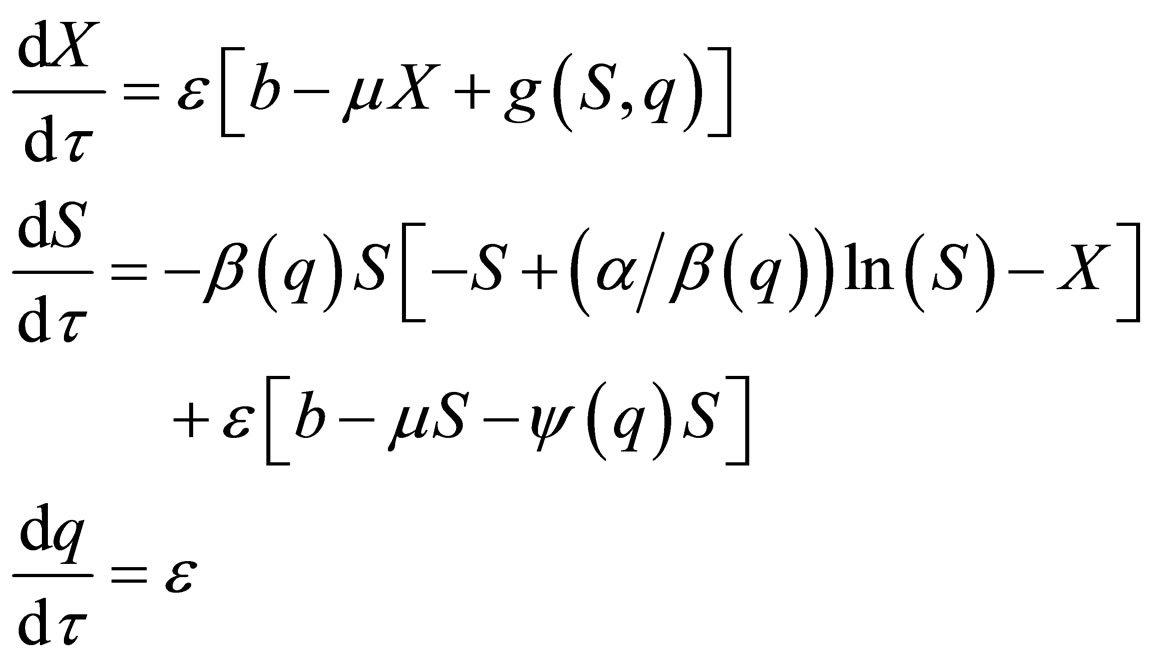 (11)
(11)
Invariant Manifold 
Consider the solution of model (1) on the invariant plane  which corresponds to the diesease free state. This plane is also invariant for the transformed system, as the transformation is regular. In the transformed system, we denote this manifold by
which corresponds to the diesease free state. This plane is also invariant for the transformed system, as the transformation is regular. In the transformed system, we denote this manifold by
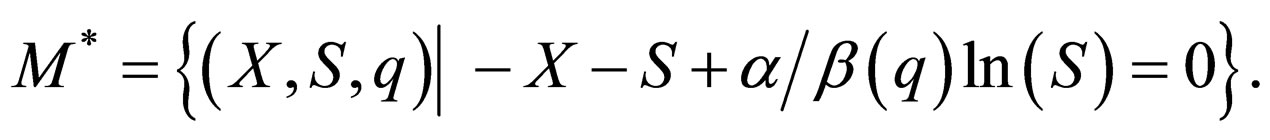
The dynamics for the 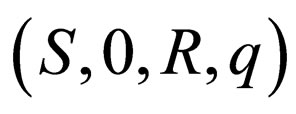 system where
system where 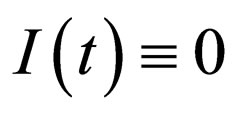 is given by the dynamics of the system
is given by the dynamics of the system 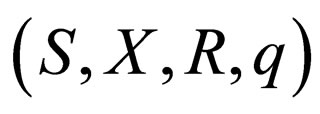 where
where 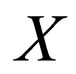 is given by
is given by 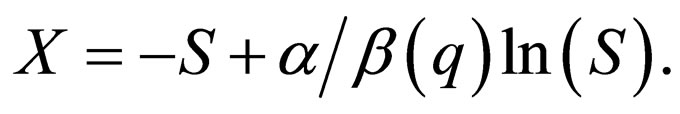 It is necessary to note that neither the manifold nor the dynamics on the manifold depends on
It is necessary to note that neither the manifold nor the dynamics on the manifold depends on . The limiting systems, when
. The limiting systems, when  (for the limiting fast as well as the slow system) do not have
(for the limiting fast as well as the slow system) do not have  dependance, hence this manifold will be conserved. This is because if we have no infected individuals we will never have infected individuals in the system; moreover,
dependance, hence this manifold will be conserved. This is because if we have no infected individuals we will never have infected individuals in the system; moreover,  only appears in terms that include
only appears in terms that include  and is not generically true for the slow manifold.
and is not generically true for the slow manifold.
All feasible initial conditions 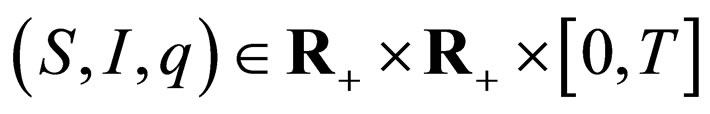 correspond to points in
correspond to points in
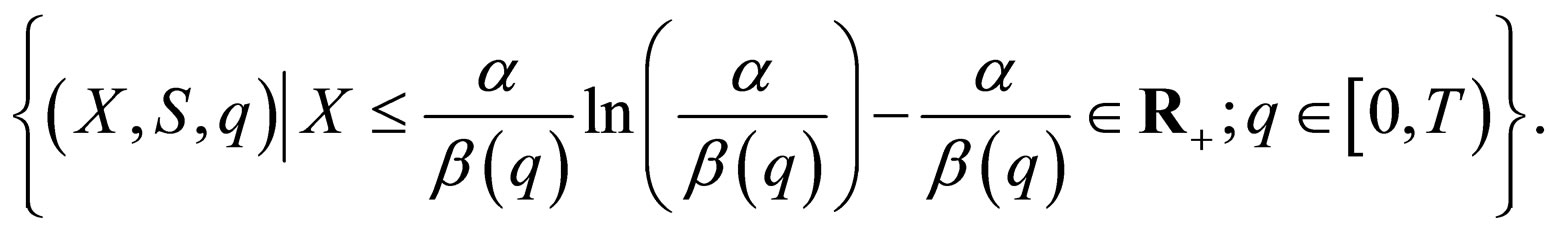
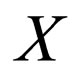 assumes values only below the maximum of
assumes values only below the maximum of 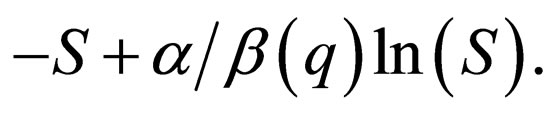 The maximum is assumed at
The maximum is assumed at 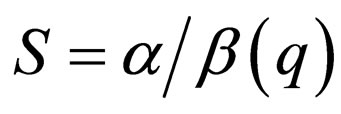 and thus
and thus 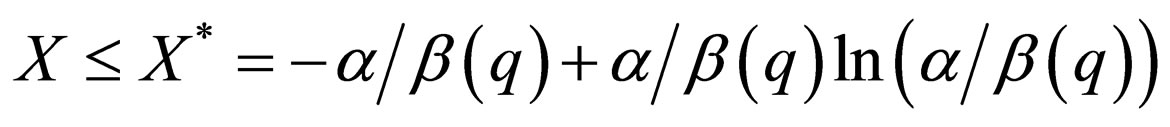 .
.
The slow manifold generically depends on the 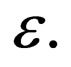 But in this special case,
But in this special case,  hence
hence 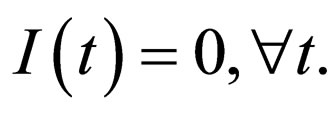 For this reason, though
For this reason, though  is non-hyperbolic, it remains invariant nevertheless. This is generally not a feature of a non-hyperbolic manifolds.
is non-hyperbolic, it remains invariant nevertheless. This is generally not a feature of a non-hyperbolic manifolds.
4.2. Limiting Systems
We do the infinite separation of time, by taking 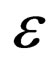 to zero for the fast system. The limiting fast system reads,
to zero for the fast system. The limiting fast system reads,
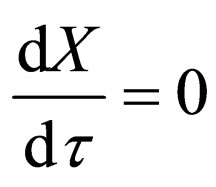
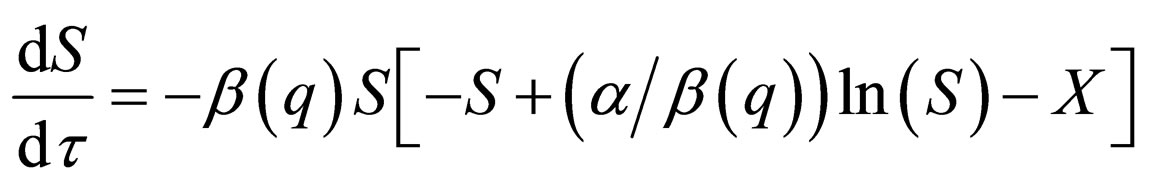 (12)
(12)
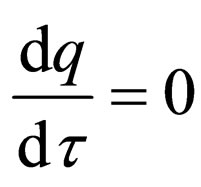
We are now on the time scale of the fast process. We determine the stationary solutions of 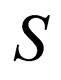 for
for 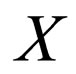 and
and 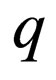 fixed. The two solution branches include
fixed. The two solution branches include , or
, or

As only  is allowed for
is allowed for 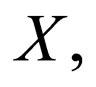 we find no additional stationary points. The stationary points in the
we find no additional stationary points. The stationary points in the  -plane are sketched in Figure 1. The dashed line indicates the unstable branch while the solid line indicates the stable branch solution. The arrows indicate the direction of the fast field.
-plane are sketched in Figure 1. The dashed line indicates the unstable branch while the solid line indicates the stable branch solution. The arrows indicate the direction of the fast field.
Now consider the slow system and take 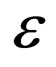 to zero,
to zero,

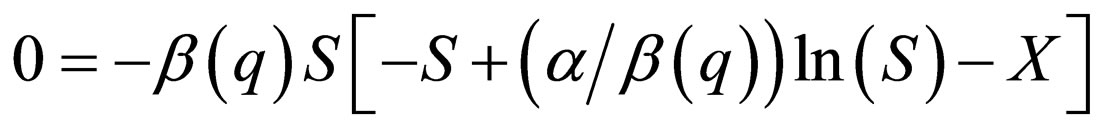 (13)
(13)
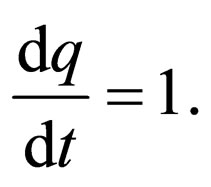
The idea is to solve for  on the slow manifold given by the zero set of the function,
on the slow manifold given by the zero set of the function,
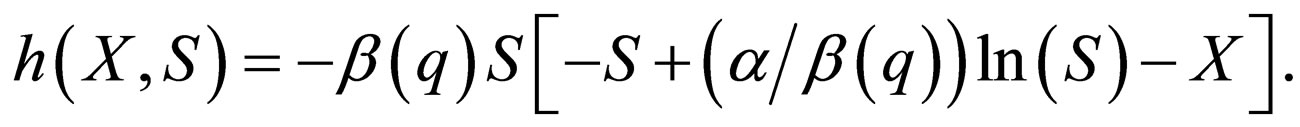
Let 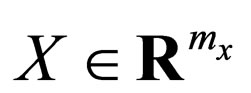 and
and  Our focus is on systems for which the zero set of
Our focus is on systems for which the zero set of 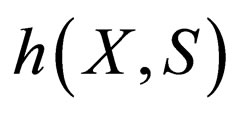 is represented by the graph of a function. That is, we assume that there exists a single-valued function
is represented by the graph of a function. That is, we assume that there exists a single-valued function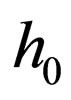 , which is defined on a compact domain in
, which is defined on a compact domain in 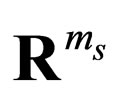 such that
such that
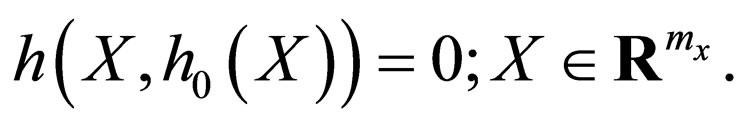
The zero set of 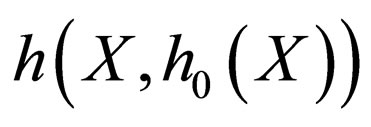 thus defines a manifold in phase space,
thus defines a manifold in phase space,
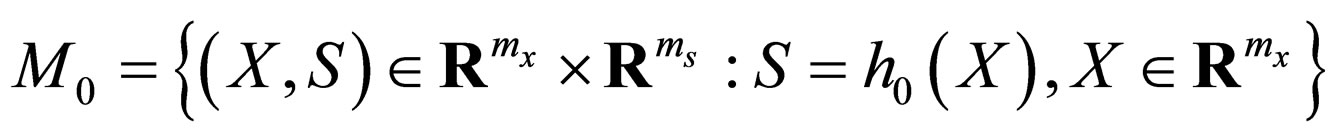
to which the motion of the reduced slow system is confined. We note that the non-linearity of 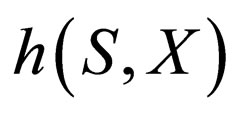 w.r.t
w.r.t  makes it difficult to obtain the representation
makes it difficult to obtain the representation  We are however interested in the stability along solution branches.
We are however interested in the stability along solution branches.
4.3. Stability along Slow Manifold
We read the slow manifold from the system (13) and denote it by
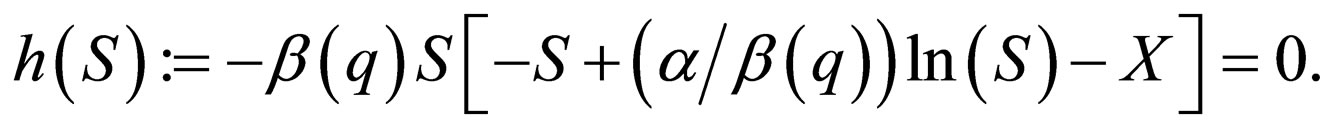
There are three solution branches along the slow manifold 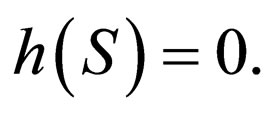 The first branch is
The first branch is 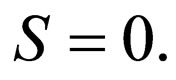 The graph
The graph 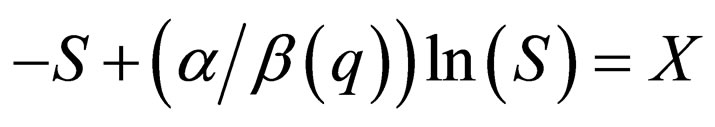 has two solution branches for
has two solution branches for  herein referred to as the middle branch and
herein referred to as the middle branch and 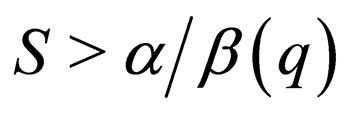 which we refer to as the right hand outer branch.
which we refer to as the right hand outer branch.
In order to determine the stability along the slow manifold, we inspect the flow on the phase portrait using the nullclines of the limiting system. The branch 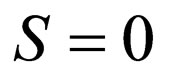 is unstable, while branch
is unstable, while branch 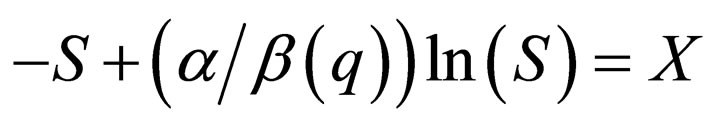 has a stable middle branch and unstable outer branch, see Figure 1, the two branches separated at the point when the derivative of
has a stable middle branch and unstable outer branch, see Figure 1, the two branches separated at the point when the derivative of 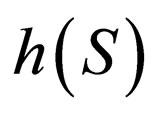 w.r.t.
w.r.t.  is equal to zero. This corresponds to the maximum point on this solution branch. On the stable part of this solution branch,
is equal to zero. This corresponds to the maximum point on this solution branch. On the stable part of this solution branch,
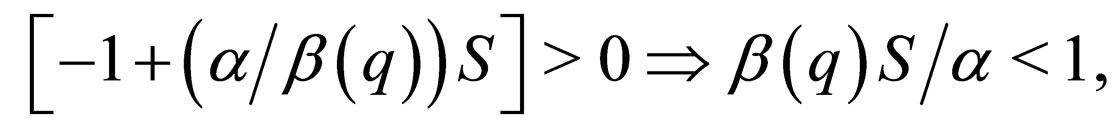
from which we define the stability threshold. Since we are on the invariant manifold 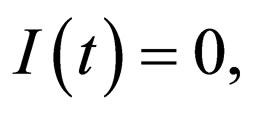 the disease free solution is stable if
the disease free solution is stable if 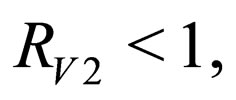 where
where  is defined below.
is defined below.

Figure 1. Solution branches on the 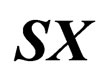 -plane, including fast and slow manifolds.
-plane, including fast and slow manifolds.
We define the instantaneous reproduction number as follows.
Definition 1 The instantaneous reproduction rate (in presence of vaccination) 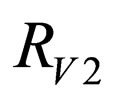 is defined by
is defined by
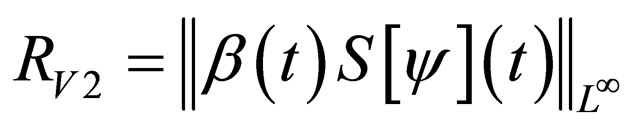
We call the uninfected periodic orbit instantaneously stable, if
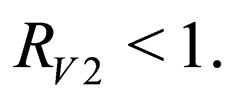
Note that 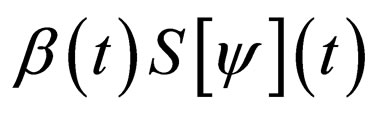 may not be well defined for every time point, since we only know that
may not be well defined for every time point, since we only know that 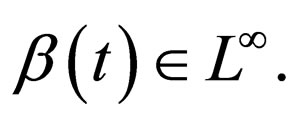 Hence our choice of the essential supremum of this function in defining
Hence our choice of the essential supremum of this function in defining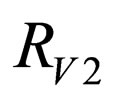 .
.
We note that 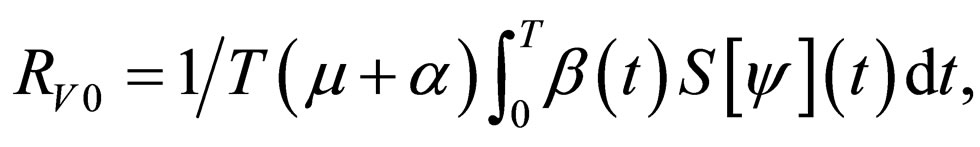
defined in section (3) is an average quantity over the period [0,T) while 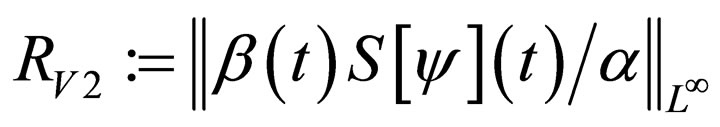 is an instantaneous stability criterion. We conjecture that there could be (for some pathological case), small epidemic outbreaks in disease
is an instantaneous stability criterion. We conjecture that there could be (for some pathological case), small epidemic outbreaks in disease  even though the overall orbital stability condition still holds
even though the overall orbital stability condition still holds 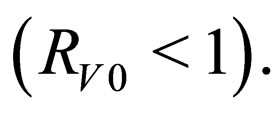 We reach the following conclusion.
We reach the following conclusion.
Proposition 2 If the uninfected periodic orbit is instantaneous stable, it is also orbital stable. In general, it is not true that orbital stability implies instantaneous stability.
4.4. Defining the Optimal Control Problem Due to Instantaneous Stability
The aim is to find a vaccination schedule that is as effective as possible. During one period for vaccination we want to spend at most 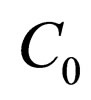 vaccination doses. The idea is to distribute the doses, such that the periodic solution minimizes the efficiency of this dose-distribution, measured in terms of instantaneous stability of disease free state.
vaccination doses. The idea is to distribute the doses, such that the periodic solution minimizes the efficiency of this dose-distribution, measured in terms of instantaneous stability of disease free state.
Problem 2 For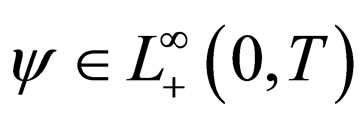 , find the vaccination schedule that minimizes
, find the vaccination schedule that minimizes
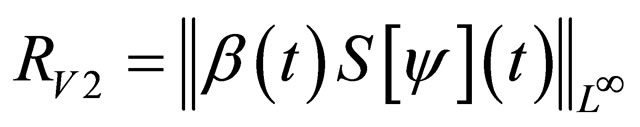
under the constraint that the number of vaccination doses, defined by
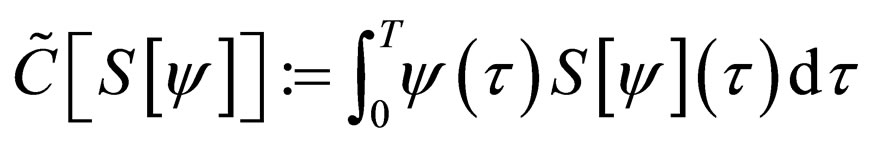
is bounded above by the maximum doses 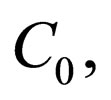 i.e.,
i.e., 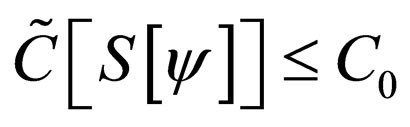 and the susceptible population is governed by the differential equation,
and the susceptible population is governed by the differential equation,
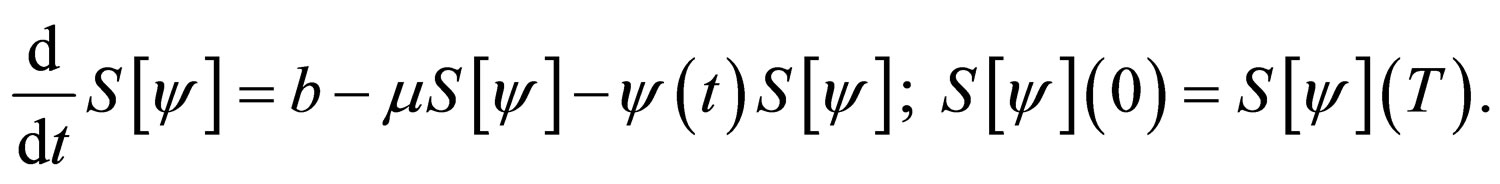
It is important to address the issue of existence for solutions for problem 4.4. We take note of the following details. One, the worst strategies maximize  Furthermore, the success of any vaccination program can be defined in terms of how many susceptible individuals are still in the population, i.e., an excellent vaccination program implies no susceptible people remain in the population (all should be immune).
Furthermore, the success of any vaccination program can be defined in terms of how many susceptible individuals are still in the population, i.e., an excellent vaccination program implies no susceptible people remain in the population (all should be immune).
We therefore study vaccination strategies in terms of a set of susceptible population profiles 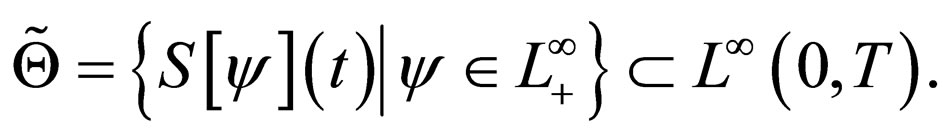 We do not seek solutions for
We do not seek solutions for  but do our search to a set
but do our search to a set , the closure of
, the closure of  in
in 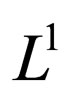 [17,18].
[17,18].
5. Optimal Vaccination Strategies
5.1. The Set  and Its Properties
and Its Properties
In the ensuing discussion, we explore the existence of solutions within the set  and by extension, in its closure
and by extension, in its closure  For ease of notation, we shall denote the susceptible profile
For ease of notation, we shall denote the susceptible profile  by
by  We shall explore the properties of the set
We shall explore the properties of the set  for purposes of existence of solutions.
for purposes of existence of solutions.
Remark 2 We begin by exploring if  is bounded. We also explore if the cost function in bounded. Consider the proof in the appendix Section 8. The susceptible population and the cost of vaccination are both uniformly bounded, i.e.,
is bounded. We also explore if the cost function in bounded. Consider the proof in the appendix Section 8. The susceptible population and the cost of vaccination are both uniformly bounded, i.e.,
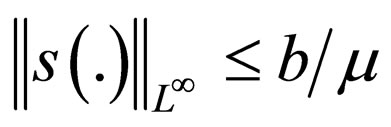
and
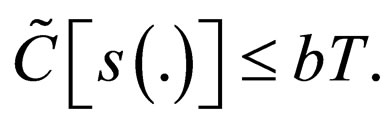
We understand the following from 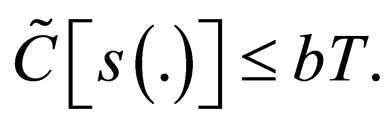 where b is birth rate and T is a vaccination period. That the maximal vaccination coverage is the total new births that occur within a period of time. The actual number of vaccination doses used is thus
where b is birth rate and T is a vaccination period. That the maximal vaccination coverage is the total new births that occur within a period of time. The actual number of vaccination doses used is thus 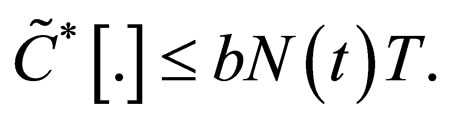
We further show in the appendix Section 8 that  is pre-compact in
is pre-compact in 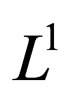 and its closure
and its closure  is a compact subset of
is a compact subset of  By this property, we can define any candidate solution in
By this property, we can define any candidate solution in  that certainly converges to a point in
that certainly converges to a point in 
Theorem 1 Let 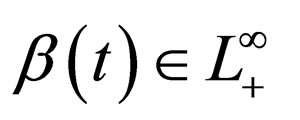 and
and 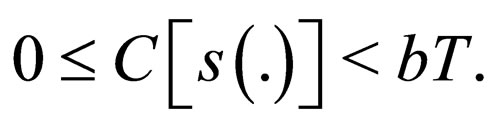 Problem 4.4 has a solution in
Problem 4.4 has a solution in .
.
Proof. Let
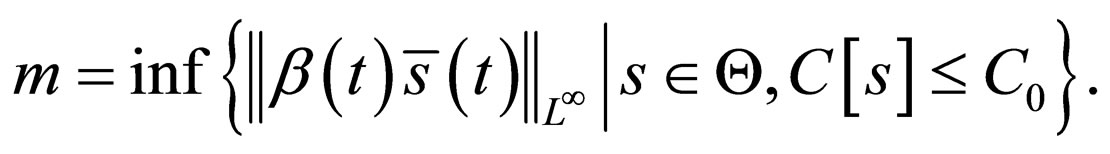
As  is bounded, and
is bounded, and , the number
, the number 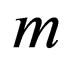 is well defined. Consider a sequence
is well defined. Consider a sequence 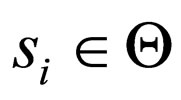 with
with  Suppose further that the sequence of values
Suppose further that the sequence of values 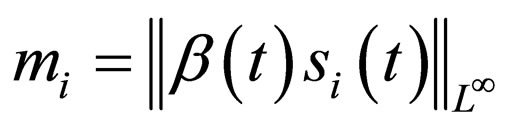 converges to
converges to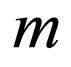 . Since
. Since  is compact w.r.t. the
is compact w.r.t. the 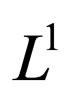 -topology (see appendix 8), there exists a subsequence
-topology (see appendix 8), there exists a subsequence 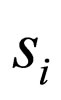 that converge in the
that converge in the 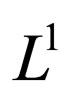 -norm to a point
-norm to a point .
.
Suppose
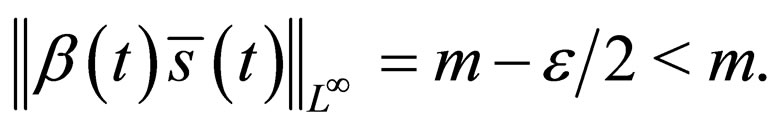
That is, there is a set of non zero measure
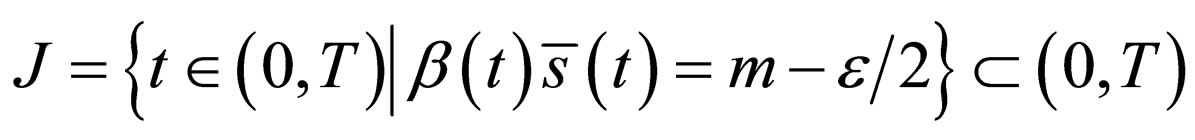
and that there exists 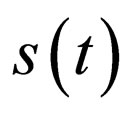 for which
for which
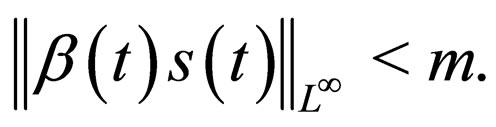
Consider 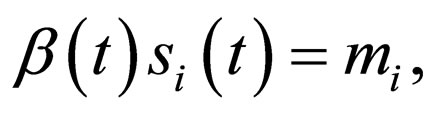 where
where  Take
Take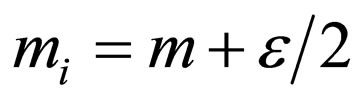 . Then
. Then
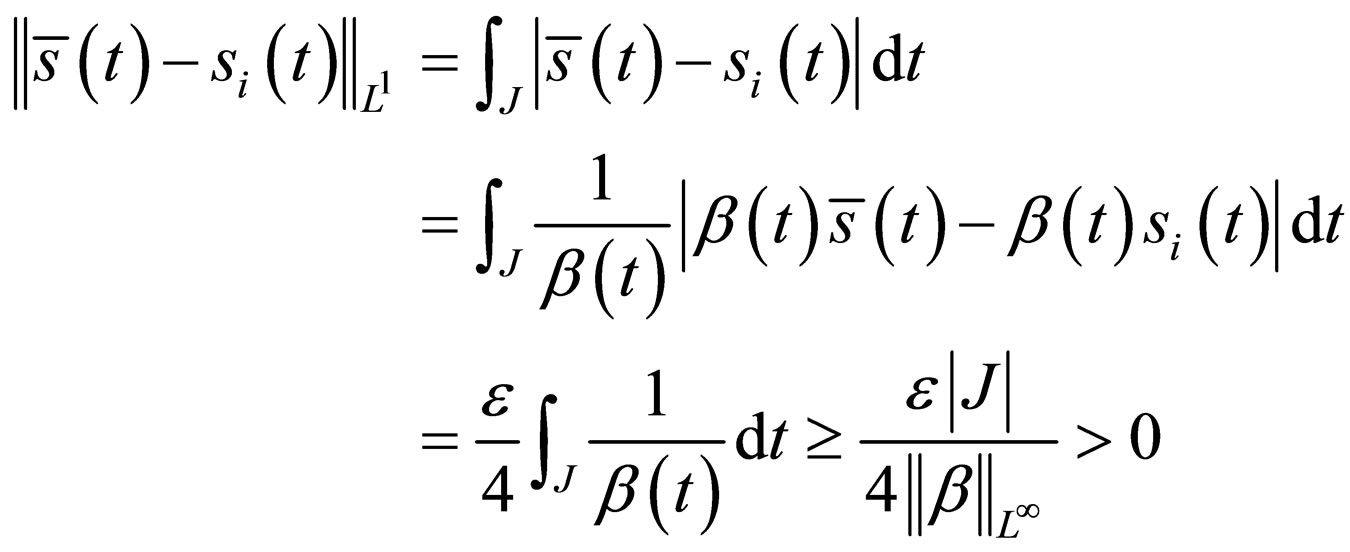
The  norm of the difference should not be larger than zero if
norm of the difference should not be larger than zero if  converges to
converges to  in the
in the 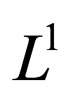 -norm. Thus, by this contradiction, we conclude that
-norm. Thus, by this contradiction, we conclude that 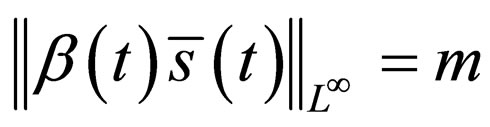 and
and 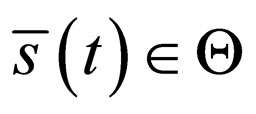 and therefore
and therefore 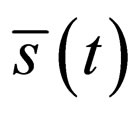 is an optimal solution of the problem.□
is an optimal solution of the problem.□
We next wish to illustrate how to characterize optimal population profiles in the sense of problem 4.4.
Remark 3 The optimal vaccination strategy utilizes the least vaccination doses for maximum effect (disease control). The more the vaccination doses used, the smaller the susceptible population in the population at the end of the day. But there is a limit on how much vaccination doses we ought to use. In fact, the less vaccination doses we use, the better. The optimal vaccination solution does not correspond to the minimum susceptible population, but to the largest susceptible population for which the disease is under control, i.e. in this case, for which,
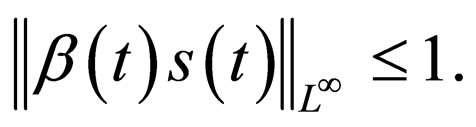
Remark 4
1) An optimal solution of problem 4.4 is a maximal element of the set
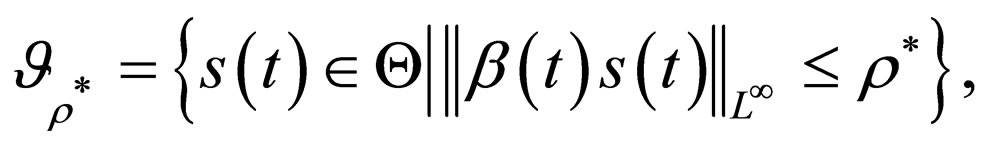
where 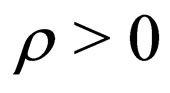 is chosen appropriately and maximality is defined via the partial order induced by the positive cone of
is chosen appropriately and maximality is defined via the partial order induced by the positive cone of .
.
2) A maximal element 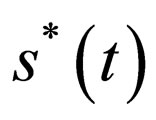 of
of  is an optimal solution of problem 4.4 at costs
is an optimal solution of problem 4.4 at costs .
.
Remark 5 As the maximal element in 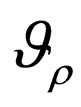 is unique, the solution of problem 4.4 is unique.
is unique, the solution of problem 4.4 is unique.
Proposition 3 Consider any vaccination point  Then the limits,
Then the limits,  and
and 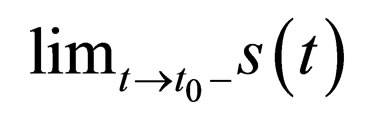 are well defined.
are well defined.
Proof. It follows from lemma (1) to lemma (3) in the appendix section B that the limit is well defined. In the notation in the appendix, we revert back to usual notation for susceptible solutions of our differential equation, 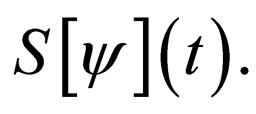 In the sections here within the text, we have used the simpler notation
In the sections here within the text, we have used the simpler notation  to denote the solution for the susceptible population.
to denote the solution for the susceptible population.
We now turn to the problem of how to construct optimal population profiles in an explicit manner.
Remark 6
1) We find that there are two different modes for optimal population profiles, resembling the bang-bang structure: either no control takes place and the profile behaves according to the non-controlled ODE 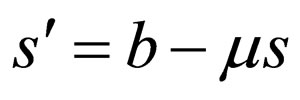 ; or, we control enough to exactly meet the critical threshold condition
; or, we control enough to exactly meet the critical threshold condition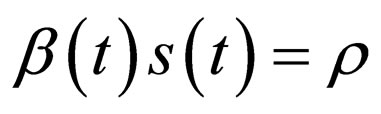 .
.
2) This observation can be formulated in a heuristic algorithm: start at time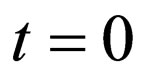 , and note that the completely unvaccinated population has size
, and note that the completely unvaccinated population has size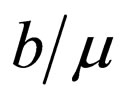 . If
. If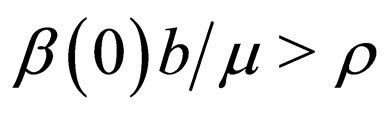 , then control the population and define
, then control the population and define 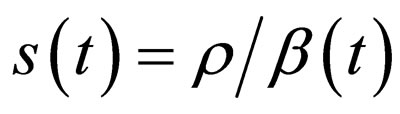 for small time intervals, else define
for small time intervals, else define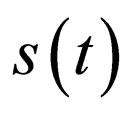 . Proceed in this manner: If
. Proceed in this manner: If 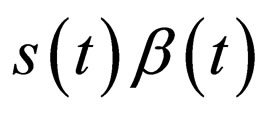 exceeds
exceeds  without control, define
without control, define ; if
; if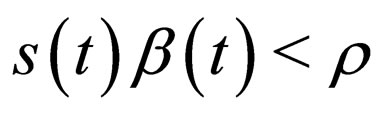 , then do not control the population, that is, define
, then do not control the population, that is, define 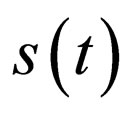 by
by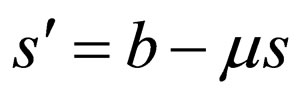 , together with continuity requirements. If this procedure eventually leads to a periodic function, this function is a good candidate for an optimal population profile.
, together with continuity requirements. If this procedure eventually leads to a periodic function, this function is a good candidate for an optimal population profile.
5.2. Candidate Optimal Vaccination Strategy
For simplicity of the function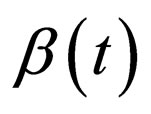 , we define two forms of periodic contact rate:
, we define two forms of periodic contact rate:
• Rectangular form, with one high and one low value within a vaccination period. This could be one calender year where contact rate is high during schooling season (assumed to be continuous with none or very short breaks) and low during holiday season (also one continuous period);
• A step function, which has high and low values in more than just two time periods.
We begin with the rectangular form of 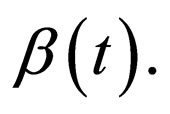
5.2.1. Rectangular Contact Rate
It is possible to represent a two level contact rate to mimic school holidays, when contact rate is low by 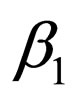 and school terms when the contact rate is higher by
and school terms when the contact rate is higher by 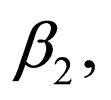 such that
such that
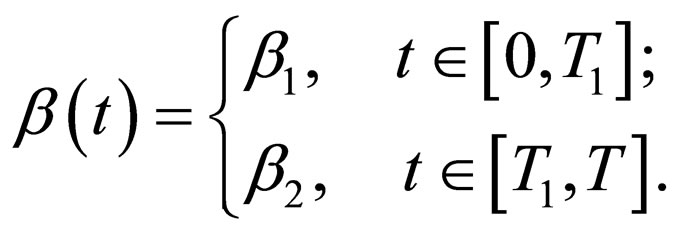
Hence 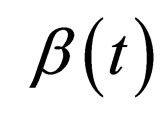 is periodic. Without restriction, we assume in this section always that
is periodic. Without restriction, we assume in this section always that 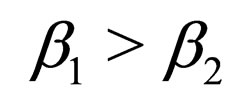 and that the jump from
and that the jump from 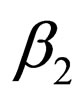 to
to  occurs at time zero and of course at time
occurs at time zero and of course at time 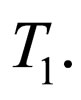
Proposition 4 Assume that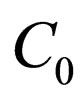 , the maximum number of vaccination doses to be used in [0,T) is fixed. The population profile for the optimal solution reads
, the maximum number of vaccination doses to be used in [0,T) is fixed. The population profile for the optimal solution reads
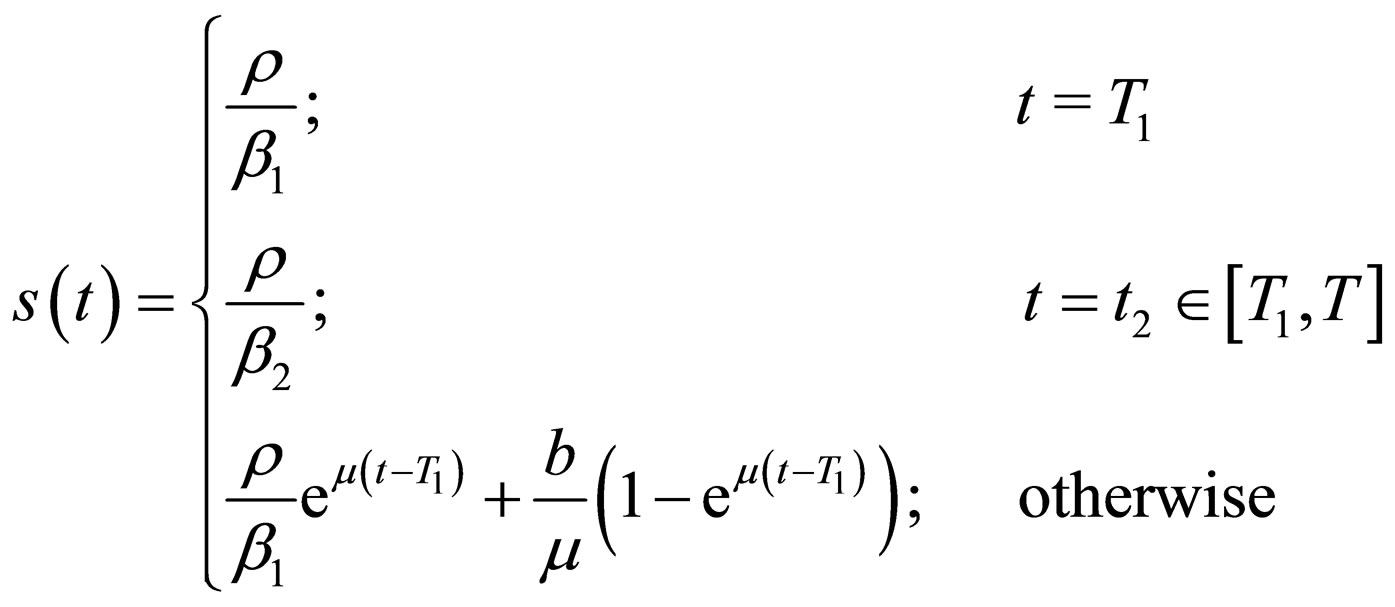
where 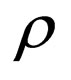 is to adapt to meet the requirement
is to adapt to meet the requirement , and the parameter
, and the parameter  is determined by the condition
is determined by the condition
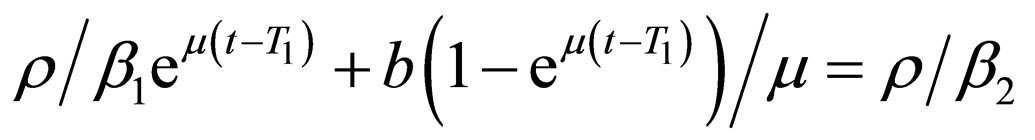
if this equation has a solution at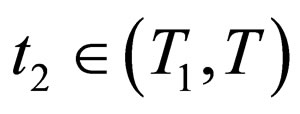 ; else, we choose
; else, we choose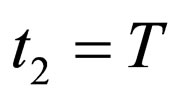 .
.
In other words, we control the population in the first time interval; if the contact rate jumps down from 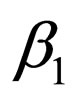 to
to  (note, that we assume
(note, that we assume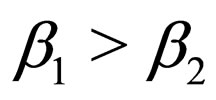 ), there is at least a small time window where no control is necessary. Depending on
), there is at least a small time window where no control is necessary. Depending on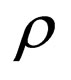 ,
,  and
and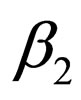 , it may (or may not) be the case that the population grows enough such that
, it may (or may not) be the case that the population grows enough such that 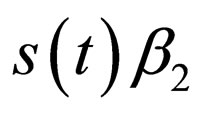 crosses the threshold
crosses the threshold  in
in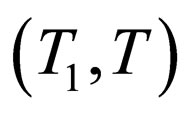 . Accordingly, we defined
. Accordingly, we defined .
.
If we consider the vaccination rate, and not the vaccination population profile, we find that at time zero there is a delta peak, as the population necessarily jumps down to balance the jump up of the contact rate; in the next interval we control with a constant vaccination rate such that the threshold is still met. If the contact rate jumps down, no control is necessary, that is, the vaccination rate is zero. At time , we again need to control the population and have again a constant vaccination rate in the time interval
, we again need to control the population and have again a constant vaccination rate in the time interval . It is straight to check (or better: we check this with the considerations in this paragraph), via the proposition 5.2 that this population is optimal, indeed. We admit that proposition 5.2 requires a continuous contact rate, whereas we have here a discontinuous contact rate. However, it is (for this simple case) possible to check that the arguments still hold true.
. It is straight to check (or better: we check this with the considerations in this paragraph), via the proposition 5.2 that this population is optimal, indeed. We admit that proposition 5.2 requires a continuous contact rate, whereas we have here a discontinuous contact rate. However, it is (for this simple case) possible to check that the arguments still hold true.
5.2.2. Contact Rate as a Step Function
Similarly, we can handle the case of a piecewise constant function (with a finite number of jumps).
Proposition 5 Assume that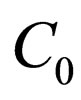 , the maximum number of vaccination doses to be used in [0,T) is fixed; let
, the maximum number of vaccination doses to be used in [0,T) is fixed; let 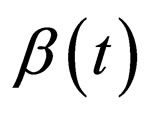 be a piecewise constant function, i.e. assume that there are time points
be a piecewise constant function, i.e. assume that there are time points  and constants
and constants 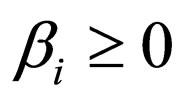 such that
such that
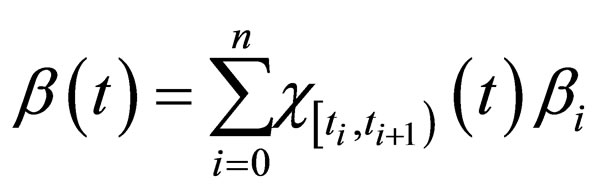
where
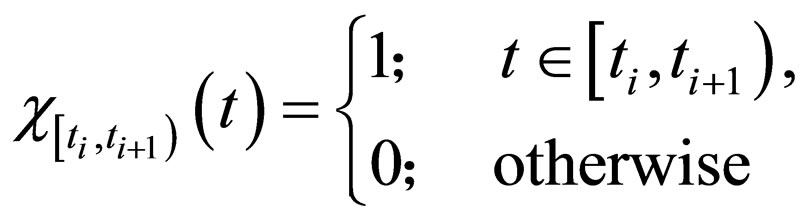
and the population profile for the optimal solution in interval 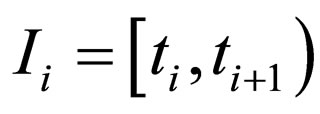 reads
reads
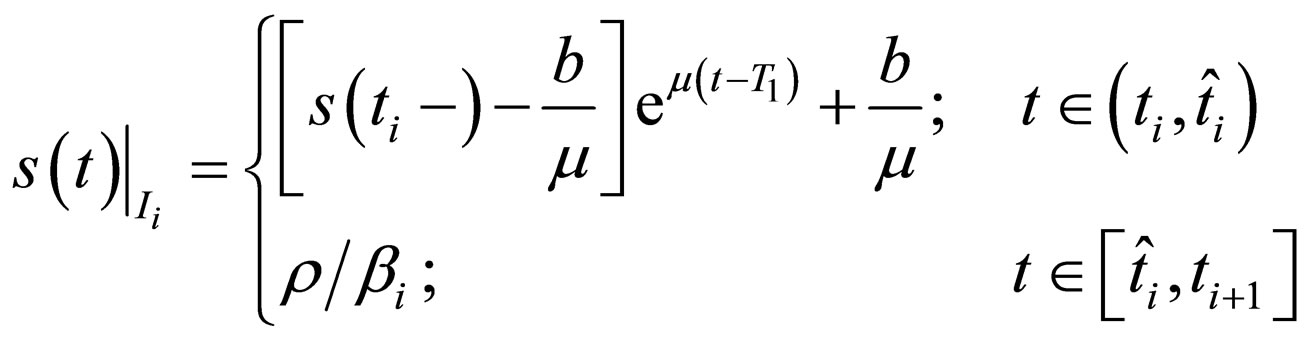
where 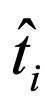 is the immediate time point when
is the immediate time point when 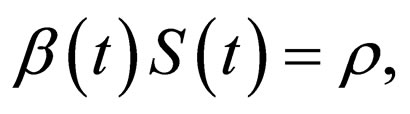
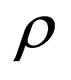 is adapted to meet the requirement
is adapted to meet the requirement , and the time points
, and the time points  are to be determined by the condition that
are to be determined by the condition that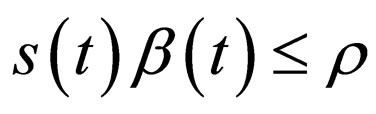 , and
, and  on
on .
.
6. Simulation
We use simulation parameters that depict measles [19]. The population is normalized such that 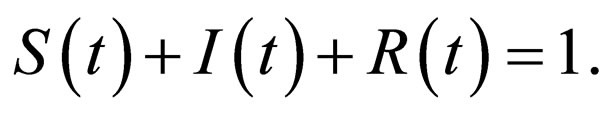 The death rate and birth rates are assumed equal and life expectancy is assumed to be approximately 50 years, typical of the developing countries, hence
The death rate and birth rates are assumed equal and life expectancy is assumed to be approximately 50 years, typical of the developing countries, hence 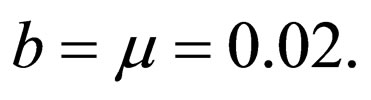 We further investigate the possible synergy between life expectancy (or residence time) and disease outbreak by considering a short residence time of only one year
We further investigate the possible synergy between life expectancy (or residence time) and disease outbreak by considering a short residence time of only one year 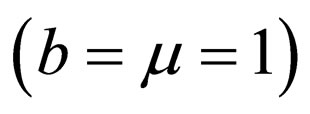 to match a contact or vaccination period. This rate may depict school/college stayperiods (students spend half to one year together in school or college). The constant contact rate is assumed to be
to match a contact or vaccination period. This rate may depict school/college stayperiods (students spend half to one year together in school or college). The constant contact rate is assumed to be 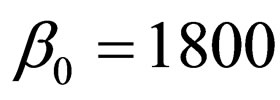 per year [19]. However, we depict a periodic contact rate by a sinusoidal function that mimics a one-year period,
per year [19]. However, we depict a periodic contact rate by a sinusoidal function that mimics a one-year period,
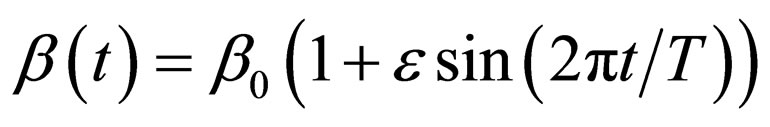
where  year, and
year, and 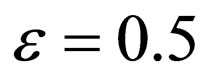 [20].
[20].
In Figure 2, we visualize the susceptible population profile during one year period, when we control the disease using the optimal control strategy derived from the instantaneous control problem. If we consider the number of susceptible individuals over time (upper panel), it is not clear why it follows such a time course or trajectory. But when we also consider the product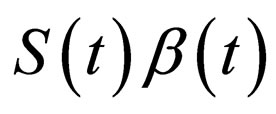 , we observe that the susceptible population is controlled in such a way that this product remains constant over most part of the period, but when the product becomes smaller than a critical value, then vaccination doses are administered and then susceptible population is left to grow freely again.
, we observe that the susceptible population is controlled in such a way that this product remains constant over most part of the period, but when the product becomes smaller than a critical value, then vaccination doses are administered and then susceptible population is left to grow freely again.
In Figures 3 and 4, we now compare three different vaccination strategies: the dotted line indicates the effect of a constant vaccination rate. This is a baseline effect that we may reach without optimization. The dashed line represents the performance of the strategy optimized with respect to the instantaneous criterion, while the solid line shows the orbital optimal strategy with respect to the Floquét criterion. On the  -axis of Figures 3 and 4, we have the average proportion of vaccination doses that are available for use, i.e.,
-axis of Figures 3 and 4, we have the average proportion of vaccination doses that are available for use, i.e.,
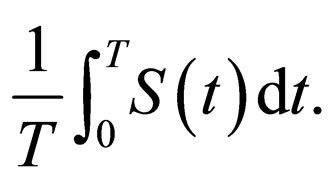
Note that this value corresponds in a one-to-one manner to the number of vaccination doses used per
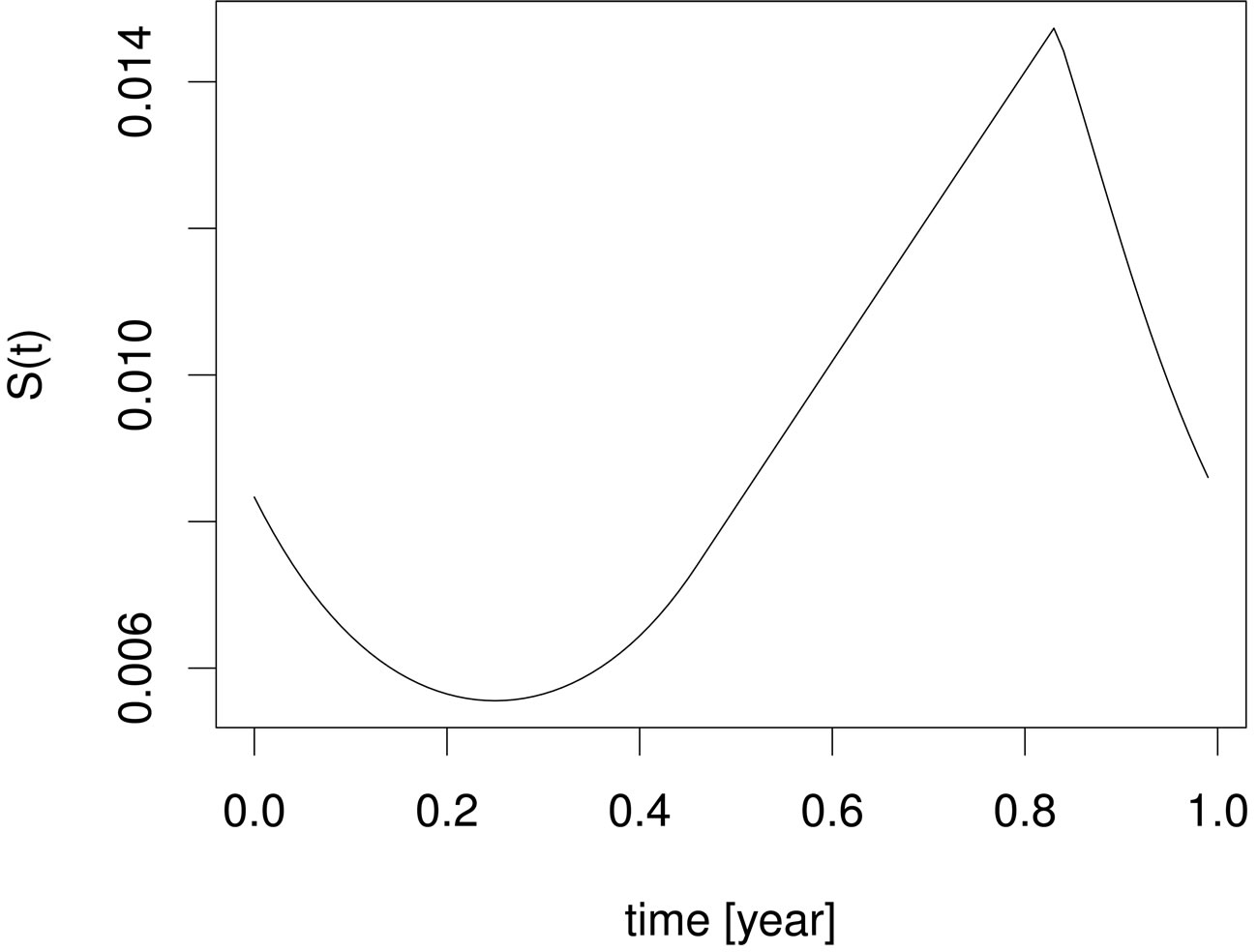
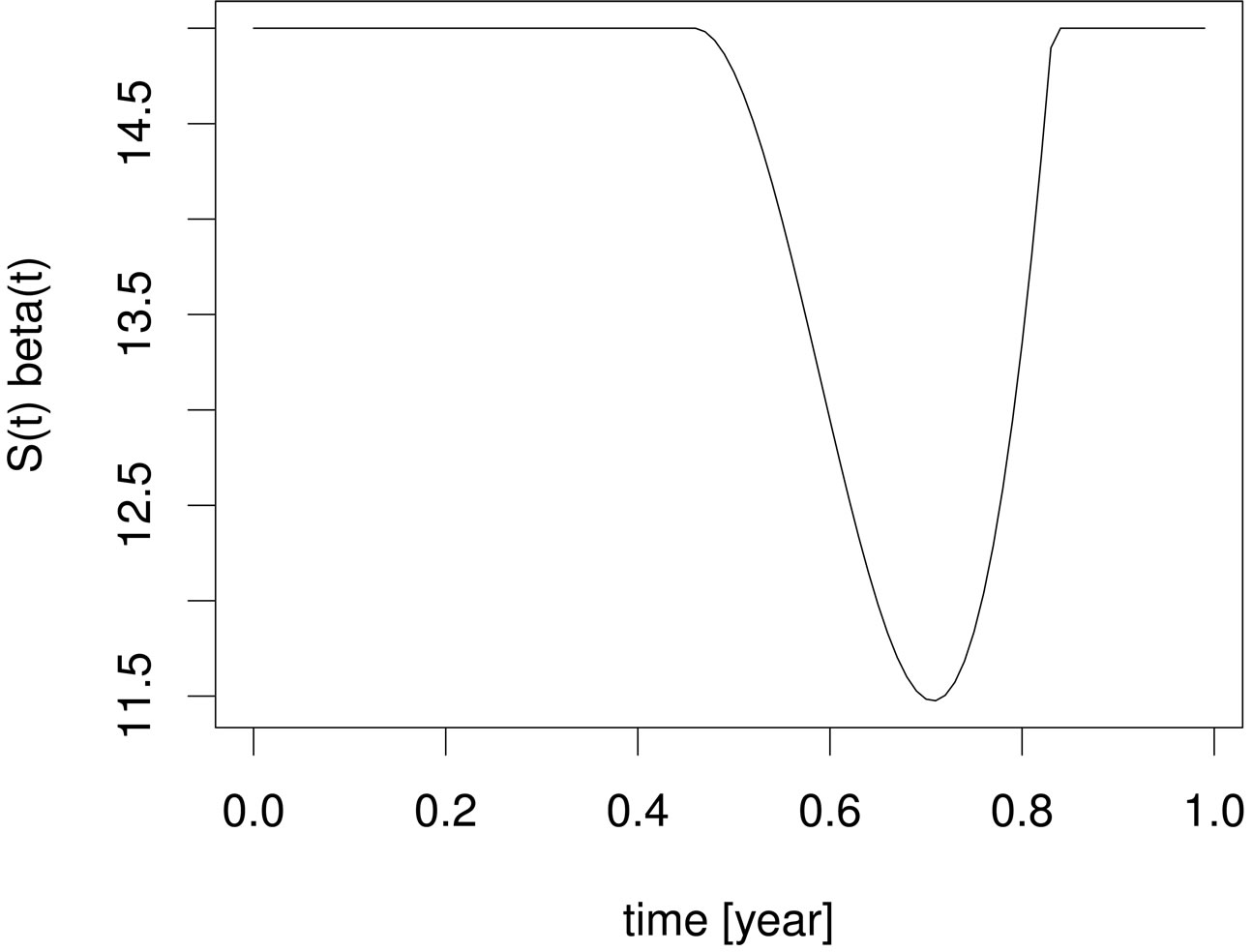
Figure 2. Susceptible population (upper panel) and susceptible population times contact rate (lower panel) under the optimal instantaneous vaccination strategy .
.
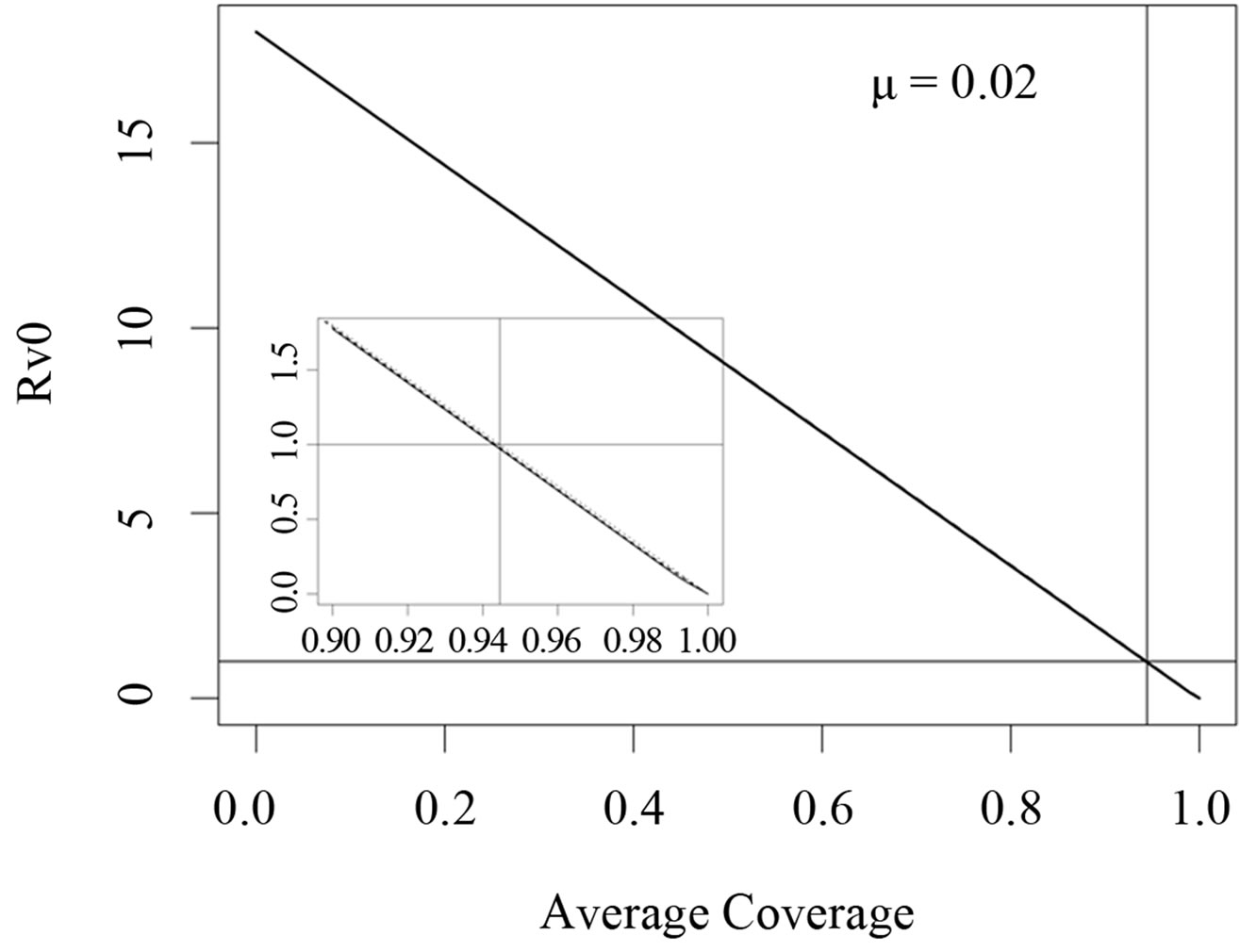
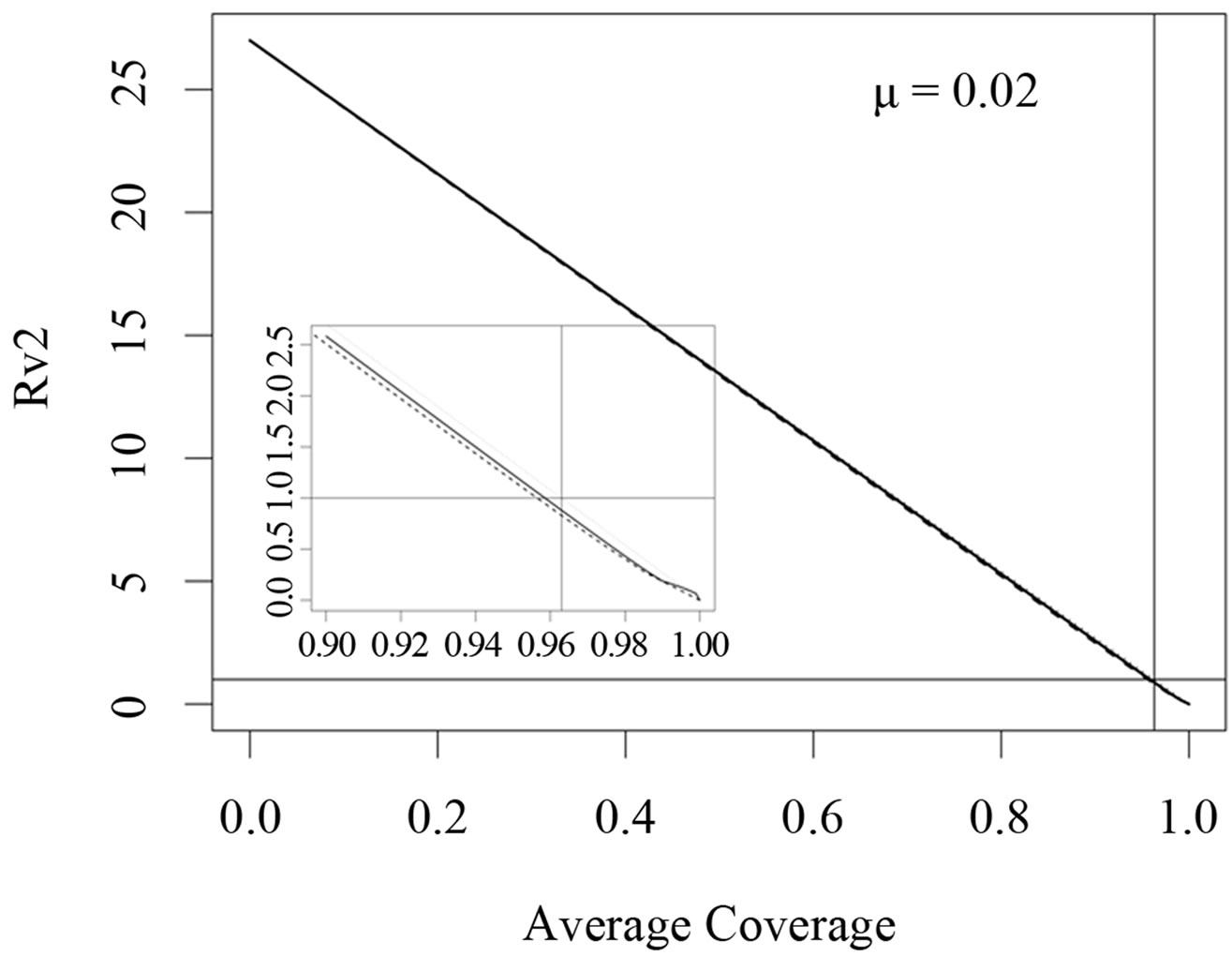
Figure 3. Costs for minimizing 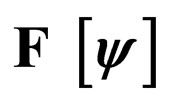 and
and 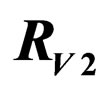 for
for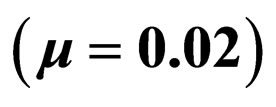 . Horizontal bar indicates
. Horizontal bar indicates 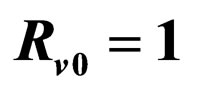 resp.
resp.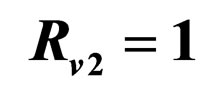 ; the dotted line is the constant case, the dashed line is the optimal solution according to instantaneous criterion, while the solid line is the optimal solution according to Floquét case. Vertical bar indicates the critical vaccination coverage of 0.944% (upper panel) and 0.963% (lower panel).
; the dotted line is the constant case, the dashed line is the optimal solution according to instantaneous criterion, while the solid line is the optimal solution according to Floquét case. Vertical bar indicates the critical vaccination coverage of 0.944% (upper panel) and 0.963% (lower panel).
period, as the costs can be represented as 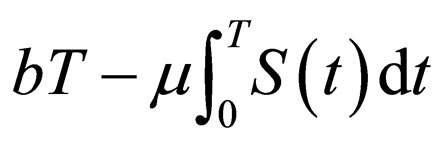 (see also [15]). On the
(see also [15]). On the  -axis of Figures 3 and 4, we represent
-axis of Figures 3 and 4, we represent
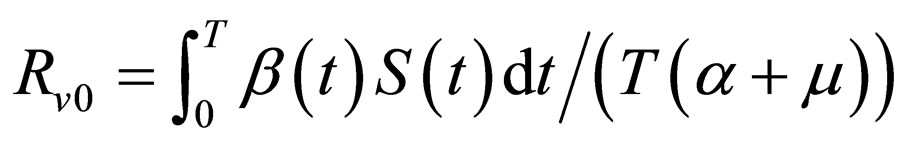 to indicate the performance w.r.t. the Floquét stability and
to indicate the performance w.r.t. the Floquét stability and  to denote the effect with respect to the instantaneous criterion. The functions are re-scaled in such a way that they agree with the reproduction number in case of constant contact rate and vaccination strategy and moreover, in such a way that always,
to denote the effect with respect to the instantaneous criterion. The functions are re-scaled in such a way that they agree with the reproduction number in case of constant contact rate and vaccination strategy and moreover, in such a way that always, 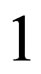 is the critical threshold. Up to a certain degree, this choice of the scaling factors are arbitrary, but obvious and intuitive.
is the critical threshold. Up to a certain degree, this choice of the scaling factors are arbitrary, but obvious and intuitive.
We have taken into account three different time scales in this exposition: time scale of the disease infection, given by 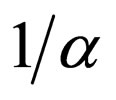 (about one week), time scale of the contact rate and vaccination rates (about one year), and the time scale of the residence time (50 years in Figure 3 where
(about one week), time scale of the contact rate and vaccination rates (about one year), and the time scale of the residence time (50 years in Figure 3 where 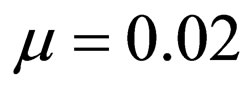 and 1 year in Figure 4 where
and 1 year in Figure 4 where  The central question is: how much can we gain by optimization and how much do we loose if we use the “wrong” optimization criterion?
The central question is: how much can we gain by optimization and how much do we loose if we use the “wrong” optimization criterion?
Let us first consider a case of life expectancy of 50 years illustrated in Figure 3. We find very little difference in the effect of the optimization strategies. Somehow, the overall number of vaccination doses applied per period matters, but the timing/pattern of applying vaccination doses appears like not so important.
The scenario however improves when we consider that the residence time is in the same magnitude like the vaccination period. This situation is depicted in Figure 4. We observe a difference in this case. This effect is stronger for the instantaneous criterion than the Floquét criterion. This observation can be explained from the fact that the Floquét criterion is an average while the instanttaneous criterion considers extreme values. Thus, the extreme values that determine the supremum norm are averaged out and are less pronounced. However, for
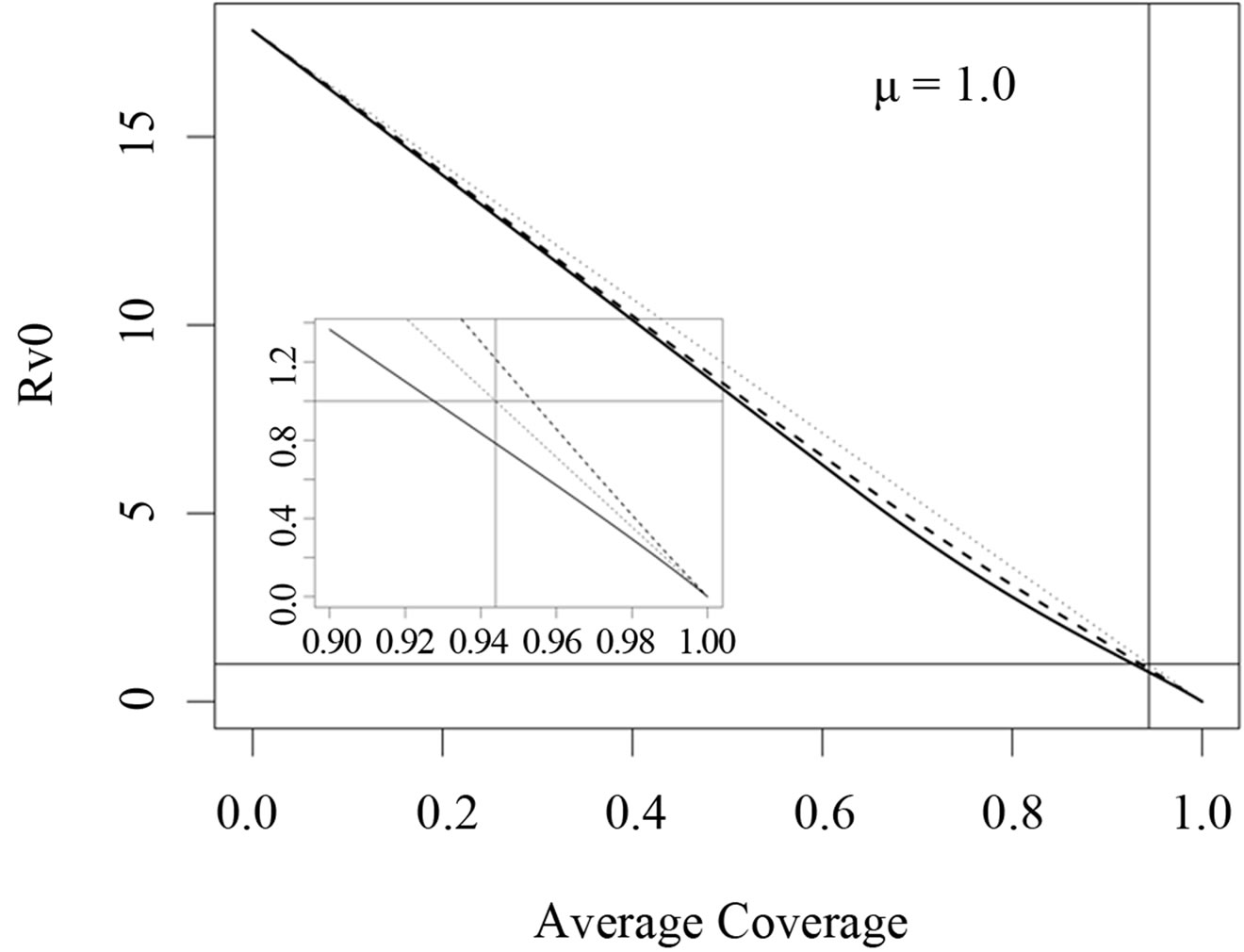
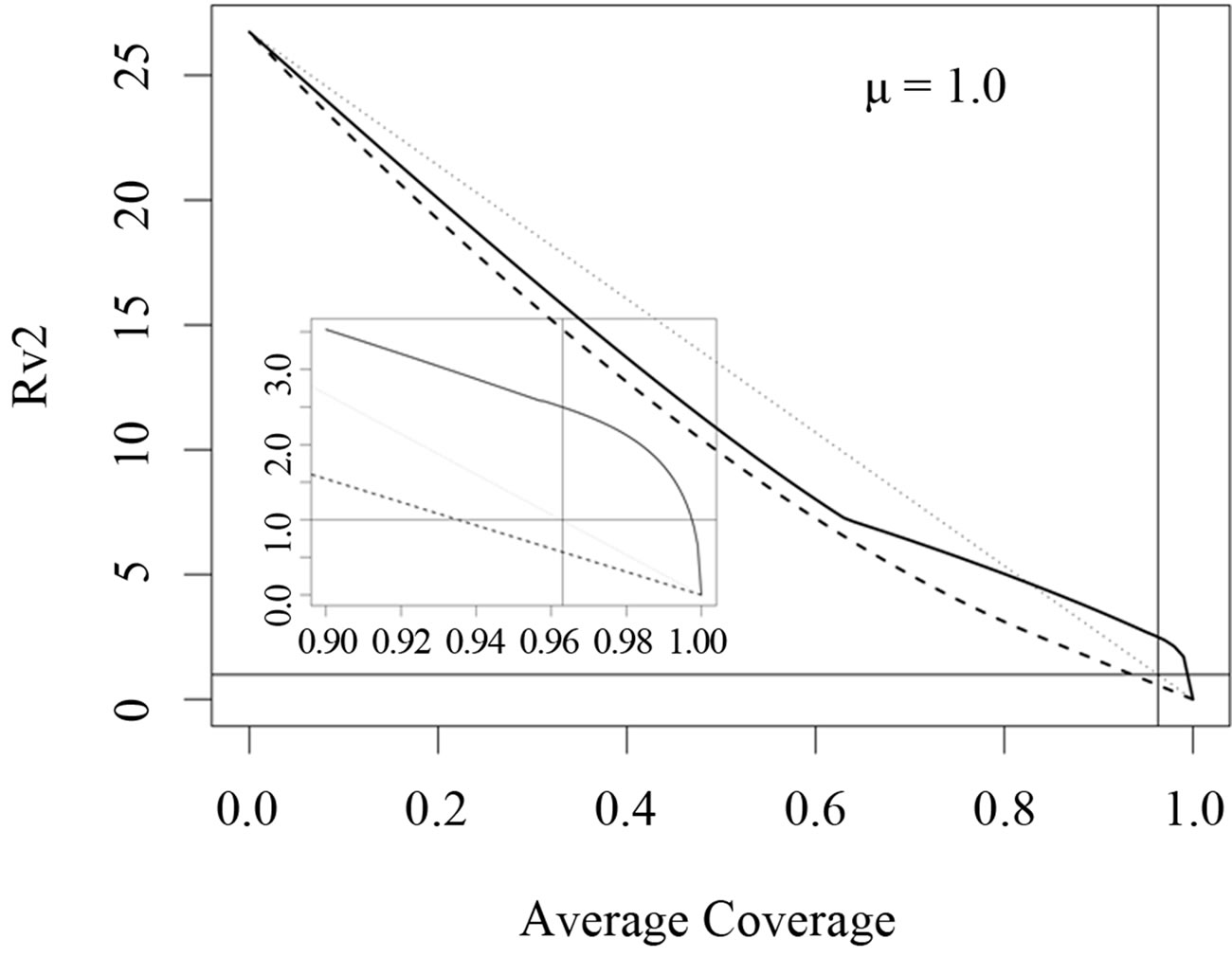
Figure 4. Costs for minimizing  and
and 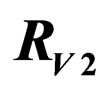 for
for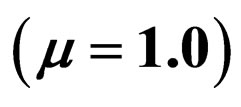 . Horizontal bar indicates
. Horizontal bar indicates 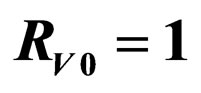 resp.
resp.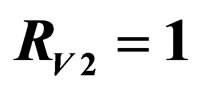 ; dotted line: constant case, dashed line: optimal solution according to instantaneous criterion, solid line: optimal solution according to Floquét case. Vertical bar indicates the critical coverage of 94.4% (upper panel) and 96.3% (lower panel).
; dotted line: constant case, dashed line: optimal solution according to instantaneous criterion, solid line: optimal solution according to Floquét case. Vertical bar indicates the critical coverage of 94.4% (upper panel) and 96.3% (lower panel).
large coverage of over 95% say, the performance of the Floquét strategy w.r.t. the instantaneous criterion is even worse than the constant strategy. In cases with a relatively short residence time, we now see that the choice of the optimization criterion obviously matters.
The fact that the critical vaccination coverage is 0.944 for the Floquét criterion and 0.963 for the instantaneous criterion is a consequence of the averaging with the Floquét term. The overall vaccination coverage necessary to eliminate the infection for a disease such as measles is always around 95%, a number that is generally hard to achieve. Especially for this reason, the organizational aspects of vaccination campaigns or vaccination days, becomes of critical importance.
7. Discussion
We investigated the influence of time scales on the stability of the uninfected solution. In the simulation, we considered the specific case of a periodic parameters including contact rate and vaccination rate. We found that the orbital stability criterion used for periodically driven systems (Floquét theory), provides an appropriate control strategy if the time scale of the disease and the contact rate are similar. If the disease is much faster (as is often the case with childhood related diseases), then singular perturbation theory defines a rather optimal control strategy; the supremum norm of the product between the susceptible population and contact rate. We used this insight to set up two different optimization problems. The first problem (the Floquét case) has been treated extensively in a different paper [15]. In this paper, we focused mainly on the instantaneous case and simulated the two strategies for comparison purposes.
The results of simulation shows that there is almost no difference in the performance of the vaccination strategies if the resident time (life expectancy) of individuals is relatively long in comparison with the period of the contact rate. This result can be also intuitively understood without the mathematical considerations: If the residence time is long, i.e., if an immunized individual lives for many time periods before he is replaced by a susceptible person again, then the importance of the time point/phase at which he is immunized does not matter. This effect is even stronger if the resident time is exponentially distributed. The results also indicate that the optimization begins (though not markedly) to matter if the residence time and the period of the contact rate do match. In this case, optimization is more important under the instantaneous criterion than under the orbital criterion, as the latter averages while the first focuses on instantaneous extreme values. The little difference in the vaccination strategies that we notice in the former case when the time scales are rather wide apart, is due to the fact that we are probably observing fast process on a slow time scale, hence we cannot see much. We must therefore separate the time scales clearly, as is the case in singular perturbation theory.
All in all, we conclusion are that in most cases, optimization will not pay if the complete population is under consideration. It only pays for small, well defined subgroups with relatively small residence times like preschool population. In this case, the importance is strengthened, from our results, by the inter-connectedness of recruitment into population, exit and contact period.
Our results support the idea of vaccination days or special vaccination periods, i.e., vaccinate when
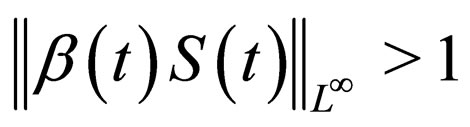
We therefore ask whether vaccination days are beneficial, over and above constantly administering vaccination doses. Despite these results, even for large populations (larger than school populations), vaccination days may be of value. Most likely, the reason is not a certain resonance or a clever use of the interaction between the dynamics of immunization and infection, but merely an organizational effect: The way vaccination days are usually organized allows for re-vaccination such that vaccination failures are removed, and persons (mostly: children) missed in one day have the opportunity to be vaccination at another vaccination day. Moreover, the concentrated effort of vaccination (in a given location as well as in time) may enhance the interest of a large part of the population on the vaccination exercise hence the compliance becomes better. All these effects may be crucial in reaching the critical vaccination coverage that is ordinarily very difficult to reach by standard and routine means. In this sense, the result presented here should be understood as a positive result, in the sense that vaccinetion days need not to be planned only according to some dynamics of the disease but also according to organizational requirements.
8. Acknowledgements
I wish to thank the DAAD (The German Academic Exchange Program) for the support award which facilitated the completion of this research work.
REFERENCES
- Z. Agur, L. Cojocaru, G. Mazor, R. Anderson and Y. Danon, “Pulse Mass Measles Vaccination across Age Cohorts,” Proceedings of the National Academy of Sciences, Vol. 90, No. 24, 1993, pp. 11698-11702. http://dx.doi.org/10.1073/pnas.90.24.11698
- M. J. Ferrari, F. G. Rebecca, B. Nita, J. K. Conlan, O. N. Bjornstad, L. J. Wolfson, P. J. Guerin, A. Djibo and B. T. Grenfell, “The Dynamics of Measles in Sub-Saharan Africa,” Nature-Articles, Vol. 451, No. 7, 2008, pp. 679- 684.
- M. E. Alexander, S. M. Moghadas, P. Rohani and A. R. Summers, “Modelling the Effect of a Booster Vaccination on Disease Epidemiology,” Journal of Mathematical Biology, Vol. 52, No. 3, 2006, pp. 290-306. http://dx.doi.org/10.1007/s00285-005-0356-0
- M. Eichner and K. P. Hadeler, “Deterministic Models for the Eradication of Poliomyelitis: Vaccination with the Inactivated (IPV) and Attenuated (OPV) Polio Virus Vaccine,” Mathematical Biosciences, Vol. 127, No. 2, 1995, pp. 149-166. http://dx.doi.org/10.1016/0025-5564(94)00046-3
- P. Rohani, D. J. D. Earn, B. Finkenstaedt and B. T. Grenfell, “Population Dynamics Interference among Childhood Diseases,” Proceedings of the Royal Society of London, Vol. 265, No. 1410, 1998, pp. 2033-2041. http://dx.doi.org/10.1098/rspb.1998.0537
- P. Rohani, M. J. Kelling and B. T. Grenfell, “The Interplay between Determinism and Stochasticity in Childhood Diseases,” The American Naturalist, Vol. 159, No. 5, 2002, pp. 469-481. http://dx.doi.org/10.1086/339467
- Y. Zhou and H. Liu, “Stability of Periodic Solutions for an SIS Model with Pulse Vaccination,” Mathematical and Computer Modelling, Vol. 38, No. 3-4, 2003, pp. 299-308. http://dx.doi.org/10.1016/S0895-7177(03)90088-4
- B. Shulgin, L. Stone and Z. Agur, “Theoretical Examination of Pulse Vaccination Policy in the SIR Epidemic Model,” Mathematical and Computer Modelling, Vol. 31, No. 4-5, 2000, pp. 207-215. http://dx.doi.org/10.1016/S0895-7177(00)00040-6
- A. d’Onofrio, “Stability Properties of Pulse Vaccination Strategy in SEIR Epidemic Model,” Mathematical Biosciences, Vol. 179, No. 1, 2002, pp. 57-72. http://dx.doi.org/10.1016/S0025-5564(02)00095-0
- K. P. Hadeler and J. Mueller, “Vaccination in Age Structured Populations I: The Reproduction Number,” In: V. Isham and G. Medley, Ed., Models for Infectious Human Diseases: Their Structure and Relation to Data, Cambridge University Press, Cambridge, 1996, pp. 90-101. http://dx.doi.org/10.1017/CBO9780511662935.013
- K. P. Hadeler and J. Mueller, “Vaccination in Age Structured Populations II: Optimal Vaccination Strategies,” In: V. Isham and G. Medley, Eds., Models for Infectious Human Diseases: Their Structure and Relation to Data, Cambridge University Press, Cambridge, 1996, pp. 102- 114. http://dx.doi.org/10.1017/CBO9780511662935.014
- R. E. O’Malley, “Introduction to Singular Perturbations,” Academic Press, New York, 1974.
- R. E. O’Malley, “Singular Perturbation Methods for Ordinary Differential Equations,” Springer-Verlag, New York, 1991. http://dx.doi.org/10.1007/978-1-4612-0977-5
- N. Fenichel, “Geometric Singular Perturbation Theory for Ordinary Differential Equations,” Journal of Differential Equations, Vol. 31, No. 1, 1979, pp. 53-98. http://dx.doi.org/10.1016/0022-0396(79)90152-9
- N. Onyango and J. Müller, “Determination of Optimal Vaccination Strategies Using an Orbital Stability Threshold from Periodically Driven Systems,” Journal of Mathematical Biology, in Press. http://dx.doi.org/10.1007/s00285-013-0648-8
- H. R. Thieme, “Mathematics in Population Biology,” Princeton University Press, Princeton, 2003.
- J. Müller, “Optimal Vaccination Patterns in Age-Structured Populations,” SIAM Journal on Applied Mathematics, Vol. 59, No. 1, 1998, pp. 222-241. http://dx.doi.org/10.1137/S0036139995293270
- J. Müller, “Optimal Vaccination Patterns in Age-Structured Populations: Endemic Case,” Mathematical and Computer Modelling, Vol. 31, No. 4-5, 2000, pp. 149-160. http://dx.doi.org/10.1016/S0895-7177(00)00033-9
- B. Shulgin, L. Stone and Z. Agur, “Pulse Vaccination Strategy in the SIR Epidemic Model,” Bulletin of Mathematical Biology, Vol. 60, No. 6, 1998, pp. 1123-1148.
- N. Bacaer, M. Gabriel and M. Gomes, “On the Final Size of Epidemics with Seasonality,” Bulletin of Mathematical Biology, Vol. 71, No. 8, 2009, pp. 1954-1966. http://dx.doi.org/10.1007/s11538-009-9433-7
- L. C. Evans, “Partial Differential Equations,” American Mathematical Society, Providence and Rhodes Island, 1998.
- K. Yosida, “Functional Analysis,” Springer-Verlag, Berlin, 1980.
Appendix
The Set  is Bounded and Pre-Compact in
is Bounded and Pre-Compact in 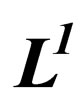
We defined the set of optimal solutions via the set of susceptible population profiles

Interest is to show that solutions of the optimal control problem exist in this set. We therefore examine the properties of this set.
We begin by considering the following proposition.
Proposition 6 For any 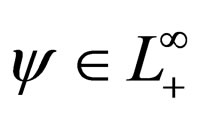 we find uniform bounds for
we find uniform bounds for 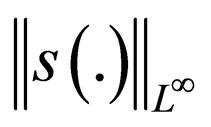 and
and 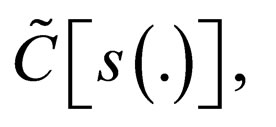 i.e.,
i.e.,
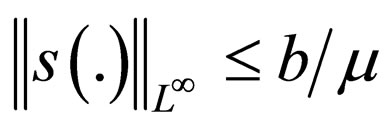
and
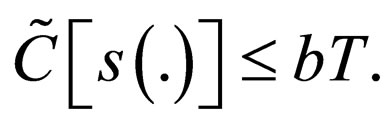
Proof. From model 1, we observe that the differential equation for the total population is,
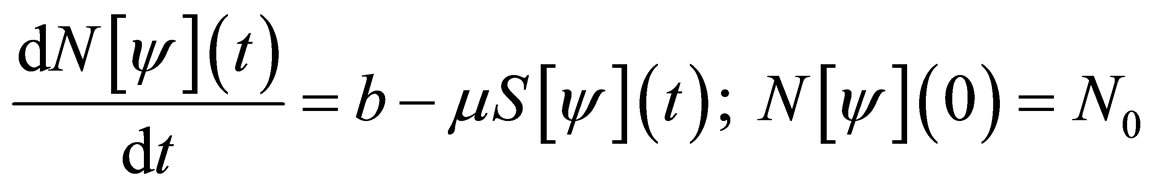
whose solution is given by
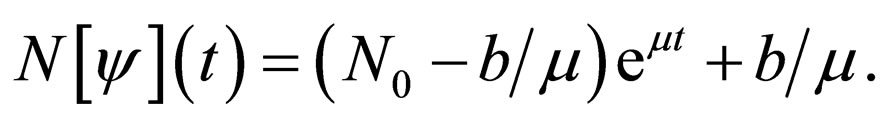
It follows that
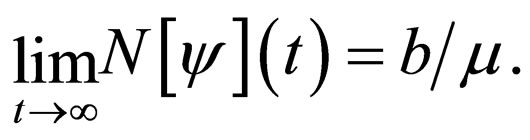
Since 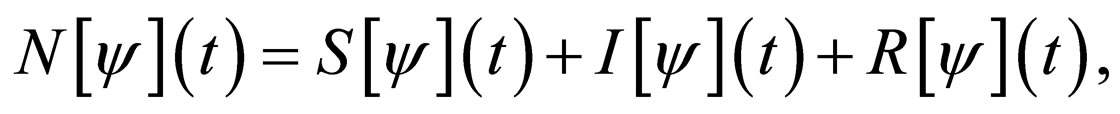 we observe that
we observe that
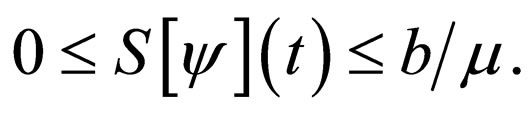
In the new notation,
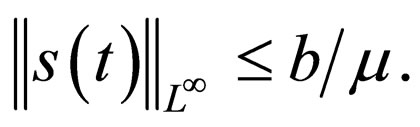
We now consider the cost functional
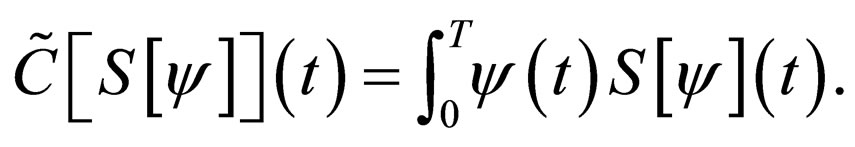
Consider the differential equation for the susceptible population,
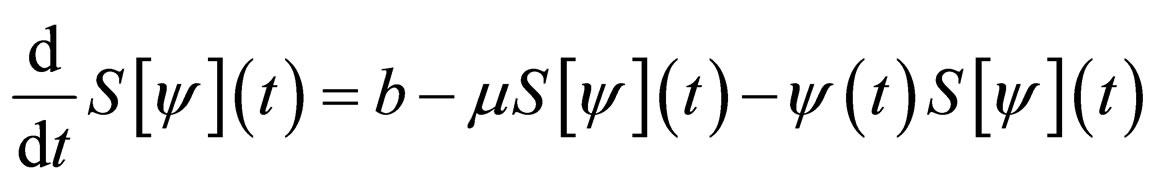

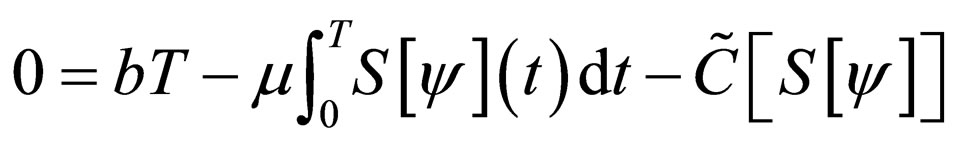
Therefore,
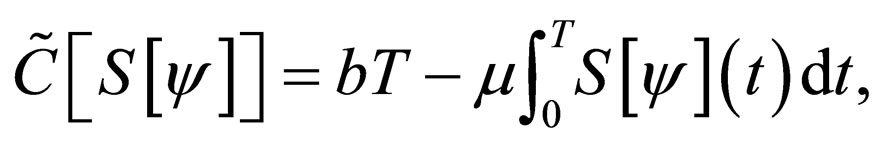
and therefore, 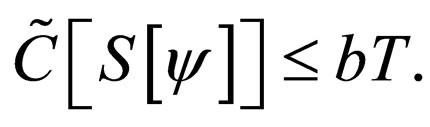
To investigate compactness, we use a remark [21, p. 274] that follows from sobolev embedding theorem in [21, Theorem 1, p. 272]. We start with both the remark and the theorem (without proof as this follows from the reference).
Theorem 2 Assume  is open, bounded and Lipschitz domain, s.t.,
is open, bounded and Lipschitz domain, s.t., 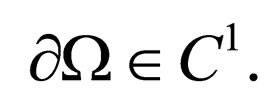 Suppose
Suppose  then
then
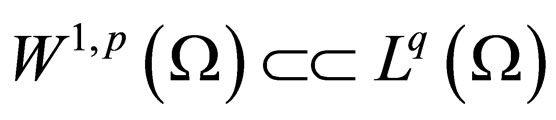
for  and
and 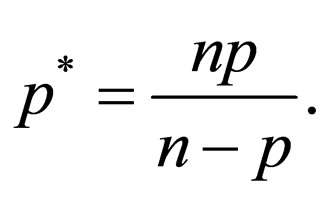
If  as
as  then
then
1)
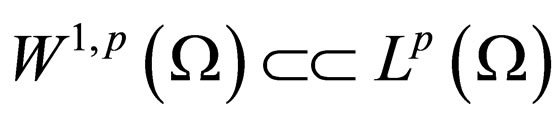
for all 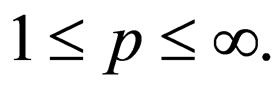
2)
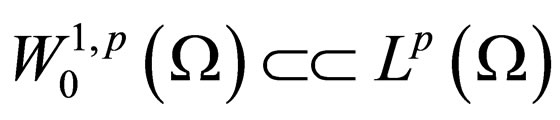
even if 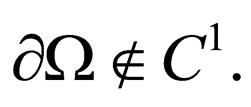
Using the above remark, we specify the following proposition.
Proposition 7 The set 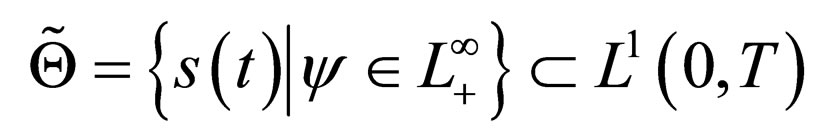 is a bounded subset in
is a bounded subset in  and is pre-compact in
and is pre-compact in .
.
Proof. We already showed that  is uniformly bounded, and thus, we only consider the bounded interval
is uniformly bounded, and thus, we only consider the bounded interval 
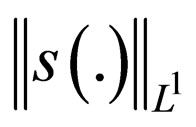 is also bounded in this interval. The norm of the derivative can be derived using the differential equation,
is also bounded in this interval. The norm of the derivative can be derived using the differential equation,

All the terms in the last line are uniformly bounded, i.e.  is a bounded subset of
is a bounded subset of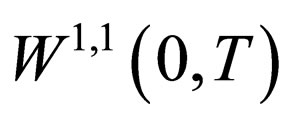 . Since
. Since 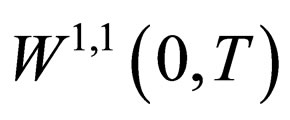 is compact embedded in
is compact embedded in  by theorem (8), then
by theorem (8), then  is pre-compact in
is pre-compact in 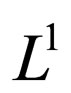 and its closure
and its closure  is a compact subset of
is a compact subset of 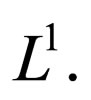
Theorem 3 If  is defined for some maximal costs
is defined for some maximal costs  i.e.,
i.e., 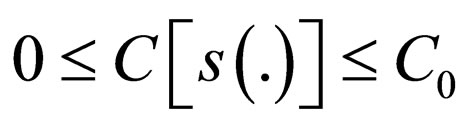 , the problem 3 has a solution in
, the problem 3 has a solution in 
Proof.  is continuous functional in
is continuous functional in 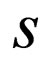 and the set
and the set
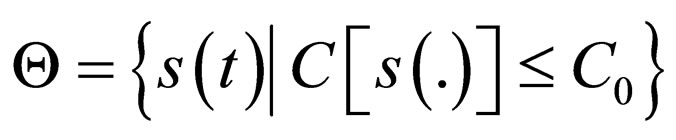
is non-empty and compact. Thus, the continuous functional 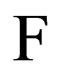 assumes its minimum within
assumes its minimum within 
Convexity of 
We show that  is convex. According to the theorem of Krein and Milman, the extremal points structure the complete set. Consequently, we investigate this special set. The inside structure we obtain here is the centerpiece for our considerations about the structure of the optimal points in
is convex. According to the theorem of Krein and Milman, the extremal points structure the complete set. Consequently, we investigate this special set. The inside structure we obtain here is the centerpiece for our considerations about the structure of the optimal points in .
.
Proposition 8 The set  is convex and so is its closure
is convex and so is its closure
Proof. Let  and
and ,
, 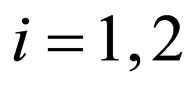 be population profiles in
be population profiles in  Since
Since  positive integer, we define
positive integer, we define 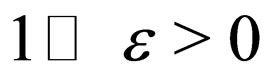 such that
such that , i.e.functions that stay in the positive domain and possibly bounded away from zero.
, i.e.functions that stay in the positive domain and possibly bounded away from zero.
We define

Does  satisfy the original differential equation for
satisfy the original differential equation for 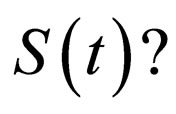
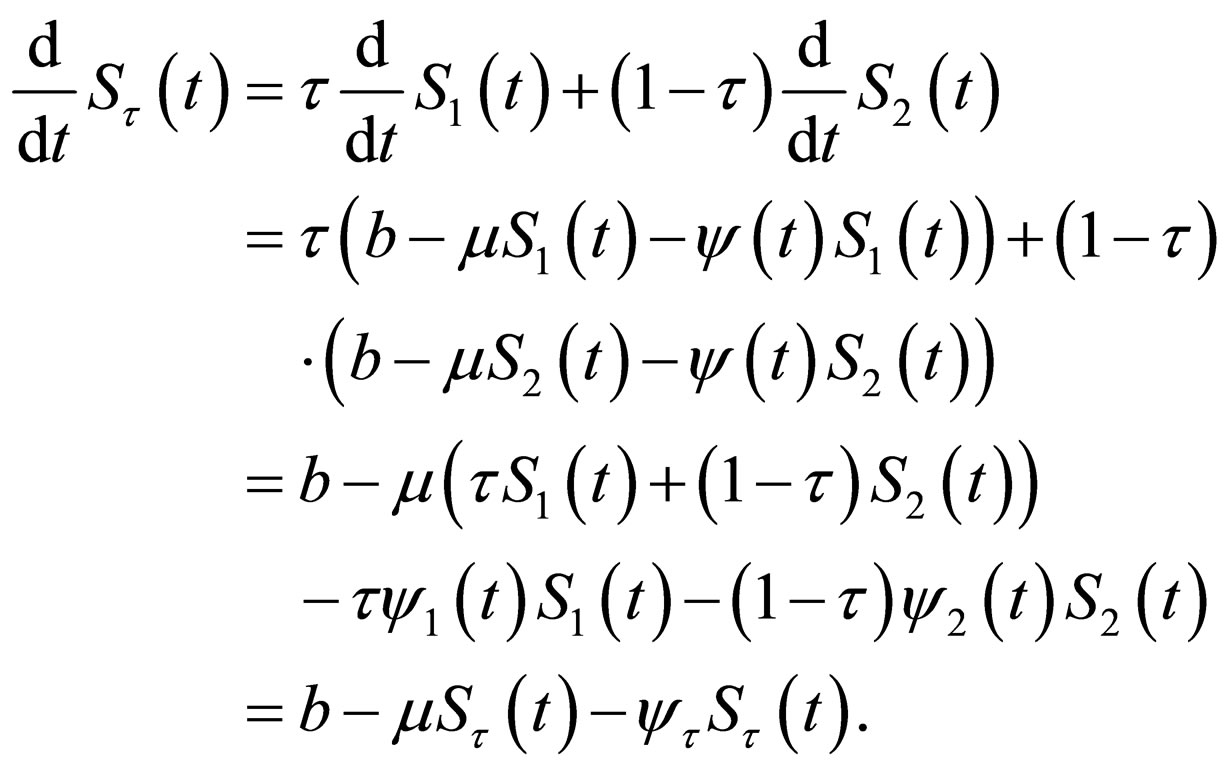 (14)
(14)
where
 (15)
(15)
Since 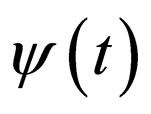 is periodic,
is periodic,  is also periodic, and so is
is also periodic, and so is  By convexity of
By convexity of  can be expressed as a convex combination of
can be expressed as a convex combination of .
.
We also show that 
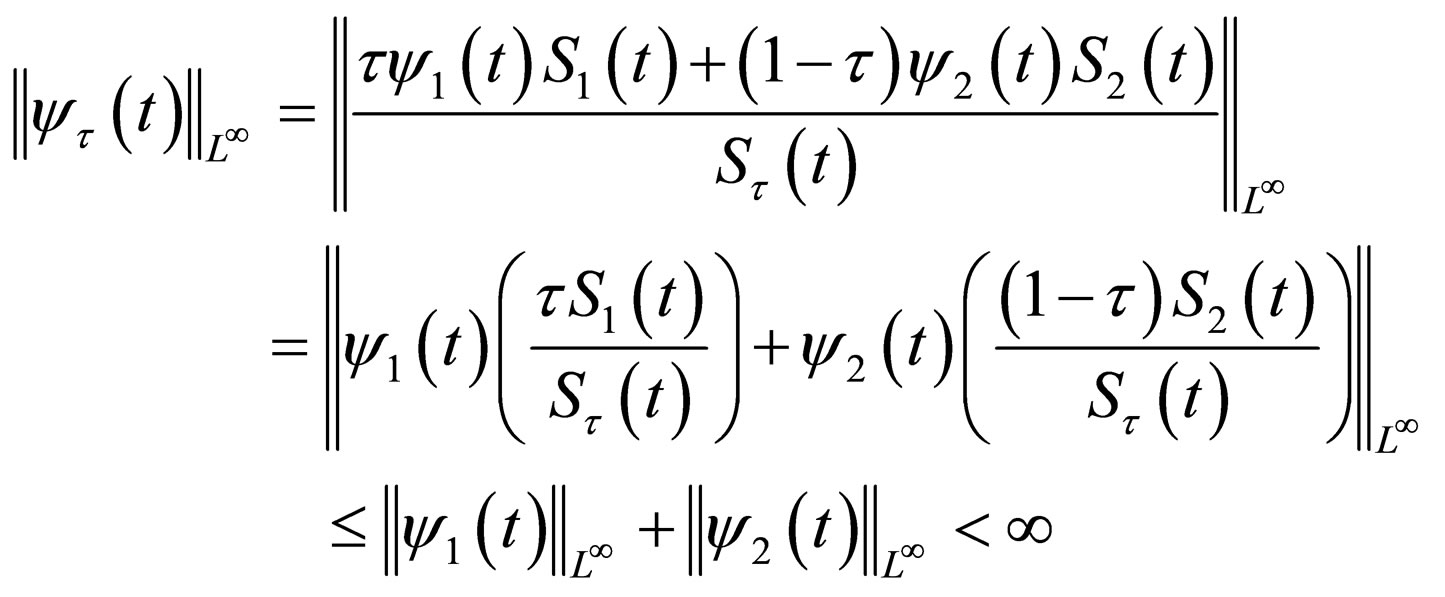
Hence 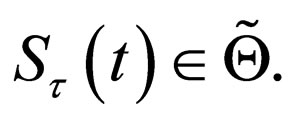
Since  is the closure of a convex set, it is also convex.
is the closure of a convex set, it is also convex.
Hence,  is a convex and compact set. The theorem of Krein-Milman [22, p. 362] tells us, that it can be characterized completely by the set of its extremal points,
is a convex and compact set. The theorem of Krein-Milman [22, p. 362] tells us, that it can be characterized completely by the set of its extremal points, .
.
Continuity of Elements of the Set  at Vaccination Points
at Vaccination Points
We wish to define candidate optimal vaccination strategies that vaccinate at discrete time points. We demonstrate that the functional  has well defined left hand and right hand limits at vaccination points,
has well defined left hand and right hand limits at vaccination points, 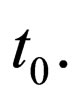
Consider following Lemmata:
Lemma 1 Let 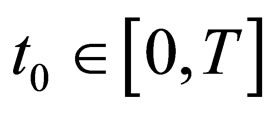 be fixed and
be fixed and 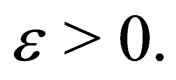 Define two functions,
Define two functions,
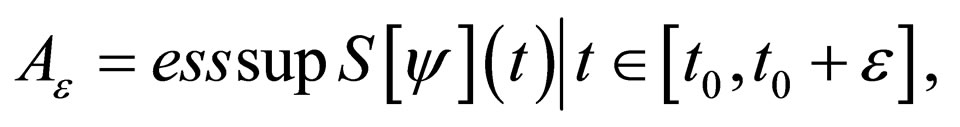

Then, for 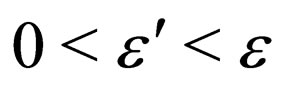
1) 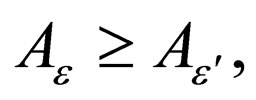
2) 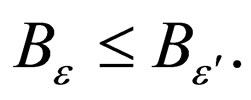
Proof. The set,
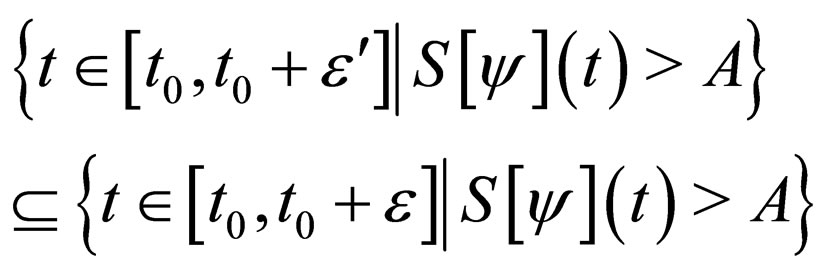
and denote 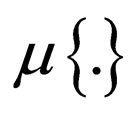 as the measure of a set, then
as the measure of a set, then
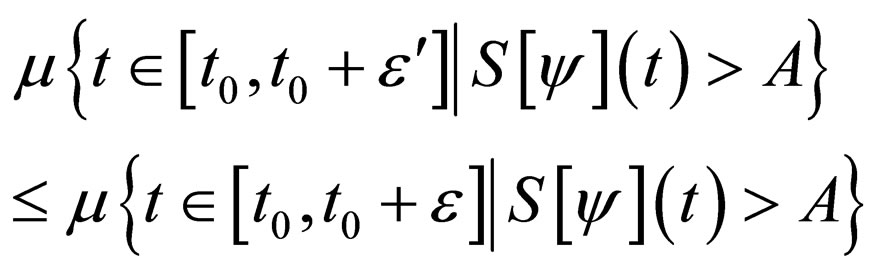
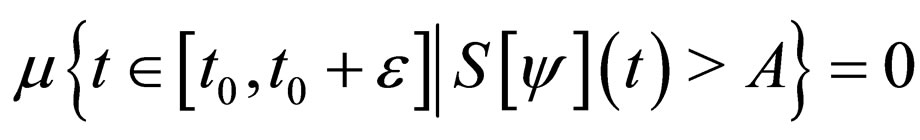

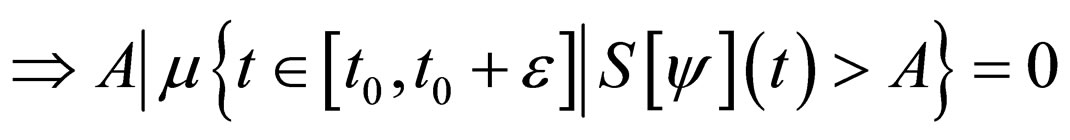
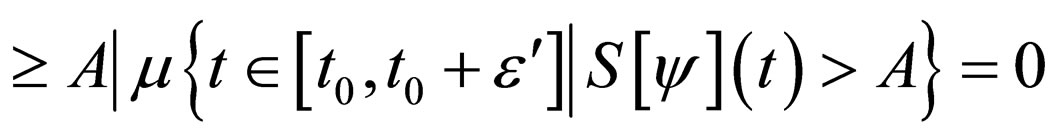

Similarly, 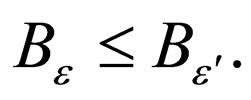
Corollary 1 It follows that,
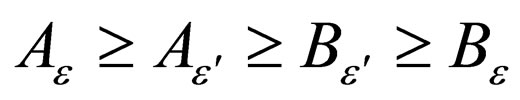
for arbitrarily small positive real values 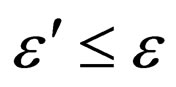
Lemma 2 The 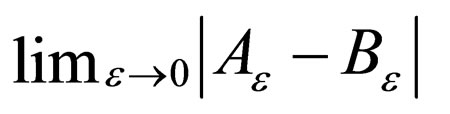 exists and is equal to zero.
exists and is equal to zero.
Proof. We know that 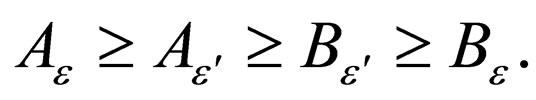
Thus  for
for 
Define 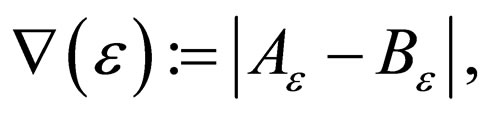 monotonously increasing in
monotonously increasing in 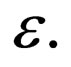
Define 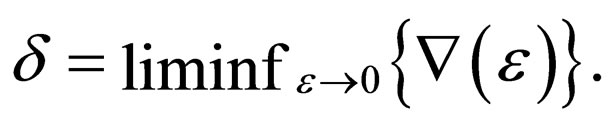 We show that the limit exists for
We show that the limit exists for 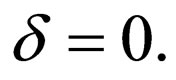 Suppose
Suppose 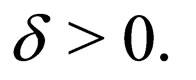 We know that for
We know that for 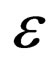 decreasing,
decreasing, 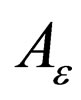 is monotonously decreasing and bounded function,
is monotonously decreasing and bounded function,  is monotonously increasing and bounded function, hence the following limits exist:
is monotonously increasing and bounded function, hence the following limits exist:
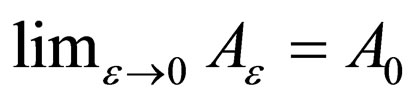
and
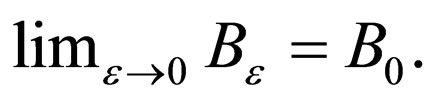
Suppose 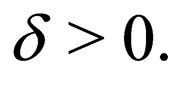 We have
We have 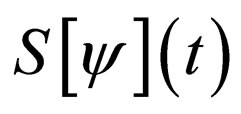 monotonically increasing in
monotonically increasing in  Since
Since 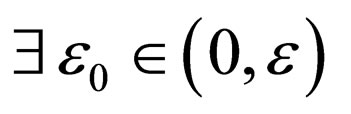
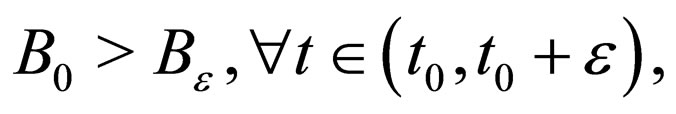 such that
such that  in the interval
in the interval  thus
thus 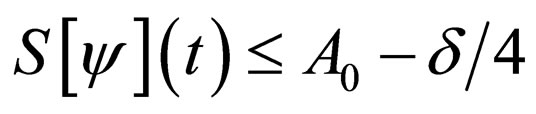 in
in 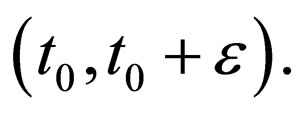 Hence
Hence
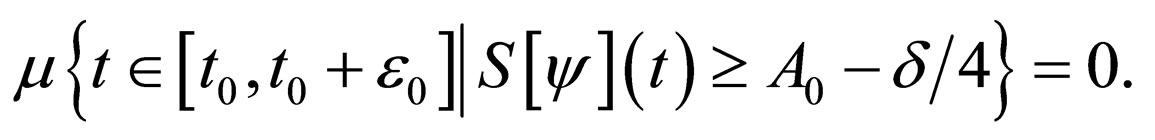
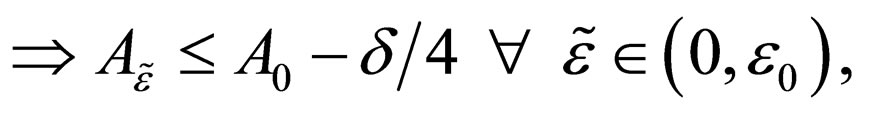
such that as 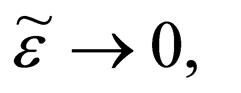
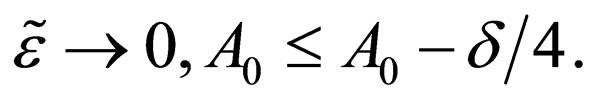
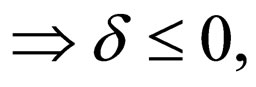
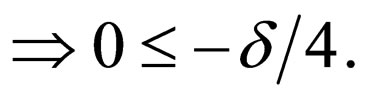 a contradiction.
a contradiction.
Lemma 3 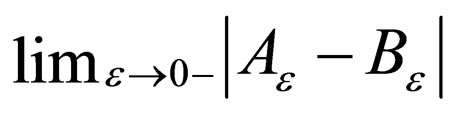 exists and is equal to zero.
exists and is equal to zero.
Proof. The proof parallels that of lemma (2), reversing time and changing the roles of the supremum and infimum.

