Received 29 October 2014; revised 26 November 2014; accepted 18 December 2014

ABSTRACT

In this article we apply and discuss El-Desouky technique to derive a generalization of the problem of selecting k balls from an n-line with no two adjacent balls being s-separation. We solve the problem in which the separation of the adjacent elements is not having odd and even separation. Also we enumerate the number of ways of selecting k objects from n-line objects with no two adjacent being of separations m, m + 1, ・・・, pm, where p is positive integer. Moreover we discuss some applications on these problems.

Keywords:

Probability Function, s-Separation, s-Successions, n-Line, n-Circle

1. Introduction

Kaplansky [1] (see also Riordan ( [2] p. 198, lemma) and Moser [3] ) studied the problem of selecting k objects from n objects arranged in a line (called n-line) or a circle (called n-circle) with no two selected objects being consecutive. Let 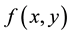and 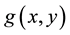denote the number of ways of such selections for n-line and n-circle respectively. Kaplansky proved that

(1.1)

and

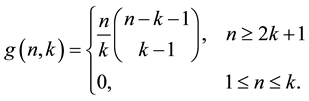(1.2)

El-Desouky [4] studied another related problem with different techniques and proved that

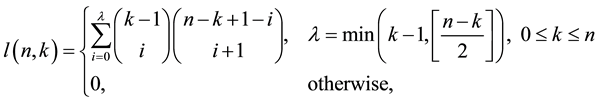(1.3)

where 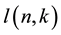is the number of ways of selecting k balls from n balls arranged in a line with no two adjacent balls being unit separation.

In the following we adopt some conventions: 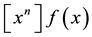denotes the coefficient of 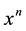in the formal power series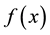; 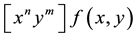denotes the coefficient of 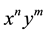in the series; 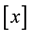is the largest integer less than or equal to x, 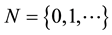and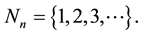

Also, El-Desouky [5] derived a generalization of the problem given in [4] as follows: let 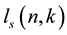denote the number of ways of selecting k balls from n balls arranged in a line with no two adjacent balls from the k selected balls being s-separation; two balls have separation s if they are separated by exactly s balls. Let denote the number of ways of selecting k balls from n balls arranged in a circle with no two adjacent balls from the k selected balls being s-separation

Let be as defined before. Then is equal to the number of k-subsets of where the difference is not allowed, so

(1.4)

Let be as defined before. Then the difference is not allowed, so

(1.5)

Let be the number of ways of selecting k balls from n balls arranged in a line with exactly m adjacent balls being of separation s or, which gives a generalization of (4.1) in El-Desouky [4] .

Thus,

(1.6)

For more details on such problems, see [3] [6] [7] .

2. Main Results

We use El-Desouky technique to solve two problems in the linear case, with new restrictions. That is if the separation of any two adjacent elements from the k selected elements being of odd separation and of even separation. Moreover, we enumerate which denotes the number of ways of selecting k objects from n objects arrayed in a line where any two adjacent objects from the k selected objects are not being of m, m + 1, ・・・, pm separations, where p is positive integer.

2.1. No Two Adjacent Being Odd Separation

Let denote the number of ways of selecting k balls from n balls arranged in a line, where the separation of any two adjacent balls from the k selected balls being of odd separation. say s, i.e.. This means that no two adjacent being of 2, 4, 6, ・・・ differences, see Table 1.

So, following Decomposition (2.3.14) see [8] (p. 55), is equal to the number of k-subsets of where the differences, are not allowed, hence, where

hence

Setting we have

Therefore, the coefficient of gives

A calculated table for the values of is given in Table 1, where,.

Remark 1. It is easy to conclude that satisfies the following recurrence relation

(2.1)

with the convention,

2.2. No Two Adjacent Being Even Separation

Let denote the number of ways of selecting k balls from n balls arranged in a line, where the separation of any two adjacent balls from the k selected balls are not being of even separation, say s i.e.. This means that no two adjacent being of 1, 3, 5,・・・ differences.

So, following Decomposition (2.3.14) see [8] (p. 55) then is equal to the number of k-subsets of where the differences are not allowed, hence, where

hence

Setting, we get

Therefore, the coefficient of gives

(2.2)

Moreover in the next subsection, we use our technique to enumerate the number of ways of selecting k objects from n objects arrayed in a line such that no two adjacent elements have the differences m + 1, m + 2, ・・・, pm + 1 i.e. no two adjacent element being of m, m + 1, ・・・, pm separations, where p is positive integer.

2.3. Explicit Formula for

Let be the number of ways of selecting k objects from n objects arrayed in a line where any two adjacent objects from the k selected objects are not being of m, m + 1, ・・・, pm separations, where p is positive integer, hence, where

Setting it is easy to find the coefficient of hence

(2.3)

3. Some Applications

Let n urns be set out along a line, that is, one-dimensional.

Suppose we have m balls of which are of colour, and we assign these balls to urns so that, see Pease [9] :

i) No urn contains more than one ball.

ii) All balls of colour are in consecutive urns,

El-Desouky proved that if the order of colours of the groups is specified, the number of arrangement is

just Hence if the total number of balls the number of arrangements is as a special case of El-Desouky results [5] .

It is of practical interest to find the asymptotic behavior of or the probability for large n and k.

Let X be a random variable having the probability function then

,

so

where we used the first aproximation

Therefore,

Putting we have

Maosen [10] considered the following problem. Let t be any nonnegative integer.

If we want to select k balls from an n-line or an n-circle under the restriction that any two adjacent selected balls are not t-separated, how many ways are there to do it? He solved these problems by means of a direct structural analysis. For the two kinds of problems, he used to denote the number of ways of selecting k balls from n balls arranged in a line with no two adjacent selected balls being t-separation and to denote the number of ways of selecting k balls from an n-circle with no two adjacent selected being t-separation. He proved that

(3.2)

(3.3)

Remark 2. In fact El-Desouky [5] has proved (3.2) in 1988.

References