Applied Mathematics
Vol.4 No.9A(2013), Article ID:36206,5 pages DOI:10.4236/am.2013.49A001
Radiation Effects on Flow past a Stretching Plate with Temperature Dependent Viscosity
Section of Applied Mathematics and Engineering Research, Department of Mathematics, University of Ioannina, Ioannina, Greece
Email: mxenos@cc.uoi.gr
Copyright © 2013 Michalis Xenos. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 22, 2013; revised May 22, 2013; accepted June 1, 2013
Keywords: Radiation; Stretching Plate; Optically Thin Gray Fluid; Viscosity as a Function of the Temperature
ABSTRACT
The effect of radiation on the flow over a stretching plate of an optically thin gray, viscous and incompressible fluid is studied. The fluid viscosity is assumed to vary as an inverse linear function of the temperature. The partial differential equations (PDEs) and their boundary conditions, describing the problem under consideration, are dimensionalized and the numerical solution is obtained by using the finite volume discretization methodology which is suitable for fluid mechanics applications. The numerical results for the velocity and temperature profiles are shown for different dimensionless parameters entering the problem under consideration, such as the temperature parameter, θr, the radiation parameter, S, and the Prandtl number, Pr. The numerical results indicate a strong influence of these parameters on the non-dimensional velocity and temperature profiles in the boundary layer.
1. Introduction
At high temperature, radiation has significant effects on the flow field. These effects have substantial applications in many industrial areas, such as electrical power generation, solar power technology, and aerospace engineering.
There has been extensive research on the effects of radiation on fluid flow. The free convection flow in the presence of radiation has been previously studied by Ali et al. [1], Seddeek and Abdelmeguid [2], Raptis and Toki [3], and Malekzadeh et al. [4]. The magnetohydrodynamic (MHD) flow in the presence of radiation has been investigated by Chamkha et al. [5], Raptis et al. [6], Duwairi [7], Ouaf [8], Abd-El Aziz [9], Pal and Mondal [10] and Shit and Haldar [11]. The flow through a porous medium in the presence of radiation has been studied by Murthy et al. [12], Al-Harbi [13], Al-Odat et al. [14], Raptis and Perdikis [15], Duwairi [16] and Badruddin et al. [17], and Awad et al. [18]. Raptis [19], Datti et al. [20], Abel et al. [21], Siddheshwar and Mahabaleswar [22] and Khan [23] have investigated the effects of radiation on the viscoelastic flow. The above studies, however, are under the assumption that the fluid is considered to be a thick gray fluid.
Bestman and Adiepong [24] studied the unsteady hydromagnetic free-convection flow with radiative heat transfer in a rotating thin gray fluid. The unsteady flow under the radiation effect of a thin gray fluid over a moving vertical plate was studied by Raptis and Perdikis [25]. Rajesh [26] studied the radiation effects of a thin gray fluid on MHD free convective flow near a vertical plate with ramped wall temperature under small magnetic Reynolds number. Rajput and Kumar [27] investigated the rotation and radiation effects on MHD flow of a thin gray fluid past an impulsively started vertical plate with variable temperature. Raptis [28] studied the free convective oscillatory flow and mass transfer past a porous plate in the presence of radiation of an optically thin fluid.
In the present study, we determine the effect of radiation on the flow field over a stretching plate of an optically thin gray fluid. We consider the fluid as viscous and incompressible, with temperature dependent viscosity.
The presented results are obtained after dimensionalization of the PDEs using a numerical approach. This approach is based on the finite volume (FV) discretization scheme. The discretization was performed with the use of a specialized symbolic package created in Mathematics.
2. Governing Equations
We consider the flow of a viscous and incompressible fluid due to an isothermal stretching flat surface. The fluid properties are assumed to be isotropic and constant, except for the fluid dynamic viscosity. The x-axis is taken along the plate and the y-axis normal to it, as depicted in Figure 1. The radiation heat flux in the x-direction is considered negligible in comparison to that in the y-direction.
The equations governing the problem are given by:
Continuity equation
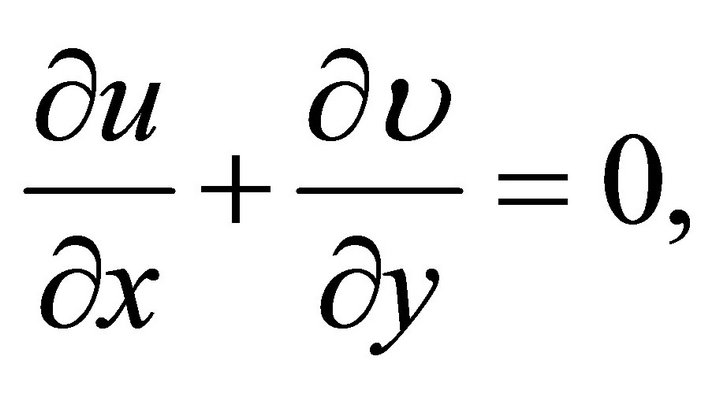 (1)
(1)
Momentum equation
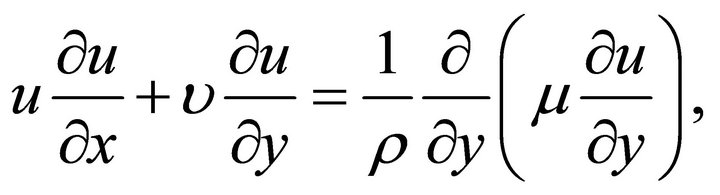 (2)
(2)
Energy equation
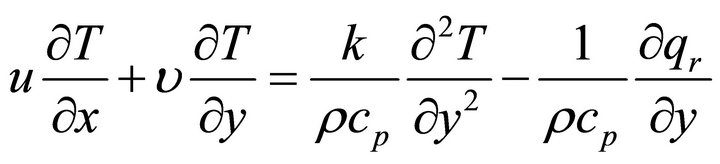 . (3)
. (3)
where 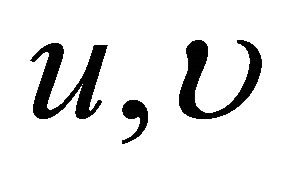 are the components of the velocity in the x and y directions respectively,
are the components of the velocity in the x and y directions respectively, 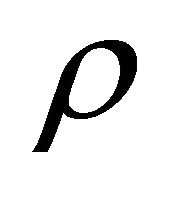 is the fluid density,
is the fluid density, 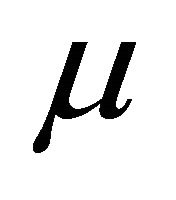 is the dynamic viscosity, T is the fluid temperature, k is the thermal conductivity,
is the dynamic viscosity, T is the fluid temperature, k is the thermal conductivity, 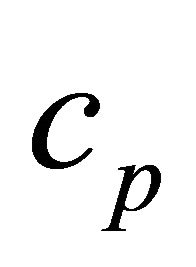 is the specific heat of the fluid under constant pressure and
is the specific heat of the fluid under constant pressure and  is the radiative heat flux.
is the radiative heat flux.
The dynamic viscosity is assumed to be an inverse linear function of temperature [29].
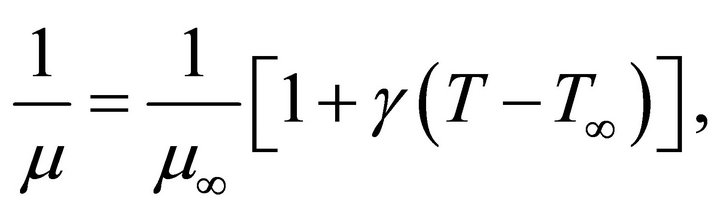 (4)
(4)
or
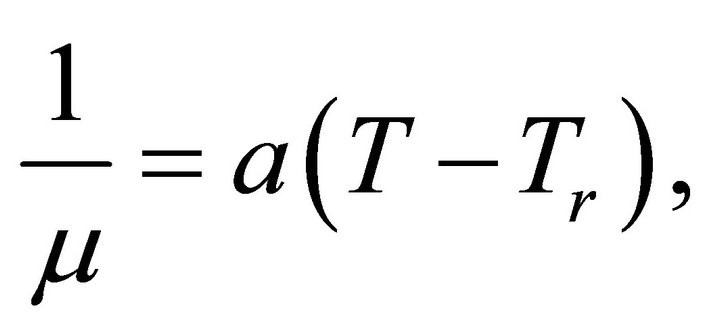 (5)
(5)
where
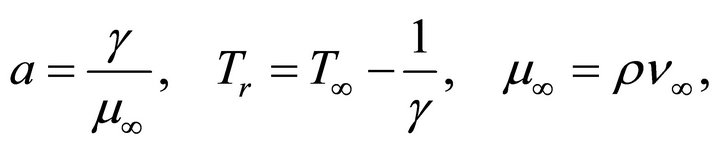 (6)
(6)
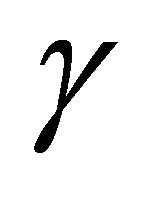 is a constant,
is a constant, 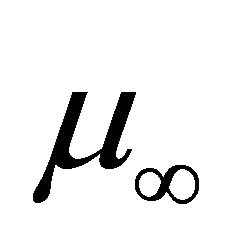 is the dynamic viscosity at infinity,
is the dynamic viscosity at infinity, 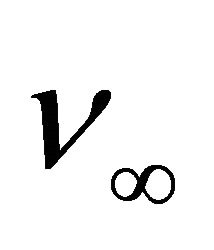 is the kinematic viscosity at infinity,
is the kinematic viscosity at infinity, 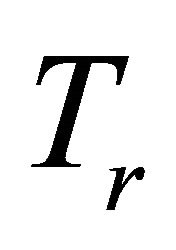 is a reference temperature,
is a reference temperature, 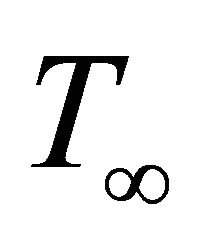 is the temperature at infinity,
is the temperature at infinity, 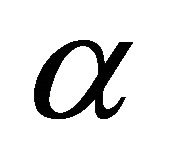 is a constant which in general is positive for liquids and
is a constant which in general is positive for liquids and
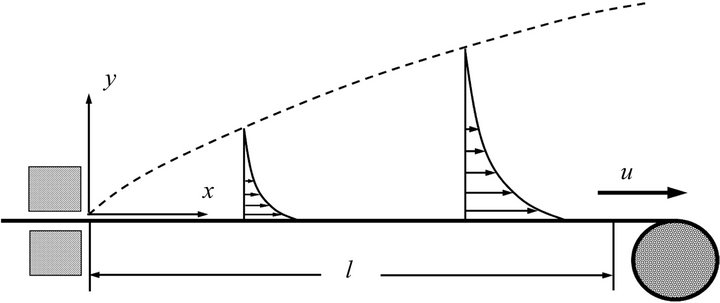
Figure 1. Physical model and co-ordinate system of the problem.
negative for gases.
The boundary conditions are defined as follows:
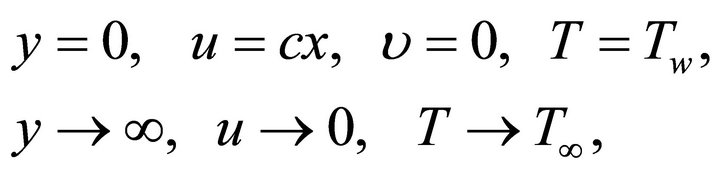 (7)
(7)
where  is a constant and
is a constant and 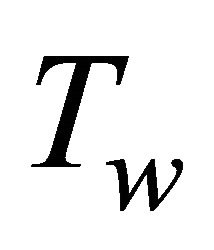 is the temperature of the stretching flat surface. In the case of an optically thin gray fluid the local radiant absorption is expressed as [8, 25,28],
is the temperature of the stretching flat surface. In the case of an optically thin gray fluid the local radiant absorption is expressed as [8, 25,28],
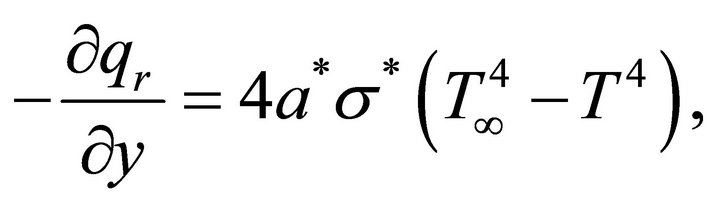 (8)
(8)
where  is the absorption coefficient and
is the absorption coefficient and  is the Stefan-Boltzman constant. We assume that the temperature differences within the flow are sufficiently small such that
is the Stefan-Boltzman constant. We assume that the temperature differences within the flow are sufficiently small such that  may be expressed as a linear function of the temperature. This is accomplished by expanding
may be expressed as a linear function of the temperature. This is accomplished by expanding  in a Taylor series about
in a Taylor series about 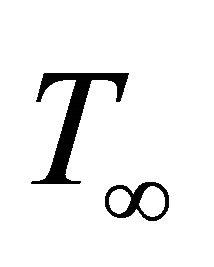 and neglecting higher-order terms, thus
and neglecting higher-order terms, thus
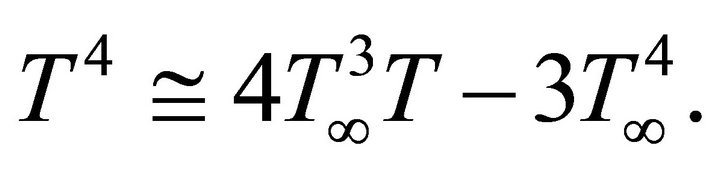 (9)
(9)
Equation (8) through (9) takes the form:
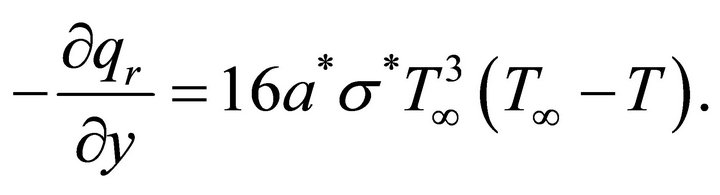 (10)
(10)
Introducing the following transformations
 (11)
(11)
where a prime denotes differentiation with respect to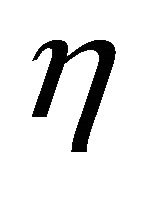 . In view of (10) and (11), Equation (1) is satisfied identically and Equations (2) and (3) reduce to
. In view of (10) and (11), Equation (1) is satisfied identically and Equations (2) and (3) reduce to
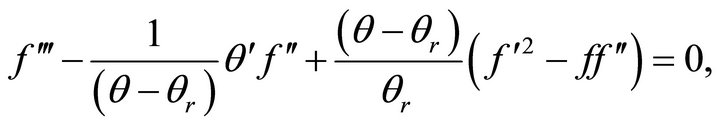 (12)
(12)
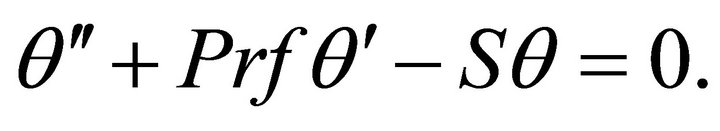 (13)
(13)
The boundary conditions (7) are transformed to
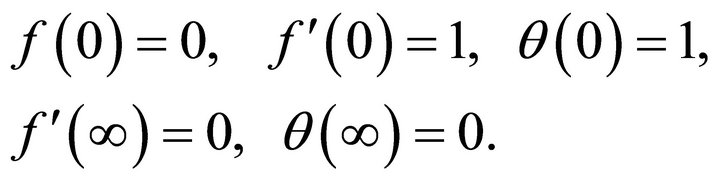 (14)
(14)
3. Numerical Solution
The non-linear system of coupled differential Equations (12) and (13) subject to the boundary conditions (14) has been solved following a symbolic approach. For this purpose we have used the Computer Algebra System (CAS) Mathematica [30].
The analysis begins by obtaining the discretized form of the system of equations by using a symbolic package developed for that purpose [31]. To discretize the coupled set of ordinary differential equations the finite volume method on a collocated grid is used [32]. Having obtained the discretized system, we construct the system of algebraic equations. Then the system is solved algebraically by Mathematica’s function Solve in respect to the grid values of the functions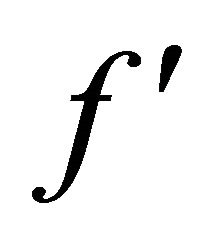 ,
, . More details about the numerical approach can be found elsewhere [31]. Grid independence studies were performed to establish that the results are not grid dependent.
. More details about the numerical approach can be found elsewhere [31]. Grid independence studies were performed to establish that the results are not grid dependent.
4. Results and Discussion
In the present study we numerically investigate the effect of radiation on the flow field over a stretching plate of an optically thin gray fluid, Figure 1. The fluid was considered viscous and incompressible. The viscosity was temperature dependent as shown in Equation (4). The results are presented in figures for the non-dimensional velocity,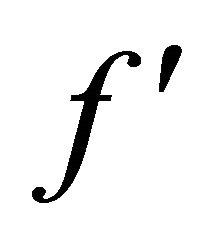 , and non-dimensional temperature,
, and non-dimensional temperature,  in respect to the temperature parameter,
in respect to the temperature parameter, 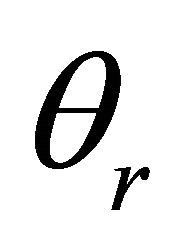 , radiation parameter,
, radiation parameter, 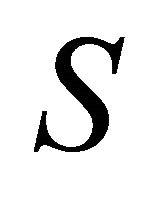 , and the Prantdl number,
, and the Prantdl number,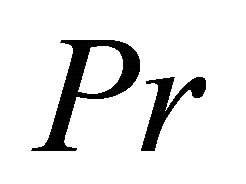 .
.
In Figure 2, the effect of the temperature parameter 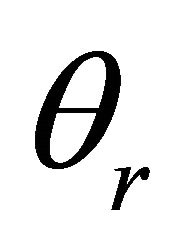
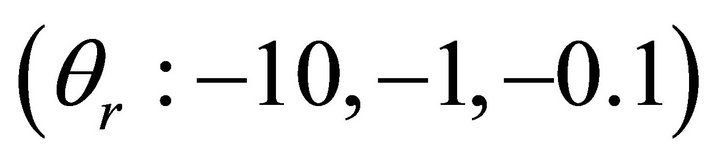 on the non-dimensional velocity,
on the non-dimensional velocity, 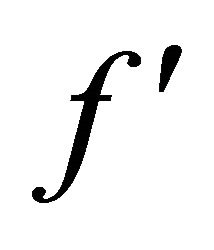 , when
, when 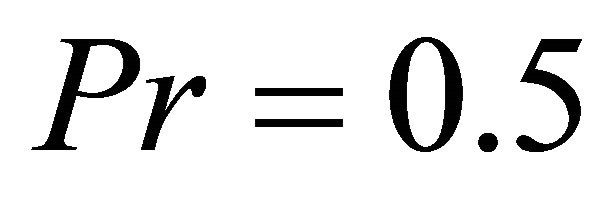 and
and 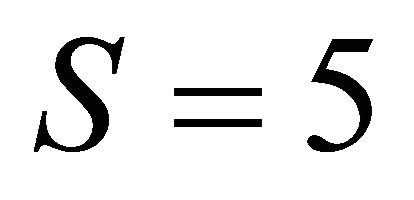 is presented. Velocity decreases with the increase of the temperature parameter. Especially for
is presented. Velocity decreases with the increase of the temperature parameter. Especially for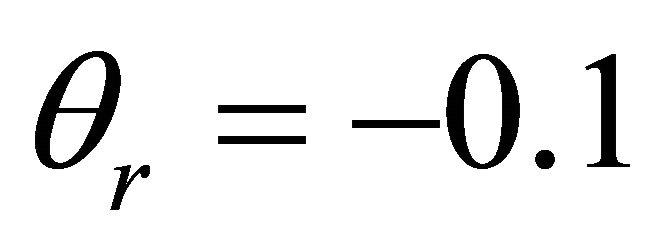 , the velocity is substantially reduced leading to a thinner boundary layer (Figure 2, line 3).
, the velocity is substantially reduced leading to a thinner boundary layer (Figure 2, line 3).
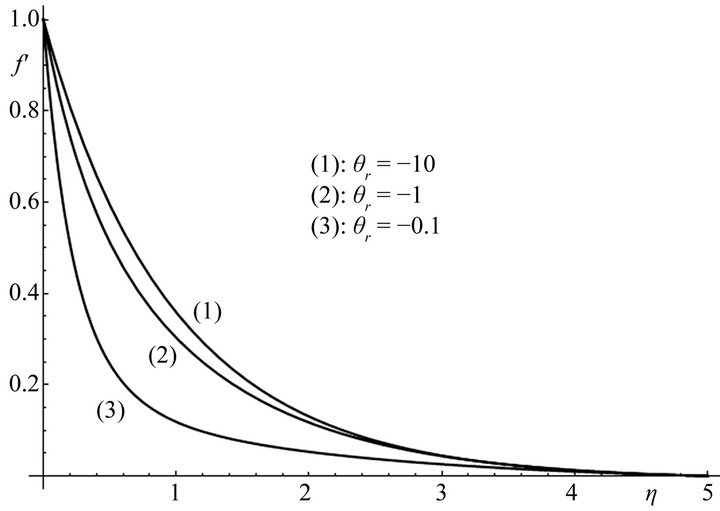
Figure 2. Velocity profiles for different values of the temperature parameter θr and for Pr = 0.5, S = 5.
The effect of the radiation parameter S (S: 0.1, 1, 7) on the non-dimensional velocity 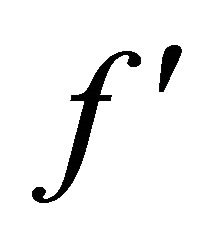 is shown in Figure 3, when Pr = 0.5 and
is shown in Figure 3, when Pr = 0.5 and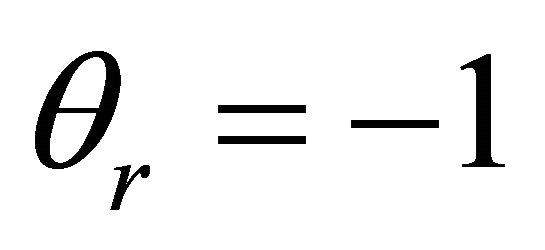 . The velocity increases with the increase of the radiation parameter. This effect is more pronounced when the radiation parameter has larger values, as depicted in Figure 3.
. The velocity increases with the increase of the radiation parameter. This effect is more pronounced when the radiation parameter has larger values, as depicted in Figure 3.
The effect of the radiation parameter S (S: 0.1, 1, 7) on the non-dimensional temperature  is shown in Figure 4, when Pr = 0.5 and
is shown in Figure 4, when Pr = 0.5 and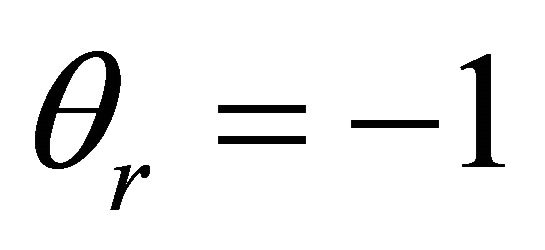 . When the radiation parameter increases the temperature decreases, and this effect is more pronounced as the radiation parameter increases.
. When the radiation parameter increases the temperature decreases, and this effect is more pronounced as the radiation parameter increases.
The effect of the Prandtl number, Pr, on the non-dimensional temperature  is presented in Figure 5 for three different values of Prandtl (Pr: 0.5, 0.7, 1), when
is presented in Figure 5 for three different values of Prandtl (Pr: 0.5, 0.7, 1), when 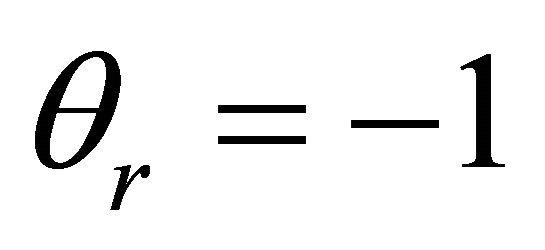 and S = 1. The increase of Prandtl number leads to a decrease of the temperature in the boundary layer.
and S = 1. The increase of Prandtl number leads to a decrease of the temperature in the boundary layer.
Finally, Figures 6 and 7 show the effect of the temperature parameter 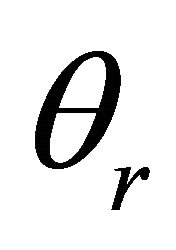 on the non-dimensional velocity
on the non-dimensional velocity  and temperature
and temperature  when Pr = 0.7, S = 1 and for
when Pr = 0.7, S = 1 and for
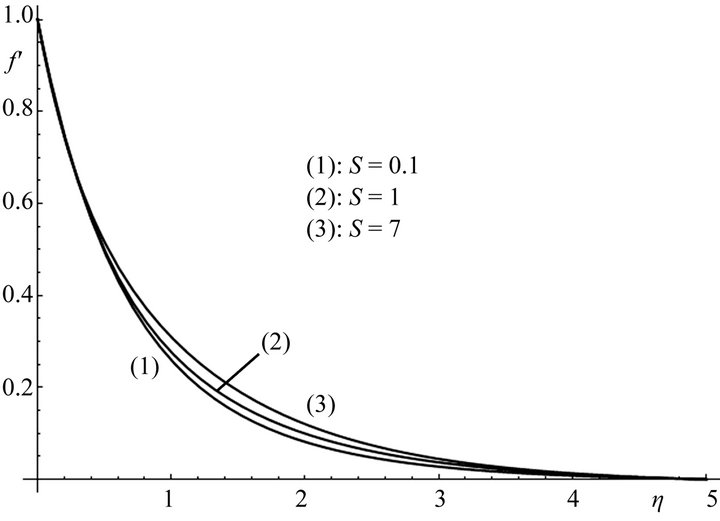
Figure 3. Velocity profiles for different values of the radiation parameter S and for Pr = 0.5, θr = −1.
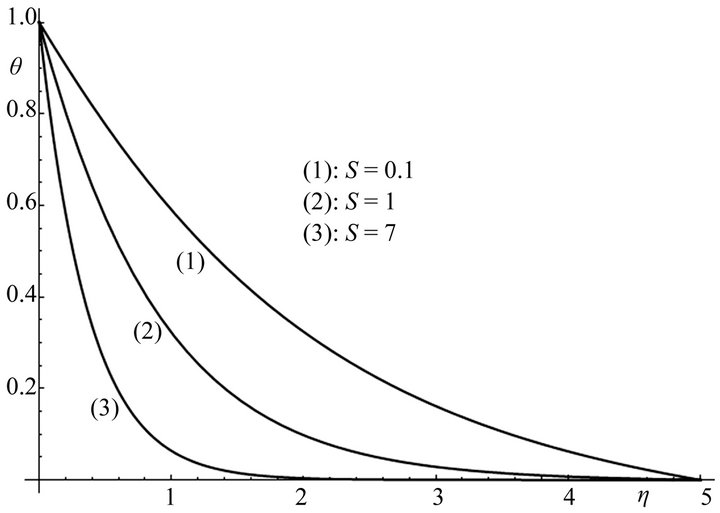
Figure 4. Temperature profiles for different values of the radiation parameter S and for Pr = 0.5, θr = −1.
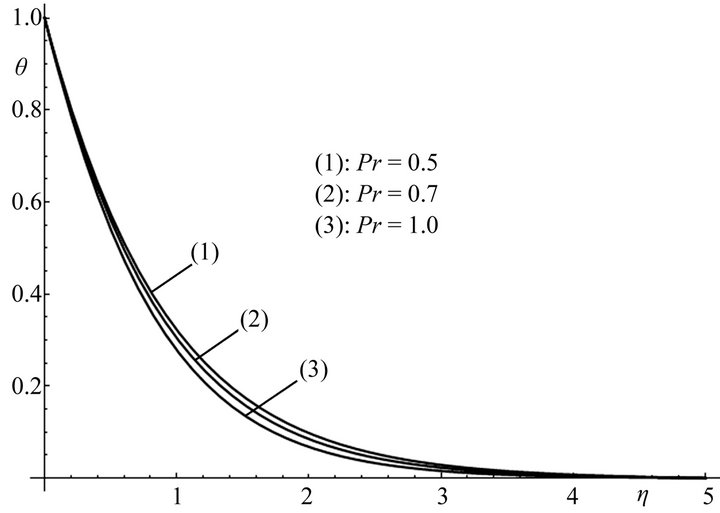
Figure 5. Temperature profiles for different values of the Prandtl number Pr and for θr = −1 and S = 1.
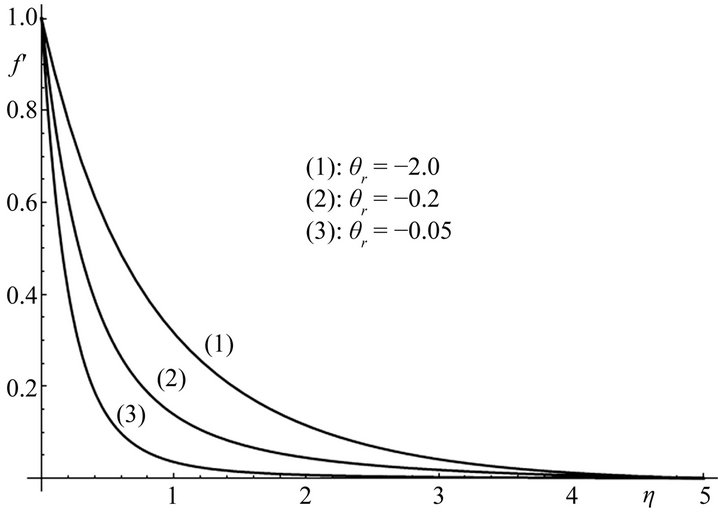
Figure 6. Velocity profiles for different values of the temperature parameter θr and for Pr = 0.7, S = 1.
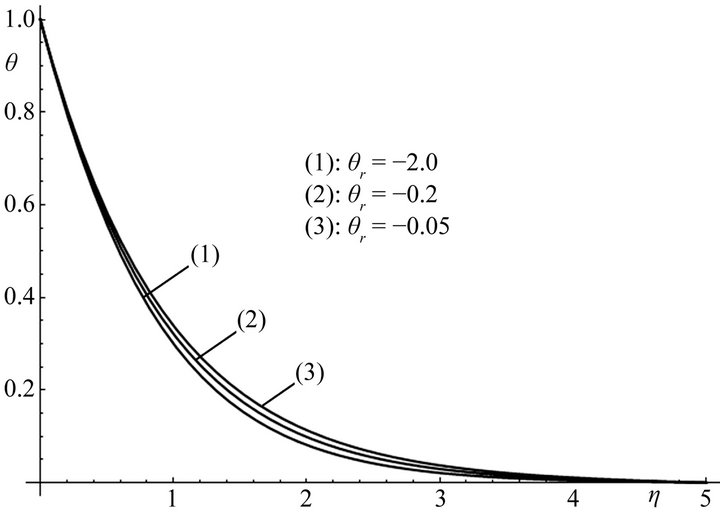
Figure 7. Temperature profiles for different values of the temperature parameter θr and for Pr = 0.7, S = 1.
three different values of the temperature parameter. Temperature increases with the increase of the temperature parameter, 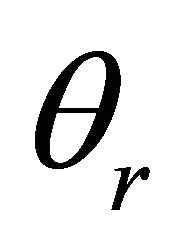 (
(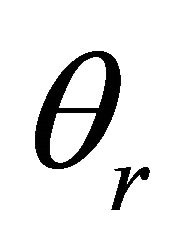 : –2, –0.05, –0.01). However, the effect of the temperature parameter is more pronounced on the non-dimensional velocity
: –2, –0.05, –0.01). However, the effect of the temperature parameter is more pronounced on the non-dimensional velocity 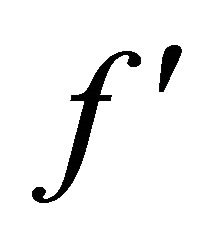 and it decreases as the parameter
and it decreases as the parameter 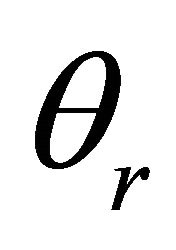 increases, Figure 6.
increases, Figure 6.
The numerical results of this study could bring new insight on the effect of thermal radiation on the flow past a stretching plate with temperature dependent viscosity. These results could be utilized in many industrial and practical areas, including glass and semiconductor processing, atmospheric flows with application to global climate change, electrical power generation, solar power technology, and aerospace engineering.
5. Conclusion
The effects of thermal radiation on the flow and temperature fields over a stretching plate of an optically thin gray fluid were numerical investigated. The fluid was considered incompressible with temperature dependent viscosity. The main findings of this study could be summarized in the following: (1) Increase of the radiation parameter increases the velocity profile but decreases the temperature profiles. (2) On the other hand, increase of the temperature parameter decreases the velocity profile and increases the temperature profile in the boundary layer. (3) Increase of Prandtl number decreases the temperature profile in the boundary layer.
REFERENCES
- M. M. Ali, T. S. Chen and B. F. Armaly, “Natural Convection-Radiation Interaction in Boundary-Layer Flow over Horizontal Surfaces,” AIAA Journal, Vol. 22, No. 12, 1984, pp. 1797-1803. doi:10.2514/3.8854
- M. A. Seddeek and M. S. Abdelmeguid, “Effects of Radiation and Thermal Diffusivity on Heat Transfer over a Stretching Surface with Variable Heat Flux,” Physics Letters A, Vol. 348, No. 3-6, 2006, pp. 172-179. doi:10.1016/j.physleta.2005.01.101
- A. Raptis and C. J. Toki, “Thermal Radiation in the Presence of Free Convective Flow past a Moving Vertical Porous Plate—An Analytical Solution,” International Journal of Applied Mechanics and Engineering, Vol. 14, No. 4, 2009, pp. 1115-1126.
- P. Malekzadeh, M. A. Moghimi and M. Nickaeen, “The Radiation and Variable Viscosity Effects on Electrically Conducting Fluid over a Vertically Moving Plate Subjected to Suction and Heat Flux,” Energy Conversion and Management, Vol. 52, No. 5, 2011, pp. 2040-2047. doi:10.1016/j.enconman.2010.12.006
- A. J. Chamkha, M. Mujtaba, A. Quadri and C. Issa, “Thermal Radiation Effects on MHD Forced Convection Flow Adjacent to a Non-Isothermal Wedge in the Presence of a Heat Source or Sink,” Heat and Mass Transfer, Vol. 39, No. 4, 2003, pp. 305-312.
- A. Raptis, C. Perdikis and H. S. Takhar, “Effect of Thermal Radiation on MHD Flow,” Applied Mathematics and Computation, Vol. 153, No. 3, 2004, pp. 645-649. doi:10.1016/S0096-3003(03)00657-X
- H. M. Duwairi, “Viscous and Joule Heating Effects on Forced Convection Flow from Radiate Isothermal Porous Surfaces,” International Journal of Numerical Methods for Heat & Fluid Flow, Vol. 15, No. 5-6, 2005, pp. 429- 440. doi:10.1108/09615530510593620
- M. E. M. Ouaf, “Exact Solution of Thermal Radiation on MHD Flow over a Stretching Porous Sheet,” Applied Mathematics and Computation, Vol. 170, No. 2, 2005, pp. 1117-1125. doi:10.1016/j.amc.2005.01.010
- M. Abd-El Aziz, “Thermal Radiation Effects on MagneTohydrodynamic Mixed Convection Flow of a Micropolar Fluid past a Continuously Moving Semi-Infinite Plate for High Temperature Differences,” Acta Mechanica, Vol. 187, No. 1-4, 2006, pp. 113-127. doi:10.1007/s00707-006-0377-9
- D. Pal and H. Mondal, “Effects of Soret Dufour, Chemical Reaction and Thermal Radiation on MHD Non-Darcy Unsteady Mixed Convective Heat and Mass Transfer over a Stretching Sheet,” Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 4, 2011, pp. 1942-1958. doi:10.1016/j.cnsns.2010.08.033
- G. C. Shit and R. Haldar, “Effects of Thermal Radiation on MHD Viscous Fluid Flow and Heat Transfer over Non-Linear Shrinking Porous Sheet,” Applied Mathematics and Mechanics-English Edition, Vol. 32, No. 6, 2011, pp. 677-688. doi:10.1007/s10483-011-1448-6
- P. V. S. N. Murthy, S. Mukherjee, D. Srinivasacharya, and P. V. S. S. S. R. Krishna, “Combined Radiation and Mixed Convection from a Vertical Wall with Suction/Injection in a Non-Darcy Porous Medium,” Acta Mechanica, Vol. 168, No. 3-4, 2004, pp. 145-156. doi:10.1007/s00707-004-0084-3
- S. M. Al-Harbi, “Numerical Study of Natural Convection Heat Transfer with Variable Viscosity and Thermal Radiation from a Cone and Wedge in Porous Media,” Applied Mathematics and Computation, Vol. 170, No. 1, 2005, pp. 64-75. doi:10.1016/j.amc.2004.10.093
- M. Q. Al-Odat, F. M. S. Al-Hussien and R. A. Damseh, “Influence of Radiation on Mixed Convection over a Wedge in Non-Darcy Porous Medium,” Forschung Im Ingenieurwesen-Engineering Research, Vol. 69, No. 4, 2005, pp. 209-215. doi:10.1007/s10010-005-0004-2
- A. Raptis and C. Perdikis, “Flow through a High Porosity Medium in the Presence of Radiation,” Journal of Porous Media, Vol. 9, No. 2, 2006, pp. 169-175. doi:10.1615/JPorMedia.v9.i2.60
- H. M. Duwairi. “Radiation Effects on Mixed Convection over a Nonisothermal Cylinder and Sphere in a Porous Media,” Journal of Porous Media, Vol. 9, No. 3, 2006, pp. 251-259. doi:10.1615/JPorMedia.v9.i3.60
- I. A. Badruddin, Z. A. Zainal, P. A. A. Narayana and K. N. Seetharamu, “Numerical Analysis of Convection Conduction and Radiation Using a Non-Equilibrium Model in a Square Porous Cavity,” International Journal of Thermal Sciences, Vol. 46, No. 1, 2007, pp. 20-29. doi:10.1016/j.ijthermalsci.2006.03.006
- F. G. Awad, P. Sibanda, S. S. Motsa and O. D. Makinde, “Convection from an Inverted Cone in a Porous Medium with Cross-Diffusion Effects,” Computers & Mathematics with Applications, Vol. 61, No. 5, 2011, pp. 1431-1441. doi:10.1016/j.camwa.2011.01.015
- A. Raptis, “Radiation and Viscoelastic Flow,” International Communications in Heat and Mass Transfer, Vol. 26, No. 6, 1999, pp. 889-895.
- P. S. Datti, K. V. Prasad, M. S. Abel and A. Joshi, “MHD Visco-Elastic Fluid Flow over a Non-Isothermal Stretching Sheet,” International Journal of Engineering Science, Vol. 42, No. 8-9, 2004, pp. 935-946. doi:10.1016/j.ijengsci.2003.09.008
- S. Abel, K. V. Prasad and A. Mahaboob, “Buoyancy Force and Thermal Radiation Effects in MHD Boundary Layer Visco-Elastic Fluid Flow over Continuously Moving Stretching Surface,” International Journal of Thermal Sciences, Vol. 44, No. 5, 2005, pp. 465-476. doi:10.1016/j.ijthermalsci.2004.08.005
- P. G. Siddheshwar and U. S. Mahabaleswar, “Effects of Radiation and Heat Source on MHD Flow of a Viscoelastic Liquid and Heat Transfer over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 40, No. 6, 2005, pp. 807-820.
- S. K. Khan, “Heat Transfer in a Viscoelastic Fluid Flow over a Stretching Surface with Heat Source/Sink, Suction/Blowing and Radiation,” International Journal of Heat and Mass Transfer, Vol. 49, No. 3-4, 2006, pp. 628- 639. doi:10.1016/j.ijheatmasstransfer.2005.07.049
- A. R. Bestman and S. K. Adjepong, “Unsteady HydroMagnetic Free-Convection Flow with Radiative HeatTransfer in a Rotating Fluid. Compressible Optically Thin Fluid,” Astrophysics and Space Science, Vol. 143, No. 2, 1988, pp. 217-224. doi:10.1007/BF00637135
- A. Raptis and C. Perdikis, “Thermal Radiation of an Optically Thin Gray Gas,” International Journal of Applied Mechanics and Engineering, Vol. 8, No. 1, 2003, pp. 131-134.
- V. Rajesh, “Radiation Effects on MHD Free Convective Flow near a Vertical Plate with Ramped Wall Temperature,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 21, 2010, pp. 60-77.
- U. S. Rajput and S. Kumar, “Rotation and Radiation Effects on MHD Flow past an Impulsively Started Vertical Plate with Variable Temperature,” International Journal of Mathematical Analysis, Vol. 5, No 24, 2011, pp. 1155- 1163.
- A. Raptis, “Free Convective Oscillatory Flow and Mass Transfer past a Porous Plate in the Presence of Radiation for an Optically Thin Fluid,” Thermal Science, Vol. 15, No. 3, 2011, pp. 849-857. doi:10.2298/TSCI101208032R
- F. C. Lai and F. A. Kulacki, “The Effect of Variable Viscosity on Convective Heat-Transfer Along a Vertical Surface in a Saturated Porous-Medium,” International Journal of Heat and Mass Transfer, Vol. 33, No. 5, 1990, pp. 1028-1031. doi:10.1016/0017-9310(90)90084-8
- Wolfram-Research, “Mathematica Edition: Version 8.0,” Wolfram-Research, Inc., Champaign, 2010.
- M. Xenos, S. Dimas and A. Raptis, “MHD Free Convective Flow of Water near 4˚C past a Vertical Moving Plate with Constant Suction,” Applied Mathematics, Vol. 4, No. 1, 2013, pp. 52-57.
- S. V. Patankar, “Numerical Heat Transfer and Fluid Flow,” McGraw-Hill, New York, 1980.

