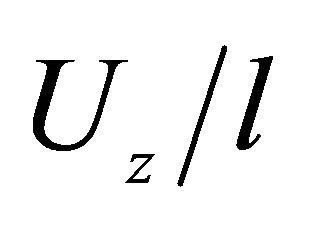Applied Mathematics
Vol. 4 No. 8A (2013) , Article ID: 34604 , 6 pages DOI:10.4236/am.2013.48A001
Mathematical Modeling of Cardiomyocytes’ and Skeletal Muscle Fibers’ Membrane: Interaction with External Mechanical Field
Department of Molecular Biomedicine, State Scientific Center of Russian Federation, Institute of Biomedical Problems of the Russian Academy of Sciences, Moscow, Russia
Email: iogneva@yandex.ru
Copyright © 2013 Irina V. Ogneva, Nikolay S. Biryukov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 25, 2013; revised April 25, 2013; accepted May 3, 2013
Keywords: Mathematical Modeling in Biology; Muscle Cell; Cell Mechanosensitivity; Microgravity
ABSTRACT
We propose a mathematic model of muscle cell membrane based on thin-walled elastic rod theory. A deformation occurs in rodents’ skeletal and cardiac cells during a period of antiorthostatic suspension. We carried out a quantitative evaluation of the deformation using this model. The calculations showed the deformation in cardiac cells to be greater than in skeletal ones. This data corresponds to experimental results of cell response that appears intense in cardiomyocytes than in skeletal muscle cells. Moreover, the deformation in skeletal and heart muscle cells has a different direction (stretching vs. compression), corresponding to experimental data of different adaptive response generation pathways in cells because of external mechanical condition changes.
1. Introduction
Every mechanical system, including living cells, in an external mechanical field is exposed to forces intrinsic to this field. The action of these forces results in mechanical tension that appears in cells. An external influence change (in direction or magnitude) leads to mechanical tension changes in cells and to deformation. The significance of the deformation for the cell depends on its inherent mechanical characteristics and the sensitivity of its mechanosensors.
An external physical signal transformation results in proper cell response generation. At the same time, the clue is the magnitude of the applied force that is able to induce cell response.
All living cells can be divided into two groups: cells that form internal tension only against external influence and cells that can additionally generate force themselves —muscle cells. Muscle cells have a specific structure, a developed cytoskeleton, which occupies most of the cell volume and forms a contractile apparatus. Taking these features into account, one can suppose that a muscle cell mechanosensor is connected to the contractile apparatus, for example with the M-line [1].
However, the muscle cell submembrane cytoskeleton is quite similar to that in non-muscle cells except for certain areas (particularly in areas of M-line and Z-disk projections on the membrane). Hence, cell formation takes place under constant external force action, so one can assume that the first mechanoreception acts to connect with the cell compartment, typical for every living cell. This compartment appears to comprise a membrane and a cortical (submembrane) cytoskeleton. Therefore, the question is what deformations emerge in the muscle fiber membrane after the gravity vector or the fiber contraction rate changes and whether these changes can result in muscle fiber mechanical characteristic change and cell response initiation.
To answer these questions, we need a numerical evaluation of deformations that arise in the sarcolemma after external mechanical conditions change. Such an evaluation requires data about longitudinal and transversal stiffness because muscle cells appear to have a three-dimensional structure [2]. However, this problem turns out to be hard to solve because the contractile apparatus contribution to linear stiffness is several orders greater than the contribution of the sarcolemma. Previously, we succeeded in determining the transversal stiffness of the sarcolemma using atomic force microscopy [3], changing mechanical conditions for both skeletal and cardiac muscles in rodents (Figure 1) [4].
An external mechanical condition change was implemented through the common animal antiorthostatic suspension method by tail at an angle of 30˚ respective to the cage floor (the Ilyin-Novikov method with the MoreyHolton modification is widely used in space physiology to model microgravity effects on a surface [5]). Animal suspension resulted, on the one hand, in a reduction of the external mechanical field on the hind limbs and, on the other hand, in increased mechanical tension in cardiomyocytes. The orientation of the muscle cells (muscle fibers) in the gravity field changed, too.
Nevertheless, the data for only the transversal stiffness of the membrane and cortical cytoskeleton do not afford us the influence of the gravity vector change on the muscle cell membrane and its probable involvement in primary mechanoreception acts. All of the above indicates the necessity of developing a membrane mathematical model.
2. Mathematical Model
2.1. Statement of the Problem
Let δ define the thickness of the membrane and cortical cytoskeleton, d is the muscle fiber diameter, and l is its length. Then, we can write the following relations:
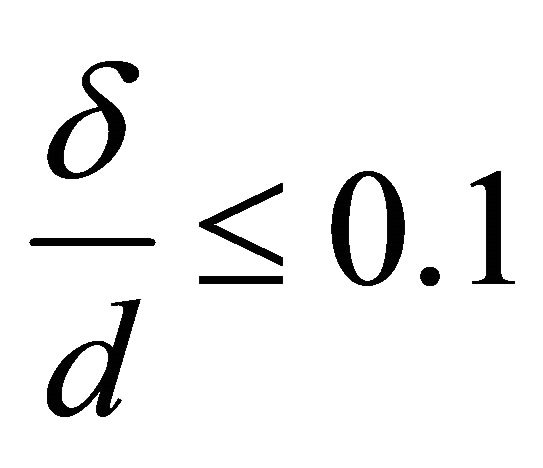 ,
, 
This enables us to consider the fiber a long, cylindrical envelope called a thin-walled rod [6].
It is typical for transversal sections of this kind of objects to initially be plane distorted on a surface: W(x, z). W(x, z) is usually called a sectional warping. For closed envelope rods, including muscle fibers, axial uniform warping is also typical, so we can rewrite W(x, z) as W(x). We have 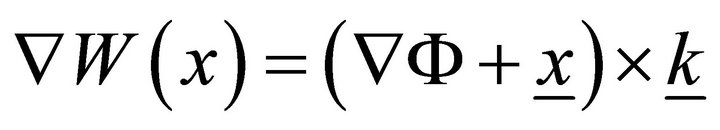 in Saint-Venant’s prob-
in Saint-Venant’s prob-
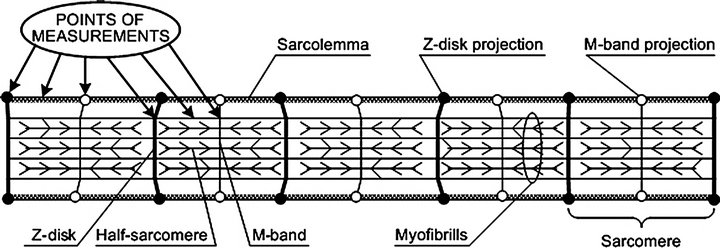
Figure 1. Scheme of muscle fiber with indicated measurement points. Using the AFM surface images, we were able to measure the transverse stiffness of all specific regions of the fiber, such as the contractile apparatus and membrane at different points. For this study, the main parameter is the membrane stiffness between the Z-disk and M-line projections. The structure of this region is universal for all cell types (not just muscle cells).
lem, where Ф is the Prandtl function (underlining indicates that the underlined value is a vector). We can take a sectorial area as W for a thin section. Then, for the part of membrane between the Z-disk and M-line to be considered, we use the thin-walled theory statements. We will consider the cylindrical rod with thin simply connected section F and with volume load f. For simplicity, we suppose the 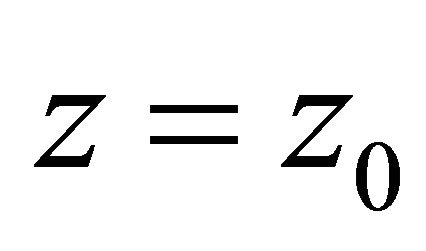 end to be fixed, and we have the surface load
end to be fixed, and we have the surface load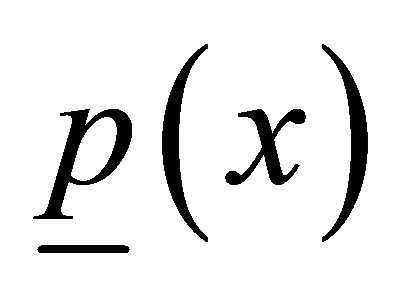 , which is a net load between the Zdisk and M-line (to be determined later) on the other end
, which is a net load between the Zdisk and M-line (to be determined later) on the other end . We describe this three-dimensional case using the method of variations [7]:
. We describe this three-dimensional case using the method of variations [7]:
 , (1)
, (1)
 ,
, 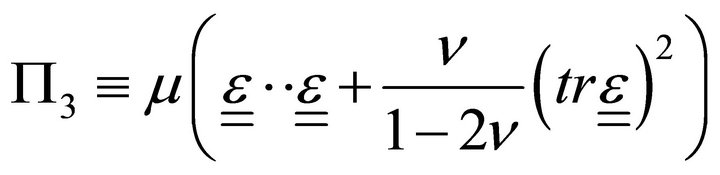 where
where  is the translation vector,
is the translation vector,  is the volumetric energy,
is the volumetric energy, 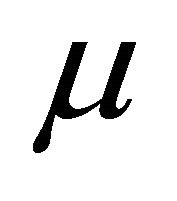 is the Lamé constant,
is the Lamé constant, ![]() is the Poisson ratio,
is the Poisson ratio, 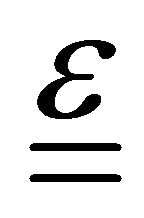 is the deformation tensor, and
is the deformation tensor, and  is the trace of deformation tensor, the first invariant (double underlining indicates tensors).
is the trace of deformation tensor, the first invariant (double underlining indicates tensors).
To derive equations from the variation principle, we approximate the translation as:
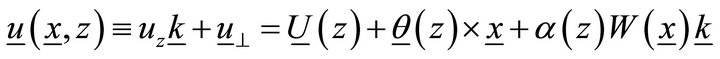 , (2)
, (2)
where 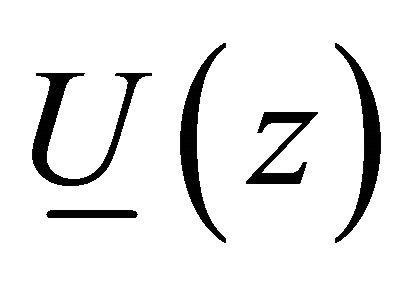 is the linear translation,
is the linear translation, 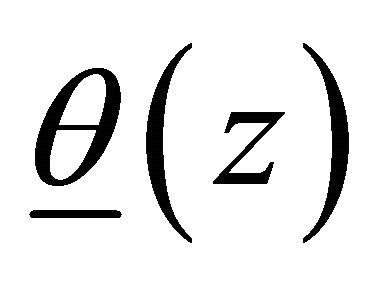 is the rotation vector,
is the rotation vector, 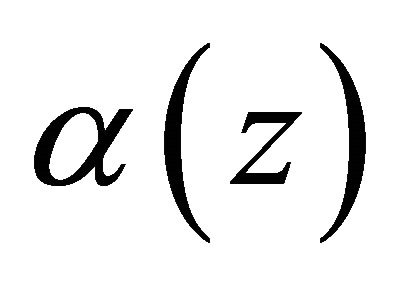 is the rotation angle per unit length, and
is the rotation angle per unit length, and 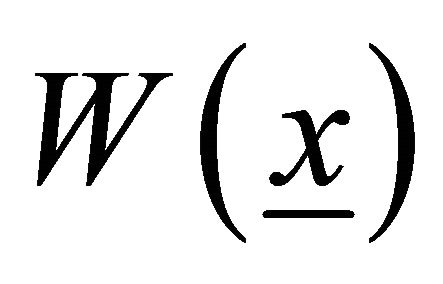 is the warping function:
is the warping function:
 ,
, 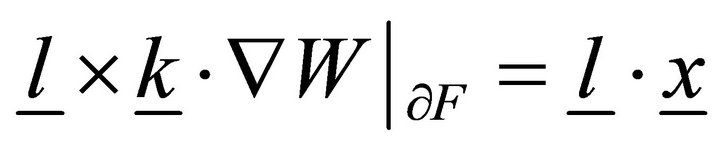 ,
,
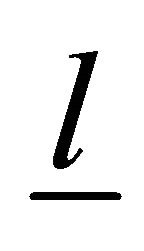 is the basis vector of the Lagrangian coordinate.
is the basis vector of the Lagrangian coordinate.
Let us suppose that there is a lack of transversal shifts; then:
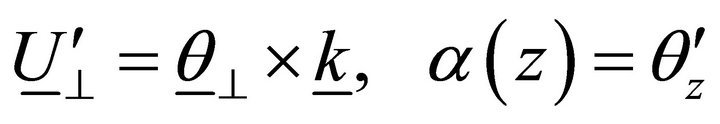 . (3)
. (3)
Taking into account Equation (3), approximation (2) becomes:
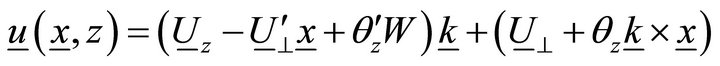 , (4)
, (4)
That is:
 . (5)
. (5)
From the classical theory of elasticity, we know that:
 , (6)
, (6)
where S is the symmetrization symbol.
Using (4), Equation (6) can be rewritten:
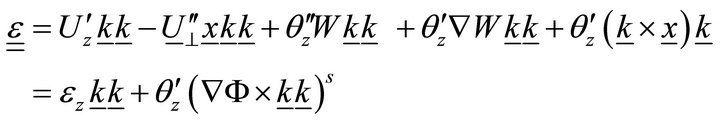 , (7)
, (7)
where 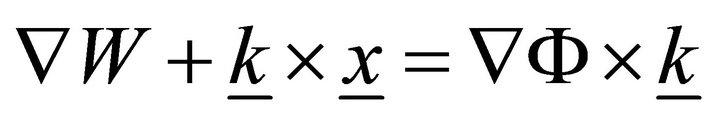 and
and  .
.
Then:
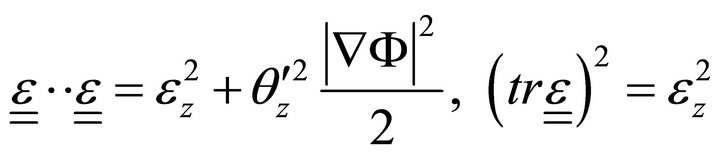 (8)
(8)
Substituting (8) into (1), we obtain a new volumetrical energy density:
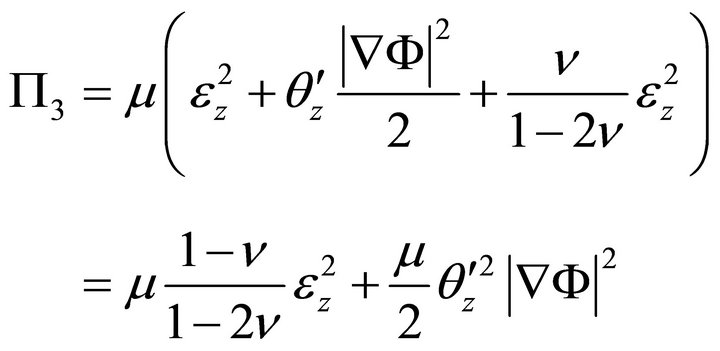
Since 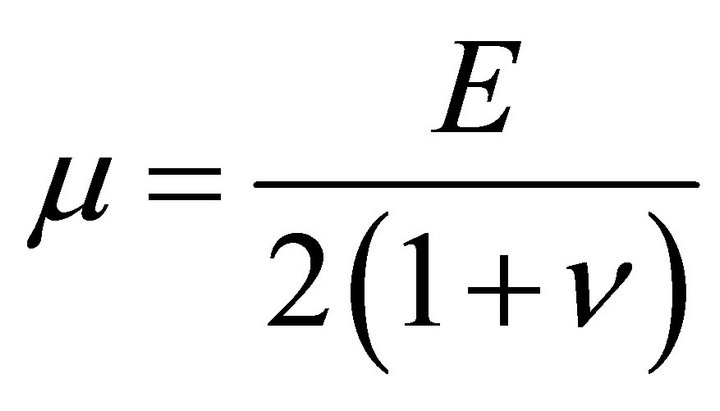 :
:
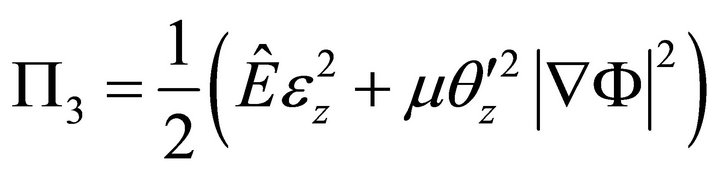 , (9)
, (9)
where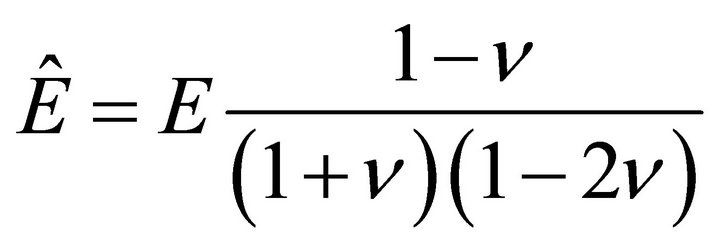 , and
, and  is Young’s modulus.
is Young’s modulus.
Taking into account (7), (9) becomes:
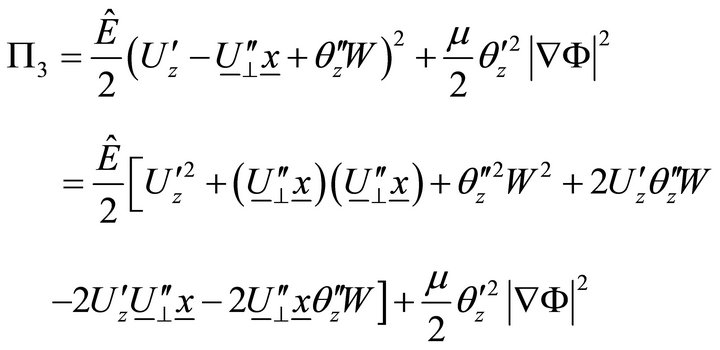 . (10)
. (10)
Integrating (10) in the section:
 , (11)
, (11)
where ,
, 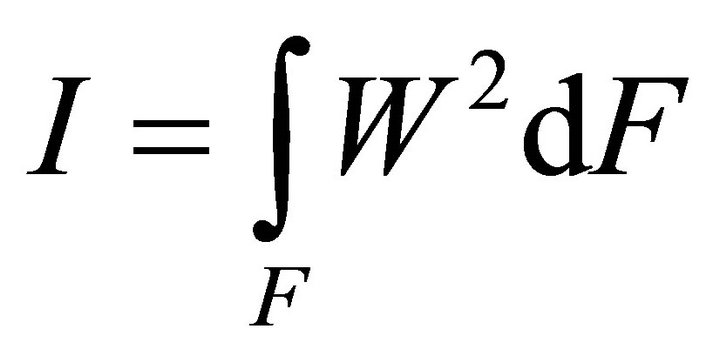 ,
, 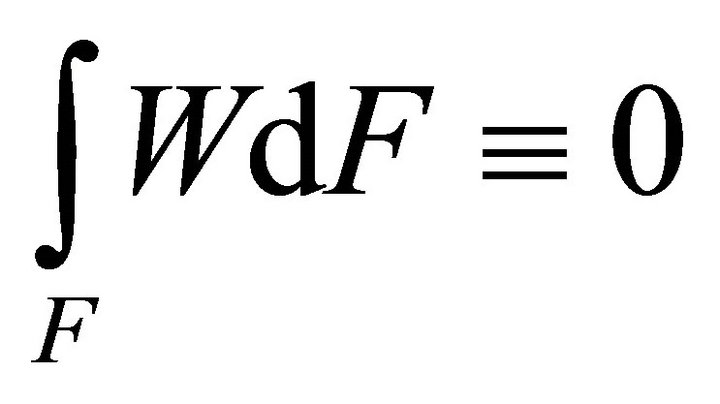 ,
,  ,
, 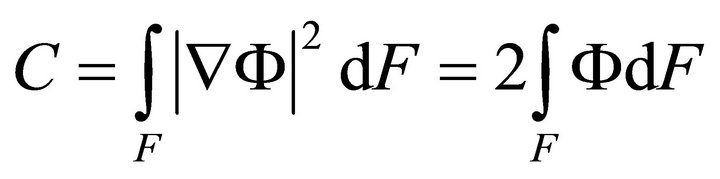 .
.
Let us now determine the work of volume loads:
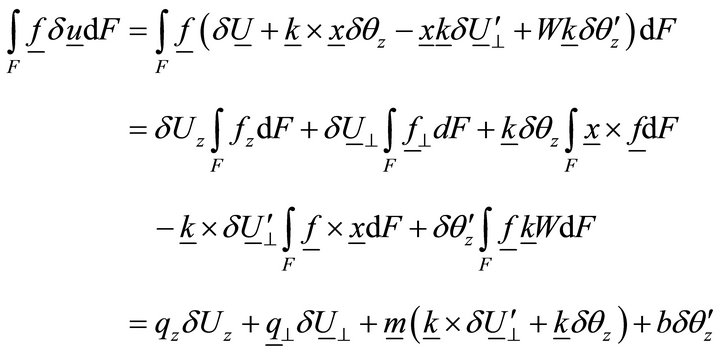 , (12)
, (12)
where ,
,  ,
, 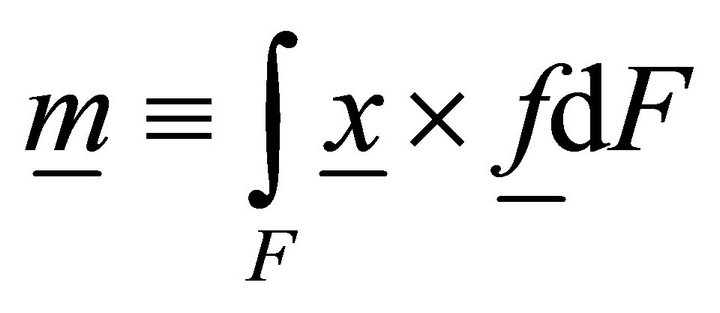 ,
, 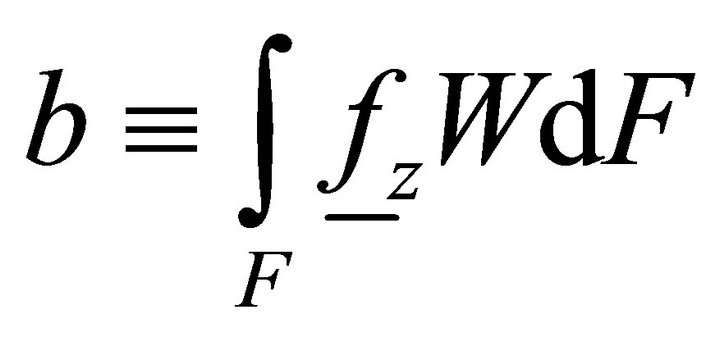 is the distributed bimoment per unit length.
is the distributed bimoment per unit length.
Similarly, a work of the volume load on the end:
 , (13)
, (13)
where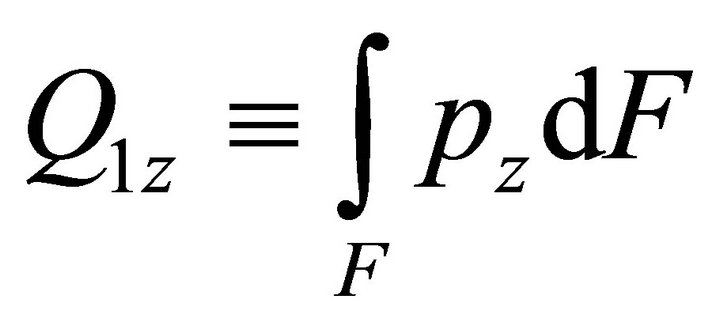 ,
,  ,
, 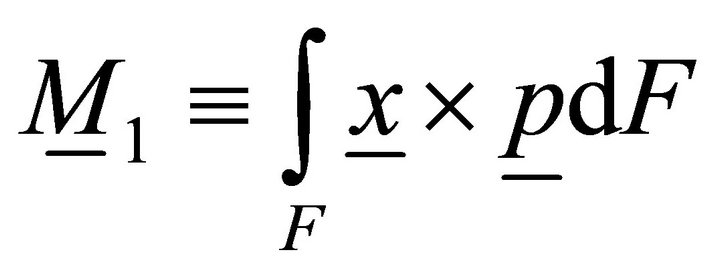 ,
, 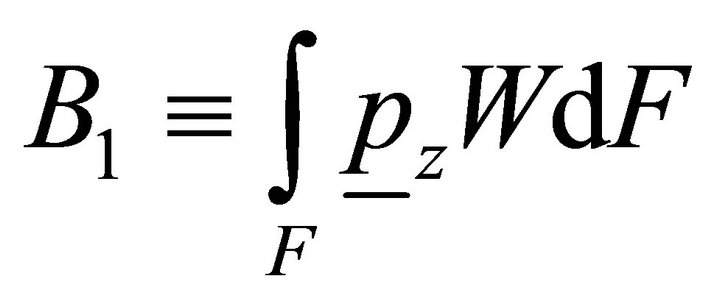 is the bimoment on the end.
is the bimoment on the end.
Taking into account Equations (12) and (13), the variational equation becomes:
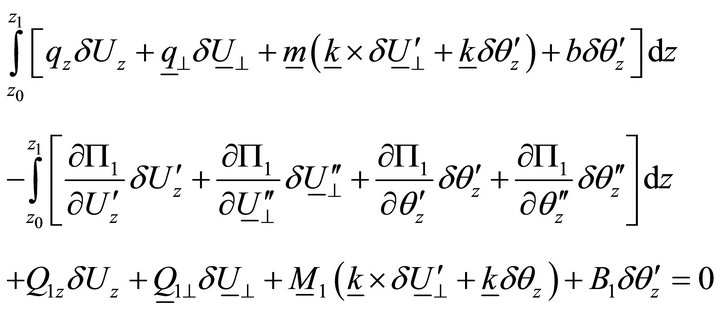 . (14)
. (14)
From (14), we obtain differential equations and limits:
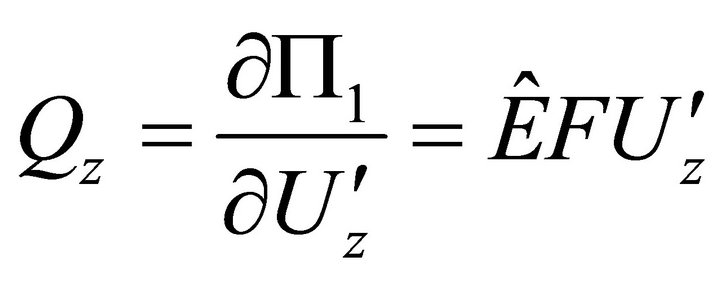
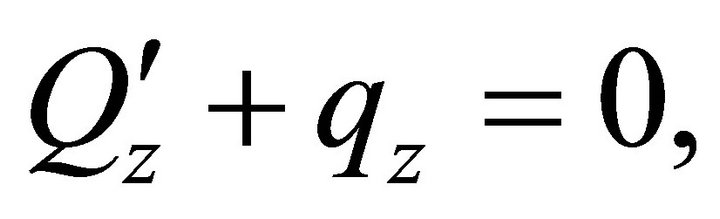 ,
,
![]() :
: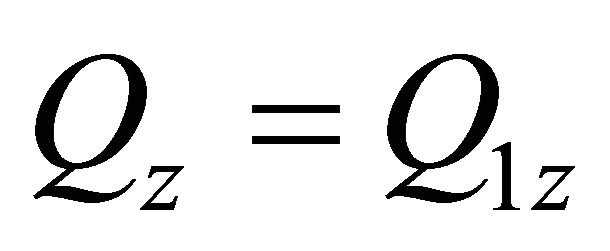 ,
, 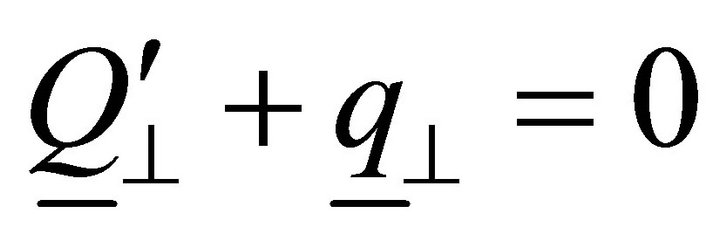 ,
,  ,
,
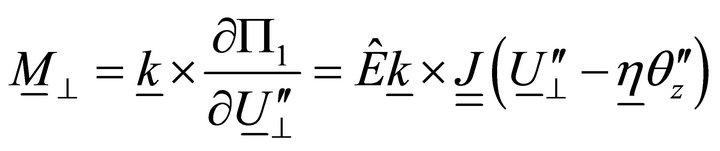 , (15)
, (15)
![]() :
: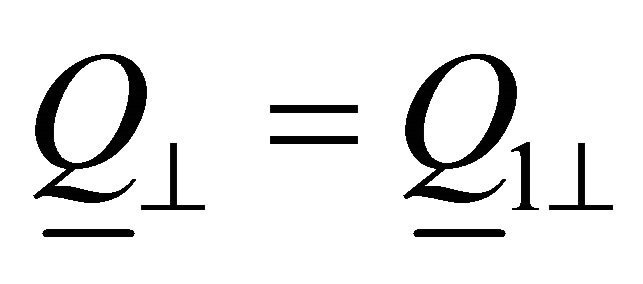 ,
, 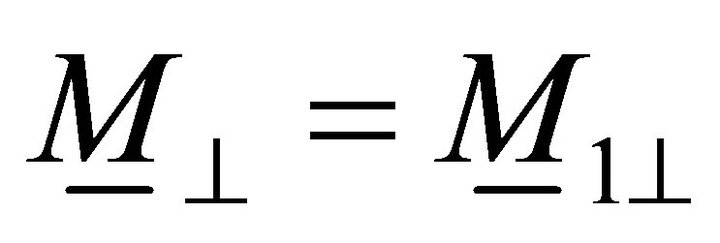
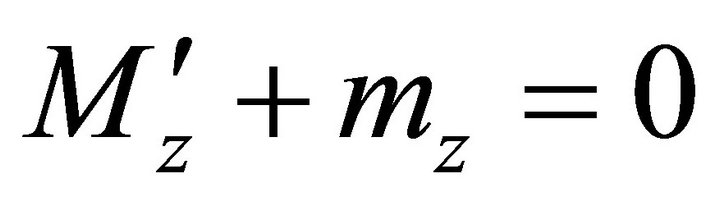 ,
, 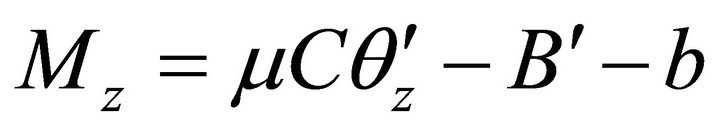 ,
,
 ,
,
![]() :
: ,
,  ,
, 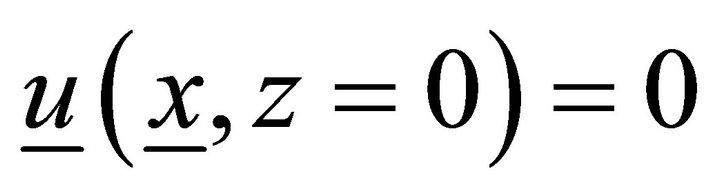
The set of equations derived in (15) gives us a chance to completely describe muscle fiber membrane behavior as a long cylindrical envelope and to find the potential energy  in the case described.
in the case described.
Let us assume that there is no external moment influence and that section warping and transversal shift contribution are negligible in comparison with the longitudinal component. This assumption is justified because of the specific muscle cell structure. Then, solving (15), we can find :
:
 , (16)
, (16)
where  is the volume load,
is the volume load, 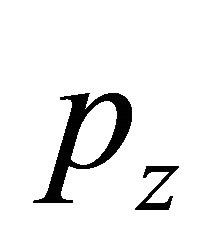 is the surface load, F is the section area,
is the surface load, F is the section area,  is the adduced Young’s modulus, and
is the adduced Young’s modulus, and ![]() is the Poisson ratio.
is the Poisson ratio.
2.2. External Mechanical Loading
An external mechanical field acts on the whole organism and launches a number of processes, leading to nervous activation change in skeletal muscles, a liquid shift in the cranial direction, and, as a result, to a volume load change in the heart.
These processes results in the muscle fiber membrane becoming subjected to the following forces:  by the contractile apparatus as a result of nervous activation,
by the contractile apparatus as a result of nervous activation,  , hydrostatic pressure (only for cardiomyocytes), and
, hydrostatic pressure (only for cardiomyocytes), and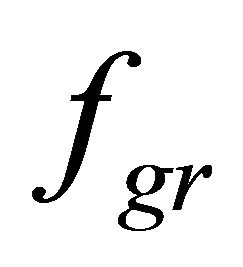 , the gravity. Nervous activation by intracellular signal mechanisms launch results in mechanical tension that arises in a muscle fiber because of myosin head and actin filament interaction, which is transmitted into the sarcolemma by the cortical cytoskeleton. Let us suppose that this interaction is uniform distributed over the length of the contractile apparatus. Therefore, it can be represented as a periodical function with the period of Т, which equals the distance between two successive myosin heads.
, the gravity. Nervous activation by intracellular signal mechanisms launch results in mechanical tension that arises in a muscle fiber because of myosin head and actin filament interaction, which is transmitted into the sarcolemma by the cortical cytoskeleton. Let us suppose that this interaction is uniform distributed over the length of the contractile apparatus. Therefore, it can be represented as a periodical function with the period of Т, which equals the distance between two successive myosin heads.
Then , where
, where 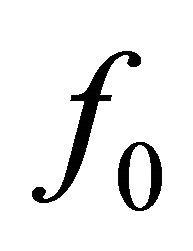 is the force generated by the single bridge, approximately 3 - 5 pN, n represents a number of bridges, which can be determined as the ratio of the fiber length (l) to the distance between two successive bridges, approximately 43 nm, per fiber volume. Gravity also acts on a muscle cell depending on the cell orientation. The specific volumetric force in this case may be represented as
is the force generated by the single bridge, approximately 3 - 5 pN, n represents a number of bridges, which can be determined as the ratio of the fiber length (l) to the distance between two successive bridges, approximately 43 nm, per fiber volume. Gravity also acts on a muscle cell depending on the cell orientation. The specific volumetric force in this case may be represented as , where
, where
![]() is the angle between the gravity vector and the fiber longitudinal axis direction,
is the angle between the gravity vector and the fiber longitudinal axis direction, ![]() is the free-fall acceleration, and
is the free-fall acceleration, and 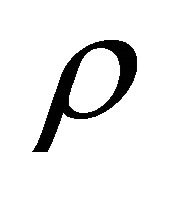 is the liquid density. The surface load on the end is a net load of gravity and hydrostatic pressure;
is the liquid density. The surface load on the end is a net load of gravity and hydrostatic pressure;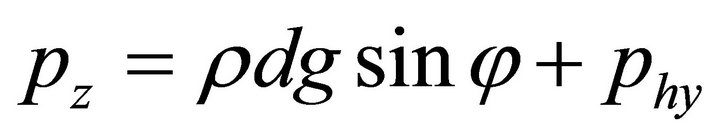 , where d is the fiber diameter.
, where d is the fiber diameter.
Then, the external forces become:
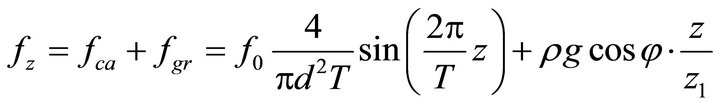 ,
,
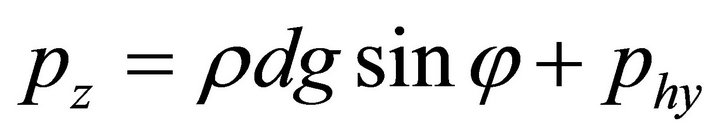 . (17)
. (17)
3. Numerical Examples
As an experimental model, we use a rodent’s antiorthostatic suspension (Figure 2).
We have determined in previous experiments Young’s modulus of the sarcolemma of different skeletal muscles [4] and a rat’s left ventricle [8,9]. Moreover, the introduction of the nifedipin system into rats resulted in increased sarcolemma transversal stiffness in skeletal muscles [10]. We have also determined the muscle fiber diameter. Based both on these data and ratio (16), we can find characteristic longitudinal deformations of M. soleus fibers and cardiomyocytes (Table 1).
4. Discussion and Conclusions
Interaction between a cell and an external mechanical field is still an unsolved problem in modern cell biophysics. A case of gravity vector change appears to be
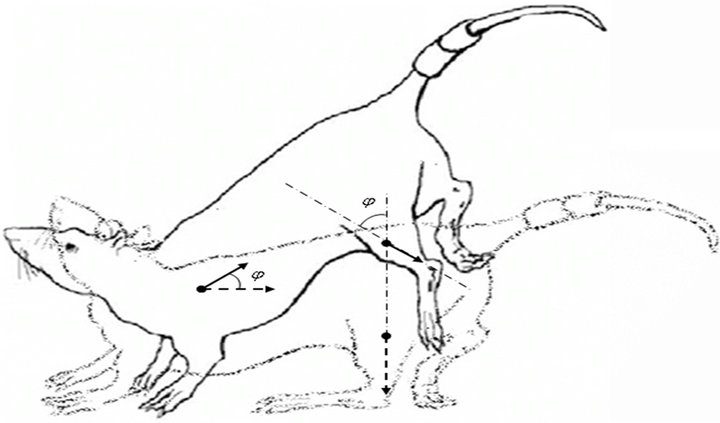
Figure 2. The Ilyin-Novikov method with the Morey-Holton modification of a rodent’s antiorthostatic suspension [5]. The dotted arrows indicate the direction of muscle cells’ dominant axis (z axis) under normal conditions, and the solid arrows represent the suspension case.
Table 1. Longitudinal absolute and relative deformations of different muscle cells after antiorthostatic suspension at an angle of 30˚.
Muscle Object | M. soleus | Heart | |
Rats |
| 4.29 | 9.5 |
| 2.15 × 10−4 | 6.31 × 10−2 | |
Rats + nifedipin (10 mg per day per 1 kg of animal weight) |
| 1.98 | - |
| 0.99 × 10−4 | ||
Results obtained for the following initial data: δ = 30 nm, r = 103 kg/m3, g = 9.8 m/s2, j = 30˚, f0 = 4 × 10−12 N, l = 2 × 10−2 m (for m. soleus fibers), and l = 1.5 × 10−4 m, d = 2 × 10−5 m, phy = 50 Pa (for cardiomyocytes), Т = 43 × 10−9 m, z = 2.4 × 10−6 m, z1 = 1.8 × 10−6 m.
the most complicated one since its magnitude is directly proportional to cell mass, so it is extremely small. Even more ambiguous is the situation with changes in the direction of the gravity vector rather than its magnitude. However, for cells in tissue, such a change launches a number of other processes connected with the nervous activation level (for skeletal muscle fibers) or the redistribution of hydrostatic pressure (in cardiomyocytes). That is why determining the cellular mechanosensor is a rather difficult problem. At the same time, a solution to this problem is necessary for adequate methods of cell protection (from external mechanical condition changes that occur during, for example, a space flight) to be developed.
We have previously supposed that the submembrane cytoskeleton, the most universal compartment for different types of cells, is a mechanosensor [4,9,11,12]. However, the question regarding the significance of deformations arising in the cortical cytoskeleton still cannot be experimentally proved.
Therefore, in this work, we decided to theoretically evaluate deformations that appear due to the effects described above. To obtain a proper estimation, we developed a muscle fiber sarcolemma model as a thin-walled rod. A series of assumptions enabled us to obtain an analytical solution, which makes it possible to estimate the deformation to the lower limit. The results showed that the absolute deformations in skeletal muscles and in the heart are comparable, but the relative deformation of the myocardium is dramatically greater. Nifedipin introduction changes the mechanical properties of muscle cells such that the deformations there appear to be minimal.
The numerical estimation results highly correspond with experimental data about the cell response formation speed: changes in cardiomyocytes occur intense than in soleus fibers, and this fact remains unexplained [4,8]. We should note the different signs of deformations in the heart and in the soleus: one case involved stretching and the one compression, which could mean the launching of different cell response signal pathways.
Thus, according to the results of the mathematical model developed and numerical experiments indicate that the external mechanical load change could lead to cortical cytoskeleton deformation. The deformation of cardiomyocytes is greater than that of soleus muscle fibers. Furthermore, the deformations have different signs in the heart and in the soleus: one involves describes stretching and the other compression. One can suppose that the different signs of deformation result in different cell responses, probably due to various proteins dissociating from the cortical cytoskeleton in each case. In addition, the deformation magnitude may influence the speed of the cell response; this fact corresponds to experimental data. In total, the results obtained from mathematical modeling explain a series of experimental data, particularly various start-up times of the cell response in the heart and soleus muscles, as well as different adaptive protein patterns in these cells as a result of external mechanical condition changes and suggests a new approach to the search for cellular mechanosensors.
REFERENCES
- A. A. Shabarchin and A. K. Tsaturyan, “Proposed Role of the M-Band Sarcomere Mechanics and Mechano-Sensing: A Model Study,” Biomechanics and Modeling in Mechanobiology, Vol. 9, No. 2, 2010, pp. 163-175. doi:10.1007/s10237-009-0167-0
- J. M. Ervasti, “Costameres: The Achille’s Heel of Herculean Muscle,” The Journal of Biological Chemistry, Vol. 278, No. 16, 2003, pp. 13591-13594. doi:10.1074/jbc.R200021200
- I. V. Ogneva, D. V. Lebedev and B. S. Shenkman, “Transversal Stiffness and Young’s Modulus of Single Fibers from Rat Soleus Muscle Probed by Atomic Force Microscopy,” Biophysical Journal, Vol. 98, No. 3, 2010, pp. 418-424. doi:10.1016/j.bpj.2009.10.028
- I. V. Ogneva, “Transversal Stiffness of Fibers and Desmin Content in Leg Muscles of Rats under Gravitational Unloading of Various Durations,” Journal of Applied Physiology, Vol. 109, No. 6, 2010, pp. 1702-1709. doi:10.1152/japplphysiol.00793.2010
- E. Morey-Holton, R. K. Globus, A. Kaplansky and G. Durnova, “The Hindlimb Unloading Rat Model: Literature Overview, Technique Update and Comparison with Space Flight Data,” Advances in Space Biology and Medicine, Vol. 10, 2005, pp. 7-40.
- V. Z. Vlasov, “Thin-Walled Elastic Rods,” Fizmatgiz, USSR, Moscow, 1959, 574 pages.
- V. V. Eliseev, “Mechanics of Elastic Bodies,” Izdatelstvo SPbSTU, Saint-Peterburg, 1999, 336 pages.
- I. V. Ogneva and I. B. Ushakov, “The Transversal Stiffness of Skeletal Muscle Fibers and Cardiomyocytes in Control and after Simulated Microgravity,” In: C. L. Frewin, Ed., Atomic Force Microscopy Investigations into Biology: From Cell to Protein, InTech, Chroatia, 2012, 354 pages.
- I. V. Ogneva, T. M. Mirzoev, N. S. Biryukov, O. M. Veselova and I. M. Larina, “Structure and Functional Characteristics of Rat’s Left Ventricle Cardiomyocytes under Antiorthostatic Suspension of Various Duration and Subsequent Reloading,” Journal of Biomedicine and Biotechnology, Vol. 2012, 2012, Article ID: 659869, 11 pages. doi: 10.1155/2011/659869
- I. V. Ogneva and E. G. Altaeva, “Effects of Nifedipine on the Mechanical Properties of Sarcolemma and Modulation of Calcium Accumulation Dynamics in Fibers of the Rat Soleus Muscle under Short-Term Hypogravity Conditions,” Biofizika, Vol. 55, No. 5, 2010, pp. 918-924.
- I. V. Ogneva, “Transversal Stiffness and Beta-Actin and Alpha-Actinin-4 Content of the M. soleus Fibers in the Conditions of a 3-Day Reloading after 14-Day Gravitational Unloading,” Journal of Biomedicine and Biotechnology, Vol. 2011, 2011, Article ID: 393405, 7 pages.
- I. V. Ogneva, “Cell Mechanosensitivity: Mechanical Properties and Interaction with Gravitational Field,” BioMed Research International, Vol. 2013, 2013, Article ID: 598 461, 17 pages.


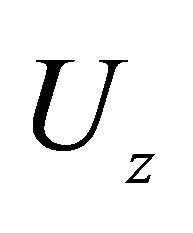 , μm
, μm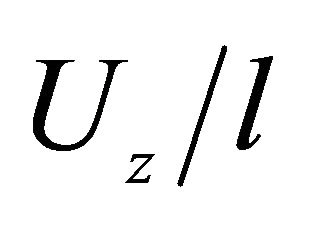
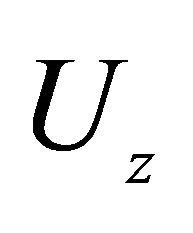 , μm
, μm