Applied Mathematics
Vol.4 No.7A(2013), Article ID:33946,4 pages DOI:10.4236/am.2013.47A001
On Isoperimetric Inequalities of Riesz Potentials and Applications
Institute of Mathematics and Mathematical Modeling, Almaty, Kazakhstan
Email: bolus91.ark@mail.ru
Copyright © 2013 Tynysbek Sh. Kalmenov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 17, 2013; revised April 18, 2013; accepted April 25, 2013
Keywords: Isoperimetric Inequalities; Eigenvalues of the Laplacian; Riesz Potentials
ABSTRACT
In this article, we prove certain isoperimetric inequalities for eigenvalues of Riesz potentials and show some applications of the results to a non-local boundary value problem of the Laplace operator.
1. Introduction
Historically, the minimization of the first eigenvalue of the Dirichlet Laplacian is probably the first such problem which appeared in the scientific literature. In Rayleigh’s famous book “Theory of Sound” [1] (first published in 1877), by using some explicit computation and physical interpretations, he stated that a circle minimizes (among all domains of the same area) the first eigenvalue of the Laplacian with the Dirichlet boundary condition. The proof of this conjecture was obtained only after 30 years later, simultaneously (and independently) by G. Faber and E. Krahn. Nowadays, the Rayleigh-Faber-Krahn inequality has been expanded many other boundary value spectral problems and operators; see [2,3] for further references.
In the present paper, we give simple proofs of some isoperimetric inequalities for the eigenvalues of Riesz potential by using methods of symmetrical decreasing rearrangements of positive measurable functions and variational principles. Riesz potentials, that is convolution operators with fractional powers of the distance to a point in , have important roles in fractional calculus theory. We also apply these results for the Laplacian with a nonlocal boundary conditions, in particular, we prove Rayleigh-Faber-Krahn inequality for the obtained non-local boundary value spectral problem of the Laplacian.
, have important roles in fractional calculus theory. We also apply these results for the Laplacian with a nonlocal boundary conditions, in particular, we prove Rayleigh-Faber-Krahn inequality for the obtained non-local boundary value spectral problem of the Laplacian.
2. Main Results
Let in an open bounded domain  of
of 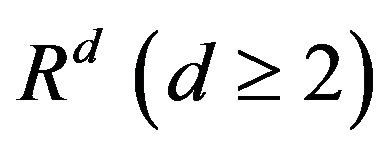 the following spectral eigenvalue problem of the Riesz potential has discrete spectrum:
the following spectral eigenvalue problem of the Riesz potential has discrete spectrum:
 (2.1)
(2.1)
where

is the distance between  and
and
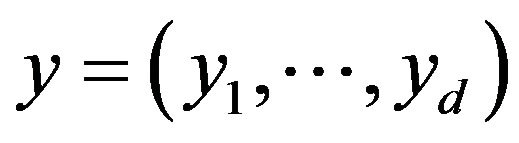 in the
in the  -dimensional Euclidean space
-dimensional Euclidean space
 ,
, 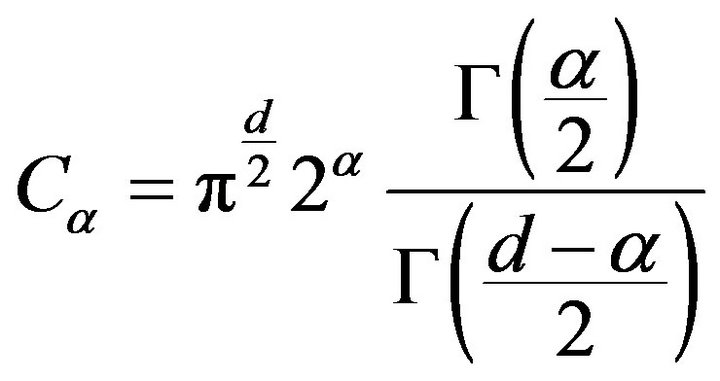 and Г is the gamma function. The potential
and Г is the gamma function. The potential  satisfies in the distributional sense (
satisfies in the distributional sense ( is the characteristic function of the set
is the characteristic function of the set )
)
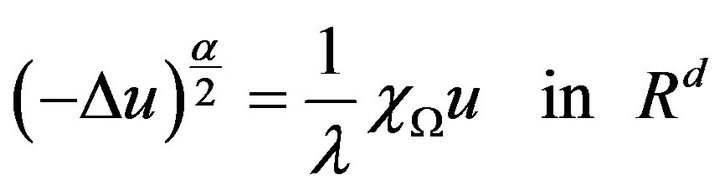 .
.
Note that when  and
and  Riesz potential coincides with the classical Newtonian potential and for
Riesz potential coincides with the classical Newtonian potential and for 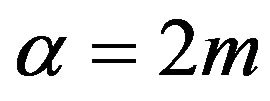 satisfies a polyharmonic equation in
satisfies a polyharmonic equation in  (cf. [4]). We denote eigenvalues of the Reisz potential by
(cf. [4]). We denote eigenvalues of the Reisz potential by 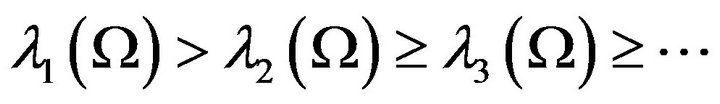 (enumerate their eigenvalues in decreasing order) each time repeated according to multiplicity. For the spectral problem (2.1), we obtain the following results:
(enumerate their eigenvalues in decreasing order) each time repeated according to multiplicity. For the spectral problem (2.1), we obtain the following results:
Theorem 1. Let 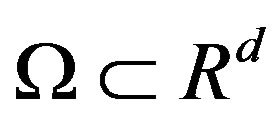 open simple-connected bounded domain and
open simple-connected bounded domain and 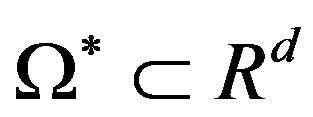 is a ball of the same measure as the
is a ball of the same measure as the , i.e.
, i.e.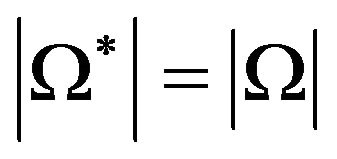 , then
, then
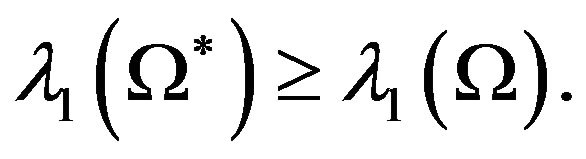 (2.2)
(2.2)
Theorem 2. Let  open simple-connected bounded domain and
open simple-connected bounded domain and  is a ball of the same measure as the
is a ball of the same measure as the , i.e.
, i.e. , and the following series has convergence then
, and the following series has convergence then
 (2.3)
(2.3)
3. Preliminary
Let  bounded measurable set in
bounded measurable set in . Its symmetric rearrangement
. Its symmetric rearrangement  is an open ball originated at 0 with a volume equal to the volume of
is an open ball originated at 0 with a volume equal to the volume of , i.e.
, i.e.  and
and
 where
where 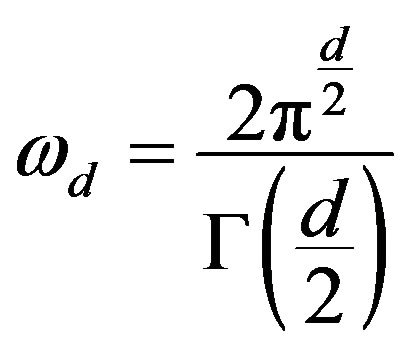 is the surface area of the unit sphere in
is the surface area of the unit sphere in . Let
. Let 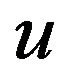 be a nonnegative measurable function vanishing at infinity, in the sense that all its positive level sets have finite measure,
be a nonnegative measurable function vanishing at infinity, in the sense that all its positive level sets have finite measure,
In the definition of the symmetric decreasing rearrangement of  can be used the layer-cake decomposition (see, for example, [5]), which expresses a nonnegative function
can be used the layer-cake decomposition (see, for example, [5]), which expresses a nonnegative function  in terms of its level sets as
in terms of its level sets as
 (3.1)
(3.1)
where 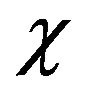 is the characteristic function of the corresponding domain.
is the characteristic function of the corresponding domain.
Definition. A function

is called a symmetric decreasing rearrangement of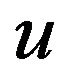 .
.
As its level sets are open domains 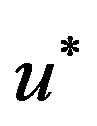 is lower semicontinuous function, and it is uniquely determined by the distribution function
is lower semicontinuous function, and it is uniquely determined by the distribution function
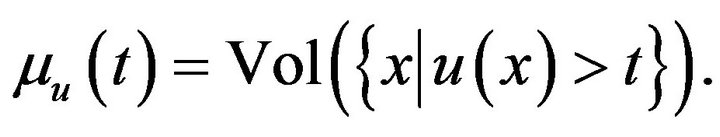
By construction, 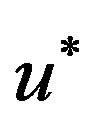 is equimeasurable with
is equimeasurable with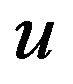 , i.e. corresponding level sets of the two functions have the same volume,
, i.e. corresponding level sets of the two functions have the same volume,
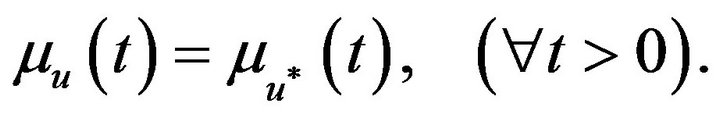 (3.2)
(3.2)
Lemma 1. For each non-negative function of 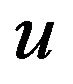 from
from , we have
, we have
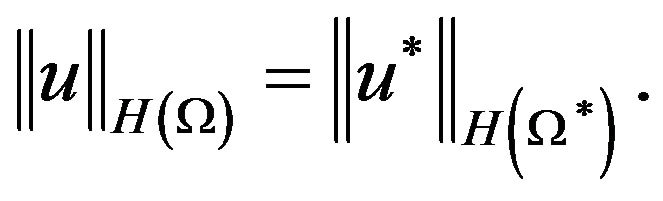
Proof. Using the layer-cake decomposition (3.1), Fubini’s theorem and (3.2), we obtain
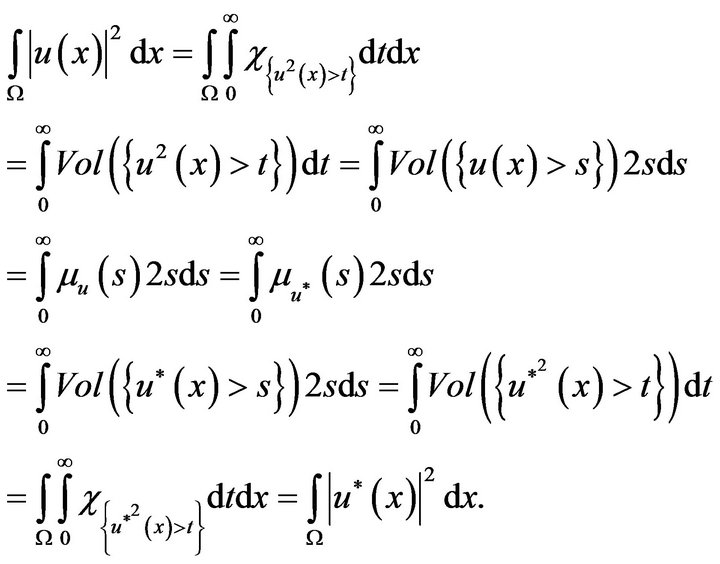
Lemma 1 is proved.
In proofs of the theorems we use the following F. Riesz’s inequality [5,6]
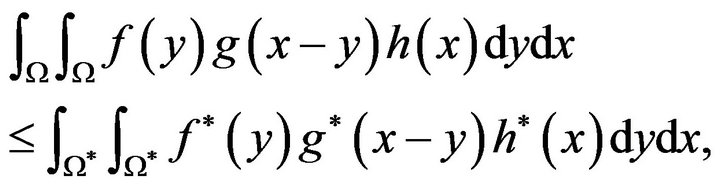 (3.3)
(3.3)
where 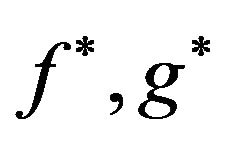 and
and 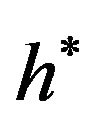 symmetric and non-increasing rearrangement of positive measurable functions
symmetric and non-increasing rearrangement of positive measurable functions 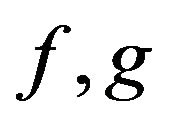 and
and 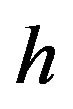 respectively.
respectively.
4. Proofs of Theorems 1 and 2
Since Riesz kernel of the potential (2.1) is symmetric and positive, by Ench theorem [7], its largest eigenvalue  is positive and simple, and the corresponding eigenfunction
is positive and simple, and the corresponding eigenfunction  can be chosen positive in
can be chosen positive in .
.
Let us use the denotation .
.
Using the Riesz inequality (3.3) and the fact that  is positive, symmetric and decreasing for all
is positive, symmetric and decreasing for all , we have
, we have

Hence by Lemma 1 and the variational principle for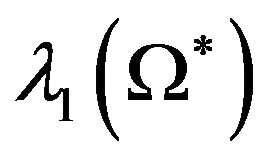 , we have
, we have
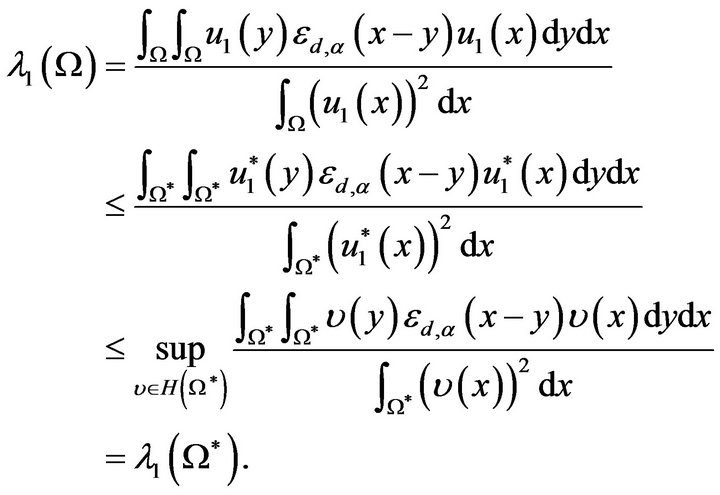
Theorem 1 is completely proved.
Note 1. One may wonder whether the ball is only maximizer of  among all domains of the same volume. But the answer is no. For example, if we remove a set of zero capacity from the ball, a new domain also maximizes the value of
among all domains of the same volume. But the answer is no. For example, if we remove a set of zero capacity from the ball, a new domain also maximizes the value of 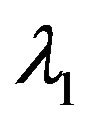 since the Hilbert space
since the Hilbert space 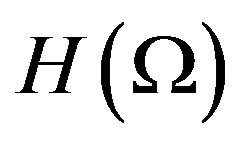 does not change if we remove from
does not change if we remove from  a set of zero capicity.
a set of zero capicity.
Now we prove Theorem 2. By bilinear decomposition of repeated kernel, we have
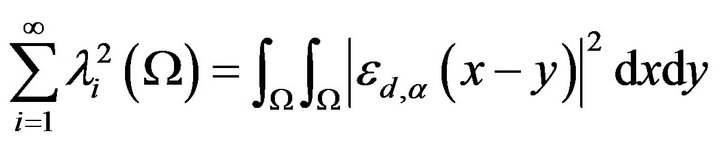 (4.1)
(4.1)
From (3.3) and the fact that 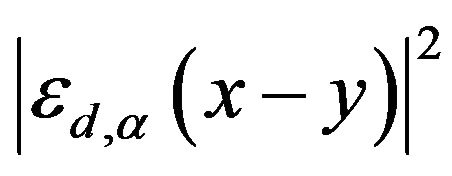 is a symmetric and positive decreasing function, we obtain
is a symmetric and positive decreasing function, we obtain
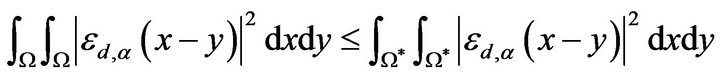
According to (4.1),
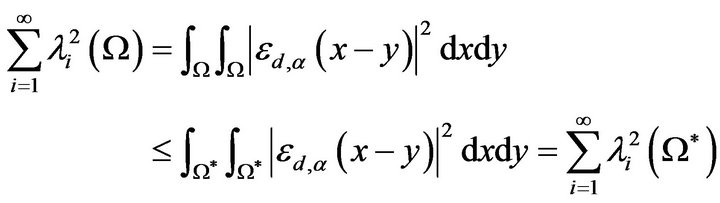
Theorem 2 is proved.
Note 2. We can generalize Theorem 2 writing in the following form
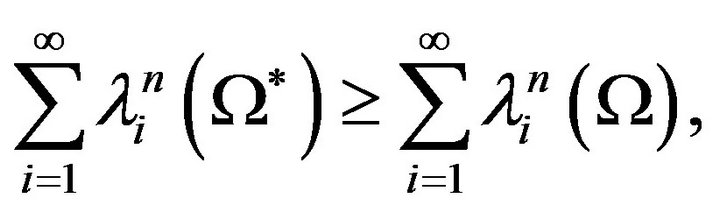 (4.2)
(4.2)
but obviously, in this case we need some restrictions on 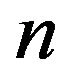 depending on the dimension of the Euclidean space
depending on the dimension of the Euclidean space  and
and .
.
5. On Applications of Results for Boundary Value Problems of the Laplacian
Let 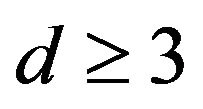 and
and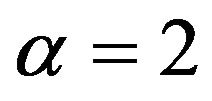 . In this case, the Riesz potential coincides with the classical Newton potential, that is, the kernel of the Riesz potential is
. In this case, the Riesz potential coincides with the classical Newton potential, that is, the kernel of the Riesz potential is
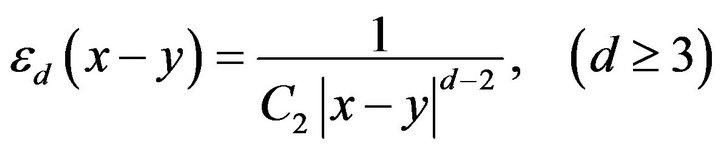
where  is a natural number.
is a natural number.
Lemma 2. For any function  suppf
suppf 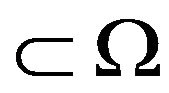 the Newton potential
the Newton potential
 (5.1)
(5.1)
satisfies the boundary condition
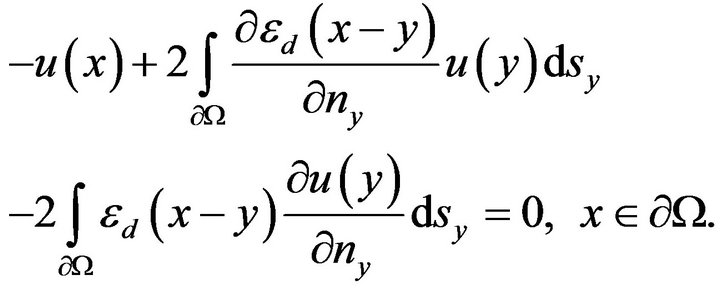 (5.2)
(5.2)
Conversely, if a function  satisfies
satisfies
 (5.3)
(5.3)
and the boundary condition (5.2), then the function 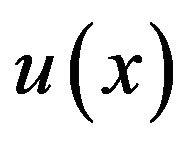 coincides with the Newton potential (5.1), here
coincides with the Newton potential (5.1), here
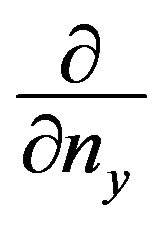 denotes the outer normal derivative on the boundary.
denotes the outer normal derivative on the boundary.
Proof. Suppose that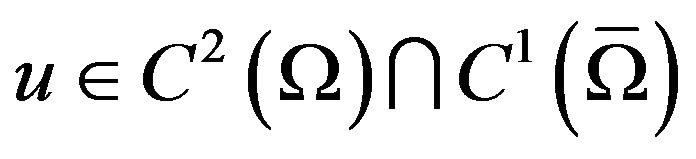 . A direct calculation shows that, for any
. A direct calculation shows that, for any , we have
, we have
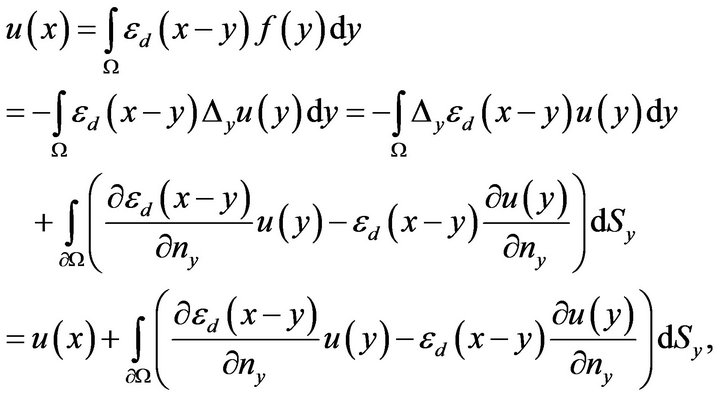
where 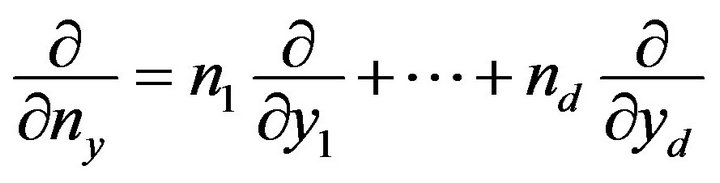 and
and  are components of the unit normal.
are components of the unit normal.
This implies, for , we get
, we get
 (5.4)
(5.4)
Applying properties of single-layer and double-layer potentials [8] to Formula (5.4) with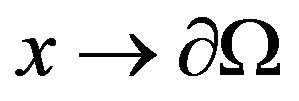 , we get
, we get
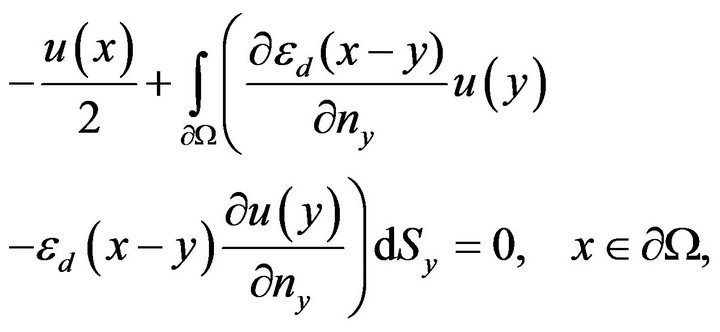 (5.5)
(5.5)
i.e. (5.5) is a boundary condition for the Newton potential (5.1). Passing to the limit we can easily show that (5.5) remains valid for all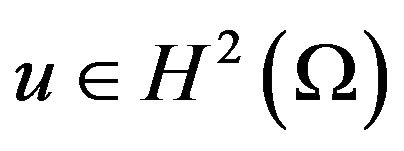 . Thus, the Newton potential (5.1) satisfies the boundary condition (5.2).
. Thus, the Newton potential (5.1) satisfies the boundary condition (5.2).
Conversely, if the function  satisfies
satisfies 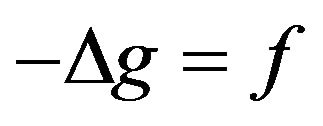 and the boundary condition (5.2), then it coincides with the Newtonian potential (5.1). Indeed, if this is not so, then the function
and the boundary condition (5.2), then it coincides with the Newtonian potential (5.1). Indeed, if this is not so, then the function , where
, where  is the Newton potential (5.1) satisfies the homogeneous equation
is the Newton potential (5.1) satisfies the homogeneous equation  with the boundary condition of
with the boundary condition of
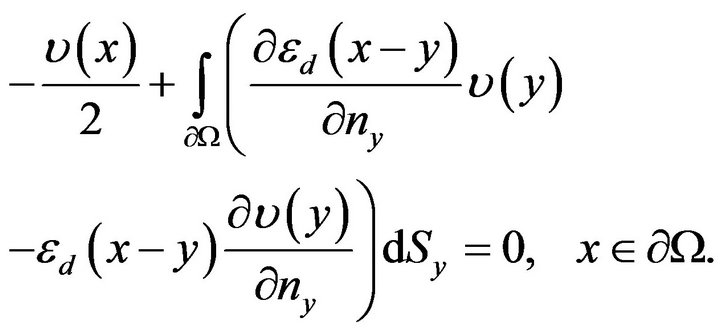 (5.6)
(5.6)
As above, applying Green’s formula to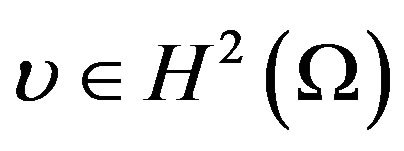 , we see that
, we see that
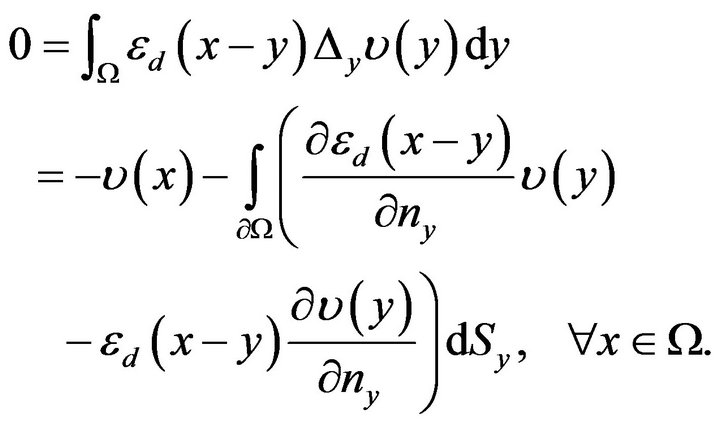
Passing the limit as , we obtain
, we obtain
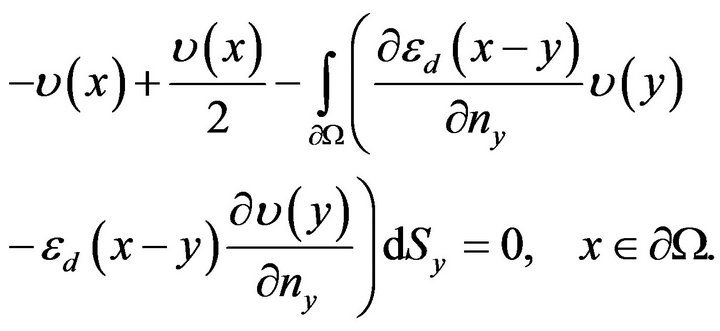
From (5.6), it implies
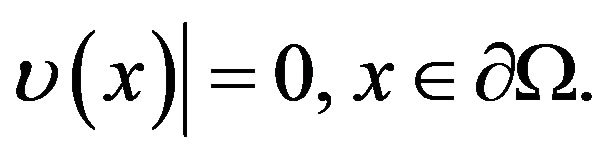 (5.7)
(5.7)
By virtue of the uniqueness of a solution of the Dirichlet problem for the Laplace equation, we have 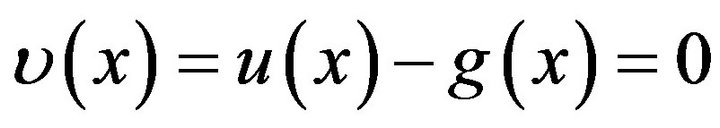 for all
for all , that is,
, that is,  ,
,  coincides with the Newton potential. This completes the proof of Lemma 2.
coincides with the Newton potential. This completes the proof of Lemma 2.
Lemma 2 shows that the eigenvalue problem of the Newton potential is equivalent to spectral boundary problem for the Laplace equation
 (5.8)
(5.8)
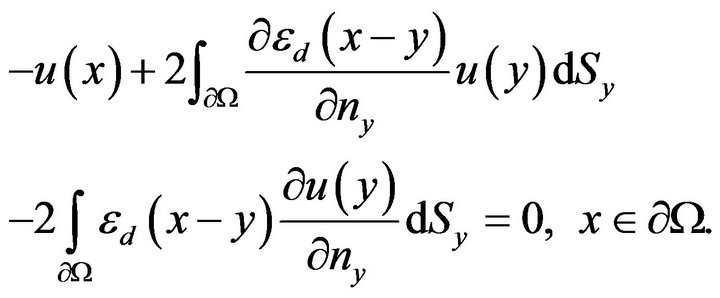 (5.9)
(5.9)
Finally, by Theorem 1, we obtain Rayleigh-FaberKrahn inequality for the first eigenvalue  of the Laplacian boundary value problems (5.8) and (5.9).
of the Laplacian boundary value problems (5.8) and (5.9).
Proposition 1. A ball minimizes the first eigenvalue of the Laplacian (5.8) with a special type of non-local boundary condition (5.9) among all domains of the same measure.
And from Theorem 2 we obtain the following analogue of Dittmar’s result [9].
Proposition 2. Series made up of squares of reciprocal eigenvalues of the Laplacian with the boundary condition (5.9),

is minimized in a ball among all domains of the same measure.
Note that in [10] in the case of two-dimensional ball and three-dimensional ball we calculated all eigenvalues of the the Laplacian with the boundary condition (5.9).
REFERENCES
- J. W. Rayleigh, “The Theory of Sound,” Dover Publishing, New York, 1945.
- A. Henrot, “Extremum Problems for Eigenvalues of Elliptic Operators,” Birkhauser, Basel, 2006.
- D. Daners, “A Faber—Krahn Inequality for Robin Problems in Any Space Dimension,” Mathematische Annalen, Vol. 335, 2006, pp. 767-785. doi:10.1007/s00208-006-0753-8
- T. Sh. Kalmenov and D. Suragan, “Boundary Conditions for the Volume Potential for the Polyharmonic Equation,” Differential Equations, Vol. 48, No. 4, 2012, pp. 595-599.
- A. Burchard, “A Short Course on Rearrangement Inequalities,” 2009. www.math.toronto.edu/almut/rearrange.pdf
- F. Riesz, “Sur Une Inregalitre Intregrale,” Journal of the London Mathematical Society, Vol. 5, No. 3, 1930, pp. 162-168. doi:10.1112/jlms/s1-5.3.162
- B. S. Vladimirov, “Equations of Mathematical Physics,” Nauka, Moscow, 1981.
- N. S. Landkoff, “Foundations of Modern Potential Theory,” Springer-Verlag, Berlin, 1972. doi:10.1007/978-3-642-65183-0
- B. Dittmar, “Sums of Reciprocal Eigenvalues of the Laplacian,” Mathematische Nachrichten, Vol. 237, No. 1, 2002, pp. 45-61. doi:10.1002/1522-2616(200204)237:1<45::AID-MANA45>3.0.CO;2-M
- T. Sh. Kalmenov and D. Suragan, “To Spectral Problems for the Volume Potential,” Doklady Mathematics, Vol. 428, No. 1, 2009, pp. 16-19.

