Applied Mathematics
Vol.4 No.5A(2013), Article ID:31480,7 pages DOI:10.4236/am.2013.45A001
Finite Element Modeling of Crack Tip Blunting for Estimation of Energy Release Rate Component of Mode I Crack near a Strength Mismatched Interface
1School of Mechanical and Building Sciences, VIT University, Vellore, India
2Department of Mechanical Engineering, Indian Institute of Technology, Mumbai, India
Email: *ss.bht@rediffmail.com
Copyright © 2013 Sunil Bhat, Vijay G. Ukadgaonker. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 28, 2013; revised April 23, 2013; accepted April 30, 2013
Keywords: Crack Tip Blunting; Interface; J Integral; Strength Mismatch; Mode I Crack
ABSTRACT
The paper presents finite element modeling of crack tip blunting for numerical estimation of fracture parameter of a Mode I crack, in weak alloy steel, which is near and normal to the interface of elastically identical but stronger maraging steel. The bimetallic body is subjected to monotonic load in K dominated regime. Crack tip yield zone across the interface, treated as Dugdale’s cohesive zone, is isolated from the bimetallic domain and is modeled alone under the action of respective cohesive stress over yield zones for obtaining the contribution of mismatch between yield strength of the steels in crack energy release rate component, . Effect of far field load on
. Effect of far field load on  is found separately from a theoretical model. Numerical and theoretical results of
is found separately from a theoretical model. Numerical and theoretical results of  are in good agreement.
are in good agreement.
1. Introduction
The effect of strength mismatch between two un-identical bodies is felt by the crack tip in parent body as it approaches the interface body [1] due to crack tip plasticity or yield zone spreading over into the interface body. If plasticity is modeled by Dugdale’s hypothesis, then the part of yield zone in interface body is subjected to closing cohesive stress different from that acting over the part of yield zone in parent body tip due to strength mismatch between the bodies. As such, the plasticity induced load transfer towards the interface or parent body, depending upon the direction of strength gradient across the interface, changes the stress field around the crack which induces shielding or amplification effects at its tip. This phenomenon has also been confirmed with the help of finite element analysis [2]. J integral over the path far away from the crack tip around the interface provides the applied value of J integral, 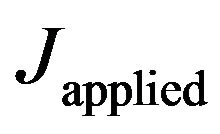 , whereas the integral over the path near the crack tip in parent body without crossing the interface results in J integral at the crack tip,
, whereas the integral over the path near the crack tip in parent body without crossing the interface results in J integral at the crack tip, .
.  is less or more than
is less or more than 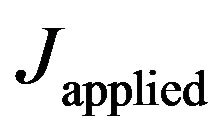 depending upon the crack approaching a stronger or weaker material respectively. Difference in strength between the bodies results in non-homogeneity effect of the mismatched interface that is represented by,
depending upon the crack approaching a stronger or weaker material respectively. Difference in strength between the bodies results in non-homogeneity effect of the mismatched interface that is represented by, 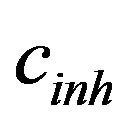 , or J integral at the interface,
, or J integral at the interface,  [3].
[3].
Previously, Bhat and Ukadgaonker [4], while adopting a different approach to simplify the analysis, isolated the Dugdale’s cohesive zone from the bimetallic domain of elastically identical but strength and plastically mismatched steels viz., Mode I cracked ASTM 4340 alloy steel joined with ultra strong MDN 250 maraging steel and modeled it alone under the effect of cohesive stress over yield zones by finite element method. J integral,  , over the path in yield zones around the interface was obtained from the numerical solution whereas J integral,
, over the path in yield zones around the interface was obtained from the numerical solution whereas J integral,  , representing the effect of far field load at the interface was determined separately from a theoretical model. Evaluation of
, representing the effect of far field load at the interface was determined separately from a theoretical model. Evaluation of in such a manner was justified by the fact that finite element analysis of the crack under far field load is a common exercise which previously was undertaken by many researchers with their results matching closely with the theoretical estimations.
in such a manner was justified by the fact that finite element analysis of the crack under far field load is a common exercise which previously was undertaken by many researchers with their results matching closely with the theoretical estimations.  and
and  were superimposed to obtain
were superimposed to obtain . The effect of crack tip blunting was however not presented in that work although it was included in the analysis. Since blunting is of significance in the problem, this paper reports the methodology of its inclusion in evaluation of
. The effect of crack tip blunting was however not presented in that work although it was included in the analysis. Since blunting is of significance in the problem, this paper reports the methodology of its inclusion in evaluation of  for the crack that is near and normal to the interface between the stated steels using Dugdale’s plasticity model. Numerical value of
for the crack that is near and normal to the interface between the stated steels using Dugdale’s plasticity model. Numerical value of is found to be in good agreement with that obtained from the theoretical model.
is found to be in good agreement with that obtained from the theoretical model.
2. Theoretical Model
Refer Figure 1. As the crack in ductile homogenous body is subjected to monotonic far field load, its tip blunts by opening in load line direction by distance, 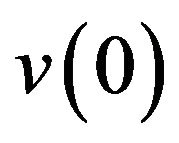 , from the axis and by extending longitudinally by distance,
, from the axis and by extending longitudinally by distance,![]() .
. ![]() represents the size of, highly stressed, process or fracture zone at the crack tip in which the material degradation or damage occurs by nucleation of voids [5]. The parent crack finally merges with the process zone. The value of
represents the size of, highly stressed, process or fracture zone at the crack tip in which the material degradation or damage occurs by nucleation of voids [5]. The parent crack finally merges with the process zone. The value of ![]() is approximately of the order of 1.6 to 2 times the value of crack tip opening displacement (CTOD) or 3.2 to 4 times the value of
is approximately of the order of 1.6 to 2 times the value of crack tip opening displacement (CTOD) or 3.2 to 4 times the value of . The yield zone surrounds the process zone. The concept holds good for the crack in strength mismatched bi-material as well although the value of
. The yield zone surrounds the process zone. The concept holds good for the crack in strength mismatched bi-material as well although the value of ![]() may not be exactly same as that in homogenous body.
may not be exactly same as that in homogenous body.
Refer Figure 2. The crack is in the parent body, A, with its tip at distance, a, from the interface body, B. Its cohesive zone has penetrated into the interface body by distance, l, with total length of cohesive zone, b, being equal to . The height of cohesive zone above the crack axis,
. The height of cohesive zone above the crack axis, 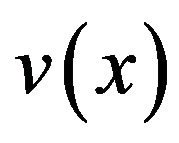 , and crack tip stress intensity parameter,
, and crack tip stress intensity parameter, 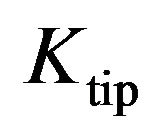 , under the action of applied stress intensity parameter,
, under the action of applied stress intensity parameter, 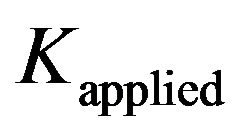 , due to far field tensile load and cohesive stress
, due to far field tensile load and cohesive stress 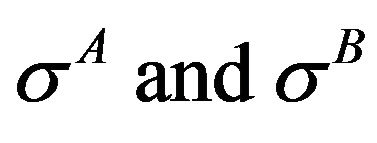 over cohesive zones in parent and interface bodies respectively in small scale yielding (SSY) or K dominated regime are given as follows [6]:
over cohesive zones in parent and interface bodies respectively in small scale yielding (SSY) or K dominated regime are given as follows [6]:
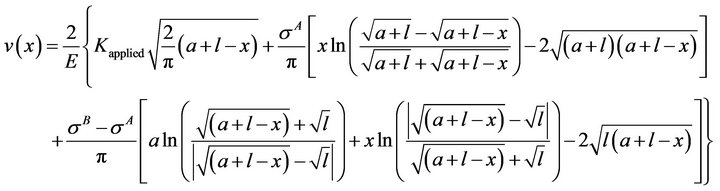 (1)
(1)
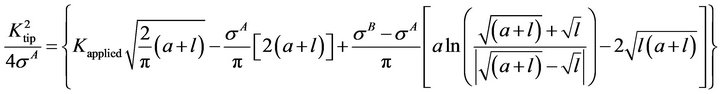 (2)
(2)
 in the case of Dugdale’s cohesive zone across the interface is written as [7]:
in the case of Dugdale’s cohesive zone across the interface is written as [7]:
 (3)
(3)
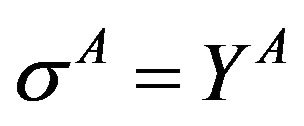 (Yield strength of body, A) and
(Yield strength of body, A) and 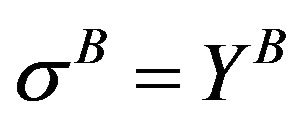 (Yield strength of body, B) in plane stress condition.
(Yield strength of body, B) in plane stress condition. 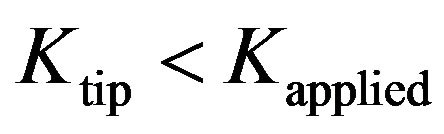 if
if 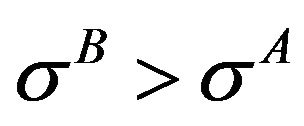 and vice versa. Difference between
and vice versa. Difference between  and
and  depends upon,
depends upon, ![]() , and the mismatch between
, and the mismatch between 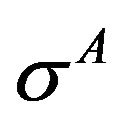 and
and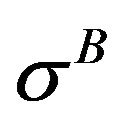 . Equation (2) and Equation (3) are solved by numerical iterative convergence scheme. Input values are
. Equation (2) and Equation (3) are solved by numerical iterative convergence scheme. Input values are 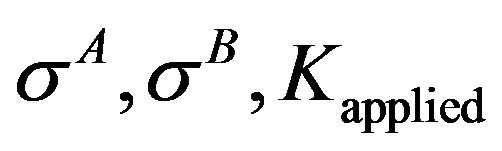 and a, the output values being
and a, the output values being 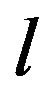 and
and . With the known value of
. With the known value of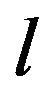 , the value of
, the value of 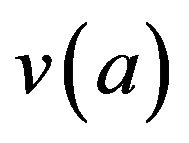 is obtained from Equation (1).
is obtained from Equation (1).  is equal to
is equal to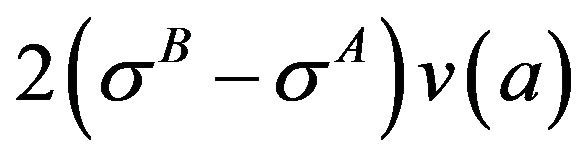 . At fracture, Equations (1)-(3) are rewritten by replacing
. At fracture, Equations (1)-(3) are rewritten by replacing 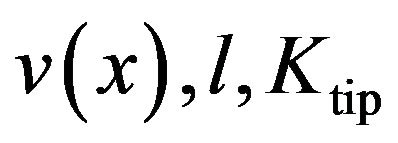 and
and 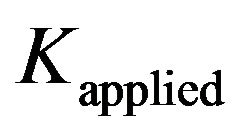 by
by 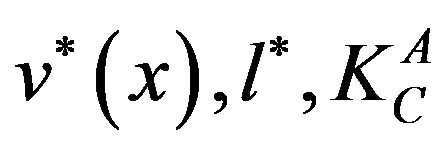 and
and 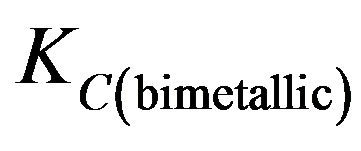 respectively where
respectively where 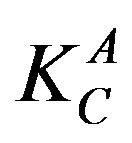 is plane stress fracture toughness of cracked body A and
is plane stress fracture toughness of cracked body A and  is plane stress fracture toughness of the bimetallic body.
is plane stress fracture toughness of the bimetallic body.  in such a condition is equal to
in such a condition is equal to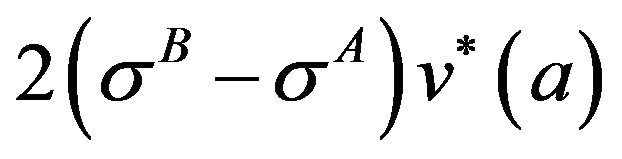 .
.

Figure 1. Opening and blunting of loaded crack.
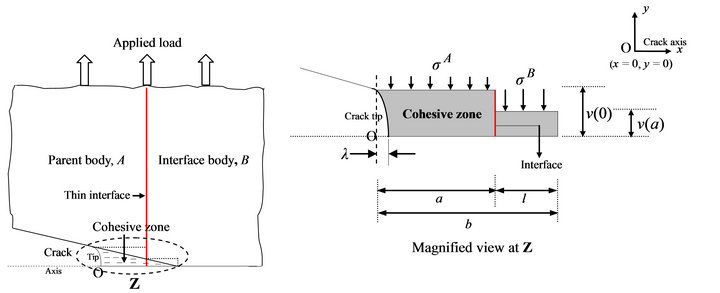
Figure 2. Cohesive zone across the bimerallic interface.
3. Case Study
The stated theoretical model is applied to material combination of weak ASTM 4340 alloy steel, A, and strong MDN 250 maraging steel, B. Refer Table 1. The results presented as Case I and Case II, represent fracture data of alloy steel at different positions of crack near the interface of maraging steel when subjected to monotonic load in SSY regime under plane stress condition. Material and crack data are suitably selected. Refer Figure 3. Stress field at the interface of maraging steel in both the cases, defined conventionally by,
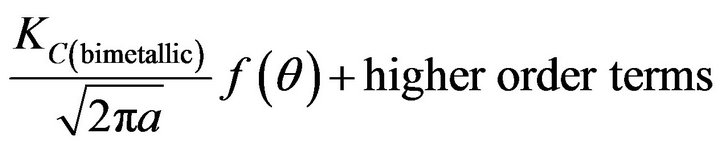 reveals nil yielding of maraging steel at and beyond the interface. But on viewing the bimetallic domain in comparison with the homogenous body of alloy steel, load is still transferred elastically to maraging steel due to its higher yield limit than that of alloy steel. Elastically strained zone in maraging steel under stress less than its yield strength is replaced by much smaller cohesive zone under the action of larger cohesive stress to make the application of the theoretical model possible. However, maraging steel shall also yield as the crack grows nearer towards the interface. Before undertaking the finite element analysis, the results of the selected cases are verified in the following manner:
reveals nil yielding of maraging steel at and beyond the interface. But on viewing the bimetallic domain in comparison with the homogenous body of alloy steel, load is still transferred elastically to maraging steel due to its higher yield limit than that of alloy steel. Elastically strained zone in maraging steel under stress less than its yield strength is replaced by much smaller cohesive zone under the action of larger cohesive stress to make the application of the theoretical model possible. However, maraging steel shall also yield as the crack grows nearer towards the interface. Before undertaking the finite element analysis, the results of the selected cases are verified in the following manner:
Case I
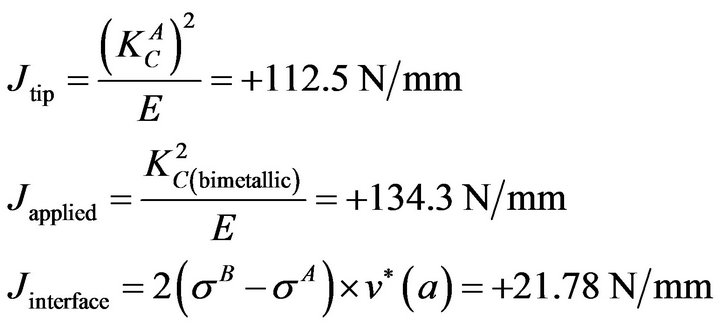
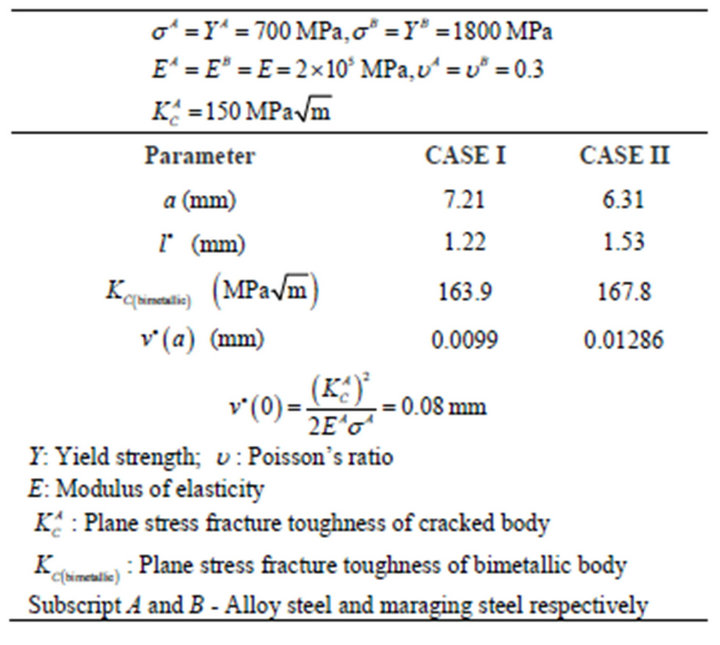
Table 1. Results of case study.
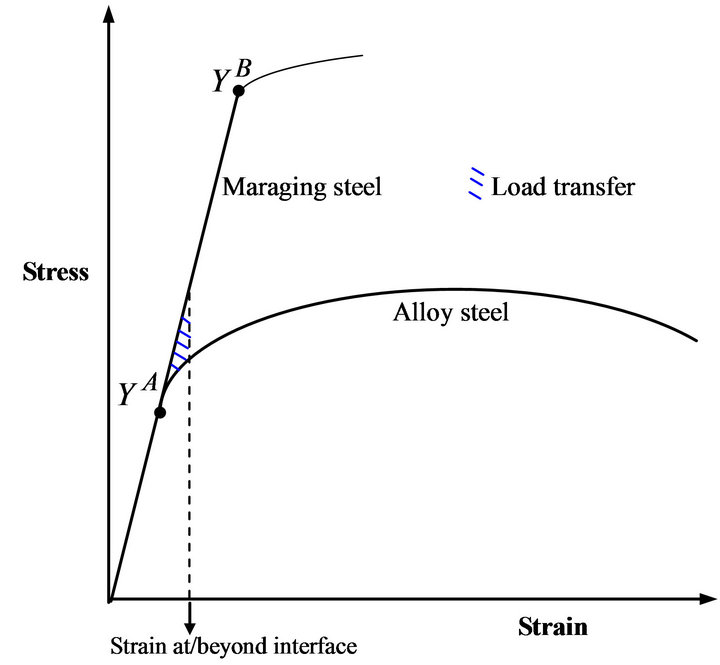
Figure 3. Load transfer effect.
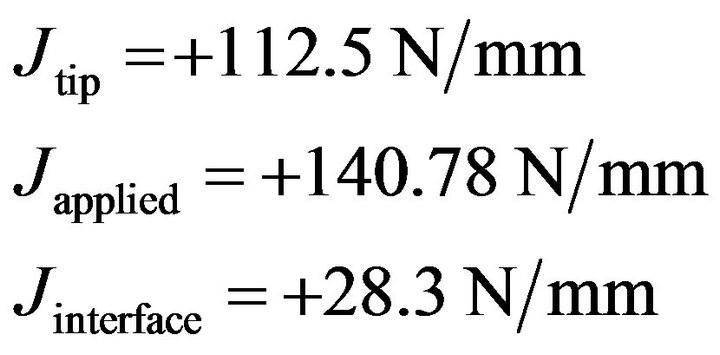
 of the alloy steel is assumed as
of the alloy steel is assumed as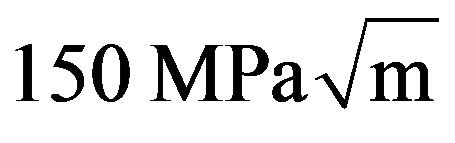 .
.  is considered as equal to
is considered as equal to 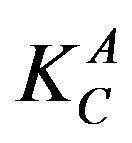 in the theoretical model due to fracture conditions. The value of l is iteratively assumed in Equation (3) till the output
in the theoretical model due to fracture conditions. The value of l is iteratively assumed in Equation (3) till the output 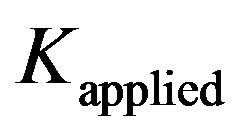 satisfies Equation (2). Final value of
satisfies Equation (2). Final value of  equals
equals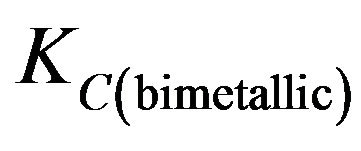 . Since the crack faces a stronger steel (weak-strong interface),
. Since the crack faces a stronger steel (weak-strong interface), 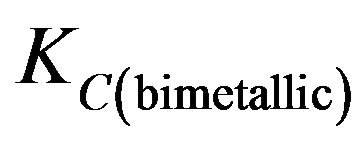 is greater than
is greater than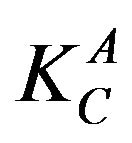 . The value of
. The value of 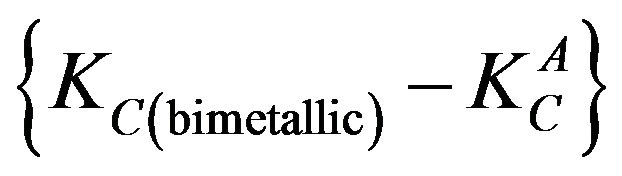 is more in Case II than in Case I because the crack is nearer to the interface in Case II. The conservation of energy release rate criterion,
is more in Case II than in Case I because the crack is nearer to the interface in Case II. The conservation of energy release rate criterion, 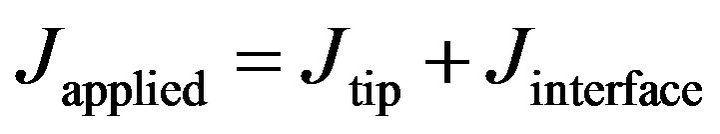 , is satisfied in both the cases. Due to stronger interface,
, is satisfied in both the cases. Due to stronger interface, 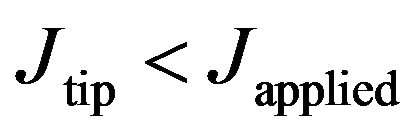 and
and  has a positive value in both the cases.
has a positive value in both the cases.4. Finite Element Analysis and Results
The cohesive zones of both the cases are modeled by finite element method. Half of the cohesive zone is only considered in each case due to symmetry. , at fracture, tapers from
, at fracture, tapers from  at crack tip to
at crack tip to 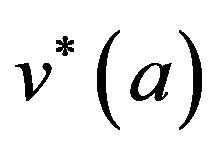 at the interface, finally reducing to zero at the tip of the cohesive zone. As cohesive zone has minimal lateral dimensions when compared to its length, its height is assumed constant as
at the interface, finally reducing to zero at the tip of the cohesive zone. As cohesive zone has minimal lateral dimensions when compared to its length, its height is assumed constant as 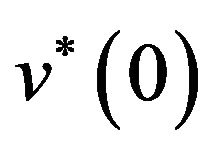 over distance, a, in alloy steel and
over distance, a, in alloy steel and  over distance, l, in maraging steel to facilitate modeling.
over distance, l, in maraging steel to facilitate modeling.
Refer Figure 4. 2D, 8 noded quadrilateral plane 82 elements are chosen for meshing. Cohesive stress, 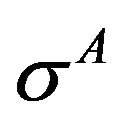 and
and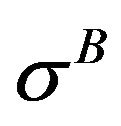 , are applied as pressure in -ve y direction over the boundary nodes of cohesive zones in steels A and B respectively. Plane stress with thickness option is adopted. Since the blunting zone is unsupported and the value of
, are applied as pressure in -ve y direction over the boundary nodes of cohesive zones in steels A and B respectively. Plane stress with thickness option is adopted. Since the blunting zone is unsupported and the value of ![]() is not exactly known, nodes ahead of the crack tip, up to the distance of
is not exactly known, nodes ahead of the crack tip, up to the distance of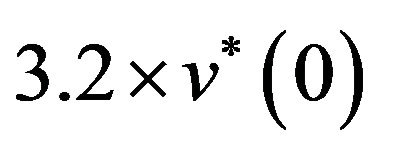 , are initially left unconstrained. Remaining nodes on crack axis are constrained in y direction. The mesh model is displayed in Figure 5.
, are initially left unconstrained. Remaining nodes on crack axis are constrained in y direction. The mesh model is displayed in Figure 5.
Using the post-processor displacement and stress solutions, the required values are mapped over chosen path, P, around the interface to obtain J integral, J1, from the expression,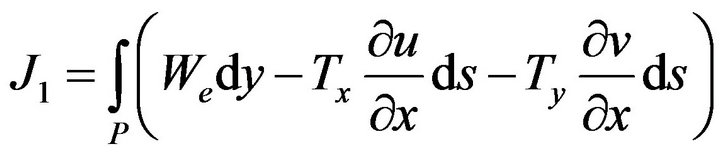 [8], where
[8], where
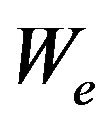 is the strain energy density,
is the strain energy density,  and
and 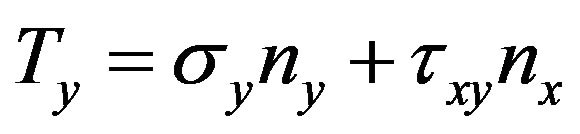 are the traction components with nx and ny representing unit vectors in x and y directions and u and v as displacements in the stated directions. Since cohesive stress has a closing or compressive effect over the crack that opposes the effect of far field tensile load, the value of J1 is taken with a negative sense. Sample stress and displacement plots near the crack tip in cohesive zone of alloy steel in Case I and Case II are presented in Figure 6 and Figure 7 respectively. The plots at the interface are available elsewhere [4]. Since the material properties employed in the analysis are linear in nature, very high stresses are found to develop at certain top locations in the cohesive zone due to bending caused by the unsupported part. This however can be eliminated by using the actual elastic-plastic properties of alloy steel. However, to avoid these hypothetical values, J integral paths are made to pass only through those areas that are elastically stressed. Different cyclic paths are tried. Appropriate value of
are the traction components with nx and ny representing unit vectors in x and y directions and u and v as displacements in the stated directions. Since cohesive stress has a closing or compressive effect over the crack that opposes the effect of far field tensile load, the value of J1 is taken with a negative sense. Sample stress and displacement plots near the crack tip in cohesive zone of alloy steel in Case I and Case II are presented in Figure 6 and Figure 7 respectively. The plots at the interface are available elsewhere [4]. Since the material properties employed in the analysis are linear in nature, very high stresses are found to develop at certain top locations in the cohesive zone due to bending caused by the unsupported part. This however can be eliminated by using the actual elastic-plastic properties of alloy steel. However, to avoid these hypothetical values, J integral paths are made to pass only through those areas that are elastically stressed. Different cyclic paths are tried. Appropriate value of  is obtained on path P that reaches right up to the crack tip where displacement values are
is obtained on path P that reaches right up to the crack tip where displacement values are
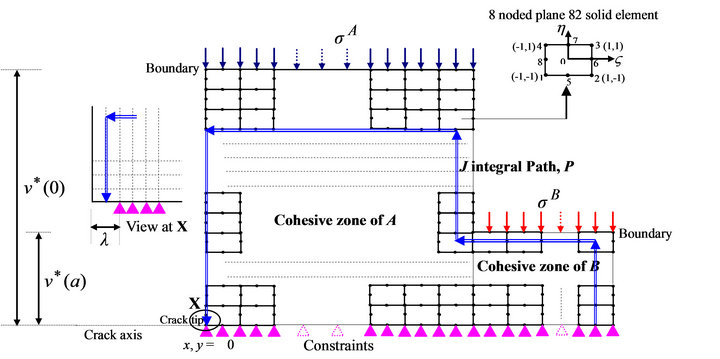
Figure 4. Finite element discretization of cohesive zone.
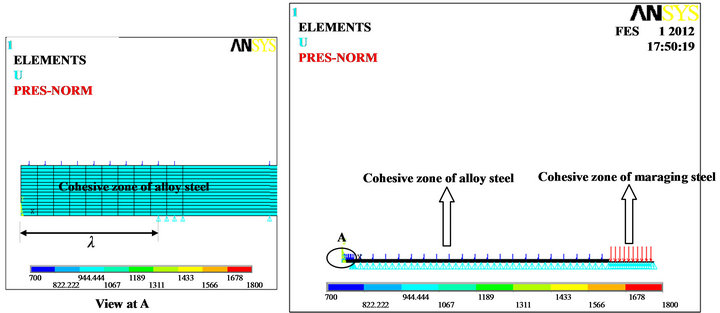
Figure 5. Mesh model.

Figure 6. Stress and displacement plots near crack tip at λ = 0.272 mm of Case I.
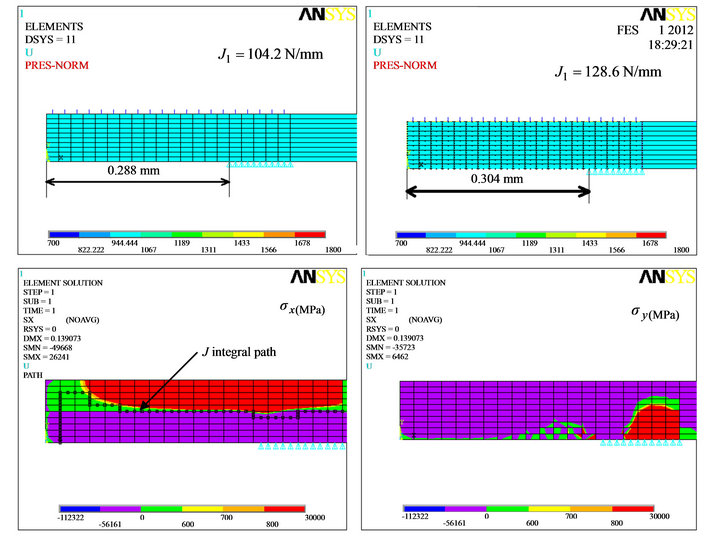
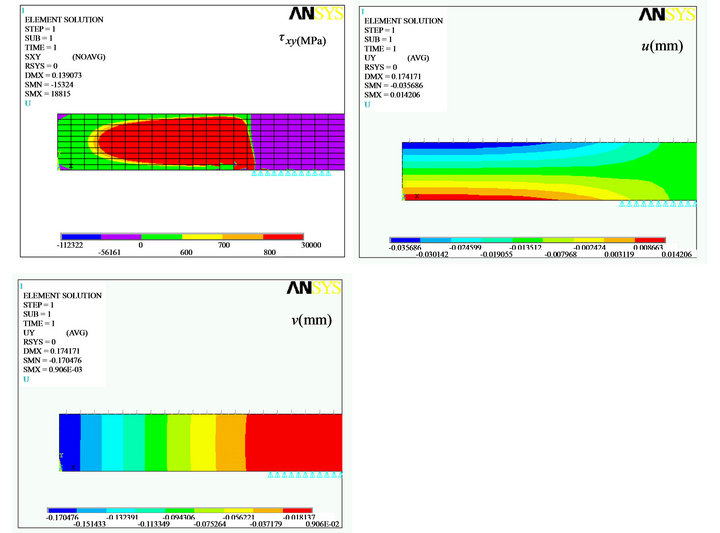
Figure 7. Stress and displacement plots near crack tip at λ = 0.288 mm of case II.
higher. The size of  or the number of unconstrained nodes is then increased and J1 is determined in each state till
or the number of unconstrained nodes is then increased and J1 is determined in each state till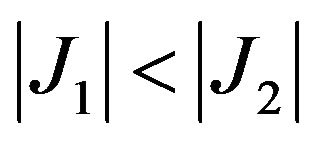 . The iterative scheme is finally stopped when
. The iterative scheme is finally stopped when 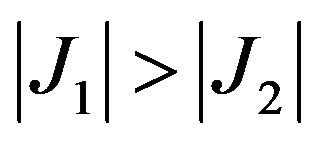 because
because  has a positive value in the present cases. Average of J1 obtained at all the values of
has a positive value in the present cases. Average of J1 obtained at all the values of  provides its magnitude. Refer Equation (1). Contribution of far field load over,
provides its magnitude. Refer Equation (1). Contribution of far field load over, 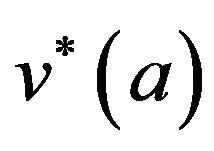 , is determined by the term
, is determined by the term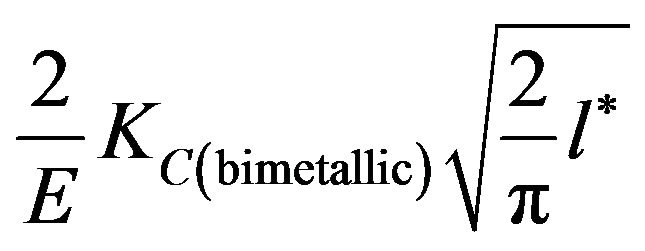 . Integral,
. Integral,  , is therefore equal to
, is therefore equal to
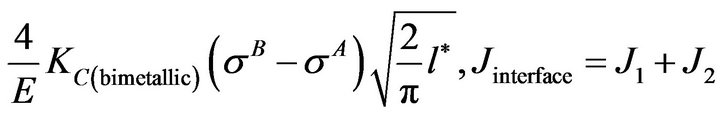
In Case I, the condition, 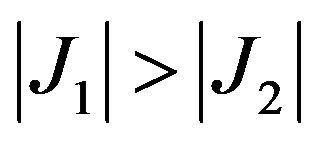 , is satisfied at and beyond the
, is satisfied at and beyond the  of 0.288 mm. At
of 0.288 mm. At  of 0.256 mm and 0.272 mm, J1 is -67.54 N/mm and -88.10 N/mm respectively. Average of J1 values is –77.82 N/mm.
of 0.256 mm and 0.272 mm, J1 is -67.54 N/mm and -88.10 N/mm respectively. Average of J1 values is –77.82 N/mm. 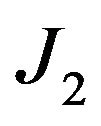 is obtained as +100.46 N/mm.
is obtained as +100.46 N/mm.  given by
given by 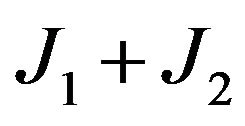 is equal to 22.64 N/mm. This value is close to +21.78 N/mm obtained from the theoretical model. Likewise in Case II,
is equal to 22.64 N/mm. This value is close to +21.78 N/mm obtained from the theoretical model. Likewise in Case II, 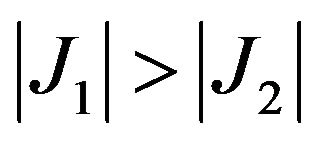 , is satisfied at and beyond
, is satisfied at and beyond  of 0.304 mm. At
of 0.304 mm. At  of 0.256 mm, 0.272 mm, 0.288 mm, J1 is –65.0 N/mm, –87.1 N/mm and –104.2 N/mm respectively. Average of J1 values is –85.44 N/mm.
of 0.256 mm, 0.272 mm, 0.288 mm, J1 is –65.0 N/mm, –87.1 N/mm and –104.2 N/mm respectively. Average of J1 values is –85.44 N/mm.  and
and  are equal to +115.18 N/mm and +29.74 N/mm respectively. Value of
are equal to +115.18 N/mm and +29.74 N/mm respectively. Value of  is again in good agreement with the theoretical value of +28.3 N/mm.
is again in good agreement with the theoretical value of +28.3 N/mm.
J1 is not found to be path independent. As mentioned earlier, appropriate values of this integral are obtained over paths reaching up to the crack tip nodes where displacements are higher. On paths terminating at constrained nodes, the displacements are less that result in reduced value of the integral. As the result,  is also not path independent.
is also not path independent.
5. Conclusion
Blunted crack tip near the interface of elastically identical but strength and plastically mismatched bodies is modeled by finite element method to numerically obtain J integral, J1 ,that represents the contribution of mismatch in yield strength between the bodies on crack energy release rate component, . Numerical results are well validated thereby supporting the feasibility of isolating the cohesive zone from the bimetallic domain and modeling it alone under the dual action of un-identical cohesive stress over yield zones in parent and interface bodies. The approach is simple and reasonably accurate.
. Numerical results are well validated thereby supporting the feasibility of isolating the cohesive zone from the bimetallic domain and modeling it alone under the dual action of un-identical cohesive stress over yield zones in parent and interface bodies. The approach is simple and reasonably accurate.
6. Acknowledgements
Support received from the School of Mechanical Building Sciences, VIT University, Vellore, India during the course of this work is gratefully acknowledged.
REFERENCES
- S. Suresh, Y. Sugimura and E. K. Tschegg, “The Growth of a Fatigue Crack Approaching a Perpendicularly-Oriented, Bimaterial Interface,” Scripta Metallurgica et Materialia, Vol. 27, No. 9, 1992, pp. 1189-1194. doi:10.1016/0956-716X(92)90597-8
- Y. Sugimura, P. G. Lim, C. F. Shih and S. Suresh, “Fracture Normal to a Bimaterial Interface: Effects of Plasticity on Crack Tip Shielding and Amplification,” Acta Metallurgica et Materialia, Vol. 43, No. 3, 1995, pp. 1157- 1169. doi:10.1016/0956-7151(94)00295-S
- J. Predan, N. Gubeljak and O. Kolednik, “On the Local Variation of the Crack Driving Force in a Double Mismatched Weld,” Engineering Fracture Mechanics, Vol. 74, No. 11, 2007, pp. 1739-1757. doi:10.1016/j.engfracmech.2006.09.015
- S. Bhat and V. G. Ukadgaonker, “Dugdale Cohesive Zone Modeling to Evaluate J Integral at the Interface of Strength Mismatched Steels: A Simplified Numerical Approach,” Finite Elements in Analysis and Design, Vol. 46, No. 7, 2010, pp. 601-610. doi:10.1016/j.finel.2010.02.007
- K. Hellan, “Introduction to Fracture Mechanics,” MaGraw-Hill Book Company, 1985, p. 92.
- D. Wappling, J. Gunnars and P. Stahle, “Crack Growth across a Strength Mismatched Bimaterial Interface,” International Journal of Fracture, Vol. 89, No. 3, 1998, p. 238.
- F. O. Reimelmoser and R. Pippan, “The J-Integral at Dugdale Cracks Perpendicular to Interfaces of Materials with Dissimilar Yield Stresses,” International Journal of Fracture, Vol. 103, No. 4, 2000, p. 404.
- J. R. Rice, “A Path Independent Integral and Approximate Analysis of Strain Concentration by Notches and Cracks,” Journal of Applied Mechanics, Vol. 35, No. 2, 1968, pp. 379-386. doi:10.1115/1.3601206
NOTES
*Corresponding author.

