Applied Mathematics
Vol.4 No.2(2013), Article ID:27957,8 pages DOI:10.4236/am.2013.42041
Bifurcation Analysis of Homoclinic Flips at Principal Eigenvalues Resonance*
1College of Science, University of Shanghai for Science and Technology, Shanghai, China
2Department of Mathematics, East China Normal University, Shanghai, China
Email: zhangts1209@163.com
Received December 15, 2012; revised January 15, 2013; accepted January 22, 2013
Keywords: Orbit Flip; Inclination Flips; Homoclinic Orbit; Resonance
ABSTRACT
One orbit flip and two inclination flips bifurcation is considered with resonant principal eigenvalues. We introduce a local active coordinate system to establish bifurcation equation and obtain the conditions when the original homoclinic orbit is kept or broken. We also prove the existence and the existence regions of double 1-periodic orbit bifurcation. Moreover, the complicated homoclinic-doubling bifurcations are found and expressed approximately, and are well located.
1. Introduction
Homoclinic bifurcations have been comprehensively investigated from the initial work of Silnikov in [1] who gave a detailed study of a system which permits an orbit homoclinic to a saddle-focus. After that many flips cases attract researcher’s interests, including resonant eigenvalues case in [2], orbit flips in [3,4], inclination flips in [5-7], and also resonant homoclinic flips in [8-11]. In these cases homoclinic-doubling bifurcation has been expensively studied, which is a codimension-two transition from an n-homoclinic to a 2n-homoclinic orbit. Some applications of these cases may be referred to a model for electro-chemical oscillators, the FitzHugh-Nagumo nerveaxon equations [12], a Shimitzu-Morioka equation for convection instabilities [13], and a Hodgkin-Huxley model of thermally sensitive neurons [14], etc.
More recently, the flip of heterodimensional cycles or accompanied by transcritical bifurcation is got attention, see [15-17], the double and triple periodic orbit bifurcation are proved to exist, and also some coexistence conditions for the homoclinic orbit and the periodic orbit. But the research is not concerned with multiple flips. While multiple cases may have more complicated bifurcation behaviors and even chaos, it is necessary to give a deep study. This paper produces mainly a theoretical study of homoclinic bifurcation with one orbit flip and two inclination flips, which can take place at least in a fourdimensional system. Compared with the above work mentioned, our problem has higher codimension with resonant, and we get not only the existence of 1-periodic orbit, 1-homoclinic orbit, and double periodic orbit, but also the  -homoclinic orbit and their corresponding bifurcation surfaces.
-homoclinic orbit and their corresponding bifurcation surfaces.
In the present context, we consider the following 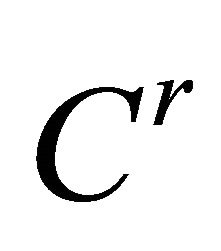 system
system
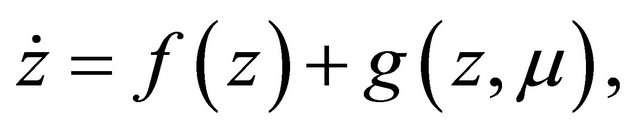 (1.1)
(1.1)
and its unperturbed system
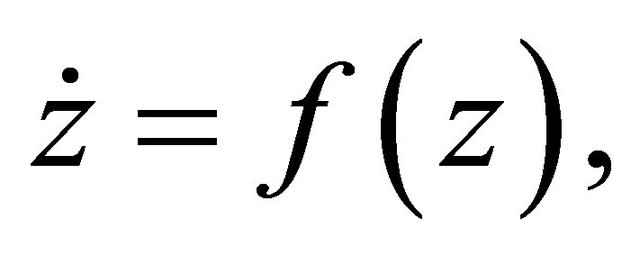 (1.2)
(1.2)
where 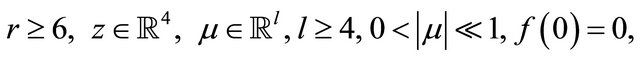
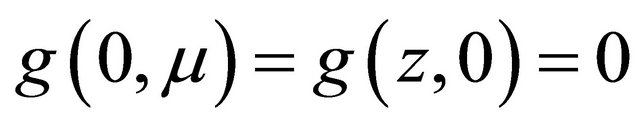 .
.
Hypothesis
We assume that system (1.2) has a homoclinic orbit 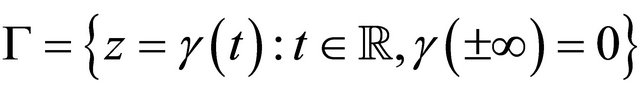 to an equilibrium
to an equilibrium , which is hyperbolic and has two negative and two positive eigenvalues, denoted by
, which is hyperbolic and has two negative and two positive eigenvalues, denoted by , and additionally
, and additionally . Set
. Set 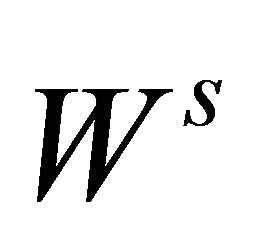 (resp.
(resp.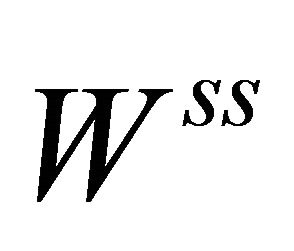 ) and
) and 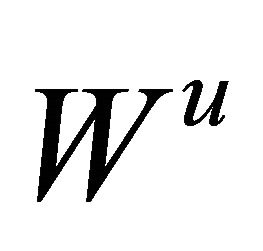 (resp.
(resp. ) the stable (resp. strong stable) manifold and unstable (resp. strong unstable) manifold of the equilibrium
) the stable (resp. strong stable) manifold and unstable (resp. strong unstable) manifold of the equilibrium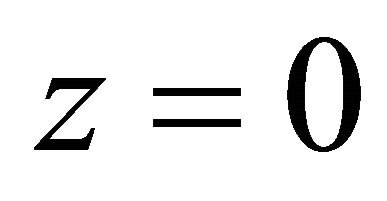 , respectively. Now we further make three assumptions:
, respectively. Now we further make three assumptions:
(H1) (Resonance)  for
for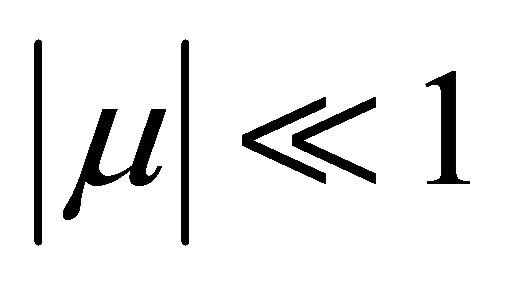 , where
, where
 and
and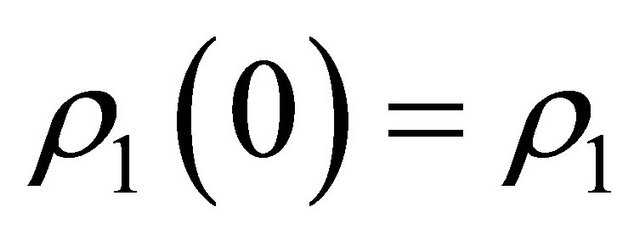 .
.
(H2) (Orbit flip) Define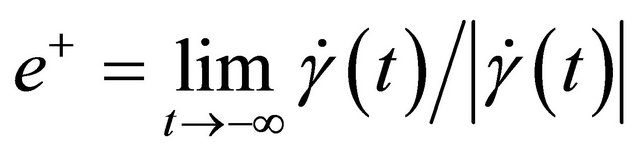 ,
,
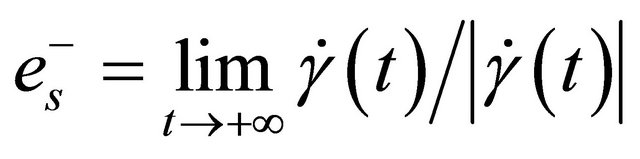 , then
, then 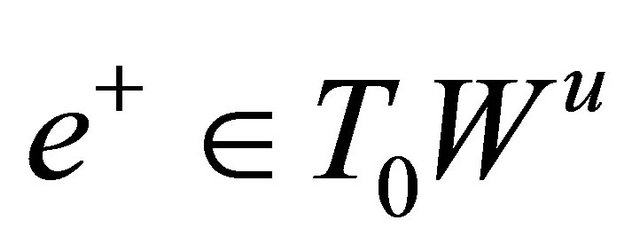 and
and  are unit eigenvectors corresponding to
are unit eigenvectors corresponding to 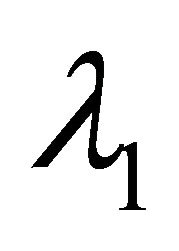 and
and  respectively, where
respectively, where 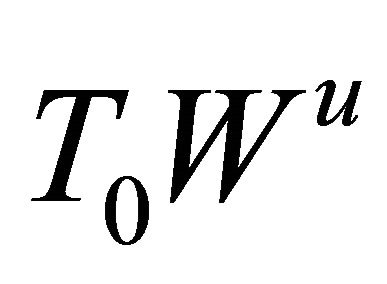 is the tangent space of the corresponding manifold
is the tangent space of the corresponding manifold 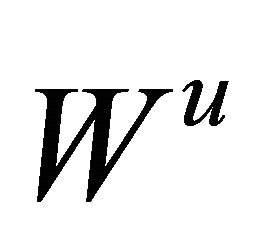 at the saddle
at the saddle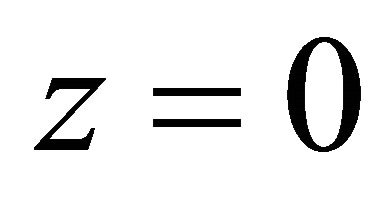 , and the similar meaning for
, and the similar meaning for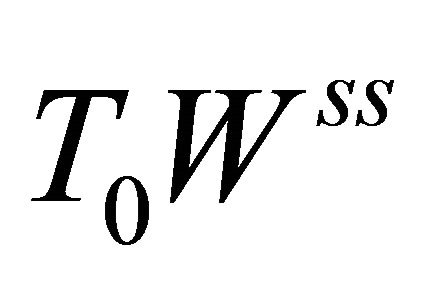 .
.
(H3) (Inclination flips) Denote by 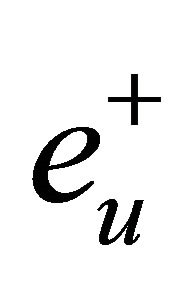 and
and 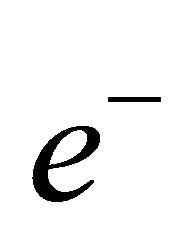 the unit eigenvectors corresponding to
the unit eigenvectors corresponding to 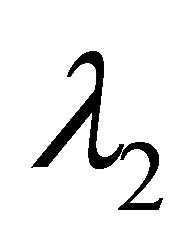 and
and 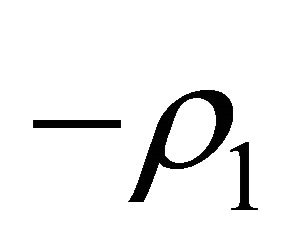 respectively, let
respectively, let

The paper is organized as follows. In Section 2 we will construct the Poincaré map by the method used in [18] to get the associated successor function. In Section 3, we first establish bifurcation equation. Then a delicate study shows our main results about the existence of double 1-periodic orbit, 1-homoclinic orbit and also 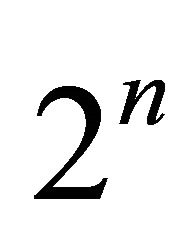 -homoclinic orbit. The last section gives a conclusion of the work.
-homoclinic orbit. The last section gives a conclusion of the work.
2. Two Normal Forms and Successor Function
From the above hypotheses, the normal form theory provides a 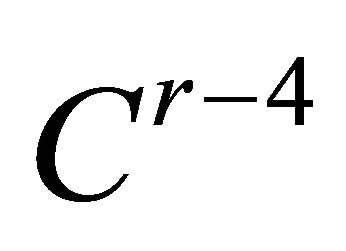 system as follows after four successive
system as follows after four successive 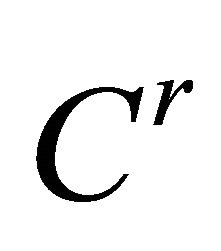 to
to 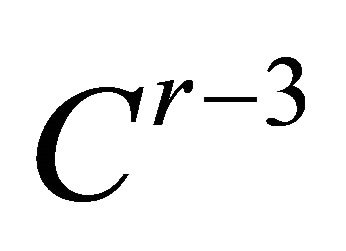 transformations in
transformations in 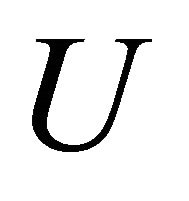 (see [10,11,18])
(see [10,11,18])
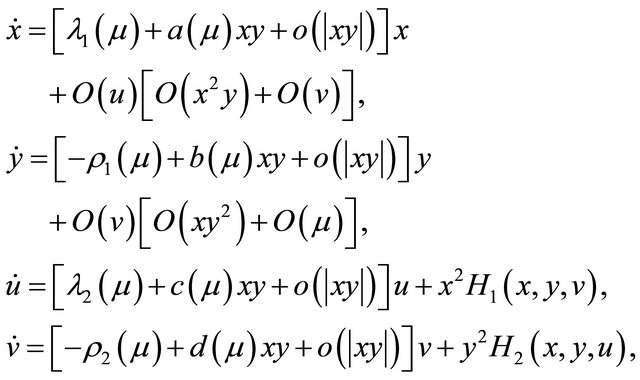 (2.1)
(2.1)
with the assumption
(H4)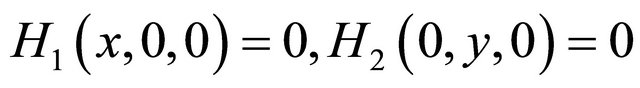 .
.
Indeed we have
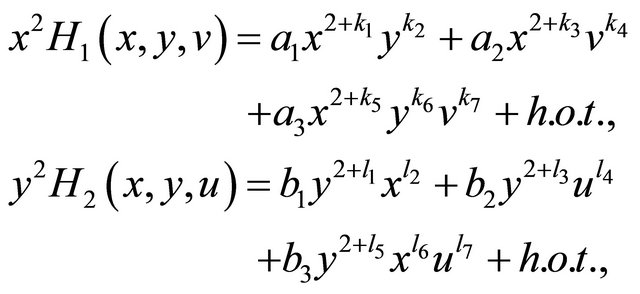
where
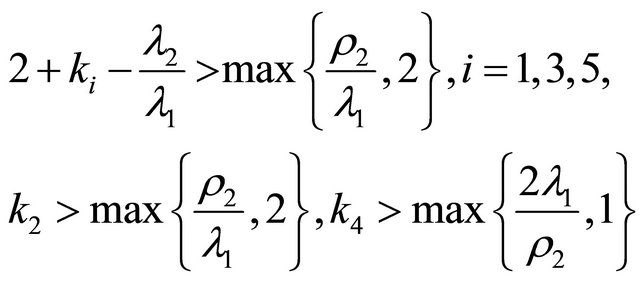
and

and
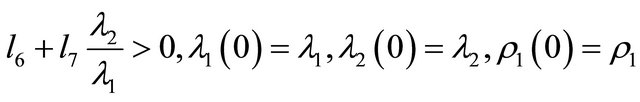
and
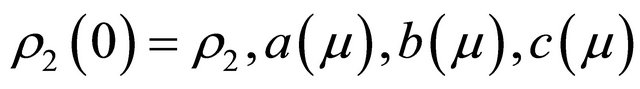
and 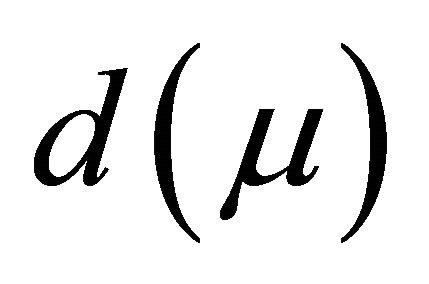 are parameters depending on
are parameters depending on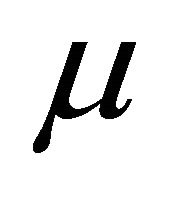 . Notice that we have straightened the corresponding invariant manifolds. So it is possible to choose some moment
. Notice that we have straightened the corresponding invariant manifolds. So it is possible to choose some moment![]() , such that
, such that 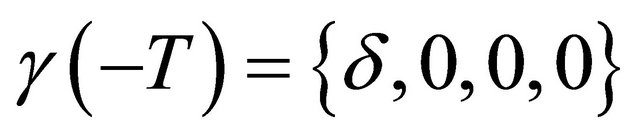 and
and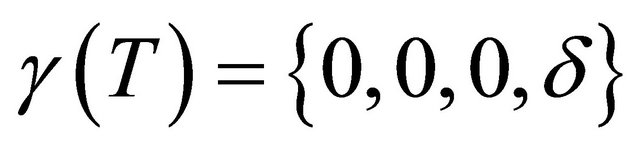 , where
, where ![]() is small enough and
is small enough and
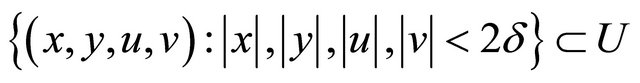 .
.
Now we turn to consider the linear variational system and its adjoint system
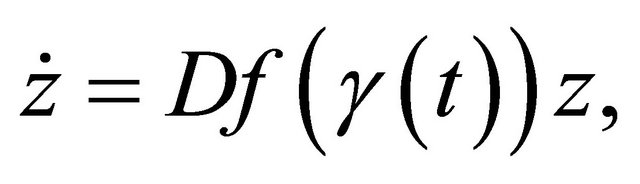 (2.2)
(2.2)
 (2.3)
(2.3)
First we introduce a lemma, see [10,11]
Lemma 2.1 There exists a fundamental solution matrix 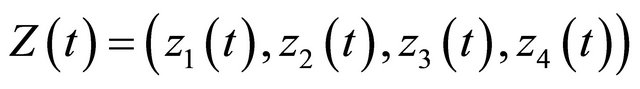 of system (2.2) satisfying
of system (2.2) satisfying

where
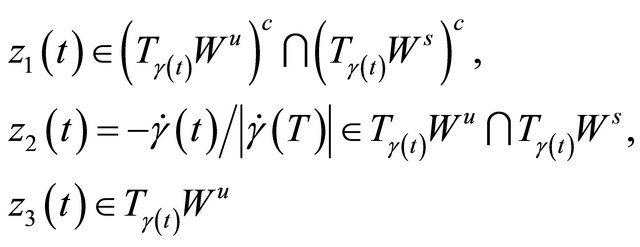
and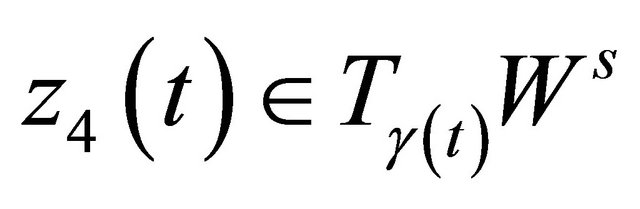 , and
, and .
.
Remark 2.1 The matrix  is a fundamental solution matrix of system (2.3), denote by
is a fundamental solution matrix of system (2.3), denote by
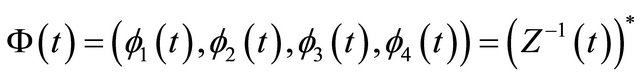 then
then
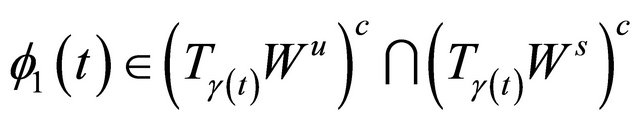
is bounded and tends to zero exponentially as 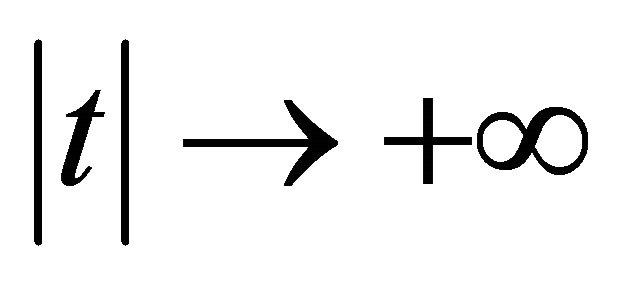 due to
due to 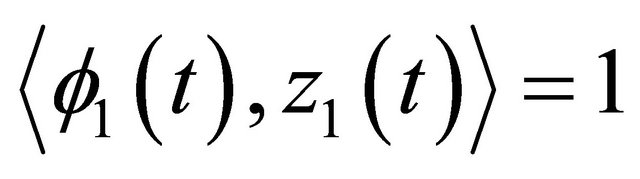 and
and 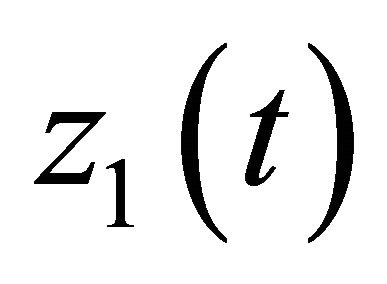 tends exponentially to infinity.
tends exponentially to infinity.
Let
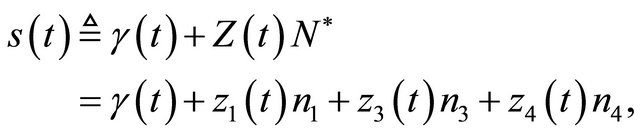 (2.4)
(2.4)
where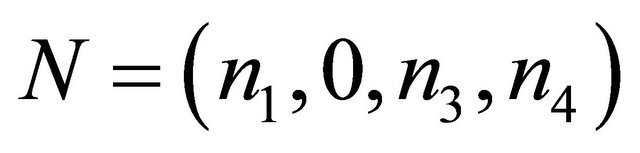 . We can well regard
. We can well regard
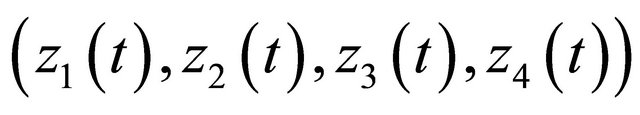 as a new local coordinate system along
as a new local coordinate system along![]() , and choose
, and choose
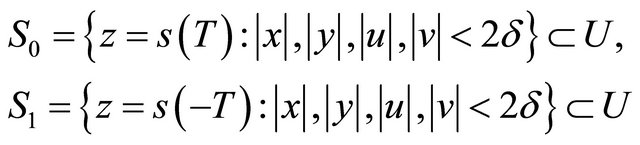
as the cross sections of ![]() at
at  and
and 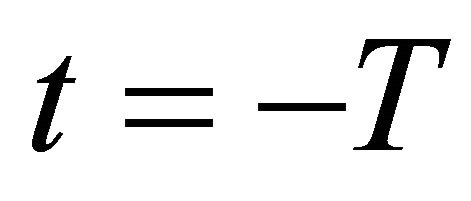 respectively. Under the transformation of (2.4), system (1.1) becomes
respectively. Under the transformation of (2.4), system (1.1) becomes

A simple integrating of both sides from  to
to ![]() of the above equation, we further achieve
of the above equation, we further achieve
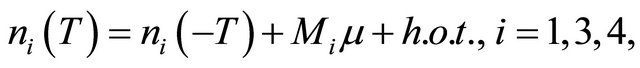 (2.5)
(2.5)
where
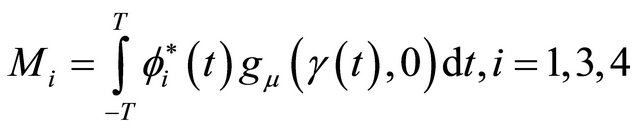
are the Melnikov vectors (see [18]).
Lemma 2.2
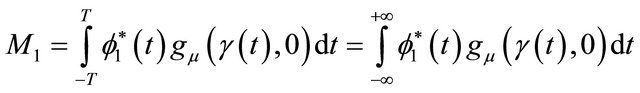 .
.
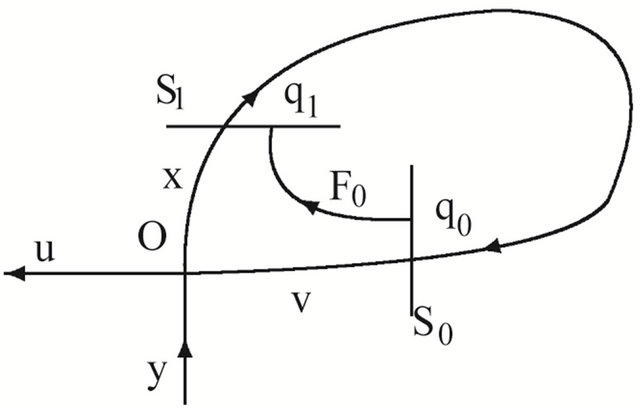
Actually a regular map is given by (2.5) as (see Figure 1(a))
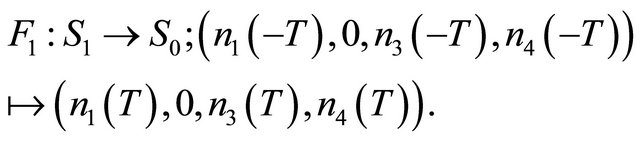
But this map is established in the new coordinate system, so we should look for the relationship between two coordinate systems. Set
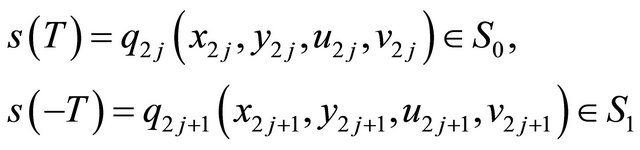
and
 (a)
(a)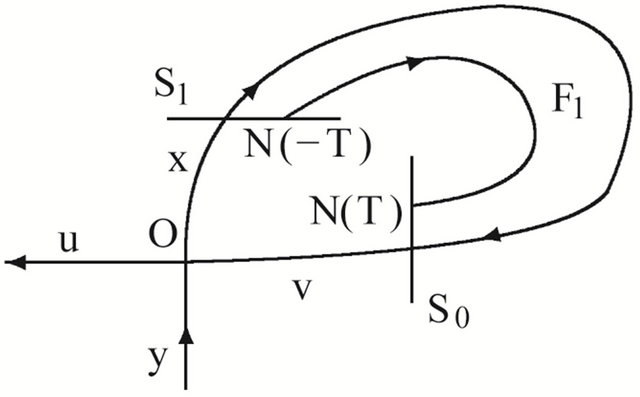 (b)
(b)
Figure 1. Transition maps. (a) F1: S1→S0; (b) F0: S0→S1.
Take 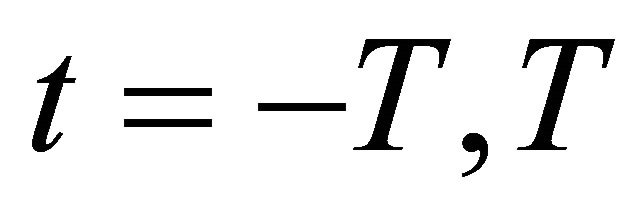 respectively in (2.4), we have
respectively in (2.4), we have
 (2.6)
(2.6)
 (2.7)
(2.7)
and
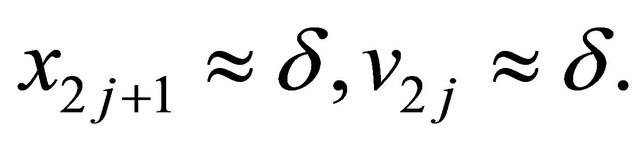 (2.8)
(2.8)
Next, we start to set up a singular map
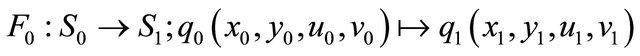
(see Figure 1(b)) induced by the solutions of system (2.1) in the neighborhood , for example
, for example
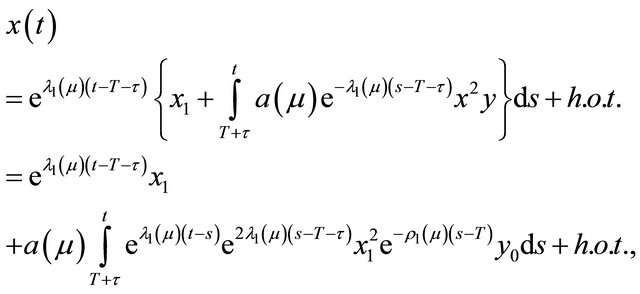
where ![]() is the time going from
is the time going from 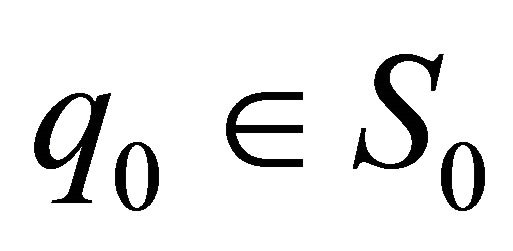 to
to . Denote the Silnikov time
. Denote the Silnikov time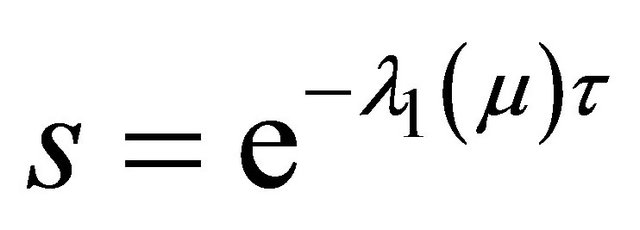 , then there is
, then there is
 .
.
Similarly, there are
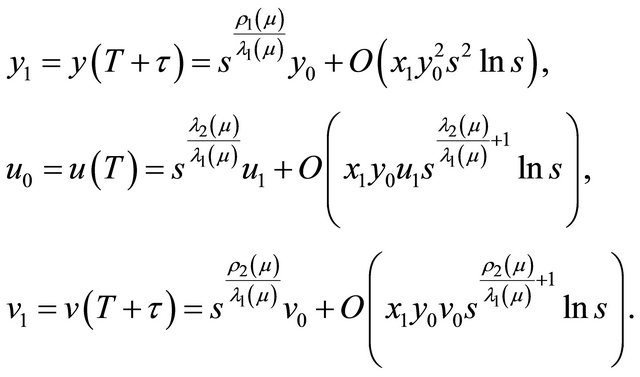 (2.9)
(2.9)
With Equations (2.6)-(2.9), Equation (2.5) well defines the Poincaré map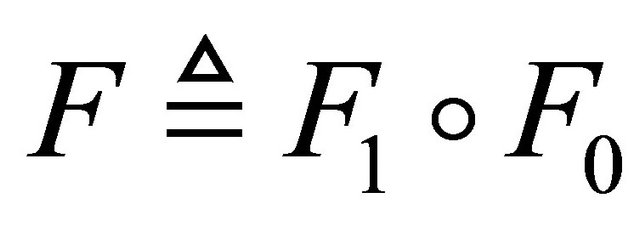 ,
,
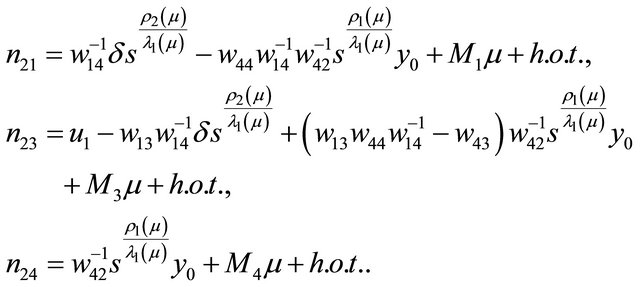
The above fact enables one to achieve the associated successor function 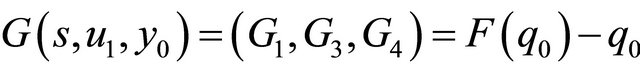 as follows:
as follows:
 (2.10)
(2.10)
3. Main Results
To begin the bifurcation study, 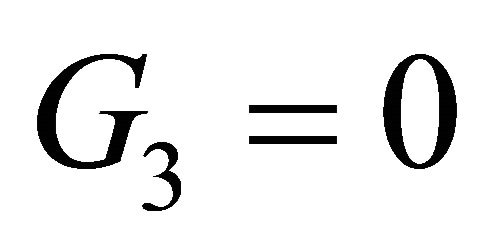 and
and 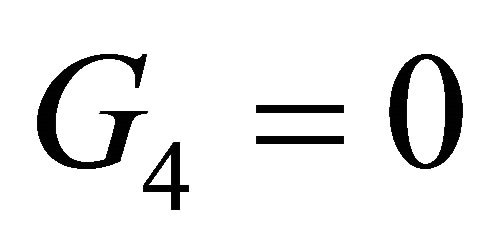 first give
first give
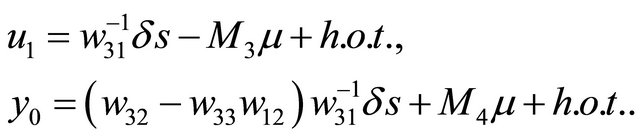
Substitute them into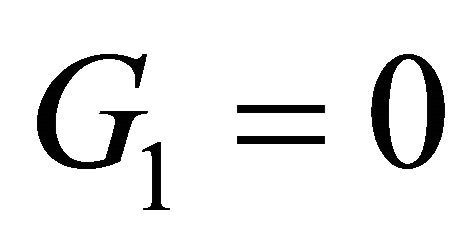 , we get
, we get
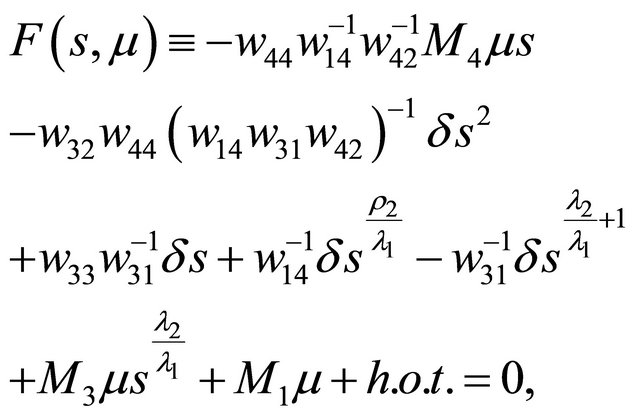 (3.1)
(3.1)
this is the bifurcation equation. Here we have omitted the parameter  in
in  and
and , and replaced the exponent
, and replaced the exponent 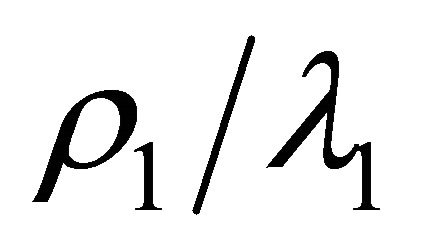 by one owing to (H1) for concision.
by one owing to (H1) for concision.
Set , we find that, when
, we find that, when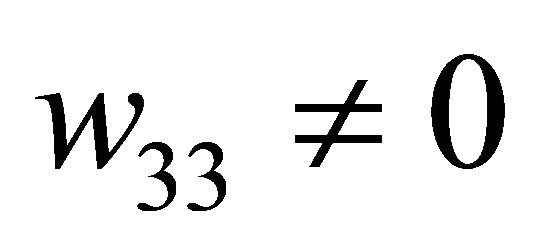 ,
,
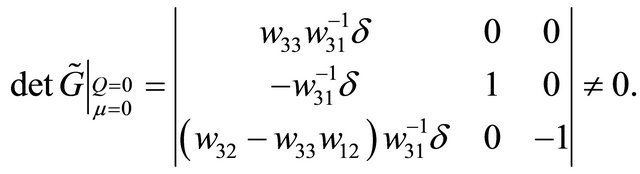
The implicit function theorem reveals that 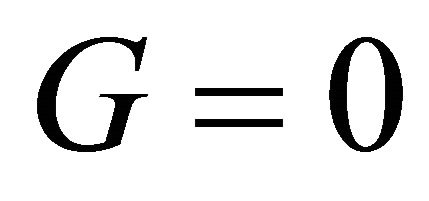 has a unique solution
has a unique solution
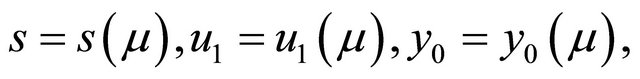
satisfying 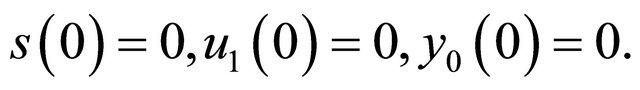 So system (1.1) has a unique periodic orbit as
So system (1.1) has a unique periodic orbit as 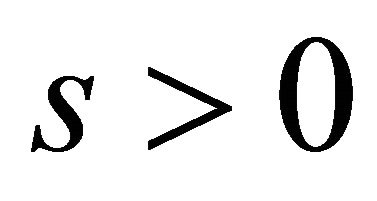 or a unique homoclinic orbit as
or a unique homoclinic orbit as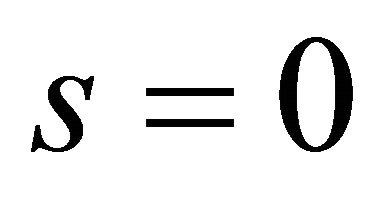 , and they do not coexist. Furthermore,
, and they do not coexist. Furthermore, 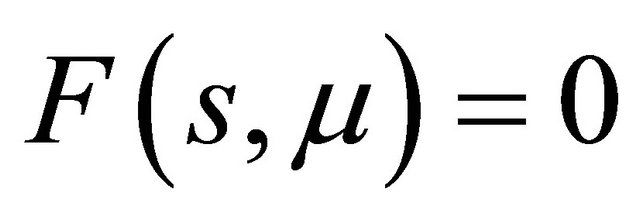 has explicitly a sufficiently small positive solution
has explicitly a sufficiently small positive solution  if
if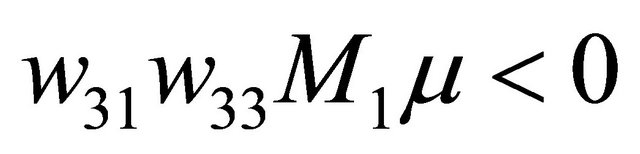 . On the other hand, it has a solution
. On the other hand, it has a solution 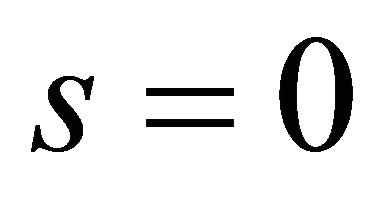 when
when , so we have Theorem 3.1 Suppose that
, so we have Theorem 3.1 Suppose that 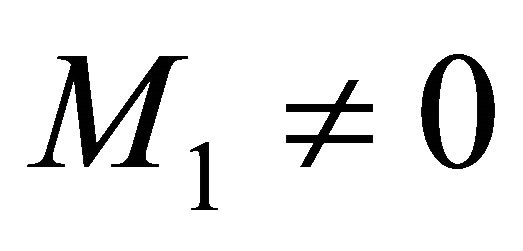 and
and 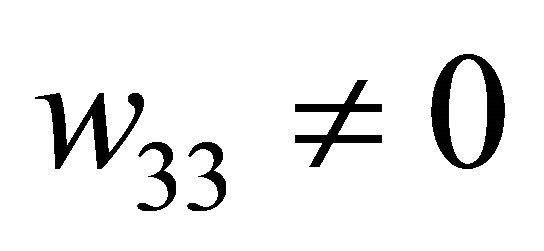 hold, then system (1.1) has at most one 1-periodic orbit or one 1-homoclinic orbit in the neighborhood of
hold, then system (1.1) has at most one 1-periodic orbit or one 1-homoclinic orbit in the neighborhood of![]() . Moreover an 1-periodic orbit exists (resp. does not exist) as
. Moreover an 1-periodic orbit exists (resp. does not exist) as 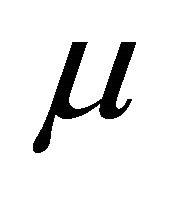 in the region defined by
in the region defined by  (resp.
(resp. ) and an 1-homoclinic orbit exists as
) and an 1-homoclinic orbit exists as , but they do not coexist.
, but they do not coexist.
In the following stage, we try to look for bifurcations according to the case 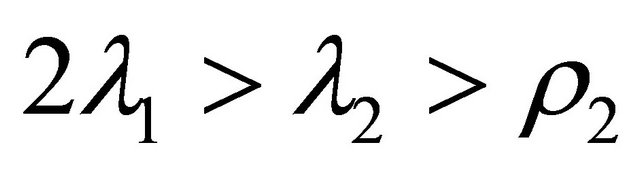 for
for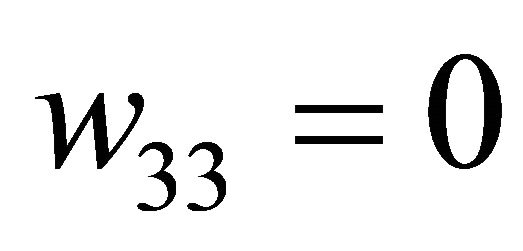 .
.
To begin with we divide (3.1) into two parts:
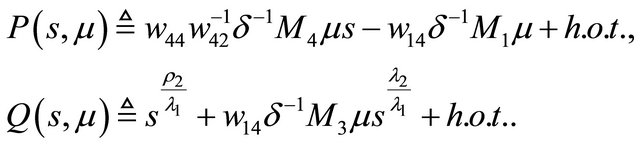
Therefore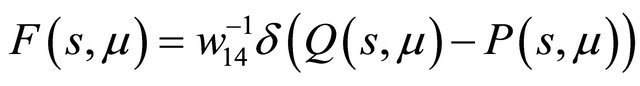 , where
, where
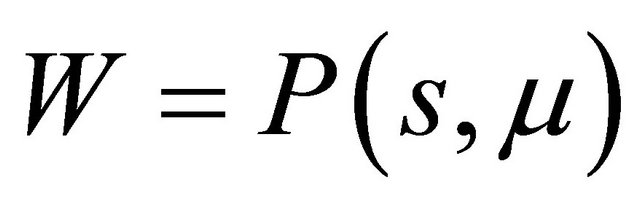 is a line and
is a line and 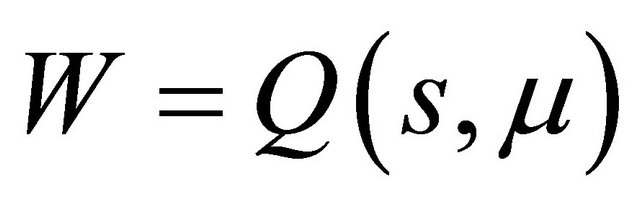 is a curve with
is a curve with 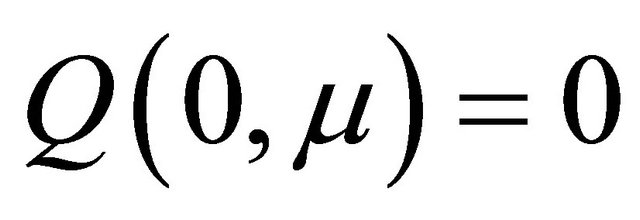 according to the variable
according to the variable![]() .
.
Theorem 3.2 Suppose that 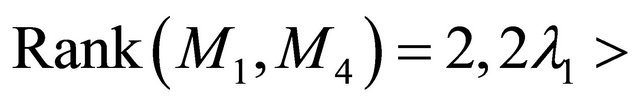
 and
and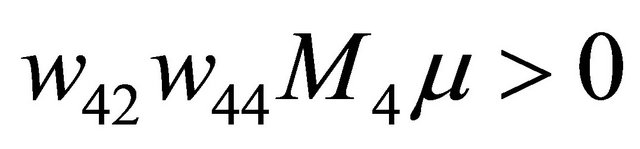 , system (1.1) then has a unique double 1-periodic orbit near
, system (1.1) then has a unique double 1-periodic orbit near![]() , and two (resp. not any) 1-periodic orbits near
, and two (resp. not any) 1-periodic orbits near ![]() when
when 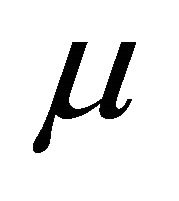 lies on the side of
lies on the side of  which points to the direction
which points to the direction  (resp. in the opposite direction of
(resp. in the opposite direction of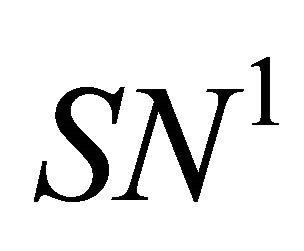 ). The corresponding double 1-periodic orbit bifurcation surface
). The corresponding double 1-periodic orbit bifurcation surface 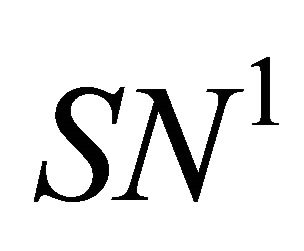 is
is
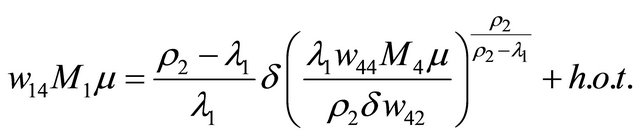
with the normal vector  at
at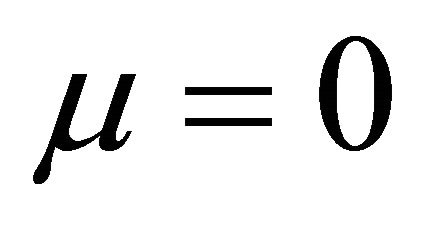 .
.
Proof Consider equations 
 and
and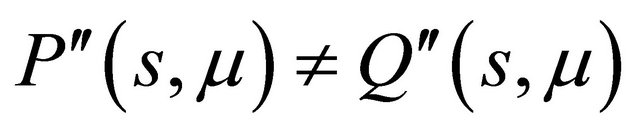 , that is,
, that is,
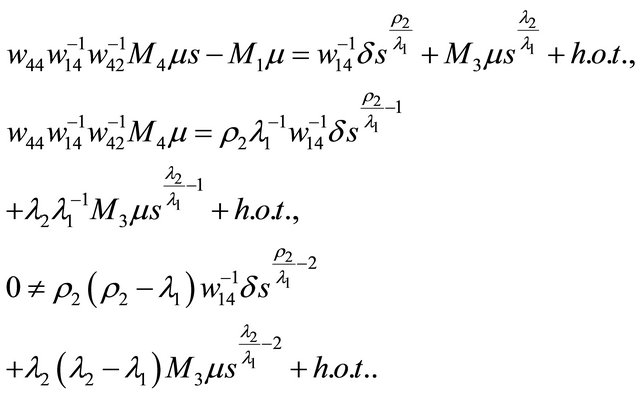 (3.2)
(3.2)
The second equation permits a solution
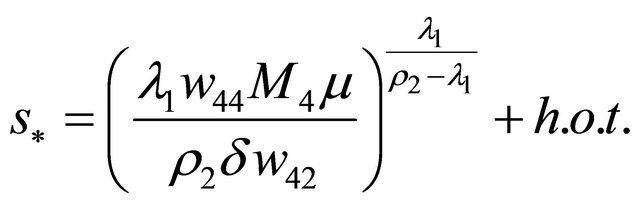
as
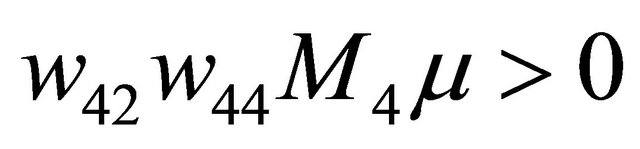 .
.
Substituting it into the first equation of (3.2), we obtain the tangency condition, which corresponds to the existence of the double periodic orbit bifurcation surface 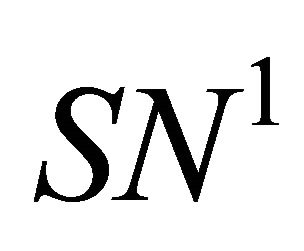 situated in the region
situated in the region 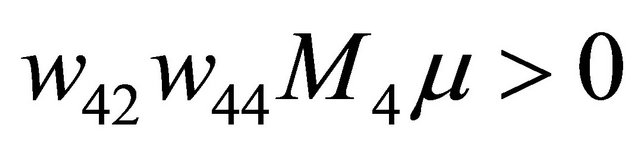 and
and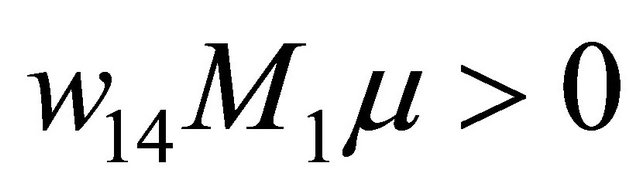 . Notice that, when the tangency takes place, the line
. Notice that, when the tangency takes place, the line 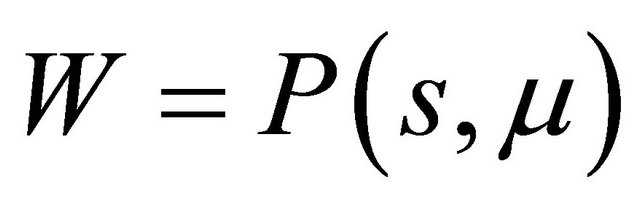 lies under the curve
lies under the curve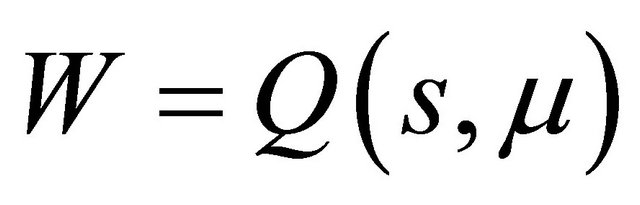 . So if
. So if 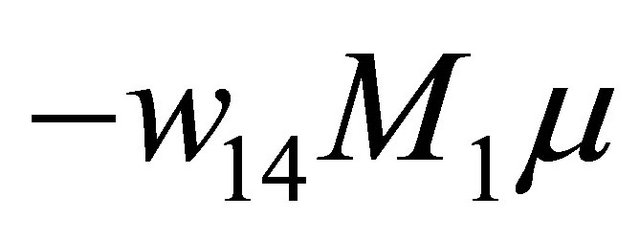 increases (resp. decreases), the line must intersects the curve at two (resp. no) sufficiently small positive points. Now the proof is complete.
increases (resp. decreases), the line must intersects the curve at two (resp. no) sufficiently small positive points. Now the proof is complete.
Theorem 3.3 Suppose that  and
and 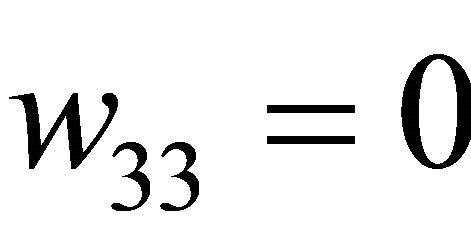 are true, then there exists two codimension-one hypersurfaces
are true, then there exists two codimension-one hypersurfaces
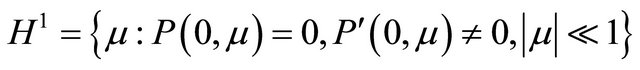
and
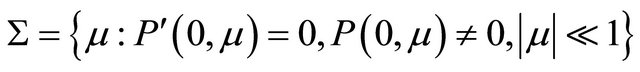 such that System (1.1) has only one 1-homoclinic orbit near
such that System (1.1) has only one 1-homoclinic orbit near ![]() as
as 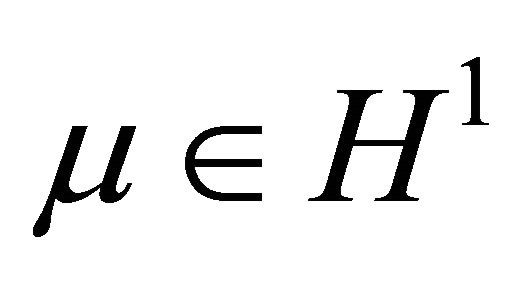 and
and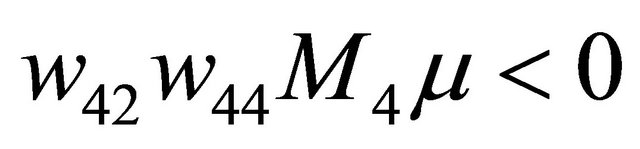 ;
;
System (1.1) has only one 1-periodic orbit near ![]() as
as 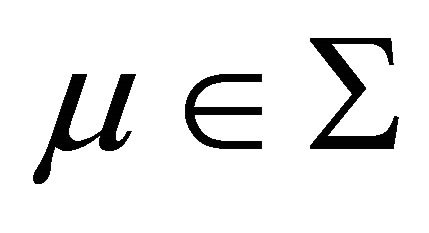 and
and ;
;
System (1.1) has exactly one 1-homoclinic orbit and one 1-periodic orbit near  as
as 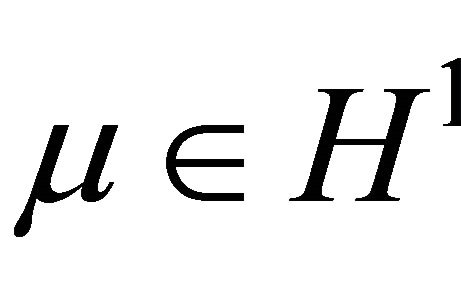 and
and 
 ;
;
System (1.1) has not any 1-periodic orbit or 1-homoclinic orbit as 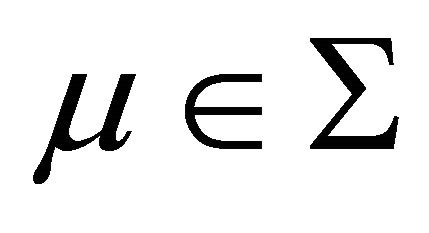 and
and .
.
Proof When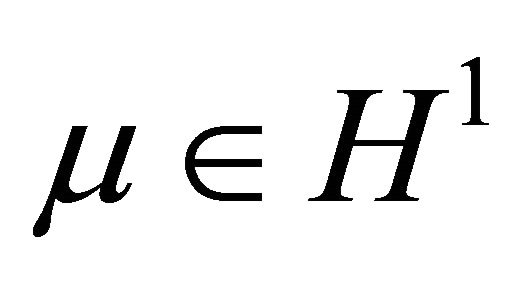 , we have at once
, we have at once
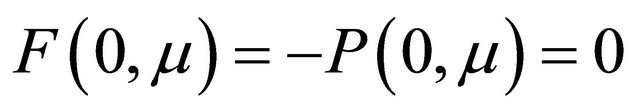
and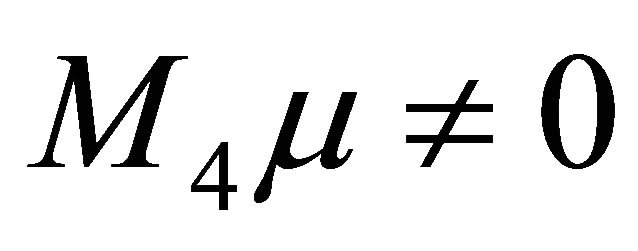 , therefore
, therefore
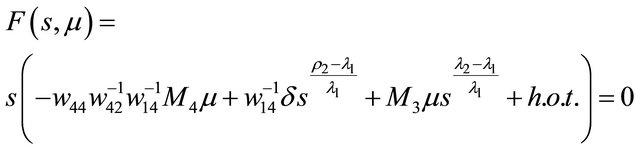
has always two nonnegative solutions  and
and
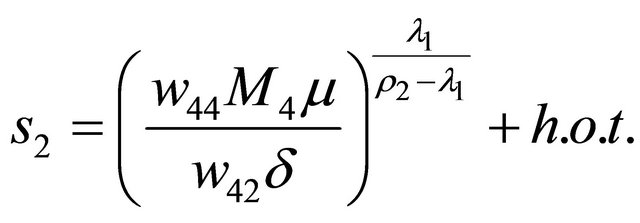
for  or has only a zero solution
or has only a zero solution 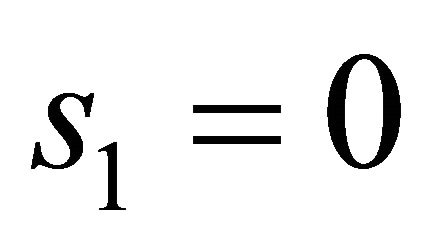
for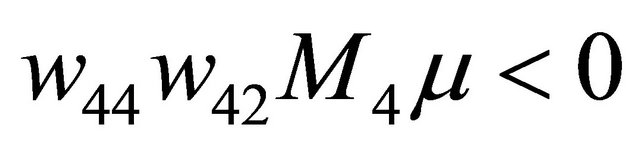 . If
. If , there is, on the contrary,
, there is, on the contrary, 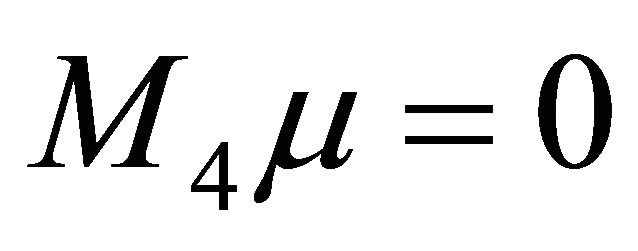 but
but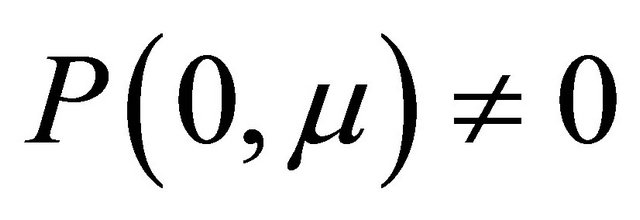 , apparently the line
, apparently the line  is horizontal. So
is horizontal. So 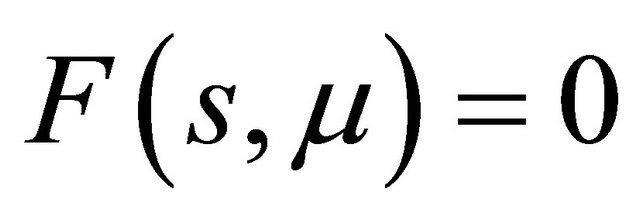 has a solution
has a solution
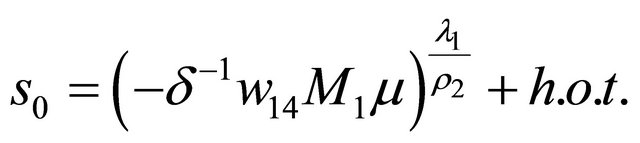
if and only if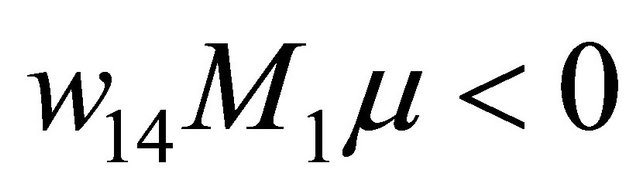 . The proof is complete.
. The proof is complete.
From the above proof, we see that if the line 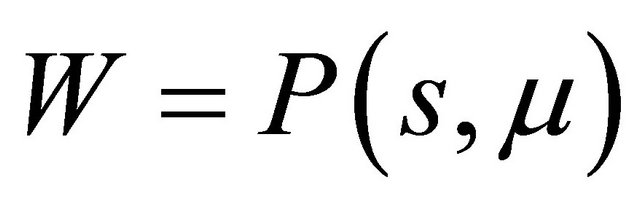 has a small positive section with the
has a small positive section with the  - axis or small positive slope, then there exists a small positive
- axis or small positive slope, then there exists a small positive 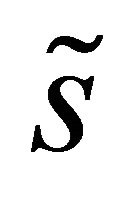 such that
such that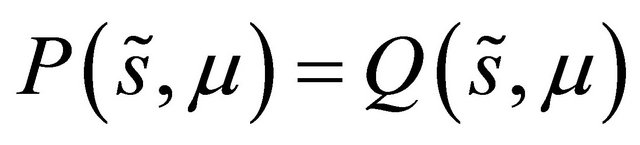 . Thus the following corollary is valid, which is a complement of Theorem 3.2.
. Thus the following corollary is valid, which is a complement of Theorem 3.2.
Corollary 3.4 Assume that the hypotheses of Theorem 3.2 are valid, system (1.1) then has a unique 1-periodic orbit near ![]() as
as 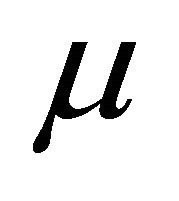 is situated in the region defined by
is situated in the region defined by
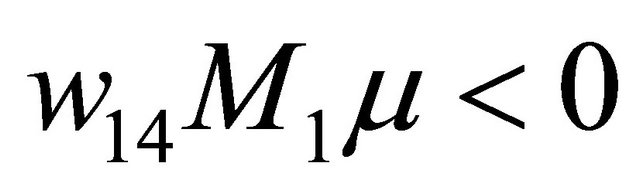 and
and  or
or ,
,  and
and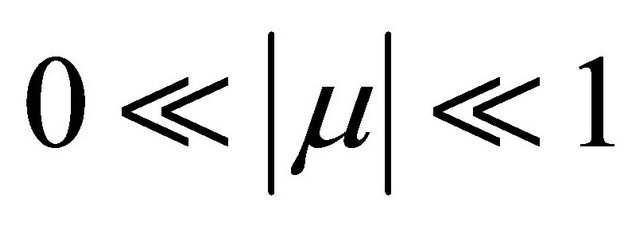 ; has not any 1-periodic orbit as
; has not any 1-periodic orbit as 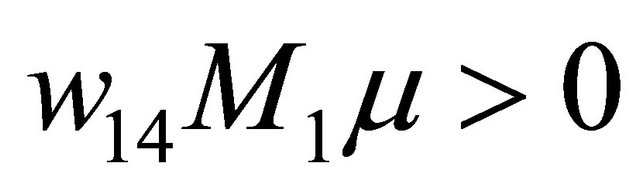 and
and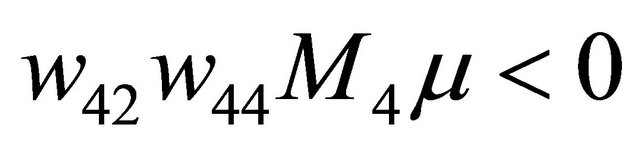 .
.
Notice that in Theorem 3.3, system (1.1) has a codimension-1 1-homoclinic orbit, see Figure 2(a), that is the existing homoclinic orbit has no longer orbit flip. But an orbit flip homoclinic orbit could still exist if
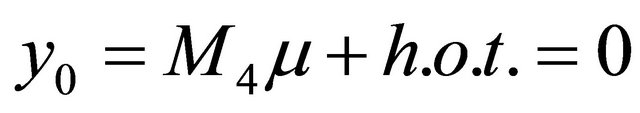 see Figure 2(b).
see Figure 2(b).
Corollary 3.5 Suppose that 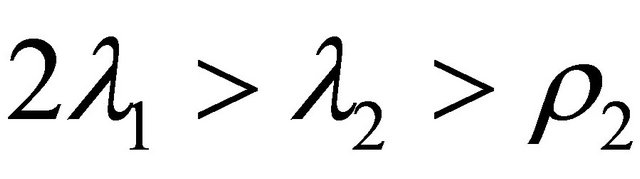 and
and 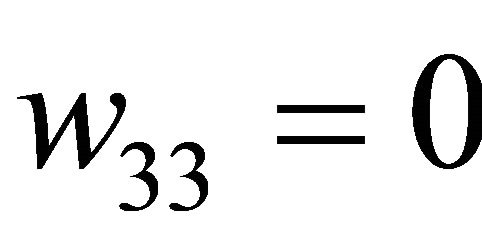 hold, system (1.1) has a codimension-2 orbit-flip homoclinic orbit as
hold, system (1.1) has a codimension-2 orbit-flip homoclinic orbit as
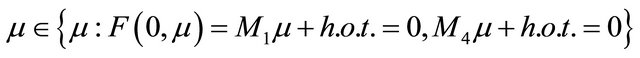 .
.
Now we turn to study the homoclinic doubling bifurcations. To begin with we look for the 2-homoclinic orbit and 2-periodic orbit bifurcation surfaces. Reset ![]() and
and 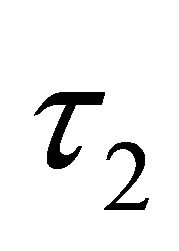 be the time going from
be the time going from 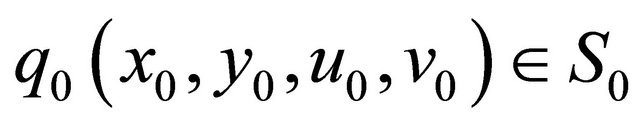 to
to
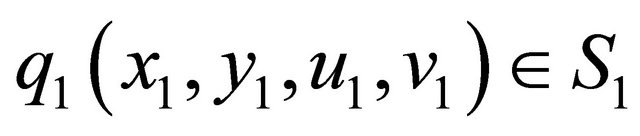 and from
and from  to
to  respectively,
respectively, 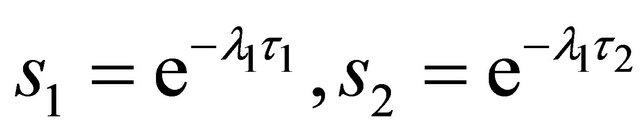 and
and
 .
.
Then recall the process of the establishment of (2.10), similarly we may get the associated second returning successor function 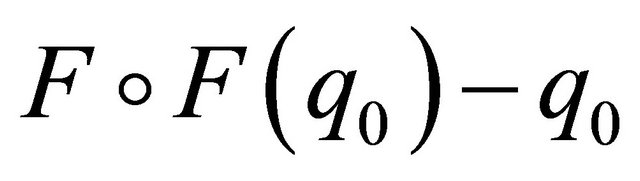 expressed as
expressed as
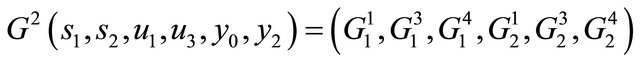 :
:
 (a)
(a) (b)
(b)
Figure 2. 1-homoclinic orbit (1-H) and (1-OH). (a) μ ∈ Σ1; (b) F(0, μ) = 0, y0 = M4μ + h.o.t. = 0.
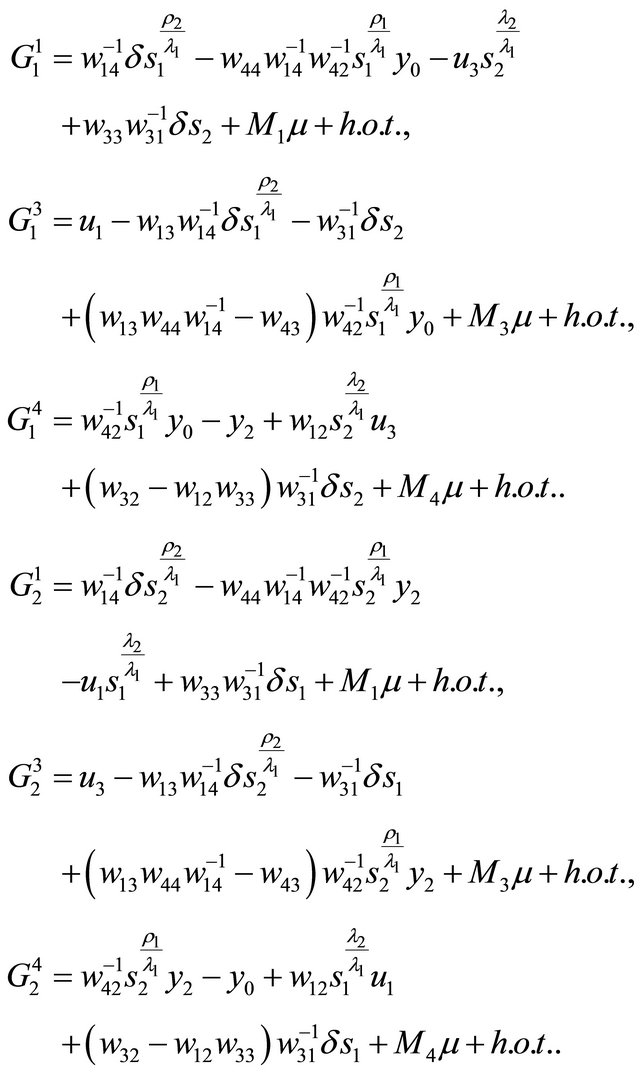
Eliminating again  and
and  from
from  and
and , and assuming
, and assuming

we obtain
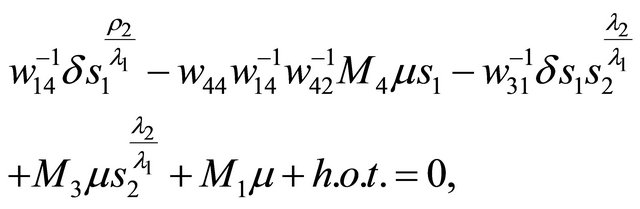 (3.3)
(3.3)
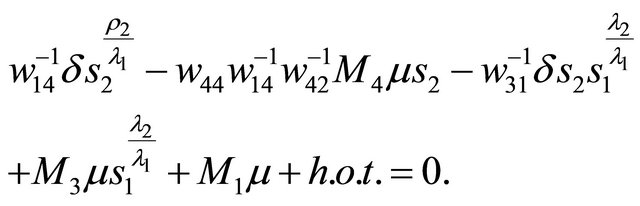 (3.4)
(3.4)
We know that a 2-homoclinic orbit 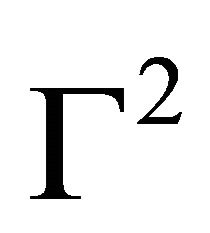 corresponds to the solution
corresponds to the solution 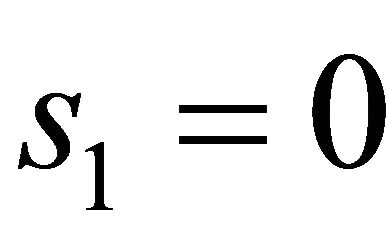 and
and 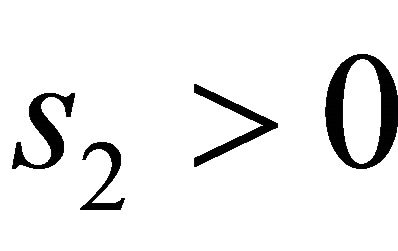 or
or 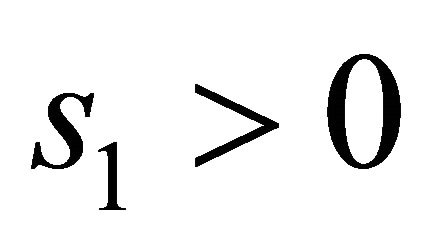 and
and 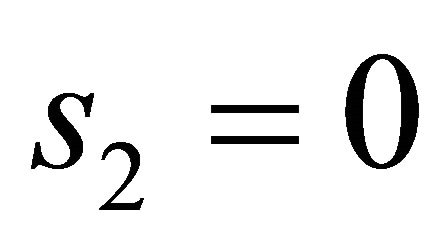 of (3.3) and (3.4), that means an orbit returns once nearby the singular point in limit time and twice in limitless time. So it is sufficient to seek the small solutions of
of (3.3) and (3.4), that means an orbit returns once nearby the singular point in limit time and twice in limitless time. So it is sufficient to seek the small solutions of 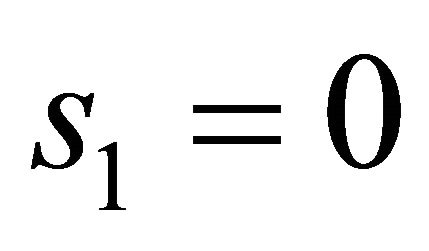 and
and 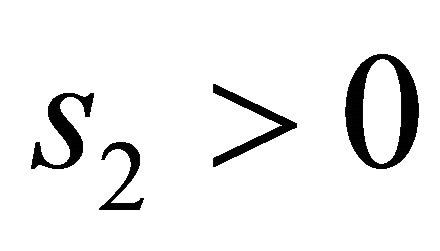 by symmetry of
by symmetry of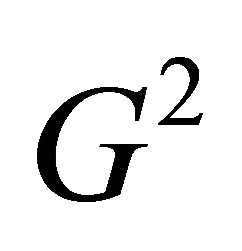 . Therefore
. Therefore
 (3.5)
(3.5)
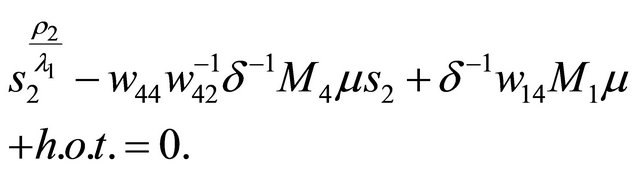 (3.6)
(3.6)
Clearly (3.5) yields
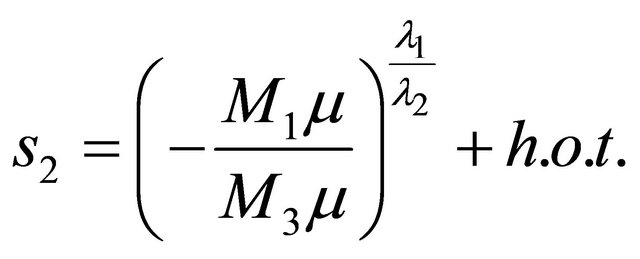
for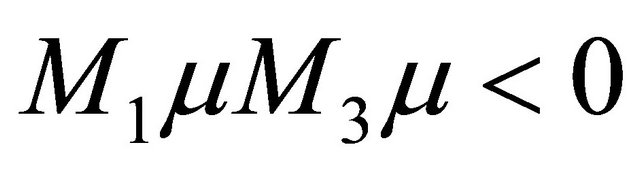 , and
, and 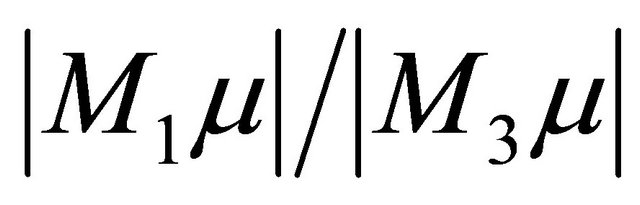 sufficiently small. With this, Equation (3.6) determines a 2-homoclinic orbit bifurcation surface
sufficiently small. With this, Equation (3.6) determines a 2-homoclinic orbit bifurcation surface
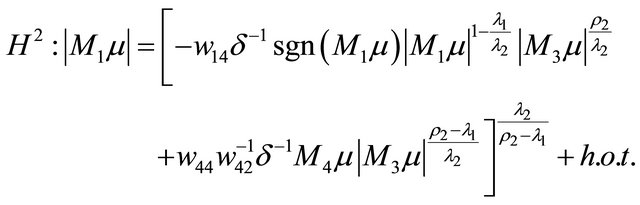
for  and
and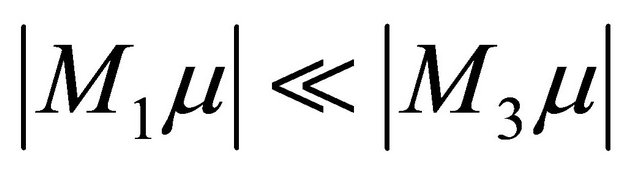 , which has a normal vector
, which has a normal vector 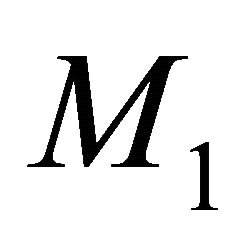 at
at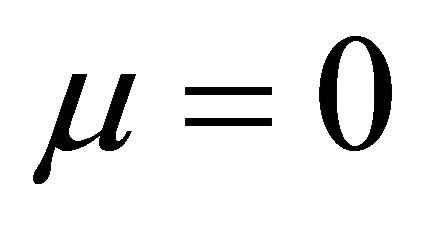 .
.
Continually, differentiating both sides of (3.3) and (3.4) with respect to 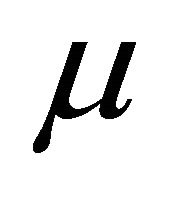 and for
and for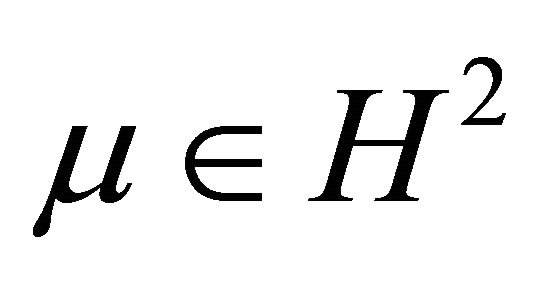 , we obtain
, we obtain
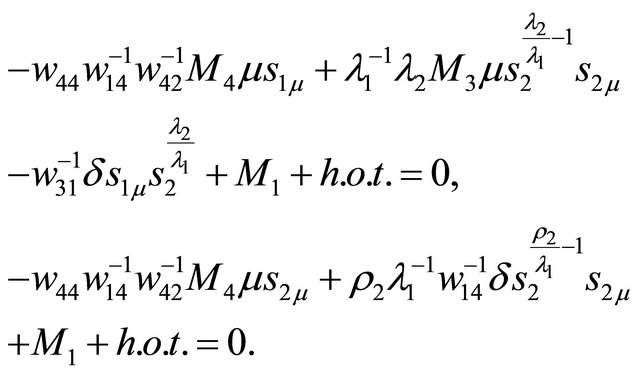
In the region defined by
 and
and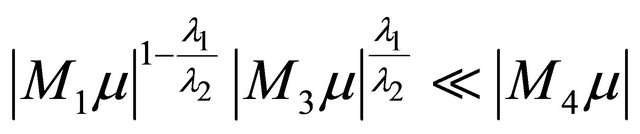 the 2-homoclinic orbit bifurcation surface
the 2-homoclinic orbit bifurcation surface  is simplified to be
is simplified to be
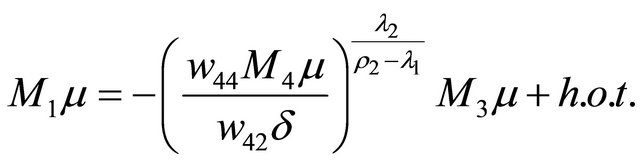 .
.
Accordingly
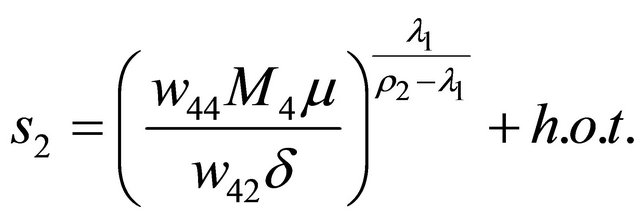 .
.
Then one may derive
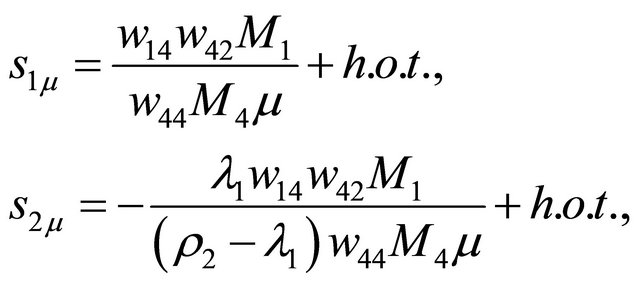
which informs that ![]() increases (resp. decreases) as
increases (resp. decreases) as 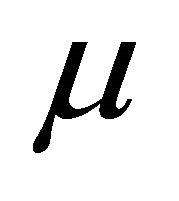 moves along the direction
moves along the direction 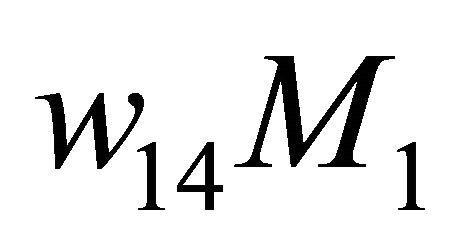 (resp. the opposite direction) such that a
(resp. the opposite direction) such that a 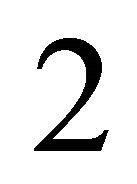 -periodic orbit bifurcates from the
-periodic orbit bifurcates from the 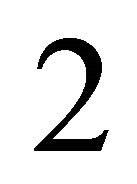 -homoclinic orbit
-homoclinic orbit  as
as  leaves
leaves 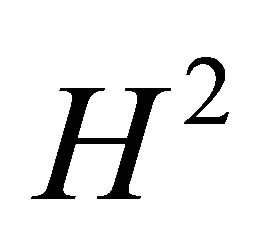 for the side pointed by
for the side pointed by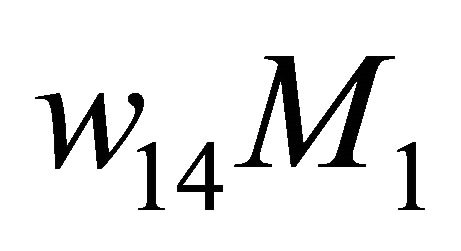 .
.
Notice that confined on the surface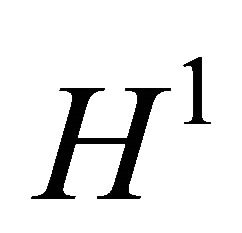 , (3.3) and (3.4) has a unique positive solution, meanwhile Theorem 3.3 indicates exactly the existence of one 1-periodic orbit when
, (3.3) and (3.4) has a unique positive solution, meanwhile Theorem 3.3 indicates exactly the existence of one 1-periodic orbit when 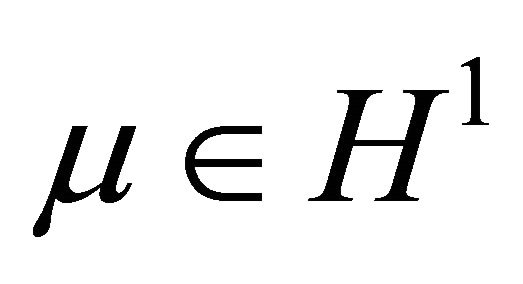 for
for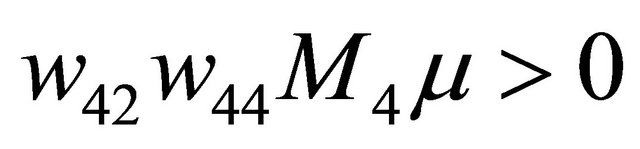 , so there does not exist any 2-periodic orbit when
, so there does not exist any 2-periodic orbit when 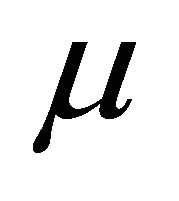 is near
is near . Therefore in the region bounded by the surfaces
. Therefore in the region bounded by the surfaces 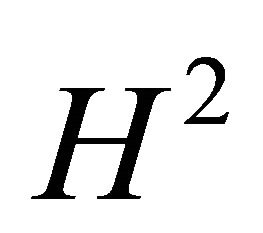 to
to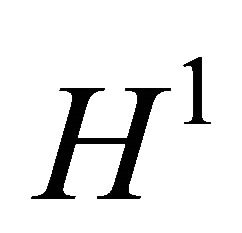 , there must exist another bifurcation surface which merges the 1-periodic orbit and the 2-periodic orbit into a new 1-periodic orbit with the different stability from the original one. We call this surface the period-doubling bifurcation surface and denote it by
, there must exist another bifurcation surface which merges the 1-periodic orbit and the 2-periodic orbit into a new 1-periodic orbit with the different stability from the original one. We call this surface the period-doubling bifurcation surface and denote it by .
.
The above reasonings can repeat itself many times to find the 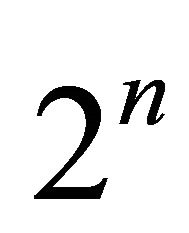 -homoclinic orbit bifurcation surface
-homoclinic orbit bifurcation surface

in the same region of  space and simultaneously the presence of period-doubling bifurcation surface
space and simultaneously the presence of period-doubling bifurcation surface 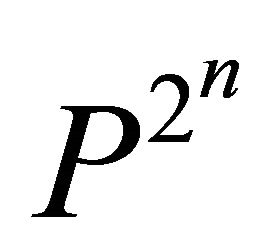 of
of 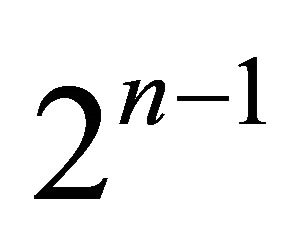 -periodic orbit.
-periodic orbit.
In short, we conclude that:
Theorem 3.6 Suppose that

and 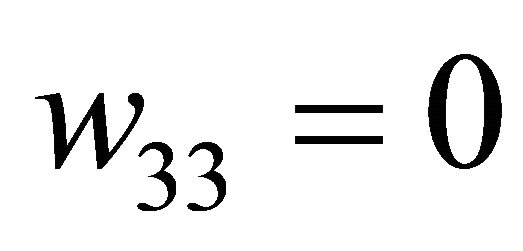 hold, then for
hold, then for
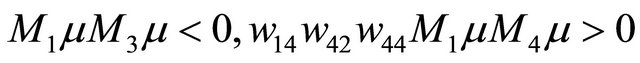
and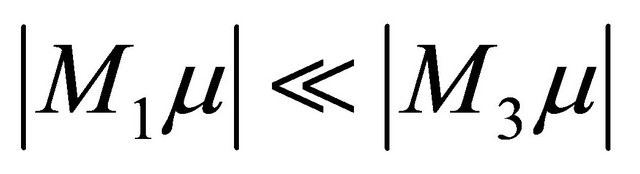 , there exists a
, there exists a 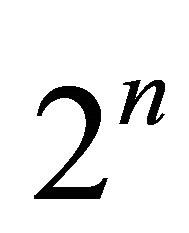 -homoclinic orbit bifurcation surface
-homoclinic orbit bifurcation surface 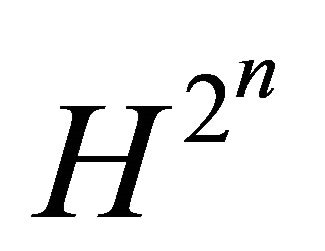 with the normal vector
with the normal vector 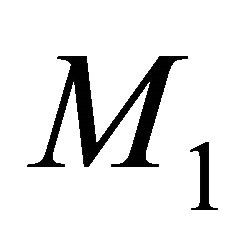 at
at 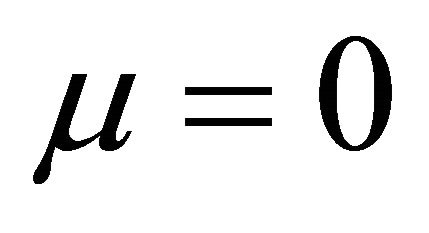 and the period-doubling bifurcation surface
and the period-doubling bifurcation surface 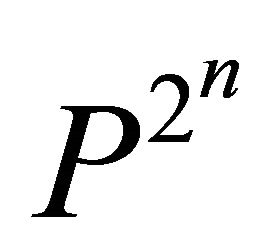 of
of 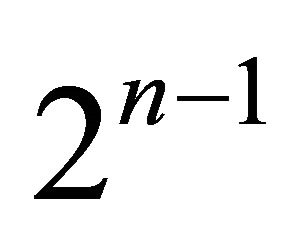 -periodic orbit in the small neighborhood of the origin of
-periodic orbit in the small neighborhood of the origin of  space. Moreover system (1.1) has exactly a
space. Moreover system (1.1) has exactly a 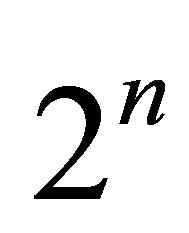 -homoclinic orbit as
-homoclinic orbit as  and a
and a 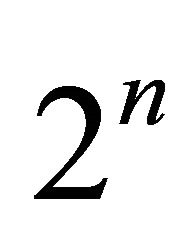 -periodic orbit as
-periodic orbit as 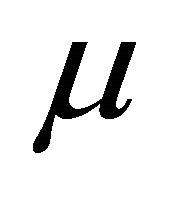 moves away to the side of
moves away to the side of 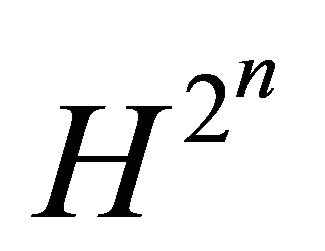 pointing to the direction
pointing to the direction 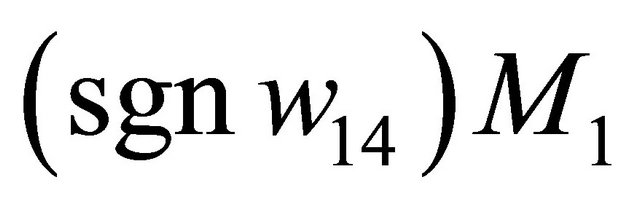 and none on the other side.
and none on the other side.
To well illustrate our results, a bifurcation diagram is drawn in Figure 3, where 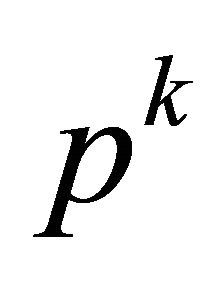 represents a
represents a  -periodic orbit.
-periodic orbit.
4. Conclusion
Homoclinic orbits generically occur as a codimensionone phenomenon, while if the genericity conditions are

Figure 3. Location of bifurcation surfaces for rank (M1, M3, M4) = 3, w33 = 0, 2λ1 > λ2 > ρ2.
broken, some high codimension instance including the resonant and flips cases, concomitant usually with chaotic behavior, may take place. Homburg and Oldeman studied two kinds of resonant homoclinic flips in [8,9] with unfolding techniques and numerical methods respectively. Zhang in [10,11] continued to research on these problems and gave some theoretical proofs of the existence of ![]() -periodic orbit and
-periodic orbit and ![]() -homoclinic orbit and also their existence regions via the method initially established in [18]. Besides these the flip heterodimensional cycles have also attracted attentions nowadays, see [16]. In this paper, we extend the method to fit a higher codimension case of 3 flips with resonant. With the delicate analysis, the existence of 1-periodic orbit, 1-homoclinic orbit, and double periodic orbit are proven and also the
-homoclinic orbit and also their existence regions via the method initially established in [18]. Besides these the flip heterodimensional cycles have also attracted attentions nowadays, see [16]. In this paper, we extend the method to fit a higher codimension case of 3 flips with resonant. With the delicate analysis, the existence of 1-periodic orbit, 1-homoclinic orbit, and double periodic orbit are proven and also the 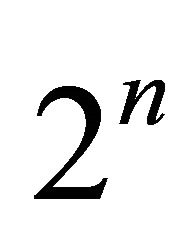 -homoclinic orbit and their corresponding bifurcation surfaces. With the work, we find the extensive existence of the double periodic orbit bifurcation and the homoclinic-doubling bifurcation, which efficiently advance the development of the flips homoclinic study.
-homoclinic orbit and their corresponding bifurcation surfaces. With the work, we find the extensive existence of the double periodic orbit bifurcation and the homoclinic-doubling bifurcation, which efficiently advance the development of the flips homoclinic study.
REFERENCES
- L. Silnikov, “A Case of the Existence of a Denumerable Set of Periodic Motions,” Soviet Mathematics Doklady, Vol. 6, 1965, pp. 163-166.
- S. Chow, B. Deng and B. Fiedler, “Homoclinic Bifurcation at Resonant Eigenvalues,” Journal of Dynamics and Differential Equations, Vol. 2, No. 2, 1990, pp. 177-244. doi:10.1007/BF01057418
- B. Sandstede, “Constructing Dynamical Systems Having Homoclinic Bifurcation Points of Codimension Two,” Journal of Dynamics and Differential Equations, Vol. 9, No. 2, 1997, pp. 269-288. doi:10.1007/BF02219223
- C. Morales and M. Pacifico, “Inclination-Flip Homoclinic Orbits Arising from Orbit-Flip,” Nonlinearity, Vol. 14, No. 2, 2001, pp. 379-393. doi:10.1088/0951-7715/14/2/311
- M. Kisaka, H. Kokubu and H. Oka, “Bifurcations to NHomoclinic Orbits and N-Periodic Orbits in Vector Fields,” Journal of Dynamics and Differential Equations, Vol. 5, No. 2, 1993, pp. 305-357. doi:10.1007/BF01053164
- V. Naudot, “Bifurcations Homoclines des Champes de Vecteurs en Dimension Trois,” PH.D. Thesis, l'Université de Bourgogne, Dijon, 1996.
- A. Homburg, H. Kokubu and V. Naudot, “HomoclinicDoubling Cascades,” Archive for Rational Mechanics and Analysis, Vol. 160, No. 3, 2001, pp. 195-243. doi:10.1007/s002050100159
- A. Homburg and B. Krauskopf, “Resonant Homoclinic Flip Bifurcations,” Journal of Dynamics and Differential Equations, Vol. 12, No. 4, 2000, pp. 807-850. doi:10.1023/A:1009046621861
- B. Oldeman, B. Krauskopf and A. Champneys, “Numerical Unfoldings of Codimension-Three Resonant Homoclinic Flip Bifurcations,” Nonlinearity, Vol. 14, No. 3, 2001, pp. 597-621. doi:10.1088/0951-7715/14/3/309
- T. Zhang and D. Zhu, “Homoclinic Bifurcation of Orbit Flip with Resonant Principal Eigenvalues,” Acta Mathematica Sinica, Vol. 22, No. 3, 2006, pp. 855-864.
- T. Zhang and D. Zhu, “Bifurcations of Homoclinic Orbit Connecting Two Nonleading Eigendirections,” International Journal of Bifurcation and Chaos, Vol. 17, No. 3, 2007, pp. 823-836. doi:10.1142/S0218127407017574
- M. Krupa, B. Sandstede and P. Szmolyan, “Fast and Slow Waves in the FitzHugh-Nagumoequation,” Journal of Differential Equations, Vol. 133, No. 1, 1997, pp. 49-97. doi:10.1006/jdeq.1996.3198
- U. Feudel, A. Neiman, X. Pei, W. Wojtenek, H. Braun, M. Huber and F. Moss, “Homoclinic Bifurcation in a Hodgkin-Huxley Model of Thermally Sensitive Neurons,” Chaos, Vol. 10, No. 1, 2000, pp. 231-239. doi:10.1063/1.166488
- A. Champneys, Kuznetsov and A. Yu, “Numerical Detection and Continuation of Codimension-Two Homoclinic Bifurcation,” International Journal of Bifurcation and Chaos, Vol. 4, No. 4, 1994, pp. 785-822. doi:10.1142/S0218127494000587
- F. Geng and D. Zhu, “Bifurcations of Generic Heteroclinic Loop Accompanied by Transcritical Bifurcation,” International Journal of Bifurcation and Chaos, Vol. 18, 2008, pp. 1069-1083. doi:10.1142/S0218127408020847
- Q. Lu, Z. Qiao, T. Zhang and D. Zhu, “Heterodimensional Cycle Bifurcation with Orbit-Filp,” International Journal of Bifurcation and Chaos, Vol. 20, No. 2, 2010, pp.491-508. doi:10.1142/S0218127410025569
- X. Liu, “Homoclinic Flip Bifurcations Accompanied by Transcritical Bifurcation,” Chinese Annals of Mathematics, Series B, Vol. 32, No. 6, 2011, pp. 905-916. doi:10.1007/s11401-011-0675-y
- D. Zhu and Z. Xia, “Bifurcation of Heteroclinic Loops,” Science in China, Series A, Vol. 41, No. 8, 1998, pp. 837- 848. doi:10.1007/BF02871667
NOTES
*Project supported by National Natural Science Foundation of China (Grant: 11126097) and by SRF for ROCS, SEM.

