ABSTRACT

The main object of this paper is to study some properties of certain subclass of analytic functions with negative coefficients defined by a linear operator in the open unit disc. These properties include the coefficient estimates, closure properties, distortion theorems and integral operators.

1. Introduction

Let be the class of analytic functions in the open unit disc

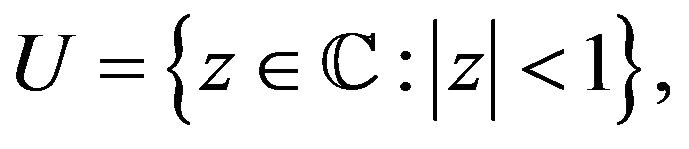
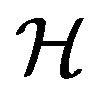and be the subclass of consisting of functions of the form

Let denote the class of functions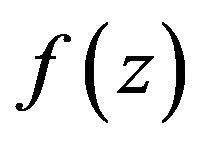 normalized by

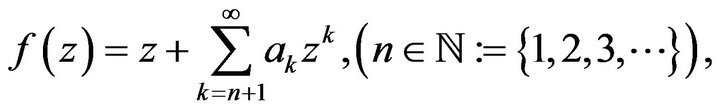(1)

which are analytic in the open unit disc. In particular,

For two functions 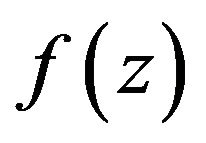given by (1) and 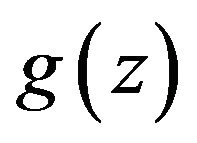given by

the Hadamard product (or convolution) is defined, as usual, by

Let the function 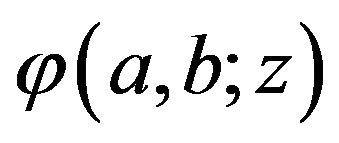be given by:

where denotes the Pochhammer symbol (or the shifted factorial) defined by:

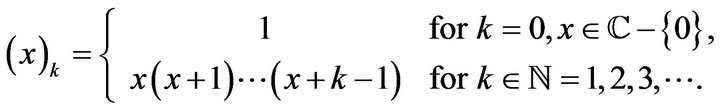
Carlson and Shaffer [1] introduced a convolution operator on involving an incomplete beta function as:

(2)

Our work here motivated by Catas [2], who introduced an operator on as follows:

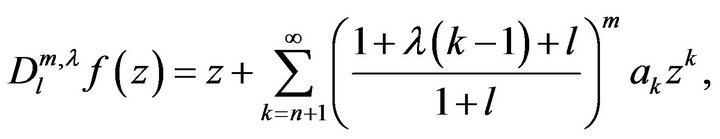
where

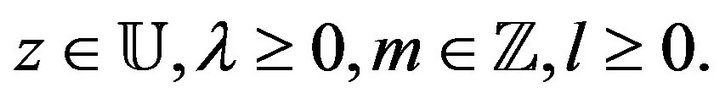
Now, using the Hadamard product (or convolution), the authors (cf. [3,4]) introduced the following linear operator:

Definition 1.1 Let

where

and is the Pochhammer symbol. We defines a linear operator by the following Hadamard product:

(3)

where

and the Pochhammer symbol .

Special cases of this operator include:

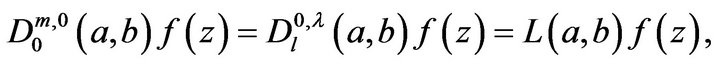• see [1].

• the Catas drivative operator [2]:

• the Ruscheweyh derivative operator [5] in the cases:

•

• the Salagean derivative operator [6]: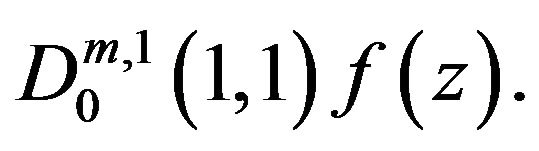

• the generalized Salagean derivative operator introduced by Al-Oboudi [7]:

• Note that:

Let 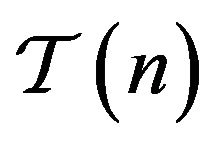denote the class of functions 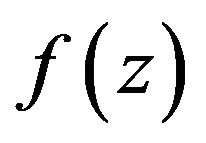of the form

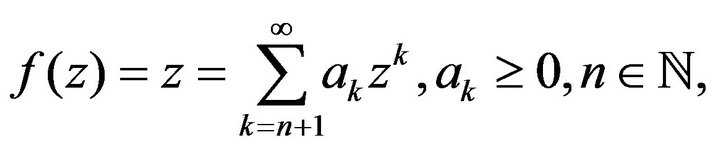(4)

which are analytic in the open unit disc.

Following the earlier investigations by [8] and [9], we define -neighborhood of a function by

or,

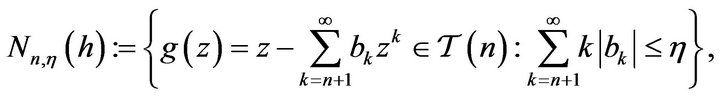
where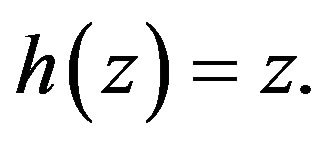

Let denote the subclass of consisting of functions which satisfy

A functio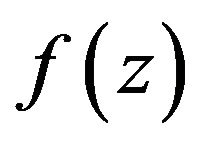n in is said to be starlike of order in.

A function is said to be convex of order it it satisfies

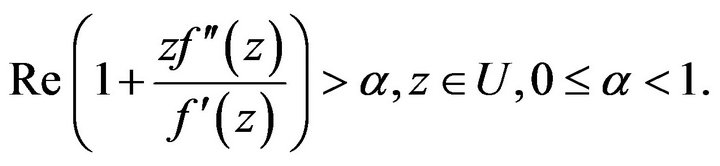
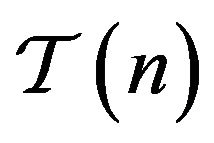We denote by the subclass of consisting of all such functions [10].

The unification of the classes and 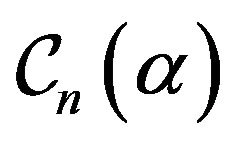is provided by the class of functions which also satisfy the following inequality

The class 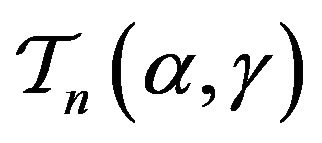was investigated by Altintas [11].

Now, by using 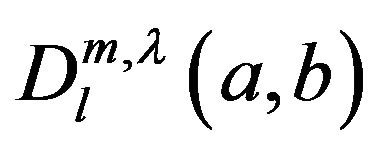we will define a new class of starlike functions.

Definition 1.2 Let

A function 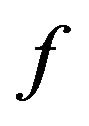belonging to 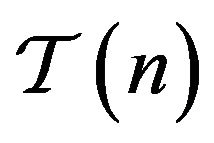is said to be in the class 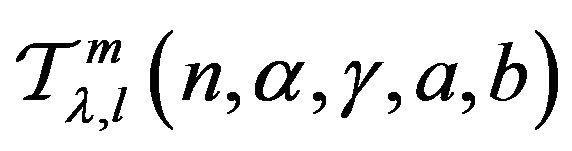if and only if

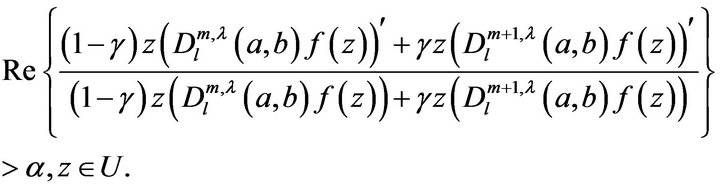(6)

Remark 1.3 The class 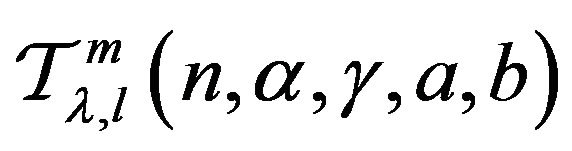is a generalization of the following subclasses:

i) and

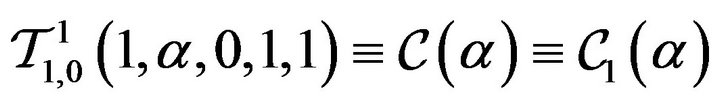defined and studied by [12];

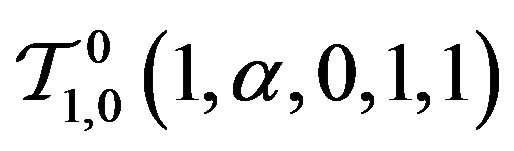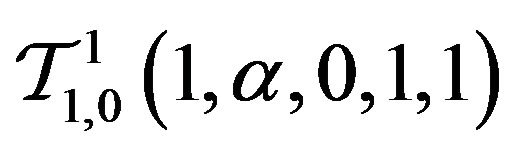ii) and studied by [13] and [14];

iii) 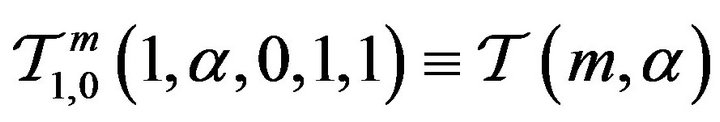studied by [15];

iv) studied by [16].

Now, we shall use the same method by [17] to establish certain coefficient estimates relating to the new introduced class.

2. Coefficient Estimates

Theorem 2.1 Let the function be defined by (1). Then 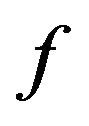belongs to the class if and only if

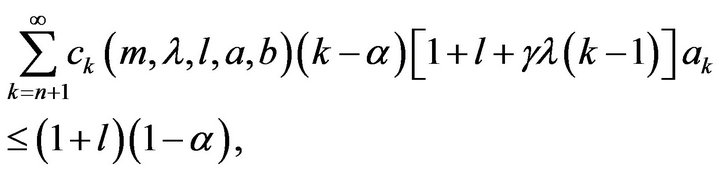(7)

where

(8)

The result is sharp and the extremal functions are

(9)

Proof: Assume that the inequality (7) holds and let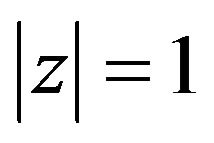. Then we have

Consequently, by the maximum modulus theorem one obtains

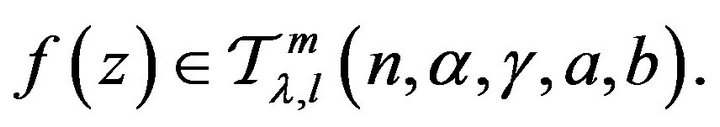
Conversely,suppose that

.

Then from (6) we find that

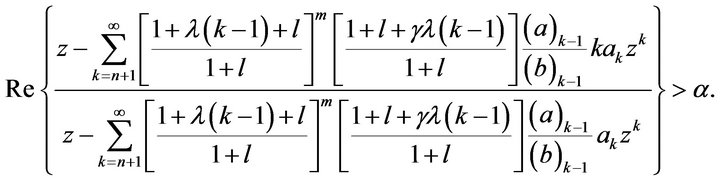
Choose values of on the real axis such that

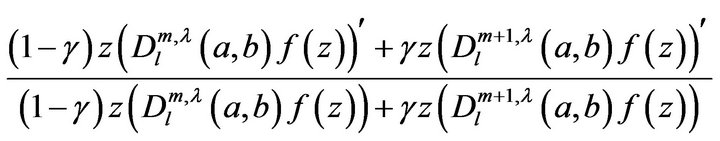
is real. Letting 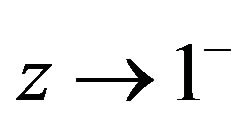through real values, we obtain

or, equivalently

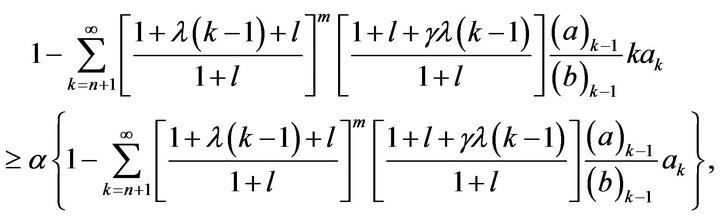
which gives (7).

Remark 2.2 In the special case 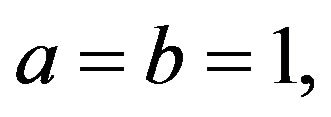Theorem 2.1 yields a result given earlier by [17].

Remark 2.3 In the special case 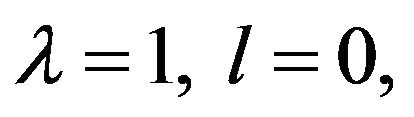Theorem 2.2 yields a result given earlier by [6].

Theorem 2.4 Let the function 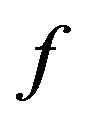defined by (3) be in the class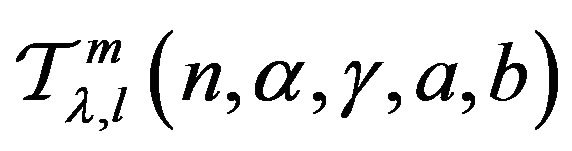. Then

(10)

and

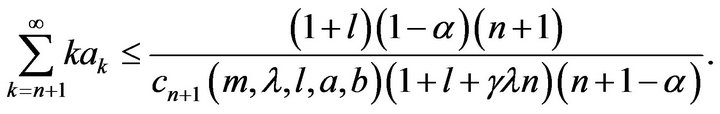(11)

The equality in (10) and (11) is attained for the function 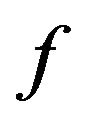given by (9).

Proof: By using Theorem 2.2, we find from (6) that

which immediately yields the first assertion (10) of Theorem 2.3.

On the other hand, taking into account the inequality (6), we also have

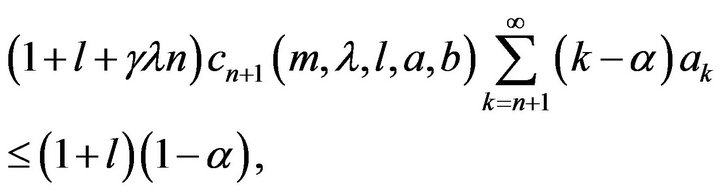
that is

which, in view of the coefficient inequality (10), can be put in the form

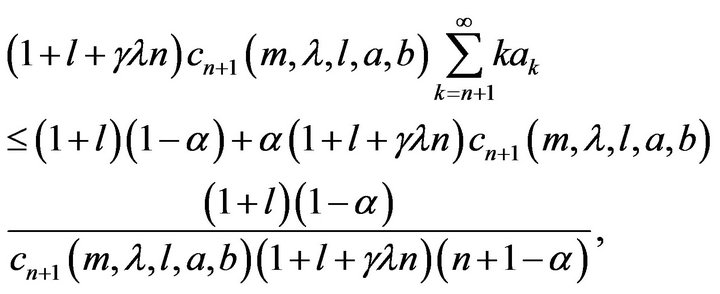
and this completes the proof of (11).

3. Closure Theorem

Theorem 3.1 Let the function 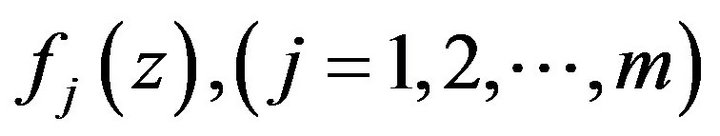be defined by

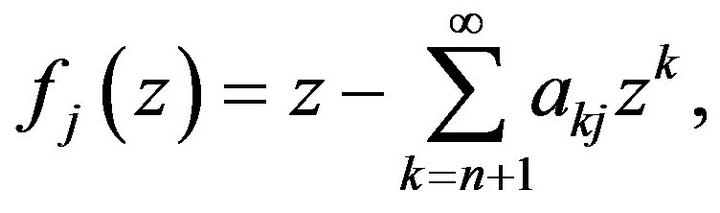
for 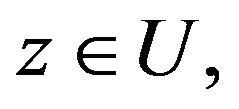be in the class 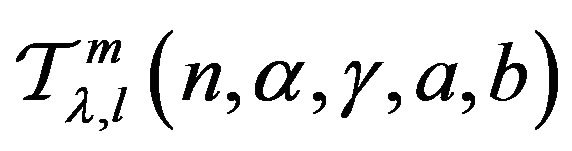then the function defined by

also belongs to the class, where

Proof: Since 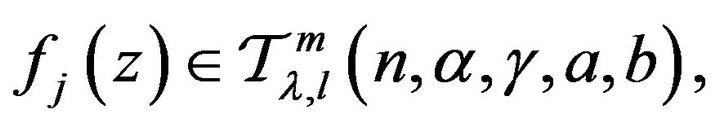it follows from Theorem 2.1, that

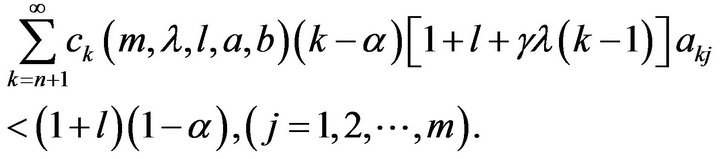
Therefore,

Hence by Theorem 2.1, also.

Morever, we shall use the same method by [17] to prove the distrotion Theorems.

4. Distortion Theorems

Theorem 4.1  Let the function 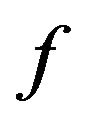defined by (1) be in the class. Then we have

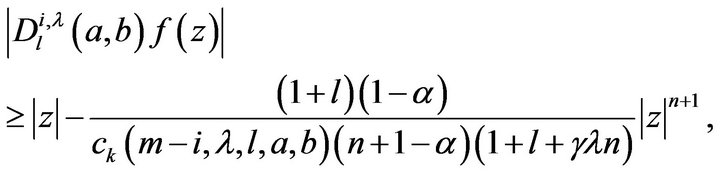(12)

and

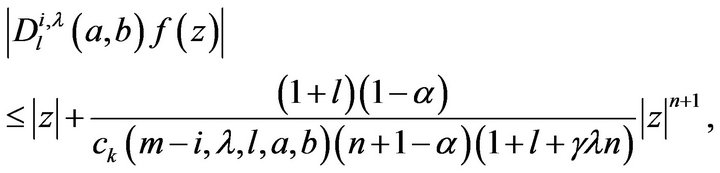(13)

for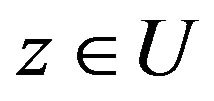, where 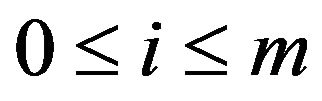and 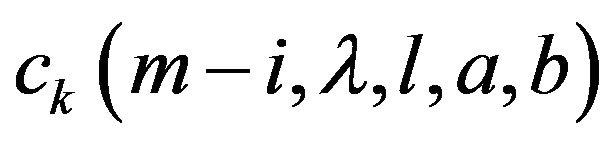is given by (8).

The equalities in (12) and (13) are attained for the function 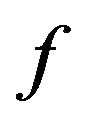given by

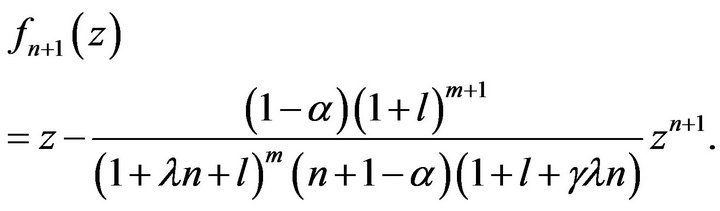(14)

Proof: Note that if and only if

, where

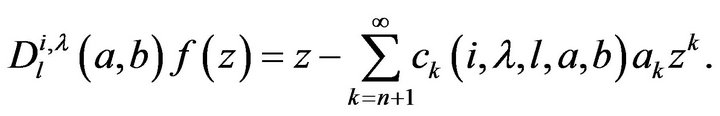
By Theorem 2.2, we know that

that is

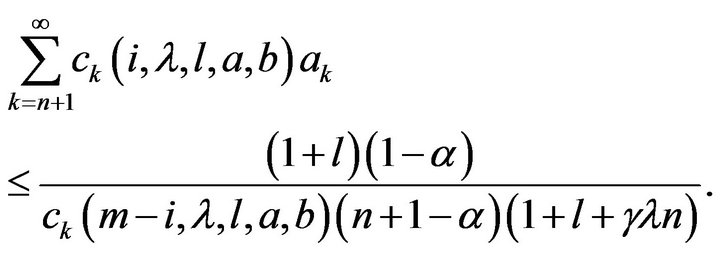
The assertions of (12) and (13) of Theorem 4.1 follow immediately. Finally, we note that the equalities (12) and (13) are attained for the function defined by

This completes the proof of Theorem 4.1.

Remark 4.2 In the special case Theorem 4.1 yields a result given earlier by [17].

Corollary 4.3  Let the function defined by (1) be in the class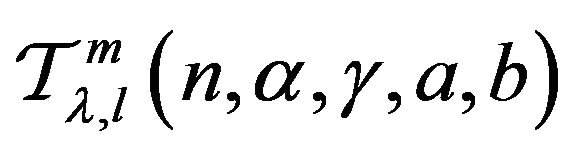. Then we have

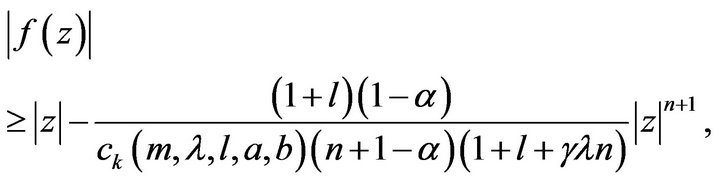(15)

and

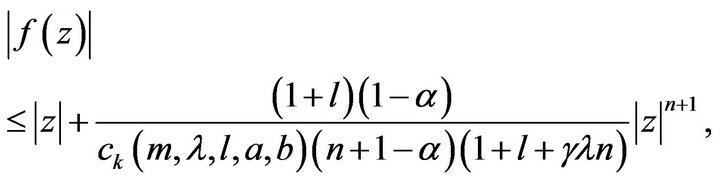(16)

for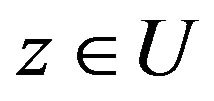. The equalities in (15) and (16) are attained for the function given in (14).

Corollary 4.4 Let the function defined by (1) be in the class. Then we have

(17)

and

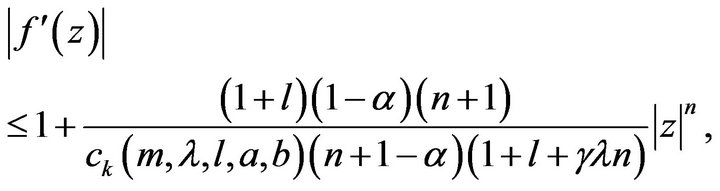(18)

for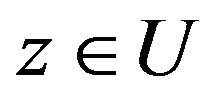. The equalities in (17) and (18) are attained for the function given in (14).

Corollary 4.5 Let the function 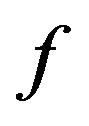defined by (3) be in the class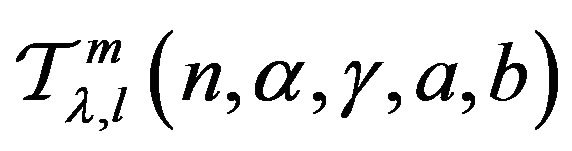. Then the unit disc is mapped onto a domain that contains the disc

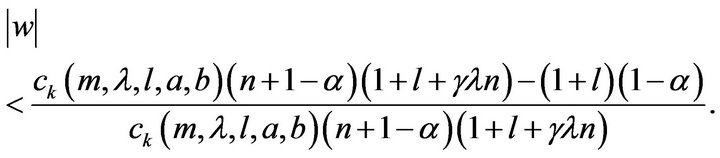
The result is sharp with the extremal function given in (14).

5. Integral Operators

Theorem 5.1 Let the function 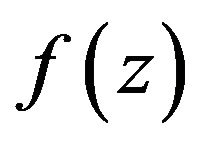defined by (1) be in the class 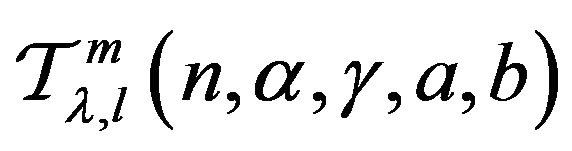and let be a real number such that 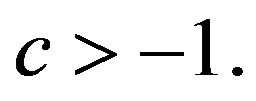Then defined by

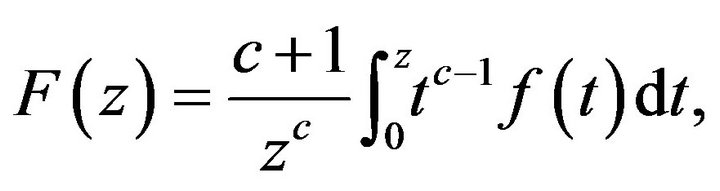
also belongs to the class

Proof: From the representation of 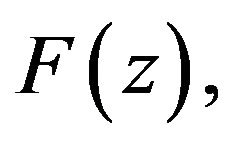it is obtained that

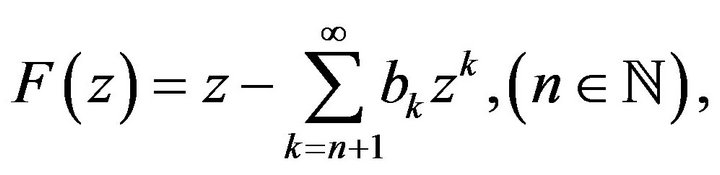
where

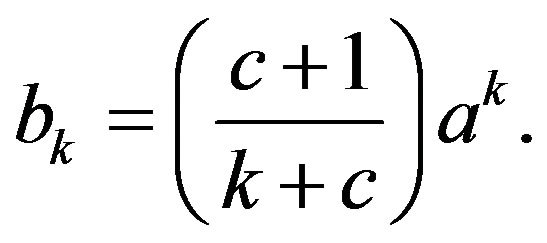
Therefore

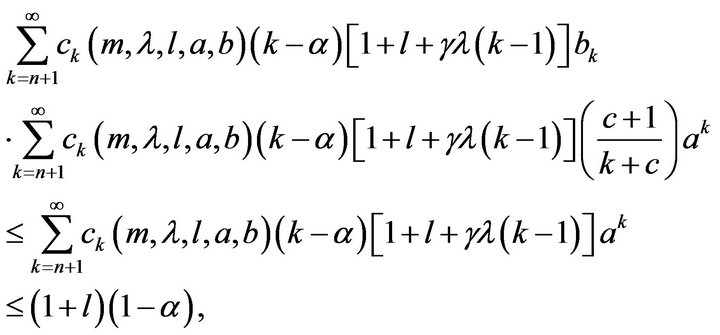
since belongs to so by virtue of Theorem 2.1, 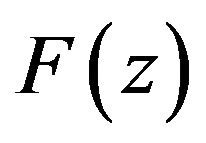is also element of

6. Acknowledgements

The work presented here was partially supported by LRGS/TD/2011/UKM/ICT/03/02.

REFERENCES

NOTES

^*Corresponding author.